2. 中国电器科学研究院有限公司,广东 广州 510300
2. China Institute of Electrical Science Limited, Guangzhou 510300, China
当今社会,化石燃料燃烧造成的环境污染及其不断消耗带来的能源危机[1],使得可再生能源的开发与应用变得越来越重要[2]. 风力发电[3]、光伏发电等新能源的不断兴起[4],使得新能源发电技术[5]成为一个研究热点.
并网逆变器是新能源发电控制系统与电网连接的重要环节[6]. 为了获得较低THD的并网电流[7],并网逆变器的输出滤波器大多采用L型滤波器或LCL型滤波器[8]. 相比L型滤波器[9],在总电感量相同的条件下,LCL型滤波器的滤波性能更好[10],对高频谐波抑制能力更强;LCL型滤波器为三阶环节[11],易造成整个控制系统不稳定[12].
针对LCL型并网逆变器,文献[13]提出非线性有源阻尼控制策略,采用桥臂侧电流环和网侧电流环内环控制;文献[14]所采用的双电感电流和电容电压反馈的三闭环解耦控制方案在实际应用中难以完全消除耦合影响. 这两种方案都增加传感器数量和系统的成本. 文献[15]利用观测值反馈, 采用零极点配置实现系统最佳阻尼,虽然减少了传感器数量,通过控制桥臂侧的电感电流间接实现对电网侧电流的控制,网侧电流与电网电压存在相位差,功率因数低.
针对上述问题,本文提出了基于状态反馈的LCL并网逆变器控制策略,采用状态观测器对控制信号做准确预测,减少传感器数量,降低成本;采用非线性误差反馈率对信号进行控制,提高系统的动态性能. 并利用仿真和实验来验证所设计的控制策略的可行性.
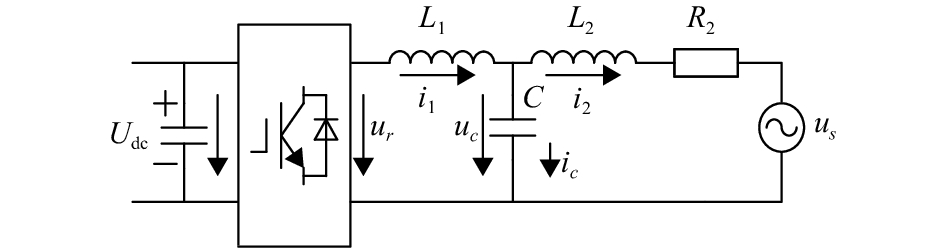
1 并网逆变器结构及模型 1.1 主电路拓扑图1为本文逆变器的主电路拓扑. 其中Udc为直流母线电压,L1、L2和C组成LCL低通滤波器,R2为电网侧等效电阻,ur为逆变器侧输出电压,us为电网电压,uc为电容C电压,i1为桥臂侧电流,i2电网侧电流,ic为通过滤波电容电流.
|
图 1 LCL单相逆变器拓扑 Figure 1 Topology of single phase LCL inverter |
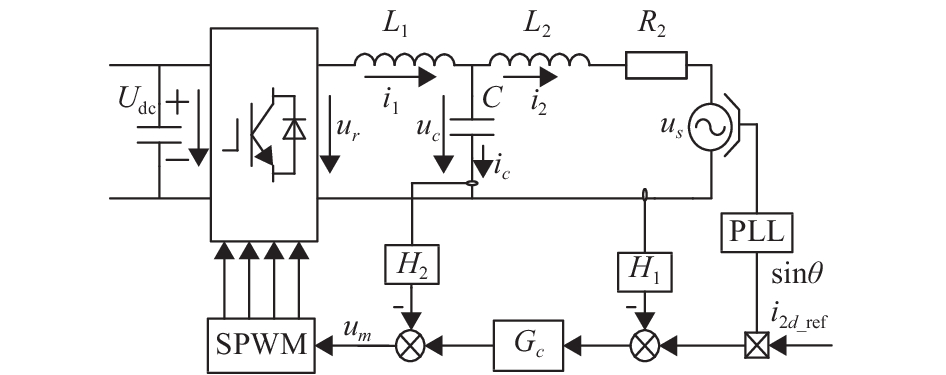
文献[16]采用电容电流反馈有源阻尼的控制方法,其控制框图如图2所示,通过电容电流比例反馈去除谐振尖峰实现有源阻尼,其中H1为并网电流反馈系数,H2为电容电流反馈系数,该控制方案增加传感器数量,并且忽略电网电压的影响,这样加大被控电流的误差.
|
图 2 电容电流反馈有源阻尼 Figure 2 Capacitor current feedback active damping |
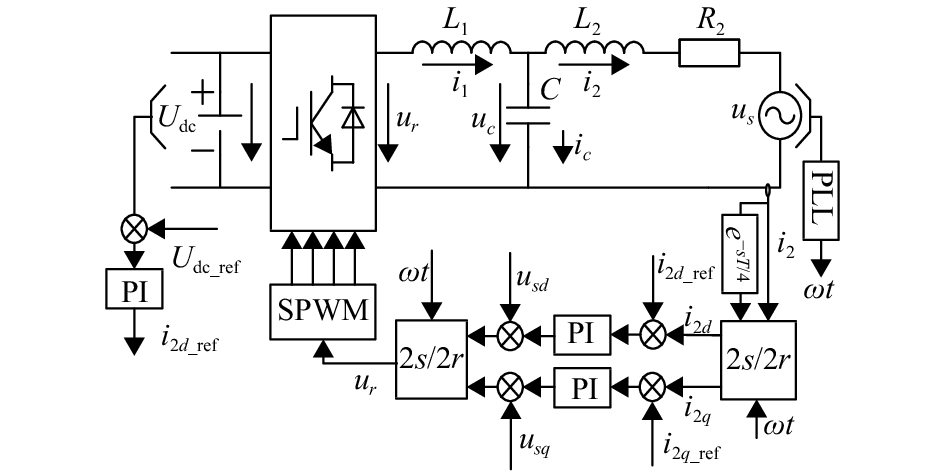
dq坐标系下的控制方案如图3所示,该控制方案通过网侧电流旋转坐标系下电流环控制,相比较图2的控制方法,该控制方法仅使用一个网侧电流传感器,且网侧电流误差相对较小,但该方案存在响应速度慢,较大的超调,微分计算不准确等问题.
|
图 3 dq坐标系下控制策略 Figure 3 Control Strategy of dq-referece Frame |
由图1所示的电路拓扑结构列出系统的微分方程如下:
| $\left\{ {\begin{array}{*{20}{l}}{\displaystyle\frac{{{\rm{d}}{i_1}}}{{{\rm{d}}t}} = \displaystyle\frac{{{u_r}}}{{{L_1}}} - \displaystyle\frac{{{u_c}}}{{{L_1}}}};\\{\displaystyle\frac{{{\rm{d}}{i_2}}}{{{\rm{d}}t}} = \displaystyle\frac{{{u_c}}}{{{L_2}}} - \displaystyle\frac{{{R_2}{i_2}}}{{{L_2}}} - \displaystyle\frac{{{u_s}}}{{{L_2}}}};\\{\displaystyle\frac{{{\rm{d}}{u_c}}}{{{\rm{d}}t}} = \displaystyle\frac{{{i_c}}}{C}};\\{{i_1} = {i_c} + {i_2}}.\end{array}} \right. $ | (1) |
取输出变量i2和输入变量ur的拉普拉斯变换表达式分别为I2(s)和Ur(s),由式(1)可得系统的开环传递函数:
| $\displaystyle\frac{{{I_2}(s)}}{{{U_r}(s)}} = \displaystyle\frac{1}{{{s^3}{L_1}{L_2}C + {s^2}{L_1}C{R_2} + s({L_1} + {L_2}) + {R_2}}}.$ | (2) |
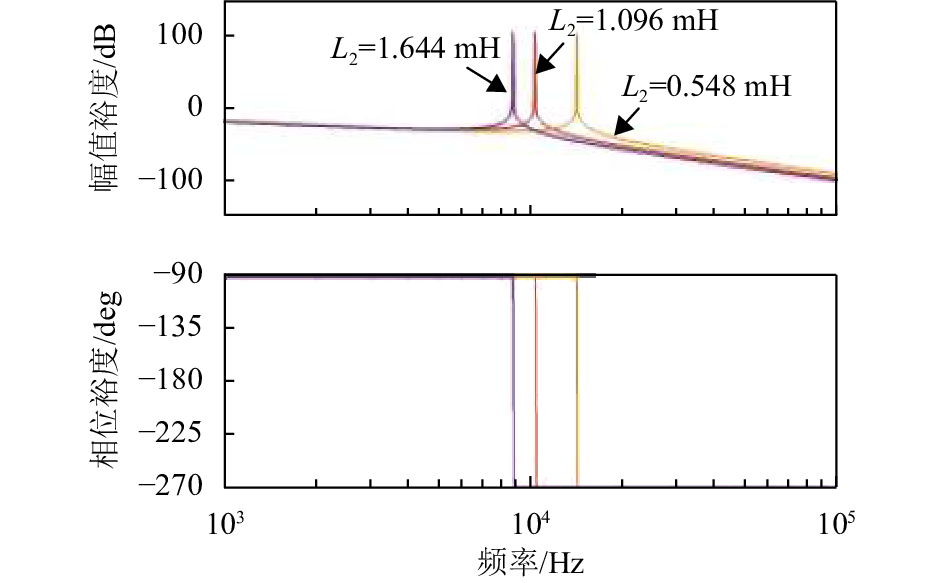
等效电阻R2的值比较小,分析系统BODE图时忽略不计. 如图4为该系统的伯德图.
|
图 4 LCL滤波器的频率特性 Figure 4 Frequency characteristics of LCL filter |
从图4可以看出,LCL滤波器存在谐振尖峰,在该谐振频率处相位发生-180°跳变,导致系统不稳定. 为了使系统稳定,需要将谐振尖峰阻尼到0 dB以下,传统的无源阻尼方法可以抑制LCL滤波器的谐振尖峰,但是会引入损耗,并降低LCL滤波器的低频增益和高频衰减能力,工程中通过控制算法的有源阻尼方法抑制谐振尖峰,但是网侧电感参数会发生变化,影响算法的阻尼效果.
为解决上述问题,本文通过dq旋转坐标系下电流解耦控制策略,将式(1)各变量延时1/4个基波周期T来构造与α轴正交的β轴虚拟分量,再经过坐标变换,可得到旋转坐标系下的微分方程.
| $\left\{ {\begin{array}{*{20}{l}}{\displaystyle\frac{{{\rm{d}}{i_{1d}}}}{{{\rm{d}}t}} = \displaystyle\frac{{{u_{rd}}}}{{{L_1}}} + \omega {i_{1q}} - \displaystyle\frac{{{u_{cd}}}}{{{L_1}}}};\\{\displaystyle\frac{{{\rm{d}}{i_{1q}}}}{{{\rm{d}}t}} = \displaystyle\frac{{{u_{rq}}}}{{{L_1}}} - \omega {i_{1d}} - \displaystyle\frac{{{u_{cq}}}}{{{L_1}}}}.\end{array}} \right.$ | (3) |
| $\left\{ {\begin{array}{*{20}{l}}{\displaystyle\frac{{{\rm{d}}{i_{2d}}}}{{{\rm{d}}t}} = \displaystyle\frac{{{u_{cd}}}}{{{L_2}}} + \omega {i_{2q}} - \displaystyle\frac{{{R_2}{i_{2d}}}}{{{L_2}}} - \displaystyle\frac{{{u_{sd}}}}{{{L_2}}}};\\{\displaystyle\frac{{{\rm{d}}{i_{2q}}}}{{{\rm{d}}t}} = \displaystyle\frac{{{u_{cq}}}}{{{L_2}}} - \omega {i_{2d}} - \displaystyle\frac{{{R_2}{i_{2q}}}}{{{L_2}}} - \displaystyle\frac{{{u_{sq}}}}{{{L_2}}}}.\end{array}} \right. $ | (4) |
| $\left\{ {\begin{array}{*{20}{l}}{\displaystyle\frac{{{\rm{d}}{u_{cd}}}}{{{\rm{d}}t}} = \displaystyle\frac{{{i_{cd}}}}{C} + \omega {u_{cq}}};\\{\displaystyle\frac{{{\rm{d}}{u_{cq}}}}{{{\rm{d}}t}} = \displaystyle\frac{{{i_{cq}}}}{C} - \omega {u_{cd}}}.\end{array}} \right. $ | (5) |
| $\left\{ {\begin{array}{*{20}{l}}{{i_{1d}} = {i_{cd}} + {i_{2d}}};\\{{i_{1q}} = {i_{cq}} + {i_{2q}}}.\end{array}} \right. $ | (6) |
将式(4)~式(6)代入式(3),化简后可得到桥臂侧电压ur在dq旋转坐标系下的方程:
| $\left\{ {\begin{array}{*{20}{l}}{{u_{rd}} = {u_{cd}} + {k_3}\displaystyle\frac{{{{\rm{d}}^2}{i_{2q}}}}{{{\rm{d}}{t^2}}} + {k_2}\displaystyle\frac{{{\rm{d}}{i_{2q}}}}{{{\rm{d}}t}} + {k_1}{i_{2q}} + {k_4}{u_{sd}}};\\{{u_{rq}} = {u_{cq}} - {k_3}\displaystyle\frac{{{{\rm{d}}^2}{i_{2d}}}}{{{\rm{d}}{t^2}}} - {k_2}\displaystyle\frac{{{\rm{d}}{i_{2d}}}}{{{\rm{d}}t}} - {k_1}{i_{2d}} + {k_4}{u_{sq}}}.\end{array}} \right. $ | (7) |
其中,
| $\left\{ {\begin{array}{*{20}{l}}{{k_1} = \omega ({L_1} + {L_2}) - {L_1}{L_2}C{\omega ^3}};\\{{k_2} = 2{L_1}C{R_2}\omega };\\{{k_3} = 3{L_1}{L_2}C\omega };\\{{k_4} = 1 - {L_1}C{\omega ^2}}.\end{array}} \right. $ | (8) |
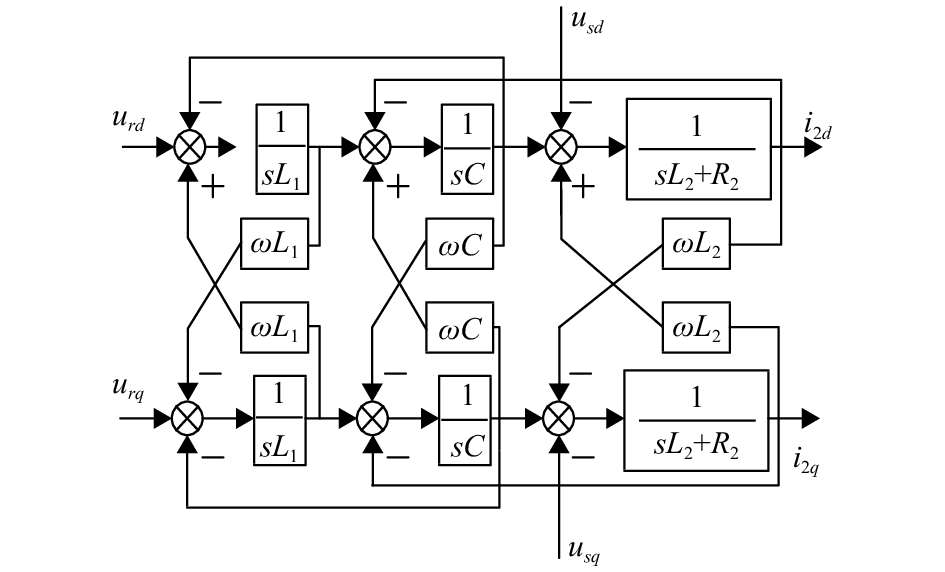
坐标变换后系统dq旋转坐标系下的模型结构如图5所示.
|
图 5 同步坐标下系统的模型图 Figure 5 Model of system under synchronous coordinate |
通过式(7)可看出存在观测量的一次微分和二次微分,本文通过引入状态观测器实现对并网工作电流i2d和i2q的状态变化实现有效跟踪和观测,得到其各阶“广义微分信号”,进而有效地解决传统微分计算不准确带来的问题. 构造的状态观测器如下所示:
| $\left\{ {\begin{array}{*{20}{l}}{{x_{1d}} = {x_{2d}} - {b_1}g({e_d})};\\{{x_{2d}} = {x_{3d}} - {b_2}g({e_d})};\\{{x_{3d}} = {x_{4d}} - {b_3}g({e_d})};\\{{x_{4d}} = - {b_4}g({e_d})}.\end{array}} \right. $ | (9) |
其中,ed=x1d–i2d,状态变量x1d为i2d的观测值,x2d、x3d和x4d分别为i2d的一阶、二阶和三阶广义微分的观测值,b1、b2、b3、b4为观测器的修正系数;同理可得i2q的各阶广义微分值. 在这里取g(e)为非线性函数:
| $g(e) = {e^{1/3}}.$ | (10) |
传统的控制策略如图3所示,多采用PI控制方式. PI控制器是对信号的误差进行直接控制,会导致被控量超调,而电力电子装备普遍存承受超调能力较弱的特点;此外,PI调节器还存在调节时间和响应速度的矛盾,鲁棒性差.
针对上述问题,本文通过状态观测器对系统的网侧电流i2的状态量进行估计预测;最后通过状态反馈对系统对象进行反馈控制. 其中控制器采用非线性控制器控制网侧电流i2,从而改善了系统的动态性能.
通过上述状态观测器的状态反馈与给定参考值的误差反馈构成系统状态误差反馈的非线性控制器:
| $e = t - {{\textit{z}}_1},$ | (11) |
其中,e为误差,t为给定参考值,z1为状态观测器的位置输出.
| $u(t) = {k_1}{\rm{fal}}(e,\alpha ,\delta )$ | (12) |
其中k1,α,δ为可调参数,非线性函数fal如式(13)所示.
| ${\rm{fal}}(e,\alpha ,\beta ) = \left\{ {\begin{array}{*{20}{l}}{{{\left| e \right|}^\alpha }{\rm{sgn}}(e)}, & {\left| e \right| > \delta };\\{e/{\delta ^{1 - \alpha }}}, & {\left| e \right| \leqslant \delta }.\end{array}} \right.$ | (13) |
|
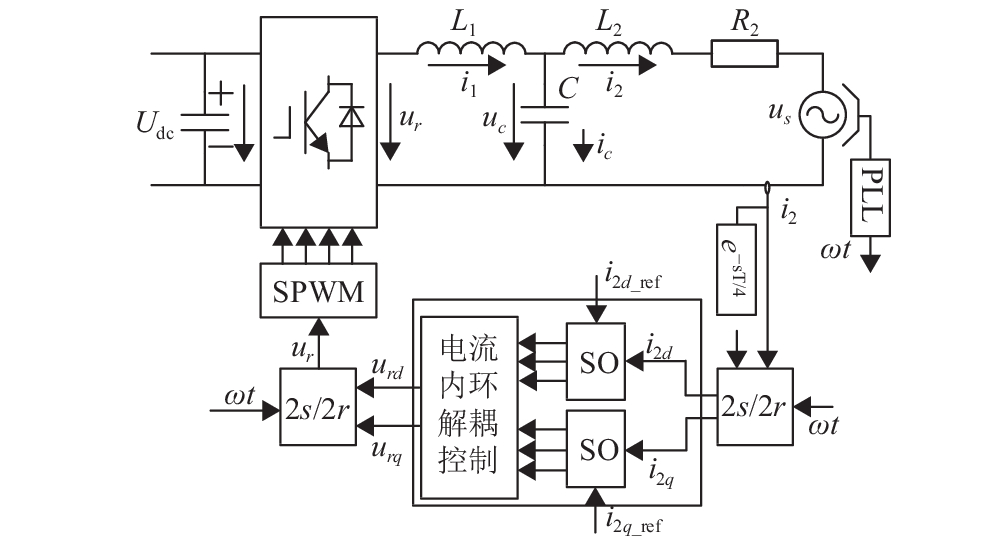
图 6 电流d-q轴控制结构图 Figure 6 d-q Axis control structure diagram of grid connected current |
如图6和图7所示为本文LCL逆变器控制结构图和电流环解耦控制框图.
图6中SO为状态观测器,其输入量是网侧电流i2,利用观测值反馈,通过极点配置实现了整个系统的最佳阻尼,只需要一个并网电流传感器就能对系统网侧电流i2进行有效控制.
由图7可知,通过状态观测器SO可分别得到i2d和i2q对应的状态观测值x1d、x2d、x3d和x1q、x2q、x3q. x1d经比例增益环节k1、x2d经比例增益环节k2和x3d经比例增益环节k3得到前馈补偿控制量抵消d轴中由q轴变量带来的耦合量;同理可实现对q轴中由d轴变量带来的耦合量补偿,从而实现系统的完全解耦. 把观测值x1d与其给定值i2d_ref进行比较得到的位置偏差经非线性控制器调节器Gc,得到输出电流i2d的控制量. 此外,电网电压us通过k4前馈补偿可消除电网电压的扰动对逆变器的影响.
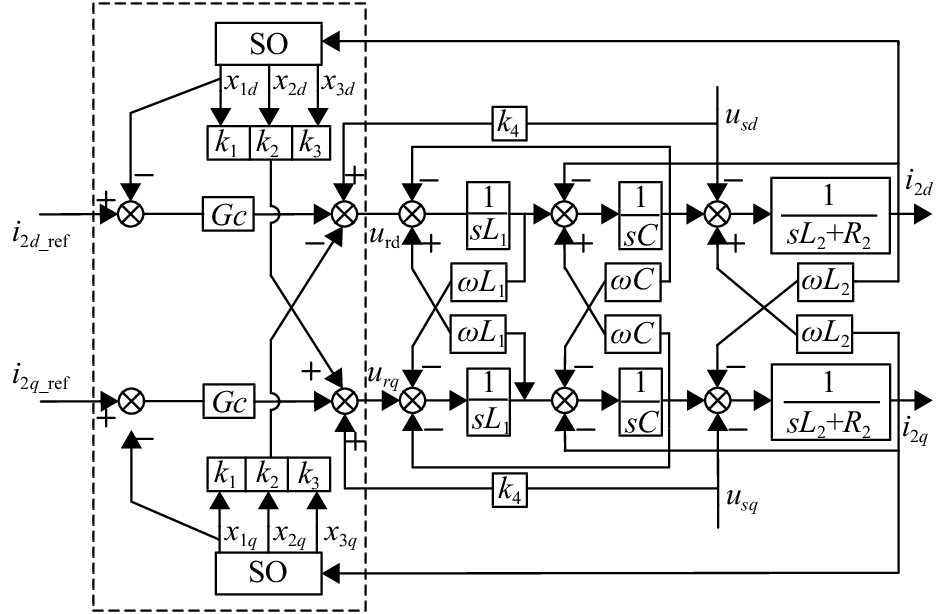
|
图 7 电流环解耦控制框图 Figure 7 Current loop decoupling control block diagram |
为验证本文所提出控制策略的有效性,搭建如图1所示的仿真模型,其中电路仿真参数如表1所示.
图8给出了加入状态观测器后网侧电压和网侧电流稳态波形. 可以看出,加入状态观测器后可以达到满意的稳态效果.
| 表 1 仿真参数 Table 1 Selection of simulation parameters |
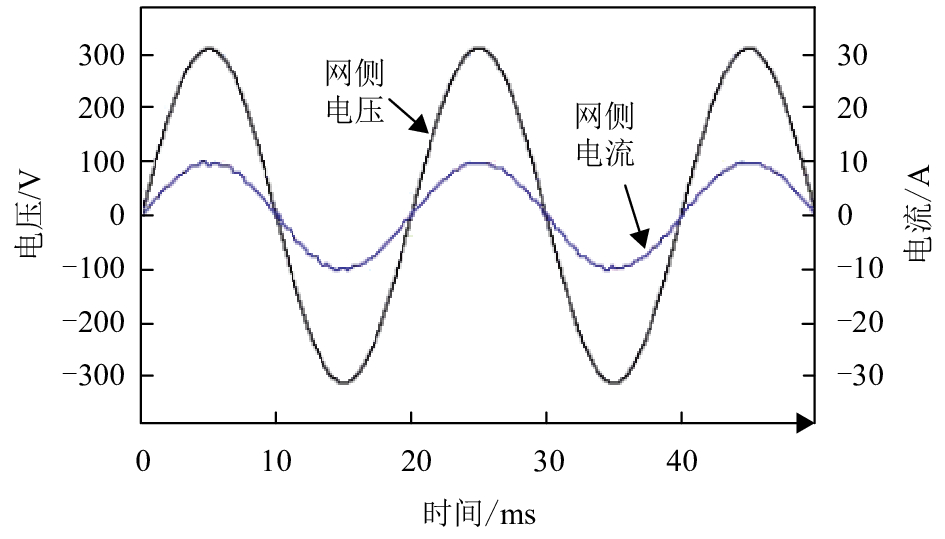
|
图 8 加入状态观测器后网侧电压和电流稳态波形 Figure 8 Steady state performance of grid voltage and current with state observer |
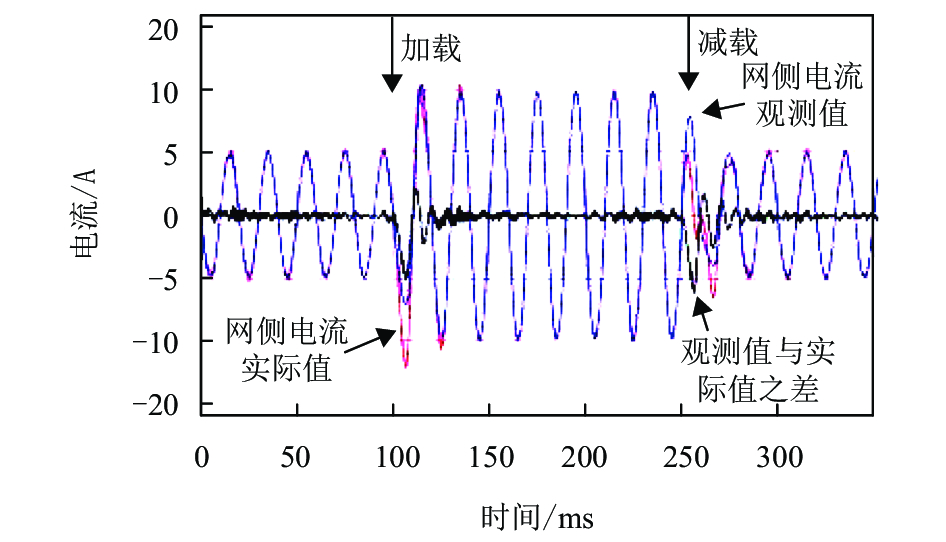
图9为加入状态观测器后网侧电流动态响应效果图. 由图9可以知,状态观测器的观测值与实际电流值的偏差很小,观测器的观测效果好.
|
图 9 加入状态观测器后网侧电流的动态响应波形 Figure 9 Dynamic performance of grid current with state observer |
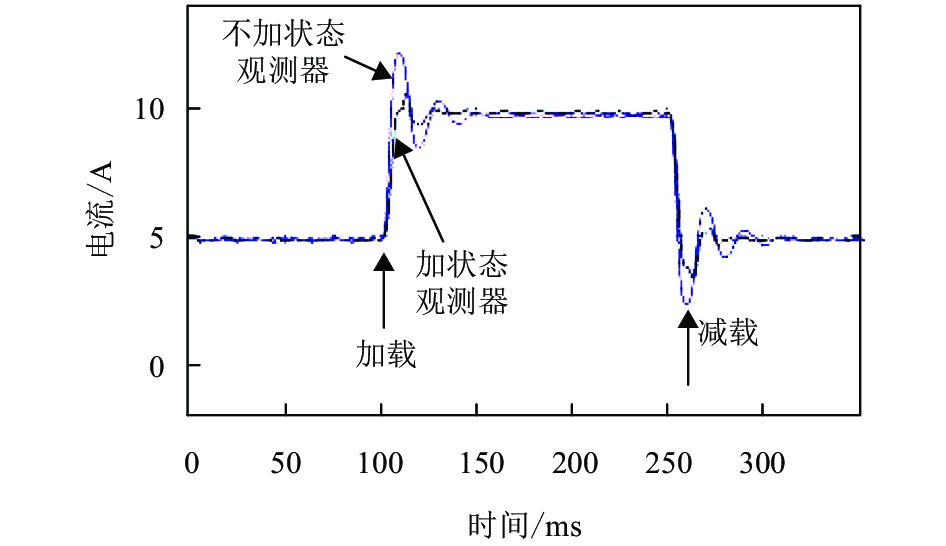
图10为加入状态观测器和不加状态观测器d轴电流响应对比图. 经过对比,可发现在加入状态反馈后系统的动态性能得到了改善. 在加载和减载时,电流的超调量明显减少,并且调节时间减小.
|
图 10 d 轴电流响应对比波形 Figure 10 Comparison of d axial current response |
仿真结果表明,本文提出的控制策略是有效的. 在网侧电流给定值突变时,电路具有良好的跟随性,且电路网侧电流具有良好的动态性能.
3.2 实验验证基于上述理论分析与仿真结果,设计了一台单相LCL并网逆变器样机. 开关频率为10 kHz,其他参数与表1对应.
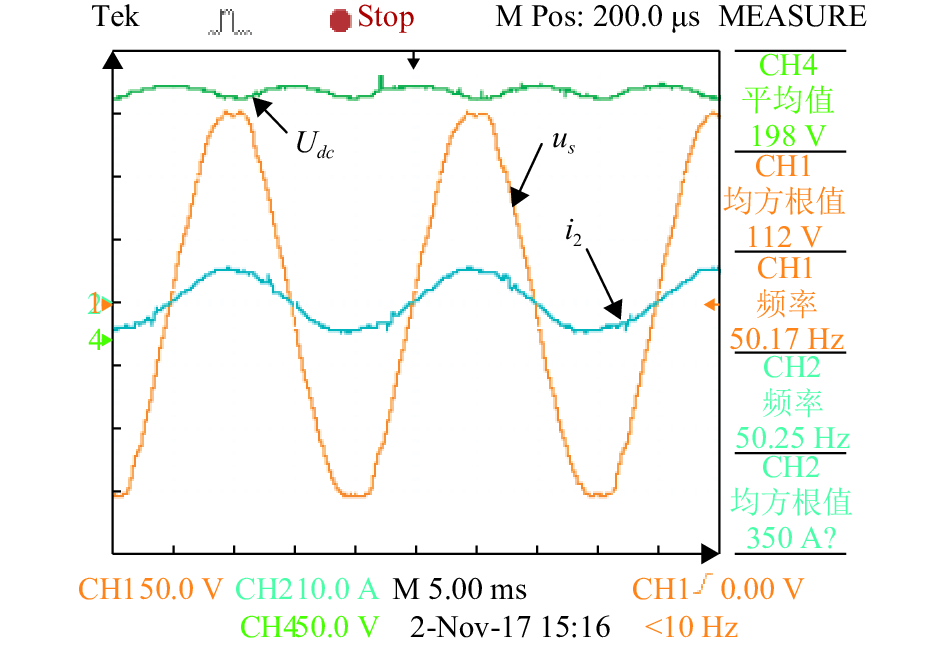
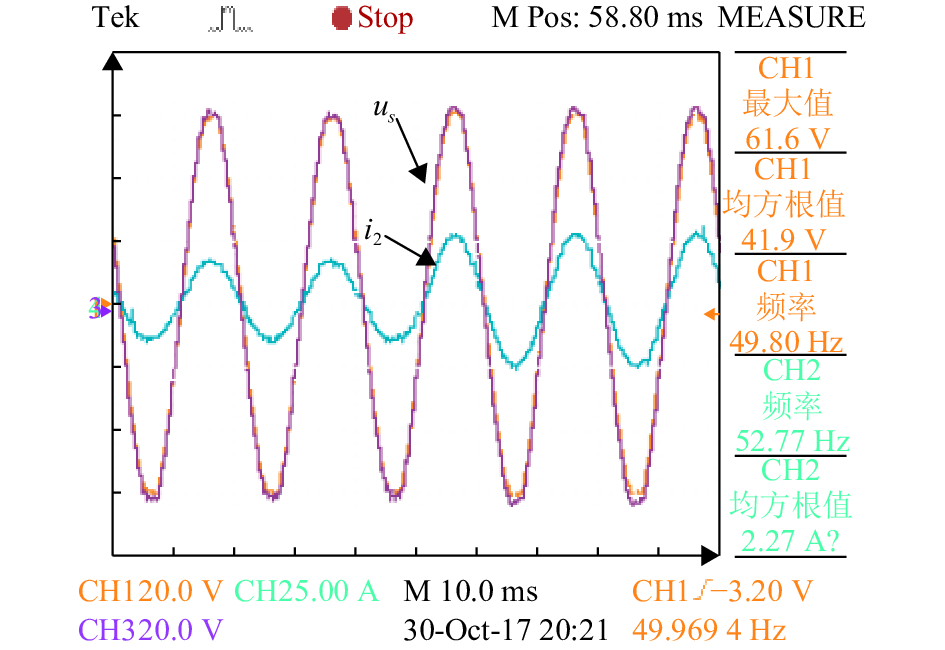
图11为基于状态反馈控制策略的稳态实验波形,图12为基于状态反馈的网侧电压和网侧电流动态响应实验波形. 从图11和图12可看出在该控制策略下满足稳态性能的同时,具有良好的动态性能.
|
图 11 网侧电压和网侧电流稳态实验 Figure 11 Steady state performance of grid voltage and current |
|
图 12 网侧电压和网侧电流动态响应实验 Figure 12 Dynamic performance of grid voltage and current |
本文提出了一种基于状态反馈的LCL逆变器的控制策略,该控制策略通过状态观测器解决了传统做法微分计算不准确问题,减少传感器数量,降低成本. 该控制策略可较好地消除dq轴间的耦合,系统有良好的动态性能. 实验结果验证了本文所提出方案是可行的.
| [1] |
FANTINO R, BUSADA C, SOLSONA J. Grid-voltage sensorless control of an LCL filter with low resonance frequency[C]// Conference on Phd Research in Microelectronics and Electronics. America, Latin:[s.n.], 2017: 1-4.
|
| [2] |
WANG X, BLAABJERG F, & LOH P C. Grid-current-feedback active damping for LCL resonance in grid-connected voltage-source converters[J].
IEEE Transactions on Power Electronics, 2016, 31(1): 213-223.
DOI: 10.1109/TPEL.2015.2411851. |
| [3] |
张淼, 苏协飞. 基于比例谐振和谐波补偿控制技术的单相逆变并网研究[J].
广东工业大学学报, 2016, 33(5): 59-64.
ZHANG M, SU X F. Research on proportional-resonant controller and harmonic compensation for grid-connected inverter[J]. Journal of Guangdong University of Technology, 2016, 33(5): 59-64. DOI: 10.3969/j.issn.1007-7162.2016.05.011. |
| [4] |
KOMURCUGIL H, BAUHAN S, ABU-RUB H. Lyapunov-function based control approach with cascaded PR controllers for single-phase grid-tied LCL-filtered quasi-Z-source inverters[C]// IEEE international conference on compatibility, Power Electronics and Power Engineering, 2017: 510-515.
|
| [5] |
秦为坤, 胡存刚. 基于改进的PR调节的单相LCL双闭环电流控制并网逆变器的研究[J].
电气工程学报, 2015, 10(8): 40-44.
QIN W L, HU C G. Research on single-phase LCL dual-loop grid current control based on the modified PR regulator[J]. Journal of Electrical Engineering, 2015, 10(8): 40-44. |
| [6] |
侯朝勇, 胡学浩, 惠东. 基于离散状态空间模型的LCL滤波并网变换器控制策略[J].
中国电机工程学报, 2011, 31(36): 8-15.
HOU C Y, HU X H, HUI D. Control strategy of grid-connected converter with LCL filter based on discrete state-space model[J]. Proceedings of The CSEE, 2011, 31(36): 8-15. |
| [7] |
TAMBARA R V, KANIESKI J M, MASSING J. A discrete-time robust adaptive controller applied to grid-connected converters with LCL filter[J].
Journal of Control Automation & Electrical Systems, 2017, 28(3): 1-9.
|
| [8] |
KOMURCUGIL H, ALTIN N, OZDEMIR S, et al. Lyapunov function and proportional resonant based control strategy for single phase grid connected VSI with LCL Filter[J].
IEEE Transactions on Industrial Electronics, 2016, 63(5): 2838-2849.
DOI: 10.1109/TIE.2015.2510984. |
| [9] |
宋修奎, 唐雄民, 章云, 等. 一种适合于单相电压型逆变电源的并联控制方案研究[J].
广东工业大学学报, 2015, 2(15): 79-85.
SONG X K, TANG X M, ZHANG Y, et al. A method of parallel control for single-phase voltage source inverters[J]. Journal of Guangdong University of Technology, 2015, 2(15): 79-85. |
| [10] |
ABDELDJABAR B, XU D, WANG X, et al. Robust active damping control of LCL filtered grid connected converter based active disturbance rejection control[C]// Power Electronics and Motion Control Conference.[S.l.]: IEEE, 2016: 2611-2666.
|
| [11] |
MISKOVIC V, BLASKO V, JAHNS T, et al. Observer based active damping of LCL resonance in grid connected voltage source converters[C]// Energy Conversion Congress and Exposition.[S.l.]: IEEE, 2013: 4850-4856.
|
| [12] |
陈东, 张军明, 钱照明. 带LCL滤波器的并网逆变器单电流反馈控制策略[J].
中国电机工程学报, 2013, 33(9): 10-16.
CHEN D, ZHANG J M, QIAN Z M, Single current feedback control strategy for grid-connected inverters with LCL filters[J]. Single current feedback control strategy for grid-connected inverters with LCL filters[J]. Proceedings of The CSEE, 2013, 33(9): 10-16. |
| [13] |
杨仁增, 张光先. LCL并网滤波器的非线性阻尼控制[J].
电工技术学报, 2015, 30(24): 152-159.
YANG R Z, ZHANG G X. Nonlinear damping controller for grid-connected LCL filter[J]. Transactions of China Electro Technical Society, 2015, 30(24): 152-159. DOI: 10.3969/j.issn.1000-6753.2015.24.020. |
| [14] |
屈克庆, 李文旗, 叶天凯. 基于状态反馈的LCL型逆变器解耦控制策略[J].
电工技术学报, 2016, 31(20): 130-138.
QU K Q, LI W Q, YE T K. State feedback based decoupling control strategy for grid-connected inverter with LCL filter[J]. Transactions of China Electro Technical Society, 2016, 31(20): 130-138. DOI: 10.3969/j.issn.1000-6753.2016.20.013. |
| [15] |
李宾, 姚文熙, 杭丽君, 等. 基于状态观测器的LCL滤波器型并网逆变器状态反馈最优化设计[J].
电工技术学报, 2014, 29(6): 80-90.
LI B, YAO W X, HANG L J, et al. Optimized design of state variable feedback of grid-connected inverter with LCL-filter based on state observer[J]. Transactions of China Electro Technical Society, 2014, 29(6): 80-90. DOI: 10.3969/j.issn.1000-6753.2014.06.011. |
| [16] |
鲍陈磊, 阮新波, 王学华, 等. 基于PI调节器和电容电流反馈有源阻尼的LCL型并网逆变器闭环参数设计[J].
中国电机工程学报, 2012, 32(25): 133-142.
BAO C L, RUAN X B, WANG X H, et al. Design of grid-connected inverters with LCL filter based on PI regulator and capacitor current feedback active damping[J]. Proceedings of The CSEE, 2012, 32(25): 133-142. |
 2018, Vol. 35
2018, Vol. 35
