SIR舱室模型是传染病动力学中非常经典的一类模型. 该模型将疫区人群分为S(易感者)、I(感染者)、R(恢复者)3个舱室，对于大范围大区域低干扰的传染病预测结果往往与实际情况非常贴合. 但随着医疗水平的提高，以及对传染病的研究和认识，人类对传染病的干预力有了显著提高. 对于新型传染病，由于防疫手段的更新，对模型的精度提出了更高的要求，同时希望对各种传播的影响因素进行直观或间接的描述和解释^[1]. 另外，微分模型对边界和初值的依赖使得其较难描述复杂随机行为，在求解证明方面也较为复杂^[2]. 相对而言，利用元胞自动机(Cellular Automata)研究传染病将有效地克服计算和证明上的困难，同时随机行为的设置也更加方便. 在结果方面，元胞自动机不仅能给出疫病在时间上的传播特征，而且能对空间上的传播特征进行模拟^[3].

对于经典动力系统的元胞自动机实现，一些学者考虑了宏观尺度上的因素，如：文献[3]在设计一种基于SEIR的元胞自动机模型对元胞赋予服从(0，1)均匀分布的传染力和感染力来体现异质性；文献[4]建立了一种基于SIR动力系统的元胞自动机模型，并考虑了人口在元胞上分布不均匀的问题；文献[5]针对人口分布、地域文化等因素，利用元胞自动机研究了大地域尺度下基于SIR和SEIR模型的流行病动态；对于媒介传染病，文献[6]对蜱媒介传染的莱姆病进行了建模，主要探讨了不同林地碎裂模式如何通过感染蜱的数量影响莱姆病的风险；文献[7]则基于媒介对于季节的敏感性建立了由3个种群层级构成的元胞自动机，并研究了由季节敏感导致的疫病周期性爆发. 人口异质性也是影响疾病传播的重要因素之一. 文献[8]则利用元胞自动机在研究HIV/AIDS疾病时赋予不同个体不同的传染率与抵抗率；文献[9]则根据人口年龄结构的异质性建立研究HIV的元胞自动机模型. 此外，随着医疗水平的发展，人为干预行为，包含隔离、注射疫苗和及时就医等能有效抑制传染病的扩散，从而对传染病爆发初期的影响越来越大^[10-11]. 而对于疫病传染阶段人口流动带来的影响，上述文献主要采用以下几种方法进行模拟，(1) 感染者接触易感者服从泊松分布的复杂网络；(2) 易感者感染率与感染者距离成反比例函数；(3) 随机行走交换. 在解决该问题上本文将采取新的方法.

本文主要分为3个部分，第一部分介绍了元胞自动机的定义，并对基于SIR动力系统建立传染病元胞自动机模型原理进行了叙述，初步实现了一个简易的传染病元胞自动机模型；第二部分介绍了为实现考虑多因素的传染病传播仿真，本文提出了3个内嵌子结构，并针对结构功能、效果进行了对比实验；第三部分利用本文建立的元胞自动机对2010年一段时间内我国内陆的H1N1感染情况进行了仿真，给出仿真结果并解释其生物学意义.

1 SIR元胞自动机模型 1.1 元胞自动机

元胞自动机是一种离散的实验模型，一般来说，其时间、空间、状态均是离散的^[12]. 元胞自动机的构成，可看成一个四元组，即： $C = \left( {{L_ \propto },S,N,f} \right)$ . 其中 ${L_ \propto }$ 为元胞空间，S为状态集，N为邻居，f为演化规则. 简单来说，一个元胞自动机模型仅需定义其规模、状态集合中的元素及元胞间以何种位置关系互为邻居、邻居状态又以何种演化规则进行转化，那么这个元胞自动机模型就能进行自我迭代，从而在对某种演化现象(如森林火灾、种群繁衍、捕食模型等)的模拟实验中得到每一个离散的单位时间内各状态元胞的空间分布以及元胞数量随时间的演化情况.

1.2 简单的SIR元胞自动机实现

为建立基于SIR方程的元胞自动机模型，首先列出SIR微分方程组如下：

$\left\{ {\begin{array}{{l}}{\displaystyle\frac{{{\rm{d}}S\left( t \right)}}{{{\rm{d}}t}} = - \beta S\left( t \right)I\left( t \right)},\\{\displaystyle\frac{{{\rm{d}}I\left( t \right)}}{{{\rm{d}}t}} = \beta S\left( t \right)I\left( t \right) - \gamma I\left( t \right)},\\{\displaystyle\frac{{{\rm{d}}R\left( t \right)}}{{{\rm{d}}t}} = \gamma I\left( t \right)}.\end{array}} \right.$

显然， $\displaystyle\frac{{{\rm{d}}S\left( t \right)}}{{{\rm{d}}t}} + \displaystyle\frac{{{\rm{d}}I\left( t \right)}}{{{\rm{d}}t}} + \displaystyle\frac{{{\rm{d}}R\left( t \right)}}{{{\rm{d}}t}} = 0$ ，即这是一个封闭的系统，总人数保持不变. 在SIR元胞自动机中，这体现为元胞的总数不变；β表示疾病的感染力，代表在元胞的转化规则上，易感状态下的元胞将以一定的几率转化成感染元胞；γ表示疾病的移出率或者恢复率，代表感染元胞将以一定的概率转化为痊愈元胞.

根据以上描述，结合现实有可能发生的随机事件，SIR元胞自动机模型可进一步作下述定义^[13-18]：

1) 元胞空间：n×n大小的正方形网格；

2) 状态集合：设 ${\rm{S}}_{i,j}^t$ 为第i行，第j列的元胞在t时刻的状态. 同时，我们有 $S_{i,j}^t = \left\{ {0,1,2} \right\}$ ，其中0代表S易感者，1代表I感染者，2代表R痊愈者；

3) 邻居关系：Moore型邻元关系；

4) 演化规则：

(1) 当 $S_{i,j}^t = 0$ ，若它的邻居中存在感染者，则每个感染者以概率b对其进行感染，若成功， $S_{i,j}^{t + 1} = 1$ . 否则， $S_{i,j}^{t + 1} = 0$ ；

(2) 当 $S_{i,j}^{t } = 1$ 在每个单位时间步，感染者都以概率r痊愈，若成功， $S_{i,j}^{t + 1} = 2$ ，否则， $S_{i,j}^{t + 1} = 1$ ；

(3) 当 $S_{i,j}^{t } = 2$ ， $S_{i,j}^{t + 1} = 2$ ，即当元胞进入痊愈状态，它的状态将不再改变.

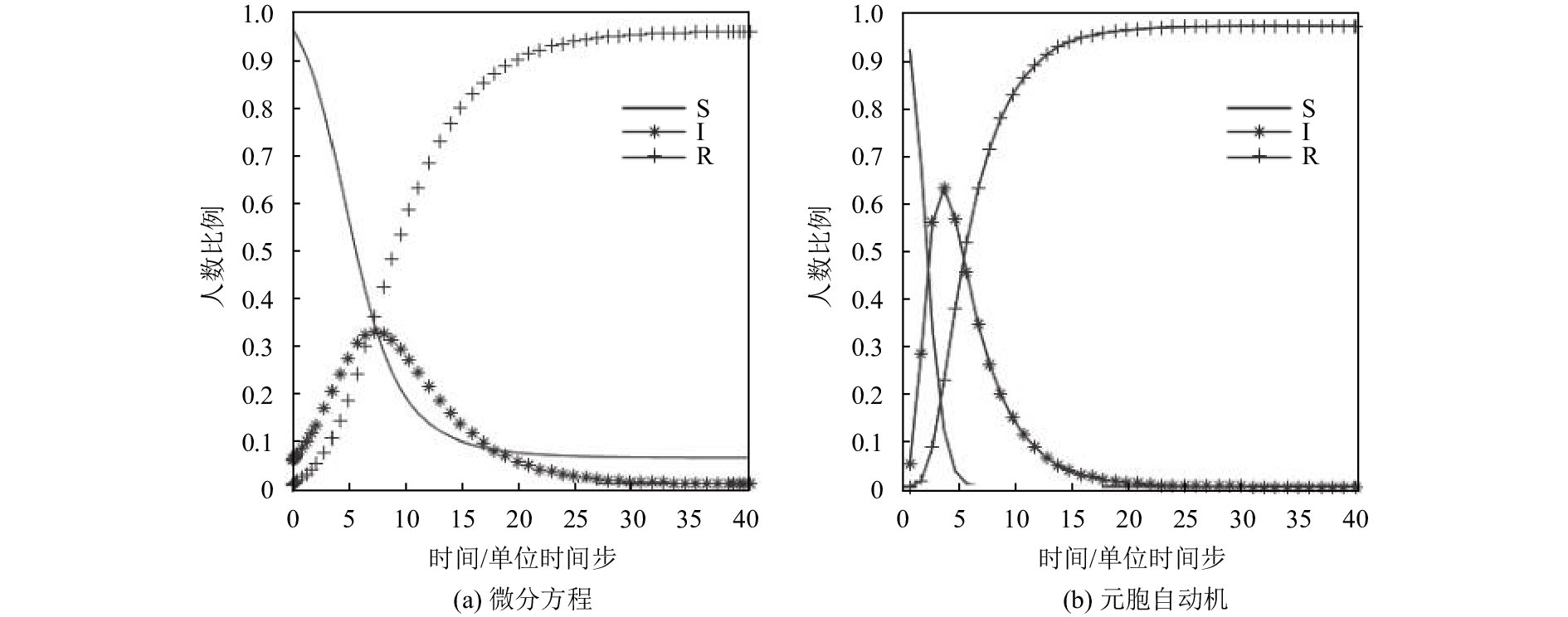
按照以上规则，设计对比实验. 对于SIR微分方程组，取定β=0.75，γ=0.25，SIR各舱室初值为S=0.95，I=0.05，R=0. 对于“简易”SIR元胞自动机模型，进行初始化，随机令约0.05%的元胞置1，其余为0，每个处于状态1的感染者元胞在每个单位时间步以b=0.75的概率对邻居进行感染，并在每个单位时间步以r=0.25的概率痊愈. 同时进行40个单位时间，实验结果如图1所示.

显然，“简易”元胞自动机的易感者被快速大量感染. 实际上，感染率一般并不会达到0.75这样高的水平，影响疫病传播的随机因素也很多，因此本文将在几乎完全模拟微分方程编写的“简易”元胞自动机基础上，加入一些仿真模块，以达到模拟真实的疫病传播情景的目的.

2 考虑多因素的仿真模块

首先，为了进行后续仿真模块的搭建，在利用MATLAB进行编程工作时，首先声明以下变量，见表1.

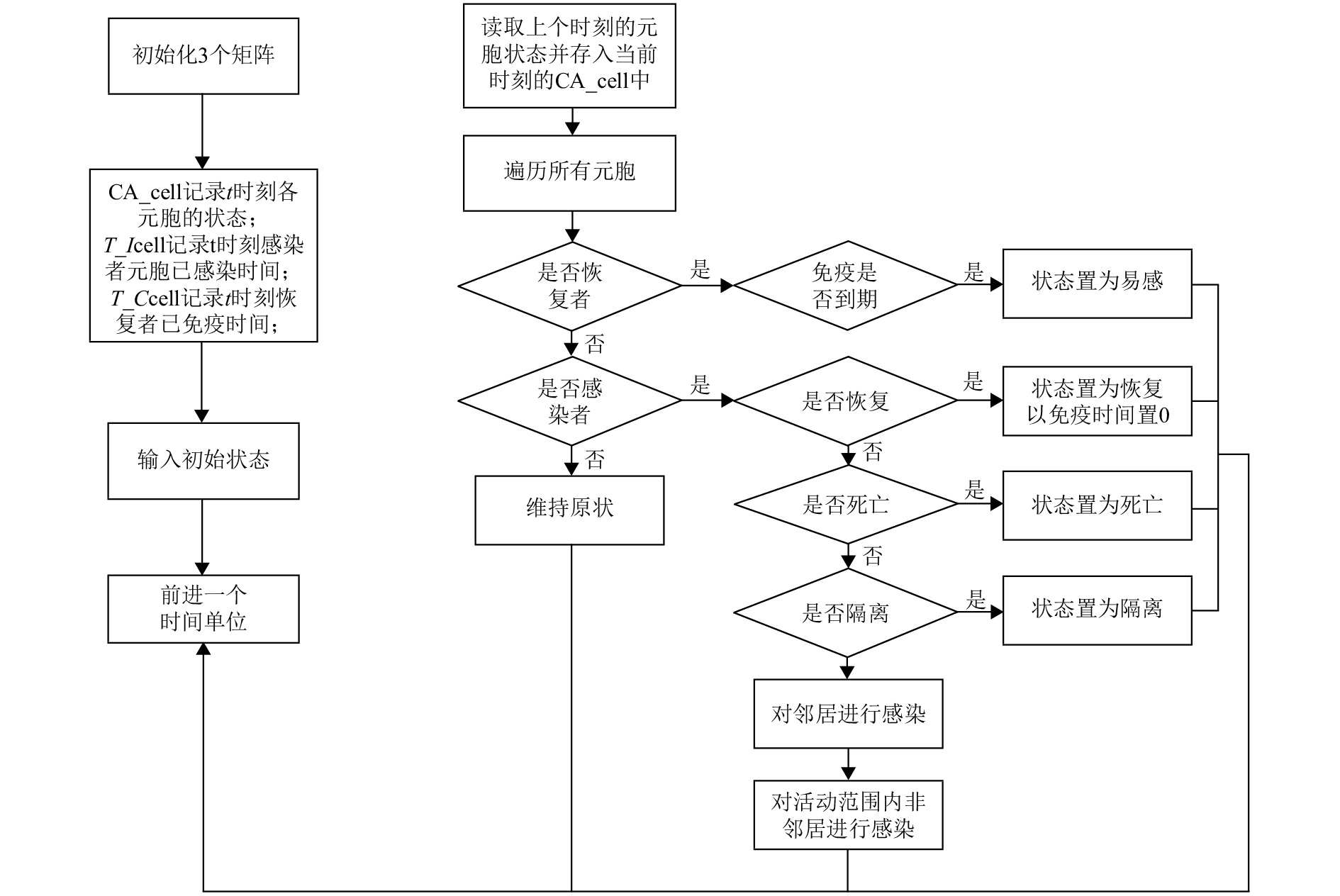
其次，根据本文提出的元胞自动机模型结构，作流程图如图2所示.

2.1 非邻体高斯传染模型

现实中，未被隔离的感染者通常不只与某几个地理位置相邻的人接触，其活动范围将设定在一定的半径大小区域内，这意味着在元胞自动机模拟中的邻体结构并不只局限于具有8个邻体的摩尔临体结构. 文献[3]介绍了一种随机行走模式，而文献[19]则采用符合泊松分布的随机数匹配来模拟随机行走. 本文则结合人群移动的特点，做出如下假设^[20-21]：

(1) 非邻体区域感染的几率比邻体区域感染几率要小；

(2) 距离某位感染者越远的区域越不容易涉及，反之，感染者更可能在距离自身较近的区域活动；

(3) 感染者没有对某一方向的趋向性，即对各个方向移动的概率相同，且相互独立；

(4) 人的活动范围有限.

根据假设，本文采用二维高斯分布函数对感染者周边非邻体区域的活动概率进行赋值. 根据二维高斯分布概率密度函数：

$\begin{split}&f\left( {x,y} \right) = {\left( {2{\rm{}}{\sigma _1}{\sigma _2}\sqrt {1 - {\rho ^2}} } \right)^{ - 1}} \times \\&{\rm{exp}}\left[ { - \displaystyle\frac{1}{{2\left( {1 \!-\! {\rho ^2}} \right)}}\left( {\displaystyle\frac{{{{\left( {x \!-\! {\mu _1}} \right)}^2}}}{{\sigma _1^2}} \!-\! \displaystyle\frac{{2\rho \left( {x \!-\! {\mu _1}} \right)\left( {y \!-\! {\mu _2}} \right)}}{{{\sigma _1}{\sigma _2}}} + }\right.}\right.\\&\left.{\left.{\displaystyle\frac{{{{\left( {y - {\mu _2}} \right)}^2}}}{{\sigma _2^2}}} \right)} \right].\end{split}$

基于假设(3)，有 $\sigma = {\sigma _1} = {\sigma _2}$ ，ρ=0，则式(1)可化简为

$f\left( {x,y} \right) = \frac{1}{{2{\text{π}} {\sigma ^2}}}{\rm{exp}}\left[ { - \frac{{{{\left( {x - {\mu _1}} \right)}^2} + {{\left( {y - {\mu _2}} \right)}^2}}}{{2{\sigma ^2}}}} \right].$

为控制感染率，将上式乘以感染期望b₂，得到每个感染个体对自身非邻体周边的感染率：

$g\left( {x,y} \right) = \frac{{{b_2}}}{{2{\text{π}} {\sigma ^2}}}{\rm{exp}}\left[ { - \frac{{{{\left( {x - {\mu _1}} \right)}^2} + {{\left( {y - {\mu _2}} \right)}^2}}}{{2{\sigma ^2}}}} \right].$

为进一步说明非邻体高斯传染模型中各参数对结果的影响，本文给出不同非邻居感染期望b₂，不同方差σ，以及不同活动范围r下的仿真结果.

首先，调整方差σ与活动范围r，为控制活动范围内感染的概率和相同. 在增大方差σ的同时需要增加活动范围r，经过计算，选定3组取值分别为(其中 ${P_\omega }$ 为活动范围内概率和，确定σ和r后可通过计算得到， ${P_\omega } \leqslant 1$ ):

(1) $\left[ {\sigma = 1,r = 3} \right]$ ， ${P_\omega } $ =0.989；

(2) $\left[ {\sigma = 2,r = 6} \right]$ ， ${P_\omega } $ =0.989；

(3) $\left[ {\sigma = 3,r = 9} \right]$ ， $ {P_\omega }$ =0.989.

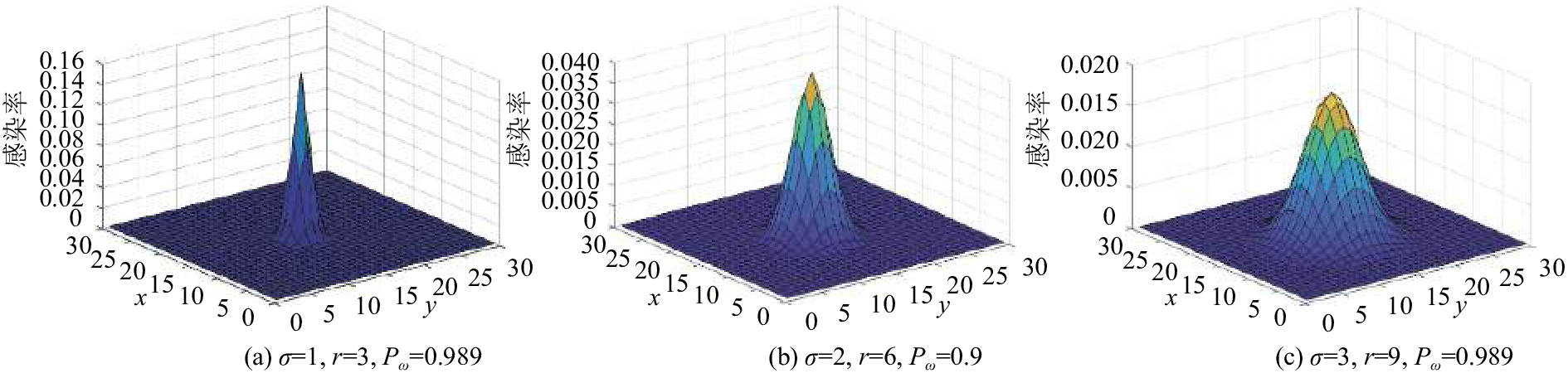
将活动范围内感染率画成曲面图如图3所示.

在此3种参数设置下，利用本文提出的模型进行了多次仿真，为使结果更明显，使用不采取隔离措施的模型. 根据图3容易发现，随着σ的增大，图形趋于扁平，这意味着以感染者为中心的中心疫区感染概率下降，边缘地区的感染概率上升. 本实验控制在活动范围r内，单个感染者对环境造成的感染率和保持一致.

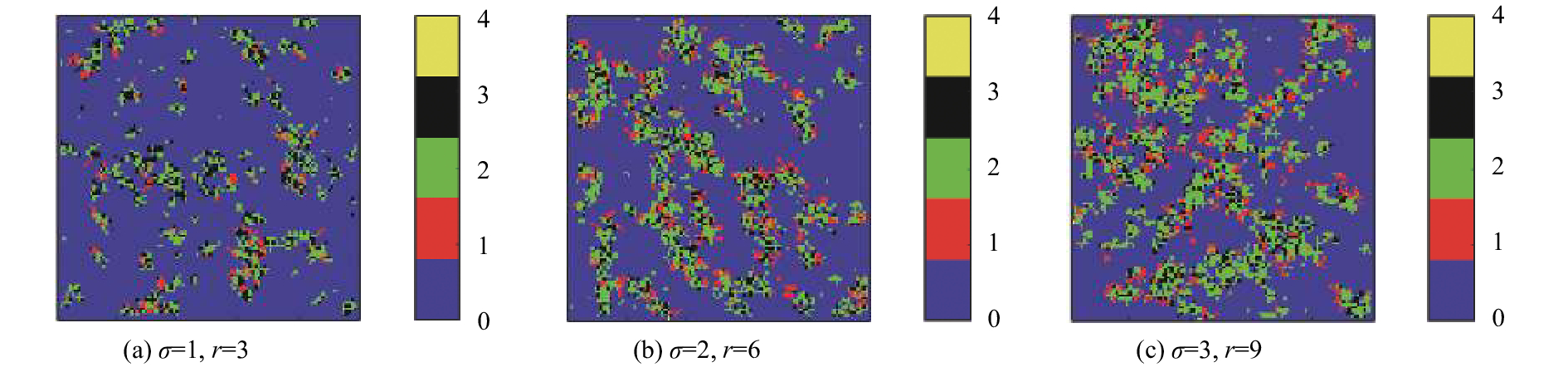
图4为分别采用图3的3种参数进行仿真实验得到的空间分布. 由图3可以看出随着活动范围r的增大，疾病的感染力明显提高，波及的范围变大. 该结果也印证了虽概率和一致，但活动范围和方差仍对结果产生巨大影响的猜想.

由图5可知，尽管范围内感染概率和相近，但活动范围越大，感染扩散越快. 说明了在疫情爆发时，限制人口流动是防止疫病感染扩散的有效手段.

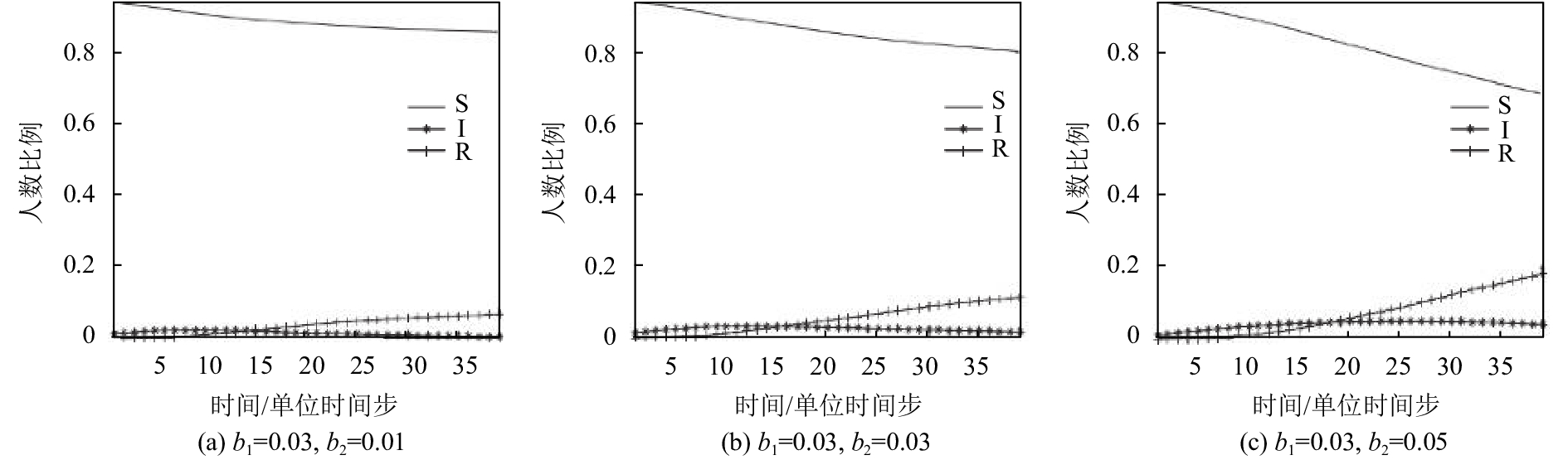
另外，对于不同的b₂取值，人群空间分布及比例动态分别见图6和图7，随着b₂的增大，流行病有显著的扩散，可见非邻体感染是流行病扩散的重要途径之一.

对于实验设定的参数，3次实验都走向衰退，意味着该种“疾病”的感染率不足以使其在感染者康复、死亡或被隔离之前传播出去，不同的是疾病虽然最终都被遏制，但影响的范围随b₂的增大而增大. 本实验选取的死亡率较低，因此出现了大批痊愈者. 若死亡率高于传染率，虽然疾病终会被遏制，但将造成大量死亡.

2.2 高斯压力死亡模型

经典的SIR模型假设人口总量不变，即无外来人口涌入，也不考虑出生率和死亡率. 对于中短期的疫病传染预测和分析，忽略人口的自然出生率和死亡率并不会带来很大的影响，但对于致死率高的疾病，这样的假设将会对结果造成较大的扰动，故本文将状态集扩充为{0，1，2，3}，其中3代表胞体“死亡”，不再进行传染，也不会重置为易感者.

结合一般经验和概率统计结果，本文对元胞“死亡”的转化规则做出以下假设：

(1) 感染者越多的疫区中心，越容易出现死亡病例(即“死亡压力”，压力越大死亡几率越大)；

(2) 对某个感染者元胞来说，其他感染者元胞距离他越近，对其造成的压力越大；

(3) 患病时间越久，若感染者无法痊愈，则更有可能“不治身亡”；

(4) 处在疫区中心，即使感染时间较短，患病“暴毙”的几率也较高.

基于以上假设，本文设计的高斯压力死亡函数由两部分组成，其中一部分为二维高斯分布概率密度函数

$p\left( {x,y} \right) = \frac{1}{{2{\text{π}} {\sigma ^2}}}{\rm{exp}}\left[ { - \frac{{{{\left( {x - {\mu _1}} \right)}^2} + {{\left( {y - {\mu _2}} \right)}^2}}}{{2{\sigma ^2}}}} \right].$

其中， $p\left( {x,y} \right)$ 代表处于 $ \left( {x,y} \right)$ 坐标上的感染者对中心元胞造成的“死亡压力”，由于 $ p\left( {x,y} \right)$ 是二维高斯分布的概率密度函数，所以有 $\mathop \sum { p\left( {x,y} \right) }\leqslant 1$ ；另一部分为患病时间加权函数，即根据假设(3)和假设(4)，感染者个体由感染时长导致的趋向死亡的程度，权重越大，死亡的概率越高，本文选取sigmoid函数作为患病时间加权函数. 其中sigmoid函数为

$S\left( x \right) = \frac{1}{{1 + {{\rm{e}}^{ - x}}}}\;.$

这里将患病时间T_Icell(x, y, t)代入上式，得到 $ \left( {x,y} \right)$ 坐标上的感染者的患病时间加权. 最后将两个部分的函数相乘得到该坐标上对中心元胞的加权“死亡压力”，而所有这样的加权压力之和即中心元胞所承受的最终“死亡压力”为

$\begin{split}&\mathop \sum { P\left( {x,y} \right) }=\\&\mathop \sum \limits_{x,y} \frac{1}{{1 + {{\rm{e}}^{ - T\_{\rm{Icell}}\left( {x,y,t} \right)}}}}\frac{1}{{2{\text{π}} {\sigma ^2}}}{\rm{exp}}\left[ { - \frac{{{{\left( {x - {\mu _1}} \right)}^2} + {{\left( {y - {\mu _2}} \right)}^2}}}{{2{\sigma ^2}}}} \right].\end{split}$

显然， $S\left( t \right) \leqslant 1$ ，进而 $ 1\geqslant \mathop \sum { p\left( {x,y} \right) \times S\left( t \right) }\geqslant 0$ ，本文把这个值设置为t时刻该中心元胞死亡的概率.

2.3 基于sigmoid函数的痊愈率与隔离率设置

经典SIR微分方程并不考虑人群的异质性，即系统中的每个人都具有相同的痊愈率. 事实上，疾病的恢复率依群体差异、环境差异和季节变化等存在一定的不均衡性. 已有文献[3]通过假设不同元胞具有随机产生的抵抗系数，用以抵消一部分的感染率或者感染的随机实验成功率，从而设置了疾病传播的群体异质性. 本文则从另一个角度，不考虑个体异质性，而考虑个体的时间异质性：即对于一般的急性流行病而言，患病时间越长，痊愈几率越高，故使用sigmoid函数对感染者元胞赋予随时间变化的痊愈率

$R\left( {x,y,t} \right) = c\_ {\rm{rate}}\times\frac{1}{{1 + {{\rm{e}}^{ - {c_1}\left( {T\_I {\rm{cell}}\left( {x,y,t} \right) - {c_2}} \right)}}}}.$

其中c₁，c₂用来调整函数的上升速度和横向平移.

隔离，是一种未取得有效疫苗之前限制流行病大规模爆发的主要防疫手段. 然而，通常情况下，感染者无法准确判断自身病情，或症状不明显时未及时到医院就诊，又或者出于对隔离的恐慌等原因，疾病防控人员无法在短时间内准确地隔离所有感染者^[22]. 在本文中，我们假设当地已发现疫情，并采取了相应的隔离措施：感染者随着患病时间增加，去医院求医或者被发现隔离的几率不断增大，表达为

$Q\left( {x,y,t} \right) = q\_ {\rm{rate}}\times\frac{1}{{1 + {{\rm{e}}^{ - {c_3}\times\left( {T\_I {\rm{cell}}\left( {x,y,t} \right) - {c_4}} \right)}}}}.$

$Q\left( {x,y,t} \right)$ 代表t时刻位于 $\left( {x,y} \right) $ 坐标的感染者被隔离的概率，c₃，c₄用来调整函数的上升速度和横向平移. 为方便运算，本文将状态集再次扩充为{0，1，2，3，4}. 其中4代表被隔离的元胞，被隔离元胞有可能被治愈，有可能死亡，但不再对周围的元胞进行感染.

为讨论隔离措施对防止疫病扩散的效果，做以下实验. 采用上述模型，控制一组元胞自动机采取隔离措施，另一组无隔离. 实验中隔离组取 $Q\left( {x,y,t} \right) = $ $ \displaystyle\frac{1}{{1 + {{\rm{e}}^{ - 0.2\left( {T\_I {\rm{cell}}\left( {x,y,t} \right) - 14} \right)}}}}$ ，即取c₃=0.2，c₄=14，q_rate=0. 其他参数如下：T_C=360，b₁=0.03，b₂=0.02，c_rate=0.5，r=5，σ=2. 而无隔离组设置q_rate=0，即 $Q\left( {x,y,t} \right) = 0$ ，其他参数与隔离组相同.

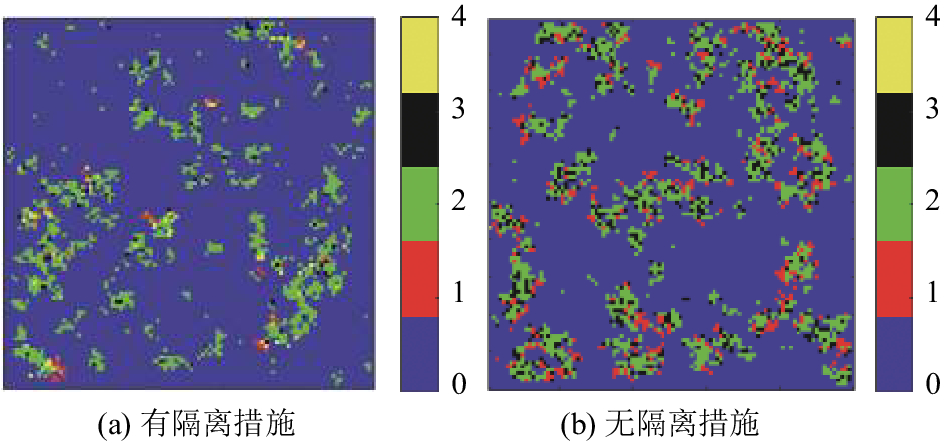
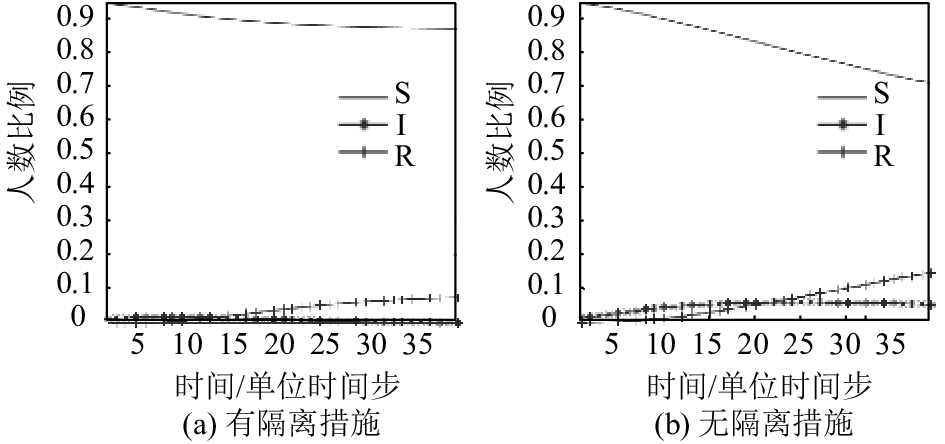
根据实验，本文的模型对于隔离措施反应灵敏，图8和图9说明了在流行病防治初期隔离感染源的重要性. 通过实验发现，只需要在流行病爆发初期隔离相对较少的感染者，就能极大程度上地抑制疫病的扩散. 图9中无隔离干预的实验，易感者人数比例降至0.7，说明截至t=40为止，至少有30%的人在该次流行病中受到感染，且在t=40之后感染者人数比例仍在上升，说明疾病仍处于扩散的态势. 而采取隔离干预的实验组，在t=40时，易感者人数比例只下降至0.87左右，即仅有13%的人被感染，且易感者人数比例曲线已趋于平缓，这表示该次流行病爆发已进入衰退阶段，将不会再有新的感染者出现.

3 数值仿真

为测试本文所提出的模型性能，选取表1数据作为仿真实验对照组. 为排除特殊性，选取相同参数，进行50次实验，记录平均值与对照组方差，给出最优情况和最差情况.

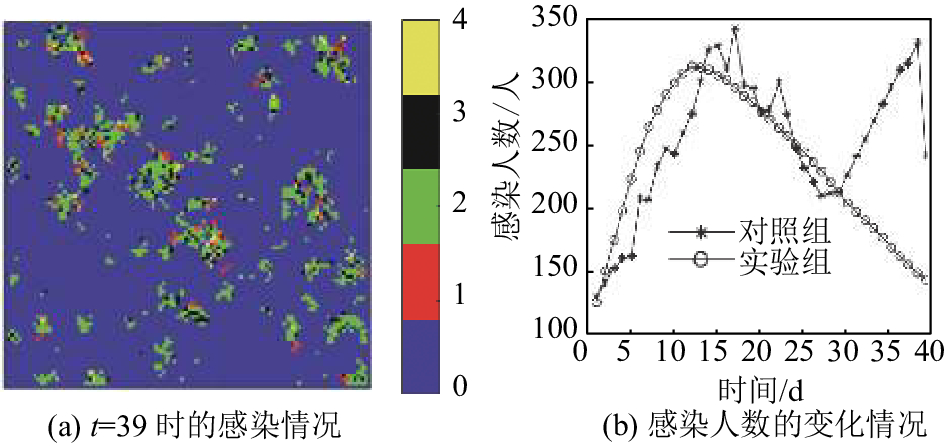
经过多次实验，设置参数为：m=100，n=100，T=39，T_C=360，b₁=0.03，b₂=0.01，c_rate=0.5，q_rate=0.35，r=5，σ=2，times=50.实验结果见图10.

如表3所示，50次实验方差的平均值为3 745.145，最小值为2 096.051，最大值为8 274.359. 由图10可以看出，模型在30 d以前拟合程度良好，30 d以后，对照组感染人数回升. 原因在于，实际中感染率b₂和b₁，隔离强度q_rate和基础治愈率c_rate受疾病严重性、政府关注程度、人群恐慌程度、特效药开发等多种因素的影响，并不是定值，感染人数增多意味着感染率在诸因素影响下有所提高，因此为进行更精确的分析，将时间离散后对每个细分进行参数的微调，理论上可得到非常趋近实际数据的模型，进而得到每个细分的参数. 本文接下来根据对照组数据特点进行微调.

根据图形特点，在疾病开始爆发的0~16 d，由于疾病未引起重视，隔离强度和治愈率并不高，设为b₁=0.02，b₂=0.02，q_rate=0.2，c_rate=0.2;在爆发前中段16~27 d，疾病进入公众视野，采取了一定的人群限流措施，减少了非邻体传染率b₂，增强了隔离强度和治愈率，设为b₁=0.02，b₂=0.01，q_rate=0.3，c_rate=0.3；在疾病爆发的中后段，疑似病毒发生变异或气候原因导致感染率提升，同时引发了广泛关注，隔离强度与治愈率均随之提升，设为b₁=0.05，b₂=0.02，q_rate=0.5，c_rate=0.5；在疾病后段，特效药物研制成功，康复率大幅度提升，感染率也由于预防措施降低，隔离强度进一步增强，设为b₁=0.02，b₂=0.01，q_rate=0.8，c_rate=1.

多段调整后拟合结果如图11所示. 显然，结果与对照组拟合良好，相对于固定值的参数，多段细分的结果大幅改善，方差从3 745.145降低到444.936，经实验，划分段数越多，拟合程度越高. 但划分段数过多会导致计算复杂度提高，同时也容易出现过拟合现象. 一般而言，传染病在某个地区的爆发大致分为感染、扩散、衰退3个阶段. 一些受季节影响的疾病，如流感，候鸟或昆虫媒介传播的疾病，甚至呈现周期性. 然而由于人类医疗干预的介入，以及种种隐性因素的影响，曲线并不总是符合明显规律. 此时，通过本文提出的模型进行多段细分拟合可帮助分析是何参数的浮动影响了疫情，从而获得解释其生物学意义的线索.

4 结语

本文提出的考虑多因素的元胞自动机传染病模型，在结构设计方面，引入了高斯非邻体传染模型，高斯压力死亡模型，基于sigmoid函数的痊愈率与隔离率设置，在元胞自动机的转化规则中加入随机条件，利用蒙特卡洛方法的思想^[23]，将参数设置的概率转化为服从一定分布的随机事件. 同时完善了目前传染病元胞自动机模型较少关注的参数时间异质性，主要考虑了流行病传播随时间发展的各个阶段，感染率、死亡率、痊愈率、隔离强度等参数随时间的变化. 由于考虑较多因素，多参数可调，因此模型的精确性，可扩展性都较为优秀，泛用性广，是一种较为稳定的元胞自动机传染病模型.