2. 桂林电子科技大学 数学与计算科学学院,广西 桂林 541004;
3. 贵州大学 管理学院,贵州 贵阳 550025
2. School of Mathematics and Computing Science, Guilin University of Electronic Technology, Guilin 541000, China;
3. School of Management, Guizhou University, Guiyang 550025, China
金融业是国民经济的主要支柱行业,其功能推动了国家和地区经济的快速发展. 随着科学技术的进步和人们投资和消费方式的变化,特别是互联网技术的普及,在金融业的运行过程中,逐渐形成了形形色色的金融交易活动. 在各种各样的金融交易过程中,产生了不同类型的交易数据. 例如股票交易过程中会产生股票价格的最高价、最低价、开盘价、收盘价、成交量、成交金额、买入数量、卖出数量、投资者数量等大量数据. 互联网金融的快速发展,产生了大量非规范的金融大数据. 金融大数据是指在金融行业的运行过程中产生满足大数据4V特征的数据,即大容量、高速率、多样性、真实性. 例如,量化交易产生的高频交易数据满足大容量、高速率和真实性的特征,投资者情绪满足非结构化数据的多样性特征. 金融大数据不仅具有传统金融数据的特征而且其研究方法和处理技术正在深入影响传统金融学的基本功能.
在金融大数据的处理过程中,研究金融市场波动在资产定价和风险管理等方面有着重要作用. 在波动测量方面,Engle[1]和Bollerslev[2]提出的ARCH/GARCH类模型是刻画金融资产波动的有效方法,已经成功地应用于测量股票市场波动、汇率市场波动、债券市场波动等. 受宏观经济不确定性等因素的影响,不同金融市场之间具有很强的相关性,如股票市场和债券市场,股票市场和汇率市场. 为了刻画这种相关性,Bollerslev[3]年提出了相关矩阵为常数的多元GARCH模型. 然而,金融资产之间的相关性往往具有时变性,为此,Engle[4]提出了带有正态分布的动态条件相关模型(DCC-GARCH)计算不同资产收益率间非线性时变相关关系. Creal等[5]提出了带有重尾分布的DCC-GARCH模型,Zhang等[6]提出了带有双曲分布的DCC-GARCH模型. 在DCC框架下的多元波动模型,存在的主要问题是统计参数数量非常多,这为在高频数据或者大数据情境下分析随机时间序列之间的相关性带来了很大困难. 为此,Fan等[7]提出条件非相关成分(CUC)方法对多元波动过程进行建模,将多维问题转化为多个一维子问题,简化了计算维度和参数数目. 王明进和陈奇志[8]利用独立成分分解(ICA)提出了一类IC-GARCH模型,从多维金融资产收益率中提取相互独立成分,再对独立成分建立GARCH模型. 孟庆浩和张卫国[9]利用独立成分分析(ICA)方法研究了金融市场的波动溢出效应. 赵丽丽和张波[10]放宽了ICA关于独立成分是IID的假设,考虑独立成分为ARMA模型的平稳过程,提出了基于自相关结构的IC-GARCH估计方法. 在数据库处理方面,李桥兴等[11]提出了大数据基元的HBase 数据库存储模型,为金融大数据的应用提供了技术手段.
然而,随着估计参数的增加,需要快速有效地优化算法求解条件非相关成分(CUC)模型. 为此,本文提出了单纯形搜索法,通过构造单纯形来逼近极小点,确定其最高点和最低点,然后通过扩展、压缩反射构造新的单纯形,目的是使得极小点能够包含于单纯形内. 该算法极大地提高了估计参数的速度和精度. 为了验证算法的有效性,本文检验了股票市场、债券市场、基金市场、外汇市场与期货市场的条件非相关性问题.
1 CUC-GARCH模型Fan等[7]提出条件非相关成分(CUC)方法将高维问题转化为多个一维子问题进行处理,而且可以刻画多维变量间的动态相关结构,下面简述其主要内容.
假定有d个不同金融资产,
| ${\rm{E}}\left( {{{{X}}_t}|{{\rm F}_{t - 1}}} \right) = 0,\;\;\;\;{\rm{Cov}}({{{X}}_t}|{{\rm F}_{t - 1}}) = {{{\varSigma}} _t} \equiv \left( {{\sigma _{ijt}}} \right),$ | (1) |
其中
CUC分解方法将
| ${{{X}}_t} = {{A}}{{{Z}}_t},$ | (2) |
其中,转移矩阵A为常数矩阵.
条件非相关成分满足
| ${\rm{E}}\left( {{Z_{i,t}}{Z_{j,t}}|{{\rm{F}}_{t - 1}}} \right) = 0,\;\;\;\;\;\;\;\;\;i \ne j.$ | (3) |
因此,
| ${\rm{Cov}}\left( {{{{X}}_t}} \right) = {\rm{Cov}}\left( {{{A}}{{{Z}}_t}} \right) = {{A}}{\rm{Cov}}\left( {{{{Z}}_t}} \right){{A}}' = {{AA}}' = {{{I}}_d},$ |
则转移矩阵A为自由度为
| ${{{Z}}_t} = {{{A}}^{{\rm{ - }}1}}{{{X}}_t} = {{A}}'{{{X}}_t}.$ | (4) |
令
| ${\rm{Cov}}\left( {{{{Z}}_t}|{{\rm{F}}_{t - 1}}} \right) = {\rm{diag}}\left( {\sigma _{1,t}^2,\sigma _{2,t}^2,\cdots,\sigma _{d,t}^2} \right).$ |
计算CUC-GARCH模型分为两步. 第一步,通过优化方法估计转移矩阵A,利用(1)式得到对应的条件非相关成分
由(1)式可得,当
| $\varPsi \left( {{A}} \right) \equiv \sum\limits_{1 \leqslant i < j \leqslant d} {\sum\limits_{B \in {{\rm{B}}_t}} {\omega \left( B \right)} } \sum\limits_{k = 1}^{{k_0}} {\left| {{\rm{E}}\left\{ {{{a'}_i}{{{X}}_t}{{{{X}}'}_t}I\left( {{{{X}}_{t - k}} \in B} \right){a_j}} \right\}} \right|} ,$ | (5) |
其中
| ${\varPsi _n}\left( {{A}} \right)\!=\!\!\!\!\!\!\sum\limits_{1 \leqslant i < j \leqslant d} {\sum\limits_{B \in {\rm{B}}} {\frac{1}{{{m_B}}}} } \!\sum\limits_{k = 1}^d \!{\frac{1}{{n \!-\! 1}}\left| {{{a_i'}}\sum\limits_{t = 2}^n {{{{X}}_t}{{{{X}_t'}}}I\left( {{X_{t - 1,k}}\! \leqslant\! x} \right)} {a_j}} \right|} .$ | (6) |
通过A的估计与式(3)得到
| ${\rm{Var}}\left( {{Z_{i,t}}|{{\rm{F}}_{t - 1}}} \right) \equiv \sigma _{i,t}^2 = {\omega _i} + {\alpha _i}Z_{i,t - 1}^2 + {\beta _i}\sigma _{i,t - 1}^2,\;\;\;i = 1,2, \cdots ,d,$ | (7) |
其中
由此,
| $ \begin{array}{l}{\rm{Cov}}({{{X}}_t}|{{\rm{F}}_{t - 1}}) = {{{\varSigma}} _t}{\rm{ = Cov}}\left( {{{A}}{{{Z}}_t}|{{\rm{F}}_{t - 1}}} \right) = {{A}}{{{\varLambda}} _t}{{A}}',\\ {{{R}}_t} = {{D}}_t^{ - 1/2}{{{\varSigma}} _t}{{D}}_t^{ - 1/2},{{{D}}_t} = {\rm{diag}}\left( {{\sigma _{11,t}},{\sigma _{22,t}}, \cdots ,{\sigma _{dd,t}}} \right),\end{array} $ | (8) |
其中,
单纯形搜索算法是通过构造单纯形来逼近极小点,每构造一个单纯形,确定其最高点和最低点,然后通过扩展、压缩反射构造新的单纯形,目的是使得极小点能够包含于单纯形内. 用单纯形搜索法求解无约束优化问题(6),其算法步骤如下:
Step1:选取初始单纯形
Step2:将单纯形的
| ${\varPsi _n}\left( {{{{A}}^0}} \right) \leqslant {\varPsi _n}\left( {{{{A}}^1}} \right) \leqslant \cdots {\varPsi _n}\left( {{{{A}}^{h - 1}}} \right) \leqslant {\varPsi _n}\left( {{{{A}}^h}} \right).$ |
Step3:令
| ${\left\{ {\frac{1}{{h + 1}}{{\sum\limits_{j = 0}^h {\left[ {{\varPsi _n}\left( {{{{A}}^j}} \right) - {\varPsi _n}\left( {{{{A}}^{j + 1}}} \right)} \right]} }^2}} \right\}^{1/2}} \leqslant \varepsilon ,$ |
则停止迭代并输出
Step4:计算
Step5:计算
Step6:令
Step7:令
Step8:令
本文选取上证综合指数作为股票市场指数,中信公司债指数作为债券市场指数,上证基金指数作为基金市场指数,美元兑人民币汇率作为外汇市场指数,中证商品期货综合指数作为期货市场指数. 上证综合指数样本从1990年12月19日~2017年10月27日,中信公司债指数从2008年1月2日~2017年10月27日,上证基金指数样本从2000年5月9日~2017年10月27日,美元兑人民币汇率样本从2009年11月2日~2017年10月27日,中证商品期货指数样本从2011年4月12日~2017年10月27日. 样本数据均为每日收盘价数据,扣除节假日以及未交易的天数,选取5个金融市场同时进行交易的数据,数据均来自东方财富Choice数据. 由于5个金融市场的指数样本数据起始时间不同,同时进行5个金融市场间相关性的研究会造成大量数据遗失,因此本文进行相关性实证研究时采取任意两市场间进行匹配的方式. 本文中的收益率采用对数收益率,其计算方式为
由图1可知,5个金融市场的日收益率均在0附近上下波动,并且均表现出波动聚集效应. 表1为上述5个金融市场收益率的描述性统计特征. 从不同金融市场收益率的均值、方差来看,股票市场、债券市场、基金市场、外汇市场的收益率序列均值都大于0,而期货市场收益率小于0. 从收益率标准差来看,股票市场最大,基金市场与期货市场次之,而后为债券市场与外汇市场,说明股票市场的波动最大,风险最高. 峰度、偏度与Jarque–Bera检验表明,5个金融市场收益率序列均不满足正态性假设,并且呈现出尖峰厚尾现象. ADF单位根检验表明在置信水平为1%的情况下,5个金融市场收益率序列均平稳. 序列平方的Ljung-Box Q统计量Q2(12)与拉格朗日乘子检验LM(12)均表明,所有序列均具有波动聚集效应,即ARCH效应.
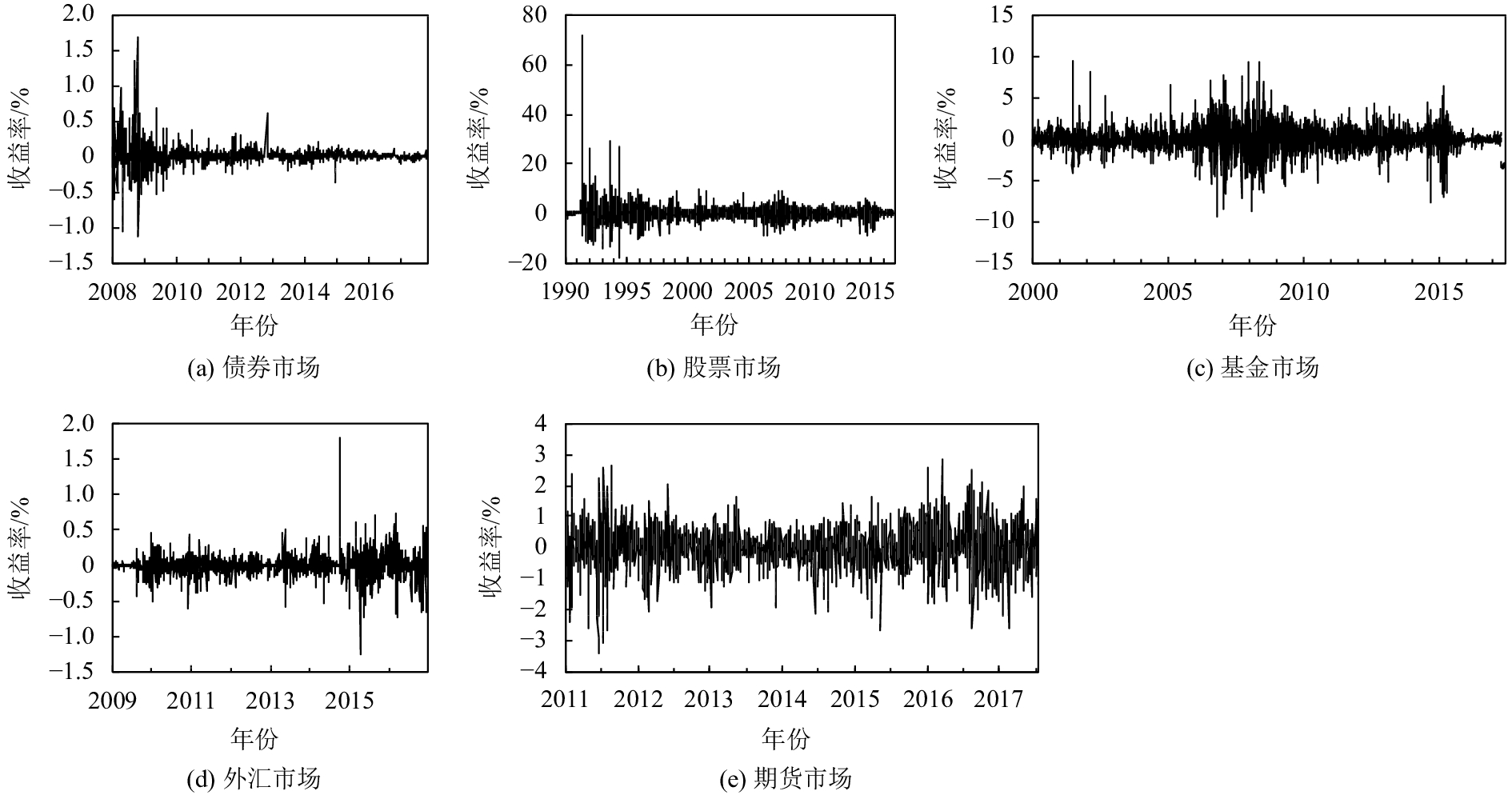
|
图 1 金融市场收益率时序 Figure 1 Return sequences of financial markets |
| 表 1 金融市场收益率序列的统计描述1) Table 1 Statistical description of the returns of financial markets |
在计算中,为满足假设
| 表 2 金融市场间的动态相关系数 Table 2 Dynamical correlations between financial markets |
从均值与标准差可知,股票市场与基金市场的相关系数均值最大,达到了0.877 7,表明股票市场与基金市场在收益率上的信息传递最强,联动效应最强,其次为股票市场与期货市场以及基金市场与期货市场. 从相关系数的正负个数及比例可知,股票市场与基金市场、股票市场与债券市场、股票市场与期货市场、债券市场与基金市场、基金市场与期货市场的正相关系数超过50%,表明其更多呈现正相关关系,即表现出“同涨同跌”现象. 而股票市场与外汇市场、基金市场与外汇市场、外汇市场与期货市场的正相关系数少于50%,表明其更多呈现负相关关系,即表现出“跷跷板”现象.
3 结论金融大数据中的相关分析是一个非常重要的研究课题,计算多维金融时间序列波动的相关性尤为重要. 为了解决多维金融资产相关性计算中降维问题,提出了快速有效的单纯形搜索优化算法,求解条件非相关成分(CUC)模型. 该算法极大地提高了估计参数的速度和精度. 为了验证算法的有效性,分析了中国股票市场、债券市场、基金市场、外汇市场与期货市场的条件非相关性问题. 本文研究结果的学术贡献体现为:1) 在理论方面,提出了求解条件非相关成分(CUC)模型的单纯形搜索优化算法,为处理金融大数据的相关性提供了快速有效的方法;2) 在应用方面,用文中提出的方法分析了中国五类金融市场之间的相关性,发现股票市场与基金市场、股票市场与债券市场、股票市场与期货市场、债券市场与基金市场、基金市场与期货市场之间更多呈现正相关关系,而股票市场与外汇市场、基金市场与外汇市场、外汇市场与期货市场时间更多呈现负相关关系. 综上,本文的研究方法为金融大数据相关分析提供了新方法,具有重要的理论意义和应用价值.
| [1] |
ENGLE R F. Autoregressive conditional heteroskedasticity with estimates of the variance of UK inflation[J].
Econometrica, 1982, 50(4): 987-1008.
DOI: 10.2307/1912773. |
| [2] |
BOLLERSLEV T. Generalized autoregressive conditional heteroskedasticity[J].
Journal of Econometrics, 1986, 31(3): 307-327.
DOI: 10.1016/0304-4076(86)90063-1. |
| [3] |
BOLLERSLEV T. Modeling the coherence in short-run nominal exchange rates: a multivariate generalized ARCH model[J].
The Review of Economics and Statistics, 1990, 72(3): 498-505.
DOI: 10.2307/2109358. |
| [4] |
ENGLE R F. Dynamic Conditional correlation: a simple class of multivariate generalized autoregressive conditional heteroskedasticity models[J].
Journal of Business and Economic Statistics, 2002, 20(3): 339-350.
DOI: 10.1198/073500102288618487. |
| [5] |
CREAL D, LUCAS A. A dynamic multivariate heavy-tailed model for time-varying volatilities and correlations[J].
Journal of Business & Economic Statistics, 2011, 29(4): 552-563.
|
| [6] |
ZHANG X,CREAL D,KOOPMAN S J, et al. Modeling dynamic volatilities and correlations under skewness and fat tails: 2011 Tinbergen Institute Discussion Paper: 11-078/2/DSF22[R/OL].(2011-05-11)[2017-12-10].http://dx.doi.org/10.2139/ssrn.1920839
|
| [7] |
FAN J, WANG M, YAO Q. Modelling multivariate volatilities via conditionally uncorrelated components[J].
Journal of the Royal Statistical Society, 2008, 70(4): 679-702.
DOI: 10.1111/rssb.2008.70.issue-4. |
| [8] |
王明进,陈奇志. 基于独立成分分解的多元波动率模型[J].
管理科学学报, 2006, 9(5): 56-64.
WANG M J, CHEN Q Z. Multivariate volatilities modeling based on independent components[J]. Journal of Management Sciences in China, 2006, 9(5): 56-64. DOI: 10.3321/j.issn:1007-9807.2006.05.008. |
| [9] |
孟庆浩,张卫国. 基于ICA的多元金融市场波动溢出及实证研究[J].
系统工程, 2015, 33(10): 115-121.
MENG Q H, ZHANG W G. Volatility spillover effect and empirical study on multi-financial markets based on independent component analysis[J]. Systems Engineering, 2015, 33(10): 115-121. DOI: 10.3969/j.issn.1001-2362.2015.10.086. |
| [10] |
赵丽丽,张波. 基于改进ICA模型的高维波动率估计[J].
数理统计与管理, 2017, 36(1): 38-50.
ZHAO L L, ZHANG B. Estimation of high dimension volatility based on improved ICA model[J]. Journal of Applied Statistics and Management, 2017, 36(1): 38-50. |
| [11] |
李桥兴,强保华,杨春燕. 大数据基元的HBase数据库存储模型与实现[J].
广东工业大学学报, 2014, 31(3): 8-13.
LI Q X, QIANG B H, YANG C Y. The storage model of big data basic-elements in HBase database and its realization[J]. Journal of Guangdong University of Technology, 2014, 31(3): 8-13. DOI: 10.3969/j.issn.1007-7162.2014.03.002. |
 2018, Vol. 35
2018, Vol. 35