不失一般性,多目标优化问题(multi-objective optimization-problem, MOP)可以表示为
| $\left\{\begin{array}{l}{\rm{min}}\;{{F}}(x) = {({f_1}(x),{f_2}(x), \cdots ,{f_m}(x))^{\rm{T}}},\\{\rm{s.}}{\rm{t.}}\quad{{x}} \in \Omega .\end{array}\right.$ | (1) |
其中
令
和单目标优化不同,MOP的最优解不是单个解而是一个解集,即Pareto优化集. 一些多目标进化算法已经被成功地应用到解决MOP上,在过去的十几年间逐渐成熟. 目前多目标进化算法主要有3种基本方法:(1) 基于Pareto支配的方法,代表算法有NSGA-II、SPEA-II、NSGA-III等[1-3];(2) 基于指标的方法,如IBEA、SMS-EMOA、HypE等[4-6];(3) 基于分解的方法,如MOEA/D、MOEA/D-DE等[7-11]. 本文则着重讨论第3种方法.
Zhang Q[7]在2007年提出了基于分解的多目标进化算法的基本框架,其主要的思想是通过聚合函数把MOP问题分解为一系列的目标子问题,一个子问题可以用一个权重向量来表示,每个子问题都可以视为一个单目标优化问题,并通过互相协助的方法求解它们. 对于标准的MOEA/D,当前进化种群内的每个个体和子问题之间是一一对应关系,一个个体对应着一个子问题,个体间的优胜劣汰并不依靠个体的目标函数值,而是通过比较聚合函数来完成. 基于此框架,许多MOEA/D的变种算法近几年不断被提出来,以应对不同的MOP问题,如使用差分变异算子的MOEA/D-DE[8],具有自适应权重的MOEA/D-AWA[10]和自动调配计算资源的MOEA/D-GRA[11]. Trivedi对最近的MOEA/D发展进行了详细的报告[12].
如上述所说,聚合函数被用于作为衡量一个个体优劣的适应值函数. 聚合函数通常是一个在给定权重
目前MOEA/D主要使用的有3个聚合函数[7, 12]:加权和(Weighted Sum)、切比雪夫方法(Tchebycheff)和PBI方法(Penalty-based Boundary Intersection).
基于上述方法,本文提出一种新的聚合函数. 不同于上述的方法,其特点和优势包括以下方面:
(1) 该聚合函数是一个二次函数,其个体的等高线是一条二次光滑曲线,不同于切比雪夫方法和PBI方法,这两者的个体等高线都是一次非光滑的. 因此该方法可以看成是对上述3种聚合函数的一种泛化及光滑化方法.
(2) 该聚合函数在局部控制个体的收敛性,而在全局则控制其散布性,达到收敛性和散布性之间的平衡.
(3) 有异于PBI方法,该聚合函数的等高线形状与权重无关,只受参数的影响,即若参数一定,则该聚合函数的等高线形状处处相同. 这也使得该方法对参数的调节不敏感,对不同的MOP使用固定参数也能有较好的表现.
2 双曲线聚合函数 2.1 建立首先,为了方便说明,本文省略了对参考点的讨论,即在假设
在这一节提出一个聚合函数,因为其函数值的等高线是一条双曲线,所以以下称之为双曲线方法(HYB 方法).
在数学上,考虑最优化以下函数:
| ${\rm{min}}\;{g^{{\rm{HYB}}}}({{x}}|{{\lambda }})\;{\rm{ = }}{f_1}^\prime - \sqrt {{\alpha ^2} + {{(\theta {f_2}^\prime )}^2}} ,$ | (2) |
其中
| $\left\{ {\begin{array}{*{20}{c}}{{f_1}^\prime = \displaystyle\frac{{ - 1}}{{\sqrt 2 }}(\displaystyle\frac{{{f_1}({{x}})}}{{{{{\lambda }}_1}}} + \displaystyle\frac{{{f_2}({{x}})}}{{{{{\lambda }}_2}}})},\\[15pt]{{f_2}^\prime = \displaystyle\frac{1}{{\sqrt 2 }}(\displaystyle\frac{{{f_1}({{x}})}}{{{{{\lambda }}_1}}} - \displaystyle\frac{{{f_2}({{x}})}}{{{{{\lambda }}_2}}})},\end{array}} \right.$ | (3) |
事实上,该聚合函数的参数调节是很直观的:该函数的函数值等高线是一条双曲线,而这两个参数就是用于控制该双曲线的形状的. 参数
控制两个参数可以得到不同形状的聚合函数. 特别地,若令
| $\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{{f_1}^\prime = \displaystyle\frac{{ - 1}}{r}({{{\lambda }}_1}{f_1}({{x}}) + {{{\lambda }}_2}{f_2}({{x}})),}\\[13pt]{{f_2}^\prime = \displaystyle\frac{1}{r}({{{\lambda }}_2}{f_1}({{x}}) - {{{\lambda }}_1}{f_2}({{x}}));}\end{array}} \right.\\[25pt]r = \sqrt {{{{\lambda }}_1}^2 + {{{\lambda }}_2}^2} .\end{array}$ | (4) |
则该方法即为PBI方法,式(3)和式(4)两者都是旋转变换,它们的区别在于式(3)在变换前多做了一个标准化变换;若令
下面考察
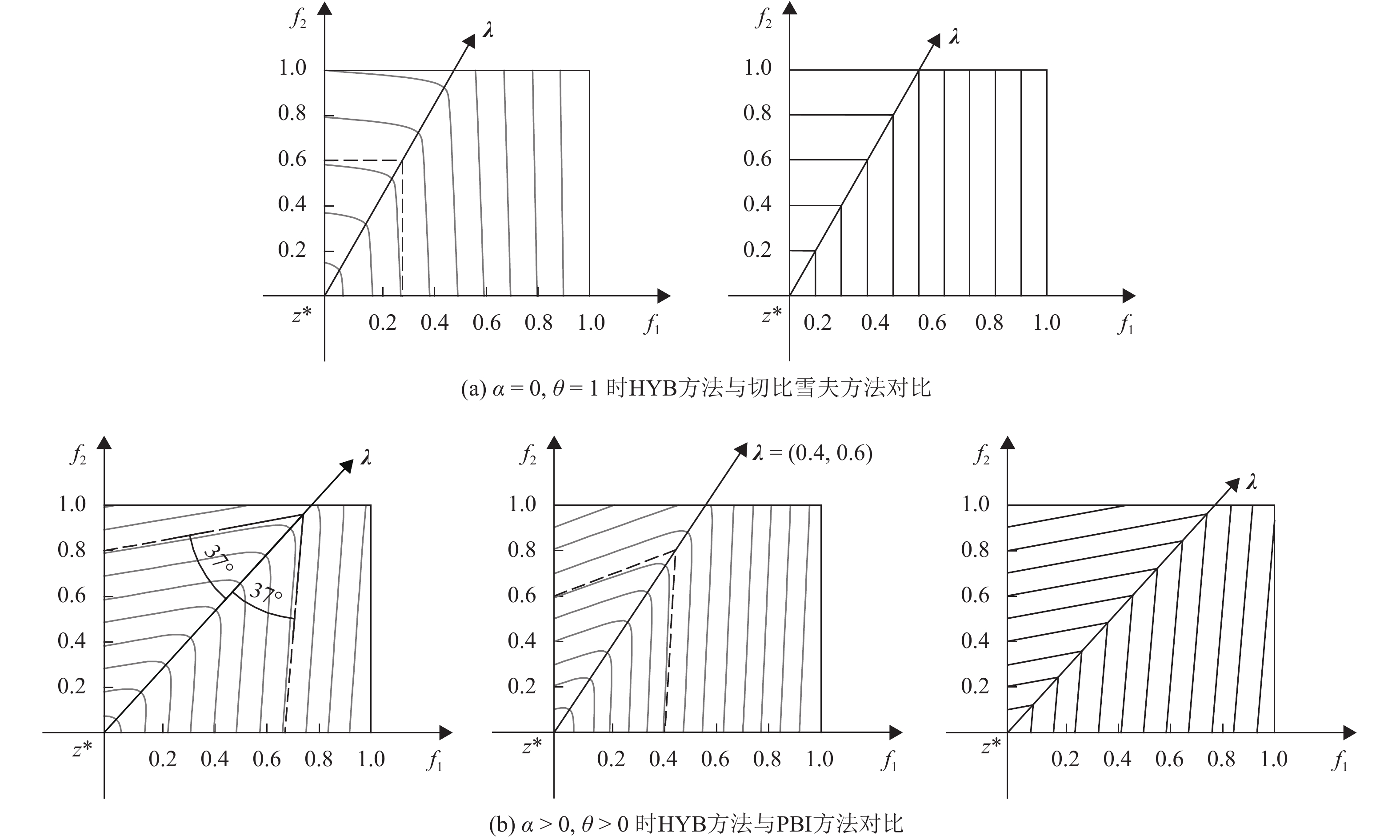
由此可以画出双曲线方法对应的个体等高线,并与其他聚合函数的等高线进行对比,如图2所示,其中
图2(a)展示了
|
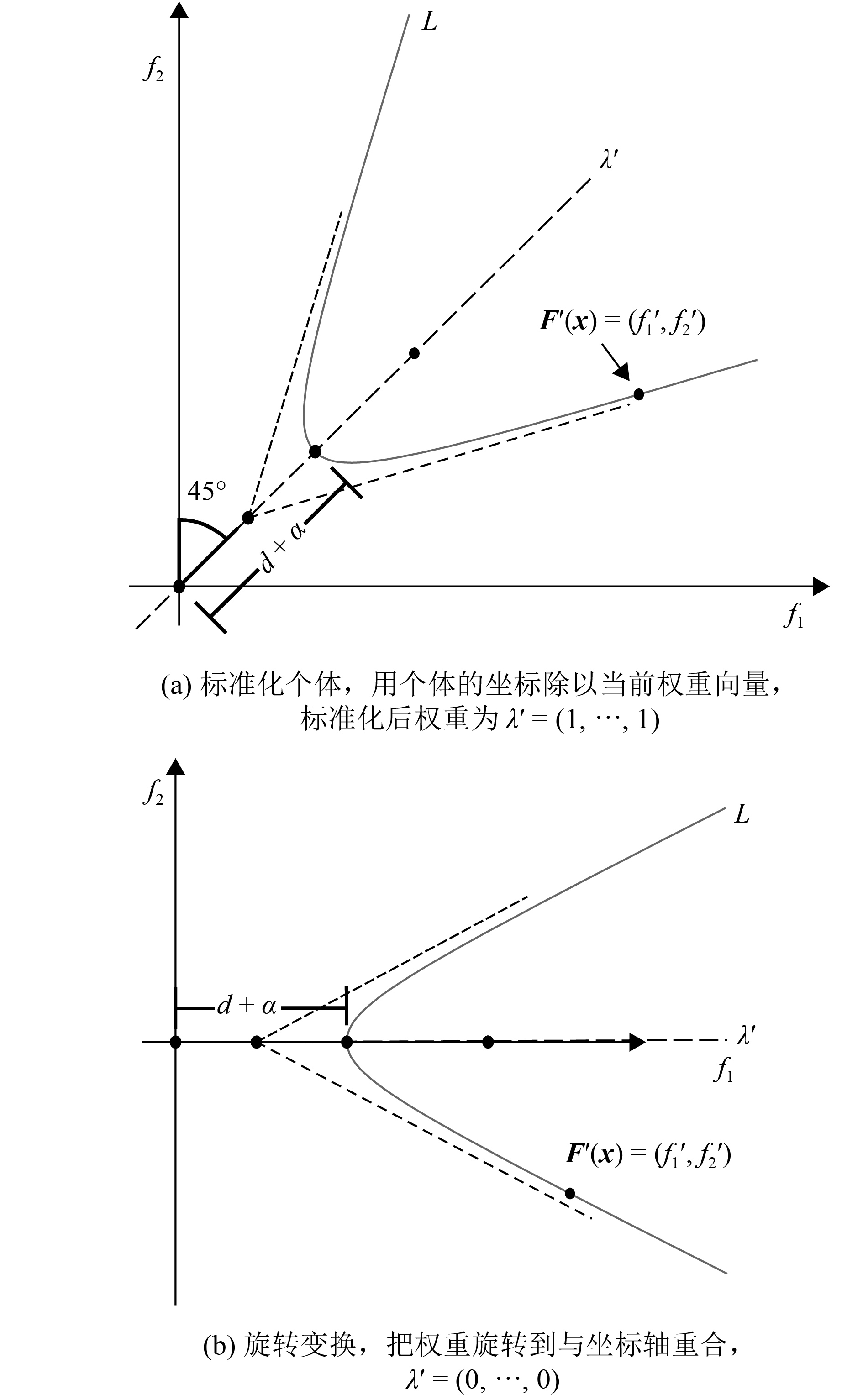
图 1 双曲线聚合函数式(2)的几何意义 Figure 1 The geometric meaning of Eq.(2) |
从该函数等高线可以知道,如果两个体都比较靠近权重
|
图 2 各聚合函数的等高线对比图 Figure 2 The contour comparison of each scalarizing function |
这一节本文进一步讨论该聚合函数的推导过程及推广. 首先考虑式(4)变换的情况,设个体
因为曲线L为双曲线,故曲线L函数表达式为
| ${({f_1} - d - \alpha )^2} - {(\theta {f_2})^2} = {\alpha ^2}.$ | (5) |
又因为曲线
| $d + \alpha {\rm{ = }}\;{f_1}^\prime - \sqrt {{\alpha ^2} + {{(\theta {f_2}^\prime )}^2}} .$ | (6) |
于是,可以有
下面讨论式(3)变换的情况,同理,先对
下面进行推广,把聚合函数式(2)和式(3)推广到高维上,以解决超多目标问题(MaOPs). 事实上,要做到这一步,只需要建立一个包含向量
在
| ${g^{{\rm{HYB}}}}({{x}}|{{\lambda }}) = {f_1}^\prime - \sqrt {{\alpha ^2} + {{(\theta {{f'}_2})}^2} + \cdots + {{(\theta {{f'}_m})}^2}} ,$ | (7) |
其中,
| $\left( {\begin{array}{*{20}{c}}{{f_1}^\prime }\\[8pt] \vdots \\[8pt]{{f_m}^\prime }\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{\displaystyle\frac{1}{{\sqrt m }}} & \cdots & {\displaystyle\frac{1}{{\sqrt m }}}\\[8pt] \vdots & {} & \vdots \\[8pt]{\displaystyle\frac{1}{{\sqrt {i + {i^2}} }}} & \cdots & {\displaystyle\frac{1}{{\sqrt {i + {i^2}} }}}\\[8pt] \vdots & {} & \vdots \\[8pt]{\displaystyle\frac{1}{{\sqrt 2 }}} & \cdots & {\displaystyle\frac{1}{{\sqrt 2 }}}\end{array}} \right){\rm{*}}{{A}}\left( {\begin{array}{*{20}{c}}{\displaystyle\frac{{{f_1}}}{{{\lambda _1}}}}\\[8pt] \vdots \\[8pt]{\displaystyle\frac{{{f_m}}}{{{\lambda _m}}}}\end{array}} \right),$ |
| ${{A}}{\rm{ = }}\left( {\begin{array}{*{20}{c}}{ - 1} & { - 1} & \cdots & { - 1} & { - 1} & { - 1} \\[5pt]1 & 1 & \cdots & 1 & 1 & {1 - m} \\[5pt]1 & 1 & \cdots & 1 & {2 - m} & 0 \\[5pt]1 & 1 & \cdots & {3 - m} & 0 & 0 \\[5pt]\vdots & \vdots & {} & \vdots & \vdots & \vdots \\[5pt]1 & { - 1} & \cdots & 0 & 0 & 0\end{array}} \right).$ | (8) |
其中*表示Hadamard乘积,
为了证明本文提出的聚合函数的有效性,本文通过实验的方法来测试该聚合函数的健壮性、稳定性和性能效果.
3.1 实验设置下面的讨论和实验均在标准MOEA/D下进行,即第1章介绍的MOEA/D算法框架. 标准MOEA/D把问题(1)分解为
本文比较了5个算法的性能表现,前4个是标准MOEA/D算法,分别使用了切比雪夫、PBI、逆PBI和双曲线方法4个聚合函数[7, 13],其中邻居数目统一为
在测试函数方面,测试了离散多目标背包问题(MOKP)[14]和连续多目标优化问题DTLZ系列[15]. DTLZ的问题定义在Deb的文献[15]上有详细介绍,此处不做说明.
MOKP问题若作为最小化问题进行求解,则可以定义为优化以下式子:
| $\left\{ {\rm{ }}\begin{array}{*{20}{l}}{{\rm{min}}}\;{{{f'}_j}({{x}}) = \displaystyle\sum\nolimits_{i = 1}^n {{{{p}}_{i,j}}} - \displaystyle\sum\nolimits_{i = 1}^n {{{{x}}_i} {{{p}}_{i,j}},} }\\[10pt]{{\rm{s.t.}}}\quad{{g_j}({{x}}) = \displaystyle\sum\nolimits_{i = 1}^n {{{{x}}_i} \cdot {{{w}}_{i,j}}} \leqslant {{{c}}_j}.}\end{array} \right.$ | (9) |
其中
为了测试该方法的可用性及可扩展性,本文不仅比较了多目标优化问题的算法表现性能,也测试了算法在超多目标优化问题上的性能(MaOPs),即令
对于MOKP问题,决策变量(自变量)数目
| 表 1 种群规模设置 Table 1 The setting of population size |
| 表 2 不同算法在求解DTLZ系列上的平均HV测量值及性能比较 Table 2 The average HV measurement and performance comparison among the different algorithms in DTLZs |
为了估计搜索性能,本实验使用超体积度量(HV)作为求解的评价标准[17]. 令
| ${\rm{HV}}(A,{{r}}) = {\rm{volume}}(\bigcup\limits_{f \in A} {[{f_1},{r_1}] \times \cdots \times [{f_m},{r_m}]} ).$ | (10) |
式(10)使用QHV算法[18]计算,HV度量值同时刻画了一个解集合的散布性和收敛性,是目前多目标优化算法评价标准用得最多的指标之一,HV测量值大意味着该解集合有更好的效果. 在实验中本实验使用
本文对上述的5个算法进行了性能比较,其中HYB方法本文令参数设置为最优参数
|
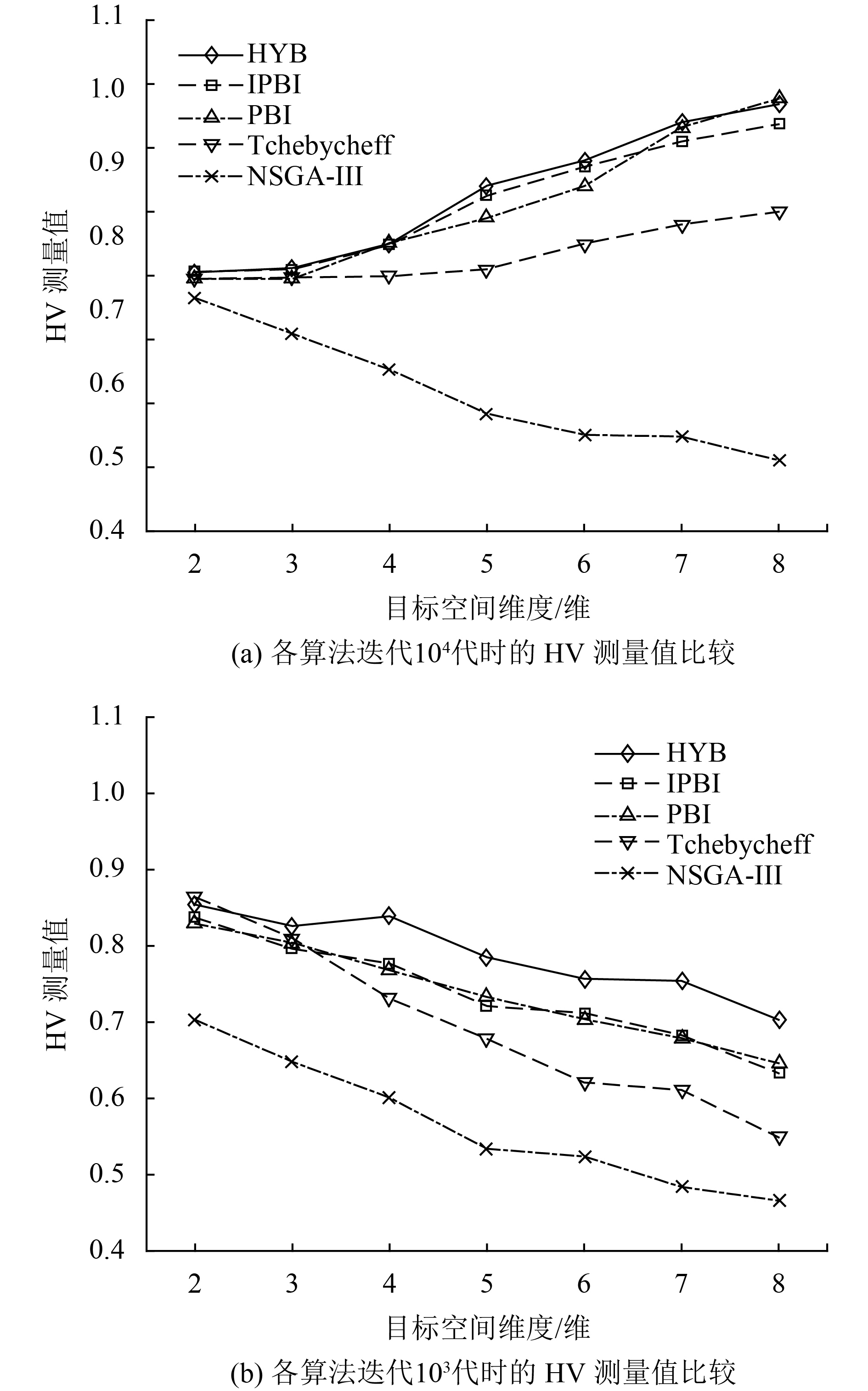
图 3 当目标数(维度)变化时,各算法求解MOKPs问题的HV测量值比较 Figure 3 The HV measurement comparison of each algorithm in MOKPs when objectives (dimensions) change |
图3(a)为MOKPs问题迭代
由于HYB方法加大了个体的被支配区域(图2(b)中曲线的左下方部分变大),因此该方法其中一个优势在于加快了收敛速度,图3(b)展示了当迭代
由于单纯比较HV测量值是片面而不可信的,所以除了比较HV 测量值外,本实验还比较了部分算法的IGD测量值[3, 19],结果如图4所示. 与HV度量相似, IGD度量也是一个综合性的评价指标,同时评价了种群的散布性和收敛性.
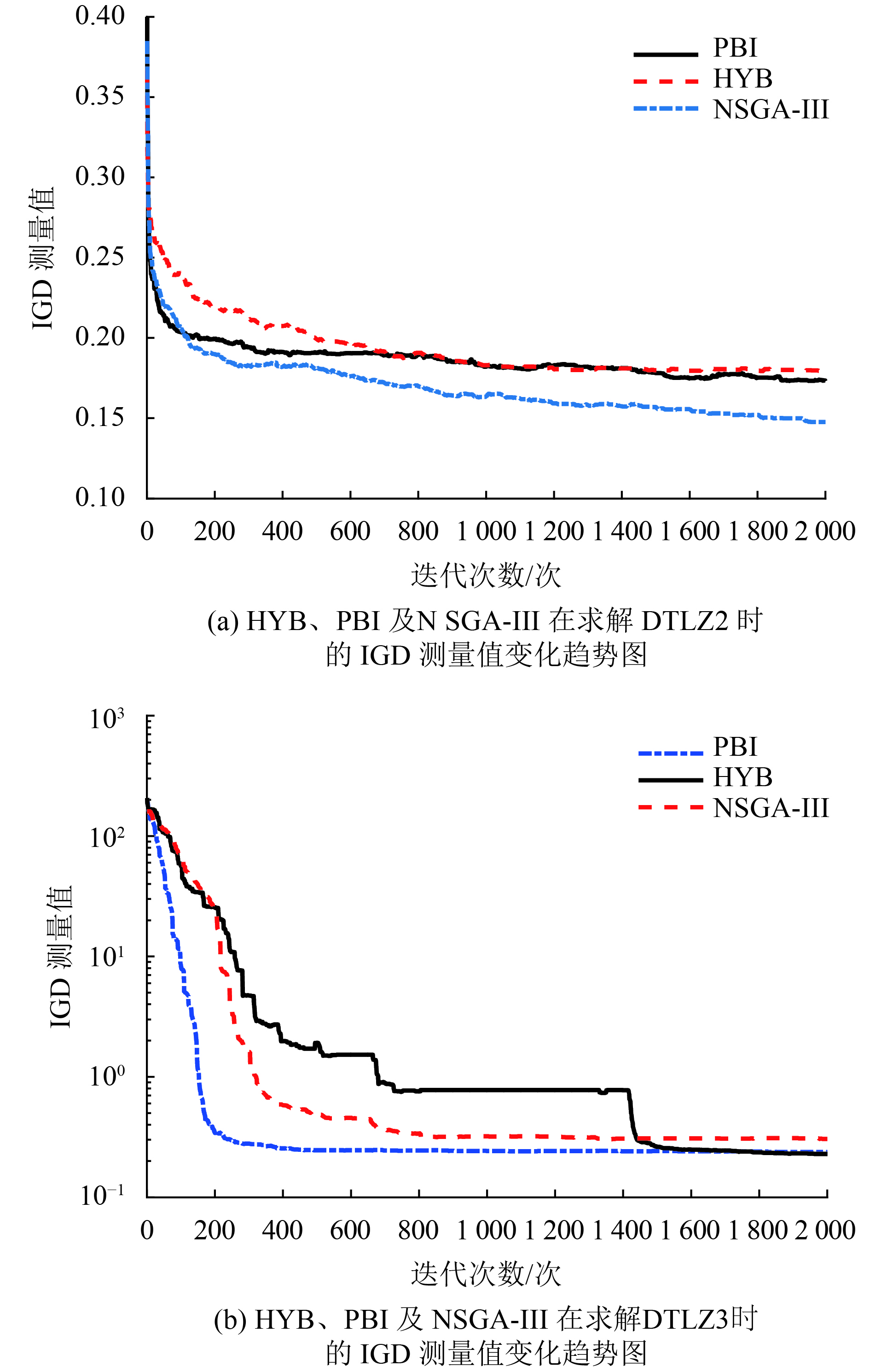
下面讨论算法在DTLZ系列的表现性能,与MOKPs问题相反,对于该系列问题NSGA-III算法是占有一定优势的,无论在HV测量上还是IGD测量上,具体的分析可以参考Deb的文章[3],做此实验对比主要是证明HYB方法在不同问题上均有稳定求解效果,且效果不差. 图4展示了NSGA-III、PBI和HYB方法随迭代的代数变化,对应的IGD对比图,这里本文只展示了高维的IGD测量值比较,
|
图 4 各算法求解DTLZ问题的IGD测量值变化,m=8 Figure 4 The IGD measurement change of each algorithm in DTLZ when m=8 |
DTLZ系列的HV测量值在表2中展示,其中加粗字体的数值表示一行中获得最好表现性能的测量数值. NSGA-III依然占有一定优势,而HYB、PBI和IPBI同样的性能相当,与IGD有相似的结论,在DTLZ2问题上PBI和IPBI方法比HYB方法要好上一些. DTLZ1和DTLZ3问题则相反,HYB方法要比两者效果好,原因同上. 尽管这一系列的实验表现总体上没有NSGA-III好,但HYB方法也具有不错的求解效果,效果比PBI方法要好.
综上所述,在面对不同的MOPs或MaOPs问题上,HYB方法都是具有稳定且不错的求解效果,尽管一些问题上没有达到最佳求解结果,但差别不会很大. HYB方法在求解过程中更强调的是收敛性,尤其局部搜索,HYB 方法的一个优势是该方法具有比其他方法更快的收敛速度. 但同样的,在散布性方面HYB方法要较PBI和IPBI方法差一些,因为受其函数曲线弯曲部分的影响.
4 结论本文提出了一种新的聚合函数,该聚合函数是对目前存在的聚合函数的一种泛化及光滑化操作,其个体函数值的等高线是一条二次曲线,并给出了该函数的一种推导过程,从等高线出发,推导出其函数表达式. 该聚合函数有两个参数,本文给出了参数适当的范围及建议的参数值,同时通过实验比较了它与其他算法的性能,使用该聚合函数稳定有效,且种群在收敛速度上有一定提高. 在接下来的工作,会对聚合函数进行更苛刻严谨的测试,并分析其劣势,从理论上证明该聚合函数比目前存在的其他聚合函数具有更优的等高线形状. 另外,将会深入研究自适应参数与方案,做出不依赖于参数的聚合函数方法.
| [1] | SRINIVAS N, DEB K. Multiobjective optimization using nondominated sorting in genetic algorithms[J]. Evolutionary Computation, 1994, 2(3): 221-248. DOI: 10.1162/evco.1994.2.3.221. |
| [2] | ZITZLER E, LAUMANNS M, THIELE L. SPEA2: improving the performance of the strength pareto evolutionary algorithm[J]. Lecture Notes in Computer Science, 2004, 3242(4): 742-751. |
| [3] | DEB K, JAIN H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: solving problems with box constraints[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(4): 577-601. DOI: 10.1109/TEVC.2013.2281535. |
| [4] | ZITZLER E, KÜNZLI S. Indicator-based selection in multiobjective search[J]. Lecture Notes in Computer Science, 2004, 3242: 832-842. DOI: 10.1007/b100601. |
| [5] | BEUME N, NAUJOKS B, EMMERICH M. SMS-EMOA: multiobjective selection based on dominated hypervolume[J]. European Journal of Operational Research, 2007, 181(3): 1653-1669. DOI: 10.1016/j.ejor.2006.08.008. |
| [6] | BADER J, ZITZLER E. HypE: an algorithm for fast hypervolume-based many-objective optimization[J]. Evolutionary Computation, 2011, 19(1): 45. DOI: 10.1162/EVCO_a_00009. |
| [7] | ZHANG Q, LI H. MOEA/D: a multiobjective evolutionary algorithm based on decomposition[J]. IEEE Trans Evol Comput, 2007, 11(6): 712-731. DOI: 10.1109/TEVC.2007.892759. |
| [8] | LI H, ZHANG Q. Multiobjective optimization problems with complicated Pareto sets, MOEA/D and NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(2): 284-302. DOI: 10.1109/TEVC.2008.925798. |
| [9] | CHENG R, JIN Y, OLHOFER M, et al. A reference vector guided evolutionary algorithm for many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2016, 20(5): 773-791. DOI: 10.1109/TEVC.2016.2519378. |
| [10] | QI Y, MA X, LIU F, et al. MOEA/D with adaptive weight adjustmen[J]. Evolutionary Computation, 2014, 22(2): 231-264. DOI: 10.1162/EVCO_a_00109. |
| [11] | ZHOU A, ZHANG Q. Are all the subproblems equally important? resource allocation in decomposition-based multiobjective evolutionary algorithms[J]. IEEE Transactions on Evolutionary Computation, 2016, 20(1): 52-64. DOI: 10.1109/TEVC.2015.2424251. |
| [12] | TRIVEDI A, SRINIVASAN D, SANYAL K, et al. A survey of multiobjective evolutionary algorithms based on decomposition[J]. IEEE Transactions on Evolutionary Computation, 2017, 21(3): 440-462. |
| [13] | SATO H. Analysis of inverted PBI and comparison with other scalarizing functions in decomposition based MOEAs[J]. Journal of Heuristics, 2015, 21(6): 819-849. DOI: 10.1007/s10732-015-9301-6. |
| [14] | ISHIBUCHI H, AKEDO N, NOJIMA Y. A study on the specification of a scalarizing function in MOEA/D for many-objective knapsack problems[J]. Proc of Learning and Intelligent Optimization 7 (LION 7), 2013, 7997: 231-246. DOI: 10.1007/978-3-642-44973-4. |
| [15] | DEB K, THIELE L, LAUMANNS M.Scalable test problems for evolutionary multiobjective optimization[C]// Evolutionary Multiobjective Optimization. London: Springer London Ltd, 2005:105-145. |
| [16] | LI K, DEB K, ZHANG Q, et al. An evolutionary many-objective optimization algorithm based on dominance and decomposition[J]. IEEE Transactions on Evolutionary Computation, 2015, 19(5): 694-716. DOI: 10.1109/TEVC.2014.2373386. |
| [17] | ZITZLER E, THIELE L. Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach[J]. IEEE Transactions on Evolutionary Computation, 1999, 3(4): 257-271. DOI: 10.1109/4235.797969. |
| [18] | RUSSO L M S, FRANCISCO A P. Quick hypervolume[J]. IEEE Transactions on Evolutionary Computation, 2012, 18(4): 481-502. |
| [19] | ZITZLER E, THIELE L, LAUMANNS M, et al. Performance assessment of multiobjective optimizers: an analysis and review[J]. IEEE Transactions on Evolutionary Computation, 2003, 7(2): 117-132. DOI: 10.1109/TEVC.2003.810758. |
 2018, Vol. 35
2018, Vol. 35

