超磁致伸缩材料机–磁耦合理论模型的研究,逐渐成为国内外专家学者研究的焦点[1]. 在磁性材料能量采集装置运行过程中,受到预应力和外加磁场的两重载荷耦合作用,两个载荷耦合场的数学模型构成超磁致伸缩材料的本构关系[2]. 机–磁耦合场间的作用互相叠加,使得针对超磁致伸缩材料的理论模型的研究,难度大大增加. 在现有的工程应用中,通常采用近似线性的压磁本构关系来简化超磁致伸缩材料的理论模型,来研究超磁致伸缩材料的机–磁耦合关系[3]. 其中,Delince等[4]将磁致伸缩材料的应变能量引入机械能量方程中,建立二维线性静态有限元模型;Benatarl[5]通过矢量磁位求解的方法,提出应力和磁场之间的线性本构关系模型;Karim[6]等通过修正机械胡克定律,提出磁致伸缩材料的线性有限元静态三维模型;贺西平[7]等对磁致伸缩换能器中的动力学方程进行研究,提出有限元磁致伸缩材料线性模型. 国内外所建立的磁性材料的线性本构关系能够简单描述机–磁间的耦合关系,计算速度快,适用范围广,但只能应用在低精度的工程中描述超磁致伸缩材料内机–磁间的内在能量转换关系[8]. 目前已提出的超磁致伸缩材料模型只能描述有限线性区域内的磁性材料本构关系,并不能透彻地反映磁性材料中的非线性机–磁耦合关系,因此未能满足较高精度工程计算的需要.
磁材料是国民经济的一种不可缺少的重要功能材料[9]. 根据磁性材料的物理特性,磁性材料的磁致伸缩效应具有正、反两向效应[10]. 磁性材料在较低的外加磁场作用下将产生较强的磁致伸缩效应,此时,磁性材料的长度或体积均可改变,可作为智能驱动材料[11]. 在外部磁场或应力作用下,其磁畴结构的运动方向和转变方式,直接决定了磁性材料的宏观磁性能[12]. 因此,通过描述磁畴结构的动态变化,可对磁畴及磁性材料的磁化性能进行分析,为磁性材料的应用提供理论依据. 所以磁畴的图像观测以及磁畴磁化性能的研究对磁性材料的应用十分重要.
根据以往实验测量表明,单晶铁磁材料中的任何宏观可观测的磁化和磁致伸缩状态都是其磁畴和原子轨道配置的直接后果. 磁畴和原子轨道结构反过来强烈依赖于外部变量,例如应力和施加磁场的强度和方向以及内部材料的各向异性. 这表明,我们可以先描述材料中固定量的磁化强度在所有方向之间的分布,然后通过以下方式获得特定方向上的磁化强度的值,从而有效描述材料的磁畴偏转行为.
本文取磁性材料内单畴颗粒作为研究磁致伸缩磁畴偏转模型的对象,应力和外加磁场载荷的共同作用,将使得单畴颗粒内磁化强度M发生角度的偏转和跃迁,进而影响磁性材料的磁化性能. 求解超磁致伸缩材料内部的非线性单畴颗粒自由能方程极值,观察分析超磁致伸缩材料内磁畴角度偏转的规律,进而描述材料的磁化及机–磁耦合特性,获得外加磁场和应力的最佳取值,即可计算出磁性材料产生的磁化强度,为步行能量采集器提供更加精确的重要参数[13].
1 机磁耦合特性 1.1 坐标变换在外加应力σ和磁场H的共同作用下,磁晶中产生的各向异性能Ek,外加应力引起的各向异性能Eσ和外加磁场所产生的各向异性能EH都会影响磁畴角度的偏转和跃迁[14]. 求解材料内部的非线性单畴颗粒自由能方程组极值,可用于描述超磁致伸缩材料内磁畴角度偏转的规律,但由于求解过程复杂、计算量大,且有效极值点的判定困难,本文采取极坐标变换来简化非线性自由能方程极值的求解. 其中,原始坐标系X以
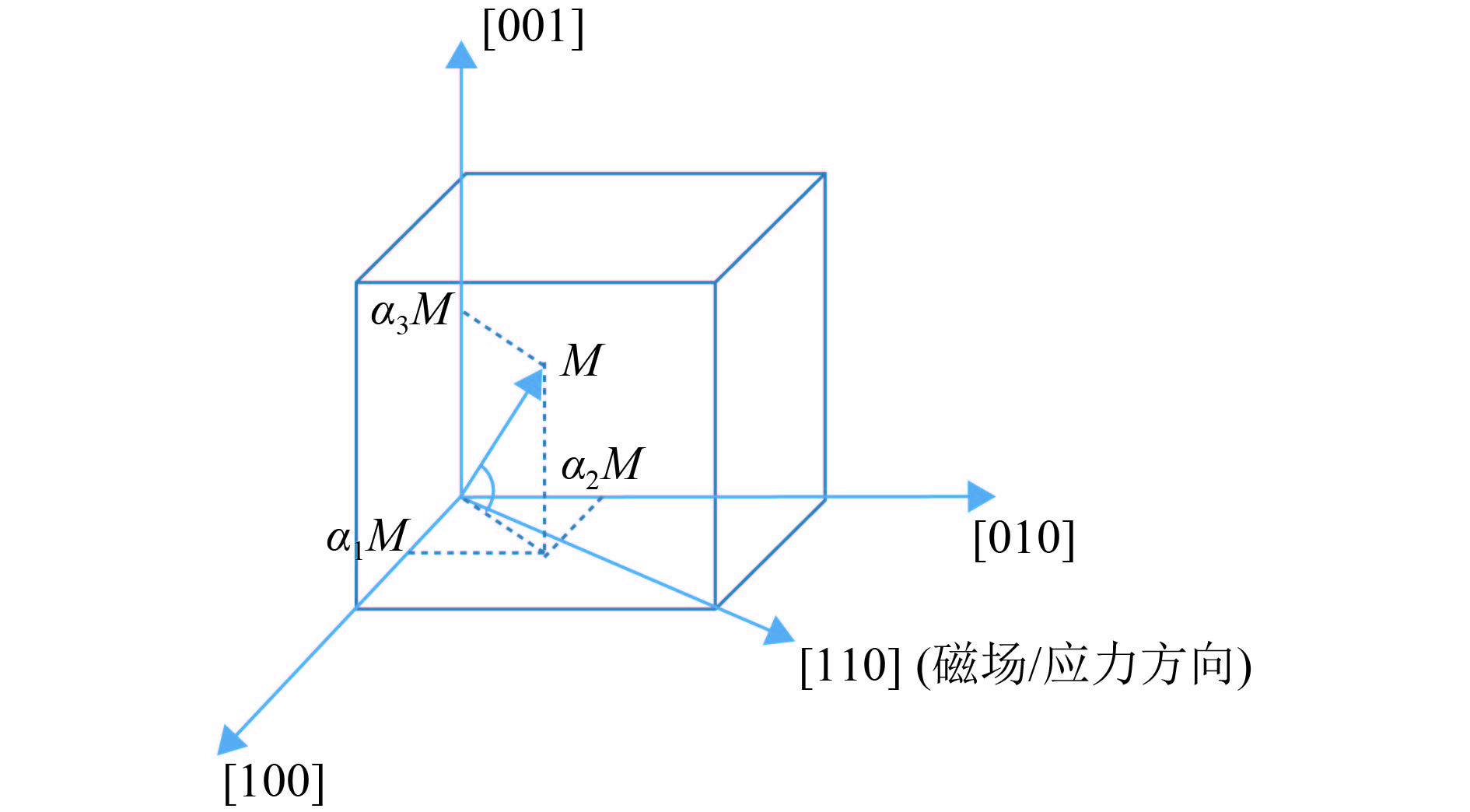
|
图 1 超磁致伸缩晶体颗粒中磁畴矢量关系示意图 Figure 1 Schematic diagram of the magnetic domain vector in the giant magnetostrictive crystal particles |
单畴颗粒的自由能可表示为
| $\begin{split}E = & {K_1}(\alpha _1^2\alpha _2^2 + \alpha _2^2\alpha _3^2 + \alpha _1^2\alpha _3^2) + {K_2}(\alpha _1^2\alpha _2^2\alpha _3^2) - \\ &\frac{3}{2}{\lambda _{100}}\sigma (\alpha _1^2\beta _1^2 + \alpha _2^2\beta _2^2 + \alpha _3^2\beta _3^2) - \\ &3{\lambda _{111}}\sigma ({\alpha _1}{\alpha _2}{\beta _1}{\beta _2} + {\alpha _2}{\alpha _3}{\beta _2}{\beta _3} + {\alpha _1}{\alpha _3}{\beta _1}{\beta _3}) - \\ &{\mu _0}{M_s}H({\alpha _1}{\beta _1} + {\alpha _2}{\beta _2} + {\alpha _3}{\beta _3}).\end{split}$ | (1) |
通过以下两种坐标变换步骤简化非线性自由能方程:
1) 三角坐标变极坐标,坐标系依旧为X:
| $\left( \begin{array}{l}{\beta _1}\\[4pt]{\beta _2}\\[4pt]{\beta _3}\end{array} \right) = \left( \begin{array}{l}{\alpha _1}\\[4pt]{\alpha _2}\\[4pt]{\alpha _3}\end{array} \right) = \left( \begin{array}{l}\sin {\theta _n} \cos {\varphi _n}\\[4pt]\sin {\theta _n} \sin {\varphi _n}\\[4pt]\cos {\theta _n}\end{array} \right).$ | (2) |
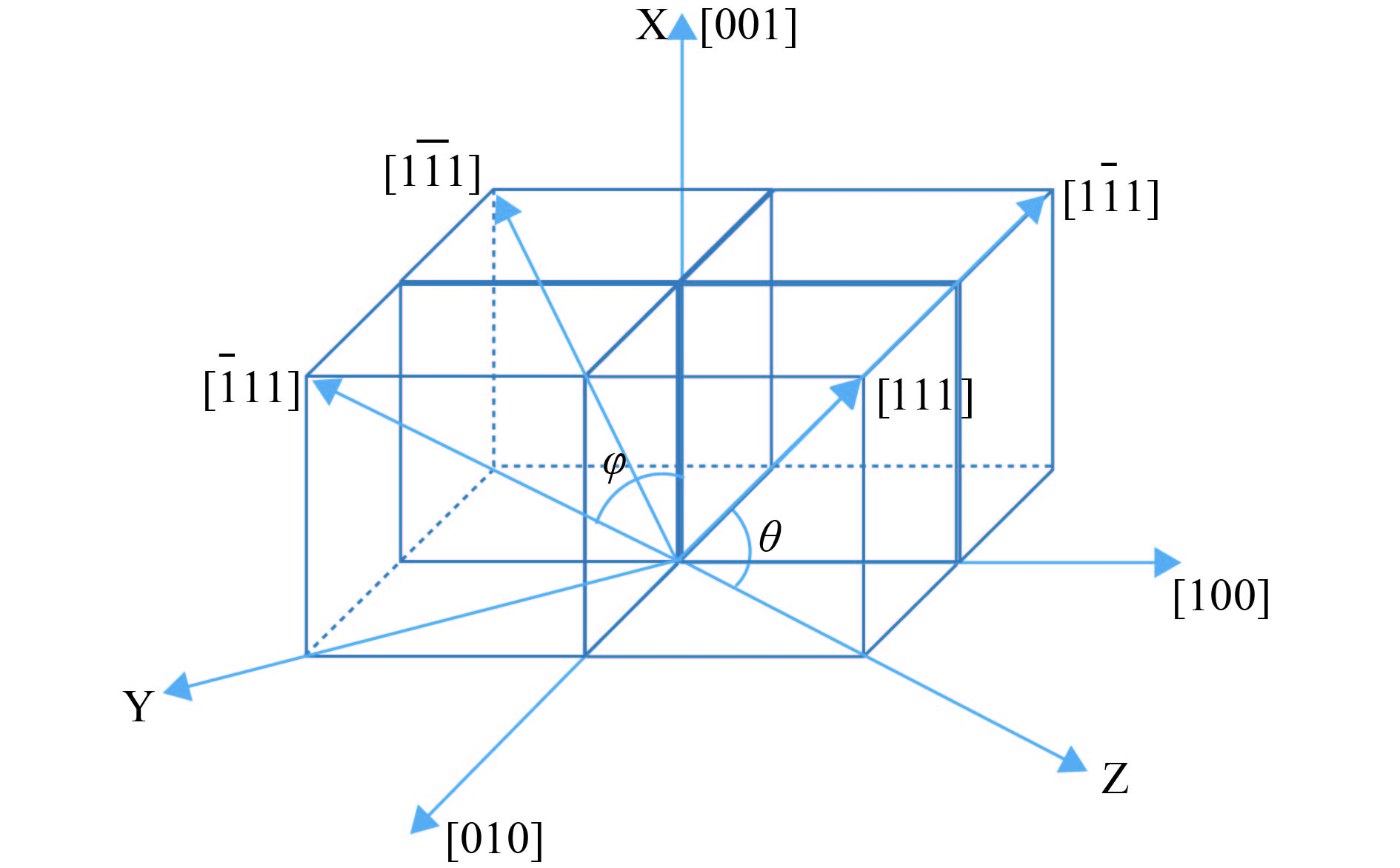
2) 三坐标变换:以[110]方向为z轴,取垂直于[110]方向的平面[110]建立
| $\begin{split}&\left( \begin{array}{l}{\beta _1}\\[4pt]{\beta _2}\\[4pt]{\beta _3}\end{array} \right) = \left( \begin{array}{l}{\alpha _1}\\[4pt]{\alpha _2}\\[4pt]{\alpha _3}\end{array} \right) = \\&\left( {\begin{array}{*{20}{c}}0&0&1\\[4pt]{\cos - \displaystyle\frac{{\rm{{\text{π}} }}}{{\rm{4}}}}&{\sin - \displaystyle\frac{{\rm{{\text{π}} }}}{{\rm{4}}}}&0\\[10pt]{ - \sin - \displaystyle\frac{{\rm{{\text{π}} }}}{{\rm{4}}}}&{\cos - \displaystyle\frac{{\rm{{\text{π}} }}}{{\rm{4}}}}&0\end{array}} \right) \times \left( \begin{array}{l}\sin {\theta _n} \cos {\varphi _n}\\[4pt]\sin {\theta _n} \sin {\varphi _n}\\[4pt]\cos {\theta _n}\end{array} \right) = \\&\left( {\begin{array}{*{20}{c}}0&0&1\\[4pt]{\displaystyle\frac{{\sqrt 2 }}{2}}&{ - \displaystyle\frac{{\sqrt 2 }}{2}}&0\\[10pt]{\displaystyle\frac{{\sqrt 2 }}{2}}&{\displaystyle\frac{{\sqrt 2 }}{2}}&0\end{array}} \right) \times \left( \begin{array}{l}\sin {\theta _n} \cos {\varphi _n}\\[4pt]\sin {\theta _n} \sin {\varphi _n}\\[4pt]\cos {\theta _n}\end{array} \right).\end{split}$ | (3) |
外加磁场所产生的各向异性能Ek,预应力引起的各向异性能Eσ和磁晶中产生的各向异性能EH都会影响磁畴角度的偏转. 较大的磁晶各向异性能料是产生磁致伸缩效应的关键,经过两次坐标变换之后化简各能量的具体表达式[17]:
| $\begin{aligned}{E_k} = & {K_1}({\cos ^2}[{\theta _n}](\frac{{\sqrt 2 }}{2}\sin [{\theta _n}]\cos [{\varphi _n}] - \\ &\frac{{\sqrt 2 }}{2}\sin [{\theta _n}]\sin [{\varphi _n}]{)^2} + \left( {\frac{{\sqrt 2 }}{2}\sin [{\theta _n}]\cos [{\varphi _n}] - } \right.\\ &{\left. {\frac{{\sqrt 2 }}{2}\sin [{\theta _n}]\sin [{\varphi _n}]} \right)^2} \times \left( {\frac{{\sqrt 2 }}{2}\sin [{\theta _n}]\cos [{\varphi _n}] + } \right.\\ &{\left. {\frac{{\sqrt 2 }}{2}\sin [{\theta _n}]\sin [{\varphi _n}]} \right)^2} + {\cos ^2}[{\theta _n}]\left( {\frac{{\sqrt 2 }}{2}\sin [{\theta _n}]\cos [{\varphi _n}] + } \right.\\ &{\left. {\frac{{\sqrt 2 }}{2}\sin [{\theta _n}]\sin [{\varphi _n}]{)^2}} \right)^2} + {K_2}\left( {{{\cos }^2}[{\theta _n}]} \right.\times\\ &{\left( {\frac{{\sqrt 2 }}{2}\sin [{\theta _n}]\cos [{\varphi _n}] - \frac{{\sqrt 2 }}{2}\sin [{\theta _n}]\sin [{\varphi _n}]} \right)^2} \times \\ &\left. {{{\left( {\frac{{\sqrt 2 }}{2}\sin [{\theta _n}]\cos [{\varphi _n}] + \frac{{\sqrt 2 }}{2}\sin [{\theta _n}]\sin [{\varphi _n}]} \right)}^2}} \right).\quad\quad (4)\end{aligned}$ |
磁晶中所产生的各向异性能是由每单位体积内的磁畴,磁化旋转离开晶体内部固有方向时释放的能量,K1和K2为磁晶中所产生的各向异性常数.
| $\begin{split}{E_\sigma } = & - \frac{3}{2}{\lambda _{100}}\sigma (\frac{{\sqrt 2 }}{2}\sin [{\theta _n}]\cos [{\varphi _n}] + \\ &\frac{{\sqrt 2 }}{2}\sin [{\theta _n}]\sin [{\varphi _n}]{)^2}.\end{split}$ | (5) |
预应力所引起的各向异性能由所施加的应力σ与应变的相互作用产生.
| $\begin{split}{E_H} = & - {\mu _0}{M_s}H(\frac{{\sqrt 2 }}{2}\sin [{\theta _n}]\cos [{\varphi _n}] + \\ &\frac{{\sqrt 2 }}{2}\sin [{\theta _n}]\sin [{\varphi _n}]).\end{split}$ | (6) |
磁场各向异性能等于磁场的强度H、饱和磁化强度MS以及磁化方向和施加的磁场方向之间角度的乘积,当磁化方向与施加磁场垂直时,磁化强度为零,当磁化方向与施加磁场平行时,磁化强度可取得最大值.
根据一组典型的棒状Terfenol-D材料基本参数取值进行计算[19]. 饱和磁化强度Ms取值0.765 A/m,磁晶各向异性常数K1取值–60 000 J/m3,磁晶各向异性常数K2取值–200 000 J/m3,材料在[100]方向的磁致伸缩系数λ100取值50×10–6.
2 磁畴偏转规律超磁致伸缩材料的磁化特性十分复杂,可采用唯象理论来解释磁畴随外加磁场偏转变化的情况[20]. 基于磁畴偏转机理的本构理论[21-25],一部分磁畴的自发磁化方向与外加磁场方向形成小角度[26],当磁性材料处于外部施加的磁场中时,随着施加的外磁场增大,这些磁畴的体积也不断增大,并且磁畴的磁化方向逐渐向外部施加的磁场方向偏转[27]. 其余部分磁畴的自发磁化方向与外部施加的磁场方向形成大角度,相应的该方向上的磁畴体积则随之减小,此时磁致伸缩材料对外反映出宏观磁性[28]. 当外部施加的磁场增大到一定的高度时,超磁致伸缩材料内部磁畴排列整齐,几乎均与外部施加的磁场方向平行,此时,超磁致伸缩材料便到了饱和磁致伸缩状态[29-30]. 当应力σ=0,磁场H=0时,云图中有8个极小值,对应在三角坐标上的最小值方向分别为:

|
图 2 磁化能二维云图 Figure 2 Magnetization energy two-dimensional cloud |
|
图 3 磁畴方向示意图 Figure 3 Schematic diagram of magnetic domain |
施加外加磁场,磁场增加到H=10 000 A/m,8个极小值随着磁场的增加而旋转,逐渐靠近θ=0的方向(θ为所取方向和Z轴的夹角),如图4(a)所示;当外部施加的磁场达到H=50 000 A/m,

|
图 4 磁场作用下磁畴变化二维云图 Figure 4 Two-dimensional cloud diagram of magnetic field change under magnetic field |
观察图4可知,磁畴角度随着磁场增加,将逐渐偏转、跃迁至[110]方向,但并不呈线性关系, 当应力σ=0 MPa时,施加外加磁场,起初磁致伸缩材料的磁化强度随着磁场增加,直到磁场增加到H=80 000~100 000 A/m左右,磁化强度的增长程度趋于平缓,单轴机械应力下的磁化曲线如图5所示. 8个极小值随着外部施加的磁场数值的增大逐渐向θ=0的方向偏移,即磁畴方向逐渐向磁化方向偏转,不断增大外部施加的磁场,直到每个磁畴中个单元磁矩都沿外磁场方向排列整齐,达到饱和磁致伸缩状态,磁性材料对外产生最大的磁化强度,产生磁致伸缩效应[31]. 因此考虑到效率的提升,外加磁场的取值应在H=80 000~100 000 A/m范围内选择.
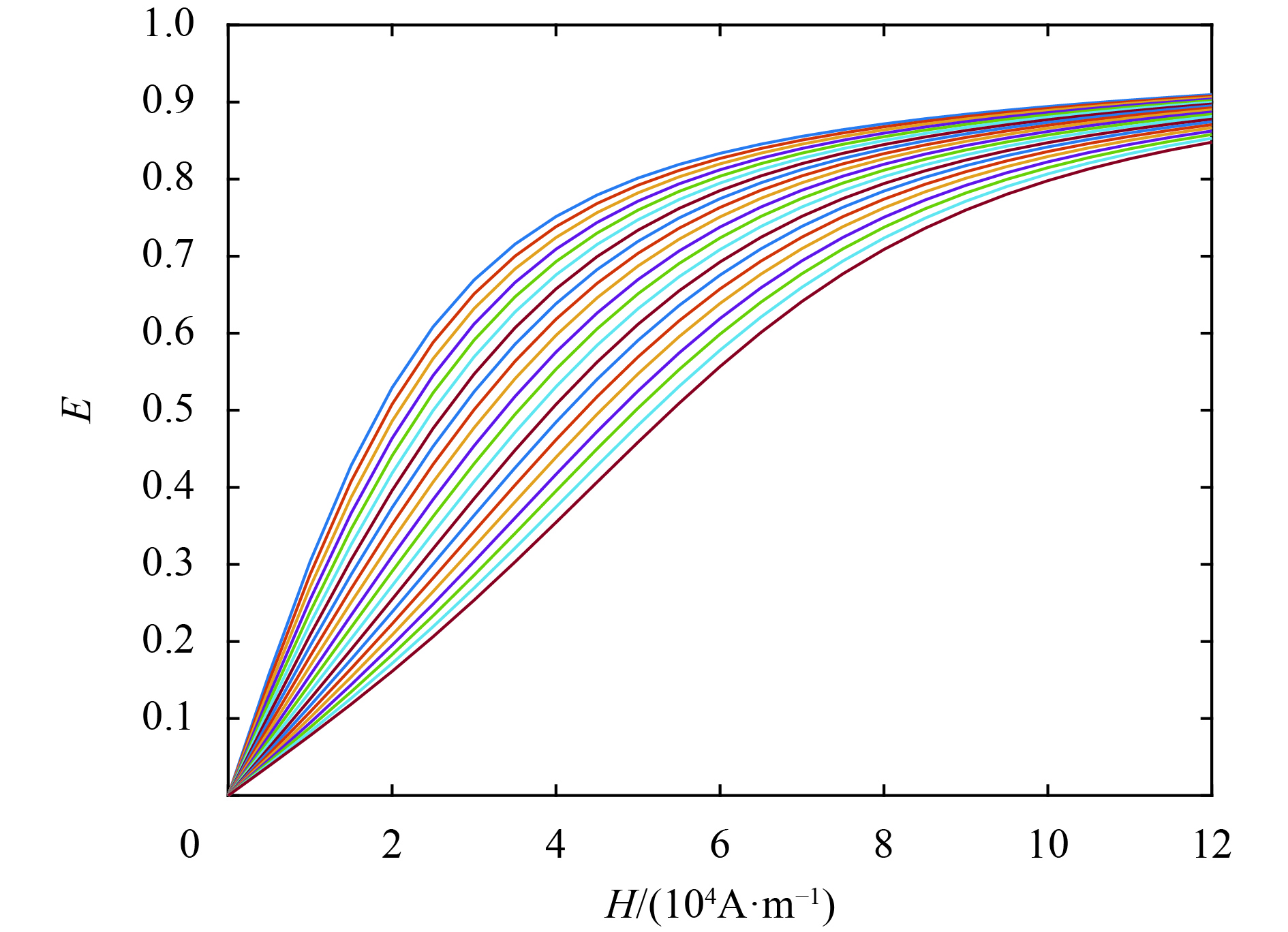
|
图 5 单轴机械应力下的磁化曲线 Figure 5 Magnetization curves under uniaxial mechanical stress |
当外加磁场H=0 A/m时,应力增加到σ= –1 MPa,有利于
由图6显示,当应力不断增大,曲线在极小值
在超磁致伸缩材料的磁弹性效应中,磁畴的偏转相对较为复杂,外部施加的磁场,以及预加压应力使得磁弹性过程中磁畴的偏转更加的复杂,磁弹性过程中存在压应力和磁场间的相互作用[32]. 从能量转换的角度来看,应力各向异性能不利于超磁致伸缩材料磁化的进行,使超磁致伸缩材料的磁化更加困难,所以应力的取值不应过大. 磁性材料对外产生的磁化强度可表示为
| $M = {M_s}\cos {\theta _n}.$ | (7) |
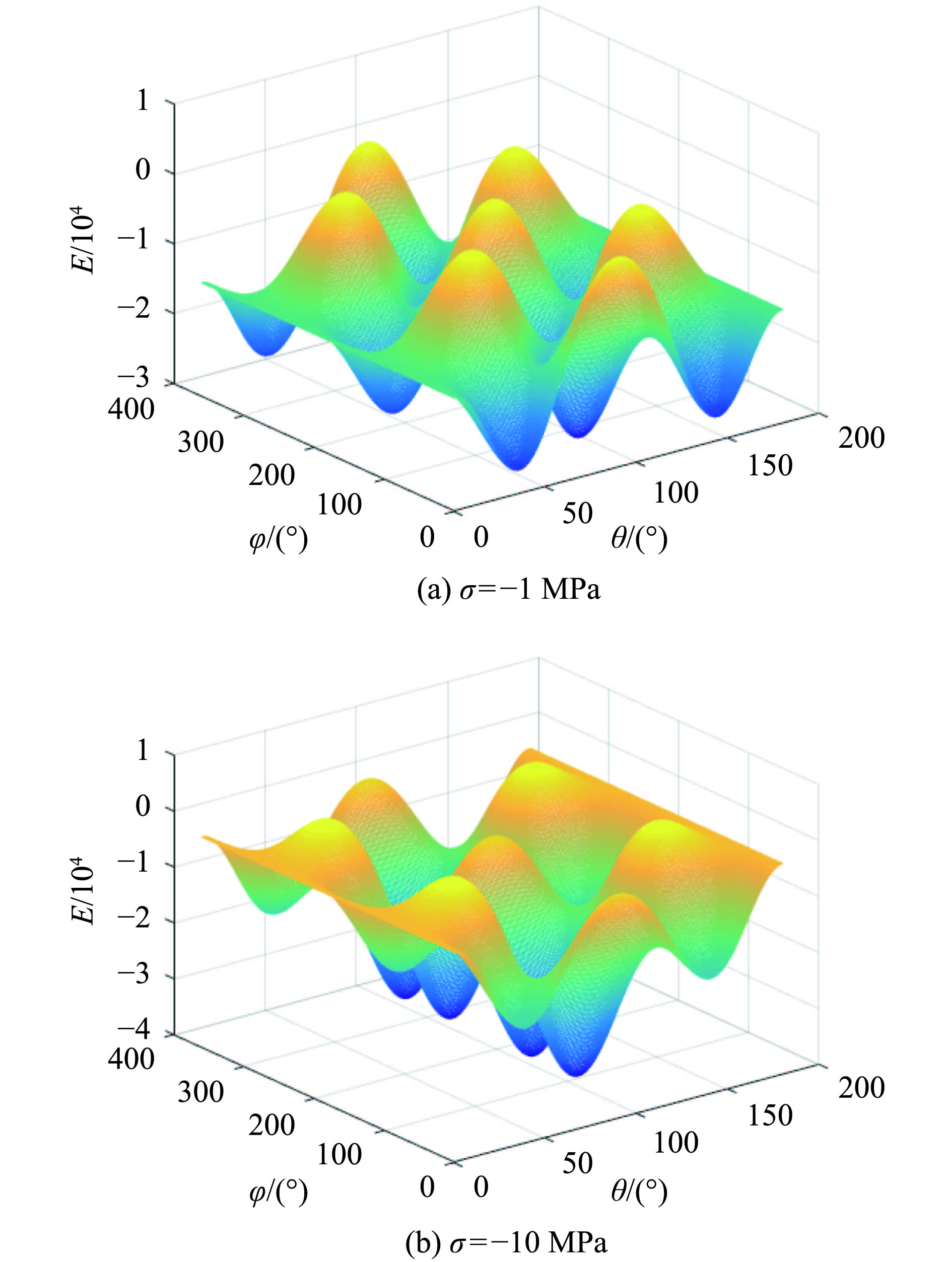
|
图 6 应力作用下磁畴变化图 Figure 6 Variation of magnetic domain under stress |
为得到较大的磁化强度,以及较高的效率. 取磁场H=100 000 A/m,应力
| $M = \frac{1}{2}{M_s}(\cos {\theta _1} + \cos {\theta _2}) = 0.73\;{\rm{A/m}}{\rm{.}}$ |

|
图 7 磁场H=100 000 A/m,应力σ=-5 Mpa下的磁畴方向云图 Figure 7 Magnetic field H=100 000 A/m, stress σ=-5 Mpa under the magnetic domain direction cloud |
本文主要针对磁化角度θn进行研究,提出以上直观、简化的数值分析方法,进行磁性材料磁畴偏转角度的求解,应力和磁场双重载荷作用下,磁畴偏转角度的计算过程被简化. 求解材料内部非线性单畴颗粒自由能方程的极值,分析各向异性能以及应力和磁场双重载荷能量对磁畴角度偏转的影响,描述在不同磁场和应力双重载荷作用下的磁性材料磁畴角度偏转以及跃迁特性,结合磁畴偏转角度和路径,分析磁畴角度偏转的规律及压磁和磁弹性效应,直观透彻地解释了磁性材料的磁化特性.
(1) 压磁效应对材料中
(2) 磁性材料产生磁致伸缩效应的关键即为对磁畴在压磁效应以及磁弹性效应中的偏转和跃迁的分析描述.
| [1] |
方岱宁, 万永平, 冯雪, 等. 功能铁磁材料的变形与断裂的研究进展[J].
力学进展, 2006(4): 485-506.
FANG D N, WAN Y P, FENG X, et al. Research progress on deformation and fracture of functional ferromagnetic materials[J]. Advances in Mechanics, 2006(4): 485-506. DOI: 10.6052/1000-0992-2006-4-J2004-139. |
| [2] |
杨勇, 李琳. 磁致伸缩作动器的电–磁–机耦合动力特性[J].
应用力学学报, 2009, 26(3): 558-563+631.
YANG Y, LI L. Electric-magnetic-mechanical coupling dynamic characteristics of magnetostrictive actuator[J]. Chinese Journal of Applied Mechanics, 2009, 26(3): 558-563+631. |
| [3] |
闫荣格, 王博文, 曹淑瑛, 等. 超磁致伸缩致动器的磁–机械强耦合模型[J].
中国电机工程学报, 2003(7): 107-111.
YAN R G, WANG B W, CAO S Y, et al. Magnetic-mechanical strong coupling model of giant magnetostrictive actuator[J]. Proceeding of the CSEE, 2003(7): 107-111. |
| [4] | DELINCE F, GENON A, GILLARD J M. Numerical computation of the Magnetostrictive effect in ferromagnetic materials[J]. Journal of Applied Physics, 1991, 69(72): 5794-5710. |
| [5] | BENATAR J G, FLATAU A B. FEM implementation of a magnetostrictive transducer[J]. Smart Structures and Materials, 2005, 57(64): 482-493. |
| [6] | KARIM A, MONDHER B. 3D FEM of magnetostriction phenomena using coupled constitutive laws[J]. International Journal of Applied Electromagnetics and Mechanics, 2004, 19(39): 367-371. |
| [7] |
贺西平, 孙进才, 李斌. 低频大功率稀土磁致伸缩弯张换能器的有限元设计理论及实验研究: Ⅰ. 理论部分[J].
声学学报, 2000(6): 521-527.
HE X P, SUN J C, LI B. Finite element design theory and experimental research on low frequency high power rare earth magnetostrictive bending transducer: Ⅰ. Theoretical part[J]. Journal of Acoustics, 2000(6): 521-527. |
| [8] |
王博文, 闫荣格. 稀土超磁致伸缩材料、应用与器件[J].
河北工业大学学报, 2004(2): 16-22.
WANG B W, YAN R G. Rare earth giant magnetostrictive materials, applications and devices[J]. Journal of Hebei University of Technology, 2004(2): 16-22. |
| [9] |
孙泓, 何玉定, 胡社军. 两相纳米晶稀土永磁材料的研究进展[J].
广东工业大学学报, 2003, 20(4): 11-18.
SUN H, HE Y D, HU S J. Research progress on two-phase nanocrystalline rare earth permanent magnetic materials[J]. Guangdong University of Technology, 2003, 20(4): 11-18. |
| [10] |
刘敬华, 张天丽, 王敬民, 等. 巨磁致伸缩材料及应用研究进展[J].
中国材料进展, 2012, 31(4): 1-12.
LIU J H, ZHANG T L, WANG J M, et al. Recent advances in research on giant magnetostrictive materials and their applications[J]. Progress in Materials Research, 2012, 31(4): 1-12. |
| [11] |
陈善飞, 王遵义, 薛立新, 等. 基于磁性液体磁致伸缩的微位移驱动实验研究[J].
兵工学报, 2010, 31(3): 350-354.
CHEN S F, WANG Z Y, XUE L X, et al. Experimental study on micro-displacement based on magnetostriction of magnetic liquid[J]. Journal of Bing Eng, 2010, 31(3): 350-354. |
| [12] |
刘亚丕, 王子生, 韩宝善, 等. 磁性材料磁畴动态观测仪的研制[J].
磁性材料及器件, 2006(5): 42-45.
LIU Y P, WANG Z S, HAN B S, et al. Development of magnetic domain dynamic observer[J]. Magnetic Materials and Devices, 2006(5): 42-45. |
| [13] |
李立毅, 严柏平, 张成明. 驱动频率对超磁致伸缩致动器的损耗和温升特性的影响[J].
中国电机工程学报, 2011, 31(18): 124-129.
LI L B, YAN B P, ZHANG C M. Effect of driving frequency on loss and temperature rise of giant magnetostrictive actuator[J]. Proceeding of the CSEE, 2011, 31(18): 124-129. |
| [14] |
吴义政. 自旋转向相变中的条纹磁畴研究[J].
物理, 2005(2): 104-108.
WU Y Z. Study of stripe magnetic domain in the spin-steering phase transition[J]. Physics, 2005(2): 104-108. |
| [15] |
黎连修. 磁致伸缩和磁记忆问题研究[J].
无损检测, 2004(3): 109-112.
LI L X. Research on magnetostrictive and magnetic memory problems[J]. Nondestructive Testing, 2004(3): 109-112. |
| [16] |
刘达, 韩晓冰, 房龙. 3维直角坐标系直接转换算法的研究与实现[J].
测绘与空间地理信息, 2012, 35(5): 175-178, 182.
LIU D, HAN X B, FANG L. Research and implementation of direct conversion algorithm for 3-D cartesian coordinate system[J]. Mapping & Spatial Information, 2012, 35(5): 175-178, 182. |
| [17] | ZHANG H, ZENG D C. Magnetostriction and its inverse effect in Tb0.3Dy0.7Fe2 alloy[J]. J Appl Phys, 2010, 107(74): 123-128. |
| [18] |
余晋岳, 朱军, 周狄, 等. 微型NiFe磁性薄膜元件中Neel畴壁极性的转变过程[J].
金属学报, 2000(4): 359-363.
YU J Y, ZHU J, ZHOU D, et al. Changes in neel domain wall polarity in micro NiFe magnetic thin films[J]. Acta Metallurgica Sinica, 2000(4): 359-363. |
| [19] | MEI W, OKANE T, UMEDA T. Magnetostriction of Tb-Dy-Fe crystals[J]. J Appl Phys, 1998, 84(49): 6208-6216. |
| [20] |
李素珍. 稀土超磁致伸缩材料与器件发展现状[J].
稀土信息, 2005(4): 28-29.
LI S Z. Recent developments of rare earth giant magnetostrictive materials and devices[J]. Rare Earth Information, 2005(4): 28-29. |
| [21] | JILES D C. Introduction to Magnetism and Magnetic Materials[M]. New York: Chapman and Hall, 1991: 79-100. |
| [22] | JILES D C, ATHERTON D L. Theory of ferromagnetic hysteresis[J]. J Magn Magn Mater, 1986, 61(98): 48-60. |
| [23] | WANG B L, JIN Y M. Magnetization and magnetostriction of terfenol-D near spin reorientation boundary[J]. J Appl Phys, 2012, 111(l0): 103-108. |
| [24] | ZHANG C S, MA T Y, YAN M. Induced additional anisotropy influences on magnetostriction of giant magnetostrictive materials[J]. J Appl Phys, 2012, 112(10): 103-108. |
| [25] | MEI W, OKANE T, UMEDA T. Magnetostriction of Tb-Dy-Fe crystals[J]. J Appl Phys, 1998, 84(37): 6208-6216. |
| [26] |
刘美全, 徐章遂, 陈鹏, 等. 磁场作用下缺陷微磁生成机理研究[J].
计算机测量与控制, 2010, 18(2): 437-439.
LIU M Q, XU Z S, CHEN P, et al. Study on mechanism of defective micro-magnetism generated by magnetic field[J]. Computer Measurement and Control, 2010, 18(2): 437-439. |
| [27] |
王建国, 邵雪辉. 磁滞回线的物理机理[J].
河北建筑工程学院学报, 2001(3): 90-92.
WANG J G, SHAO X H. Physical mechanism of hysteresis loop[J]. Journal of Hebei Institute of Architecture and Civil Engineering, 2001(3): 90-92. |
| [28] |
王跃虎, 王博文, 王莉, 等. 磁致伸缩材料的磁–热–力耦合模型及其仿真分析[J].
磁性材料及器件, 2015, 46(6): 1-5.
WANG Y H, WANG B W, WANG L, et al. Magnetic-thermo-mechanical coupling model of magnetostrictive material and its simulation analysis[J]. Magnetic Materials and Devices, 2015, 46(6): 1-5. |
| [29] | OUANDELI R C. Modern Magnetic Materials Principle And Application [M]. Beijing: Chemical Industry Press. 2004: 256-258. |
| [30] |
郭雪涛, 王修勇, 孟庆甲. 超磁化条件下超磁致伸缩作动器迟滞现象研究[J].
湖南工程学院学报(自然科学版), 2013, 23(4): 62-67.
GUO X T, WANG X Y, MENG Q J. Study on hysteresis of giant magnetostrictive actuator under super magnetization conditions[J]. Journal of Hunan Institute of Engineering: Natural Science Edition, 2013, 23(4): 62-67. |
| [31] |
冯红亮, 杨志红, 扈晓斌. 磁致伸缩效应原理及在工业测量中的应用[J].
仪表技术与传感器, 2009(S1): 344-346.
FENG H L, YANG Z H, HU X B. Magnetostrictive effects and its application in industrial measurement[J]. Instrumentation Technology and Sensor, 2009(S1): 344-346. |
| [32] |
代前国, 周新志. 大位移磁致伸缩传感器的弹性波建模与分析[J].
传感技术学报, 2013, 26(2): 195-199.
DAI Q G, ZHOU X Z. Elastic wave modeling and analysis of large displacement magnetostrictive sensor[J]. Chinese Journal of Sensors and Actuaries, 2013, 26(2): 195-199. |
 2018, Vol. 35
2018, Vol. 35
