随着全球的能源与环境问题的日益严重，分布式发电技术得以快速发展且广泛应用. 然而分布式电源与大电网存在大量协调控制问题，为了解决这些问题，微电网应运而生^[1-3]. 微电网是一个既包含负荷也包含多种分布式电源的独立可控系统，可以并网运行，保证微电网的可靠性；也可以孤岛运行，提高供电的灵活性^[4].

近年来，随着纯电动汽车巡航里程的不断增加及充电技术的不断革新，可以预料，在不久的将来，纯电动汽车将会大规模使用，而纯电动汽车的能量来源于大电网或微电网^[5]. 因此，微电网与纯电动汽车的有机结合、经济运行是极具潜力的研究方向，而微电网优化调度往往存在运行成本、环境成本等多个目标函数同时寻优^[6].

目前，对于微电网多目标优化调度研究，学者们已取得一定的实验及理论成果. 文献[7]建立了考虑发电成本及污染物排放的微电网优化模型，利用模糊决策法赋予经济成本和环境成本不同权系数值，再通过改进的粒子群算法进行求解，但是权系数的确定仍然受主观因素影响. 文献[8]提出一个综合考虑微电网运行成本、电压偏差和微网削峰填谷能力的微电网多目标模型，并采用粒子群–细菌觅食算法(PSO-BF)进行求解. 文献[9]在分时电价的条件下建立了以用户满意度最大为目标函数的日前优化调度模型，并采用遗传和禁忌混合算法对其进行求解. 文献[10]建立了峰谷分时电价的电动汽车有序充放电模型，以微电网发电成本和环境效益最优为目标函数，采用改进的遗传算法进行求解. 然而遗传算法的运算时间较长，并不适用于实时调度需求.

在多目标模型的求解方法上，使用最多的是人工智能方法，如遗传算法、粒子群算法、免疫算法等. 遗传算法等进化算法，因其基因编码、选择交叉变异等手段，其优化结果及精度比较理想，但是运算时间较长，不满足实时调度需求. 而粒子群算法则因其寻优速度快，结果在一定精度下满足需求，较适合实时调度. 而很多学者也在标准粒子群算法的基础上，进行了很多改进. 如文献[11]在粒子群算法的基础上，引入拥挤网格和外部存档来进一步提升算法全局寻优能力，从而提高算法精度. 文献[12]的文化粒子群多目标优化算法中群体空间采用多目标粒子群算法更新，同时新的形势知识、规范化知识和历史知识定义使信念空间更适用于多目标优化. 文献[13]提出一种自适应惯性权重的混沌粒子群算法，利用立方映射的混沌序列对粒子位置初始化，同时在寻优过程中自适应调整惯性权重，提高收敛速度. 文献[14]在粒子群初始化时引入组合混沌映射，在粒子更新过程时引入动态惯性权重，提高算法全局寻优能力.

本文综合考虑线路、微源等约束条件，建立了以微电网运行维护费用最小、环境效益最高的多目标优化调度模型^[15-17]. 针对多个目标函数难以协调问题，引入动态模糊目标函数进行处理；针对标准粒子群算法(PSO)易陷入局部最优、遍历性差的缺点，引入可变惯性权重、混沌理论来改进粒子群算法，提出动态模糊多目标混沌粒子群优化算法(FCPSO)，并通过仿真算例，证明该算法的高效性及优越性.

1 含电动汽车微电网多目标优化调度模型 1.1 纯电动汽车(BEV)充放电模型 1.1.1 BEV充电模型

虽然车主的行驶习惯具有极大的个体独立性，但是从一定规模的车主行为可归类分析出车主的行驶特性规律. 本文参照美国交通部(National Household Travel Survey，NHTS)2009年调查结果来研究BEV车主的行驶持性，得出无序充电情况下，即无序模式下，BEV日行驶里程L近似服从对数正态分布，充电时刻T₀近似服从正态分布.

日行驶里程 $L$ 服从对数正态分布，其概率密度函数为

$f(L) = \displaystyle\frac{1}{{L \times \sigma \times \sqrt {2{\rm{\text{π} }}} }}\exp [ - \displaystyle\frac{{{{(\ln L - \mu )}^2}}}{{2{\sigma ^2}}}].$

(1)

其中， $\mu {\rm{ = 3}}.{\rm{2}}$ 、 $\sigma {\rm{ = 0}}.{\rm{88}}$ ； $L$ 为日行驶里程， ${\rm{0}} \leqslant L \leqslant {\rm{200}}$ .

无序模式下BEV充电时刻服从正态分布，其概率密度函数为

$f({T_0}) = \left\{ {\begin{array}{*{20}{l}}{\displaystyle\frac{1}{{\sigma \times \sqrt {2{\rm{\text{π} }}} }}\exp [ - \displaystyle\frac{{{{({T_0} - \mu )}^2}}}{{2{\sigma ^2}}}],} \;{(\mu - 12) < {T_0} \leqslant 24;}\\[13pt]{\displaystyle\frac{1}{{\sigma \times\!\! \sqrt {2{\rm{\text{π} }}} }}\exp [ - \displaystyle\frac{{{{({T_0} \!+\! 24 \!-\! \mu )}^2}}}{{2{\sigma ^2}}}],} \;{0 \!< \!{T_0} \leqslant (\mu \!-\! 12).}\end{array}} \right.$

(2)

其中， $\mu {\rm{ = 17}}.{\rm{6}}$ ， $\sigma {\rm{ = 3}}.{\rm{4}}$ ； ${T_0}$ 为充电开始时刻.

1.1.2 BEV放电模型

根据日负荷曲线可知，纯电动汽车在人们普遍处于室内环境时候提供电能最为合适，此时也是电动汽车闲置时间，在保证纯电动车满足一定行驶里程的情况下，可以令电量较足的电动车作为电源就近为微电网提供电能，达到削峰效果.

根据路程、速度及时间之间的关系，可得持续放电时长为

${T_{{\rm{cdis}}}} = \displaystyle\frac{{(90\% - 10\% ) \times {C_{{\rm{BEV}}}} - W \times {L_{\rm{e}}}}}{{{P_{{\rm{cd}}}}}}.$

(3)

其中， ${T_{{\rm{cdis}}}}$ 为持续放电时长； ${C_{{\rm{BEV}}}}$ 为电动车电池额定容量； $W$ 为电动车行驶里程平均能耗； ${L_{\rm{e}}}$ 为电动车期望行驶里程； ${P_{{\rm{cd}}}}$ 为电动车放电功率.

1.2 目标函数

微电网优化调度是在满足负荷需求及各种约束条件的情况下，合理配置各微源出力，实现微电网运行维护成本最低、环境污染最小的目的.

目标函数 $F$ 为运行维护成本 ${F_{\rm{1}}}$ （计及燃料成本、维护成本、启动成本、交互成本）最低，同时环境污染物对环境影响 ${F_2}$ 最小.

$\min F = \{ {F_{\rm{1}}},{F_{\rm{2}}}\}. $

(4)

1) 目标函数 ${F_{\rm{1}}}$ ：运行维护成本

${F_{\rm{1}}}{\rm{ = }}{C_{\rm{F}}} + {C_{\rm{M}}} + {C_{\rm{s}}} + {C_{\rm{g}}}.$

(5)

其中， ${F_{\rm{1}}}$ 为微电网的运行维护成本； ${C_{\rm{F}}}$ 为微型燃气轮机与燃料电池的燃料成本； ${C_{\rm{M}}}$ 为维护成本，包括各微源及电动汽车电池的维护成本； ${C_{\rm{s}}}$ 为微型燃气轮机、燃料电池的启动成本； ${C_{\rm{g}}}$ 为并网交互成本，正值表示微电网从大电网中购电，负值表示微电网向大电网卖电.

2) 目标函数 ${F_{\rm{2}}}$ ：环境污染物成本

${F_2} = {E_{\rm{m}}} + {E_{\rm{g}}}.$

(6)

其中， ${F_2}$ 为微电网的环境污染物成本； ${E_{\rm{m}}}$ 为各微源产生的各类污染物的折算量； ${E_{\rm{g}}}$ 为大电网供应给微电网电量而产生各类污染物的折算量.

1.3 约束条件 1.3.1 功率平衡约束

$\sum\limits_{i = 1}^N {{P_i}} + {P_{\rm{g}}} = {P_{{\rm{Load}}}} + {P_{{\rm{BEV}}}}.$

(7)

其中， ${P_i}$ 为各微源功率； ${P_{\rm{g}}}$ 为并网功率，正值代表微电网从大电网吸收功率，负值代表微电网向大电网输出功率； ${P_{{\rm{Load}}}}$ 为负荷吸收的功率； ${P_{{\rm{BEV}}}}$ 为纯电动汽车充电功率，正值代表纯电动汽车从微电网吸收功率，负值代表纯电动汽车向微电网输出功率.

1.3.2 各微源及大电网交互功率限制

$\left\{ {\begin{array}{*{20}{c}}{{P_{i{\rm{min}}}} \leqslant {P_i} \leqslant {P_{i{\rm{max}}}},}\\[5pt]{{P_{{\rm{gmin}}}} \leqslant {P_{\rm{g}}} \leqslant {P_{{\rm{gmax}}}}.}\end{array}} \right.$

(8)

其中， ${P_i}$ 为各微源实际功率； ${P_{i{\rm{min}}}}$ 、 ${P_{i{\rm{max}}}}$ 为第 $i$ 个微源的功率上下限； ${P_{\rm{g}}}$ 为微电网与大电网的交互功率； ${P_{{\rm{gmin}}}}$ 、 ${P_{{\rm{gmax}}}}$ 为微电网与大电网交互功率的上下限.

1.3.3 蓄电池荷电状态限制

蓄电池电池状态常常用荷电状态来描述，而荷电状态是指剩余电量与满电容量的比值. 为了延长蓄电池的使用寿命，需对蓄电池的荷电状态进行限制.

${\rm{so}}{{\rm{c}}_{{\rm{min}}}} \leqslant {\rm{soc}}(t) \leqslant {\rm{so}}{{\rm{c}}_{{\rm{max}}}}.$

(9)

其中， ${\rm{soc}}(t)$ 为某时刻 $t$ 的荷电状态； ${\rm{so}}{{\rm{c}}_{{\rm{min}}}}$ 、 ${\rm{so}}{{\rm{c}}_{{\rm{max}}}}$ 分别为荷电状态的上下限.

1.3.4 可控微源的爬坡约束

$r_i^{\rm{d}} \cdot \Delta t \leqslant {P_{i,t + 1}} - {P_{i,t}} \leqslant r_i^{\rm{u}} \cdot \Delta t.$

(10)

其中， $r_i^{\rm{d}}$ 和 $r_i^{\rm{u}}$ 分别为第 $i$ 个可控微源的向上、向下爬坡速率； $\Delta t$ 为爬坡时间； ${P_{i,t}}$ 和 ${P_{i,t + 1}}$ 分别为第 $i$ 个可控微源这时刻和下个时刻的功率.

2 动态模糊混沌粒子群算法 2.1 标准pso优化算法

粒子群算法是根据鸟群觅食而开发的一种群智能优化方法. 其通过粒子自身信息及粒子群的信息来更新各个粒子的位置，从而不断趋近最优位置. 因其原理简单、参数易于控制、收敛速度快等优点被用于解决各种寻优问题，其更新公式为

$\left\{\begin{array}{l}V_i^{k + 1} = \omega V_i^k + {{\rm{c}}_{\rm{1}}}{r_1}(P_{{\rm{best}}}^k - x_i^k) + {{\rm{c}}_{\rm{2}}}{r_2}(G_{{\rm{best}}}^k - x_i^k),\\[5pt]X_i^{k + 1} = X_i^k + V_i^{k + 1}.\end{array}\right.$

(11)

其中， $V_i^{k + 1}$ 为此次粒子更新速度； $V_i^k$ 为上次粒子更新速度； $X_i^{k + 1}$ 为更新后的粒子位置； $X_i^k$ 为更新前的粒子位置， $i = 1,2, \cdots , M$ ； $M$ 为粒子规模； $k$ 为迭代次数； $P_{{\rm{best}}}^k$ 为粒子自身更新 $k$ 代后的最优位置； $G_{{\rm{best}}}^k$ 为种群更新 $k$ 代后全局最优的粒子位置； ${c_{\rm{1}}}$ 、 ${c_{\rm{2}}}$ 为加速因子，用于匹配 $P_{{\rm{best}}}^k$ 与 $G_{{\rm{best}}}^k$ 对粒子更新的影响； ${r_1}$ 、 ${r_2}$ 为 $[0,1]$ 间的随机数，用于增加粒子更新的多样性； $\omega $ 为惯性权重，代表历史信息对速度的影响，其值较大时有利于全局位置优化，其值较小时有利于局部位置优化.

2.2 动态模糊多目标混沌粒子群算法(FCPSO) 2.2.1 可变惯性权重

惯性权重是粒子位置更新中代表历史数据的信息比重，较大的惯性权重可以增加粒子在全局的搜索能力，较小的惯性权重则有利于局部的寻优. 本文利用式(12)调整惯性权重，使算法前期更注重全局搜索，后期更注重局部搜索.

权重系数公式为

$\omega {\rm{ = }}{\omega _{{\rm{min}}}} + \displaystyle\frac{{{\rm{Maxiter}} - {\rm{iter}}}}{{{\rm{Maxiter}}}} ({\omega _{{\rm{max}}}} - {\omega _{{\rm{min}}}}).$

(12)

其中， $\omega $ 为惯性权重； ${\omega _{{\rm{min}}}}$ 为惯性权重最小值； ${\omega _{{\rm{max}}}}$ 为惯性权重最大值； ${\rm{iter}}$ 为当前迭代次数； ${\rm{Maxiter}}$ 为最大迭代次数.

2.2.2 混沌粒子群优化算法

为了增加PSO算法初始化和迭代后期种群多样性，本文在粒子初始化和更新过程中引入混沌思想，增加算法的遍历性，从而避免算法陷于局部最优. 更新过程中引入典型的Logistic映射方程：

${x_{n + 1}} = {\rm{\partial }}{x_n}(1 - {x_n}).$

(13)

由于Logistic混沌映射受初值的影响较大，因此本文在初始化过程中引入Logistic混沌映射与Chebyshev混沌映射的组合混沌序列，以增加粒子的遍历性，提高粒子的均匀程度.

组合混沌序列映射方程为

$\left\{ \begin{array}{l}{y_0} = {x_0},\\[5pt]{y_{k + 1}} = {\rm{cos}}({\rm{narccos}}{y_n}),\\[5pt]{\rm{temp}} = \partial {x_k}(1 - {x_k}) + \left| {{y_{k + 1}}} \right|,\\{x_{k + 1}} = od ({\rm{temp}},1).\end{array} \right.$

(14)

其中， ${x_{n + 1}}$ 、 ${x_n}$ 为粒子这次和上次状态值； ${x_0}$ 、 ${y_0}$ 为粒子的初始值； ${\rm{\partial }}$ 、n为控制参数.

2.2.3 基于模糊理论的动态多目标决策

在多目标优化问题中，常常出现各目标函数之间存在一定交集与矛盾，无法同时使多个目标达到最优. 而在多目标求解中，使用最多的是加权系数求和法，把多目标函数转化为单目标函数. 但是加权系数的选取极大影响了优化结果，存在较大的主观因素. 本文借用模糊隶属度函数，把各目标函数转化为隶属度，通过最大最小理论得出非劣解集，从而把多目标优化问题转化为非线性单目标问题进行求解. 算法通过自身的隶属程度决定目标函数，从而避免了主观赋权值的过程，降低了人为因素造成多目标函数配置权值的不合理性.

由于算法寻优以适应度最小为目标，而微电网运行维护成本及环境成本也希望越低越好，因此本文采用式(15)的升半型梯形隶属度函数把各目标函数转化为隶属度 ${\lambda _1}$ 、 ${\lambda _2}$ ，按照最大最小原则，取 ${\rm{max\{ }}{\lambda _1}, {\lambda _2}{\rm{\} }}$ 作为目标函数，得出pareto非劣解，可以证明pareto非劣解为可行解集. 当 ${\rm{max\{ }}{\lambda _1}, {\lambda _2}{\rm{\} }}$ 达到足够低的数值时，那么pareto非劣解也趋于最优.

升半梯形隶属度函数为

$\lambda = \left\{ {\begin{array}{*{20}{l}}{0,} & {X \leqslant {X_{\min }};}\\[5pt]{\displaystyle\frac{{X - {X_{\min }}}}{{{X_{\max }} - {X_{\min }}}},} & {{X_{\min }} < X < {X_{\max }};}\\[12pt]{1,} & {X \geqslant {X_{\max }}.}\end{array}} \right.$

(15)

其中， $\lambda $ 为隶属度； $X$ 为待转化的函数，本文取为目标函数 ${F_{\rm{1}}}$ 、 ${F_{\rm{2}}}$ . ${X_{{\rm{max}}}}$ 、 ${X_{{\rm{min}}}}$ 为待转化函数的最大值、最小值，本文取目标函数 ${F_{\rm{1}}}$ 、 ${F_{\rm{2}}}$ 的最大值、最小值.

由于隶属度函数转化需要已知待转化函数的最大、最小值，因此迭代前期，以加权系数法确定目标函数，借此过程记录待转化函数的最大最小值. 目标函数在算法寻优过程中动态地变换. 在迭代前期，目标函数以加权系数法确定，在迭代中后期，目标函数为转化后的隶属度函数最大值，即 ${\rm{max\{ }}{\lambda _1}, {\lambda _2}{\rm{\} }}$ . 动态的微电网目标函数 $F$ (式(16))有利于避免算法陷入局部最优，达到更好的优化效果.

微电网动态模糊总目标函数 $F$ 为

$F = \left\{ {\begin{array}{*{20}{c}}{{R_1}{F_1} + {R_2}{F_2},} & {{\rm{iter}} \leqslant Z \cdot {\rm{Maxiter}};}\\[5pt]{\max \{ {\lambda _1}, {\lambda _2}\} ,} & {{\rm{iter}} > Z \cdot {\rm{Maxiter}}.}\end{array}} \right.$

(16)

其中， ${R_{\rm{1}}}$ 、 ${R_{\rm{2}}}$ 为加权系数、 $Z$ 为变换系数，决定迭代过程中转换目标函数的临界点，其中 $Z$ 取 $[0,1]$ 之间.

2.3 动态模糊多目标混沌粒子群优化算法流程

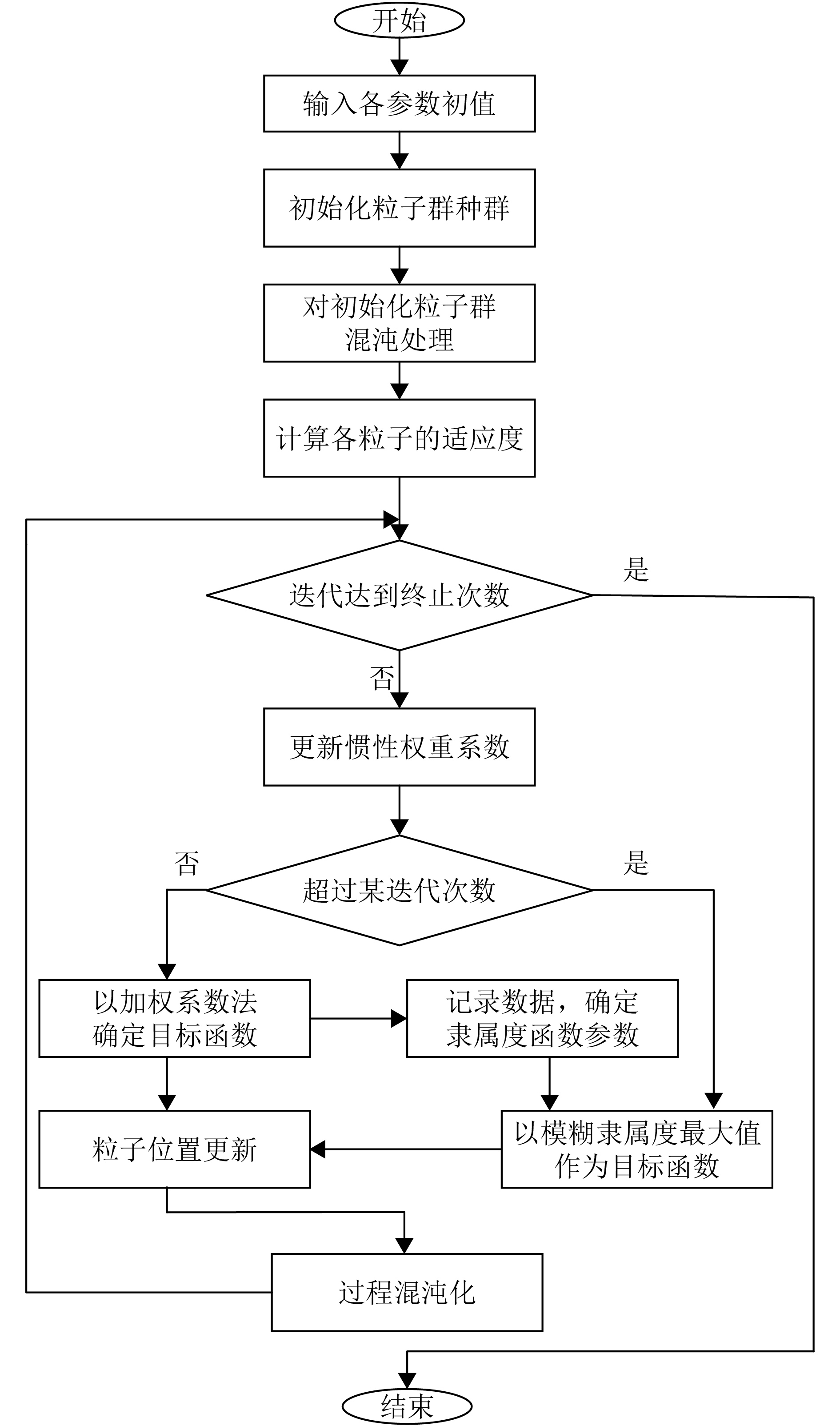
针对本文的微电网多目标优化调度模型，运用动态模糊多目标混沌粒子群优化算法求解的流程如图1所示，具体步骤如下.

1) 初始化粒子群算法各参数，在满足各约束条件下产生初始种群，即各微源出力及并网功率.

2) 以式(14)对初始化的种群进行混沌处理，判断是否满足各约束条件，如不满足，则进行越限处理，即等于最大值或最小值.

3) 计算各粒子的适应度，若未超过某迭代次数，则以加权系数法确定的目标函数作为筛选出P_best及G_best的标准，并记录各目标函数的数值；若超过某迭代次数，则以之前记录的各目标函数最大最小值，用模糊隶属度函数对原目标函数进行隶属度换算(即式(15))，把各目标函数转化为隶属度 ${\lambda _1}$ 、 ${\lambda _2}$ ，取 ${\rm{max\{ }}{\lambda _1}, {\lambda _2}{\rm{\} }}$ 作为目标函数，筛选出P_best及G_best(即式(16)).

4) 以式(12)更新惯性权重，前期加大惯性权重利于全局寻优，后期减少惯性权重利于局部寻优，以式(11)进行粒子位置更新，更新后进行越限处理.

5) 以式(13)对迭代过程进行混沌处理，增加迭代过程的遍历性，避免陷入早熟.

6) 重复步骤3)、4)、5)，直至达到最高迭代次数，结束算法寻优，输出结果.

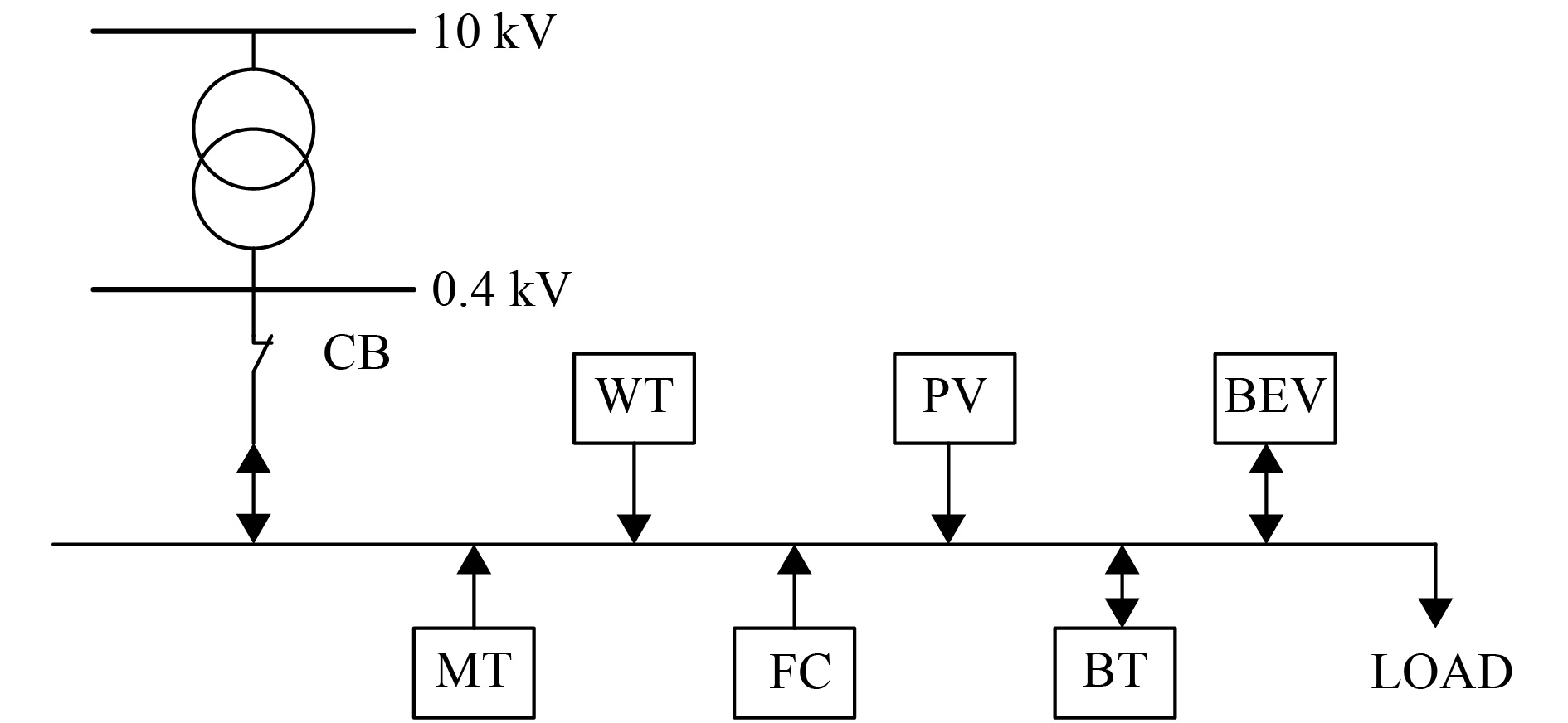
3 算例分析 3.1 仿真参数设置

如图2所示，本文以风力发电机WT、光伏发电装置PV、微型燃气轮机MT、燃料电池FC、蓄电池BT、纯电动汽车BEVs组成的微电网为例进行多目标寻优. 图中单向箭头代表功率只能单向流动，双向箭头代表功率可双向流动.

微电网从大电网购售电价参照北京分时电价进行设置，如表1所示.

MT及FC均使用天然气作为燃料，天然气的低热值为9.7 kW·h/m³，价格取2.5元/m³. MT及FC具体参数如表2所示，FC、MT及并网的污染物排放因子及处理费用如表3所示. 蓄电池容量为1000 A·h；纯电动汽车4辆，每辆容量为50 kW·h.

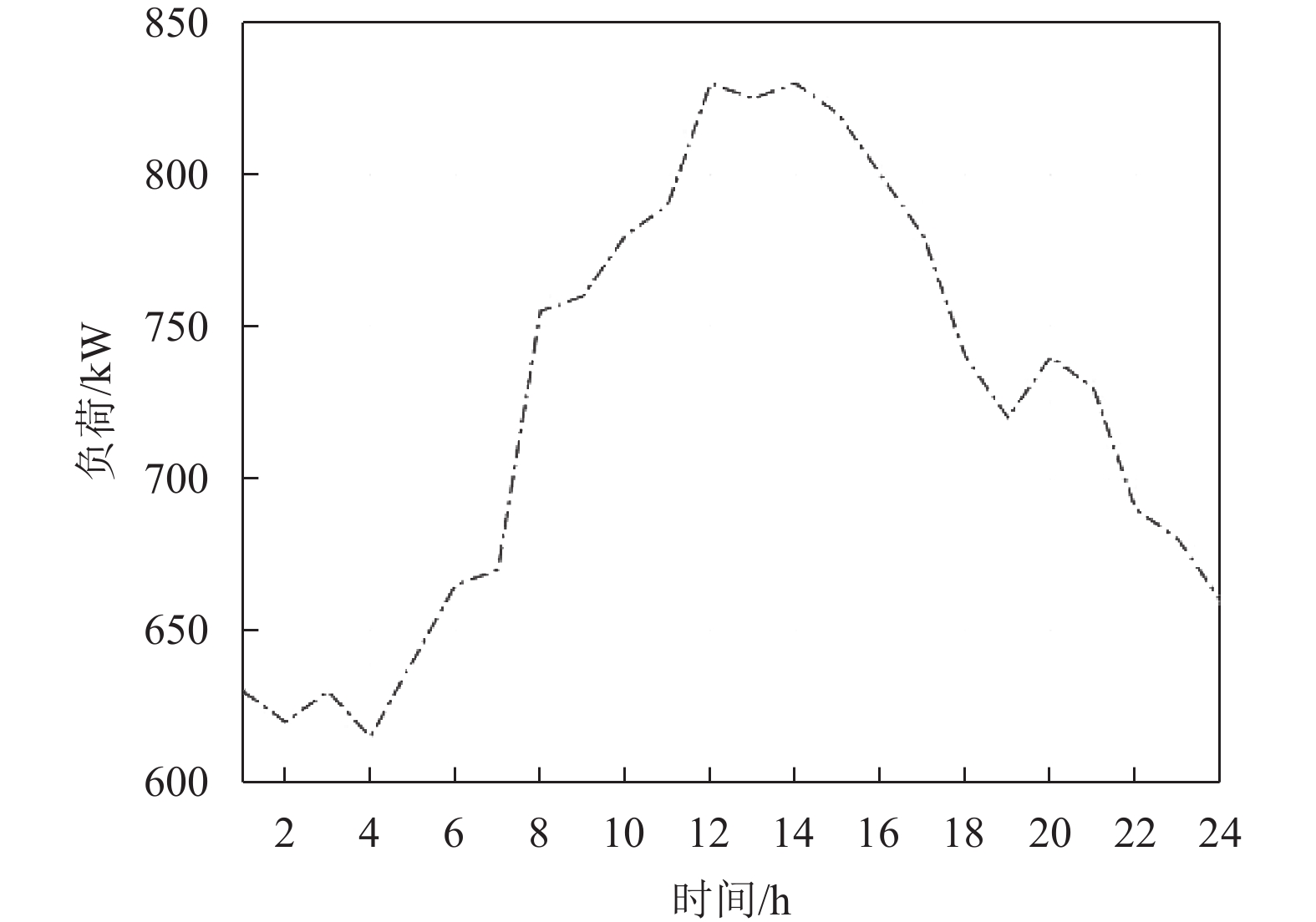
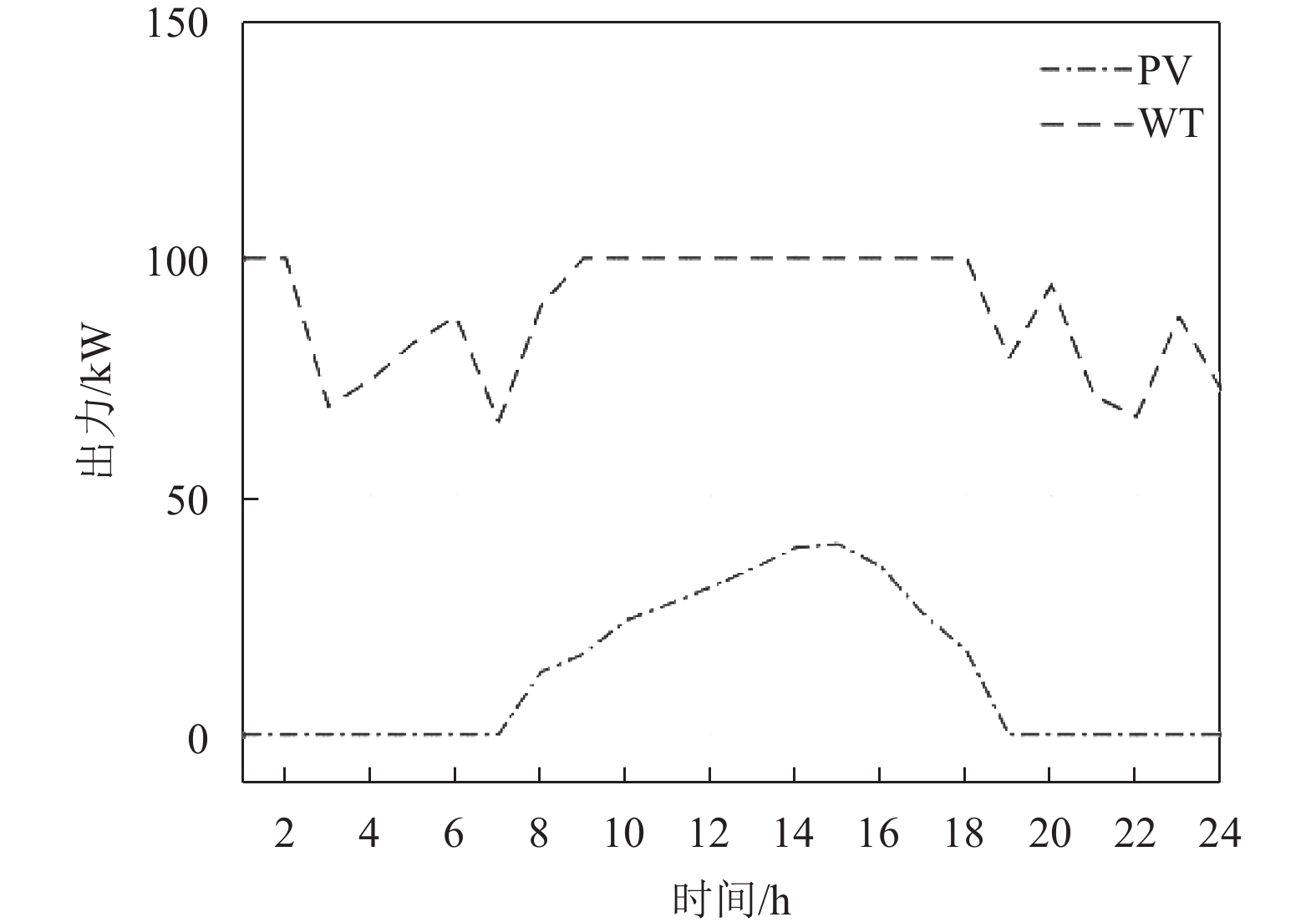
算例计算周期为一天，分为24个时段，根据历史数据预测微电网的负荷数据及PV、WT的出力如图3、图4所示.

求解模型时，标准粒子群算法(PSO)、混沌粒子群算法(CPSO)、动态模糊混沌粒子群算法(FCPSO)的参数均设置为：粒子规模 $M = {\rm{60}}$ ；惯性权重 $\omega $ 在 $[0.4,0.9]$ 之间；加速因子 ${c_{\rm{1}}}{\rm{ = }}{c_{\rm{2}}}{\rm{ = 2}}$ ；最大速度 ${V_{{\rm{max}}}}{\rm{ = 20}}$ ；最大迭代次数 ${\rm{Maxiter = 100}}$ .

3.2 结果分析

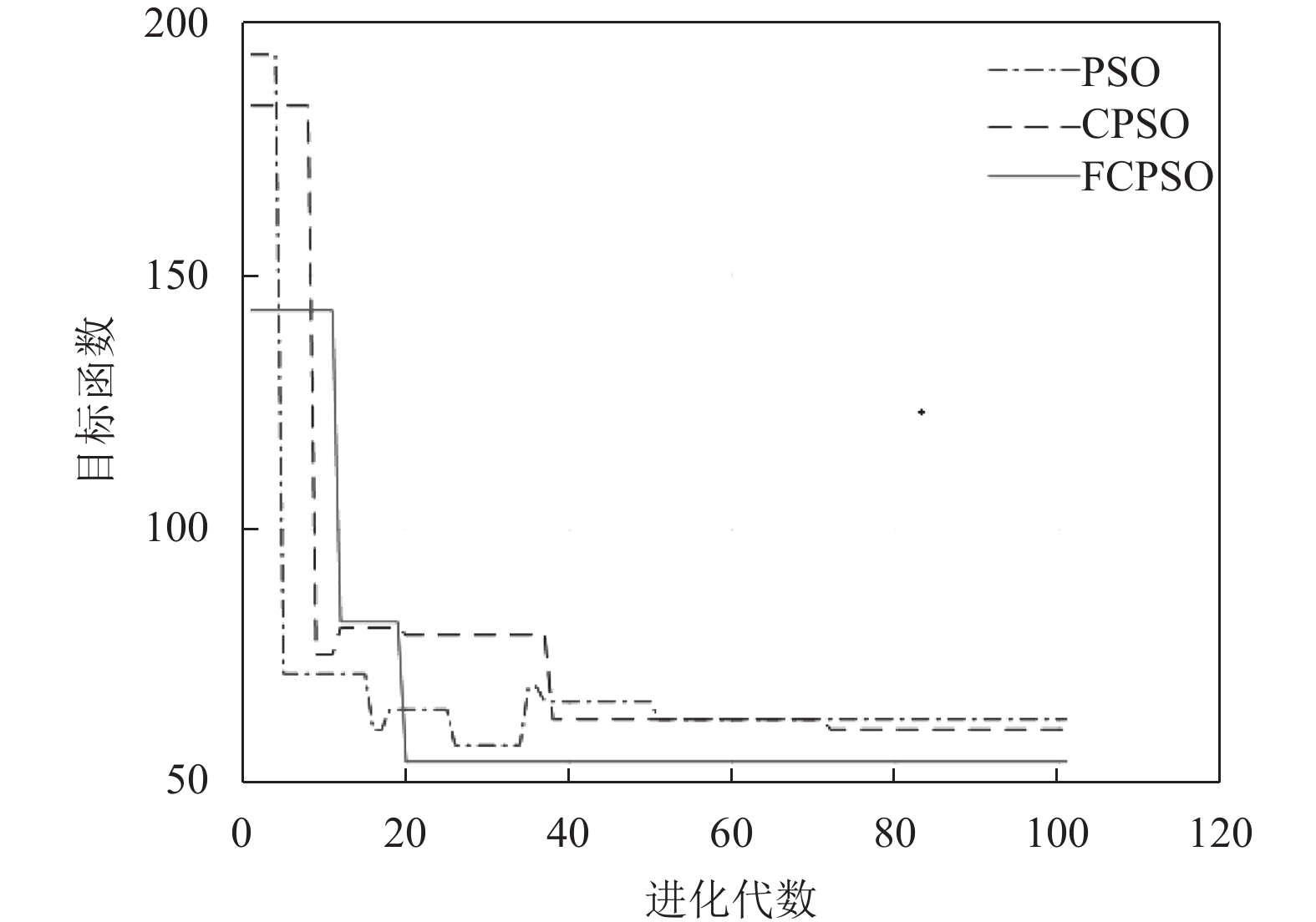
从图5可看出，因初始化混沌处理，CPSO算法与FCPSO算法的初值效果更好，成本更低. 3种算法的收敛速度都非常快，但是PSO算法在中段寻优规则性较差，且陷入局部最优，其遍历性较差；CPSO算法逐渐趋于最优，较为平稳，但是在后期成本无法继续降低；FCPSO算法前期收敛速度稍慢，但是中后期收敛逐渐趋于最优，因目标模糊化处理，FCPSO算法最终成本比CPSO算法成本更低. 从表4看出，FCPSO算法运算效率高，其求解时间最快，求解时间比PSO算法缩短了70%，比CPSO算法缩短了10%. 虽然FCPSO算法的环境成本最高，但是从最终结果可看出，FCPSO算法优化效果最好，运行维护成本及总成本最低. 这是因为目标函数转换为隶属度后，运行维护成本的隶属程度更高，因此优先考虑对运行维护成本进行优化.

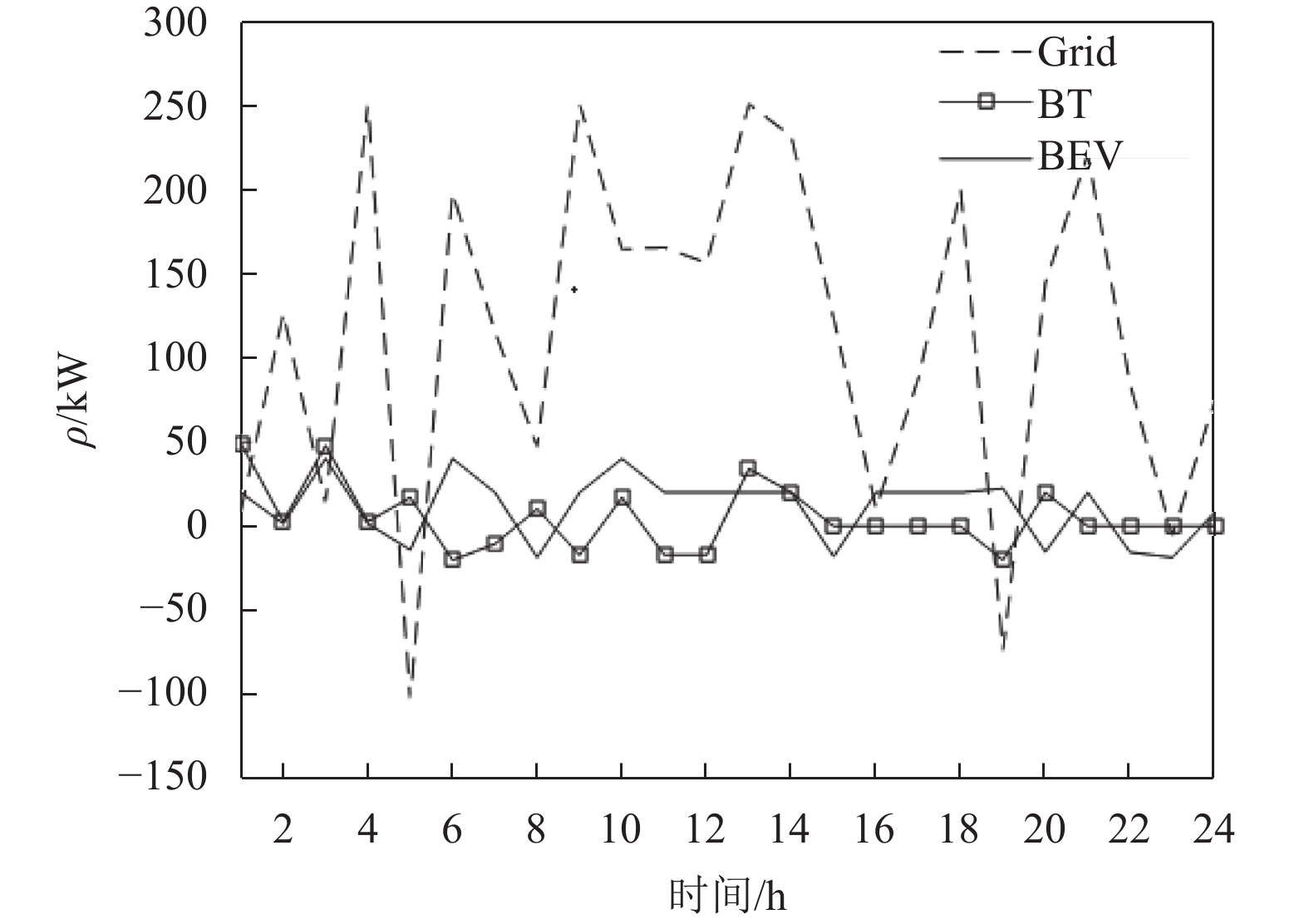
在满足负荷需求、并网功率约束、蓄电池荷电限制、电动汽车无序随机充放电、可控微源出力上下限及爬坡速率的条件下，FCPSO优化算法求解含电动汽车微电网多目标优化调度模型，输出最优方案. 图6为微电网并网功率、蓄电池充放电功率及电动汽车充放电功率最优方案；表5为可控微源最优出力方案.

4 结论

本文综合考虑了运行维护成本和环境成本两个目标函数，采用动态模糊决策方法建立含电动汽车的微电网多目标优化调度模型. 在传统粒子群优化算法的基础上，引入可变惯性权重及混沌理论，提高了算法的运算效率及寻优能力. 仿真结果表明，与CPSO和PSO算法相比，改进的FCPSO算法对微电网调度更具有高效性和可行性，为微电网调度提供一种新思路和新方法. 本文的电动汽车模型参考了美国2009年的NTTS调查数据，与现今中国的实际情况有一定偏差，今后的模型采样将更多使用国内数据，使优化调度的结果更具实用价值.