广东工业大学 土木与交通工程学院,广东 广州 510006
收稿日期:2017-11-30
基金项目:国家自然科学基金资助项目(51608132);广东省大学生创新创业训练项目(201711845132);广东工业大学大学生创新实验项目(yj201511845082)
Public Participation in Decision-making of PPP Project Based on Bayesian Network
School of Civil and Transportation Engineering, Guangdong University of Technology, Guangzhou 510006, China
十九大报告指出,我国社会主要矛盾已经转化为人民日益增长的美好生活需要和不平衡不充分的发展之间的矛盾. 而社会公众对公共产品日益增长的需求同公共产品供给短缺、性能低下之间的矛盾则是我国社会主要矛盾在实践中的具体体现. 随着社会对基础设施项目及公共服务需求的增加,政府财政预算日趋紧张. 为了解决这一问题,很多国家政府都通过对公共服务项目引入社会资本方式,即公私合营模式(PPP, Public Private Partnership)为社会公众提供质量更高、价格更低廉的公共产品或服务. 与传统的采购模式相比,我国的PPP项目集中于大型基础设施项目,其历时更长,涉及的项目各方关系复杂. 如何平衡项目主要参与方,政府与社会资本的相关利益,以及提升基础设施或公共服务的最终使用者——社会公众的满意度,成为PPP项目成功的关键. 本文在研究公众参与评价工具与信息来源主要途径的基础上,以贝叶斯方程为手段建立了一个辅助PPP项目规划设计阶段方案选择的多目标决策支持模型. 该模型能帮助项目决策者在考虑社会公众行为习惯和相关喜好的前提下,平衡投资者和社会公众的利益关系,获得双方都较满意的项目规划设计方案,从而保证项目的顺利实施.
1 研究背景
在20世纪的公法学中,人们引入一种髙度效仿立法程序思路的“公众参与”,让公民通过民主参与做更为直接的利益表达. Chambers[1]认为公众参与是通过一系列的正规及非正规的机制直接使公众介入决策. Creighton[2]将公众参与定义为一个过程,公众意见、公众需求以及公众价值通过此过程被引入政府及法人组织的决策之中,是一种双向沟通交互,公众的支持使总体目标得到更好的实施. 因此,许多学者纷纷主张,公共政策制定、环境评价等领域应当充分征求和体现利益相关人和社会公众的意见,不能由行政主体自行决定[3]. 由于公私合营项目往往涉及公共产品和公共服务,其目的是以最有效的方式为社会公众提供更好的产品和服务. 因此,将公众参与模式引入公私合营项目方案制定,能够从程序层面大幅拉升PPP项目的民主形象. 不过,类似探讨还仅仅停留在倡导阶段,尚未涉及公私合营项目公众参与的具体操作技术.
要完善公众参与PPP项目方案决策,在通过确定公众参与的法律地位,细化公众参与的实体性和程序性内容之外,应建立公众参与PPP项目的具体实施方式. 而这种具体的实施方式一般包含两个方面,一是公众意愿或喜好信息的来源途径,二是基于信息的决策分析. 目前,公众各种意见或喜好的获得主要是通过一些公众主动参与的方式,例如普通投票、听证会、公众意见调查、协商规则谈判、舆论会议、公众法庭、公众顾问委员会、参与工作组等[3]. 对于公众主动参与方式获得的相关信息,业界也形成了一批评价工具. 例如,社会评价[4]、利益相关群体分析[5]、受益评价[6]等,但这些评价方法都是以社会公众主动参与为前提. 由于成本和时间的限制,主动参与方式中参与公众样本数往往仅为样本总数的一小部分,其代表性容易受到质疑. 因此,利用这些数据进行分析而得到结果的可靠性较差.
为了提高公众参与的有效性和全面性,可视技术[7]、地理信息系统[8]、3D技术[9]、移动互联网技术[10]等也日益应用于公众参与的信息收集之中,成为公众被动参与项目决策的主要方式,为决策过程提供了有效和可靠的数据信息. 但通过被动参与方式获得的数据信息量非常庞大,需要可靠的决策分析手段对海量数据信息进行分析整理. 在过去的二十年间,计算机决策支持系统(Decision Support Systems,DSSs)在学术研究、商业、工业和政府管理层面都有广泛的应用. 它可以辅助决策者增加信息处理容量,解决复杂、耗时的决策问题. DSSs被定义为在一个或多个决策者的控制下通过对决策事项的结构化分析辅助决策,提高最终决策的有效性[11]. 因此,本文主要以公众被动参与方式获得公众意愿/喜好相关大数据作为数据信息来源,构建适合PPP项目的决策支持系统,辅助项目决策者选择公众满意度和投资者满意度都较高的PPP项目规划决策方案.
2 研究现状
在国际上,关于公众参与工程项目的研究已经有一定的基础,其中包括一些对公众参与的定义[12-13]、必要性、主体 [2, 14]以及对公众参与工程项目决策优点的讨论[15-16]. 在工程实践中,以世界银行为代表的国际工程项目在推进公众参与应用于工程建设项目方面做出了很大的贡献. 1996年,世行出版了专门的《世界银行参与手册》[17],该手册总结了世行实施参与式发展项目的经验和教训,指导如何在项目周期中具体落实公众参与. 亚洲开发银行、非洲开发银行等区域性银行也将公众参与作为发展项目贷款的首要条件. 国内关于工程建设中公众参与的研究较少,但已有部分学者认识到公众参与公共投资建设项目决策的必要性. 其中杨秋波[18]在分析国外公众参与的发展趋势的基础上提出我国工程建设项目实施公众参与的建议,并尝试构建了公众参与工程项目决策、设计、施工、运营及后评价的博弈模型;Li等[19]提出应将我国基础设施中的公众参与模式由仅在环境评价阶段的参与拓展到整个工程周期;Liu等[20]比较了北京3个不同节能改造项目的公众参与对项目的影响程度,认为在项目中实施公众参与应充分考虑参与人的参与动机和生活习惯.
在计算机辅助决策方面,自上世纪70年代起很多工程项目的实践者和研究者都尝试使用决策支持系统辅助决策. DSSs可以通过对项目延误的分析提出防止进一步延误的建议[21],协助对承包商的资格预审[22],辅助招投标决策[23],用于政府机构对公共设施修复的决策[24],用于工程质量监督[25],以及协助公路工程运送方式的选择[26]等. Haag[27]总结了DSSs的3个特征:(1) DSSs是专门为辅助决策过程设计的;(2) DSSs是作为辅助决策的工具而非自动生成决策;(3) DSSs能快速应对决策者需求的变化. 它将决策者和专家经验通过IT技术进行结合. 建筑工程项目非常适合使用决策支持系统辅助决策,因为一般建筑工程项目在规划阶段具有很大的不确定性. 根据营销学的消费者黑箱理论,此时决策者实际处于使用者黑箱中,在使用者做出使用行为之前,决策者无法了解使用者的使用行为与使用意愿. 因此,决策者非常希望在不断变化的客观环境中能提高决策的最终效果.
而对于PPP项目规划阶段的各种方案,决策者必须从多方面进行评价,要同时考虑经济和非经济因素. 其中PPP方案的非经济因素分析通常需要使用一定评价规则进行评分或评级,这就需要一组决策者、专家或社会公众对每个备选方案按照评分标准进行打分. 这一过程实际上是非常耗时耗力的,也需要大量的资金投入. 如果方案中的某些指标改变了,评价过程就需要重新进行. 因此,决策过程实际是非常繁重和重复性强的工作,当决策者仅仅根据自己的经验、知识和直觉做出的判断往往是很难让人信服的. 为此,针对PPP项目方案的评价问题而建立的决策支持系统应可以模仿决策者在不确定条件下进行推理,从数据库、经验和社会公众参与大数据中获取有用信息,有效地解决决策问题,并在情况变化时能迅速重新决策. 在众多的决策支持系统中,有学者使用规范的概率方法进行推理来解决这种复杂的问题[28]. 这种决策模型通常采用一种图形化概率模型,即贝叶斯网络进行建模和推理. 本文也将采用贝叶斯网络模型,建立公众参与PPP项目方案决策的多目标决策模型,并以公众被动参与方式获得的大数据作为模型的输入,获得公众与投资者满意度均较高的PPP项目方案.
3 基于贝叶斯网络的项目决策支持模型构建
3.1 多目标决策贝叶斯网络模型构建
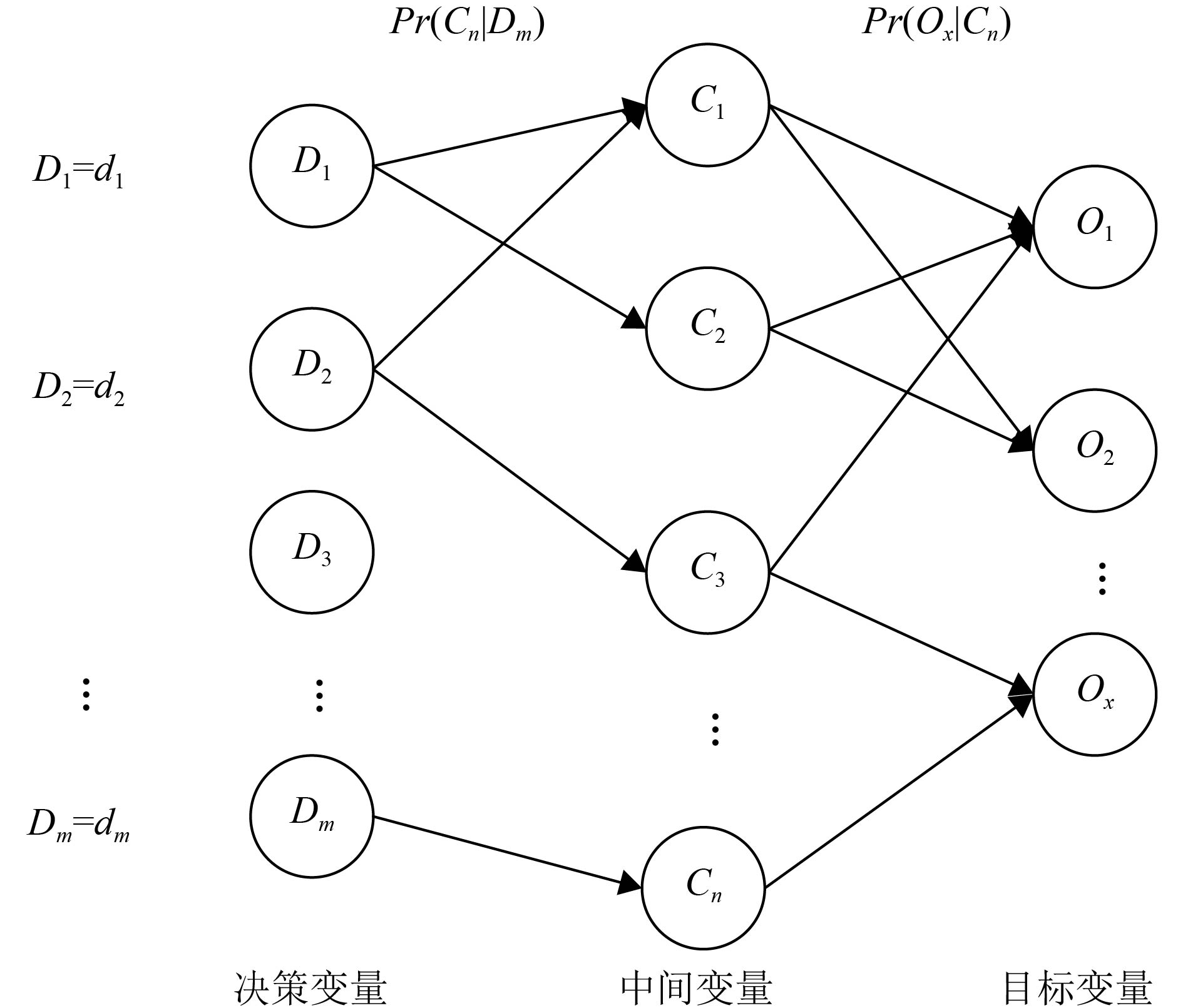
贝叶斯网络常用于表达和分析不确定性和概率性的事件,应用于有条件地依赖多种控制因素的决策,可以从不完全、不精确或不确定的知识或信息中做出推理. 贝叶斯网络是进行问题诊断和预测的重要工具. 基于公众参与项目决策问题的贝叶斯网络通常包括决策者控制下的决策变量(即方案)、表达参与者喜好的目标变量以及一些必要的中间变量. 贝叶斯网络可以简要描述为变量之间的概率依赖关系或独立关系,其中用节点表示变量,用节点之间的箭线代表两个变量之间的因果关系,并以条件概率表示. 具体地说,对于贝叶斯网络B = (V, E),V代表一系列的节点(或变量),E代表节点之间的箭线集合,联合概率分布可表示为
|
$Pr\left( {{X_V}} \right) = \prod\nolimits_{v \in V} {Pr} \left( {{X_v} = {x_v}{\rm{|}}{X_{pa\left( v \right)}} = {x_{pa\left( v \right)}}} \right),$
|
(1) |
其中, XV 为变量值的集合{X1,X2,…,Xv},Xv是其中某个变量的可能值(v∈V),Xpa(v)为Xv父节点的集合(pa(v)∈V),
$Pr\left( {{X_v}{\rm{|}}{X_{pa\left( v \right)}}} \right)$
代表节点v的条件概率,即当父节点
${X_{pa\left( v \right)}}$
为
${x_{pa\left( v \right)}}$
时,Xv为
${x_v}$
的概率.
因此,可利用贝叶斯网络通过图形建立连接决策因素、中间变量和目标变量之间的关系来辅助解决多目标决策问题(见图1). 每个连接节点之间的关系可用概率分布的形式表示,概率分布的数值可基于决策者主观经验数据或社会工作日常行为大数据的统计信息获取. 当对每个决策变量进行赋值,使其代表某种可能的决策选项,那么目标值可沿着箭线方向最终计算得到.
为了获得与项目相对应的贝叶斯网络结构及参数,本文利用Noisy-or gate模型来近似确定贝叶斯网络的条件参数[29]. 式(2)~(4)举例说明计算单个目标期望值的过程,其中式(2)表示在决策变量D1=d1,D2=d2时,中间变量C1=c1的概率;式(3)表示,在中间变量C1=c1,C2=c2时,目标变量O2=o2的概率. 式(4)表示目标变量Ox在不同中间变量影响下可能的取值集合{o1,o2,…,on}的期望值,通过这种方法可以得到所有目标的期望值. 最后根据决策者对各目标重要性的权衡设定单个目标权重,目标期望值与相应权重的乘积之和为项目决策综合加权值,见式(5).
|
$\begin{split}&Pr\left( {{C_1} = {c_1}{\rm{|}}{D_1} = {d_1};{D_2} = {d_2}} \right) = \\&1 - Pr\left( {{C_1} = {c_1}{\rm{|}}{D_1} \ne {d_1}} \right) \times Pr\left( {{C_1} = {c_1}{\rm{|}}{D_2} \ne {d_2}} \right),\end{split}$
|
(2) |
|
$\begin{split}& Pr\left( {{O_2} = {o_2}{\rm{|}}{C_1} = {c_1};{C_2} = {c_2}} \right) =\\& 1 - Pr\left( {{O_2} = {o_2}{\rm{|}}{C_1} \ne {c_1}} \right) \times Pr\left( {{O_2} = {o_2}{\rm{|}}{C_2} \ne {c_2}} \right),\end{split}$
|
(3) |
|
$E\left( {{O_x}} \right) = \mathop \sum \nolimits^ {o_x}Pr\left( {{O_x} = {o_x}} \right),$
|
(4) |
|
$E\left( O \right) = \mathop \sum \nolimits^ {W_{Ox}} \times E\left( {{O_x}} \right).$
|
(5) |
将以上公式用于PPP项目辅助决策时,首先应确定方案选项(决策变量Dm)、被影响因素(中间变量Cn)以及决策目标(目标变量Ox),以其为节点构成贝叶斯网络. 关系概率的确定主要依据可获得的行为数据或主观经验评价,其中每一对节点之间的关系概率均揭示了各个方案选项值对被影响因素影响的概率分布,以及该影响因素对决策目标的影响. 在确定方案选项值和各节点之间的关系概率后,此贝叶斯网络模型就可对PPP项目中不同决策方案进行打分.
3.2 贝叶斯网络模型辅助PPP项目决策应用分析
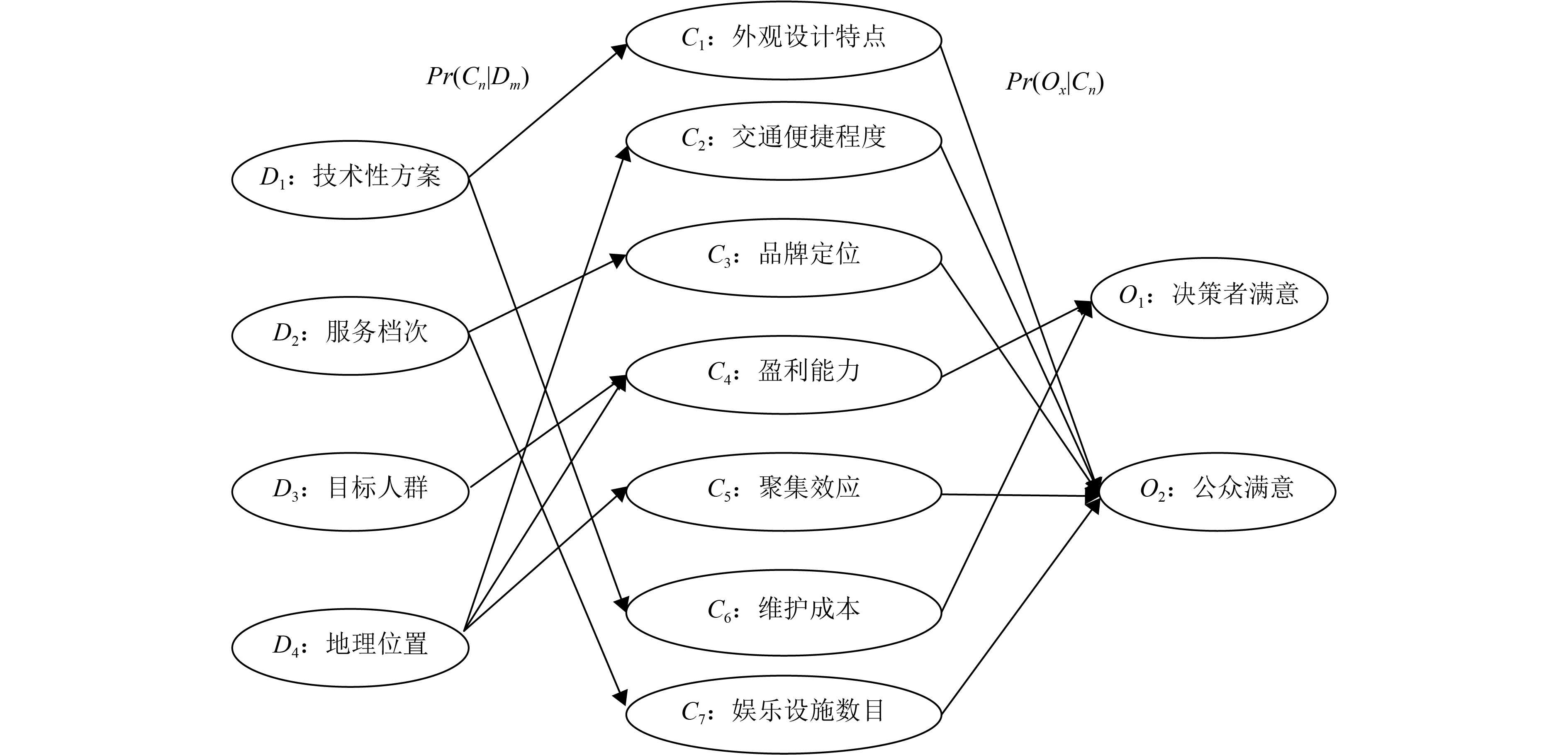
针对公众参与PPP项目决策问题,数值部分主要依据Fang等[24]的方法获得反映社会公众喜好的大数据信息,并利用数据挖掘和分析技术确定各变量之间的关系概率,具体方法将在另一篇论文中讨论. 本文以某商业性项目方案规划为例讨论模型实际应用方法. 根据对工程项目经理、咨询顾问以及一般公众的访谈结果,初步确定模型中主要变量包括4个决策变量分别是工程相关技术性方案选择(D1)、服务档次设定(D2)、目标人群设定(D3)以及地理位置选择(D4). 确定这4个决策变量主要的影响因素有7项中间变量,分别是外观设计特点(C1)、交通便捷程度(C2)、品牌定位(C3)、盈利能力(C4)、聚集效应(C5)、维护成本(C6)以及其他娱乐设施数目(C7)等. 决策问题的目标节点为投资者满意度(O1)与社会公众满意度(O2),通过贝叶斯网络决策模型可获得双方满意度最高的决策变量数值(见图2). 这些中间变量是投资者与社会公众满意度的父变量,各自独立影响最终双方满意度的分布,而对于这7个中间变量,左右其各种情况出现概率的父变量则为4个决策变量值的选择.
根据式(4)~(5),假设当投资者或公众满意度为高时的分值为o11或o21,投资者或公众满意度为低时的分值为o12或o22,将目标变量满意度为高或低概率与对应的满意度为高或低时的分值相乘得到投资者或社会公众各自对项目的满意度期望值(E(O1),E(O2)),并根据决策者设定的在进行项目决策时投资者与社会公众满意度的权重,确定权衡后的双方满意度综合加权值E(O)(式(6)~(8)). 最大的E(O)即为最优决策方案,即在确定的决策变量条件下,双方的满意度最大化,在给定的所有方案组合中,使这个目标期望值最大的方案组合为最优组合.
|
$E({O_1}) = Pr\left( {{O_1} = {o_{11}}} \right) \times {o_{11}} + Pr\left( {{O_1} = {o_{12}}} \right) \times {o_{12}},$
|
(6) |
|
$E({O_2}) = Pr\left( {{O_2} = {o_{21}}} \right) \times {o_{21}} + Pr\left( {{O_2} = {o_{22}}} \right) \times {o_{22}},$
|
(7) |
|
$E\left( O \right) = E\left( {{O_1}} \right) \times {W_{O1}} + E\left( {{O_2}} \right) \times {W_{O2}}.$
|
(8) |
本文用以讨论模型具体操作过程的数据也通过访谈形式初步设定. 表1对工程相关技术性方案、服务档次、目标人群和地理位置4个决策变量的不同可选方案进行赋值. 表2-7为受到单个决策因素影响的中间变量条件概率值,表8为受到两个决策因素影响的中间变量值(即盈利能力). 例如表8多因素影响中间变量条件概率表中第三列,假设当人均开销为100元、地理位置为极佳的条件下,盈利能力为强的概率为0.7,盈利能力为弱的概率为0.3. 具体概率数值可根据历史数据、决策者经验或大数据分析结果确定. 投资者满意度主要受到盈利能力和维护成本的影响(见表9),公众满意度与项目的外观设计、交通便捷性、品牌定位、聚集效应以及娱乐设施数目之间的存在概率关系(见表10).
表 1(Table 1)
表 1 决策变量赋值表
Table 1 Values of decision variables
| 决策变量 |
变量值1 |
变量值2 |
| 技术性方案 |
复杂 |
普通 |
| 服务档次 |
高 |
低 |
| 目标人群 |
人均消费100元 |
人均消费200元 |
| 地理位置 |
优越 |
偏僻 |
|
表 1 决策变量赋值表
Table 1 Values of decision variables
|
表 2(Table 2)

表 2 单因素影响中间变量条件概率表(外观设计)
Table 2 Conditional probability of interim variables (single affect factor- appearance design)
| 中间变量 |
技术性方案 |
| 复杂 |
普通 |
| 外观设计 |
新颖 |
1 |
0 |
| 普通 |
0 |
1 |
|
表 2 单因素影响中间变量条件概率表(外观设计)
Table 2 Conditional probability of interim variables (single affect factor- appearance design)
|
表 3(Table 3)

表 3 单因素影响中间变量条件概率表(交通便捷性)
Table 3 Conditional probability of interim variables (single affect factor- traffic)
| 中间变量 |
地理位置 |
| 优越 |
偏僻 |
| 交通便捷程度 |
便利 |
0.8 |
0.2 |
| 不便 |
0.2 |
0.8 |
|
表 3 单因素影响中间变量条件概率表(交通便捷性)
Table 3 Conditional probability of interim variables (single affect factor- traffic)
|
表 4(Table 4)

表 4 单因素影响中间变量条件概率表(品牌定位)
Table 4 Conditional probability of interim variables (single affect factor- brand)
| 中间变量 |
服务档次 |
| 高 |
低 |
| 品牌定位 |
高端 |
0.8 |
0.4 |
| 一般 |
0.2 |
0.6 |
|
表 4 单因素影响中间变量条件概率表(品牌定位)
Table 4 Conditional probability of interim variables (single affect factor- brand)
|
表 5(Table 5)

表 5 单因素影响中间变量条件概率表(聚集效应)
Table 5 Conditional probability of interim variables (single affect factor- aggregation effect)
| 中间变量 |
地理位置 |
| 优越 |
偏僻 |
| 聚集效应 |
有 |
0.8 |
0.2 |
| 无 |
0.2 |
0.8 |
|
表 5 单因素影响中间变量条件概率表(聚集效应)
Table 5 Conditional probability of interim variables (single affect factor- aggregation effect)
|
表 6(Table 6)

表 6 单因素影响中间变量条件概率表(维护成本)
Table 6 Conditional probability of interim variables (single affect factor- maintenance cost)
| 中间变量 |
技术性方案 |
| 复杂 |
普通 |
| 维护成本 |
高 |
1 |
0 |
| 底 |
0 |
1 |
|
表 6 单因素影响中间变量条件概率表(维护成本)
Table 6 Conditional probability of interim variables (single affect factor- maintenance cost)
|
表 7(Table 7)

表 7 单因素影响中间变量条件概率表(娱乐设施)
Table 7 Conditional probability of interim variables (single affect factor- maintenance cost)
| 中间变量 |
服务档次 |
| 高 |
底 |
| 娱乐设施数目 |
多 |
0.8 |
0.6 |
| 一般 |
0.2 |
0.4 |
|
表 7 单因素影响中间变量条件概率表(娱乐设施)
Table 7 Conditional probability of interim variables (single affect factor- maintenance cost)
|
表 8(Table 8)

表 8 多因素影响中间变量条件概率表(盈利能力)
Table 8 Conditional probability of interim variables (multi affect factor- profitability)
|
目标人群
人均消费100元
|
|
目标人群
人均消费200元
|
地理位置
优越
|
地理位置
偏僻
|
地理位置
优越
|
地理位置
偏僻
|
| 盈利能力 |
强 |
0.7 |
0.1 |
|
0.9 |
0.3 |
| 一般 |
0.3 |
0.9 |
|
0.1 |
0.7 |
|
表 8 多因素影响中间变量条件概率表(盈利能力)
Table 8 Conditional probability of interim variables (multi affect factor- profitability)
|
表 9(Table 9)

表 9 多因素影响目标变量条件概率表(投资者满意度)
Table 9 Conditional probability of objective variable (multi affect factor- investor’s satisfaction)
|
盈利能力强 |
|
盈利能力一般 |
| 维护成本高 |
维护成本低 |
维护成本高 |
维护成本低 |
| 投资者满意度 |
高 |
0.6 |
1 |
|
0 |
0.5 |
| 低 |
0.4 |
0 |
|
1 |
0.5 |
|
表 9 多因素影响目标变量条件概率表(投资者满意度)
Table 9 Conditional probability of objective variable (multi affect factor- investor’s satisfaction)
|
表 10(Table 10)

表 10 多因素影响目标变量条件概率表(公众满意度)
Table 10 Conditional probability of objective variable (multi affect factor- public’s satisfaction)
| 外观设计 |
交通情况 |
品牌定位 |
聚集效应 |
娱乐设施 |
公众满意度 |
| 高 |
低 |
| 新颖 |
便利 |
多 |
有 |
多 |
1 |
0 |
| 少 |
0.8 |
0.2 |
| 无 |
多 |
0.8 |
0.2 |
| 少 |
0.6 |
0.4 |
| 一般 |
有 |
多 |
0.8 |
0.2 |
| 少 |
0.6 |
0.4 |
| 无 |
多 |
0.6 |
0.4 |
| 少 |
0.4 |
0.6 |
| 不便 |
多 |
有 |
多 |
0.8 |
0.2 |
| 少 |
0.6 |
0.4 |
| 无 |
多 |
0.6 |
0.4 |
| 少 |
0.4 |
0.6 |
| 一般 |
有 |
多 |
0.6 |
0.4 |
| 少 |
0.4 |
0.6 |
| 无 |
多 |
0.6 |
0.4 |
| 少 |
0.4 |
0.6 |
| 普通 |
便利 |
多 |
有 |
多 |
0.8 |
0.2 |
| 少 |
0.6 |
0.4 |
| 无 |
多 |
0.6 |
0.4 |
| 少 |
0.4 |
0.6 |
| 一般 |
有 |
多 |
0.6 |
0.4 |
| 少 |
0.4 |
0.6 |
| 无 |
多 |
0.6 |
0.4 |
| 少 |
0.2 |
0.8 |
| 不便 |
多 |
有 |
多 |
0.6 |
0.4 |
| 少 |
0.4 |
0.6 |
| 无 |
多 |
0.4 |
0.6 |
| 少 |
0.2 |
0.8 |
| 一般 |
有 |
多 |
0.4 |
0.6 |
| 少 |
0.2 |
0.8 |
| 无 |
多 |
0.2 |
0.8 |
| 少 |
0 |
1 |
|
表 10 多因素影响目标变量条件概率表(公众满意度)
Table 10 Conditional probability of objective variable (multi affect factor- public’s satisfaction)
|
鉴于多目标决策贝叶斯网络模型的复杂性,本文使用了GeNIe 软件作为贝叶斯网络计算模拟工具. GeNIe 软件是一款搭建可视化贝叶斯网络平台的计算机辅助工具,可进行贝叶斯推理,为处理贝叶斯网络中大容量数据和状态建模提供帮助. 依据图2在GeNIe中构建贝叶斯网络模型(见图3),并根据表1-10对各决策变量、中间变量和目标变量进行赋值和确定关系概率. 通过GeNIe软件对贝叶斯决策模型进行运算,得到的某次运行结果如图3所示. 根据该运行结果,当技术性方案为复杂,服务档次为高,人均开销为100元以及地理位置为极佳的情况下,该项目公众满意度为高的概率为84%,公众满意度为低的概率为16%;投资者满意度为高的概率为42%,投资者满意度为低的概率为58%.
若设定满意度为高时分值为5分(o11=o21=5),满意度为低时分值为1分(o12=o22=1). 且在决策者进行决策时,公众满意度和投资者满意度同等重要(即WO1=WO2=0.5),根据式(6)~(8),在这种决策条件下E(O1)=5×84%+1×16%=4.36,E(O2)= 5×42%+1×58%=2.68,E(O)=0.5×(4.36+2.68)=3.52. 随着决策变量值的变化,各次模拟结果的期望值E(O)不断变化. 由于本案例决策变量有4个,且每个都有两个选项,对应有24=16种决策变量值的组合方案,计算结果如表11所示.
根据计算结果的对比,当决策变量中工程相关技术性方案为普通,服务档次为高,目标人群人均开销为200元,地理位置为极佳时(即第11次模拟运算结果),目标变量期望值E(O)最大为4.20,此时该规划方案中对4个决策点的选择,即为公众和投资者平均满意度最高的方案. 在该决策变量组合中,尽管公众满意度并不是所有满意度中的最高值,但由于投资者满意度的值为最大且较高,使该方案组合的综合满意度最大. 此外,在16个方案组合中,公众满意度最低的为组合14和16,即在技术性方案选择一般方案,服务档次为低,地理位置较为偏僻情况下,两类消费群体的消费欲望都较低(公众满意度2.16). 与之相反,当技术性方案复杂,服务档次设定较高,地理位置极佳时,两类消费群体的满意度都较高(公众满意度4.36). 因此,说明在商业性项目进行规划决策时,技术性方案、服务档次和地理位置对社会公众的满意度影响较大,应重点考虑. 对于投资者来说,组合2和组合6的满意度最差,即技术性方案复杂,服务人群消费水平较低,地理位置偏僻时,无论服务档次高低,投资者的收益都不高(投资者满意度1.24). 与之相反,选择一般的工程技术性方案,服务人群消费水平较高,地理位置处于市中心时,无论服务档次高低,投资者都将获得较高收益(投资者满意度4.8). 因此,作为投资者更为关心工程技术性方案、项目选址和服务对象定位. 作为最终决策者,则应将两者的满意度进行权衡,确定最终的方案组合. 最后,通过访谈方式对运行结果进行验证,受访者认为利用贝叶斯网络模型获得的决策过程运算结果与实际情况较为相符.
综上所述,利用贝叶斯网络模型辅助项目决策,决策者可在较短时间内获得较为可靠的方案组合. 该方法将以往需要依赖决策者主观经验的抽象决策过程定量化,增强了决策过程的科学性.
表 11(Table 11)

表 11 公众参与PPP项目决策模型模拟运算结果
Table 11 Simulation results of public participation model for PPP project
| 编号 |
决策变量 |
|
目标变量数值 |
| 技术性方案 |
服务档次 |
人均开销/元 |
地理位置 |
|
公众满意度 |
投资者满意度 |
综合满意度 |
| 1 |
复杂 |
高 |
100 |
极佳 |
|
4.36 |
2.68 |
3.52 |
| 2 |
复杂 |
高 |
100 |
偏僻 |
|
3.52 |
1.24 |
2.38 |
| 3 |
复杂 |
高 |
200 |
极佳 |
|
4.36 |
3.16 |
3.76 |
| 4 |
复杂 |
高 |
200 |
偏僻 |
|
3.52 |
1.72 |
2.62 |
| 5 |
复杂 |
低 |
100 |
极佳 |
|
3.88 |
2.68 |
3.28 |
| 6 |
复杂 |
低 |
100 |
偏僻 |
|
3.24 |
1.24 |
2.24 |
| 7 |
复杂 |
低 |
200 |
极佳 |
|
3.88 |
3.16 |
3.52 |
| 8 |
复杂 |
低 |
200 |
偏僻 |
|
3.24 |
1.72 |
2.48 |
| 9 |
普通 |
高 |
100 |
极佳 |
|
3.60 |
4.40 |
4.00 |
| 10 |
普通 |
高 |
100 |
偏僻 |
|
2.64 |
3.20 |
2.92 |
| 11 |
普通 |
高 |
200 |
极佳 |
|
3.60 |
4.80 |
4.20 |
| 12 |
普通 |
高 |
200 |
偏僻 |
|
3.60 |
2.64 |
3.12 |
| 13 |
普通 |
低 |
100 |
极佳 |
|
3.12 |
4.40 |
3.76 |
| 14 |
普通 |
低 |
100 |
偏僻 |
|
2.16 |
3.20 |
2.68 |
| 15 |
普通 |
低 |
200 |
极佳 |
|
3.12 |
4.80 |
3.96 |
| 16 |
普通 |
低 |
200 |
偏僻 |
|
2.16 |
3.60 |
2.88 |
|
表 11 公众参与PPP项目决策模型模拟运算结果
Table 11 Simulation results of public participation model for PPP project
|
4 结论与展望
目前我国绝大部分PPP项目在工程决策时并没有充分考虑公众参与对于项目未来运营所带来的正面作用,更多的是凭借决策者主观意志和专家意见主导着项目的立项、决策、建设运营等阶段. 因此,PPP项目在建设过程中经常遇到很多来自社会公众的不满和阻碍,项目落成后出现效益不佳的情况. 本文提出在PPP项目决策时引入公众参与项目决策,并利用贝叶斯网络模型辅助项目决策方案的选择,使社会公众与投资者两大利益相关者的满意度达到最优组合. 随着大数据技术的发展,公众参与的途径将不断完善,更高价值的数据信息可有效引入项目决策,决策者将更加清楚了解终端用户的需求. 利用基于贝叶斯网络的多目标决策模型,决策者能更加有效、快速地获得使项目利益相关者满意程度都较高的项目规划决策方案. 在未来的研究中,将进一步考虑增加变量的取值范围,针对复杂的贝叶斯网络模型寻找更加快捷的运算过程,并引入工程实例,通过问卷调查、现场访谈和公众行为大数据搜索获得真实数据,探寻社会公众和投资者两个目标变量下项目最佳决策方案的选择途径.

 2018, Vol. 35
2018, Vol. 35
