为了规避投资风险，投资者往往将资金分散配置到多种资产上，也就是“不要把所有鸡蛋放到同一个篮子里”的组合投资思想. 1952年Markowitz^[1]提出了投资组合问题的均值–方差(Mean-Variance，MV)模型，随后被众多学者进行了广泛的推广^[2-4]. 该模型假设股票的收益为随机变量，分别用其均值与方差来量化股票的预期收益与风险. 然而，在实际应用中难以估计股票收益的均值和方差，甚至难以找到合适的概率分布刻画股票的收益. 20世纪90年代初Cover^[5]借鉴在线算法与竞争分析理论的思想，建立了在线投资组合模型. 该模型不对未来的股票价格作任何概率假设，允许股价无规律地剧烈波动，仅利用历史数据计算当期的投资比例，克服了MV模型的缺陷，更符合金融管理的实际情况.

Cover^[5]提出了第一个在线投资组合策略，并证明了该策略具有与最优定常再调整策略(Best Constant Rebalanced Portfolio，BCRP)相同的渐近收益，称这样的策略为泛证券投资组合策略(Universal Portfolio，UP). Singer^[6]研究了根据市场变化的转换策略，提高了投资的收益. Agarwal等^[7]运用数学优化中的牛顿方法给出了有效的、计算性能较好的在线投资策略. Helmbold等^[8]应用指数更新方法，提出了利用当期获得的股票价格信息确定下一期投资比例的指数梯度策略(Exponential Gradient，EG)，该策略对于惯性股票价格序列能够获得较好的收益. 张卫国等^[9]基于线性学习函数对EG策略进行了改进，构造了LFM策略，并证明它具有泛证券性. 张永等^[10]用有限个静态专家意见代表常见类投资策略，应用弱集成算法设计在线投资组合策略并分析其竞争性能. 刘善存等^[11]将交易费用引入UP策略，并证明其仍然是泛证券投资组合策略. Borodin等^[12]通过计算组合中两两股票在两个相邻历史窗口上对数收益率之间的相关性，并利用股票价格均值回归的规律调整投资比例，提出了Anticor策略. 虽然没有证明Anticor策略是泛证券投资组合策略，但是实证结果表明该策略不但远远超过了在线的UP、EG等策略，而且超过了离线的BCRP策略. 基于证券价格的反转变化假设，Li等^[13-14]利用均值复位的思想，给出了能够实现更多收益的在线投资组合策略. O'Sullivan和Edelman^[15]通过定义相对绩效度量因子，提出了适应性泛证券投资组合策略(Adaptive Universal Portfolio，AUP)，提升了UP策略的表现.

上述研究均使用获取到的所有历史数据来构造投资比例，然而实际的股票市场往往波动剧烈，过去较长时间的股票价格与当前的股票价格关系不大，甚至会对当前的投资决策产生干扰. 因此，本文考虑利用近期历史数据构造在线投资组合策略. 在策略设计过程中，不考虑投资者的风险偏好，因此所设计的策略是风险中性的. 首先，在每一期的期初，使用固定长度历史数据计算投资比例，设计一种基于移动窗口的在线投资组合策略; 然后，考虑到在实际的投资决策中移动窗口的长度应该随着市场的波动而变化，即适应性地选取合适的移动窗口长度，进一步设计了一种适应性的在线投资组合策略. 最后，采用国内外实际股票市场数据，对策略进行实证分析.

1 相关概念与记号

假设投资者选取 $m$ 只股票进行投资，整个投资过程分为 $n$ 期. 每一期所有可能采用的投资比例构成的集合用 ${\varDelta _m}$ 表示，即

${\varDelta _m} = \left\{ {{b} = {{({b_1},{b_2},\cdots,{b_m})}^{\rm{T}}}:{b_i} \geqslant 0,\sum\limits_{i = 1}^m {{b_i} = 1} } \right\}.$

(1)

投资者在第 $t$ 期期初采用的投资比例表示为 ${{{b}}_t} = {({b_{t,1}},{b_{t,2}},\cdots,{b_{t,m}})^{\rm{T}}} \in {\varDelta _m}(1 \leqslant t \leqslant n)$ ，其中 ${b_{t,i}}$ 表示投资者在第 $t$ 期期初投资于第 $i$ 只股票的比例 $\left( {1 \leqslant i \leqslant m} \right)$ . 所有期的投资比例构成的序列 $\{ {{b}_t}\} _{t = 1}^n$ 称为一个在线投资组合策略，简记为 ${{{b}}_{1:n}}$ . 第 $t$ 期相对价格向量表示为 ${{{x}}_t} = {({x_{t,1}},{x_{t,2}}, \cdots ,{x_{t,m}})^{\rm{T}}} \in {\bf{R}}_ + ^m$ ，其中 ${x_{t,i}}$ 表示第 $i$ 只股票在第 $t$ 期的相对价格，即第 $i$ 只股票在第 $t$ 期收盘价与第 $t - 1$ 期收盘价的比值 $(1 \leqslant t \leqslant n)$ . 整个投资期的相对价格向量序列为 $\{ {{{x}}_t}\} _{t = 1}^n$ ，简记为 ${{{x}}_{1:n}}$ . 整个投资期的最终累积收益为

${S_n}({{{b}}_{1:n}}) = {S_0}\prod\limits_{t = 1}^n {{{b}}_t^{\rm{T}}{{{x}}_t}} = {S_0}\prod\limits_{t = 1}^n {\sum\limits_{i = 1}^m {{b_{t,i}}{x_{t,i}}} } .$

(2)

一般地，初始投资比例往往采用平均投资的方式，即 ${{{b}}_1} = (1/m, \cdots ,1/m)$ ; 投资者的初始财富值设为 ${S_0} = 1$ .

若每一期均采用相同的投资比例 ${{b}} \in {\varDelta _m}$ ，这样的策略称为定常再调整策略(Constant Rebalanced Portfolio，CRP)，其最终累积收益为

${S_n}({\rm{CRP}}({b})) = \prod\limits_{t = 1}^n {{{b}^{\rm{T}}}{{x}_t}} .$

(3)

最终累积收益 ${S_n}({\rm{CRP}}({b}))$ 最大的CRP策略称为最优定常再调整策略，记为 ${{{b}}^ * }$ ，即

${{b}^*} = \mathop {\arg \max }\limits_{{b} \in {\varDelta _m}} {S_n}({\rm{CRP}}({b})).$

(4)

这是一种事后策略，不能用于实际的投资决策. Cover^[5]证明了该策略具有一系列特性，因而往往被选作衡量在线投资组合策略性能的基准策略.

Cover^[5]的策略UP是对所有投资比例 ${{b}}$ 的加权平均. 若投资比例 ${{b}}$ 对应的CRP策略至当前期的累积收益越大，则被赋予的权重也越大. 具体地，第 $t + 1$ 期期初的投资比例为

${{{b}}_{t + 1}} = \frac{{\int_{{\varDelta _m}} {{{b}}{S_t}({{b}}){\rm{d}}{{b}}} }}{{\int_{{\varDelta _m}} {{S_t}({{b}}){\rm{d}}{{b}}} }}.$

(5)

其中 ${S_t}({{b}}) = \prod\nolimits_{\tau = 1}^t {{{{b}}^{\rm{T}}}} {{{x}}_\tau }$ .

2 策略设计 2.1 MWAUP策略

O'Sullivan和Edelman^[12]改进了Cover的UP策略，通过赋予较优CRP策略较大的权重，提出了AUP策略. 该策略使用过去所有的历史数据来确定当期投资比例. 为了避免过去较长时间的股价数据对当前投资决策的干扰，本文考虑仅利用近期固定长度窗口数据来确定投资比例.

假设每一期采用的历史数据窗口长度是固定的，用 $r(r \in {\bf{N}^ + })$ 表示. 在第 $t + 1$ 期期初，CRP策略 ${{b}}$ 最近 $r$ 期的累积收益为

${S_{t,r}}({{b}}) = \prod\limits_{\tau = t'}^t {{{{b}}^{\rm{T}}}} {{{x}}_\tau }.$

(6)

其中 $t' = \max \left\{ {t - r + 1,{\rm{ }}1} \right\}$ . 类似于UP策略，本文提出的策略是所有CRP策略的加权平均，若近期累积收益越大，则权重就越大. 为了扩大不同CRP策略权重之间的差异，引入相对绩效度量因子的概念. 相对绩效度量因子 ${\alpha _{t + 1}}$ 为从 $\left( {{\varDelta _m},\{ {{{x}}_\tau }\} _{\tau = t'}^t} \right)$ 到 $(0,1)$ 的映射， ${\alpha _{t + 1}}({{b}})$ 是关于 ${S_{t,r}}({{b}})$ 的增函数. 那么，相应的投资组合策略为

${{{b}}_{t + 1}} = \frac{{\int_{{\varDelta _m}} {{{b}}{\alpha _{t + 1}}({{b}})} {S_{t,r}}({{b}})\operatorname{d} {{b}}}}{{\int_{{\varDelta _m}} {{\alpha _{t + 1}}({{b}}){S_{t,r}}({{b}})\operatorname{d} {{b}}} }}.$

(7)

该策略称为基于移动窗口的适应性泛证券投资组合策略(Moving-Window-Based Adaptive Universal Portfolio，MWAUP).

在实际计算中，将投资比例集合 ${\varDelta _m}$ 均等离散化为集合 ${\tilde \varDelta _m}$ ，则式(7)变为

${{{b}}_{t + 1}} = \frac{{\displaystyle\sum\nolimits_{{{b}} \in {{\tilde \varDelta }_m}} {{{b}}{\alpha _{t + 1}}({{b}}){S_{t,r}}({{b}})} }}{{\displaystyle\sum\nolimits_{{{b}} \in {{\tilde \varDelta }_m}} {{\alpha _{t + 1}}({{b}}){S_{t,r}}({{b}})} }}.$

(8)

不同的相对绩效度量因子选取方式，对应不同的MWAUP策略. 在下一节的实证分析中，相对绩效度量因子的选取方式为: 对 ${\tilde \varDelta _m}$ 中所有的CRP策略 ${{b}}$ 根据其最近 $r$ 期的累积收益 ${S_{t,r}}({{b}})$ 大小进行降序排序，对排在第 $j$ 位的策略 ${{b}}$ 赋予相对绩效度量因子 ${\alpha _{t + 1}}({{b}}) = 1/{2^j}$ .

该策略的计算流程见算法1.

2.2 适应性学习的MWAUP策略

对于MWAUP策略，首先需要给定一个固定且合适的参数 $r$ . 然而，很难寻找到一个合适的 $r$ 的取值，特别是在投资决策的初期. 另外，考虑到股票市场往往存在波动，在一些新兴市场甚至有波动异常的现象出现，在整个投资决策过程中参数 $r$ 始终设定为某一个固定的常数显然也并不合理. 因此，本文进一步设计适应性学习的MWAUP策略，通过适应性学习的方式适应性地确定参数 $r$ 的取值. 将一个 $r$ 取值对应的MWAUP策略当作一个专家策略，则不同的 $r$ 取值对应不同的专家策略. 首先，选取有限个专家策略，所构成的集合为 ${\varGamma } \subseteq {\bf{N}_ + }$ ; 然后，在每一期的期初，选取当前累积收益最大的专家策略对应的 $r$ 值作为当期的 $r$ 值，进而计算当期的投资比例. 称该策略为可变的MWAUP策略(Variable Moving-Window-Based Adaptive Universal Portfolio，VMWAUP).

参数 $r$ 对应的专家策略记为

${{b}}_{t + 1}^r = \frac{{\displaystyle\sum\nolimits_{{{b}} \in {{\tilde \varDelta }_m}} {{{b}}{\alpha _{t + 1}}({{b}}){S_{t,r}}({{b}})} }}{{\displaystyle\sum\nolimits_{{{b}} \in {{\tilde \varDelta }_m}} {{\alpha _{t + 1}}({{b}}){S_{t,r}}({{b}})} }}.$

(9)

在第 $t + 1$ 期的期初，首先计算所有专家直至第 $t$ 期的累积收益 ${S_t}\left( {{b}_{1:t}^r} \right)$ ，然后选取累积收益最大的专家策略对应的 $r$ 值作为VMWAUP策略的移动窗口长度，即

${r_{t + 1}} = r_t^* = \mathop {\arg \max }\limits_{r \in {\varGamma }} {S_t}({b}_{1:t}^r).$

(10)

相应的投资比例为

${{{b}}_{t + 1}} = \frac{{\displaystyle\sum\nolimits_{{{b}} \in {{\tilde \varDelta }_m}} {{{b}}{\alpha _{t + 1}}({{b}}){S_{t,{r_{t + 1}}}}({{b}})} }}{{\displaystyle\sum\nolimits_{{{b}} \in {{\tilde \varDelta }_m}} {{\alpha _{t + 1}}({{b}}){S_{t,{r_{t + 1}}}}({{b}})} }}.$

(11)

该策略的计算流程见算法2.

3 实证分析

本节采用实际股票价格数据对上一节提出的MWAUP和VMWAUP策略进行实证分析，检验其在实际股票市场中的表现.

3.1 数据

本文实证部分选用美国市场纽约证券交易所22年的股票数据（从1962年7月3日到1984年12月31日）和中国市场上证50成份股12年的股票数据（2004年1月2日~2016年6月30日），其中上证50成份股的数据来源于Resset金融研究数据库，已经过向后复权复息处理. 构造了6个股票组合进行测试，分别由3只、4只、5只股票组成，股票名称及组合情况见表1.

本文构造的策略MWAUP和VMWAUP主要包含移动窗口长度等参数，在测试时可以针对不同的股票市场类型设置相应的参数. 对于本文采用的股票数据，设置参数 $r = 300,{\varGamma } = \{ 250,300,350\} $ .

为了更好地说明策略MWAUP和VMWAUP的表现，本节将它们与基准策略Market和BCRP以及已有的在线投资组合策略EG、ONS、OLMAR、UP及AUP进行比较. 相关策略介绍如下：

(1) Market：初始时刻平均投资的购买并持有策略;

(2) BCRP：最优定常再调整策略(事后策略);

(3) EG：指数梯度策略，采用Helmbold等^[7]的参数设置，即 $\eta = 0.05$ ;

(4) ONS：在线牛顿梯度策略^[9]，其中参数设置为 $\eta = 0,\beta = 1,\varDelta = 1/8$ ;

(5) OLMAR：在线移动均值回归策略^[11]，其中参数设置为 $\alpha = 0.5,$ ò = 10;

(6) UP：Cover的泛证券投资组合策略^[5]，其离散化可行策略集的步长设为0.05;

(7) AUP：O'Sullivan和Edelman^[12]提出的适应性泛证券投资组合策略.

3.2 结果分析

不同策略在6个股票组合上的最终累积收益见表2，其中V/B表示策略VMWAUP与BCRP的最终累积收益的比值; V/M表示VMWAUP与MWAUP的最终累积收益的比值. 另外，为便于比较，将每个股票组合上排在前两位的策略的最终累积收益加粗标出. 从表2可以看出，策略MWAUP和VMWAUP在各个股票组合上的表现明显优于已有的在线投资组合策略，并且从V/B的值可以看出，策略VMWAUP的表现均超过离线的BCRP策略，这说明仅使用近期的历史数据构造的投资策略提升了策略AUP的性能; 同时，V/M的值也超过了1，最高达到了2.03，这表明通过对移动窗口适应性学习可以进一步提升策略MWAUP的性能.

最后，为检验策略的结果是否是由随机因素造成的，表3给出了策略VMWAUP的统计检验结果. 这是在基金行业中较为常见且行之有效的做法. 具体地，因随机因素取得的超额收益的概率最大仅为0.02，均未超过0.05. 这表明策略VMWAUP的累积收益结果是可信的.

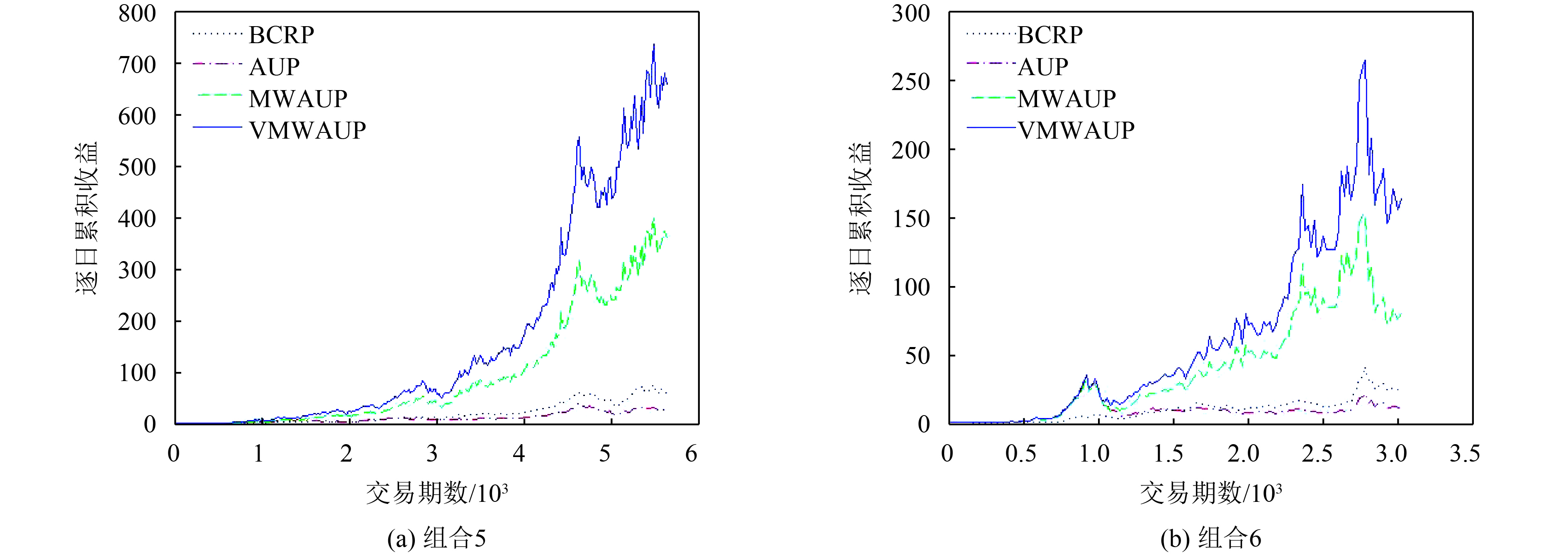
为了进一步说明策略MWAUP和VMWAUP相对于策略BCRP与AUP的性能，本文给出了策略BCRP、AUP、MWAUP以及VMWAUP在组合5和组合6，即两个5只股票组合上的逐日累积收益，见图1. 从图1可以看出，策略MWAUP和VMWAUP不但具有较高的最终累积收益，而且逐日累积收益也稳定地高于策略BCRP与AUP. 这也说明了策略MWAUP和VMWAUP具有更好的性能. 同时，策略MWAUP和VMWAUP的逐日累积收益变化趋势基本保持一致，前者一直稳定地超过后者并且随着投资期数的增加，两者之间的差距也随着扩大，这也说明了适应性学习的策略VMWAUP具有更好的性能.

3.3 敏感度分析 3.3.1 移动窗口长度 $r$ 的敏感性分析

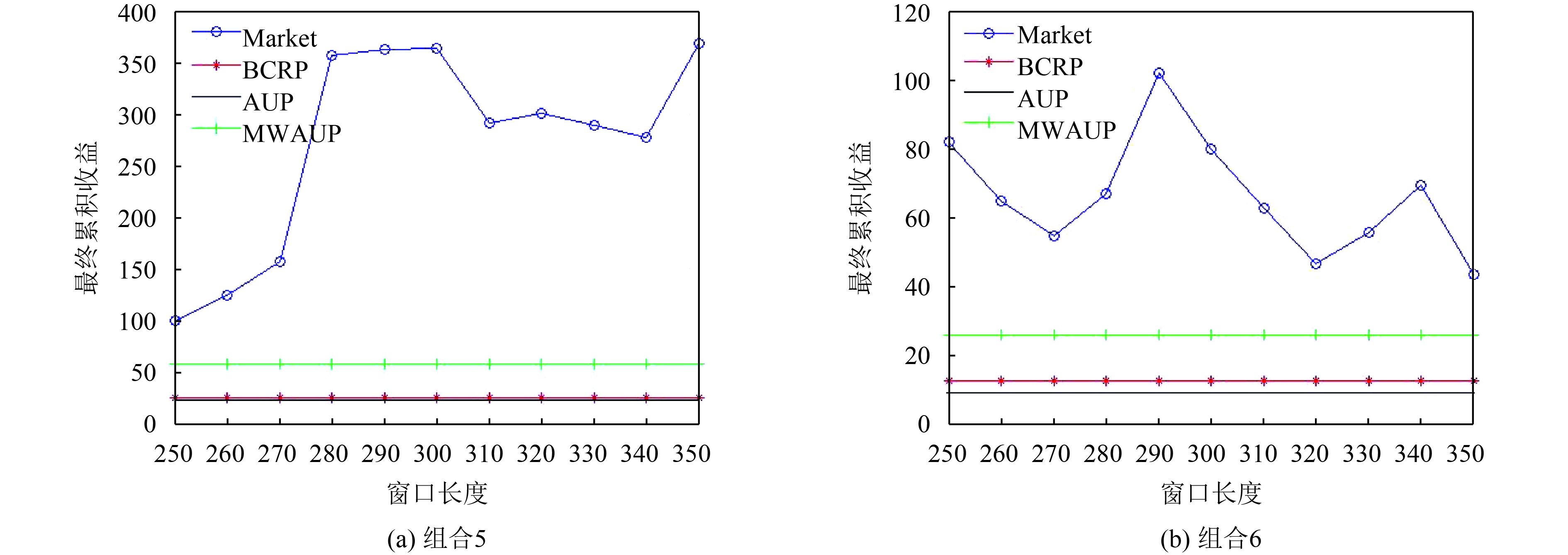
为了检验移动窗口长度 $r$ 对策略MWAUP的影响，给出了当移动窗口长度取不同值时策略MWAUP在组合5和组合6上的表现，其中参数 $r$ 的取值域为 $\left\{ {250,260, \ldots ,350} \right\}$ ，见图2. 为了便于对比，图2同时也给出了策略Market、BCRP和AUP的表现. 由图2可知，同一个移动窗口长度 $r$ 在不同的股票组合上的表现不尽相同，且无明显趋势，总体上看，当 $r$ 在250~350这一范围内时，策略MWAUP的累积收益明显优于策略AUP. 这进一步说明了过去较长时间的股票价格数据对策略会产生干扰.

3.3.2 移动窗口学习集合 ${\varGamma }$ 的敏感性分析

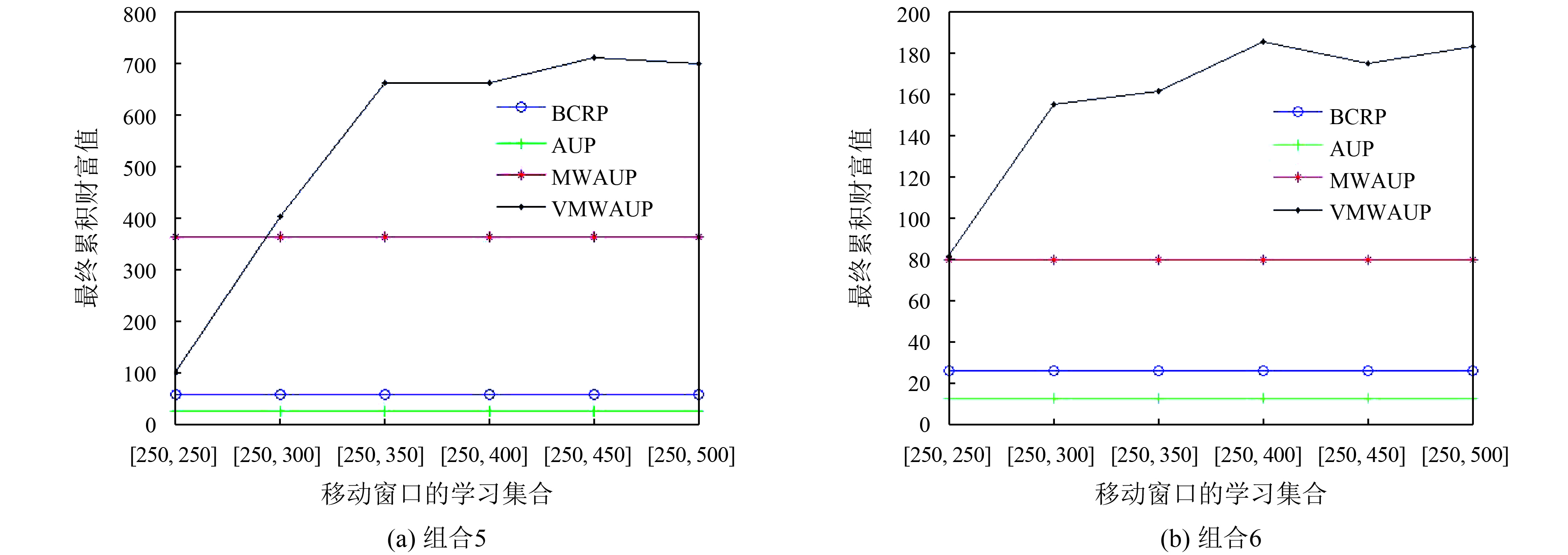
为了检验移动窗口学习集合 ${\varGamma }$ 对策略VMWAUP的影响，给出了当移动窗口学习集合取不同值时策略MWAUP在组合5和组合6上的表现，其中参数 ${\varGamma }$ 的取值域为 $\left\{ {\left[ {250,250 + 50j} \right];j = 0,1,2,3,4,5} \right\}$ ，见图3. 图中同时给出了策略BCRP、AUP和MWAUP的最终累积收益. 由图3可知，随着移动窗口的学习集合的扩大，策略VMWAUP的最终累积收益也逐步增大，这进一步说明适应性学习策略VMWAUP具有更好的性能.

4 结论

本文利用近期历史数据，基于移动窗口设计了两个风险中性的在线投资组合策略MWAUP和VMWAUP，避免了过去较长时间的历史数据对当前投资决策产生的干扰. 通过实证分析，说明了它们优于AUP等已有的在线投资组合策略. 另外，与策略MWAUP相比，适应性学习策略VMWAUP具有更好的性能，更适用于非平稳股票市场中的投资决策. 然而，本文存在一定的不足之处，主要是未能从理论上证明所设计策略的性能，这将是我们以后关注的方向.