多示例学习是一种在处理训练样本时，将训练样本当成多示例包（多个示例的集合）来进行处理的有监督分类学习方法 ^[1]. 在多示例学习中，训练集由多个多示例包构成，每个包中包含多个单示例. 对于分类任务的训练集，一个多示例包对应一个样本，样本标签只和包有关，而包中的每个示例的所属标签是无法直接获取的^[2]. 传统二分类任务中，若多示例包中至少含有一个示例为正类示例，则该多示例包被标记为正包；相反，若多示例包中的所有示例均为负类示例，则该多示例包被标记为负包. 对于二分类多示例问题，分类器将会在已知标签的多示例包中进行训练，从而对未知标签的包进行分类，预测其所属分类为正类还是负类. 多示例学习已经取得了广泛的研究与应用，如文档分类^[3]、图像识别^[4]、情感分析^[5-6]、人脸识别^[7]、对象检测^[8]等.

多示例学习问题提出后，研究者们提出了一系列多示例学习算法. Andrews等^[9]在支持向量机基础上，提出了两种基于支持向量机的多示例学习算法MI-SVM和mi-SVM. Qi Zhang等^[10]结合最大期望(EM)算法和多样性密度(DD)算法，提出了EM-DD算法. Jun Wang等^[11]在K-近邻(KNN)算法基础上，使用基于包层级的豪斯多夫距离来取代欧氏距离，提出了基于最小化豪斯多夫距离(minimum Hausdorff distance)的Citation-KNN算法.

这些多示例学习算法能够获得不错的分类效果的前提条件是，数据集中具有数量充足的训练样本. 当数据集的训练样本数量充足时，这些多示例学习算法能够获得充分的分类信息来建立准确的预测模型. 但是，当数据集的训练样本数量不充足时，由于分类信息的缺乏，训练所得模型的分类效果可能不佳^[12]. 针对训练集中样本数量可能不充足的情况，本文提出了基于抗噪声的多任务多示例学习算法(Multi-task Multi-instance Anti-noise Learning, MtMiAnL). 一方面，本文所提出的MtMiAnL算法能够在训练样本数量不足时，通过同时训练多个学习任务，利用任务间的关联性来提高各个分类任务的预测性能. 另一方面，在实际的应用中，数据可能在传输过程中受到的干扰，存在噪声信息. MtMiAnL算法通过示例加权方式，降低噪声数据对预测结果的影响.

本文提出了基于抗噪声的多任务多示例学习算法(MtMiAnL)，跟现有的多示例学习算法相比，本文的主要贡献在于：(1) 算法充分考虑了数据可能存在噪声信息，在训练过程中对示例进行加权，通过迭代更新权值来降低噪声对结果的影响；(2) 提出了在多任务框架下的抗噪声多示例学习算法，解决了在训练样本数量不充足的情况下，通过联合多个相关任务一起学习，提高分类的精度.

1 MtMiAnL算法原理

MtMiAnL算法分为多示例加权和目标函数多任务化两部分. 在多示例加权阶段，首先对样本中的示例添加初始权值，然后在训练过程中对示例的权值进行更新，以降低噪声示例对预测结果的影响. 在目标函数多任务化阶段，把算法从单任务学习环境扩展到多任务学习环境，最大化利用多个任务的关联性来提高算法性能，从而解决了分类模型因样本数量不充足而造成性能不佳的问题.

2 基于抗噪声的多任务多示例学习算法 2.1 多示例加权

假设存在T个相似的多示例加权学习任务，则第t(1<t $\leqslant$ T)个任务的数据集表示为D_t，D_t由正包集合P_t和负包集合N_t组成，即D_t= ${{{P}}_t} \displaystyle\cup{{{N}}_t}$ . 其中，正包集合 ${{{P}}_{{t}}} = \left[ {{{{B}}_{{{1t}}}},\cdots,{{{B}}_{{{it}}}},\cdots,{{{B}}_{\left| {{{{P}}_{{t}}}} \right|{{t}}}}} \right]$ ，负包集合 ${{{N}}_{{t}}} = \left[ {{{{B}}_{{{1t}}}},\cdots,}\right.$ $\left.{{{{B}}_{{{it}}}},\cdots,{{{B}}_{\left| {{{{N}}_{{t}}}} \right|{{t}}}}} \right]$ ，式中|P_t|和|N_t|分别表示任务t的正包集合P_t和负包集合N_t所包含的多示例包个数. 分类标签Y_it∈{–1, 1}为任务t的第i个多示例包B_it的标签. 当Y_it=1时，即B_it∈P_t，多示例包B_it被认定为正包；相反，当Y_it=–1时，即B_it∈N_t，多示例包B_it被认定为负包.

多示例包B_it中的m个示例 $[{{B}}_{it}^1,\cdots,{{B}}_{it}^j,\cdots,{{B}}_{it}^{{m}}]$ 被赋予不同的权值 $[{{Q}}_{it}^{1(k)},\cdots,{{Q}}_{it}^{j(k)},\cdots,{{Q}}_{it}^{{m(k)}}]$ ，权值的表达形式为

$Q_{it}^{j(k)} = Q_{it}^{j{\rm{(}}k - 1{\rm{)}}}{{\rm{e}}^{{\rm{(}}{Y_{it}} \cdot y_{it}^j - 1{\rm{)}}/{\alpha ^2}}}.$

(1)

式(1)中，Q_it^j(k)表示包中示例B_it^j在第k次迭代的权值，Q_it^j(k–1)表示第k–1次迭代的权值，α为常数调节因子，一般设为1，Y_it为多示例包B_it的标签，y_it^j为包中示例B_it^j的标签. Y_it是已知的，而y_it^j是未知的. 在第k次迭代求解中，对于多示例包B_it，若包中示例B_it^j的标签y_it^j与包标签Y_it一致，则认为该示例不是噪声示例，此时Q_it^j(k)=Q_it^j(k-1)e⁰，示例的第k次迭代权值与第k–1次权值相等，不会发生变化；相反，当示例B_it^j的标签y_it^j与包标签Y_it不一致时，则该示例为包中的噪声示例，故第k次迭代的权值为 $Q_{it}^{j(k)} = Q_{it}^{j{\rm{(}}k - 1{\rm{)}}}{{\rm{e}}^{ - 2/{\alpha ^2}}}$ ，与第k–1次的迭代权值相比，将适当缩小，从而降低该示例对结果的影响.

当多示例包B_it为正包时，用符号p_it来表示加权后的包B_it；当多示例包B_it为负包时，用符号n_it来表示加权后的包B_it，具体描述如下

${{{p}}_{{{it}}}} = \sum\nolimits_{j = 1}^{\left| {{{{B}}_{{{it}}}}} \right|} {Q_{it}^{j{\rm{(}}k{\rm{)}}}} {{B}}_{{{it}}}^{{j}}{\Bigg{/}}\sum\nolimits_{j = 1}^{\left| {{{{B}}_{{{it}}}}} \right|} {Q_{it}^{j{\rm{(}}k{\rm{)}}}} ,{\rm{ if }}\;\;\;{Y_{it}} = 1.$

(2)

${{{n}}_{it}} = \sum\nolimits_{j = 1}^{\left| {{{{B}}_{it}}} \right|} {Q_{it}^{j(k)}} {{B}}_{it}^j{\Bigg{/}}\sum\nolimits_{j = 1}^{\left| {{{{B}}_{it}}} \right|} {Q_{it}^{j(k)},{\rm{if}}\;\;\;{Y_{it}} = - 1} . $

(3)

式(2)和(3)中，|B_it|表示多示例包B_it的示例个数. 在迭代过程中，p_it和n_it分别按照式(1)进行更新，能有效降低正负示例包中噪声示例对模型的影响，从而提高模型的预测精度.

根据式(2)和式(3)中正负多示例包的加权表达形式以及约束条件，可以为这T个多示例加权分类任务构造一个优化问题，该优化问题可以表达为

$\left\{\begin{gathered} {\text{minimize}}: \hfill \\ J\left( {{{{w}}_{{t}}},{b_t},\zeta _{it}^ + ,\zeta _{it}^ - } \right) = \hfill \\ \frac{1}{2}\sum\limits_{t = 1}^T {{{\left\| {{{{w}}_{{t}}}} \right\|}^2}} + {C_0}\sum\limits_{t = 1}^T {\sum\limits_{i = 1}^{\left| {{{{P}}_{{t}}}} \right|} {\zeta _{it}^ + } } + {C_0}\sum\limits_{t = 1}^T {\sum\limits_{i = 1}^{\left| {{{{N}}_{{t}}}} \right|} {\zeta _{it}^ - } } \;.\hfill \\ {\text{subject to:}} \hfill \\ {{{w}}_{{t}}}{{{p}}_{{{it}}}} + {b_t} \geqslant {G_{it}} - \zeta _{it}^ + , 1 \leqslant i \leqslant \left| {{{{P}}_t}} \right| , \hfill \\ {{{w}}_{{t}}}{{{n}}_{{{it}}}} + {b_t} \leqslant - 1 + \zeta _{it}^ - , 1 \leqslant i \leqslant \left| {{{{N}}_t}} \right| , \hfill \\ \zeta _{it}^ + \geqslant 0,\zeta _{it}^ - \geqslant 0, 1 \leqslant t \leqslant T. \hfill \\ \end{gathered}\right.$

(4)

式(4)中， ${{{w}}_{{t}}}$ 为分类任务t的向量，约束条件中的控制变量G_it=(2–|B_it|)/|B_it|，|B_it|表示任务t的正包B_it中的示例个数，该控制变量G_it在约束条件中可保证包中的正示例个数至少为1. $C_0 \geqslant 0$ 是惩罚系数， $\zeta _{it}^+ \geqslant 0$ 和 $\zeta _{it}^- \geqslant 0$ 是松弛变量，使优化问题可以容纳一定的错误分类结果.

通过迭代求解最小化问题(4)，可以在保持包中正常示例的权值不变的情况下，将包中噪声示例的权值不断减小，从而降低噪声示例对分类器的影响.

2.2 多任务目标方程

然而，优化问题(4)只是单纯将多个分类任务进行累加求和并求解，并未考虑到多个任务间的关联性，本质上还是一种单任务学习问题. 在样本数量不充足的情况下，并不能够保证分类任务t的分类模型的预测性能. 因此，下文对优化问题(4)进行了扩展，提取任务间的关联性，把算法扩展到多任务环境中.

在多任务学习环境中，为了提取T个任务间的相似性来提高每个分类任务的预测性能，本文将任务t的向量 ${{{w}}_{{t}}}$ 表示为多任务形式： ${{{w}}_{{t}}} = {{{w}}_{{0}}} + {{{v}}_{{t}}}$ ，向量 ${{{v}}_{{t}}}$ 表示任务t所独有的向量，向量 ${{{w}}_{{0}}}$ 为T个任务所共享的向量^[13]. 因此，引入向量的多任务形式 ${{{w}}_{{t}}} = {{{w}}_{{0}}} + {{{v}}_{{t}}}$ 到优化问题(4)中，将其扩展到多任务学习环境下，从而提出了基于抗噪声的多任务多示例学习算法模型

$\left\{\begin{gathered} {\text{minimize:}} \hfill \\ J{\text{(}}{{{w}}_{{0}}},{{{v}}_{{t}}},\zeta _{it}^ + ,\zeta _{it}^ - {\text{)}} = \hfill \\ T{\lambda _0}{\left\| {{{{w}}_{{0}}}} \right\|^2} \!\!\!+\!\! {\lambda _1}\!\!\sum\limits_{t = 1}^T {{{\left\| {{{{v}}_{{t}}}} \right\|}^2}} \!\!\!+\!\! {C_0}\!\!\sum\limits_{t = 1}^T \!\!{\sum\limits_{i = 1}^{\left| {{{{P}}_t}} \right|} {\zeta _{it}^ + } } \!\!\!+\!\! {C_0}\sum\limits_{t = 1}^T {\sum\limits_{i = 1}^{\left| {{{{N}}_{{t}}}} \right|} {\zeta _{it}^ - } }\;. \hfill \\ {\text{subject to:}} \hfill \\ {{\text{(}}{{{w}}_{{0}}} + {{{v}}_{{t}}}{\text{)}}^{\text{T}}}{{{p}}_{{{it}}}} + {b_t} \geqslant {G_{it}} - \zeta _{it}^ + , 1 \leqslant i \leqslant \left| {{{{P}}_{{t}}}} \right| , \hfill \\ {{\text{(}}{{{w}}_{{0}}} + {{{v}}_{{t}}}{\text{)}}^{\text{T}}}{{{n}}_{{{it}}}} + {b_t} \leqslant - 1 + \zeta _{it}^ - , 1 \leqslant i \leqslant \left| {{{{N}}_{{t}}}} \right| , \hfill \\ \zeta _{it}^ + \geqslant 0 ,\zeta _{it}^ - \geqslant 0 , 1 \leqslant t \leqslant T. \end{gathered}\right. $

(5)

式(5)中， $\lambda _0\geqslant 0$ 和 $\lambda _1\geqslant 0$ 为多任务权重系数，用来控制任务之间的相似度.

当λ₀为一个较小的固定值，而λ₁趋近于无穷大时，训练出来的各个任务所独有的向量 ${{{v}}_{{t}}}$ 趋近于零向量，则有 ${{{w}}_{{t}}} = {{{w}}_{{0}}}$ ，所有任务的向量 ${{{w}}_{{1}}},{{{w}}_{{2}}},\cdots,{{{w}}_{{T}}}$ 将会类似，此时所有任务的相似性最高.

当λ₁为一个较小的固定值，而λ₀趋近于无穷大时，此时训练出来的任务间共享的向量 ${{{w}}_{{0}}}$ 趋近于零向量，则有 ${{{w}}_{{t}}} = {{{v}}_{{t}}}$ ，所有任务的向量 ${{{w}}_{{1}}},{{{w}}_{{2}}},\cdots,{{{w}}_{{T}}}$ 将相互独立，目标函数(5)退化为目标函数(4).

通过求解问题(5)，可以得到优化后的T个任务间所共享的向量 ${{{w}}_{{0}}}$ ，以及各个任务所独有的向量 ${{{v}}_{{t}}}$ ，此时任务t的分类函数为

${F^t}({{{B}}_{{t}}}) = {\text{sign}}\mathop {\max }\limits_{{{B}}_{{t}}^{{j}} \in {{{B}}_{{t}}}} {\text{(}}({{{w}}_{{0}}} + {{{v}}_{{t}}}){{B}}_{{t}}^{{j}} + {b_t}\;.$

(6)

式(6)中，B_t为分类任务t中的未知标签多示例包，B_t^j为该未知多示例包中的示例. 当B_t中的示例B_t^j为负示例时，则有 $({{{w}}_{{t}}} + {{{v}}_{{t}}}){{B}}_{{t}}^{{j}} + {b_t} < 0$ ；相反，当B_t^j为正示例时，则有 $({{{w}}_{{t}}} + {{{v}}_{{t}}}){{{B}}}_{{t}}^{{j}} + {b_t} > 0$ . 因此，当B_t中的所有示例都为负示例时，根据分类函数(6)可计算得出： $ F^t({{B}}_t)=-1$ ，即多示例包B_t被划分为负包；当B_t有一个或一个以上的示例为正示例时，根据分类函数(6)可计算得出： $ F^t({{B}}_t)=1$ ，即多示例包B_t被划分为正包.

2.3 优化问题求解

本文拟将式(5)转化为标准SVM形式的二次规划问题，从而求解转化后的二次规划问题. 首先，定义多任务分类模型的耦合参数 $\mu = T{\lambda _0}/{\lambda _1}$ 和惩罚系数 $C = {C_0}/{\lambda _1}$ ；然后，将|P_t|个正包p_it与|N_t|个负包n_it合并为新向量A_it，见式(7)，将|P_t|个变量G_it与|N_t|个常数1合并为新向量I_it，见式(8).

${{{A}}_{{{it}}}} = \left[ {{{{p}}_{1{{t}}}},\cdots,{{{p}}_{\left| {{{{P}}_{{t}}}} \right|{{t}}}},{{{n}}_{{\rm{(}}\left| {{{{P}}_{{t}}}} \right| + 1{\rm{)}}{{t}}}},\cdots,{{{n}}_{{\rm{(}}\left| {{{{P}}_{{t}}}} \right| + \left| {{{{N}}_{{t}}}} \right|{\rm{)}}{{t}}}}} \right],$

(7)

${{{I}}_{{{it}}}} = \left[ {{G_{1t}},\cdots,{G_{\left| {{{{P}}_{{t}}}} \right|t}},1,\cdots,1} \right].$

(8)

基于上述变量A_it和I_it的定义，问题(5)可以简化表示为

$\left\{\begin{gathered} {\rm{minimize:}} \hfill \\ J{\text{(}}{{{w}}_{{0}}},{{{v}}_{{t}}},{\zeta _{it}}{\text{)}} = \hfill \\ \frac{1}{2}(\mu {\left\| {{{{w}}_{{0}}}} \right\|^2} + \sum\limits_{t = 1}^T {{{\left\| {{{{v}}_{{t}}}} \right\|}^2}} ) + C\sum\limits_{t = 1}^T {\sum\limits_{i = 1}^{\left| {{{{P}}_{{t}}}} \right| + \left| {{{{N}}_{{t}}}} \right|} {{\zeta _{it}}} }\;. \hfill \\ {\rm{subject\;to:}} \hfill \\ {Y_{it}}\left[ {{{{\text{(}}{{{w}}_{{0}}} + {{{v}}_{{t}}}{\text{)}}}^{\text{T}}}{{{A}}_{{{it}}}} + {b_t}} \right] \geqslant {{{I}}_{{{it}}}} - {\zeta _{it}} , \hfill \\ 1 \leqslant i \leqslant \left| {{{{P}}_{{t}}}} \right| + \left| {{{{N}}_{{t}}}} \right| , \hfill \\ {\zeta _{it}} \geqslant 0 , 1 \leqslant t \leqslant T. \hfill \\ \end{gathered} \right. $

(9)

为了解决问题(9)，构建两个向量

${{W}} = {\left[ {\sqrt \mu {{w}}_{{0}}^{\rm{T}},{{v}}_{{1}}^{\rm{T}},\cdots,{{v}}_{{t}}^{\rm{T}},\cdots,{{v}}_{{T}}^{\rm{T}}} \right]^{ {\rm{T}}}},$

(10)

${{{X}}_{{{it}}}} = {\left[ {\frac{{\text{1}}}{{\sqrt \mu }}{{A}}_{{{it}}}^{\text{T}},\underbrace {0,\cdots,0}_{t - {\text{1}}},{{A}}_{{{it}}}^{\text{T}},\underbrace {0,\cdots,0}_{T - t}} \right]^{ {\text{T}}}}.$

(11)

根据上述定义的向量，可以发现 ${\left\| {{W}} \right\|^2} = \mu {\left\| {{{{w}}_{{0}}}} \right\|^2} + {\sum_{t = 1}^T {\left\| {{{{v}}_{{t}}}} \right\|} ^2}$ 和 ${{{W}}^{\text{T}}}{{{X}}_{{{it}}}} = {({{{w}}_{{0}}} + {{{v}}_{{t}}})^{\text{T}}}{{{A}}_{{{it}}}}$ . 因此，问题(9)可以进一步改写为

$\left\{\begin{gathered} {\text{minimize: }}\frac{1}{2}{\left\| {{W}} \right\|^2} + C\sum\limits_{t = 1}^T {\sum\limits_{i = 1}^{\left| {{{{P}}_{{t}}}} \right| + \left| {{{{N}}_{{t}}}} \right|} {{\zeta _{it}}} } \hfill . \\ {\text{subject to:}} \hfill \\ {Y_{it}}{\text{(}}{{{W}}^{\text{T}}}{{{X}}_{{{it}}}} + {b_t}{\text{)}} \geqslant {{{I}}_{{{it}}}} - {\zeta _{it}} , \hfill \\ 1 \leqslant i \leqslant \left| {{{{P}}_t}} \right| + \left| {{{{N}}_{{t}}}} \right| , \hfill \\ {\zeta _{it}} \geqslant 0 , 1 \leqslant t \leqslant T. \hfill \\ \end{gathered} \right.$

(12)

通过标准SVM的二次规划求解法，如LibSVM^[14]，可以对问题(12)进行求解，从中得到T个任务间所共享的向量 ${{{w}}_{{0}}}$ ，以及各个任务所独有的向量 ${{{v}}_{{t}}}$ .

2.4 算法步骤

本文算法流程如下：

输入：T个任务数据 ${{D}}_1,\cdots,{{D}}_t,\cdots,{{D}}_T$ ，权值调节因子α，多任务分类模型的耦合参数μ，惩罚系数C，终止迭代次数K；

输出：T个任务的分类器： ${{F}}^1,\cdots,{{F}}^t,\cdots,{{F}}^T$ .

算法步骤：

1) 在任务t中，初始化正包中所有示例的标签为1，负包中所有示例的标签为–1，设置示例B_it^j的初始权值为Q_it^j(0)=1/|B_it|；

2) 更新T个分类任务中，正包和负包所包含的示例B_it^j的权值Q_it^j(k)；

3) 根据表达式(2)和(3)，构建正包p_it和负包n_it；

4) 根据定义描述式(7)，(8)和(11)，构建变量A_it，I_it和X_it；

5) 求解问题(12)，得到T个任务所共享的向量 ${{{w}}_{{0}}}$ 和各个任务所独有的向量 ${{{v}}_{{t}}}$ ，并获得T个任务的分类器 ${{F}}^1,\cdots,{{F}}^t,\cdots,{{F}}^T$

6) 计算目标函数(9)的值J_k，若(J_(k–1)–J_k)/J_k<0.001或迭代次数k达到K时，跳转到步骤9)，否则进入下一步；

7) 基于分类函数(6)，更新T个任务中所有多示例包所含有的示例的标签y_it^j；

8) k=k+1并跳转到步骤2)；

9) 迭代结束，得到每个任务的分类器.

其中，J_(k–1)表示第k–1次迭代时的多任务优化问题(9)的函数值，J_k表示在第k次迭代时的优化问题(9)的函数值.

3 实验与结果分析 3.1 数据集

1) Corel数据集.

参照文献^[15]的实验设定，在Corel数据集中选取“非洲生活”“美食”“汽车”“花”“室内”“室外”“风景”和“非风景”8个类，组成4个任务，即任务1、2、3和4. 每一个任务是一个二分类问题，“非洲生活”“汽车”“风景”和“室内”分别为任务1、2、3和4的正类，而“美食”“花”“非风景”和“室外”分别为任务1、2、3和4的负类. 对于一个任务，正类和负类各有100幅图像. 在训练过程中，抽取20幅正类图和20幅负类图，其余160幅图作为测试集.

2) CIFAR数据集.

选取CIFAR数据集的“卡车”“狗”“小汽车”“猫”“飞机”“鸟”“轮船”和“马”8个类，组成四个任务，即任务1、2、3和4. 每一个任务是一个二分类问题，“卡车”“小汽车”“飞机”和“轮船”分别为任务1、2、3和4的正类，而“狗”“猫”“鸟”和“马”分别为任务1、2、3和4的负类. 对于一个任务，正类和负类各有100幅图像. 在训练过程中，抽取20幅正类图和20幅负类图，其余160幅图作为测试集.

为了研究MtMiAnL算法在处理噪声数据方面的性能，按照文献^[16]的实验方法，在Corel和CIFAR数据集中，随机选取10%的多示例包添加噪声. 具体来说，在示例的每维数据随机添加[0，σ]的噪声，其中σ是示例n维数据的标准差.

3.2 比较算法

为了使实验更具针对性，选择多种算法进行对比实验. 在多示例学习算法方面，选择了一种基于支持向量机的多示例学习算法^[9]，记为MI-SVM；在多任务学习算法方面，选择了一种基于SVM的多任务学习方法^[13]，记为MtL-SVM；在多任务多示例学习算法方面，选择了一种基于卷积神经网络的多示例多任务分类方法^[17]，记为MtMi-CNN.

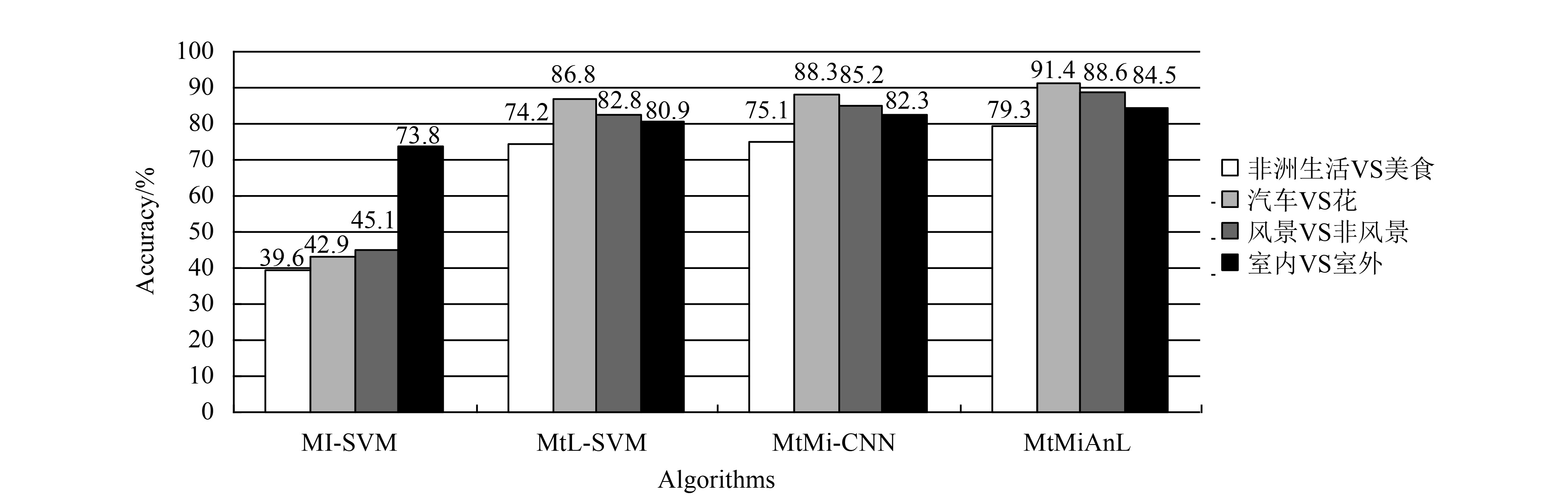
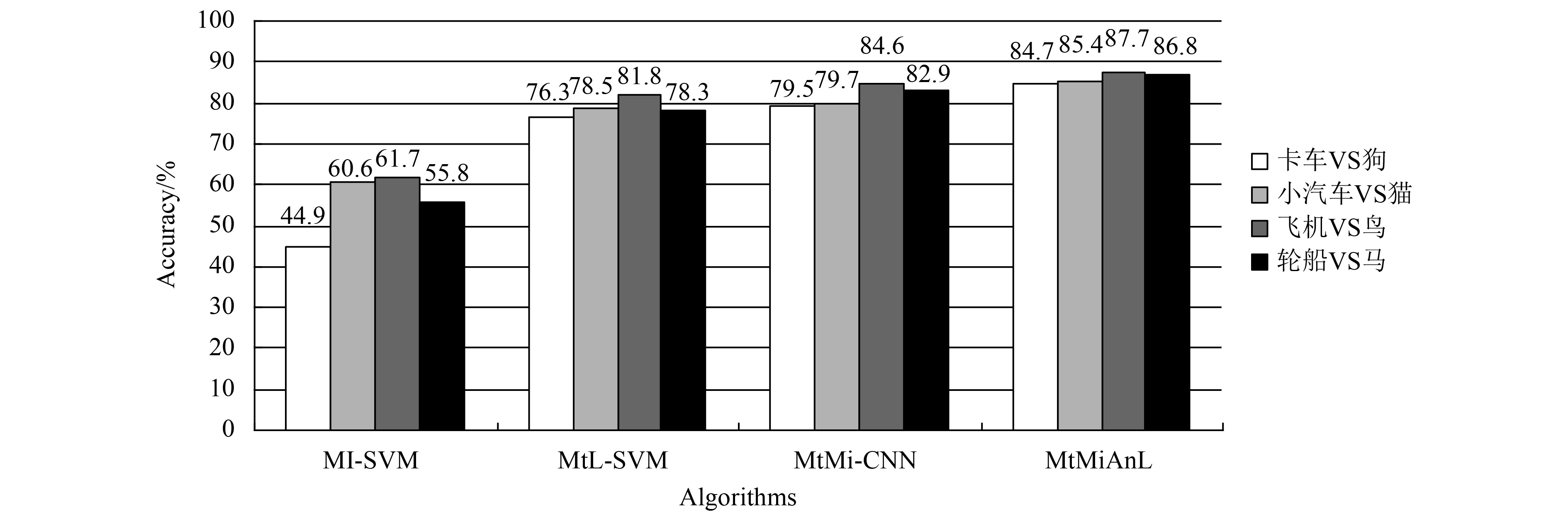
3.3 算法精度对比

分别在包含噪声的Corel和CIFAR数据集上采用MI-SVM、MtL-SVM、MtMi-CNN和MtMiAnL来训练，本文将给出这些算法在Corel和CIFAR数据集上的精度，如表1所示. 另外，在Corel和CIFAR数据集中4个任务的精度结果见图1和图2.

表1统计了各算法在Corel和CIFAR数据集上的精度，图1和图2进一步给出了在Corel和CIFAR数据集中4个任务的精度，可以看出本文MtMiAnL算法的分类效果是比较突出的. (1) 相比其他3种算法，MI-SVM的分类精度较低. MI-SVM是单任务多示例学习算法，当训练样本数量较少时，其总体精度偏低. 跟单任务多示例学习算法MI-SVM相比，MtMiAnL提出了多任务多示例学习算法，通过多个相关任务的联合训练，能够在训练样本数量较少的情况下，提高各个任务的分类精度. (2) MtMiAnL获得了比MtL-SVM更高的分类精度. MtL-SVM是多任务单示例学习算法，而MtMiAnL是多任务多示例学习算法. MtMiAnL对图像进行多示例化处理后，可以降低因图像内容的多样性和歧义性所带来的分类难度，进一步提高分类精度. (3) 跟MtMi-CNN相比，MtMiAnL具有更好的分类性能. 虽然MtMiAnL和MtMi-CNN都是多任务多示例学习算法，但是MtMi-CNN没有考虑噪声数据的影响，而MtMiAnL通过示例加权方式，降低噪声数据对分类结果的影响，因此具有更好的分类性能. 由上面各算法的结果比较得知，训练样本数量不足和噪声数据都会影响到分类预测的精度. 本文算法克服了这两类问题的局限性，从而得到较好的分类精度.

3.4 参数对精度的影响

为了研究多任务耦合参数μ和惩罚系数C对多任务分类模型的影响，本实验针对Corel和CIFAR数据集，研究在参数μ和C的变化下，MtMiAnL的分类精度的变化. 其中，多任务耦合参数μ的取值从[0.001, 0.01, 0.1, 0.5, 1, 5, 10, 100, 1 000]中进行选择，惩罚系数C的取值从2^[–5:1:5]中进行选择.

在式(9)中，分类模型的耦合参数μ通过控制 ${{{w}}_{{0}}}$ 和 ${{{v}}_{{t}}}$ 的权值大小来调整任务间的相似性. 若令μ趋近无穷大时，任务所共享的向量 ${{{w}}_{{0}}}$ 将接近零向量，此时各分类任务的相关性最低；若令μ趋近于零向量时，各分类任务所独有的向量 ${{{v}}_{{t}}}$ 将接近零向量，此时各分类任务的相关性最高. 正则化参数C用来控制ζ_it使得优化问题可以容纳一定的错误分类.

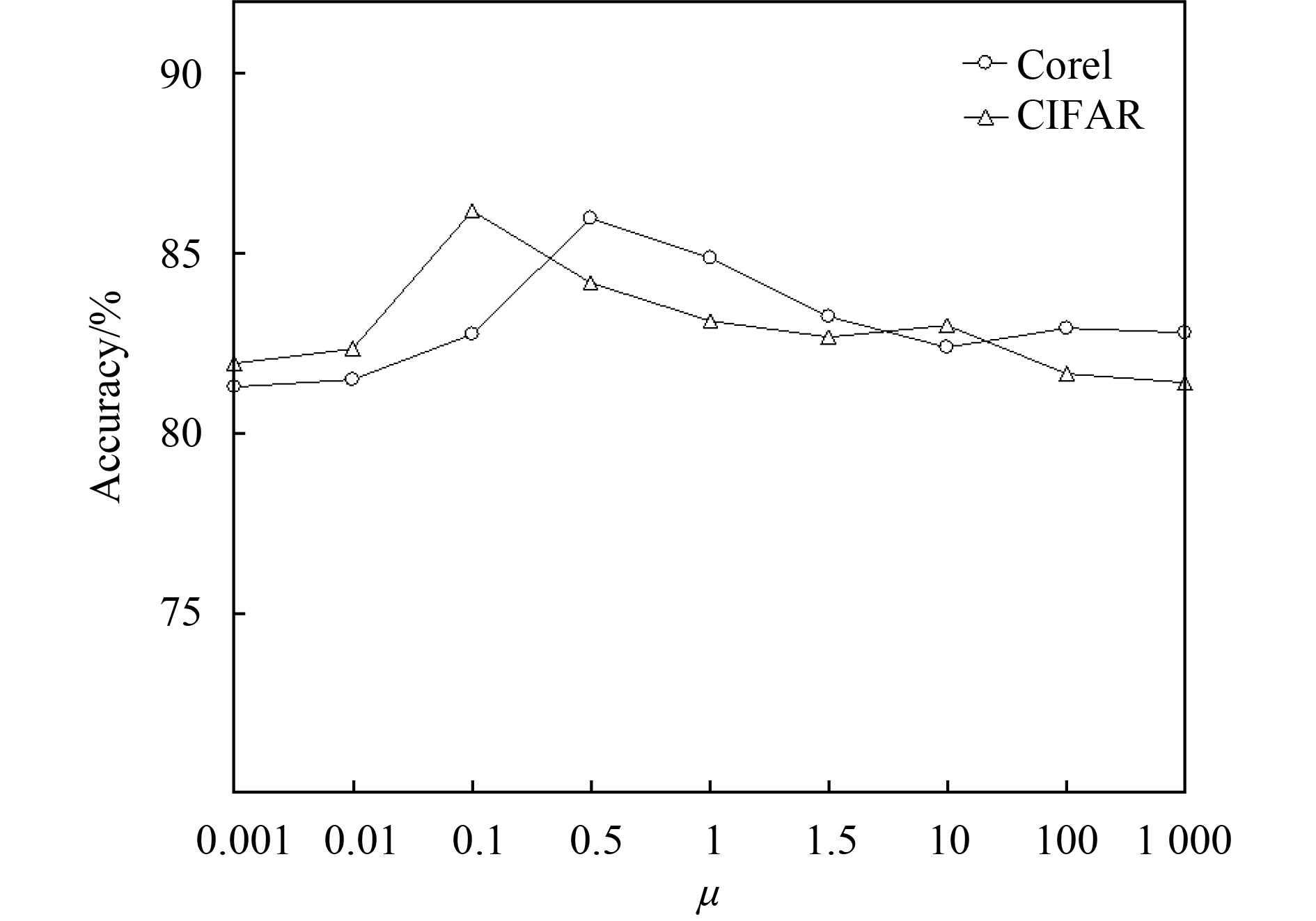
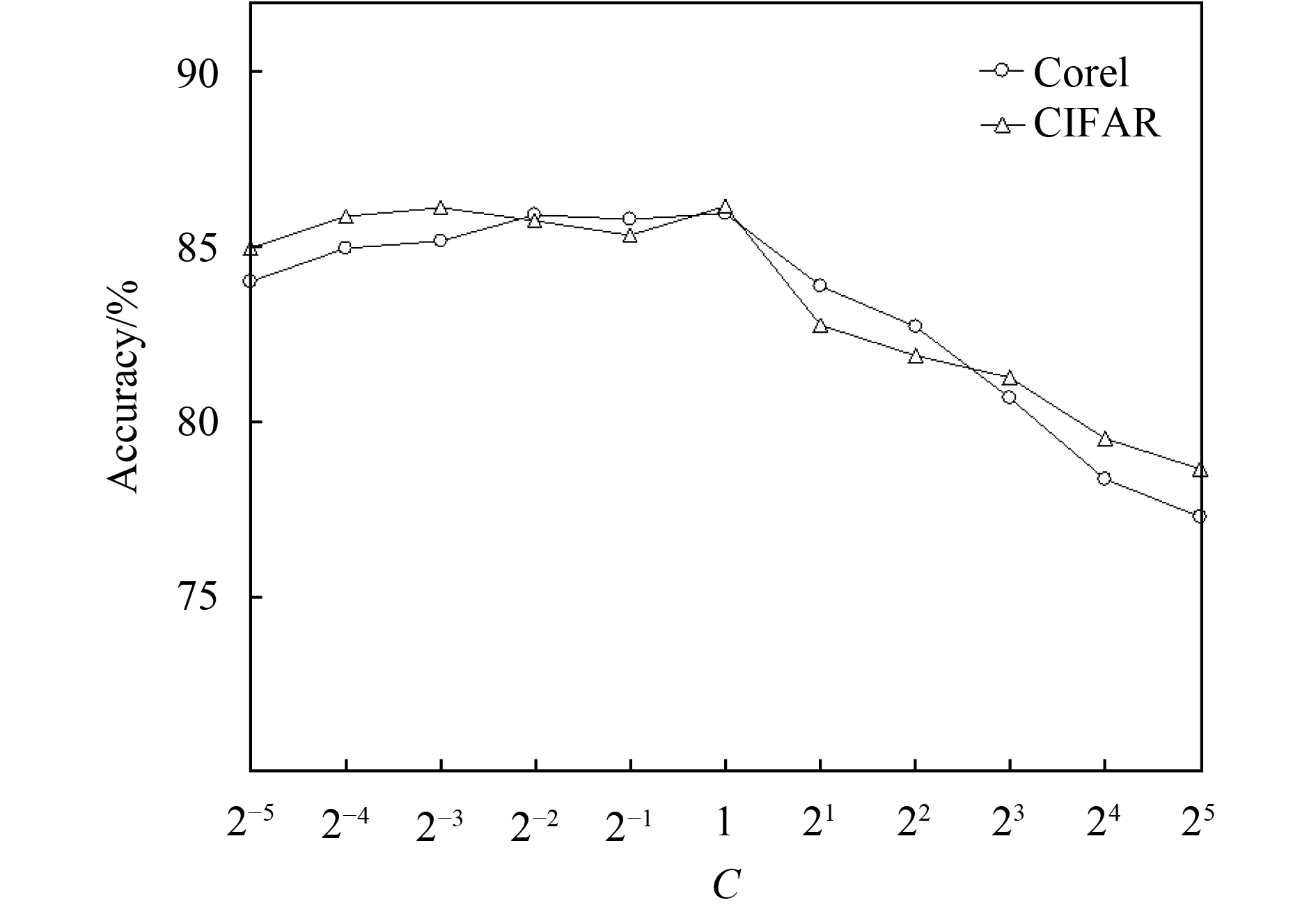
图3展示了MtMiAnL算法在参数μ取不同值时，Corel和CIFAR数据集的分类精度；图4展示了MtMiAnL算法在参数C取不同值时，Corel和CIFAR数据集的分类精度. 在实验中，当对其中一个参数进行实验时，另一个参数将被确定为最优值.

从图3可知，在Corel数据集中，当耦合参数μ=0.1时，MtMiAnL算法达到了最高的分类精度，而当0.001<μ<0.01时，算法的性能随着μ的增大而提升；当μ>0.1时，算法的性能随着μ的增大而呈现递减趋势. 在CIFAR数据集中，当耦合参数μ=0.5时，MtMiAnL算法达到了最高的分类精度，当0.001<μ<0.5时，算法的性能随着μ的增大提升；而当μ>0.5时，算法的性能随着μ的增大而呈递减趋势. 因此，根据此次实验，建议μ的取值范围为0.1~0.5.

由图4可知，在Corel和CIFAR数据集中，当正则化参数 $C\leqslant 1$ 时，MtMiAnL算法的精度较高，性能也比较稳定，而当 $C > 1$ 时，MtMiAnL算法的性能下降得很快. 因此，根据此次实验，建议C的取值范围为一个较小值，如 $C\leqslant 1$ .

4 结束语

本文提出了一种基于抗噪声的多任务多示例学习算法，通过对多示例包中的示例进行加权处理，降低噪声数据在训练过程中的影响，并对多示例加权后的目标函数进行多任务化处理，使得所有任务的数据信息得到共享，以提高分类精度，从而解决了训练样本数量不充足导致分类模型效果不佳问题. 本文分别对比了3种不同的机器学习算法，实验结果证明，本文的方法达到更优的分类性能，并且，通过在实验中观察参数对分类模型的影响，给出了参数的选取范围. 但是，在训练过程中需要对多任务分类模型进行迭代优化，损耗了时间. 因此，进一步降低时间复杂度是后续研究的方向.