语音识别技术就是通过机器对声音信号的采集，并对其加以理解和识别从而转变为相应的文本或命令的技术^[1]. 随着智能手机和个人电脑的普及，人工智能的研究和应用获得了飞速地发展，而作为智能计算机研究的主导方向和人机语音通信的关键技术，语音一直受到各国科学界的广泛关注^[2]. 在安静环境下，语音识别系统的识别率可高达95%~99%，但在实际应用中，环境噪声会导致语音识别系统的识别率大大降低^[3]. 并且，目前在语音识别的研究中仍然存在着噪声干扰、自适应性和语音模糊性等问题^[4]. 本文基于语音增强中的噪声估计算法，提出一种对平滑因子的改进算法, 旨在提高带噪语音的通信质量和可懂度.

一个完整的语音识别系统通常可以归纳为识别和匹配^[5]. 语音识别的过程可以通过两个阶段来进行概括，第一阶段是系统“训练”，第二阶段是“识别”. 训练的过程如图1所示. 将语音信号通过端点检测和求解特征参数从而形成一个语音参考的样本，即语音库，为第二阶段的识别打下基础.

图 1(Figure 1)

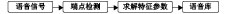
图 1 语音识别训练 Figure 1 Speech recognition training

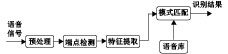
语音识别的实现过程如图2所示. 首先对输入的语音信号进行预处理，再进行端点检测及特征提取，然后与第一阶段通过训练后生成的语音库进行比对，即进行模式匹配，从而找到最佳的参量样本作为结果输出.

图 2(Figure 2)

图 2 语音识别过程 Figure 2 Speech recognition process

在复杂环境中，噪声干扰严重影响语音通信的质量，导致无法正确传达语义. 语音增强技术能从噪声背景中提取有用的语音信号，抑制与降低噪声干扰^[6]. 基于统计模型的语音增强算法^[7]，由于算法复杂度适中且效果较好被广泛研究应用. 强噪声环境下，噪声复杂多变，并且信噪比较低，现有算法往往出现信号过度失真、残余音乐噪声等现象. 例如，目前广泛应用于语音信号去噪的小波分析法，设定阈值过滤噪声时同样会过滤掉部分语音信号，造成信号失真^[8]. 如何改进现有的算法，一直是各国学者广泛研究的重要课题^[9-10]. 大多数语音增强方法都要对噪声进行估计^[11-12]，这意味着噪声估计的准确程度决定着语音增强系统的性能. 在进行语音识别前，通常需要先对语音信号进行检测，这种技术被称为语音活性检测. 在全球移动通信系统GSM的语音间断传输（即语音信号不连续发送）中，语音活性检测技术可以称得上是较为关键的部分^[13]. 并且语音活性检测算法作为一种常用的噪声估计算法，可以有效地去除带噪语音信号中的非语音片段，降低噪声并提高语音识别的准确率. 这种算法在平稳噪声和高信噪比环境下表现出的噪声估计效果较好，但是只能在语音间隙来估计噪声. 为了在含有背景噪音的环境中有效估计含有语音活动片段内的噪声频谱，本文主要介绍另外一种同样较为常用的噪声估计算法，即基于后验信噪比的时间递归平均算法，以及在此算法的基础上提出的一种对平滑因子的改进算法，通过模拟运算证明改进后的算法具有更优越的性能.

通常在语音信号频谱中，噪声产生的影响并不均匀，使得不同频谱的分量往往具有不同的实际信噪比. 时间递归平均(time-recursive averaging)算法^[14-15]可以按照不同频谱分量中的实际信噪比对噪声谱进行实时估计和更新. 时间递归平均算法具有如下的表述形式^[16]

式中， ${\left| {Y(\lambda ,k)} \right|^2}$ 是带噪语音幅度谱的平方， $\hat \sigma _d^2(\lambda ,k)$ 表示第 $\lambda $ 帧的频点k处的噪声功率谱密度估计， $\alpha \left( {\lambda ,k} \right)$ 为与时间和频率相关的平滑因子.

通过时间递归平均算法对噪声谱的估计需要在之前噪声估计与当前带噪语音谱加权平均的基础上进行，权重根据不同频谱分量中的实际信噪比自适应地发生改变. 这种基于每一频点实际信噪比来确定平滑因子的算法称为信噪比相关的(SNR-dependent)递归平均算法^[17]. 在该算法中，平滑因子 $\alpha \left( {\lambda ,k} \right)$ 使用了后验信噪比的sigmoid函数：

式中， $\beta $ 为调节因子， ${\gamma _k}(\lambda )$ 是后验信噪比的近似，式(3)中的分母为过去10帧噪声功率谱密度估计的平均值.

当调节因子 $\beta $ 分别取值2、5、10时，通过式(2)和式(3)的运算可以得到平滑因子随着后验信噪比发生变化的情况，具体结果如图3所示.

图 3(Figure 3)

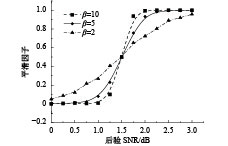
图 3 采用不同的β计算得到的平滑因子 ${\alpha \left( {\lambda ,k} \right)}$ 曲线 Figure 3 The smoothing factor curve obtained by different β calculations

从图3中可以看出，随着后验信噪比取值的增大，平滑因子α(λ, k)→1，而当后验信噪比取值逐渐减小时，α(λ, k)→0. 式(2)中的调节因子β同样对噪声谱的估计有一定的影响，从图中可以看出，随着β取值的增大，平滑因子的变化曲线趋于陡峭，使得α(λ, k)接近一个阶跃函数，导致噪声谱的估计值相比于实际值偏低.

本文提出的对平滑因子的改进方法主要针对上文提出的当β取值较大时平滑因子 $\alpha \left( {\lambda ,k} \right)$ 只有二元取值0和1的情况. 根据上文的函数关系及分析，提出新的平滑因子的表示形式

式(4)中，μ和p是两个可以设定的参数，μ的取值主要对后验SNR范围为0~1 dB时平滑因子的变化产生影响，而p的取值主要对后验SNR为1 dB以上时平滑因子的变化产生影响. 在后验SNR为0~1 dB范围内，随着μ的增大平滑因子逐渐减小，当后验SNR大于1 dB时，p值越大平滑因子增大越快. 式(4)中的 ${\gamma _k}(\lambda )$ 由上述式(3)给出. 通过对式(4)的运算，即可以确保 $\alpha \left( {\lambda ,k} \right)$ 的值始终处于范围 $0 < \alpha \left( {\lambda ,k} \right) < 1$ .

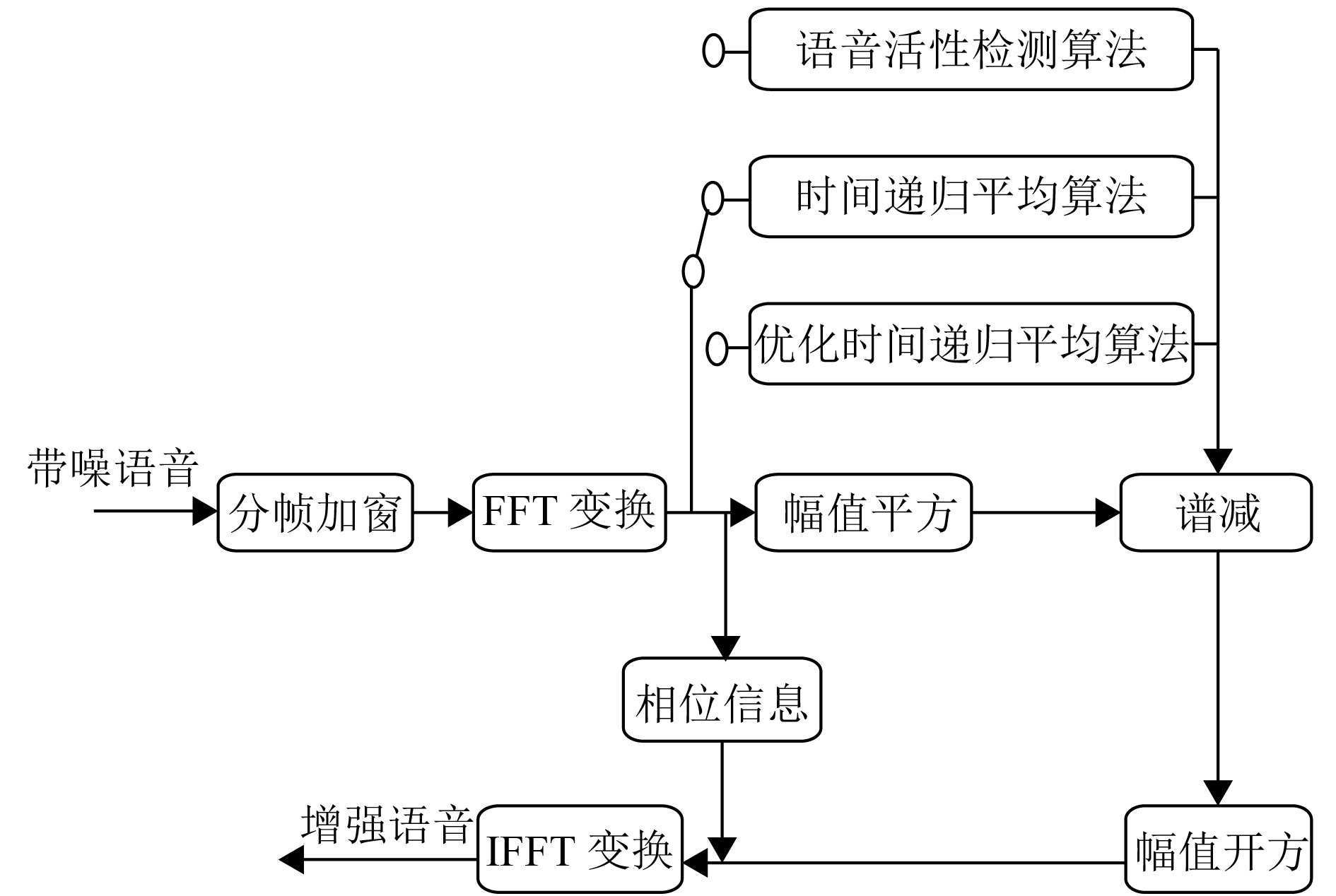
为了评估平滑因子改进后的算法的性能，本文分别将语音活性检测算法、时间递归平均算法及改进后的算法与基本谱减算法相结合，按照图4所示的流程进行语音信号的噪声估计及增强处理.

在多说话人babble噪声下将输入信噪比分别设定为0、2.5、5、7.5、10、12.5、15 dB进行仿真实验，仿真结果如图5和图6所示.

图 4(Figure 4)

图 4 结合不同噪声估计算法的功率谱减法原理图 Figure 4 The schematic diagram of power spectral subtraction of different noise estimation algorithms

图 5(Figure 5)

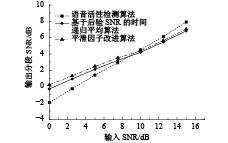
图 5 babble噪声环境下3种算法的输出分段SNR比较 Figure 5 Comparison of output segment SNR of three algorithms in babble noise environment

图 6(Figure 6)

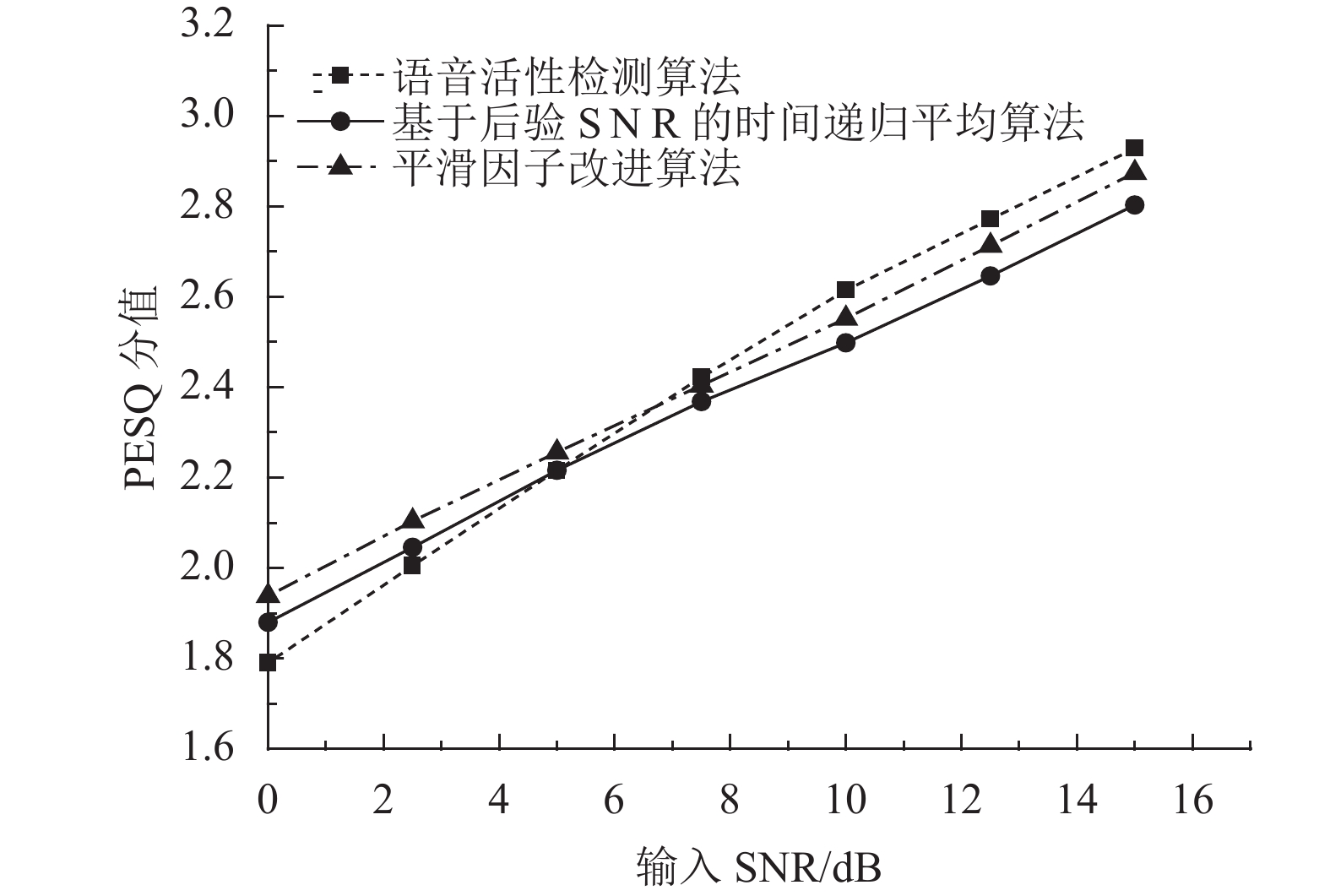
图 6 babble噪声环境下3种算法的PESQ分值比较 Figure 6 Comparison of PESQ scores of three algorithms in the babble noise environment

从图5中可以看出，当输入SNR在0~10 dB范围内时，本文提出的平滑因子改进算法相比于语音活性检测算法最高可以使输出分段SNR提高2.1 dB,而相比于原时间递归平均算法最高可以使输出分段SNR提高0.5 dB. 因此，在低输入信噪比下，本文提出的改进算法对带噪语音信号的质量有所改善.

从图6中可以看出，当输入SNR在0~7.5 dB范围内时，本文提出的平滑因子改进算法相比于语音活性检测算法最高可以使PESQ分值提高0.2,而相比于原时间递归平均算法最高仅可以使PESQ分值提高0.1. 此结果也表明，在低输入信噪比下，本文提出的改进算法对带噪语音的可懂度有所改善.

本文主要对语音增强中噪声估计算法进行了研究及改进. 在时间递归平均算法中提出了一种对平滑因子的有效改进措施. 通过仿真实验结果表明，在低信噪比的环境下，本文提出的改进算法相比于语音活性检测算法最高可以使输出分段SNR提高2.1 dB，改善PESQ分值0.2，相比于原时间递归平均算法最高可以使输出分段SNR提高0.5 dB，改善PESQ分值0.1. 因此本文提出的改进算法可以同时提高语音的质量和可懂度，对带噪语音取得了比较好的改善效果.