各种各样的数据爆炸式地产生，图片、语音、视频等海量多媒体数据给远程传输、存储带来了巨大的困难和挑战. 因此在传输和存储之前对数据进行压缩很有必要. 通过压缩，大幅减少信号存储空间以及传输带宽，并保证高重构质量，是急需解决的研究与工程应用热点^[1-6].

考虑到现实多媒体数据所具有稀疏性质，一种可行的思路为利用稀疏字典学习方法对语音数据进行压缩. 稀疏字典学习^[7]包括稀疏表示和字典学习两阶段，稀疏表示的本质是利用尽可能少的资源表示更多的知识；字典是数据特征的集合. 目前，稀疏字典学习方法被广泛运用在多媒体数据的识别、降噪、增强、检索^[8-11]等方面.

针对不断增长的实时语音数据，本文结合稀疏字典学习方法，提出一种面向增量式学习的语音字典构造方法，增量学习有助于大规模数据的特征学习^[12]. 该方法的核心是通过增量式学习构建一个字典，令字典中的基向量编号G结合相应拟合系数W组成参数对稀疏表示大部分频域信号，从而达到压缩目的. 具体流程为：

(1) 先将语音时域信号经短时傅里叶变换STFT(Short-Time Fourier Transform)处理后转换为各窗频谱幅值，然后基于喉头仪信号找到各窗内的共振峰，通过多项式拟合方法得到各窗频谱的包络.

(2) 将包络作为高维空间向量投影到低维空间，并以字典中的少数基向量线性拟合当前窗向量. 进而通过存储基向量编号G和拟合系数W完成对当前窗向量的存储；把无法拟合的窗向量利用LRU的策略加入字典，实现增量式学习.

(3) 解压过程依据用户请求将字典中指定基向量经线性拟合实现.

论文共分为五部分. 第一部分为引言；第二部简单介绍了稀疏字典学习的内容. 第三部分详细介绍本文提出的字典学习方法以及压缩应用. 第四部分列出了在公开数据集上的实验结果. 实验结果表明，该方法能大幅度压缩语音频谱包络的数据量，适用于受带宽限制下实时高采样率的流式PCM语音信号. 该算法与同类算法相比，有更好的压缩效果. 最后，第五部分对全文进行了总结并阐述了下一步工作.

1 相关工作

关于稀疏字典学习，国内外研究学者进行了大量的研究工作，已有许多研究成果. 稀疏字典学习的目标是找到一个字典 ${D} \in {{\rm{R}}^{n \times z}}$ ，能够稀疏表示原信号 ${Y} \in {{\rm{R}}^{n \times t}}$ ：

${Y} \approx {DX}.$

(1)

其中 ${D} = \left[ {{{d}_1},{{d}_2}, \cdots ,{{d}_z}} \right] \in {{\rm{R}}^{n \times z}}$ ， ${{d}_i} \in {{\rm{R}}^{n \times 1}}$ 称为字典中的一个基. ${X} = \left[ {{{x}_1},{{x}_2}, \cdots ,{{x}_t}} \right] \in {{\rm{R}}^{z \times t}}$ 是 ${Y}$ 在字典 ${D}$ 上的稀疏因子，x_i是严格 $\varGamma $ 稀疏的，即 ${\left\| {{{x}_i}} \right\|_0} \leqslant \varGamma $ . 这表明原信号Y中每一个采样点都能通过字典中的少数基的线性拟合来近似表示.

在稀疏字典学习中，求解稀疏因子的方法一般是匹配追踪(MP)或者正交匹配追踪(OMP). 同样该方法也被用于字典训练过程中，字典训练的目的是在当前稀疏度的标准下获得一个最小期望的字典 $\hat{ D}$ ，它能够稀疏表示当前训练数据^[13]：

$\hat{ D} = \mathop {{\rm{argmin}}}\limits_{{D}} \left\| {{Y} - {DX}} \right\|_F^2\;{\rm{s}}.{\rm{t}}.\forall j \in \left\{ {1:z} \right\},{\left\| {{{d}_j}} \right\|_2} = 1.$

(2)

常见的字典学习方法是K-SVD^[14]、在线字典学习(ODL)^[15]等. 文献[16]基于OMP算法和KSVD算法，在稀疏参数因子中提出池化概念和抽样选择方法，结合SVM对语音数据进行分类，分类结果比利用MFCCs作为特征的情况下准确率高，但未考虑实时在线应用的情况. 文献[17]提出一种基于图像块数据的交替迭代方案，通过严格的收敛分析证明该方法有全局收敛的特性，并且通过实验证明获得相同效果下相比KSVD具有更低的计算开销. 文献[18]提出一种分层学习结构，通过贡献字典原子能够减少训练一个大的混合字典的计算开销，但是尚未考虑到标签内在特性，文献[19]提出一种新的距离测量方法，联合KSVD稀疏字典学习方法运用于图片相似度检测，利用一个已知图片信号的信息去显著压缩另一个与之相似的图片信号的信息，两者越相似压缩比越高. 文献[20]则通过K-SVD分解字典学习方法，改进了单通道语音增强算法. 文献[21]提出了基于过完备字典稀疏表示的自适应语音增强方法，利用K-SVD算法训练字典，对含噪语音采用正交匹配追踪算法进行系数分解，再通过系数重构得到语音信号.

由于K-SVD算法在更新字典过程中，每次迭代都需要所有的训练样本集进行计算，所以基于K-SVD算法的字典更新操作过程对计算空间、存储空间要求较高. 而ODL方法则是在每次迭代过程中使用一个训练样本去更新字典，文献[15]在彩色图像恢复中提出了在线字典学习算法. 联合LARS-Lass算法，在字典的每次迭代更新只处理一个样本，从而达到计算速度快的目的. 文献[22]在降噪、提取脉冲信号的应用中，借助压缩感知理论，通过学习自适应字典稀疏提取混合在大量噪声背景下的脉冲信号，该方法相比传统方法具有自适应调整的能力以及高稀疏性等优势. 文献[23]提出利用MFCCs特征以及结合在线字典学习方法的分类算法，该算法通过字典去除了使用不同分类器带来的冗余信息，降低了高维空间向量的运算复杂度，对音乐和语音信号达到了完全分离的效果.

考虑到当前互联网研究与应用中，语音数据大量的产生，本文综合了相关理论研究，提出一种增量式语音字典构造学习方法，该方法基于语音信号的稀疏性^[24]，利用冗余稀疏字典学习和增量学习的策略对语音信号频谱包络进行流式压缩编码与解码的研究实验.

2 增量式字典构造方法 2.1 预备知识

本文涉及了几个概念，统一在此描述.

定义1 　窗：引用STFT^[25]中定义，设音频PCM序列为L，将L按照固定采样点数2n和步长θ划分成多个时间片l₁,l₂,l₃,…,l_t，其中步长θ表示两个PCM序列的起始位置之差. 且定义l_i为第i窗.

定义2 　包络：设通过STFT获取第i窗l_i的峰值谱为p_i，将p_i中各共振峰用光滑曲m_i线连接起来，则定义曲线m_i为第i窗的频谱包络.

定义3 　空间权值向量：向量 ${V} = \left( {{v_1},{v_2}, \cdots ,{v_n}} \right)$ 定义为n维空间权值向量，v₁是n维空间上第i维的权值.

由于人耳对不同频率的音频信号听觉灵敏度不同，因此在语音频域模值包络中，不同频段的模值应具有不同的权值.

定义4 　带权值的向量点积计算公式：假设n维空间中各维权值为 ${V},{a}\! = \!\left( {{a_1},{a_2}, \ldots ,{a_n}} \right)$ ， ${b} \!=\! \left( {{b_1},{b_2}, \ldots ,{b_n}} \right)$ 为n维空间中的任意两个向量，则a，b的点积定义为

${\left\langle {{a},{b}} \right\rangle _{{V}}} = \sum\limits_{i = 1}^n {{{a}_i} \cdot {{b}_i} \cdot {{v}_i}} .$

(3)

定义5 　带权值的向量模值公式：假设n维空间中各维权值为V， ${a} = \left( {{a_1},{a_2}, \ldots ,{a_n}} \right)$ 是n维空间上的向量，则a的带权值的向量模值式为

${\left\| {{a}} \right\|_{\left( {{V}} \right)}} = \left\langle {{{a}},{{a}}} \right\rangle _{{V}}^{1/2}.$

(4)

定义6 　带权值的余弦公式：假设n维空间中各维权值为V，a，b为n维空间中的任意两个向量，则a，b之间夹角的余弦值的计算式定义为

${\cos _{{V}}}\left( {{a,b}} \right) = \frac{{{{\left\langle {{a,b}} \right\rangle }_{{V}}}}}{{{{\left\| {a} \right\|}_{\left( {V} \right)}} \cdot {{\left\| {b} \right\|}_{\left( {V} \right)}}}}.$

(5)

定义7 　稀疏向量的压缩表示方式：设有n维的稀疏向量μ，若有向量G，W和函数f,

$\begin{array}{l}{G} = ({g_i}|i \in \left\{ {1:{{\mu }_0}} \right\},\forall i \ne \tau ,{g_i} \ne {g_\tau }).\\[6pt]f\left( {{G},{W},i} \right) = \left\{ {\begin{array}{*{20}{c}}{0,\;\;\;\;\;\;\;\;\;\;\;\;i \notin G};\\[6pt]{{\lambda _{\mathop {{\rm{argmin}}}\limits_\beta }}_{\left| {i - {g_\beta }} \right|},i \in G}\end{array}} \right..\\[15pt]{W} = \left( {{\lambda _i}|i \in \left\{ {1:{{\mu }_0}} \right\}} \right).\end{array}$

(6)

使得 $\forall i,f\left( {{G},{W},i} \right) = {{\mu }_i}$ ，则称为使用编号G与系数W对μ进行压缩表示.

2.2 包络压缩总体框架

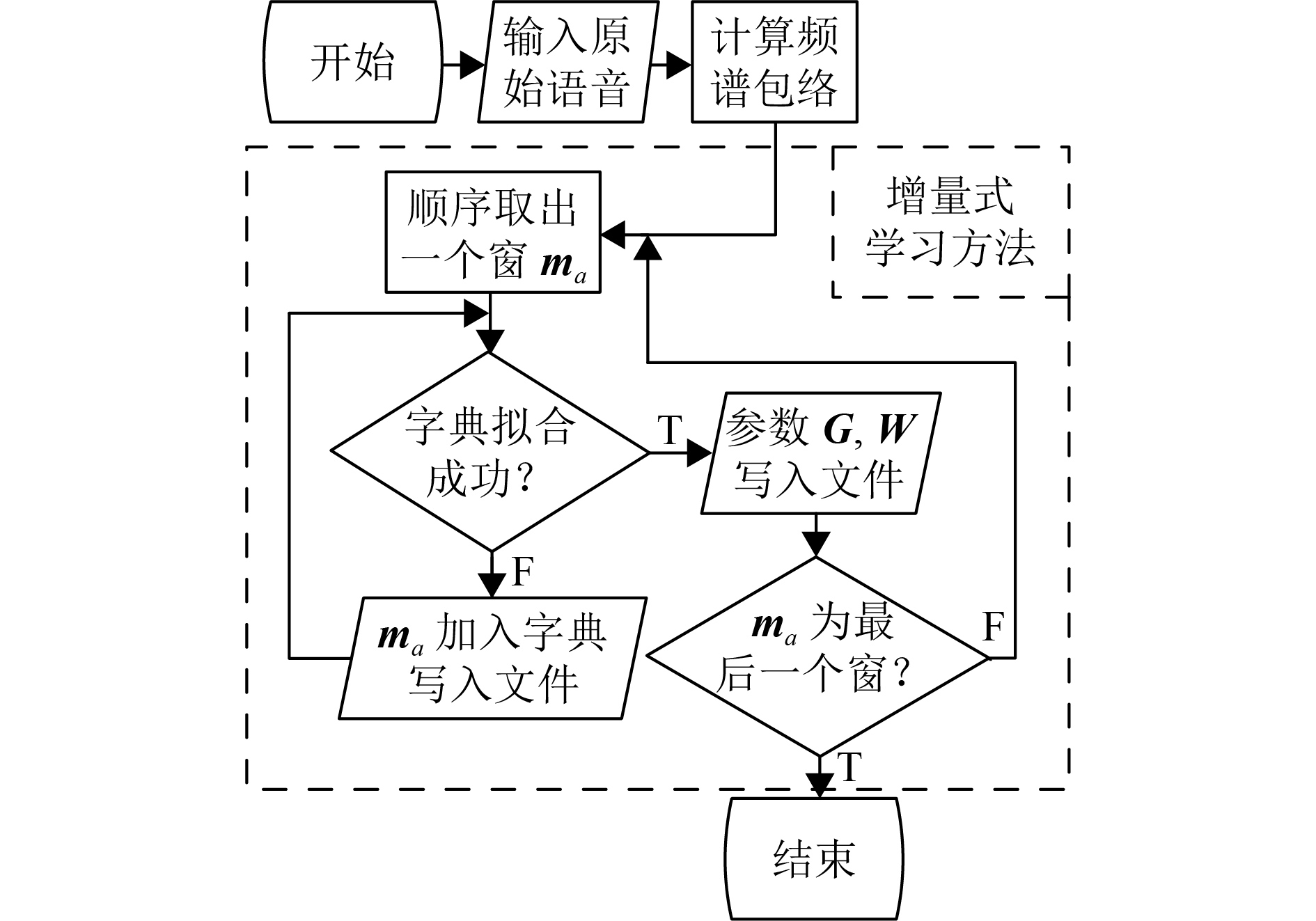
本节将结合语音压缩描述字典构造方法的总体框架以及数据流向问题. 首先需要说明的是，本方法直接求解编号G与系数W，从物理意义上，相对于ODL算法，相当于使用编号G与系数W间接表示X中的一个元素x_i. 并且本方法不一次性处理整体Y，而是通过依次处理Y中的第α个包络m_α，来实现增量式压缩. 对语音时域信号经STFT处理后得到了各窗频谱幅值，然后按照每个窗的输入顺序，利用字典中基向量进行拟合. 若拟合匹配成功，则记录字典编号G和对应系数W；若无法拟合则加入字典并写入文件，若此时字典未满，则直接加入字典；若此时字典容量已满，则选用LRU策略进行字典更新，然后再进行一次拟合匹配. 总体框架图如图1所示.

2.3 匹配与拟合

本部分描述本方法在字典学习和更新过程中利用所使用的高维向量个性化匹配算法，以下是基本实现方式.

2.3.1 二向量拟合单向量

在高维向量拟合的步骤中，因利用到了高维向量与高维空间中平面的投影关系，每次使用两个高维向量拟合一个向量，所以这个过程可视为待拟合向量在两个高维向量构成的平面上的分解拟合过程.

定义8 　投影分解系数：设n维空间上存在 ${e = a' - a }= j'{{b}} + {k'{{c - a}}}$ ，有

$\begin{array}{l}\;\;\;\;\;\;\;\;\;\;\;j,k = \mathop {{\rm{argmin}}}\limits_{j',k'} {{e}_{\left( {{V}} \right)}}.\\[6pt]{\rm{s}}.{\rm{t}}.{\cos _{{V}}}\left( {{e},{b}} \right) = 0,{\cos _{{V}}}\left( {{e},{c}} \right) = 0.\end{array}$

(7)

则称j，k为a在b，c构成超平面上的投影分解系数， ${{a}}' $ 是a在b，c构成超平面上的投影. e表示误差.

求解投影分解系数的具体方法是：首先求b施密特正交化于c的投影 ${{b}}' $ ，然后用正交基 ${{b}}' $ 和c来表示 ${{a}}' $ . 那么可得

${a' }=\frac{{{{\langle {{a',b'}} \rangle }_{{V}}}}}{{\left\| {{b'}} \right\|_{\left( {V} \right)}^2}} \cdot{b' }+\frac{{{{\langle {{a',c}} \rangle }_{{V}}}}}{{\left\| {c} \right\|_{\left( {V} \right)}^2}} \cdot {c}.$

(8)

根据几何意义，可以求得

${j = }\frac{{{{\langle {{a',b'}}\rangle }_{{V}}}}}{{\left\| {{b'}} \right\|_{\left( {V} \right)}^2}},\quad k = \frac{{\left\| {{a' - jb}} \right\|}}{{{{\left\| {c} \right\|}_{\left( {V} \right)}}}}.$

(9)

综合式(8),(9)和施密特正交化过程，设函数为 ${\mathbb{J}}$ ， ${\mathbb{K}}$ ，j和k的计算式为

$j = \mathbb{J}\left( {{a},{b},{c}} \right),\quad k = \mathbb{K}\left( {{a},{b},{c}} \right).$

(10)

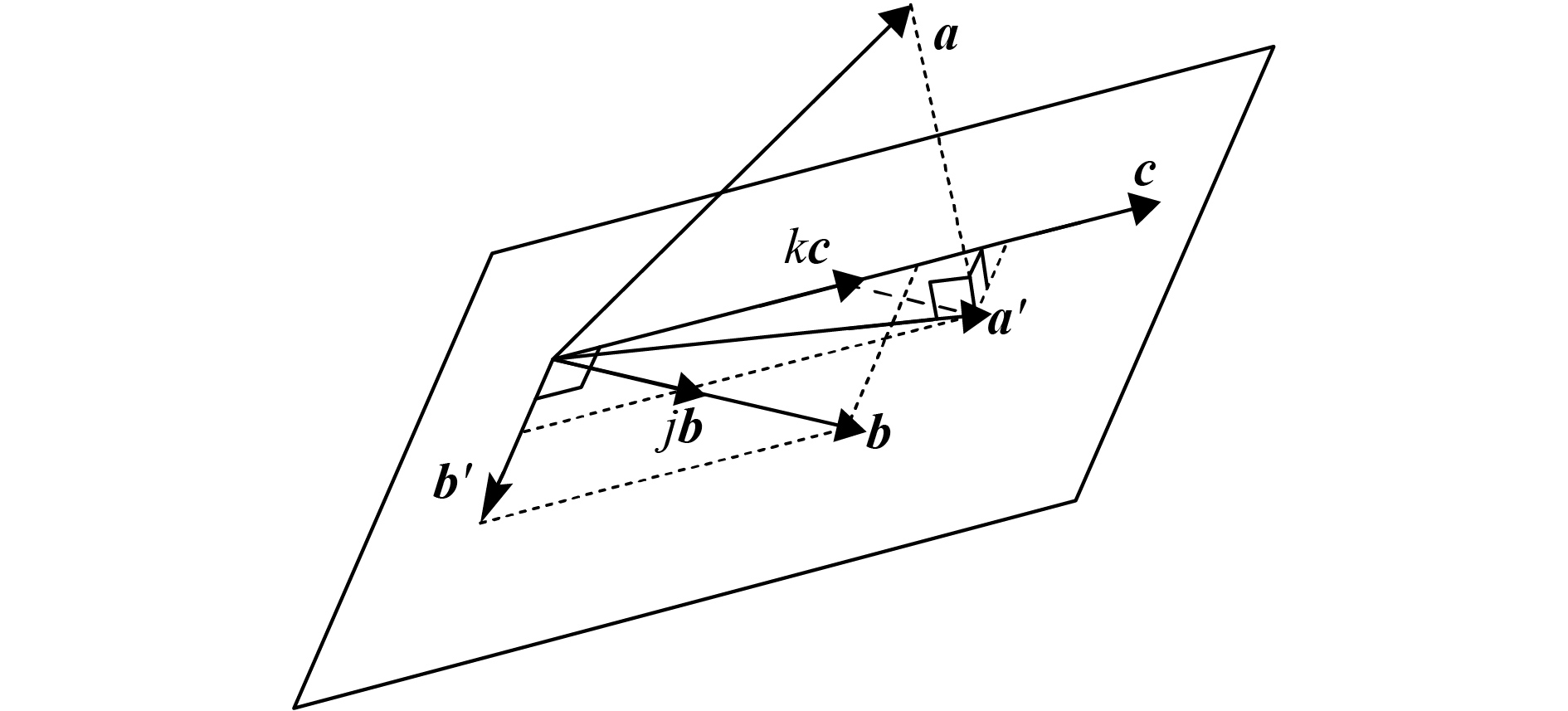
利用三维向量说明上述向量拟合的图解形式，如图2所示.

2.3.2 多向量拟合单向量

通过递归调用2.3.1中的拟合规则，本小节将描述使用多个基向量拟合一个向量的方法.

假设在n维空间中，已知给定基向量组 $\varOmega = \left( {{{\omega }_1},{{\omega }_2}, \cdots ,{{\omega }_s}} \right)$ 和向量a；拟合时所允许的最大误差阈值为ε，若存在一组系数

${W}\epsilon {{\rm{R}}^{1 \times s}},{W} = \left( {{\lambda _1},{\lambda _2}, \cdots ,{\lambda _s}} \right)$

使得

${a} = {W}\cdot{\varOmega ^{\rm{T}}} + {e},{\rm{s}}.{\rm{t}}.||{{e}||_{\left( {V} \right)}} < \varepsilon ,$

(11)

则称向量 ${a}$ 能由向量组Ω线性拟合.

2.3.3 多向量拟合的系数计算与拟合匹配

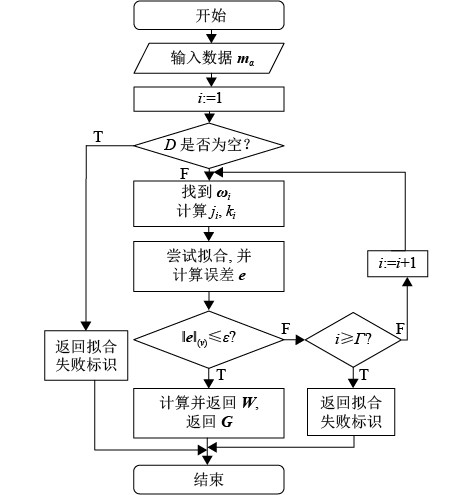
实际利用上述方法对高维向量的拟合匹配流程如图3所示. 首先G=(g₁,g₂, $ \cdots $ ,g_s)表示使用到的基向量集合，与W组成参数对. 图中m_α为待拟合向量；Γ表示该过程最多能使用的基向量个数.

假设使用了 $s,s \in \left\{ {1:\varGamma } \right\}$ 个基向量来拟合向量m_α，约定第 $i,i \in \left\{ {1:s} \right\}$ 次加入的基向量的编号为g_i，其最终系数为λ_i，记当前轮次的系数为k_i. 则

${g_i} = \left\{ {\begin{array}{*{20}{c}}{\mathop {{\rm{argmax}}}\limits_\tau {\rm{co}}{{\rm{s}}_{{V}}}\left( {{{m}_\alpha },{{d}_\tau }} \right),\;\;\;\;\;\;\;\;\;\;\;\;i = 1;}\\{_{\tau \notin \{ {g_\gamma }|\gamma \in \left( {1,i - 1} \right)\} }^{{\rm{argmax}}}{\rm{co}}{{\rm{s}}_{{V}}}\left( {{{\varphi }_{i - 1}},{{d}_\tau }} \right),i \in \left\{ {2:s} \right\}.}\end{array}} \right.$

(12)

式(12)中， ${{\omega }_i} = {{d}_{{g_i}}}$ ，当前轮次下所有选中的基向量的临时合成向量为 ${{\varphi }_i}$ ，

${{\varphi }_i} = \left\{ {\begin{array}{*{20}{c}}{{k_i}{{\omega }_i},\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1;}\\{{j_i}{{\varphi }_{i - 1}} + {k_i}{{\omega }_i},\quad i \in \left\{ {2:s} \right\}.}\end{array}} \right.$

(13)

式(13)中，套用式(10)，k_i和j_i为

${k_i} = \displaystyle\left\{ {\begin{array}{*{20}{c}}{\displaystyle\frac{{{\langle {{{m}_\alpha },{{d}_{{g_1}}}}\rangle }_{{V}}}}{||{{{d}_{{g_1}}}||_{\left( {{V}} \right)}}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1;}\\{\mathbb{K}\left( {{{m}_\alpha },{{\varphi }_{i - 1}},{{d}_{{g_i}}}} \right),\;\;\;\;\;\;\;\;i \in \left\{ {2:s} \right\}.}\end{array}} \right.$

(14)

${j_i} = \left\{ {\begin{array}{*{20}{c}}{1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = s + 1;}\\{\mathbb{J}\left( {{{m}_\alpha },{{\varphi }_{i - 1}},{{d}_{{g_i}}}} \right),\;\;\;\;i \in \left\{ {2:s} \right\}.}\end{array}} \right.$

(15)

那么，最终W中的各元素λ_i为

${{\lambda }_{i}} = {{k}_{i}} \cdot \prod\limits_{{u} = {i}}^{s} {{{j}_{{u}{\rm{ + }}1}}} .$

(16)

2.4 文件格式

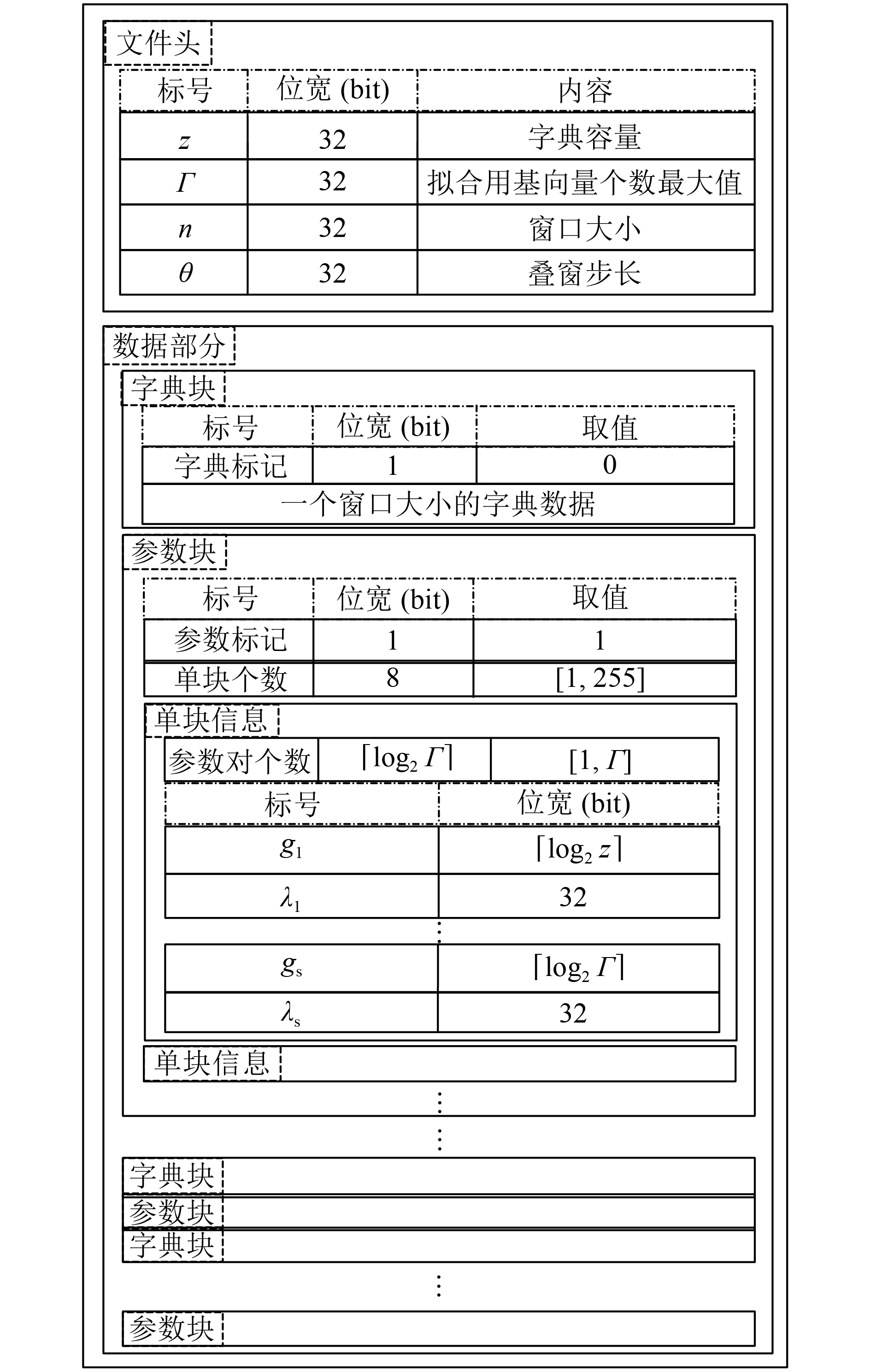
本文提出的方法可用于语音频谱模值包络的压缩，将压缩后文件分为文件头和数据两部分. 文件头记录压缩相关的参数大小，数据部分则分别记录字典和稀疏表示后的参数. 字典标记后会接一个窗口长度的字典数据；参数标记后接一个参数块个数，表示包含多少块单块信息，一个参数块最多能存255个单块，因此参数块数使用1字节表示，若在实际使用中需要超过255个连续单块，则拆分为多个参数块；而每块单块信息包含了用于拟合一个向量的编号G以及系数W. 更具体的文件格式如图4所示.

2.5 字典构建与压缩过程

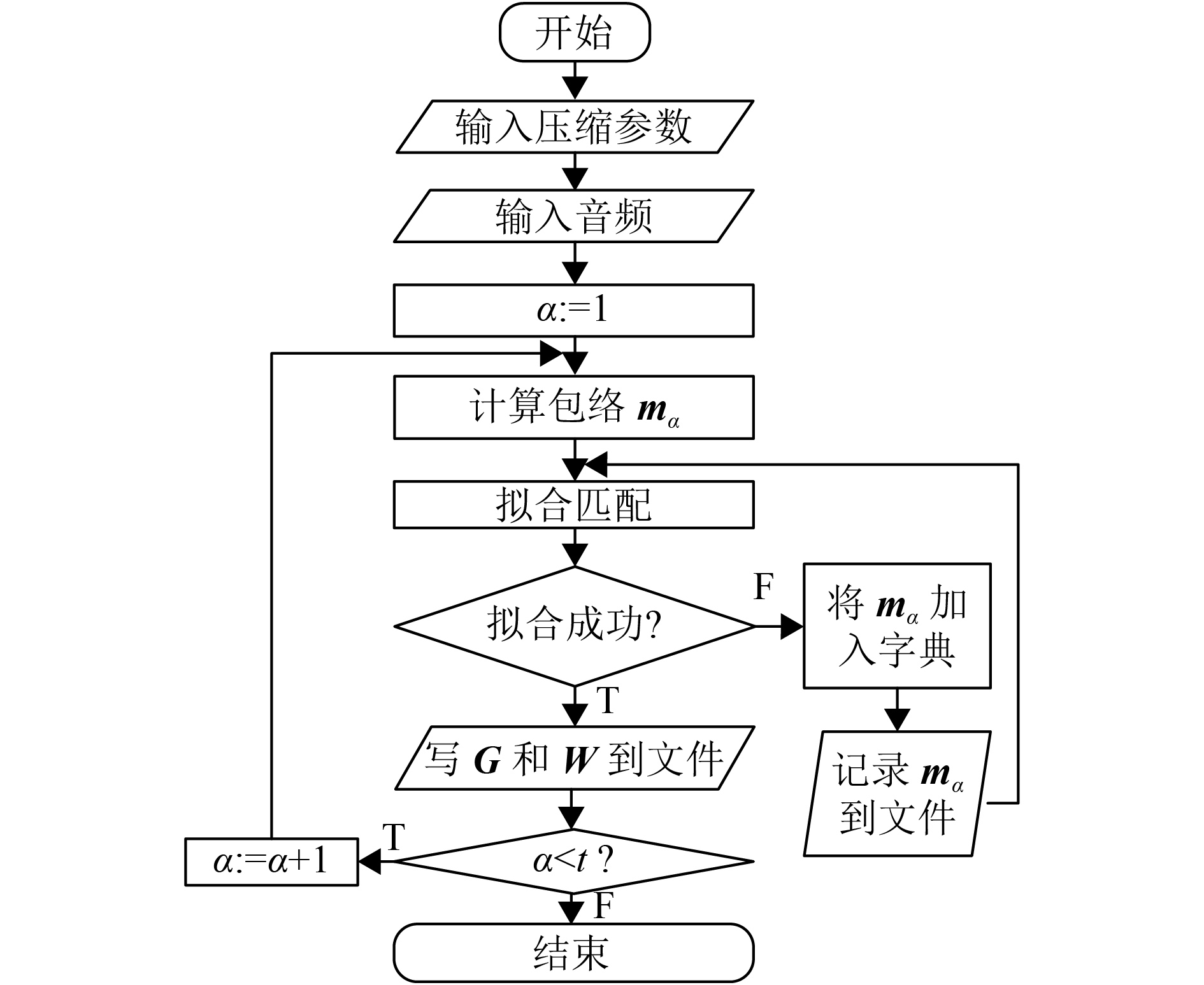
按α增序，逐个处理待拟合向量m_α，压缩流程图如图5所示. 图5中的拟合匹配使用图3的拟合方法. 若图3返回拟合失败，则需要更新字典. 更新时，当字典未达到容量上限z时直接加入向量m_α，当达到容量时当前采用的是最近最少使用(Least Recently Used, LRU)策略替换旧的基向量. 在写文件过程中，写入文件格式参照图4. 记标记位变量为Δ，如果Δ=0，则表示记录字典到文件，那么将写入字典标记和字典数据；如果Δ=1，则表示写参数到文件. 那么先写参数块个数为0并记下参数位置，之后再写入单块信息，直到再次遇到Δ=0，则将统计好的单块信息总数回填至参数位置；若单块信息的实际统计个数超过1字节(255)存储容量，则将255回填至参数位置并重新开一个参数块记录余下的单块信息.

2.6 还原过程

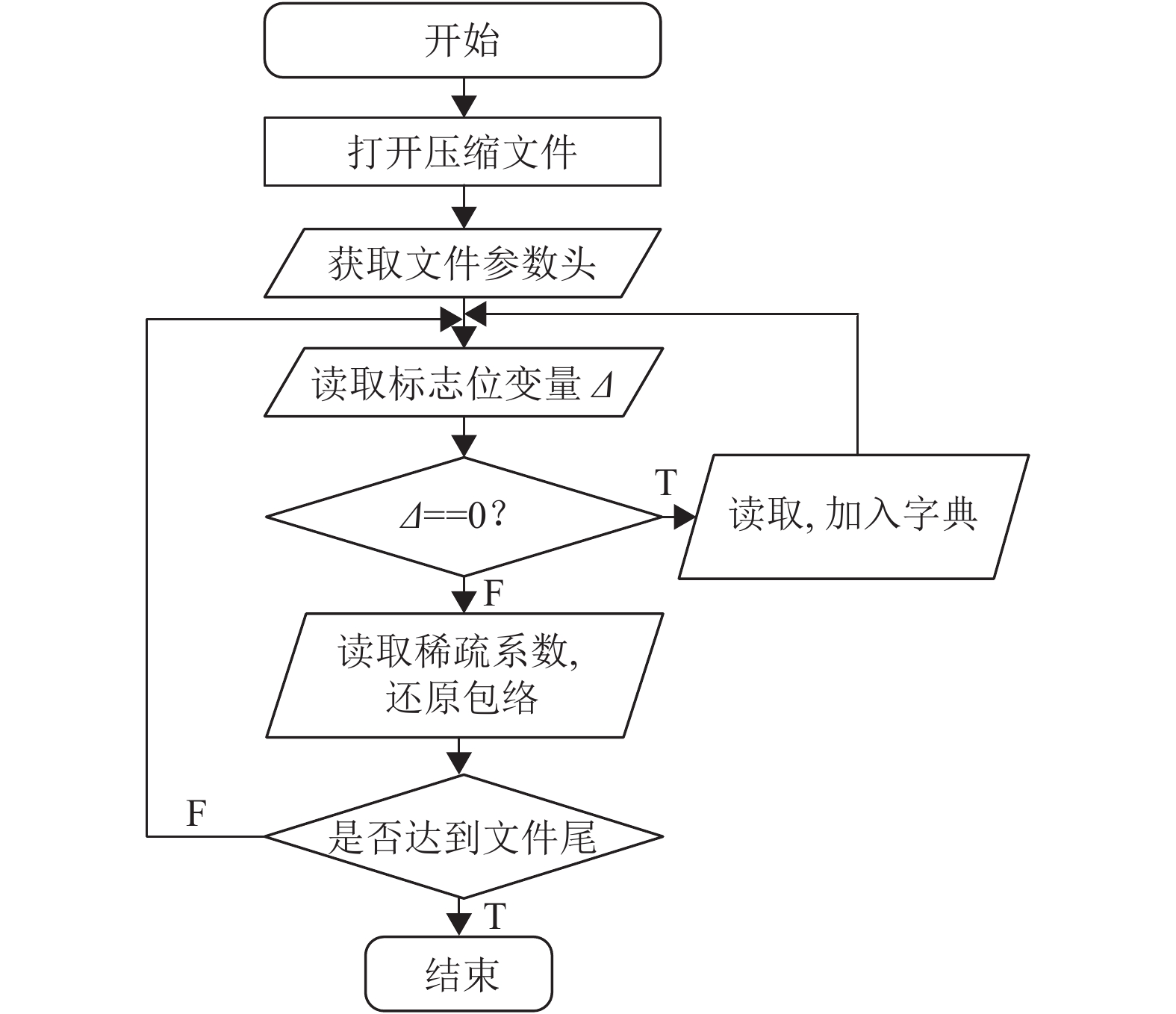
本文提出的语音字典在压缩过程中被碎片式地记录于压缩文件中，压缩过程中标志位变量记为Δ. 整个解压还原的流程图如图6所示. 首先获取文件头，根据文件头的参数对解码器做好初始化设置. 然后按顺序处理数据部分的每个块，读取Δ. 若Δ=0，则读取基向量，并按照LRU的规则加入字典；若Δ=1，则读取参数块，通过获取一个单块信息中的G和W并使用

$\varOmega = ({{d}_i}|i \in \left\{ {G} \right\}).$

(17)

${{m}_{\rm{\alpha }}}{'} = {W}\cdot{\varOmega ^{\rm{T}}}.$

(18)

得到对应的近似还原包络.

3 实验结果及分析

实验在win10系统下进行，利用Visual Studio2015编码. 开源语音数据集PTDB-TUG包含有10位女生10位男生的声音片段集. 从中随机选取5名女生和5名男生的录音集，每个人的录音大约有220个片段，采样率是44.1 kHz，按照窗长度为4 096点进行STFT实验获取频谱包络，每个窗口长度为512，表示频率范围是0~6 kHz. 最终每个人大约有70 000~90 000个窗口包络，每个人的语音量可以模拟数据不断增长的过程.

目前流行的字典学习方法是训练一个过完备字典. 过完备字典是指字典中条目的数量大于每个条目的维度^[15]，过完备字典一般从样本数据随机抽取K条，利用KSVD或在线字典学习(Online Dictionary learning, ODL)等字典学习算法进行训练，然后利用系数分解算法求解出样本数据的系数.

相比较而言ODL算法比KSVD训练字典更迅速，本次实验选择与ODL算法进行对比，ODL算法源码在文献[16]的作者主页下载，并在Matlab环境下进行运算使用. 通过调整参数使得两种算法在数据的平均相似度上尽可能一致，然后比较两种算法的压缩比和具体每一个窗的还原质量.

3.1 压缩比对比

定义9 　压缩比计算公式：假设A是原始数据大小； ${ A}{\rm{'}}$ 是压缩后数据的大小，大小单位为bit. 那么压缩比为 ${ {A}}'{ {A}}^{-1}$ .　压缩比越小表明压缩效果越好.

在本文实验中，原始频谱包络 ${Y} \in {{\rm{R}}^{n \times t}}$ 以浮点(float)的形式存储，一列为一个窗口的频谱包络. 压缩后的数据中，字典中所有系数以及基向量以浮点(float,32bit)形式存储，记字典大小为z，每个基的长度为n；计本方法生成的文件中，共有 ${\varsigma _1}$ 个参数块， ${\varsigma _2}$ 个单块信息， ${\varsigma _3}$ 对参数对. 最终字典写入的基向量个数为 $\zeta $ ，G中每一个元素g_i所占位数均为 $\left\lceil {{{\log }_2}z} \right\rceil $ bit，那么本方法中的压缩数据大小 ${ A}{\rm{'}}$ 为

$\begin{array}{l}{{A}}{\rm{'}} = \left( {32 + 1} \right)\zeta n + \left( {8 + 1} \right){\varsigma _1} + {\varsigma _2}\left\lceil{\log _2}\varGamma\right\rceil +\\[5pt]\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; {\varsigma _3}\left( {\left\lceil{{\log }_2}z\right\rceil + 32} \right).\end{array}$

(19)

对于ODL，为公平对比，在每次测试中，字典容量均与本算法的 $\zeta $ 相同，而且从直接存储X，或者G和W表示X的这两种方法中，选取最小者作为压缩数据大小，记为 ${ B}{\rm{'}}$ . 记X中非零元素的个数为 ${\varsigma _4}$ ，则

${{B}}{\rm{'}} = {\rm{min}}\left\{ {\begin{array}{*{20}{c}}{32\zeta n + {\varsigma _4}\left( {\left\lceil{{\log }_2}z\right\rceil + 32} \right)}\\[5pt]{32\left( {\zeta n + zt} \right)}\end{array}} \right\}.$

(20)

在本实验中，通过调整ODL中的lambda参数使得两种方法得到的平均相似度近似.

实验结果分成男女两组，分别记录两种方法对同一数据处理后的相似度和压缩比两个结果，详情见表1和表2. 但是在具体实验中没有针对男女的区别进行特殊处理. 由表中可得，在相同的平均近似度结果下，本文方法的压缩比均大于ODL算法的压缩比. 另外，实际应用中ODL算法一般需要预先定义字典大小，如果字典大小定义不合适，则会影响压缩效率，并且ODL算法的字典需要在已知部分数据下进行训练得到. 而本文中提出的方法能够根据流式数据进行增量式字典学习，既保证较高的压缩效率，又有着在字典训练过程不必预先获取部分数据进行训练的优势.

3.2 还原质量对比

定义10 　平均相似度计算公式：假设Y是原始频谱包络；Y_i是还原后频谱包络. 那么平均相似度C为

$C = {t^{ - 1}}\sum\limits_{i = 1}^t {{{\cos }_{{V}}}} \left( {{{m}_i},{m}_i'} \right).$

(21)

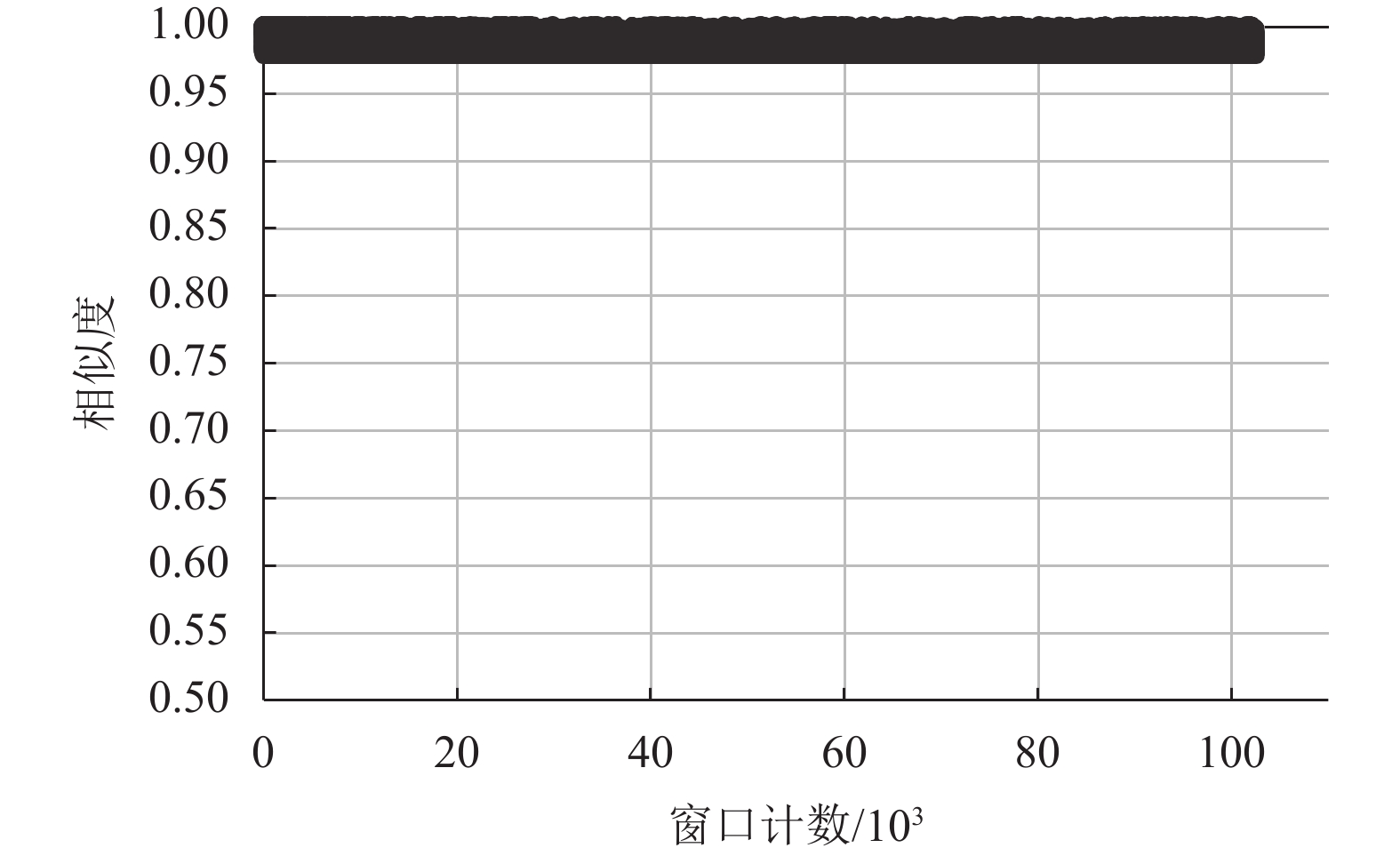
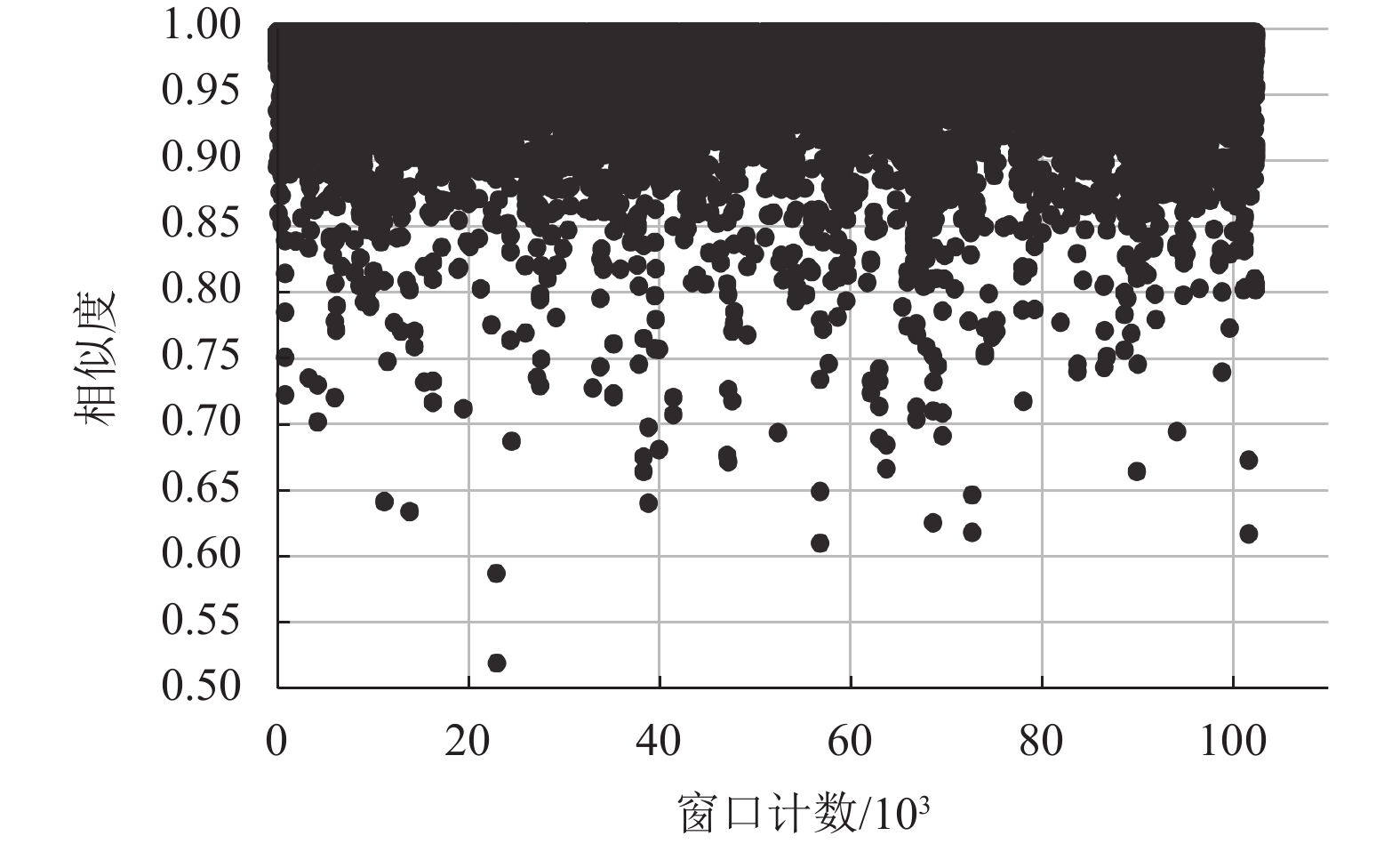
从PTDB-TUG数据集中随机选择一个人的全部录音，将两种方法的各个窗口具体还原质量绘制出相似度散点图. 对比图7和图8可看出，本文方法各窗相似度均在所设阈值以上，整体还原质量较高；而ODL算法的各窗相似度分布较为分散，这表明部分窗口包络存在较大的缺失，这会对听觉质量产生较大影响.

此外通过频谱包络图可以观察还原质量，将原包络以及两种方法还原得到的包络转换成频谱包络图（见图9），颜色越深表示数值越大.

在图9中，(a)是原始频谱包络图，(b)是本方法还原后频谱包络图，(c)是ODL还原后的频谱包络图. 从图中黑色方框可以看出，图9(c)中ODL方法对语音模值的高频部分包络过于平滑，没有保留原始包络的细节部分，例如图9(c)方框中每个窗口内数值很接近，而实际原始包络(a)方框中每个窗口内数值存在变化. 相反，本文提出的方法则能够较好地保留一些细节部分，且与图9(a)中的纹样相似. 这些细节对人耳听觉会产生一定的影响，因此如果能够正确还原细节将对语音质量有所保证.

4 结束语

针对大量产生的稀疏性模值信号包络，本文提出一种较低压缩比，易于重构还原以及还原度较高的稀疏数据压缩方法. 该方法利用稀疏字典学习的方法迭代学习提取稀疏数据的重要特征，减少存储数据中的冗余信息，同时结合增量学习策略来解决不断产生的数据流带来的特征学习困难的问题. 实验结果表明该方法在语音数据流的压缩与还原方面能取得较好的效果.

在下一步工作中，将继续研究如何降低压缩比同时保持较高的还原率以及如何提高计算效率，尤其是编码时的运算效率的问题.