2. 中国能源建设集团广东省电力设计研究院有限公司,广东 广州 510663
2. Guangdong Electric Power Design Institute Co, Ltd. of China Energy Engineering Group, Guangzhou 510663, China
在节能减排、提高能源利用率和环境效益的大背景下,以风电为代表的分布式电源得到了迅速的发展. 然而,由于风速具有随机性、间歇性和难以预测性,使风电场输出功率具有强烈的随机性和波动性. 大规模风电并网会改变系统的潮流分布,对系统的电压稳定和有功网损等方面产生不同程度的影响[1-2],从而对电力系统的安全稳定运行带来重大挑战.
在经典电力系统无功优化中,负荷的随机性对无功优化结果产生较大影响. 风电并网后,风电机组有功输出的波动性,进一步加剧了电力系统运行中不确定因素的复杂程度. 为了突出风电并网对电力系统无功优化的影响,仅考虑风电随机性对系统无功优化的影响.
长期以来,国内外众多学者为解决无功优化问题做了大量的研究工作,提出了很多算法,这些算法对解决多目标无功优化问题提供了新途径[3-4]. 由于传统算法在处理无功优化问题上具有一定的局限性,不方便处理离散变量,易陷入局部最优解,且收敛速度慢;而人工智能算法具有较强的全局搜索能力且能处理含有离散约束条件的多目标无功优化,因此人工智能算法在无功优化问题中得到了广泛的研究和应用. 包括粒子群算法[5-6],遗传算法[7-8],免疫算法[9]、差分进化算法[10-11]和混合算法[12-13].
本文分析了熵权法和模糊权值法在客观决策和主观决策方面的优势,引入模糊熵权法将多目标优化问题转化为单目标优化问题. 同时,为了提高初始粒子的随机性和均匀性,结合Chebyshev映射与Logistic映射的优越特性,将其应用于粒子初始化,并将组合混沌映射产生的父代粒子,运用于本文提出的组合混沌动态粒子群算法中,提高算法整体寻优性能. 最后,通过IEEE14节点系统仿真测试,验证了该算法的高效性和可行性.
1 双馈风力发电机组的数学描述 1.1 双馈风力发电机组稳态数学模型由图1可以推出转子输出有功功率
| ${P_2} = \frac{{{r_2}x_{{\rm{ss}}}^2(P_1^2 + Q_1^2)}}{{x_{\rm{m}}^2U_1^2}} + \frac{{2{r_2}{x_{{\rm{ss}}}}}}{{x_{\rm{m}}^2}}{Q_1} - s{P_1} + \frac{{{r_2}U_1^2}}{{x_{\rm{m}}^2}}.$ | (1) |
其中,

|
图 1 双馈风力发电机组等效电路 Figure 1 Equivalent circuit of a doubly-fed wind turbine |
| $\begin{split}{P_{\rm{e}}} = & {P_1} + {P_2} = \displaystyle\frac{{{r_2}x_{{\rm{ss}}}^2(P_1^2 + Q_1^2)}}{{x_{\rm{m}}^2U_1^2}} + \displaystyle\frac{{2{r_2}{x_{{\rm{ss}}}}}}{{x_{\rm{m}}^2}}{Q_1} + \\ &(1 - s){P_1} + \displaystyle\frac{{{r_2}U_1^2}}{{x_{\rm{m}}^2}}.\end{split}$ | (2) |
双馈风力发电机在向电网发出有功功率的同时还将输出无功功率,目前主要有恒电压控制和恒功率因数控制两种控制方式. 采用恒功率因数控制时,定子侧输出的无功功率由有功功率与功率因数角共同决定,即
| ${Q_{\rm{e}}}\!\! = \!\!{Q_1} \!\!=\!\! {P_1}\tan \varphi = \frac{{ - bU_1^2 \!\!+\!\! {U_1}\!\!\sqrt {cU_1^2 \!\!+\! 4a{P_{\rm{e}}}} }}{{2a}}\tan \varphi .$ | (3) |
其中,
从式(3)中可以看出,双馈风电机组输出无功功率由有功功率及机端电压共同决定.
1.2 双馈风力发电机组有功输出特性风电机组输出功率取决于其所对应的风速,对于风电场中多台并列运行的风电机组,采用一台或多台等值机加以处理. 对于单台风电机组,其输出有功功率与风速的对应关系为
| ${P_{\rm{w}}} = \left\{ \begin{array}{l}0,v \leqslant {v_{{\rm{ci}}}}{\text{或}}v \geqslant {v_{{\rm{co}}}};\\[8pt]{P_{\rm{r}}}\displaystyle\frac{{v - {v_{{\rm{ci}}}}}}{{{v_{\rm{r}}} - {v_{{\rm{ci}}}}}},{v_{{\rm{ci}}}} \leqslant v \leqslant {v_{\rm{r}}};\\[8pt]{P_{\rm{r}}},{v_{\rm{r}}} \leqslant v \leqslant {v_{{\rm{co}}}}.\end{array} \right.$ | (4) |
其中,
目前实际应用中的大型风电场一般由几十甚至上百台的异步风力发电机组组成. 在进行风电机组并网后的电力系统潮流计算时,必须将风力发电机组的稳态数学模型扩展到系统的潮流方程中联立求解. 如上所述双馈风机输出的无功功率与其输出的有功功率及机端电压有关,因此不能将其简单取为P-Q节点. 风电场节点对应的潮流计算功率方程为
| $\left\{ \begin{array}{l}\Delta {P_i} = \displaystyle\sum\limits_{k = 1}^M {{P_{ik}}} - {V_i}\displaystyle\sum\limits_{j \in i} {{V_j}} ({G_{ij}}\cos {\delta _{ij}} + {B_{ij}}\sin {\delta _{ij}}) = 0;\\\Delta {Q_i} = \displaystyle\sum\limits_{k = 1}^M {{Q_{ik}}} - {V_i}\displaystyle\sum\limits_{j \in i} {{V_j}} ({G_{ij}}\sin {\delta _{ij}} - {B_{ij}}\cos {\delta _{ij}}) = 0.\end{array} \right.$ | (5) |
其中,
在电力系统潮流已知的情况下,多目标无功优化的数学模型是在满足系统和发电机约束的条件下,以系统有功网损
| $\left\{ \begin{array}{l}\min {f_1} \!\!=\!\! {P_{{\rm{loss}}}} \!\!=\!\!\! \displaystyle\sum\limits_{i,j \in {N_{\rm{L}}}} \!\!{{G_{ij}}(V_i^2 + V_j^2 - 2{V_i}{V_j}\cos {\theta _{ij}});} \\[10pt]\min {f_2} = \min ({\rm{d}}V) = \displaystyle\sum\limits_{i \in {N_{\rm{L}}}} {{{\left( {\displaystyle\frac{{{V_i} - V_i^s}}{{\Delta V_i^{\max }}}} \right)}^2}} ;\\[10pt]\max {f_3} = {\delta _{\min }}.\end{array} \right.$ | (6) |
其中,
约束条件含功率方程约束和变量约束. 功率方程约束如式(5)所示,变量约束包括节点电压约束、变压器分接头约束、无功补偿约束、并联电容器投切容量约束和线路潮流约束,如下
| $\left\{ \begin{array}{l}V_i^{\min } \leqslant {V_i} \leqslant V_i^{\max };\\[8pt]{T_k}^{\min } \leqslant T{}_k \leqslant {T_k}^{\max };\\[8pt]Q_i^{\min } \leqslant {Q_i} \leqslant Q_i^{\max };\\[8pt]{S_{{\rm{Li}}}} \leqslant S_{{\rm{Li}}}^{\max }.\end{array} \right.$ | (7) |
式中:
在进行多目标决策时,基于各个目标的差异程度,基于熵权法的客观决策方法认为差异越大,所占的权值也就越大;而基于模糊权值法的主观决策方法则将待优化问题设置有
假定采用熵权法计算所得的m个目标函数权值构成的矩阵为
| ${{\mathit{\boldsymbol{\lambda}}} _j} = \displaystyle\frac{{{{\mathit{\boldsymbol{f}}}_j} \times {{\mathit{\boldsymbol{w}}} _j}}}{{\displaystyle\sum\limits_{j = 1}^m {{{\mathit{\boldsymbol{f}}}_j} \times {{\mathit{\boldsymbol{w}}} _j}} }}.$ | (8) |
综合以上,通过各目标之间的博弈,对各目标函数进行归一化后得
| $\min {\mathit{\boldsymbol{f}}} = {{\mathit{\boldsymbol{\lambda}}} _1}\overline {{{\mathit{\boldsymbol{f}}}_2}} + {{\mathit{\boldsymbol{\lambda}}} _2}\overline {{{\mathit{\boldsymbol{f}}}_3}} + {{\mathit{\boldsymbol{\lambda}}} _3}\overline {{{\mathit{\boldsymbol{f}}}_5}}. $ | (9) |
粒子群优化算法以其收敛速度快、依赖参数少和对初值不敏感的特点而被广泛运用于各种优化问题的求解,其基本思想是以速度、位置和适应度3项指标表征. 通过不断跟踪个体最优值Pbest以及种群最优极值Gbest,不断地更新粒子的速度及位置,直到达到最大迭代次数或找到满足精度的最优解.
虽然粒子群优化算法具有快速收敛性能,但其在整个优化过程中都以Gbest作为引导,前期其收敛速度较快,但后期如果Gbest陷入局部最优解,则整个种群将陷入“早熟”,使优化问题不能得到全局最优解. 因此有必要对基本的粒子群算法进行改进.
3.1 基于组合混沌序列的种群初始化改进策略混沌运动能在一定范围内按其自身“规律”不重复地遍历所有状态,常被用来改进PSO算法[14-16]. 典型的Logistic映射数学方程为
| ${x_{n + 1}} = f(\mu ,{x_n}) = \mu \;{x_n}(1 - {x_n}).$ | (10) |
典型的Logistic混沌系统对初值的依赖性比较强. 本文将Logistic映射与Chebyshev映射相结合的组合混沌序列引入到PSO算法的初始化过程中,以改善粒子分布的随机性和均匀性. 序列的数学描述为[17]
| $\left\{ \begin{array}{l}{y_0} = {x_0};\\[6pt]{y_{m+ 1}} = \cos (n\arccos {y_n});\\[6pt]{\rm{temp}} = \mu {x_m}(1 - {x_m}) + \left| {{y_{m + 1}}} \right|;\\[6pt]{x_{m + 1}} = \bmod (\rm{temp},1).\end{array} \right.$ | (11) |
其中,
惯性权重
| $\omega (t + 1) = \left\{ \begin{array}{l}\omega (t)/p,v_{\rm{avg}}^t > v_{\rm{E}}^t;\\[6pt]\omega (t),v_{\rm{avg}}^t = v_{\rm{E}}^t;\\[6pt]\omega (t) \times p,v_{\rm{avg}}^t < v_{\rm{E}}^t.\end{array} \right.$ | (12) |
其中,
实验表明
| $v_{\rm{E}}^t = {v_0}{{\rm{e}}^{ - {{[2h({T_{\max }} - {T_1})]}^2}}},$ | (13) |
其中,h=4,
电力系统无功优化是保证电力系统安全经济运行和提高电压质量的重要措施之一. 本文以系统有功网损
步骤1:初始化程序,输入各参数原始数据,计算风电机组在不同风速下的输出功率;
步骤2:在控制变量的取值范围内随机生成一个初始粒子;
步骤3:利用式(11)对步骤1中粒子的速度和位置进行N-1次操作,产生混沌初始粒子群位置和速度;
步骤4:对步骤3中产生的粒子进行归一化逆操作,将[0,1]之间的变量转化为实际数值;
步骤5:计算系统潮流,将目标函数1作为适应度函数,评估潮流计算后每个粒子的适应值,更新
步骤6:更新粒子的速度和位置,对越限粒子的速度,取边界值进行处理;
步骤7:计算种群粒子速度
步骤8:对粒子进行归一化操作,并利用式(10)对其进行混沌化操作;
步骤9:对步骤8中的粒子进行归一化逆操作,并将[0,1]之间的变量转化为实际数值;
步骤10:计算粒子在不同风速下的适应度值,确定粒子本身经历最优位置
步骤11:检查终止条件,若结果精度满足要求或达到了最大迭代次数,终止当前迭代,输出最优值,否则转步骤6;
步骤12:分别以目标函数2和3作为评估粒子适应值的适应度函数,调用步骤5~11,计算对应的变量
步骤13:计算各个目标函数的熵权值和模糊权值,然后根据式(8),得出各个目标函数基于模糊熵权法的权值
步骤14:将
步骤15:根据步骤14获得的适应度函数最终表达式,再次调用步骤5~11,计算权衡各目标函数的折衷解及在此解下的各目标函数值.
4 算例分析采用IEEE14节点系统进行含风电的无功优化,验证CCPSO算法的有效性和实用性. IEEE14节点系统有5台发电机,20条支路,3条可调变压器支路,其详细参数参见文献[19]. 考虑在9号节点接入由40台双馈风力发电机组成的风电场,单台风机额定电压为0.69 kV,额定容量为1.5 MW,切入、切出和额定风速分别为3.5 m/s、25 m/s和12 m/s. 叶片扫风面积为4 657 m2,风电场所在地空气密度为1.224 5 kg/m3,轮毂高度65 m,励磁电抗为j1.456 8 Ω,定子阻抗为0.001 692+j0.036 92 Ω,转子阻抗为0.002 423+j0.037 59 Ω. CCPSO算法参数为:种群数目M=80,维数N=8,最大迭代次数
| 表 1 不同风速下风电场潮流分布结果 Table 1 Result of wind flow distribution under different wind speeds |
表2为含风电场无功优化结果. 可以看出,风电机组接入电网之后,随着风速的增大,其网损在不断降低. 由于并网风机输入电网中的有功功率增加,减小了系统中的有功流动,因此降低了系统的网络损耗. 与此同时,与风电接入电网前(即停机状态)相比,其电压偏差逐渐减小,静态电压稳定裕度逐渐增大,说明通过风电机组的无功调节能力,系统的运行状态得到了很大改善,起到了调节电压、降低网损的效果.
| 表 2 含风电场电网无功优化结果 Table 2 Results of reactive power optimization in wind farm |
为验证CCPSO算法的有效性与可行性,本文以额定运行状态下风速15 m/s为例,对风电场接入系统进行多目标无功优化,并与CPSO算法和PSO算法所得优化结果进行比较. 表3为不同算法下变量优化前后变量结果比较.
| 表 3 变量优化前后结果比较 Table 3 The results before and after variables optimization |
表4为各算法优化前后目标函数结果比较. 可以看出,采用各种算法进行优化计算后,系统有功网损、节点电压偏移及静态稳定裕度均有明显改善. 但如果仅考虑网损这一个参数,与其他两种算法相比,CCPSO并无明显优势,如果同时计及节点电压偏移和静态电压稳定裕度这两个指标,CCPSO优化之后的结果最好,并且所需要的迭代次数也最少.
| 表 4 优化前后结果对比 Table 4 Comparison of results before and after optimization |
图2为3种算法的收敛曲线,可以看出相较于PSO和CPSO两种算法,本文提出的CCPSO算法不管是在收敛精度还是在收敛速度上都具有很大的优势.
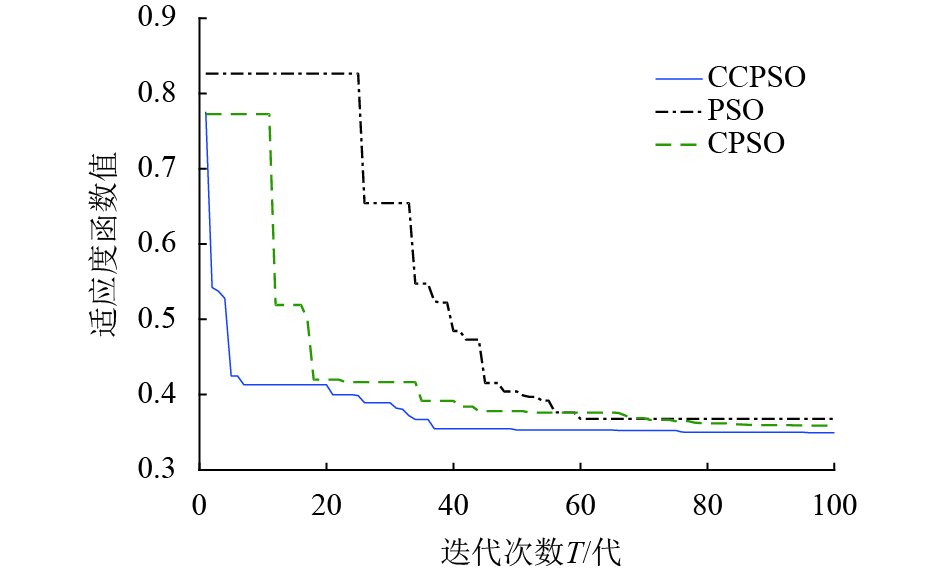
|
图 2 3种算法收敛曲线 Figure 2 Convergence curve of three algorithms |
本文综合考虑了系统网损、节点电压偏移和静态稳定裕度3个目标,结合客观决策和主观决策的优势,采用基于糊熵权法的多目标决策方法建立含风电场的多目标无功优化模型. 在传统的基于Logistic映射的CPSO算法基础上,采用种群平均速度动态改变惯性权重,防止进化过程中种群速度过早接近零而出现早熟的现象,结合Chebyshev映射和Logistic映射,在粒子初始化过程中运用组合混沌映射,增强初始粒子的均匀性,并将Logistic混沌优化引入到算法寻优过程中,使算法全局寻优能力得到加强. 仿真结果表明改进粒子群算法对电力系统无功优化具高效性和可行性,为解决含风电场的电力系统无功优化问题提供了一种新的思路和方法.
| [1] |
汪宁渤, 马彦宏, 王建东. 大规模风电集中并网对电力系统安全稳定的影响[J].
电力建设, 2011, 32(11): 77-80.
WANG N B, MA Y H, WANG J D. Analysis of power system security and stability caused by large-scale wind power grid integration[J]. Electric Power Construction, 2011, 32(11): 77-80. DOI: 10.3969/j.issn.1000-7229.2011.11.018. |
| [2] |
林章岁, 罗利群. 福建省风电出力特性及其对电网的影响分析[J].
电力建设, 2011, 32(12): 18-23.
LIN Z S, LUO L Q. Analysis of wind power output characteristics in Fujian and its impact on power grid[J]. Electric Power Construction, 2011, 32(12): 18-23. DOI: 10.3969/j.issn.1000-7229.2011.12.004. |
| [3] |
郭经韬, 陈璟华, 周俊, 等. 基于组合混度序列动态粒子群算法的电力系统无功优化[J].
广东工业大学学报, 2014, 31(2): 85-89.
GUO J T, CHEN J H, ZHOU J, et al. Reactive power optimization based on combined chaotic dynamic particle swarm optimization algorithm[J]. Guangdong University of Technology, 2014, 31(2): 85-89. |
| [4] |
严正, 陈雪青, 相年德, 等. 优化潮流牛顿算法的研究及应用[J].
清华大学学报, 1989, 29(1): 69-78.
YAN Z, CHEN X Q, XIANG N D, et al. Study of optimal power flow by newton approach and its application to var optimization[J]. Journal of Tsinghua University, 1989, 29(1): 69-78. |
| [5] | VLACHOGIANNIS J G, LEE K Y. A comparative study on particle swarm optimization for optimal steady-state performance of power systems[J]. IEEE Transactions on Power Systems, 2006, 21(4): 1718-1728. DOI: 10.1109/TPWRS.2006.883687. |
| [6] | VALLE Y, VENAYAGAMOORTHY G K, MOHAGHEGHI S, et al. Particle swarm optimization: basic concepts, variants and applications in power systems[J]. IEEE Transactions on Evolutionary Computation, 2008, 12(2): 171-195. DOI: 10.1109/TEVC.2007.896686. |
| [7] |
马立新, 王继银, 项庆, 等. 三目标混合骨干粒子群算法的电力系统无功优化[J].
电力科学与工程, 2015, 31(11): 18-23.
MA L X, WANG J Y, XIANG Q, et al. Three-objective hybrid Bare-bones particle swarm optimization for reactive power optimization[J]. Electric Power Science and Engineering, 2015, 31(11): 18-23. DOI: 10.3969/j.issn.1672-0792.2015.11.004. |
| [8] |
李智欢, 段献忠. 多目标进化算法求解无功优化问题的对比分析[J].
中国电机工程学报, 2010, 30(10): 57-65.
LI Z H, DUAN X Z. Comparison and analysis of multi-objective evolutionary algorithm for reactive power optimization[J]. Proceedings of the CSEE, 2010, 30(10): 57-65. |
| [9] | LIU M B, CANIZARES C A, HUANG W. Reactive power and voltage control in distribution systems with limited switching operations[J]. IEEE Transactions on Power Systems, 2009, 24(2): 889-899. DOI: 10.1109/TPWRS.2009.2016362. |
| [10] |
曾学强, 刘志刚, 符伟杰, 等. 改进差分进化算法在电力系统无功优化中的应用[J].
电网技术, 2012, 36(2): 121-125.
ZENG X Q, LIU Z G, FU W J, et al. Application of improved differential evolution algorithm in reactive power optimization[J]. Power System Technology, 2012, 36(2): 121-125. |
| [11] |
马玲, 于青, 刘刚, 等. 基于量子差分进化算法的电力系统无功优化[J].
电力系统保护与控制, 2013, 41(17): 39-43.
MA L, YU Q, LIU G, et al. Power system reactive power optimization based on quantum DE algorithm[J]. Power System Protection and Control, 2013, 41(17): 39-43. DOI: 10.7667/j.issn.1674-3415.2013.17.006. |
| [12] |
刘丽军, 李捷, 蔡金锭. 基于强引导粒子群与混沌优化的电力系统无功优化[J].
电力自动化设备, 2010, 30(4): 71-75.
LIU L J, L J, CAI J D. Reactive power optimization based on induction-enhanced particle swarm optimization and chaos search[J]. Electric Power Automation Equipment, 2010, 30(4): 71-75. |
| [13] |
简献忠, 李莹, 范建鹏, 等. 基于差分进化粒子群算法的多目标无功优化[J].
控制工程, 2015, 22(1): 113-117.
JIAN X Z, LI Y, FAN J P, et al. Particle swarm optimization based on differential evolution for multi-objective reactive power optimization[J]. Control Engineering of China, 2015, 22(1): 113-117. |
| [14] |
廖炎平, 刘莉, 龙腾. 基于多属性决策的气动隐身多目标优化[J].
机械工程学报, 2012, 48(13): 132-140.
LIAO Y P, LIU L, LONG T. Multi-objective aerodynamic and stealthy performance optimization based on multi-attribute decision making[J]. Journal of Mechanical Engineering, 2012, 48(13): 132-140. |
| [15] |
陈璟华, 邱明晋, 唐俊杰, 等. 基于改进差分进化和粒子群混合算法的电力系统最优潮流计算[J].
广东工业大学学报, 2017, 34(05): 22-28.
CHEN J H, QIU M J, TANG J J, et al. A hybrid algorithm based on improved differential evolution and particle swarm optimization for power system optimal power flow calculation[J]. Journal of Guangdong University of Technology, 2017, 34(05): 22-28. DOI: 10.12052/gdutxb.160149. |
| [16] |
陈璟华, 梁丽丽, 丁林军, 等. 计及风电场并网的机会约束规划的机组组合优化[J].
广东工业大学学报, 2017, 34(01): 50-54+64.
CHEN J H, LIANG L L, DING L J, et al. Unit commitment optimization based on chance-constrained programming in wind power integrated system[J]. Journal of Guangdong University of Technology, 2017, 34(01): 50-54+64. DOI: 10.12052/gdutxb.160087. |
| [17] |
俎云霄, 周杰. 基于组合混沌遗传算法的认知无线电资源分配[J].
物理学报, 2011, 60(7): 894-901.
ZU Y X, ZHOU J. Cognitive radio resource allocation based on combined chaotic genetic algorithm[J]. Acta Physica Sinica, 2011, 60(7): 894-901. |
| [18] |
张顶学, 廖锐全. 一种基于种群速度的自适应粒子群算法[J].
控制与决策, 2009, 24(8): 1257-1265.
ZHANG D X, LIAO R Q. Adaptive particle swarm optimization algorithm based on population velocity[J]. Control and Decision, 2009, 24(8): 1257-1265. |
| [19] | 张伯明, 陈寿孙, 严正.高等电力网络分析[M].北京: 清华大学出版社, 2007. |
 2018, Vol. 35
2018, Vol. 35