能量受限的无线网络运行时间较短，典型的如用电池为无线网络提供能量，如果电池电量耗尽，更换电池或者为电池充电可以延长网络的运行时间. 这种方式成本较高，甚至在有些情况下无法实现.

能量受限的无线网络面临着能量缺乏的问题，在文献[1-4]提出了属于能量收集技术的无线携能传输有助于解决这一问题. 无线能量传输和信息传输一样，随着发射机和接收机之间距离增加，使得能量衰减，导致可达速率较低. 为了解决这一问题，文献[5-6]采用了基于大规模天线阵列的波束成形技术来提高网络的传输性能. 在文献[7-9]中，发送端引入了大规模天线阵列来提高系统的传输性能. 此外，文献[10]引入了具有能量收集装置的中继节点也是一种提高无线携能传输性能的有效方法. 文献[11]介绍了一种基于无线携能中继的窄带单载波放大转发中继网络. 中继在不同的时隙里获得能量和转发信息，这意味着在不同的时隙，中继充当着能量收集机和信息转发器的角色. 文献[12-13]研究了基于无线携能的解码转发中继网络.

在多载波系统中，文献[14]研究了基于无线携能传输的单跳网络，文献[15]研究了无线携能传输的解码转发中继网络. 文献[16]提出了多载波解码转发中继系统的传输方式，中继接收到发送端的各载波的信号并将它们重新分配到不同的子载波上，再发送到接收端. 文献[17]研究了基于无线携能的单天线正交频分复用(OFDM)中继系统，提出了时间和功率资源联合的优化算法. 然而，基于大规模天线阵列的无线携能OFDM中继系统的时间和功率联合分配最优问题至今没有得到深入的研究.

对于大规模天线阵列的无线携能OFDM中继系统，本文提出了针对该系统的时间和功率联合分配最优算法. 通过时间和功率联合分配最优算法，可以达到最大化点对点可达速率的目的，并支持远距离无线携能传输.

1 系统模型

考虑由一个发送端、一个解码转发中继和一个接收端组成的两跳OFDM中继网络系统. 发送端有N_t根天线（N_t足够大），中继和接收端具有单天线. 发送端与接收端之间没有直接的通信链路，发送端的信息经过中继转发至接收端. 中继工作在时分半双工的模式. 中继需要从发送端接收能量来满足信号的处理和转发. 设系统的信息传输帧的长度为T，它被分为3个时隙，分别是 ${\beta _1}T$ 、 ${\beta _2}T$ 、 ${\beta _3}T$ ，满足 ${\beta _1} + {\beta _2} + {\beta _3} = 1$ . 在第一个时隙 ${\beta _1}T$ ，发送端向中继发送能量；在第二个时隙 ${\beta _2}T$ ，发送端向中继发送信息；在第三个时隙 ${\beta _3}T$ ，中继运用第一个时隙所接收到的能量解码第二个时隙接收到的信息并转发给接收端.

该OFDM系统有N个正交的子载波. 假设SR链路为发送端到中继的链路，RD链路为中继到接收端的链路，基于SR和RD链路信道状态信息，发送端和中继分别对各子载波进行功率的分配. $\sqrt {{{\textit{η}} _{{\rm{SR}}}}} \mathit{\boldsymbol{h}}_n^{{\rm{SR}}}$ 和 ${\sqrt{ {\textit{η}} _{{\rm{RD}}}}}\mathit{\boldsymbol{h}}_n^{{\rm{RD}}}$ 分别表示N个子载波在SR和RD链路的信道，其中 ${{\textit{η}} _{{\rm{SR}}}}$ 和 ${{\textit{η}} _{{\rm{RD}}}}$ 分别是SR和RD链路的大尺度衰落因子， $1 \times {N_t}$ 的矩阵 $\mathit{\boldsymbol{h}}_n^{{\rm{SR}}}$ 和标量 $\mathit{\boldsymbol{h}}_n^{{\rm{RD}}}$ 分别表示SR和RD链路小尺度衰落增益，它们是独立同分布的. 因此中继在第一个时隙接收到的功率为^[2]

$E = {\beta _1}{{\textit{η}} _{\rm{SR}}}T\rho \sum\limits_{n = 1}^N {p_n^{{\rm{SR}},1}} {\left| {{{(\mathit{\boldsymbol{h}}_n^{{\rm{SR}}})}^H}{\mathit{\boldsymbol{w}}_n}} \right|^2},$

(1)

其中 $p_n^{{\rm{SR}},1}$ 是第n个子载波的传输功率，ρ是能量接收效率， ${\mathit{\boldsymbol{w}}_n}$ 是第n个子载波在信息和能量传输的波束成形矩阵. 为了最大化能量的传输， ${\left| {{{(\mathit{\boldsymbol{h}}_n^{{\rm{SR}}})}^H}{\mathit{\boldsymbol{w}}_n}} \right|^2}$ 必须最大. 中继在该时隙接收到的能量为

$E = {\beta _1}\lambda .$

(2)

其中

$\lambda = {{\textit{η}} _{{\rm{SR}}}}T\rho P\mathop {\max }\limits_n {\left| {{{(\mathit{\boldsymbol{h}}_n^{{\rm{SR}}})}^H}{\mathit{\boldsymbol{w}}_n}} \right|^2}.$

(3)

式中，P是发送端的最大传输功率. 最大比传输(MRT)波束成形能够最大化E，i.e., ${\mathit{\boldsymbol{w}}_n} = \mathit{\boldsymbol{h}}_n^{{\rm{SR}}}/\left\| {\mathit{\boldsymbol{h}}_n^{{\rm{SR}}}} \right\|$ . 因此在第一时隙中继接收到的能量为

$\lambda = {{\textit{η}} _{{\rm{SR}}}}T\rho P\mathop {\max }\limits_n {\left\| {\mathit{\boldsymbol{h}}_n^{{\rm{SR}}}} \right\|^2}.$

(4)

当天线数趋近无穷大的时候，满足

$\mathop {\lim }\limits_{{N_t} \to \infty } \frac{{{{\left\| {\mathit{\boldsymbol{h}}_n^{{\rm{SR}}}} \right\|}^2}}}{{{N_t}}} = 1.$

这是信道硬化的性质^[18]，因此得到

$\lambda = {{\textit{η}} _{\rm{SR}}}T\rho P{N_t}.$

(5)

在第二个时隙，发送端通过N个子载波向中继发送信息. 第三个时隙，中继利用第一时隙接收到的能量对接收到的信息进行解码和转发到接收端. 因此这两个连续时隙的可达速率可以表示为

${R_{{\rm{SR}}}} = {\beta _2}\sum\limits_{n = 1}^N {{{\log }_2}} (1 + p_n^{{\rm{SR}},2}r_n^{{\rm{SR}}})$

(6)

和

${R_{{\rm{RD}}}} = {\beta _3}\sum\limits_{n = 1}^N {{{\log }_2}} (1 + p_n^{{\rm{RD}}}r_n^{{\rm{RD}}}),$

(7)

其中 $p_n^{{\rm{SR}},2}$ 和 $p_n^{{\rm{RD}}}$ 分别是SR和RD链路信息传输时，第n个子载波的传输功率， $r_n^{{\rm{SR}}}$ 和 $r_n^{{\rm{RD}}}$ 分别定义为

$r_n^{{\rm{SR}}} = \frac{{{{\textit{η}} _{{\rm{SR}}}}{{\left| {\mathit{\boldsymbol{h}}_n^{{\rm{SR}}}{\mathit{\boldsymbol{w}}_n}} \right|}^2}}}{{\sigma _{{\rm{SR}}}^2}},$

(8)

$r_n^{{\rm{RD}}} = \frac{{{{\textit{η}} _{{\rm{RD}}}}{{\left| {\mathit{\boldsymbol{h}}_n^{{\rm{RD}}}} \right|}^2}}}{{\sigma _{{\rm{RD}}}^2}}.$

(9)

假设这两条链路的每个子载波的噪声是相互独立并且满足方差 $\sigma _{{\rm{SR}}}^2$ 和 $\sigma _{{\rm{RD}}}^2$ 的加性高斯白噪声. 通过使用最大比合并和信道硬化， $r_n^{{\rm{SR}}}$ 可以表示为

$r_n^{{\rm{SR}}} = \frac{{{{\textit{η}} _{{\rm{SR}}}}{N_t}}}{{\sigma _{{\rm{SR}}}^2}}.$

(10)

基于文献[16], 系统从发送端到接收端的可达速率可表示为

$R = \min (R_n^{{\rm{SR}}},R_n^{{\rm{RD}}}).$

(11)

2 时间和功率联合分配最优算法

本文在中继的能量接收和发送端功率传输的限制条件下，通过时间和功率联合分配最优算法可使发送端到接收端的可达速率最大化，算法如表(1)所示.

时间和功率联合分配最优算法问题为

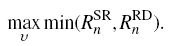
(12a)

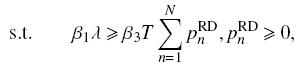
(12b)

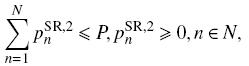
(12c)

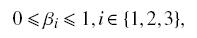
(12d)

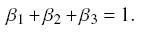
(12e)

其中 $\upsilon = \{ {\beta _1},{\beta _2},{\beta _3},p_n^{{\rm{SR}},2},p_n^{{\rm{RD}}},n \in N\} $ ，式(12b)是第一时隙内中继接收的能量限制，必须不低于中继信息处理和传输的能量损耗；式(12c)是第二时隙发送端信息传输时，分配到子载波的功率的条件限制；式(12d)和式(12e)是时间资源分配的条件.

关于目标函数(12a)，文献[12]有相关的描述，最优解 $\upsilon $ 满足

${\beta _2}\sum\limits_{n = 1}^N {{{\log }_2}} (1 + p_n^{{\rm{SR}},2}r_n^{{\rm{SR}}}) = {\beta _3}\sum\limits_{n = 1}^N {{{\log }_2}} (1 + p_n^{{\rm{RD}}}r_n^{{\rm{RD}}}).$

(13)

把式(9)和式(10)代入式(13)可以得到

$\mu = \displaystyle\frac{{\displaystyle\sum\limits_{n = 1}^N {{{\log }_2}} (1 + p_n^{{\rm{RD}}}\frac{{{{\textit{η}} _{\rm{RD}}}{{\left| {\mathit{\boldsymbol{h}}_n^{{\rm{RD}}}} \right|}^2}}}{{\sigma _{\rm{RD}}^2}})}}{{\displaystyle\sum\limits_{n = 1}^N {{{\log }_2}} (1 + p_n^{{\rm{SR}},2}\frac{{{{\textit{η}} _{{\rm{SR}}}}{N_t}}}{{\sigma _{{\rm{SR}}}^2}})}},$

(14)

其中 $\mu = \displaystyle\frac{{{\beta _2}}}{{{\beta _3}}}$ ，由时间资源分配条件(12d)和(12e), 能够得到

${\beta _3} \leqslant \frac{\lambda }{{T\displaystyle\sum\limits_{n = 1}^N {p_n^{{\rm{RD}}} + (1 + \mu )\lambda } }}.$

(15)

由式(13)可知，目标函数能够重新表示为

$\begin{array}{l}\mathop {\max }\limits_{0 \leqslant {\beta _3} \leqslant 1,p_n^{{\rm{SR}},2},p_n^{{\rm{RD}}}} R = {\beta _3}\displaystyle\sum\limits_{n = 1}^N {{{\log }_2}} (1 + p_n^{\rm{RD}}\displaystyle\frac{{{{\textit{η}} _{\rm{RD}}}{{\left| {\mathit{\boldsymbol{h}}_n^{{\rm{RD}}}} \right|}^2}}}{{\sigma _{\rm{RD}}^2}})\\[19pt]\;\;\;\;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;\;0 \leqslant \beta \leqslant 1,i \in \left\{ {1,2,3} \right\},\\[6pt]\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\beta _3} \leqslant \displaystyle\frac{\lambda }{{T\displaystyle\sum\limits_{n = 1}^N {p_n^{{\rm{RD}}} + (1 + \mu )\lambda } }}.\end{array}$

(16)

由式(16)得知目标函数是一个关于β₃的非减函数，因此最优的β₃必须满足

${\beta _3} = \frac{\lambda }{{T\displaystyle\sum\limits_{n = 1}^N {p_n^{{\rm{RD}}} + (1 + \mu )\lambda } }}.$

(17)

把式(17)代入目标函数(16)，得到

$R = \displaystyle\frac{{\lambda \displaystyle\sum\limits_{n = 1}^N {{{\log }_2}} (1 + p_n^{{\rm{RD}}}\frac{{{{\textit{η}} _{\rm{RD}}}{{\left| {\mathit{\boldsymbol{h}}_n^{{\rm{RD}}}} \right|}^2}}}{{\sigma _{{\rm{RD}}}^2}})}}{{T\displaystyle\sum\limits_{n = 1}^N {p_n^{{\rm{RD}}} + (1 + \mu )\lambda } }}. $

(18)

进而对式(18)左右两边同时求倒数得到

$\begin{split}\displaystyle\frac{1}{R} = & \displaystyle\frac{{T\displaystyle\sum\limits_{n = 1}^N {p_n^{{\rm{RD}}} + \lambda } }}{{\lambda \displaystyle\sum\limits_{n = 1}^N {{{\log }_2}} (1 + p_n^{{\rm{RD}}}\frac{{{{\textit{η}} _{{\rm{RD}}}}{{\left| {{\mathit{\boldsymbol{h}}}_n^{{\rm{RD}}}} \right|}^2}}}{{\sigma _{\rm{RD}}^2}})}} + \\[-5pt]&\frac{{\lambda \mu }}{{\lambda \displaystyle\sum\limits_{n = 1}^N {{{\log }_2}} (1 + p_n^{{\rm{RD}}}\displaystyle\frac{{{{\textit{η}} _{{\rm{RD}}}}{{\left| {{\mathit{\boldsymbol{h}}}_n^{{\rm{RD}}}} \right|}^2}}}{{\sigma _{{\rm{RD}}}^2}})}}. \end{split}$

(19)

通过最小化式(19)来达到最大化目标函数(16)的目的，因此优化问题(16)能够重新写成

$\begin{split}\mathop {\min }\limits_{p_n^{{\rm{SR}},2},p_n^{{\rm{RD}}}} \frac{{T\displaystyle\sum\limits_{n = 1}^N {p_n^{{\rm{RD}}} + \lambda } }}{{\lambda \displaystyle\sum\limits_{n = 1}^N {{{\log }_2}} (1 + p_n^{{\rm{RD}}}\frac{{{{\textit{η}} _{\rm{RD}}}{{\left| {\mathit{\boldsymbol{h}}_n^{{\rm{RD}}}} \right|}^2}}}{{\sigma _{\rm{RD}}^2}})}}+\\[-2pt]\displaystyle\frac{{\lambda \mu }}{{\lambda \sum\limits_{n = 1}^N {{{\log }_2}} (1 + p_n^{{\rm{RD}}}\displaystyle\frac{{{{\textit{η}} _{\rm{RD}}}{{\left| {\mathit{\boldsymbol{h}}_n^{{\rm{RD}}}} \right|}^2}}}{{\sigma _{{\rm{RD}}}^2}})}},\;\;\;\;\;\\{\rm{ s}}{\rm{.t}}{\rm{. }}\displaystyle\sum\limits_{n = 1}^N {p_n^{{\rm{SR}},2}} \leqslant P,p_n^{{\rm{SR}},2} \geqslant 0,p_n^{{\rm{RD}}} \geqslant 0,n \in N.\end{split}$

(20)

把式(14)代入式(20)，式(20)可以分解成

$\begin{split}&\mathop {\max }\limits_{p_n^{{\rm{SR}},2} \geqslant 0,n \in N} \displaystyle\sum\limits_{n = 1}^N {{{\log }_2}} (1 + p_n^{{\rm{SR}},2}\displaystyle\frac{{{{\textit{η}} _{{\rm{SR}}}}{N_t}}}{{\sigma_{{\rm{SR}}}^2}}),\\&{\rm{ s}}{\rm{.t}}{\rm{. }}\displaystyle\sum\limits_{n = 1}^N {p_n^{{\rm{SR}},2}} \leqslant P.\end{split}$

(21)

和

$\mathop {\max }\limits_{p_n^{{\rm{RD}}},n \in { N}} \frac{{\lambda \displaystyle\sum\limits_{n = 1}^N {{{\log }_2}} (1 + p_n^{{\rm{RD}}}\frac{{{{\textit{η}}_{{\rm{RD}}}}{{\left| {\mathit{\boldsymbol{h}}_n^{{\rm{RD}}}} \right|}^2}}}{{\sigma _{{\rm{RD}}}^2}})}}{{T\displaystyle\sum\limits_{n = 1}^N {p_n^{{\rm{RD}}} + \lambda } }}. $

(22)

很容易看出式(21)是凸问题，并且求得最优解为^[19]

$\overline {p_n^{{\rm{SR}},2}} = {(\frac{1}{\alpha } - \frac{{\sigma _{{\rm{SR}}}^2}}{{{{\textit{η}} _{{\rm{SR}}}}{N_t}}})^ + },\forall n \in N,$

(23)

其中 ${x^ + } = \max (x,0)$ ，α是拉格朗日乘子.然而，问题(22)是一个非凸问题. 根据文献[19], 目标函数(22)等于

$\lambda \sum\limits_{n = 1}^N {{{\log }_2}} (1 + p_n^{{\rm{RD}}}\frac{{{{\textit{η}} _{{\rm{RD}}}}{{\left| {h_n^{{\rm{RD}}}} \right|}^2}}}{{\sigma _{{\rm{RD}}}^2}}) - {q^*}(T\sum\limits_{n = 1}^N {p_n^{{\rm{RD}}} + \lambda } ),$

(24)

其中q^*是目标函数(22)的最优解，当 $p_n^{{\rm{RD}}}$ 等于最优值 $p_n^{{\rm{RD}}*}$ 时有 ${q^*} = \displaystyle\frac{{\lambda \displaystyle\sum\limits_{n = 1}^N {{{\log }_2}} (1 + p_n^{{\rm{R}}{{\rm{D}}^*}}\displaystyle\frac{{{\eta _{{\rm{RD}}}}{{\left| {\mathit{\boldsymbol{h}}_n^{{\rm{RD}}}} \right|}^2}}}{{\sigma _{{\rm{RD}}}^2}})}}{{T\displaystyle\sum\limits_{n = 1}^N {p_n^{{\rm{R}}{{\rm{D}}^*}} + \lambda } }}$ . 因此式(22)能够重写成

$\begin{split}&\mathop {\max }\limits_{p_n^{{\rm{RD}}} \geqslant 0,n \in N} \lambda \displaystyle\sum\limits_{n = 1}^N {{{\log }_2}} (1 + p_n^{{\rm{RD}}}\displaystyle\frac{{{{\textit{η}} _{{\rm{RD}}}}{{\left| {\mathit{\boldsymbol{h}}_n^{{\rm{RD}}}} \right|}^2}}}{{\sigma _{{\rm{RD}}}^2}}) - \\&\;\;\;\;\;\;\;\;\;\;{q^*}(T\displaystyle\sum\limits_{n = 1}^N {p_n^{{\rm{RD}}} + \lambda } ).\end{split}$

(25)

容易证明问题(25)是凸问题并且有非负的最优值. 使用KKT条件^[20]，能够得到式(25)的最优值为

$\displaystyle \overline {p_n^{{\rm{RD}}}} = {(\displaystyle\frac{\lambda }{{{q^*}T\ln 2}} - \displaystyle\frac{{\sigma _{{\rm{RD}}}^2}}{{{{\textit{η}} _{{\rm{RD}}}}{{\left| {{\mathit{\boldsymbol{h}}}_n^{{\rm{RD}}}} \right|}^2}}})^ + },\displaystyle\forall n \in N.$

(26)

问题(22)能够通过二分法搜索q^*得到最优值，q^*的下界假设 ${q^*}_l = 0$ ，上界为 ${q^*}_u = q$ ，根据文献[17]，q能够通过式(27)求得：

$\displaystyle q = N{\log _2}(1 + Q) + N\kappa {\log _2}(1 + {\kappa ^{ - 1}}),$

(27)

其中 $Q = \lambda \mathop {\max }\limits_n r_n^{{\rm{RD}}}/T$ 和 $\kappa = W\left( { - 1/e} \right)$ ，W是Lambert W函数^[21].

3 仿真结果与分析

采用计算机仿真验证所提时间和功率联合分配最优算法的性能. 系统的子载波数为N=32，对于每个子载波， $\mathit{\boldsymbol{h}}_n^{\rm{SR}}$ 和 $\mathit{\boldsymbol{h}}_n^{\rm{RD}}$ 满足均值为0、方差为1的独立复高斯分布. 仿真中，令SR和RD链路的大尺度衰落因子相等，即 ${{\textit{η}}_{{\rm{SR}}}} = {{\textit{η}} _{{\rm{RD}}}} = {\textit{η}} $ ，SR和RD链路的加性高斯白噪声的方差 ${\sigma _{{\rm{SR}}}} = {\sigma _{{\rm{RD}}}} = {\sigma ^2}/N$ ，并且假设 ${\sigma ^2} = 0.001\;{\rm{mW}}$ ，ρ₁，T=1 ms.

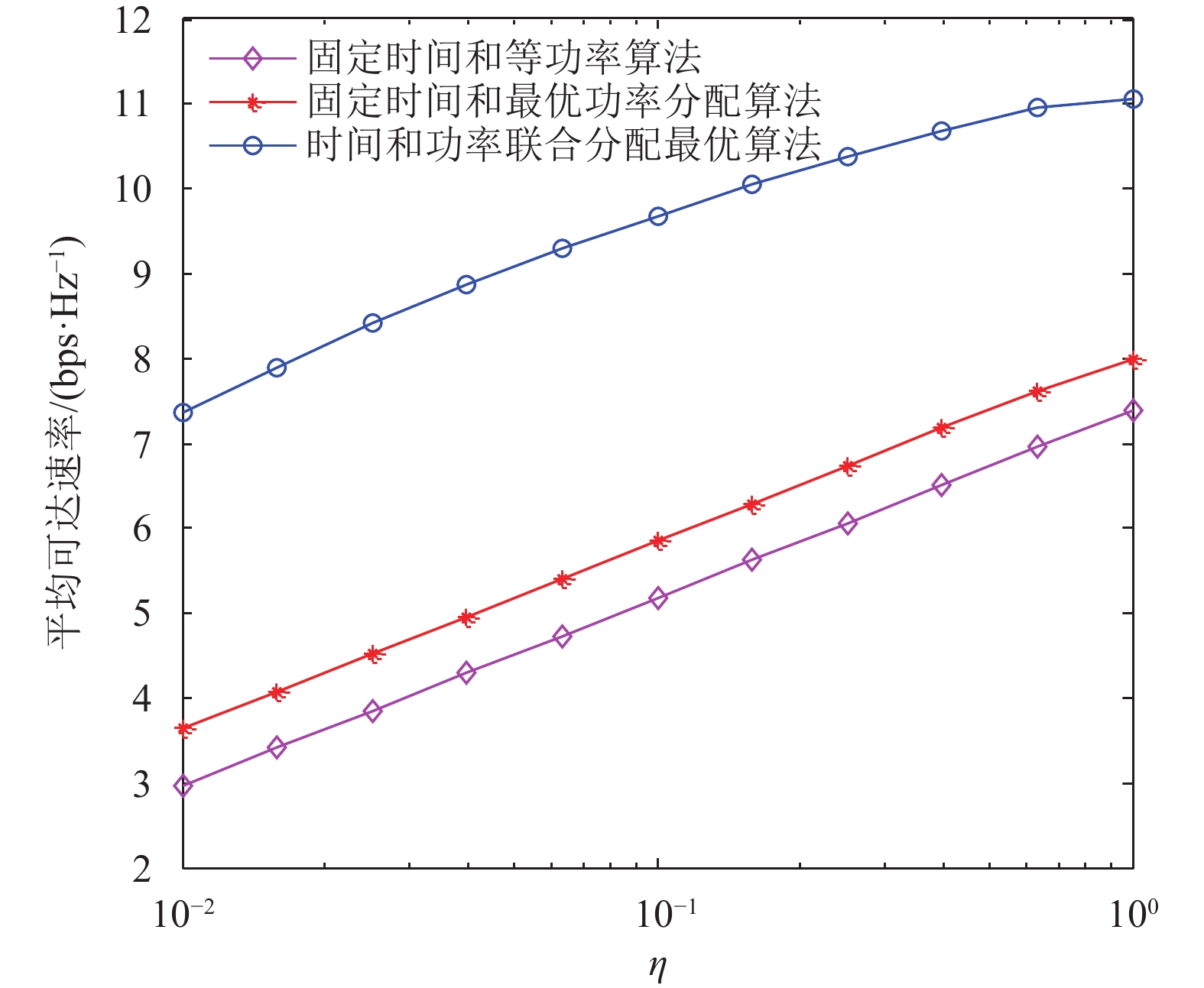
基于衰落因子的变化，图1显示的时间和功率体现应用大规模天线对系统性能的影响，本文对比了在同样的资源分配策略条件下使用单天线（文献[17]）所得到的系统性能. 联合分配算法的性能，假设天线数N_t=20和P=100 mW，对于不同的资源分布策略，发送端到接收端的平均可达速率性能的变化. “固定时间和最优功率分配算法”曲线是由固定时间和最优功率资源配置策略所得，“固定时间和等功率分配算法”曲线是由固定时间和固定功率资源配置策略所得. 固定时间和最优功率资源配置策略是假设 ${\beta _1} = {\beta _2} = {\beta _3}$ 和利用式(23)和式(26)对子载波进行功率分配. 固定时间和固定功率资源配置策略假设 ${\beta _1} = {\beta _2} = {\beta _3}$ 和对每个子载波进行等功率分配. 从仿真图可以看出时间和功率联合分配最优算法较其余两种策略有更高的性能.

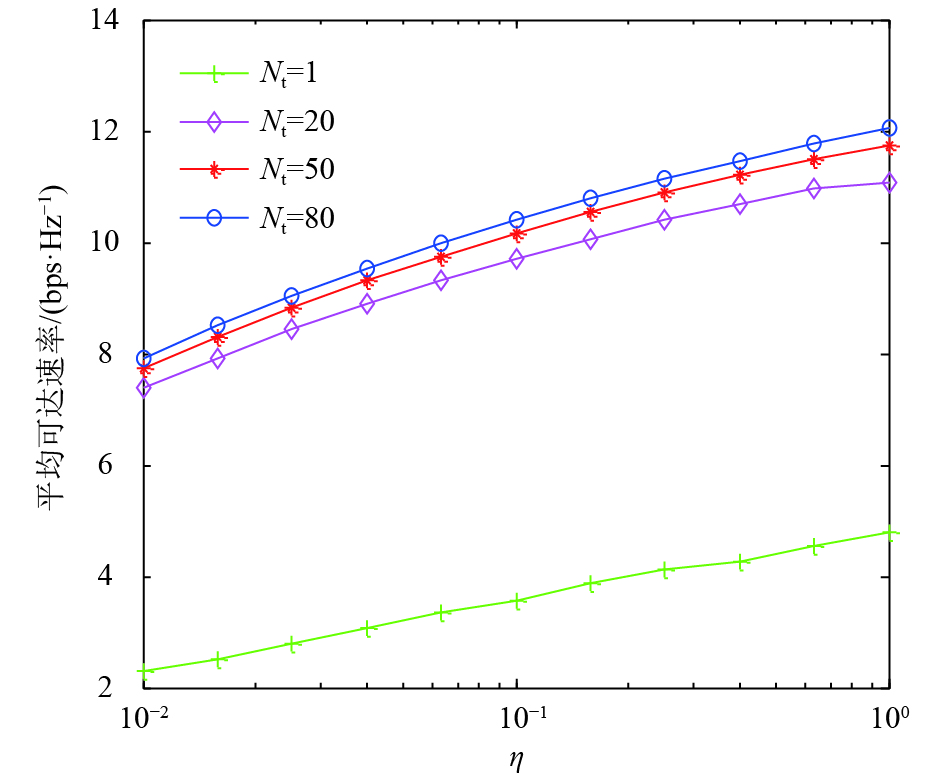
基于衰落因子的变化，图2显示了天线数对于平均可达速率的影响，在最优资源分配策略的条件下，假设P=100 mW，根据发送端的天线数量的不同所得到的不同平均可达速率. 天线数越大，平均可达速率越大. 对比天线N_t=1（参考文献[17]）所得到的可达速率，可以得出扩大天线阵容能够得到更优的系统性能.

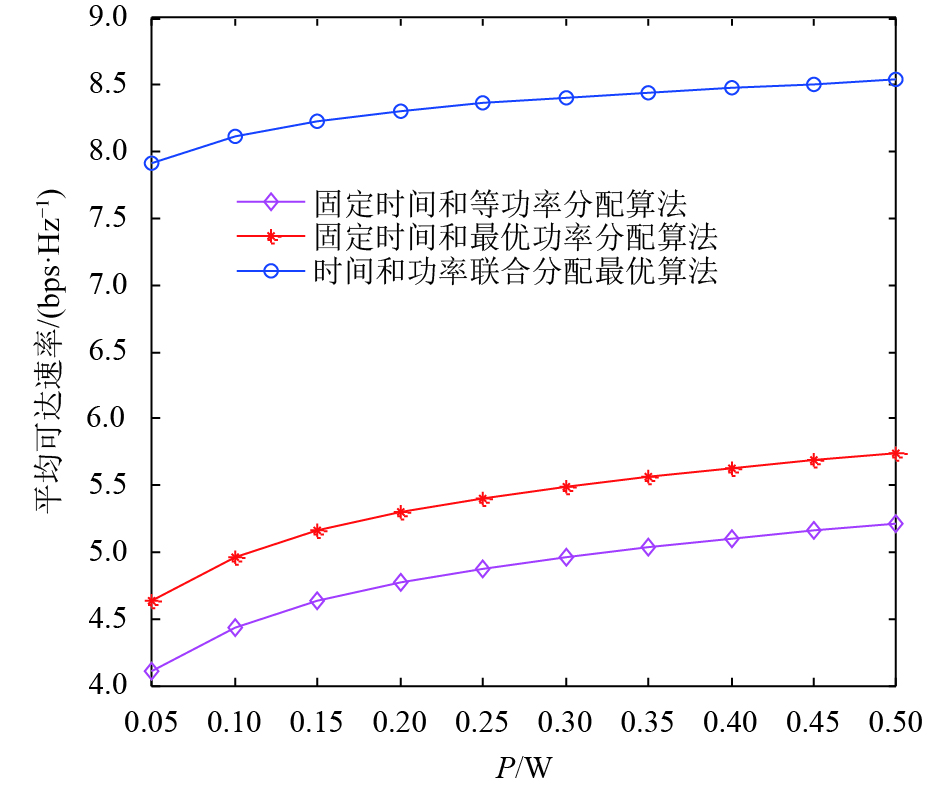
基于发送端最大传输速率的变化，图3显示了时间和功率联合分配算法的性能，假设天线数N_t=20和 $\eta = {10^{ - 0.4}}$ ，基于P的改变来对比不同策略的平均可达速率. 可以看出P越大，平均可达速率越大. 时间和功率联合分配最优算法的性能高于其余两种.

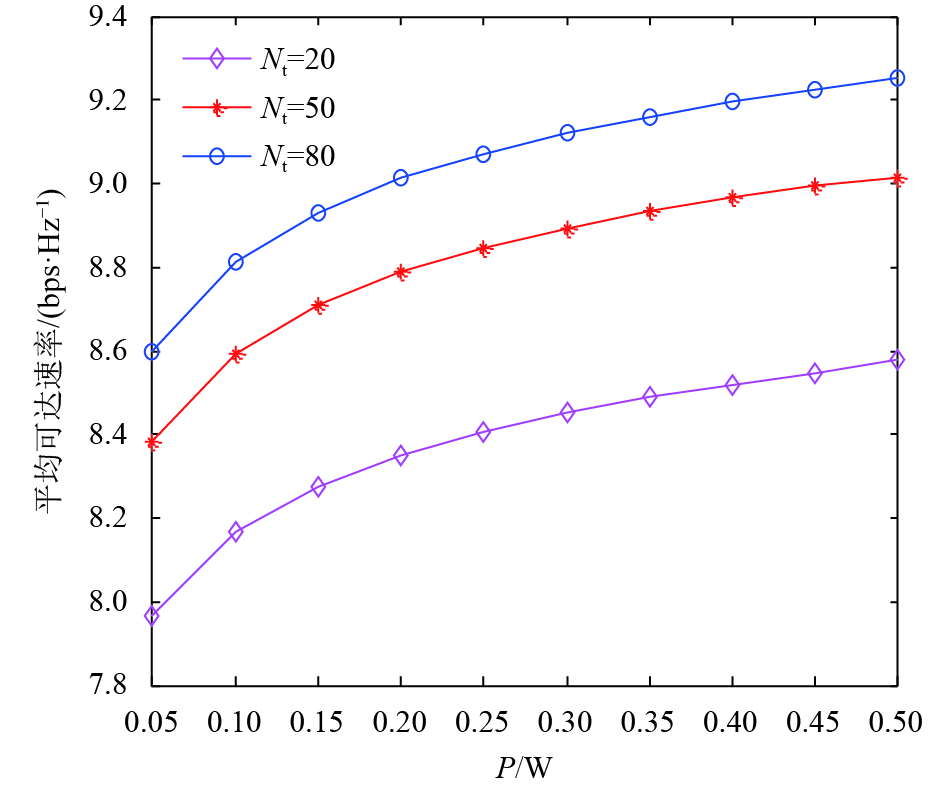
对于时间和功率联合分配最优算法，基于发送端最大传输速率的变化，图4显示了天线数对于平均可达速率的影响，在最优资源分配策略的条件下，假设 $\eta = {10^{ - 0.4}}$ ，根据发送端的天线数量的不同所得到的不同平均可达速率. 天线数N_t越大，系统平均可达速率越大.

4 结束语

本文提出了具有大规模天线阵列结构的OFDM解码转发中继系统的无线携能通信，运用时间和功率联合分配最优算法，最大化了发送机到接收机的可达速率. 仿真结果证明了适当的资源分配策略有更强的系统性能.