2. 广东工业大学 自动化学院,广东 广州 510006
2. School of Automation, Guangdong University of Technology, Guangzhou 510006, China
近年来,随着社会经济的发展、城镇化进程的加快和生活条件的改善,我国城市交通拥堵、群众出行不便和私家车保有量增加造成空气污染等问题日益明显,庞大的出行需求和有限的公共交通资源之间的矛盾更加突出.
发展智慧公交系统是解决上述问题的关键. 科学的公交车辆调度和合理的线路规划促使公交系统高效运营,而公交调度和线路规划都依赖于对公交客流准确、全面的分析和预测. 公交的高效运营对客流繁重的工作日尤为重要,因此基于交通一卡通大数据的公交工作日客流分析与预测具有重要的意义.
2011年6月起,麦肯锡咨询公司陆续发布了多份有关“大数据”的研究报告,其中一份名为《大数据:下一个竞争、创新和生产力的前沿》一文提出大数据将促进生产力增长并推动创新,大数据的充分利用将在各个领域创造巨大的价值. 此后,大数据的应用延伸至医疗、交通和金融等多个领域[1]. 交通一卡通大数据包括一卡通数据及联接与交通相关其他数据. 数据来源的丰富和数据的爆炸式增长促使一卡通大数据的形成,并且得到日益广泛的关注和研究[2-3].
目前利用大数据分析和预测客流有历史平均模型、线性回归模型和非线性回归模型等方法,Xu Wei等[4]提出了基于时间和空间,并利用线性回归方法得到预测结果的地铁客流预测方法;Mo Y等[5]提出一种基于神经网络的实时公交线路客流预测解决方案,输入变量包括预测日期、时间、客流量和天气;芦方强等[6]运用模型标定和图形处理等方法研究了居民出行时间消耗特征、分布特征和空间分布特征;张春辉等[7]在进行短时客流特性分析的基础上,利用卡尔曼滤波建立公交站点短时客流的预测模型;邹巍等[8]分析造成轨道交通客流具有不确定性、动态性和非线性的影响因素,提出基于小波神经网络与遗传算法的轨道交通短时客流预测方法.
不同的学者考虑到的客流因素不尽相同,尚没有学者在进行客流预测时考虑时间段、天气类型、最高温度、最低温度和风力等不确定因素对工作日公交客流的影响[9-11]. 本文利用公交IC卡数据分析了工作日的客流特性,并综合考虑了天气类型、最高温度、最低温度和风力,通过多元线性回归模型,准确地预测工作日高峰时段的公交客流. 希望以此方法为科学的公交车辆调度和合理的线路规划提供思路.
1 原始数据的采集与预处理 1.1 原始数据的采集 1.1.1 公交IC卡数据采集通过对公交IC卡交易数据进行综合性的采集处理,可以准确有效地获取客流出行需求信息,为分析公交客流的分布特性和公共交通治理提供基础数据支撑.
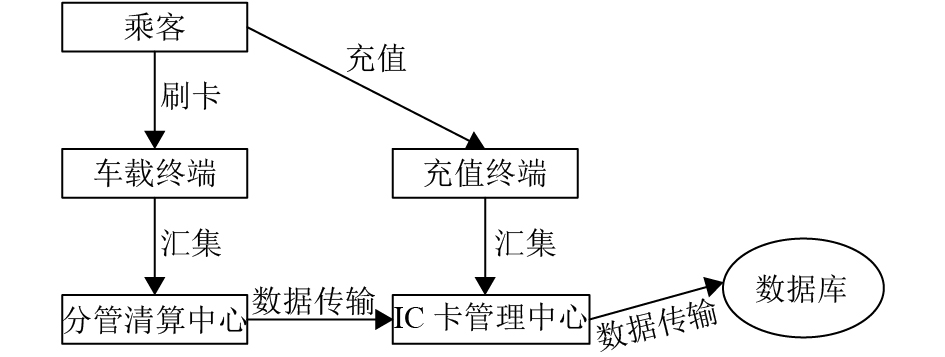
传统的公交客流调查存在耗时、耗力、复杂和繁琐等缺点. 目前公交IC卡数据采集通过经验积累和技术发展逐步形成规范化的采集流程[12],具体流程如图1所示.
(1) IC卡记录的产生:乘客将IC卡放置车载终端,卡号和刷卡时间被记录;乘客利用充值终端进行充值的信息也被记录.
(2) 数据的传递过程:数据通过导入或者无线传输等方式送至分管清算中心.
(3) 数据的接收:数据分管中心以数据通讯方式将数据传送到数据库.
|
图 1 公交IC卡数据采集流程[10] Figure 1 Bus IC card data acquisition process |
随着城市公共交通一卡通在城市普及程度的逐渐提升和使用人群增加,每时每刻都将产生大量的公交IC刷卡数据. 以广东省公交一卡通(岭南通)为例,岭南通在全省范围内每天的刷卡数据记录达到1 500多万条,公交刷卡数据量为55 GB,全年的数据量高达20 TB[12],这些数据经过上述方法采集之后形成了本文关于客流量分析与预测的重要数据来源.
本文采用的公交IC卡刷卡数据为广州市内随机选取的6条公交线路,从2014年08月01日至2015年01月31日的公交刷卡数据,经严格的预处理得出的100多万条数据记录,其中累计乘车人次达5万. 所得的IC卡交易数据结构如表1所示,包括使用地、刷卡终端ID、线路、卡片ID、发卡地、交易时间、交易金额和卡类型等信息.
| 表 1 公交IC卡刷卡数据(部分字段) Table 1 Bus IC card data |
目前分析公交客流量的方向有两个:一是根据公共服务水平和城市发展规模等确定性因素分析公交客流量的整体水平;二是根据天气状况、重大活动、突发交通事故、降雨量和修路等不确定性因素分析公交日客流量[9, 13-14].
为避免与前人研究内容的重复,突出本研究方法的创新性,本文主要探讨了天气类型、最高温度、最低温度和风力4个因素对工作日高峰期客流的影响,因此在天气网上搜集广州市对应时期(2014年10月01日至2015年01月31日)的天气状况数据,并将其汇总为天气信息表,数据格式如表2所示.
| 表 2 广州天气数据 Table 2 Guangzhou weather data |
为更好地提高数据分析结果的准确度,适应模型构建和分析,必须将采集而来的数据进行清洗、融合、变换和归约等预处理操作[15].
首先,公交IC数据可能因为刷卡动作和终端环境等的影响而产生异常数据,这些数据如果不清洗排除,可能对分析结果的准确性造成影响,以下是几种常见的异常数据情况[16]:
(1) 噪音数据:此类数据不可以随意进行删除处理,因为某些孤立数据或离群数据可能代表特定意义,需要使用适当的数据处理技术(例如聚类技术或局部平滑)进行分析,若分析过后确信数据无效才可删除;
(2) 不完整数据:是指数据中部分关键字段内容缺失或不完整,无法确定数据真实性;
(3) 冗余数据:是指在采集过程或者导入过程中多次重复操作而产生的数据,冗余的数据必须删除,只保留唯一记录;
(4) 错误数据:是指刷卡交易过程中断或错误所造成的数据字段发生错配,此类数据必须删除;
(5) 其他异常数据:是指与同时期相比有显著偏差的数据,因为此类数据不能代表整体的发展趋势,所以不能将此类数据作为分析数据使用.
其次,天气类型对于客流量的影响较为明显. 在其他因素保持一致的情况下,天气类型为晴天时的客流量明显高于其他天气类型. 同时考虑到采用多元线性回归模型进行分析和预测客流,为方便计算需将天气类型通过表3所示的对应关系进行量化处理,其中晴天定为最大值12,大雨定义为最小值2,仅为方便处理和建立模型,并非特殊的规定.
| 表 3 天气类型与量化系数之间的对应关系[1] Table 3 The relation of the weather types and coefficients |
最后,为了描述更加简单和直观,将工作日的6:00~23:00时划分为17个时间段,如表4所示.
| 表 4 具体时间与时间段的对应关系 Table 4 The relation of the concrete time and the time slot |
城市公交工作日客流具有一定的随机性和规律性,客流的分布特性可以从工作日和非工作日、普通卡和非普通卡、其他影响因素等方面进行分析.
本文以研究天气因素对客流的分布特性的影响为目的,将进行两方面的分析:(1) 各线路工作日公交客流的分布特性分析;(2) 同线路不同工作日客流的分布特性分析.
本文通过以每小时为间隔进行采集,统计对应时间段的出行人数,描绘出一卡通刷卡出行人数的变化趋势图.
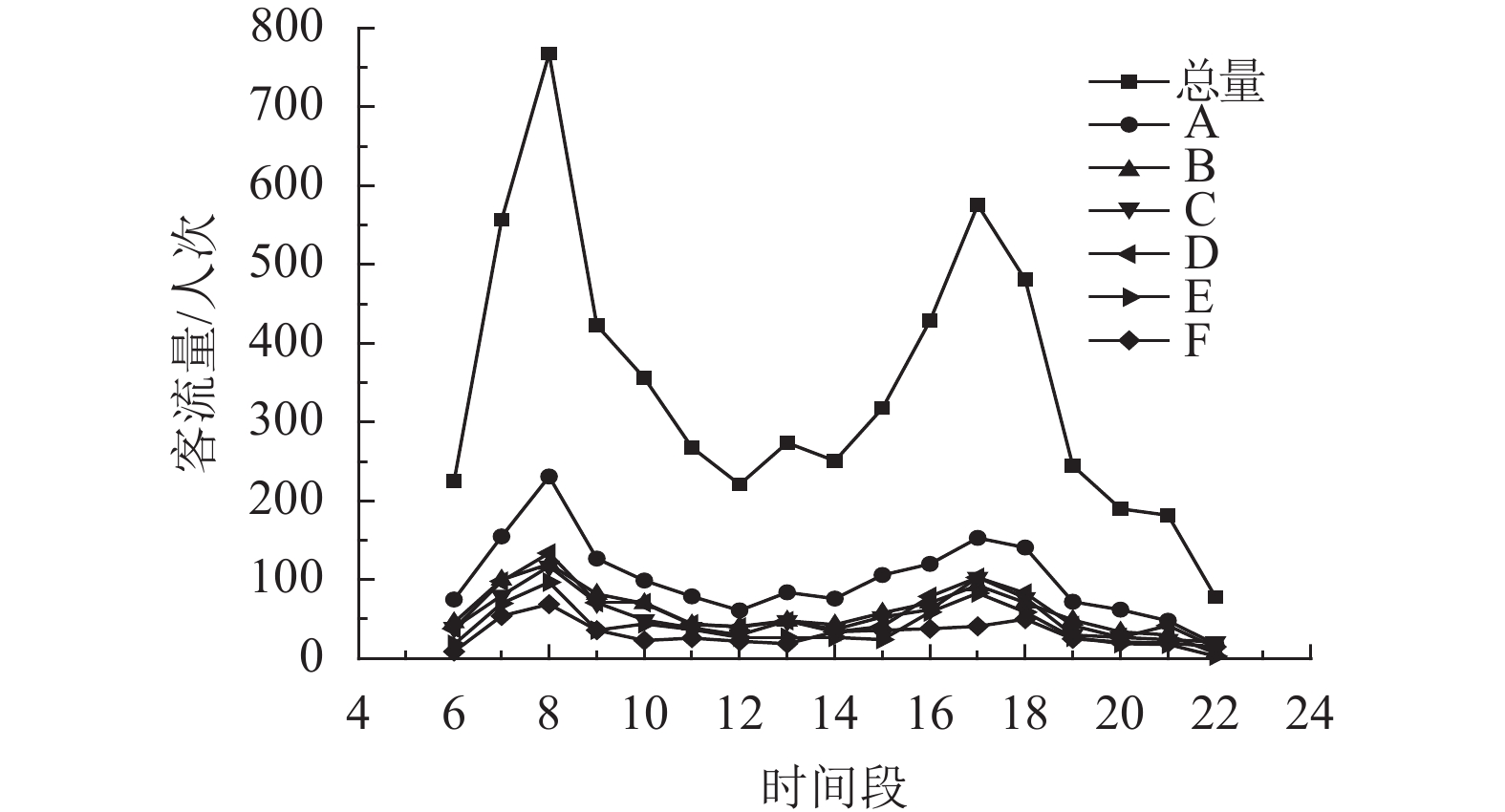
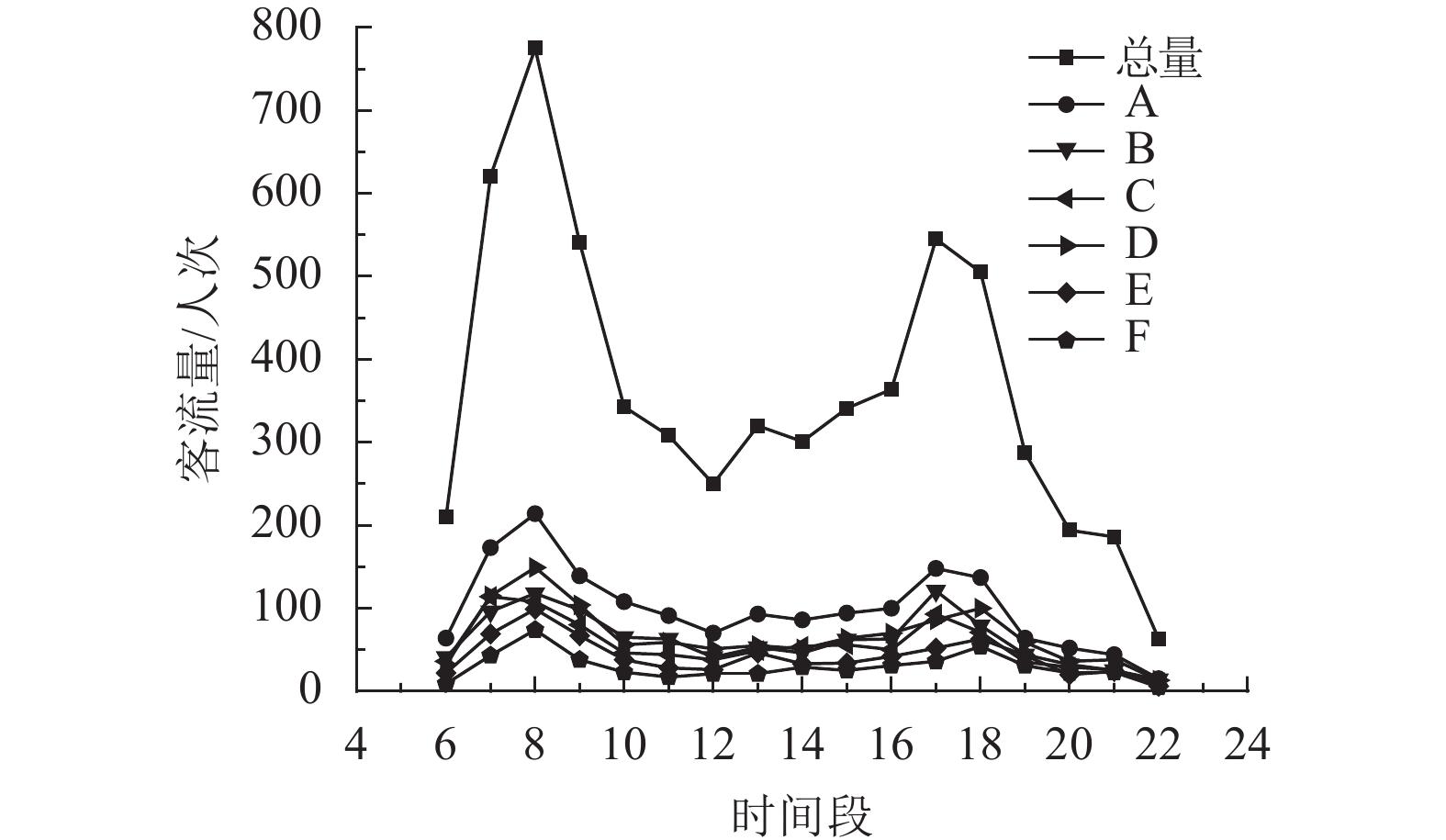
2.1 各线路工作日客流分布特性分析随机选取广州市内日均刷卡量高于500人次的6条公交线路(A、B、C、D、E和F),统计2014年11月07日和11月27日各时段的刷卡量如图2~3所示.
|
图 2 2014.11.07各公交线路各时间段客流量 Figure 2 Weekday passenger flow trend (2014.11.07) |
|
图 3 2014.11.27各公交线路各时间段客流量 Figure 3 Weekday passenger flow trend (2014.11.27) |
从图中可知,总量与分线路的工作日客流规律是相同的:客流早高峰出现在7:00~10:00,客流峰值出现在时间段8(8:00~9:00),特点是客流大而集中且增加或减少比较急剧;晚高峰出现在16:00~19:00,客流峰值出现在时间段17(17:00~18:00),其特点为峰值比早高峰低,客流分布比较均匀且较为缓和. 这主要是因为工作日早上乘客出行时间比较集中,而晚上返程时间则相对分散.
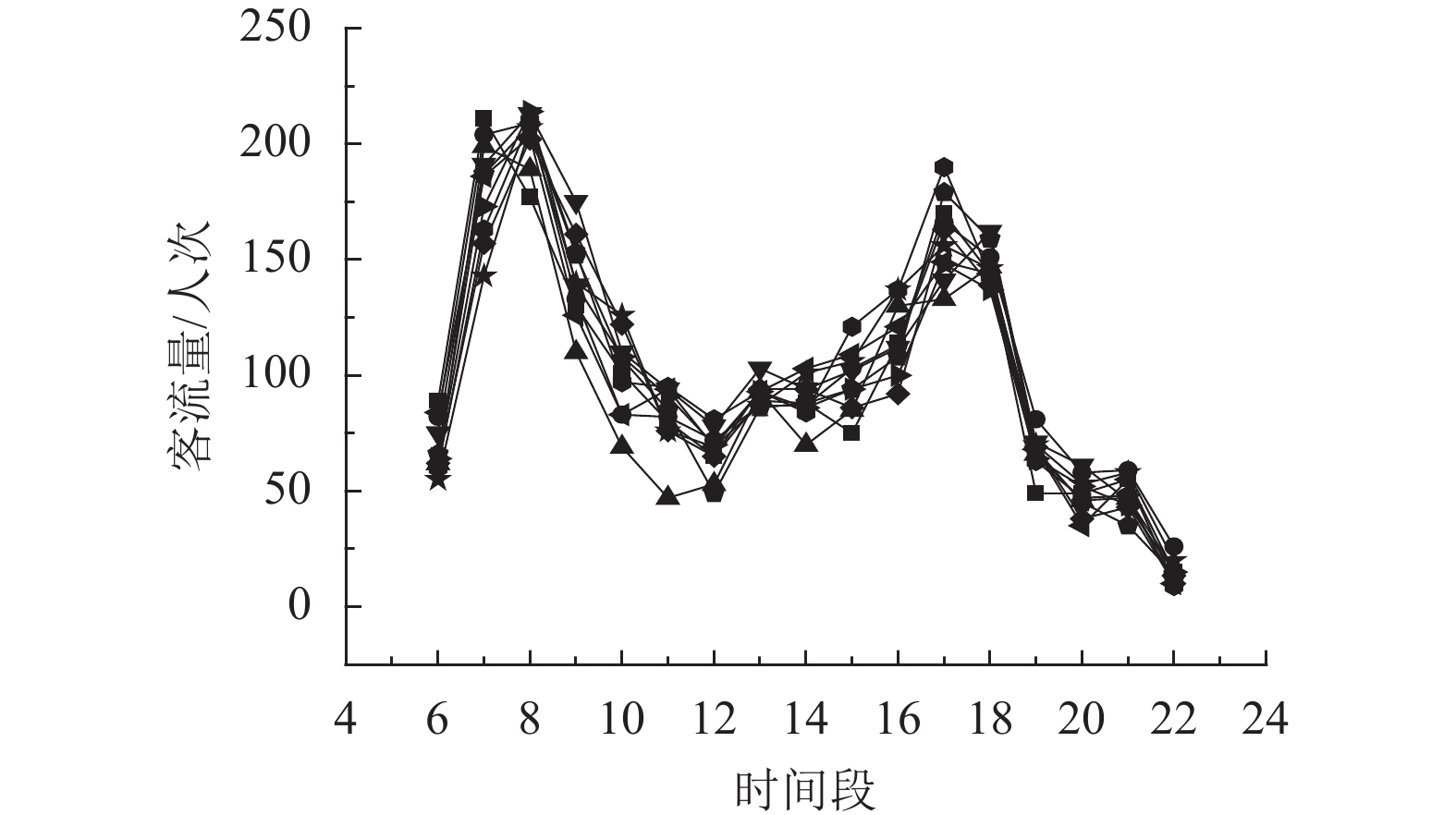
2.2 同线路不同工作日客流分布特性分析不同线路工作日客流分布特性因各自线路规划和站点数量等因素而不同. 为研究天气因素对客流分布特性的影响,对同线路不同工作日客流进行分析,因此选取日均客流量约为2 000人次的线路A为研究对象,选取2014年10月、11月和12月中连续10个星期四的数据,其结果如图4所示.
|
图 4 公交线路A连续10个星期四各时间段客流量 Figure 4 The different weekday passenger flow trend of line A |
其早晚高峰出现的时间段与2.1节所得结论基本一致,只是在不同日期内同一时间段的数据有一定的波动. 而出现波动的主要原因可能是天气因素,包括天气类型、最高温度、最低温度和风力,进一步对比不同天气因素情况下的客流量,结果如图5所示.
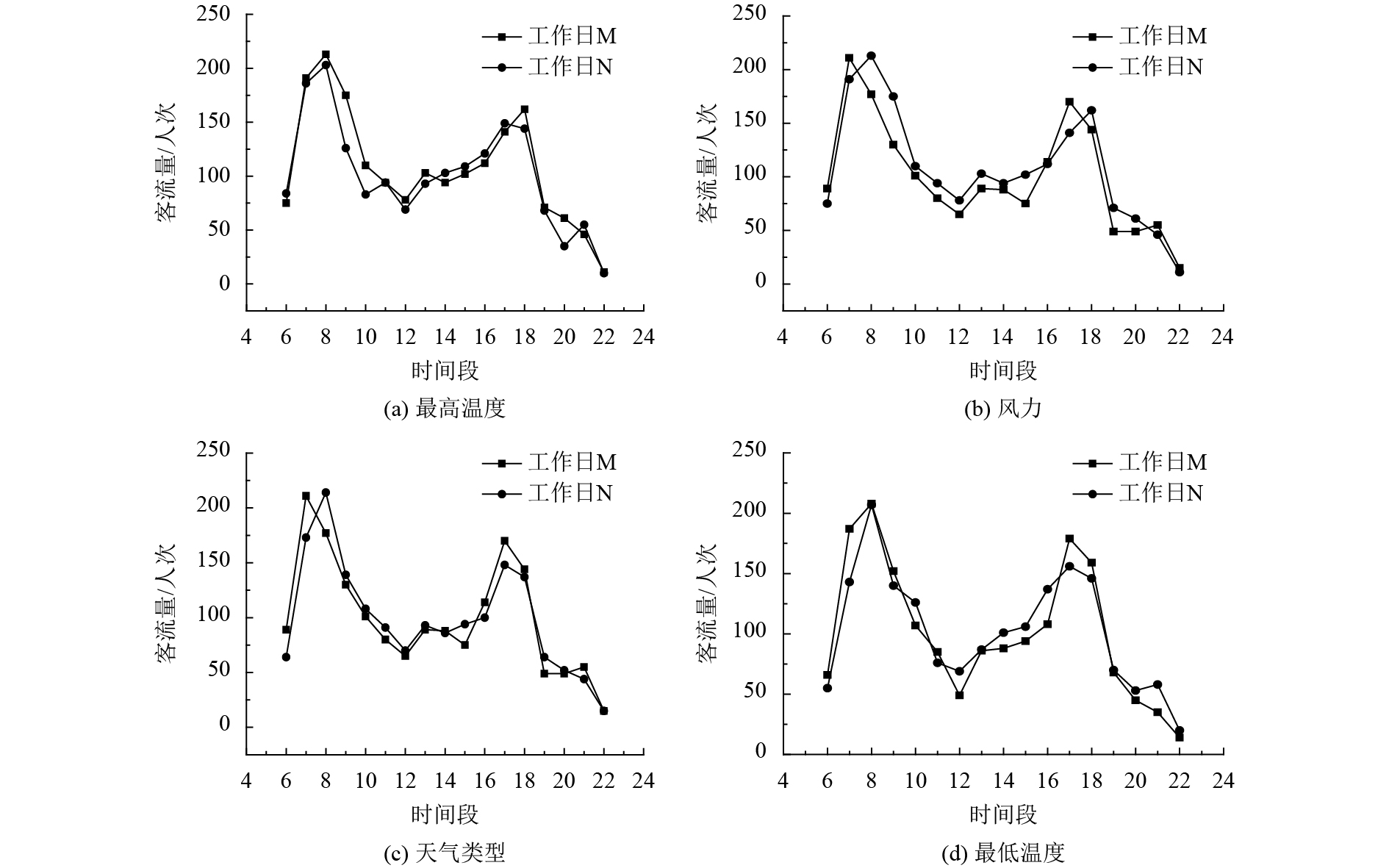
图5(a)表示天气类型、风力和最低温度相同,最高温度不同的两个工作日内各时间段的客流量;图5(b)表示天气类型、最高温度、最低温度相同,风力不同的两个工作日内各时间段的客流量;图5(c)表示最高温度、风力、最低温度相同,天气类型不同的两个工作日内各时间段的客流量;图5(d)表示天气类型、最高温度、风力相同,最低温度不同的两个工作日内各时间段的客流量. 从图中可以发现风力和天气类型对客流量的影响比较大,而最低温度和最高温度对客流量的影响比较小.
|
图 5 公交线路A不同天气因素的各时间段客流量 Figure 5 Weekday passenger flow trend of line A in different weather |
综合上述不同线路同一工作日的客流分布特性和同一线路不同工作日的客流分布特性,可以发现工作日的客流特性分布具有相似性. 工作日公交客流的趋势呈双驼峰型,相同时段客流量在一定范围内波动,同一线路不同工作日的曲线波形十分相似,不同的天气状况对客流量的影响不同,其中天气类型和风力影响较大,而最高温度与最低温度则影响较小.
3 模型的建立为了将工作日公交客流的特性更为直观地表现出来,并且能够预测公交客流,建立模型是一个较为可行的研究方法. 因为多元线性回归模型具有特征提取简易明确、线性模型简单易理解、概念清晰、特征值构建符合数据分布等多种特点[1]. 而公交工作日客流量特性分布具有相似性,所以本研究选择多元线性回归模型为建模方案.
提取公交A线路2014年10、11和12月中连续10个星期四的数据为建立模型数据,其中时间段7(7:00~8:00)数据与天气数据汇总如表5所示. y表示时间段7的客流量,x1表示依据表3中的对应关系进行量化后的天气类型,x2表示最高温度,x3表示最低温度,x4表示风力.
| 表 5 线路A的10组历史周四时段7客流数据 Table 5 10 historical period passenger flow data on Thursday of line A |
多元线性回归的预测样本点容量为10,其中y为应变量,xi(i=1, 2, 3, 4)为自变量,多元线性回归方程表示如下
| $\mathit{\boldsymbol{y}} = {b_0} + {b_1}{{x}_1} + {b_2}{{x}_2} + {b_3}{{x}_3} + {b_4}{{x}_4}.$ |
时间段7的具体数据如下:
y=(211, 204, 199, 191, 186, 173, 157, 187, 163, 143)T.
| ${\mathit{\boldsymbol{x}}} = \left[ {\begin{array}{*{20}{c}}{\rm{1}}&{{\rm{10}}}&{{\rm{29}}}&{{\rm{20}}}&{\rm{3}}\\[8pt]{\rm{1}}&{{\rm{12}}}&{{\rm{31}}}&{{\rm{21}}}&{\rm{3}}\\[8pt]{\rm{1}}&{\rm{8}}&{{\rm{23}}}&{{\rm{19}}}&{\rm{3}}\\[8pt]1&{{\rm{10}}}&{{\rm{21}}}&{16}&{\rm{3}}\\[8pt]{\rm{1}}&{{\rm{12}}}&{{\rm{24}}}&{{\rm{15}}}&{\rm{3}}\\[8pt]{\rm{1}}&{{\rm{10}}}&{{\rm{26}}}&{{\rm{19}}}&{\rm{3}}\\[8pt]{\rm{1}}&{{\rm{10}}}&{{\rm{14}}}&{\rm{8}}&{\rm{4}}\\[8pt]{\rm{1}}&{{\rm{10}}}&{{\rm{18}}}&{{\rm{11}}}&{\rm{3}}\\[8pt]{\rm{1}}&{{\rm{10}}}&{{\rm{16}}}&{\rm{5}}&{\rm{3}}\\[8pt]{\rm{1}}&{\rm{8}}&{{\rm{18}}}&{{\rm{11}}}&{\rm{3}}\end{array}} \right].$ |
通过SPSS软件的回归函数作多元线性回归得
y=(b0, b1, b2, b3, b4)T=(136.261 6, 5.150 8, –0.983 3,3.426 5,–11.104 1)T.
根据上述计算结果得时间段7的回归方程为 y=136.261 6+5.150 8x1–0.983 3x2+3.426 5x3–11.104 1x4.
可以发现天气类型和最低温度的系数为正值,说明这两个因素与客流量呈正相关;而最高温度和风力的系数为负值,说明这两个因素与客流量呈负相关. 且根据系数绝对值的大小可以知道对客流影响程度由大到小的因素分别为风力、天气类型、最低温度和最高温度.
同时,通过观察回归方程的R2(相关系数的平方),其范围在0.40~0.64之间,说明所讨论的4个因素(风力、天气类型、最低温度和最高温度)可解释客流量变化的40%~64%,剩余的需要由其他因素进行解释. 而显著性分析的P值在0.20~0.55之间,大于显著性水平0.05.
其他各时间段的建模过程与时段7相同,表6展现了其中4个时段的多元回归方程,可以发现它们的基本规律与时间段7相同.
| 表 6 线路A时间段7、8、9和18的多元回归方程 Table 6 Multiple linear regression of time 7, 8, 9 and 18 (Line A) |
模型验证是为了判断结合公交IC刷卡数据和天气数据所建立模型的实用性和有效性,利用多元线性回归方程所得的模型其允许的相对残差为8%.
通过残差检验可以对模型的实用性和有效性进行评价. 残差是指实际值与预测值之间的差值,设样本数点容量为n,y为客流实际值,y′为通过多元线性回归方程所得的客流预测值,残差为
| $\varDelta = \left| {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{y}}'} \right|;$ |
相对残差为
| $\varPhi = \frac{\varDelta }{\mathit{\boldsymbol{y}}} \times 100\% ;$ |
平均相对残差
| $\mathop \varPhi \limits^ - = \frac{1}{n}\sum\limits_{i = 1}^n {\mathop \varPhi \nolimits_i }.$ |
将2015年01月08日、15日和22日量化后的天气特征值代入表6中所得的多元回归方程,计算得到如表7~10所示的预测值,得出的相对残差为16.9%、7.6%、21.2%、7.2%、10.3%、2.7%、10.0%、1.8%、1.8%、2.0%、7.1%和4.8%,其平均相对残差7.8%,小于预设的8%,证明该多元线性回归模型是适用于公交客流预测的模型. 经分析数据可知客流量的预测值小于实际值所占比例较大,其中2015年01月22日时间段7的预测值比实际值少了44人次,相对残差也大于20%,这可能是因为1月下旬天气状况已经比较恶劣导致预测值较小,但高峰时间段上班族和学生并未改变出行时间,最终使误差相对较大.
| 表 7 时间段7的实际值与预测值对照表 Table 7 Bus passenger flow real value-predicted value contrast table (time 7) |
| 表 8 时间段8的实际值与预测值对照表 Table 8 Bus passenger flow real value-predicted value contrast table (time 8) |
| 表 9 时间段9的实际值与预测值对照表 Table 9 Bus passenger flow real value-predicted value contrast table (time 9) |
| 表 10 时间段18的实际值与预测值对照表 Table 10 Bus passenger flow real value-predicted value contrast table (time 18) |
将2015年1月份3个星期四(2015年01月01日为元旦,不是工作日)的天气状况代入各高峰时间段的多元线性回归方程中,所得结果可知多元线性回归模型的平均误差较小,能够有效地对高峰时间段客流进行预测,表明其实用性较好.
5 总结城市公共交通的发展是我国智慧城市发展过程中的必然趋势,对公共交通客流规律的分析与全面、准确并快速的预测是重要的研究方向. 只有把握客观的客流规律以及未来客流趋势,公交管理部门才能及时高效地进行优化线路和调度客运等工作,才能使我国城市公共交通的发展有质的飞越.
本文分析了工作日公交客流数据,发现工作日客流具有早晚两个高峰,同时发现天气类型和风力对客流量的影响大于最高和最低温度对客流量的影响. 因此以高峰时间段的客流量数据为研究对象,利用多元线性回归模型,综合考虑天气类型、最高温度、最低温度和风力四个影响因素得到了各高峰时间段的多元线性回归方程. 最后,利用后期的数据进行了验证,发现多元回归模型对高峰时间段客流预测的残差小于预设的8%,证明其适用于公交客流量的预测.
本文研究的是宏观上的线路高峰时间段客流预测,目前研究尚存在不足,如样本点数量有限,预测结果相对比较粗略,未来可以通过增加样本点数量建立模型,提高其精度;同时将线路各时间段客流预测与线路站点客流预测相结合,可以为线路规划和公交调度提供更加全面可靠的决策分析.
| [1] | 谢振东, 李之明, 徐锋, 等. 城市交通一卡通大数据应用[M]. 北京: 人民交通出版社, 2016: 171-188. |
| [2] |
吴金成, 谢振东, 伍冠桦, 等. 基于交通一卡通数据的交通状态分析及动态研究[J].
广东工业大学学报, 2017, 34(3): 77-82.
WU J C, XIE Z D, WU G H, et al. A study of traffic status and dynamic control based on IC card data[J]. Journal of Guangdong University of Technology, 2017, 34(3): 77-82. |
| [3] |
谢振东, 吴金成, 李之明, 等. 企业大数据能力的构建与培育研究[J].
广东工业大学学报, 2017, 34(3): 110-114.
XIE Z D, WU J C, LI Z M, et al. A study of construction and cultivation of big data capacity of enterprise[J]. Journal of Guangdong University of Technology, 2017, 34(3): 110-114. |
| [4] | XU W, QIN Y, HUA H. A new method of railway passenger flow forecasting based on spatio-temporal data mining[C]//QIN Y. The International IEEE Conference on Intelligent Transportation Systems, Proceedings. Washington, WA, USA: IEEE, 2004: 402-405. |
| [5] | MO Y, SU Y Y. Neural networks based real-time transit passenger volume prediction[C]//SU Y Y. Power Electronics and Intelligent Transportation System (PEITS), 2009 2nd International Conference on. Shenzhen: IEEE, 2009: 303-306. |
| [6] |
芦方强, 陈学武, 胡晓健. 基于公交OD数据的居民公交出行特征研究[J].
交通运输工程与信息学报, 2010, 8(2): 31-36.
LU F Q, CHEN X W, HU X J. Study on the characteristics of residents’ bus trip based on OD data[J]. Journal of Transportation Engineering and Information, 2010, 8(2): 31-36. |
| [7] |
张春辉, 宋瑞, 孙杨. 基于卡尔曼滤波的公交站点短时客流预测[J].
交通运输系统工程与信息, 2011, 11(4): 154-159.
ZHANG C H, SONG R, SUN Y. Short term passenger flow forecasting based on Calman filter[J]. Transportation Systems Engineering and Information, 2011, 11(4): 154-159. |
| [8] |
邹巍, 陆百川, 邓捷, 等. 基于遗传算法与小波神经网络的客流预测研究[J].
武汉理工大学学报(通科学与工程版), 2014, 38(5): 1148-1151.
ZHOU W, LU B C, DENG J, et al. Study on passenger flow forecasting based on genetic algorithm and wavelet neural network[J]. Journal of Wuhan University of Technology(Science and Engineering), 2014, 38(5): 1148-1151. |
| [9] |
张庆年, 高健智. 城市公共交通需求预测模型研究[J].
武汉理工大学学报, 2001, 23(8): 50-52.
ZHANG Q N, GAO J Z. Research on urban public transport demand forecasting model[J]. Journal of Wuhan University of Technology, 2001, 23(8): 50-52. |
| [10] | 李振. 基于Hadoop平台的公交客流分析与预测研究[D]. 长春: 东北师范大学信息与软件工程学院, 2015: 1-48. |
| [11] | 耿学贵. 基于IC卡的公交客流时间规律研究[D]. 昆明: 昆明理工大学交通工程学院, 2012: 1-93. |
| [12] | 刘雪琴. 基于交通一卡大数据的公客流分析与预测[D]. 广州: 广东工业大学自动化学院, 2016: 1-82. |
| [13] |
李林波, 康琳渭, 王猜. 基于天气影响分析的公交客流调查日期确定方法[J].
交通科技, 2016(1): 149-152.
LI L B, KANG L W, WANG C. A method for determining the date of bus passenger flow survey based on weather impact analysis[J]. Transportation Technology, 2016(1): 149-152. |
| [14] |
孙慧, 周颖, 范志清. 基于解释结构模型的公交客流量影响因素分析[J].
北京理工大学学报(社会科学版), 2010, 12(1): 29-32.
SUN H, ZHOU Y, FANG Z Q. Analysis of influencing factors of passenger traffic volume based on interpretative structural model[J]. Journal of Beijing Institute of Technology (SOCIAL SCIENCE EDITION), 2010, 12(1): 29-32. |
| [15] |
罗强, 何利力, 王晓菲. 数据仓库中数据清洗技术分析机[J].
电脑编程技巧与维护, 2015(2): 61.
LUO Q, HE L L, WANG X F. Data cleaning technology in data warehouse[J]. Computer Programming Skills and Maintenance, 2015(2): 61. |
| [16] |
谢振东, 吴金成, 刘雪琴. 基于交通一卡通的城市老年人出行行为特征的分析研究[J].
金卡工程, 2015(10): 18-20.
XIE Z D, WU J C, LIU X Q. Study on the characteristics of urban elderly travel behavior based on traffic card[J]. Golden Card Project, 2015(10): 18-20. |
 2018, Vol. 35
2018, Vol. 35

