磁共振成像中，自旋磁矩的动力学行为是研究磁共振成像理论的基础. Bloch方程描述了磁矩在磁场中的变化规律，并同时反映了磁矩在驰豫过程中的动力学机制^[1-3]. 求解Bloch微分方程是磁共振理论研究领域的重要内容，方法也很多^[4-5]. 矩阵传播子方法是将组织参数和磁场环境参数如主磁场磁感应强度B、外加射频场B₁、质子密度ρ、驰豫时间T₁、T₂等融合在一个矩阵中，将磁化强度矢量M作为一个向量，通过合理简化矩阵方程，直接利用矩阵表述下的Bloch方程解的形式，求解出复杂序列如反转恢复-平面回波序列(IR-EPI)下M的随时演化规律. 此方法的优点是无需求解Bloch方程的一阶偏微分方程组，同时，序列结构中任意时刻下M的求解可通过序列前一阶段计算出的M以及传播子矩阵，通过不断修正方程解的形式，最终得到其随时变化规律. 不足之处在于，计算过程较为繁琐，计算量很大，需要结合具体参数的值进行讨论，以便简化计算过程.

1 理论与方法

作为一种唯象的理论，Bloch给出了在磁场中自旋的动力学行为的描述，经过了很多实验的验证. Bloch方程的矢量形式为^[6]

$\frac{{{\rm{d}}{{\mathit{\boldsymbol{M}}}}}}{{{\rm{d}}t}} = \gamma {{\mathit{\boldsymbol{M}}}} \times {{\mathit{\boldsymbol{B}}}} - \frac{{{{{\mathit{\boldsymbol{iM}}}}_x} + {{{\mathit{\boldsymbol{jM}}}}_y}}}{{{T_2}}} + k{\rm{(}}{{{\mathit{\boldsymbol{M}}}}_0} - {{{\mathit{\boldsymbol{M}}}}_z}{\rm{)}}/{T_1},$

其中，M为磁化强度矢量，B为总的磁感应强度，M₀为热平衡下的磁化强度矢量，T₁和T₂分别为纵向驰豫时间和横向驰豫时间. 总磁感应强度B可表示为^[7-10]

${{\mathit{\boldsymbol{B}}}} = k{{{\mathit{\boldsymbol{B}}}}_0}' + {{{\mathit{\boldsymbol{B}}}}_1}(t) = k({{{\mathit{\boldsymbol{B}}}}_0} + \Delta {{\mathit{\boldsymbol{B}}}} + {\mathit{\boldsymbol{G}}}{\rm{\cdot}}{\mathit{\boldsymbol{r}}}) + {{{\mathit{\boldsymbol{B}}}}_1}{{(t),}}$

B₀为z方向的主磁场磁感应强度，∆B反映静磁场的不均匀性，G为梯度场， ${{\mathit{\boldsymbol{B}}}_1}(t) = {{\mathit{\boldsymbol{i}}}B_1}\cos {\rm{(}}\omega t{\rm{)}} - {{\mathit{\boldsymbol{j}}}B_{\rm{1}}}\sin {\rm{(}}\omega t{\rm{)}}$ 为外加射频场的磁感应强度.

综合考虑以上因素，Bloch方程的矢量形式可以用简洁的矩阵形式表示为

$\frac{{{\rm{d}}{\mathit{\boldsymbol{M}}}}}{{{\rm{d}}{{t}}}} = {\mathit{\boldsymbol{LM}}} + \frac{{{{\mathit{\boldsymbol{M}}}_0}}}{{{{{T}}_1}}},$

M为实验室系磁化强度的列向量，M₀为热平衡下磁化强度矢量的列向量；L为演变矩阵，具体形式为

${\mathit{\boldsymbol{L}}} = \left[ {\begin{array}{*{20}{c}}{ - 1/{{{T}}_2}} &\!\!\!\! {\gamma {{\mathit{\boldsymbol{B}}}_0}'} &\!\!\!\! {\gamma {{\mathit{\boldsymbol{B}}}_1}\sin (\omega {{t}})}\\[8pt]{ - \gamma {{\mathit{\boldsymbol{B}}}_0}'} &\!\!\!\! { - 1/{{{T}}_2}} &\!\!\!\! {\gamma {{\mathit{\boldsymbol{B}}}_1}\cos (\omega {{t}})}\\[8pt]{ - \gamma {{\mathit{\boldsymbol{B}}}_1}\sin (\omega {{t}})} & \!\!\!\!{ - \gamma {{\mathit{\boldsymbol{B}}}_1}\cos (\omega {{t}})} &\!\!\!\! { - 1/{{{T}}_1}}\end{array}} \right].$

为了进一步简化，引入绕z轴方向以ω旋转下的坐标系，Bloch方程简化为

$\frac{{{\rm{d}}{\mathit{\boldsymbol{M}}}}}{{{\rm{d}}{{t}}}} = {\mathit{\boldsymbol{QM}}} + \frac{{{{\mathit{\boldsymbol{M}}}_0}}}{{{{{T}}_1}}},$

(1)

其中

${\mathit{\boldsymbol{Q}}} = \left[ {\begin{array}{*{20}{c}}{ - 1/{{{T}}_2}} & {\Delta \omega } & 0\\[8pt]{ - \Delta \omega } & { - 1/{{{T}}_2}} & {{\omega _1}}\\[8pt]0 & { - {\omega _1}} & { - 1/{{{T}}_1}}\end{array}} \right],$

而 $\Delta \omega = {\omega _0}' - \omega $ ， ${\omega _0}' = \gamma {{\mathit{\boldsymbol{B}}}_0}'$ ， ${\omega _1} = \gamma {{\mathit{\boldsymbol{B}}}_1}$ .

设初始条件t=0时，M=M(0)，得到Bloch矩阵方程的解：

${\mathit{\boldsymbol{M}}}({{t}}) = {{\rm{e}}^{{\mathit{\boldsymbol{A}}}t}}{\mathit{\boldsymbol{E}}}({{t}})\chi ({{t}}){\mathit{\boldsymbol{M}}}(0) + {{\mathit{\boldsymbol{M}}}_0}[1 - {{\mathit{\boldsymbol{E}}}_1}({{t}})],$

(2)

其中， $\;\;\;\;\chi ({{t}}) = {{\rm{e}}^{ - {\mathit{\boldsymbol{T}}}t}}{{\rm{e}}^{ - {\mathit{\boldsymbol{A}}}t}}{{\rm{e}}^{{\mathit{\boldsymbol{Q}}}t}}$ ， ${\mathit{\boldsymbol{Q}}} = {\mathit{\boldsymbol{A}}} + {\mathit{\boldsymbol{T}}}$ ，

　　　 ${\mathit{\boldsymbol{A}}} = \left[ {\begin{array}{*{20}{c}} 0 & {\Delta \omega } & 0\\ { - \Delta \omega } & 0 & {{\omega _1}}\\ 0 & { - {\omega _1}} & 0 \end{array}} \right]$ ，　　　 ${\mathit{\boldsymbol{T}}} = \left[ {\begin{array}{*{20}{c}} { - 1/{T_2}} & 0 & 0\\ 0 & { - 1/{{{T}}_2}} & 0\\ 0 & 0 & { - 1/{{{T}}_1}} \end{array}} \right]$ ，　　　 ${\mathit{\boldsymbol{E}}}({{t}}) = {{\rm{e}}^{{\mathit{\boldsymbol{T}}}t}} = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{E}}}_2}} & 0 & 0\\ 0 & {{{\mathit{\boldsymbol{E}}}_2}} & 0\\ 0 & 0 & {{{\mathit{\boldsymbol{E}}}_1}} \end{array}} \right]$ ，　　　 ${{\mathit{\boldsymbol{E}}}_1} = {{\rm{e}}^{ - {{t}}/{{{T}}_1}}}$ ， ${{\mathit{\boldsymbol{E}}}_2} = {{\rm{e}}^{ - {{t}}/{{{T}}_2}}}$ .

在式(2)中，e^At被定义为矩阵Bloch方程中的传播子矩阵. 另外，解的形式中M(0)为初始条件下的磁化强度矢量的向量式，而M₀表示热平衡体系下的M表达式.

2 IR-EPI序列的简化模型

平面回波成像(echo planar imaging, EPI)是磁共振快速成像序列的一种，可在30~100 ms内采集一幅完整的图像. 作为一种数据读取模式，EPI脉冲序列需要配合一种单次激发序列，如FID、SE、IR、IRSE、GRE等，使用快速反转振荡的梯度脉冲进行数据的快速读取^[11-13].

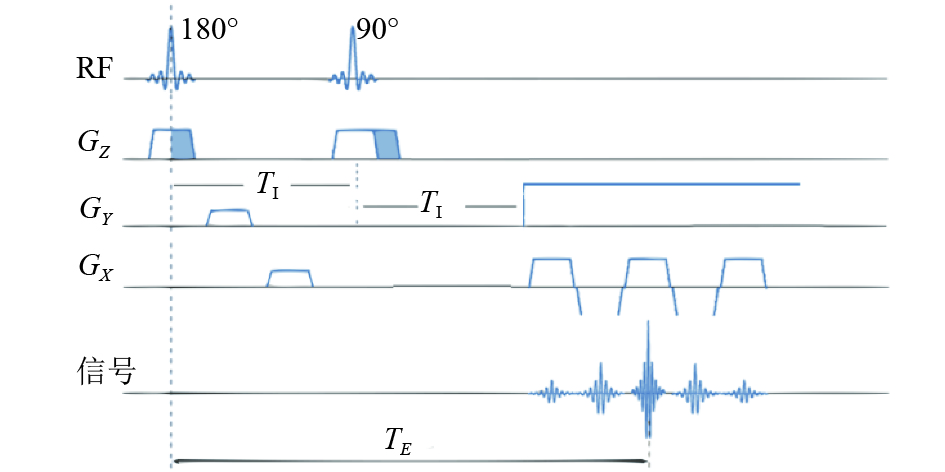
建立一个绕着z、频率为ω的旋转坐标系，主磁场B₀沿z轴方向，外加射频脉冲中的磁场分量B₁沿着坐标系的x轴方向. 为了简化模型并说明推导过程，图1给出了IR-EPI序列结构的简化模型^[14-15]，即IR序列之后进行了若干次x方向梯度场的快速切换. 在此过程中，只考虑一个周期TR结束后的M，忽略掉断层厚度中磁场不均匀，相位编码梯度以及射频场的不均匀带来的影响.

3 传播子矩阵求解磁化强度矢量

根据简化模型下序列结构的具体情况，求解序列(一个周期TR)结束后的M的向量表达式，需要根据不同时间段依次进行求解. 其中脉冲作用期间和驰豫期间，由于磁场环境的改变，传播子矩阵在表达式上有不同的简化结果.

3.1 反转恢复序列(IR)下M在各时间段内的表达式

根据Bloch方程解的形式(2)，在IR序列结果中，首先施加180° RF脉冲，脉冲作用期间，由于B₁场下章动占据主要作用，同时，驰豫效应对M的影响也比较小，近似有

${\omega _1} > > \Delta \omega ,\;\Delta \omega = 0,\;{\mathit{\boldsymbol{E}}}({{t}}) = \chi ({{t}}) = 1.$

(3)

同时，由于射频场的磁感应强度为B₁，180° RF脉冲的作用是将磁化强度矢量偏转到z轴的负方向，根据章动角度计算公式θ=γB₁t，将180° RF脉冲作用前选为时间起点，并结合之前讨论到的相关参数的近似结果，代入到方程中，可以得到

${\mathit{\boldsymbol{M}}}({{t}} = \frac{{\rm{\pi }}}{{\gamma {{{B}}_1}}}) = \left[ {\begin{array}{*{20}{c}}0\\[6pt]0\\[6pt]{ - {{\mathit{\boldsymbol{M}}}_0}}\end{array}} \right].$

此结果验证了Bloch矩阵方程解的形式，即式(2)的正确性.

考虑180° RF脉冲作用后在一个脉冲间隔时间内的驰豫过程. 由于驰豫过程中，射频场对磁场环境没有贡献，即B₁章动现象不存在. 代入方程求解M前，需要修正传播子矩阵表达式，令ω₁=γB₁=0. 以180° RF脉冲刚结束作为时间起点，在t =t_I时，可求出

$M(t = {t_I}) = \left[ {\begin{array}{*{20}{c}}0\\[6pt]0\\[8pt]{ - {M_0}(1 - 2{{\rm{e}}^{ - {t_i}/{T_1}}})}\end{array}} \right].$

设定t =t_I时，施加IR序列结果中的90° RF脉冲，脉冲作用期间，类似于前面180° RF脉冲作用过程，近似有∆ω=0，E(t)=χ(t)=1，且将t=t_I设为时间起点，此时的磁化强度矢量M将作为式(2)中的M(0). 利用章动角度计算公式θ=γB₁t，可知，90° RF脉冲施加时间π/2γB₁后，

${\mathit{\boldsymbol{M}}}({{t}} = {{{t_I}}}) = \left[ {\begin{array}{*{20}{c}}0\\[6pt]{ - {{{M}}_0}(1 - 2{{\rm{e}}^{ - {{{t_I}}}/{{{T}}_1}}})}\\[8pt]0\end{array}} \right].$

继续经过t=t_I时间的驰豫过程后，继续修改传播子矩阵的简化结果，则

${\mathit{\boldsymbol{M}}}(t = {t_I}) = \left[ {\begin{array}{*{20}{c}}{{{\rm{e}}^{ - (\displaystyle\frac{1}{{{T_1}}} + \displaystyle\frac{1}{{{T_2}}}){t_I}( - 2 + {{\rm{e}}^{{t_I}/{T_1}}}){M_0}\sin ({t_I}\Delta \omega )}}}\\[10pt]{{{\rm{e}}^{ - (\displaystyle\frac{1}{{{T_1}}} + \displaystyle\frac{1}{{{T_2}}}){t_I}( - 2 + {{\rm{e}}^{{t_I}/{T_1}}}){M_0}\cos ({t_I}\Delta \omega )}}}\\[10pt]{{M_0}(1 - {{\rm{e}}^{ - {t_I}/{T_1}}})}\end{array}} \right].$

(4)

3.2 考虑x方向梯度磁场快速切换后M的表达式

完整的单次激发IR序列之后，M表达式为式(4). EPI仅仅是一种数据读出方式，具体采用x方向连续快速地施加梯度场，不断分散和重聚M在xy平面上的分量，得到相应变化的磁共振信号，实际上，此时是 ${T_2}^*$ 加权信号. EPI序列要求在读出梯度G_x施加的同时，要结合y方向的梯度磁场，才可以填充了K空间的不同位置，从而最终填满整个K空间. 这里在y方向的梯度场采用一种比较弱的恒定相位的编码梯度G_y.

由于EPI序列中磁共振信号的一般表达式较为复杂，为了简化计算，同时得到磁共振信号的结果，将部分参数的具体数值设定为

$\begin{array}{l}{B_0} = 3.0\;\;{\rm{ T}},\;\gamma = 2.67 \times {10^8}\;\;{\rm{ rad}} \cdot {{\rm{s^{-1}}}}\cdot{{\rm{T^{-1}}}},\\[10pt]{T_1} = 1.0\;\;{\rm{ s}},\;{M_0} = 0.02\;\;{\rm{ A}} / {{\rm{m}}},\\[10pt]{G_x} = {G_y} = 0.025\;\;{\rm{ T}} / {{\rm{m}}},\\[10pt]{G_z} = 0,\;x = y = 1,\;{t_I} = 0.007\;\;{\rm{ s}}.\end{array}$

(5)

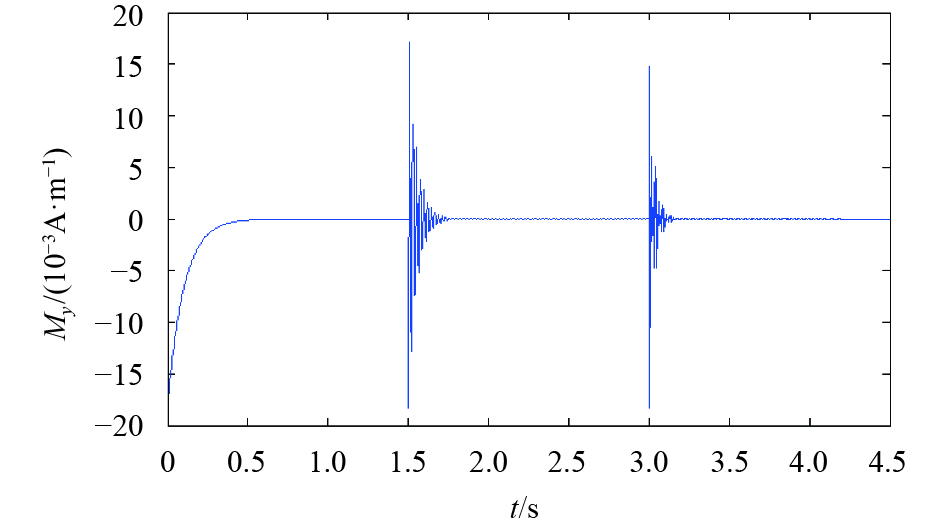
其中t=0到3 s的过程中，第1次施加方向为x轴负方向的G_x梯度场，大小为0.025 T/m，作用时间为0.5 t，即t=0到1.5 s内，磁化强度矢量M的y分量随时间变化的过程；t=3到6 s过程中，第2次施加方向为x轴正方向的G_x梯度场，大小及作用时间不变. 最后，在t=6到9 s阶段再次采用相同的操作. 需要说明的是，EPI序列作用过程中，始终存在G_y=0.025 T/m的恒定编码梯度场. 图2给出了EPI序列作用的不同阶段磁共振信号随时间演化的过程.

实际中，EPI序列结构中，梯度场需要反复施加，G_y的选择方式也多种多样，它们对应了不同的K空间填充方式，此时，对序列结构下磁共振信号的推导，同样可以通过对式(2)修改不同时间段的传播子矩阵的具体形式，并结合初始状态下的磁化强度矢量的向量式M(0)，不断的迭代计算中求出下一阶段磁化强度矢量M(t)，最终逐步得到复杂序列下在任意时刻磁共振信号的计算结果.

4 结论

本文从Bloch方程的一般矩阵形式出发，讨论了IR-EPI序列下的磁共振信号的推导过程. 在IR-EPI序列下不同时间阶段，通过对相应的传播子矩阵的形式的修改，然后代入矩阵化的Bloch方程中，逐步推演出序列结束后磁共振信号的表达式，这种方法也为更为复杂条件下的序列的磁共振信号的推导、计算和分析提供了参考.