摄影测量是通过对摄影机摄取的二维影像进行测量,确定物体在空间的位置、形状、大小以及运动形态的一门学科[1],按照摄影距离的远近,可分为航天摄影测量、航空摄影测量和近景摄影测量[2]. 近景摄影测量的摄影距离一般小于100 m,摄影方式灵活且成本低廉,可以瞬间获取被测物体大量表面信息,特别适合于测量大量点目标,在土木建筑、生物医学、工业、交通等行业有着广泛的应用[3-4].
获取影像内外方位元素是对目标进行摄影定位的基础[5-7]. 利用GPS技术辅助测定影像内外方位元素,在航空航天摄影测量中已取得很好的效果[8]. 随着近景摄影测量技术在绝对目标定位方面的应用日益受到重视[9-12],如何将GPS与传统近景摄影测量方法结合起来,提高作业效率并取得更优的定向和定位成果,成为业内十分关注的问题[13]. 本文提出一种GPS-RTK辅助近景摄影测量光束法平差方法,通过实验对该方法的可行性和有效性进行了验证,取得了较好的效果.
1 利用GPS-RTK获取近景摄站位置 1.1 GPS-RTK技术GPS是目前应用最为广泛的全球导航定位系统,通过GPS与其他观测技术的结合,带动了测绘技术的新一轮变革. 在航空摄影测量领域,利用差分动态GPS定位技术获取摄影瞬间摄站的空间位置,由所观测的摄站坐标作为空中控制点,可部分替代地面控制点的作用. 基于相似原理,近景摄影测量同样可以利用GPS获取摄站位置,以省去控制点布设的大量工作,提高作业效率.
GPS-RTK是一种由GPS载波相位观测值进行实时动态相对定位的技术,适合于获取近景摄站坐标. 进行RTK测量时,基准站通过数据通信链实时地将载波相位观测值以及站坐标等信息播发给附近的RTK接收机. 通过接收机内置的数据处理软件进行实时相对定位,再结合基准站坐标求得RTK接收机的绝对三维坐标[14]. 在近景摄影测量数据采集过程中,只需将GPS-RTK接收机安置在近景摄站上,即可快速获取摄站的空间三维坐标.
1.2 利用GPS-RTK获取摄站位置的精度控制GPS-RTK技术观测作业效率高,而其观测精度对于测量成果质量至关重要. 由于近景摄影测量测区范围较小,采用独立的物方坐标系,采取以下措施有利于提高摄站位置的观测精度:(1) 在测区四周布设足够公共点,减小WGS84坐标到独立坐标的转换误差;(2) 严格按照精度要求设定观测参数和观测时间;(3) 注意检查GPS观测结果验后精度,避免粗差;(4) 必要时进行重复观测,以多次观测均值代替单次观测值. 一般情况下,利用GPS-RTK获取的摄站坐标精度可达到厘米级,而且返工的几率低,数据采集工作量小.
2 GPS-RTK辅助近景摄影测量光束法平差方法 2.1 函数模型(1) 像点坐标观测方程.
摄影测量像点坐标观测方程即经典的共线方程[15],如式(1)所示.
| $\left\{ \begin{array}{c}x = \displaystyle- f\frac{{{a_{{\rm{i}}1}}({X_{\rm{T}}} - {X_{\rm{S}}}) + {b_{{\rm{i}}1}}({Y_{\rm{T}}} - {Y_{\rm{S}}}) + {c_{{\rm{i}}1}}({Z_{\rm{T}}} - {Z_{\rm{S}}})}}{{{a_{{\rm{i}}3}}({X_{\rm{T}}} - {X_{\rm{S}}}) + {b_{{\rm{i}}3}}({Y_{\rm{T}}} - {Y_{\rm{S}}}) + {c_{{\rm{i}}3}}({Z_{\rm{T}}} - {Z_{\rm{S}}})}} + {x_0},\\[15pt]y = \displaystyle- f\frac{{{a_{{\rm{i}}2}}({X_{\rm{T}}} - {X_{\rm{S}}}) + {b_{i2}}({Y_{\rm{T}}} - {Y_{\rm{S}}}) + {c_{i2}}({Z_{\rm{T}}} - {Z_{\rm{S}}})}}{{{a_{{\rm{i}}3}}({X_{\rm{T}}} - {X_{\rm{S}}}) + {b_{{\rm{i}}3}}({Y_{\rm{T}}} - {Y_{\rm{S}}}) + {c_{{\rm{i}}3}}({Z_{\rm{T}}} - {Z_{\rm{S}}})}} + {y_0}.\end{array} \right.$ | (1) |
式(1)中,
| $\left\{ \begin{array}{l}{a_{i1}} = \cos {\varphi _i}\cos {\kappa _i} - \sin {\varphi _i}\sin {\omega _i}\sin {\kappa _i},\\[6pt]{a_{i2}} = - \cos {\varphi _i}\sin {\kappa _i} - \sin {\varphi _i}\sin {\omega _i}\cos {\kappa _i},\\[6pt]{a_{i3}} = - \sin {\varphi _i}\cos {\omega _i},\\[6pt]{b_{i1}} = \cos {\omega _i}\sin {\kappa _i},\\[6pt]{b_{i2}} = \cos {\omega _i}\cos {\kappa _i},\\[6pt]{b_{i3}} = - \sin {\omega _i},\\[6pt]{c_{i1}} = \sin {\varphi _i}\cos {\kappa _i} + \cos {\varphi _i}\sin {\omega _i}\sin {\kappa _i},\\[6pt]{c_{i2}} = - \sin {\varphi _i}\sin {\kappa _i} + \cos {\varphi _i}\sin {\omega _i}\cos {\kappa _i},\\[6pt]{c_{i3}} = \cos {\varphi _i}\cos {\omega _i}.\end{array} \right.$ | (2) |
(2) GPS摄站坐标观测方程.
摄站坐标观测作业中实际很难保证GPS-RTK观测中心与相机摄影中心重合,两者必然存在一定偏差. 由于各摄站的偏差量不同,总体可将该偏差看作随机误差. 该偏差对定位结果产生等量偏移误差[16],通过平差可消除该偏差影响. GPS摄站坐标观测方程为
| $\left\{ \begin{array}{c}{X_{\rm{G}}} = {X_{\rm{S}}},\\[6pt]{Y_{\rm{G}}} = {Y_{\rm{S}}},\\[6pt]{Z_{\rm{G}}} = {Z_{\rm{S}}}.\end{array} \right.$ | (3) |
摄影测量平差随机模型中一般取像点坐标观测值为单位权观测值,其权P1=1. 对于GPS-RTK摄站观测值,可按其先验精度给予相应的权值. 考虑GPS-RTK观测误差及与摄影中心的位置偏差,GPS-RTK观测中心与摄影中心的偏心量一般不超过10 cm,实际可取经验标准差值σG=5 cm. 假定探测器像元尺寸为5 μm,像点坐标量测中误差为0.5像元,则摄站坐标的权
给定参数初值后,对观测方程(1)、(3)线性化展开,得到如下误差方程组
| $\left\{ \begin{array}{l}{\mathit{\boldsymbol{V}}_X} = {\mathit{\boldsymbol{A}}_{X1}}{\mathit{\boldsymbol{t}}_1} + {\mathit{\boldsymbol{A}}_{X2}}{\mathit{\boldsymbol{t}}_2} + \mathit{\boldsymbol{Cc}} + \mathit{\boldsymbol{Dx}} - {\mathit{\boldsymbol{L}}_X}{\bf{,}}\quad {\mathit{\boldsymbol{P}}_I},\\[6pt]{\mathit{\boldsymbol{V}}_{\rm{G}}} = \mathit{\boldsymbol{E}}{\mathit{\boldsymbol{t}}_I} - {\mathit{\boldsymbol{L}}_{\rm{G}}},\quad {\mathit{\boldsymbol{P}}_{\rm{G}}}.\end{array} \right.$ | (4) |
式(4)中,VX、VG分别为像点坐标、摄站坐标观测值改正数向量;t1为影像外方位线元素增量;t2为影像外方位角元素增量;c为影像内方位元素增量;x为像点对应的目标点物方坐标增量;AX1、AX2、C、D、E为相应参数的系数矩阵;LX、LG分别为像点坐标观测值、摄站坐标观测值的残差向量. PI、PG分别为像点坐标观测值、摄站坐标观测值的权.
误差方程组的矩阵形式为
| $\mathit{\boldsymbol{V}} = \mathit{\boldsymbol{Bx}} - \mathit{\boldsymbol{l,}}\;\;\mathit{\boldsymbol{P}}\mathit{\boldsymbol{.}}$ | (5) |
根据最小二乘原理列出相应的法方程,即可求出参数增量的最小二乘平差解[17]:
| $\mathit{\boldsymbol{\hat x}} = {{\bf{(}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}}{\bf{)}}^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{Pl}} = {\mathit{\boldsymbol{N}}_{BB}}^{ - 1}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{Pl}}\mathit{\boldsymbol{.}}$ | (6) |
根据误差传播定律,所求参数的协方差阵为
| ${\mathit{\boldsymbol{D}}_{\hat x\hat x}} = \hat \sigma _0^2{\mathit{\boldsymbol{Q}}_{\hat x\hat x}} = \hat \sigma _0^2\mathit{\boldsymbol{N}}_{BB}^{ - 1},$ | (7) |
其中,验后单位权中误差
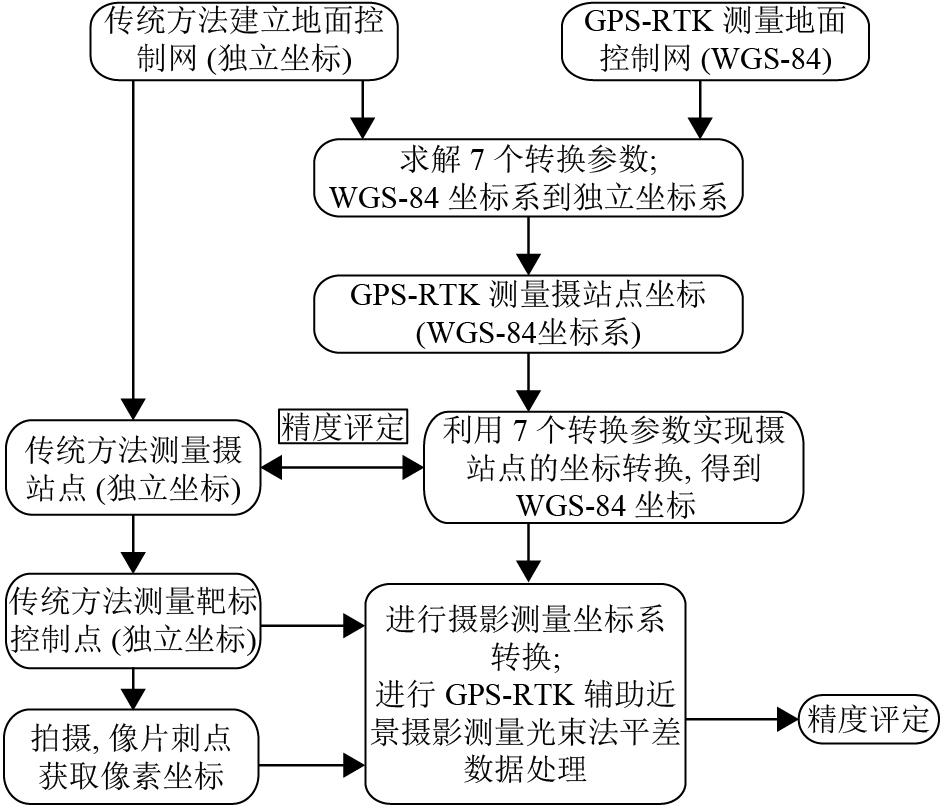
本文实验步骤如图1所示.
|
图 1 GPS-RTK辅助近景摄影测量实验流程图 Figure 1 Flow chart of GPS-RTK assisted photogrammetry experiment |
实验拍摄场景为校内教学办公建筑,实验相机型号为NIKON D610,其有效像素为2 426万. 所摄影像如图2~4所示.

|
图 2 影像DSC_0683 Figure 2 Image DSC_0683 |

|
图 3 影像DSC_0688 Figure 3 Image DSC_0688 |

|
图 4 影像DSC_0691 Figure 4 Image DSC_0691 |
所摄3幅影像分别构成两个不同基线长度的立体像对. 影像DSC_0683和DSC_0688构成立体像对1,其摄影基线约为3.5 m;影像DSC_0683和DSC_0691构成立体像对2,其摄影基线约为4.8 m. 在无GPS观测值辅助条件下进行常规光束法平差,求解过程不稳定,特别是当角元素初值误差较大时,待定参数均无法收敛而求解失败. 采用本文提出的GPS辅助近景摄影测量光束法平差,两个实验立体像对的影像定向和目标定位结果如下.
3.2.1 立体像对1立体像对1的摄影范围内有12个已知坐标点,其中6个点作为控制点,另外6个点作为检查点. 平差后影像定向结果如表1所示,各检查点目标定位精度如表2所示.
各检查点的三维定位中误差约为0.082 m,其中XY方向的定位中误差为0.020 m,而Z方向即沿相机光轴方向的定位中误差为0.080 m,为定位误差的主要部分.
3.2.2 立体像对2立体像对2中共包含10个已知坐标点. 取6个点作为控制点,另外4个点作为检查点. 平差后影像定向结果如表3所示,各检查点目标定位精度如表4所示.
| 表 1 立体像对1定向参数平差值及理论精度 Table 1 Parameter estimation value and precision of stereo image pair 1 |
| 表 2 立体像对1检查点目标定位精度 Table 2 Target location precision of CPs of Stereo image pair 1 |
| 表 3 立体像对2定向参数平差值及理论精度 Table 3 Parameter estimation value and precision of stereo image pair 2 |
| 表 4 立体像对2各检查点目标定位精度评定 Table 4 Target location precision of CPs of Stereo image pair 2 |
各检查点的三维定位中误差约为0.066 m,其中XY方向的定位中误差约为0.020 m,Z方向定位中误差为0.063 m.
3.3 结果分析从两个立体像对的平差结果可看出:
(1) 两个像对在XY方向的定位中误差大致相当,约为0.02 m. 根据近景摄影测量规范,图上点位精度应在0.5 mm以内,按比例尺计算,本文实验结果可满足1︰50比例尺平面测图要求.
(2) 两个像对的Z方向定位中误差均显著大于XY方向定位中误差,其中立体像对2的Z方向定位中误差较小. 理论而言,长基线立体像对在沿观测方向上的几何交会精度更高,本文实验结果亦符合这一规律.
(3) 像方定位验后单位权中误差约为5个像元,与物方定位中误差基本符合,但未达到像元物方分辨率水平. 究其原因,本文所用光束法平差模型未严格考虑成像几何畸变. 由于几何畸变属于系统误差,后续还需研究有效的系统误差补偿方法,进一步提高定位精度.
4 小结本文提出一种GPS-RTK辅助近景摄影测量光束法平差方法. 利用GPS-RTK技术快速获取摄站坐标观测值,并在平差函数模型中引入相应的GPS摄站定位观测方程. 在常规光束法平差基础上,GPS辅助光束法平差计算程序只需作少量改动,即可使参数求解过程的稳定性得到有效提高. 此外,采用常规方法,一般要求具有较高精度的平差参数初值以及数量较多的控制点. 而GPS-RTK观测值可一定程度上代替控制点的位置基准作用,加入GPS-RTK观测值后,近景影像光束法平差对参数初值精度及控制点数量要求有所降低,有助于改进近景摄影测量作业的效率. 在未考虑几何畸变条件下,本文实验结果中平面定位中误差达到0.02 m,后续通过系统误差补偿可望进一步提高精度.
| [1] | 冯文灏. 近景摄影测量学[M]. 武汉: 武汉大学出版社, 2002. |
| [2] | 王佩军, 徐亚明. 摄影测量学[M]. 武汉: 武汉大学出版社, 2010. |
| [3] |
陈楚, 姜兴钰, 张学民, 等. 近景摄影测量在滑坡监测中的应用研究[J].
城市勘测, 2015(1): 105-108.
CHEN C, JIANG X Y, ZHANG X M, et al. The research on the application of close-range photogrammetry in the landslide monitoring[J]. Urban Geotechnical Investigation & Surveying, 2015(1): 105-108. |
| [4] |
张国建, 于承新. 数字近景摄影测量在桥梁变形观测中的应用[J].
全球定位系统, 2016, 41(1): 91-95.
ZHANG G J, YU C X. The application of digital close-range photogrammetry in the deformation observation of bridge[J]. Global Positioning System, 2016, 41(1): 91-95. |
| [5] | MUNDY J L, ZISSERMAN A. Geometric invariance in computer vision [M]. Massachusetts: Cambridge, MIT Press, 1992. |
| [6] | 王之卓. 摄影测量原理[M]. 武汉: 武汉大学出版社, 2007. |
| [7] | FRASER C S, EDMUNDSON K L. Design and implementation of a computational processing system for off-line digital close-range photogrammetry[J]. ISPRS Journal of Photogrammetry & Remote Sensing, 2000, 55(2): 94-104. |
| [8] | 袁修孝. GPS辅助空中三角测量原理及应用[M]. 北京: 测绘出版社, 2001. |
| [9] |
赵鹏, 何珏, 汪洪慧. 内方位元素对普通数码影像光线束算法精度的影响[J].
测绘信息与工程, 2012, 37(3): 23-26.
ZHAO P, HE Y, WANG H H. The inner orientation elements influence on ordinary digital image light beam algorithm[J]. Engineering of Surveying and Mapping, 2012, 37(3): 23-26. |
| [10] |
宋立明, 章传银, 秘金钟, 等. 基于GPS的近景测量定位方法研究[J].
测绘科学, 2011, 36(2): 40-41.
SONG L M, ZHANG C Y, BI J Z, et al. Locating method of close-range photogrammetry based on GPS[J]. Science of Surveying and Mapping, 2011, 36(2): 40-41. |
| [11] | 张正禄. 工程测量学[M]. 武汉: 武汉大学出版社, 2015. |
| [12] |
李天子, 郭辉. 多基线近景摄影测量的平面地表变形监测[J].
辽宁工程技术大学学报(自然科学版), 2013, 41(08): 1098-1102.
LI T Z, GUO H. Deformation observing of plane terrain basing on multi-baseline close-range photogrammetry[J]. Journal of Liaoning Technical University (Natural Science Edition), 2013, 41(08): 1098-1102. |
| [13] |
谭瑞, 章传银, 秘金钟, 等. 新型动态定位系统的研究与应用[J].
测绘与空间地理信息, 2014, 37(8): 222-224.
TAN R, ZHANG C Y, BI J Z, et al. The researchon the dynamic positioning methods in some unreachable areas[J]. Geomatics & Spatial Information Technology, 2014, 37(8): 222-224. |
| [14] | 李征航, 黄劲松. GPS测量与数据处理[M]. 第三版. 武汉: 武汉大学出版社, 2016. |
| [15] |
池梦群, 陈曦, 杨辽, 等. 普通相机近景影像空三加密精度分析[J].
遥感信息, 2015, 30(6): 13-17.
CHI M Q, CHEN X, YANG L, et al. Aerial triangulation accuracy analysis of close-range images based on digital camera[J]. Remote Sensing Information, 2015, 30(6): 13-17. |
| [16] |
丁琼, 吕俊涛, 陈高文, 等. LiDAR安置误差对定位精度影响分析[J].
广东工业大学学报, 2015, 32(3): 115-118.
DING Q, LYU J T, CHEN G W, et al. Influence of LiDAR systematic error on positioning accuracy[J]. Journal of Guangdong University of Technology, 2015, 32(3): 115-118. |
| [17] | 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 第三版. 武汉: 武汉大学出版社, 2014. |
 2017, Vol. 34
2017, Vol. 34