机组组合问题是电力系统中一个重要的非线性混合整数优化问题,它的优化目标是在一定的调度周期内合理地安排机组的启停状态以及合理地分配运行机组的机组出力使得总的运行费用最小. 由于要满足功率平衡约束、旋转备用约束、最小开停机时间约束、爬坡约束等一些约束条件,使得机组组合问题的求解十分困难.
机组组合问题是电力系统中最难求解的问题之一,它的求解能够带来显著的经济效益,一直以来是众多学者研究的热点问题. 许多方法已经被用来求解机组组合问题,如优先列表法[1]、动态规划法[2]、拉格朗日松弛法[3]等传统方法,遗传算法[4-5]、粒子群算法[6]、差分算法[7]等人工智能算法以及一些混合算法[8-12]. 传统方法简单方便,但往往容易陷入局部最优解,特别是在求解规模比较大的系统时,传统方法存在诸多困难,甚至难以求解. 人工智能算法和混合算法由于其易于实施,求解复杂问题时的全局收敛能力强,能够寻找到最优的或者接近最优的解决方案,近年来已经得到了广泛的认可. 文献[13]采用离散PSO(Particle Swarm Optimization)分时段优化机组的启停状态,连续PSO优化机组的负荷分配,并在种群更新时引入临界算子,改进可行解的判别条件. 但是分时段优化必然会降低机组组合问题在时间维度上的耦合关系,使得问题的求解精度降低. 文献[14]采用改进的离散粒子群算法结合原对偶内点法分别对机组组合问题的整型变量和连续变量进行交替迭代优化求解,但是在处理约束问题时某些时段未能满足功率平衡约束. 文献[9]混合遗传算法和差分算法求解机组组合问题,并采用基于优先列表的方法和启发式策略修正约束问题,取得了分别比单独使用遗传算法和差分算法较好的结果,但是随着系统规模的增大,该方法收敛速度慢,并且容易陷入局部最优解.
本文在纵横交叉算法的基础上,提出一种用于求解机组组合问题的混合纵横交叉算法,离散CSO(Crisscross Optimization)和连续CSO在迭代过程中对机组的启停状态和负荷的经济分配进行交替优化求解,结合一种贪婪的选择机制,使得种群朝着全局最优的方向进化,加快了种群的收敛速度. 对于功率平衡、最小开停机时间、爬坡限制等一些约束的处理,采用启发式修正方法代替传统的罚函数法,提高和改善求解结果的精度.
1 机组组合问题的数学模型 1.1 目标函数机组组合问题的目标函数是在一定的调度周期内使总的燃料费用和启动费用之和最小,即
| ${\rm{min TC}} = \sum\limits_{t = 1}^T {\sum\limits_{i = 1}^N {[{F_i}({P_{it}}) + {\rm{S}}{{\rm{C}}_{it}}(1 - {u_{i(t - 1)}})]{u_{it}}} } ,$ | (1) |
式(1)中,TC为系统总运行费用;Pit为机组i在时段t的出力值;uit表示机组i在t时段的状态;N为机组数;
| ${F_i}({P_{it}}) = {a_i} + {b_i}{P_{it}} + {c_i}P_{it}^2,$ | (2) |
| ${\rm{S}}{{\rm{C}}_{it}}{\rm{ = }}{K_i} + {B_i}[1 - \exp ( - {\rm{toff}}_i^{t - 1}/{\tau _i})].$ | (3) |
式(2)、(3)中:
机组组合问题一般需要满足以下约束条件:
(1) 功率平衡约束.
| $\sum\limits_{i = 1}^N {({P_{it}}{u_{it}})} = {\rm{Loa}}{{\rm{d}}_t}.$ | (4) |
式(4)中,
(2) 旋转备用约束.
| $\sum\limits_{i = 1}^N {P_i^{{\rm{max}}}} {u_{it}} \geqslant {\rm{Loa}}{{\rm{d}}_t} + {\rm{S}}{{\rm{R}}_t}.$ | (5) |
式(5)中,
(3) 最小开停机时间约束.
| $\left\{ \begin{array}{l}{\rm{ton}}_i^t \geqslant {\rm{MU}}{{\rm{T}}_i},\\[6pt]{\rm{toff}}_i^t \geqslant {\rm{MD}}{{\rm{T}}_i}.\end{array} \right.$ | (6) |
式(6)中,
(4) 机组出力约束.
| ${u_{it}}P_i^{{\rm{min}}} \leqslant {P_{it}} \leqslant {u_{it}}P_i^{{\rm{max}}}.$ | (7) |
式(7)中,
(5) 机组爬坡约束.
| $\left\{ \begin{array}{l}{P_{it}} - {P_{i,t - 1}} \leqslant {\rm{U}}{{\rm{R}}_i}{\rm{,}}\\[6pt]{P_{i,t - 1}} - {P_{it}} \leqslant {\rm{D}}{{\rm{R}}_i}{\rm{.}}\end{array} \right.$ | (8) |
式(8)中,URi为机组出力增加的速度上限,DRi为机组出力的减少的速度下限.
考虑机组的爬坡约束限制时,机组的出力约束需要被修改为
| $\begin{split}&\max (P_i^{{\rm{min}}},{P_{i,t - 1}} - {\rm{D}}{{\rm{R}}_i}) \leqslant {P_{it}}\leqslant\\[4pt]&{\rm{ }}\min (P_i^{{\rm{max}}},{P_{i,t - 1}} + {\rm{U}}{{\rm{R}}_i}).\end{split}$ | (9) |
纵横交叉算法[15]是最近发展起来的新型群体智能搜索算法. 它采用一种双向搜索机制,即横向交叉和纵向交叉,结合一个简单的竞争机制,形成CSO的基本搜索行为. 在每一次迭代过程中,CSO从两个不同的方向对种群进行交叉产生子代,这些子代被称为中庸解. 随后,这些新产生的中庸解通过一个贪婪的选择机制和父代进行比较,只有比父代适应度更好的解才能够存活下来,否则就被淘汰. 这些在竞争中存活下来的解被称为占优解,作为下一次交叉的父代. 很显然,在种群迭代过程中,CSO始终保持个体的最优解,这样的竞争机制无疑会加快求解的收敛速度.
(1) 横向交叉.
横向交叉之前需要对种群中的粒子两两不重复配对,然后对配对粒子的相同维进行算术交叉. 假设对粒子X(i)和X(j)的第d维交叉,公式为
| $\left\{ \begin{array}{l}{\rm{M}}{{\rm{S}}_{id}} = {r_1} {X_{id}} + (1 - {r_1}) {X_{jd}} + {c_1} ({X_{id}} - {X_{jd}}),\\[6pt]{\rm{M}}{{\rm{S}}_{jd}} = {r_2} {X_{jd}} + (1 - {r_2}) {X_{id}} + {c_2} ({X_{jd}} - {X_{id}}).\end{array} \right.$ | (10) |
式(10)中,r1、r2为[0, 1]上的随机数;c1、c2为[–1, 1]之间的随机数;Xid和Xjd分别为粒子X(i)和X(j)的第d维;MSid和MSjd分别为横向交叉后的第d维子代.
由式(10)可以观察到横向交叉由两个部分组成:第1部分是内部信息的交换,以较大的概率在父代粒子形成的超立方体内进行搜索;第2部分是外部信息的探索,通过在父代粒子之间施加一个扩展系数,以较小的概率在超立方体的外缘进行搜索. 这种搜索机制可以有效地减少搜索盲点,提高CSO的全局搜索能力.
(2) 纵向交叉.
与横向交叉不同的是,纵向交叉是在同一个粒子不同维的交叉,假设对粒子X(i)的第d1和d2维执行纵向交叉,公式为
| $\begin{split}&{\rm{M}}{{\rm{S}}_{i,d_1}} = r \cdot {X_{i,d_1}} + (1 - r) \cdot {X_{i,d_2}}i \in (1,M),\\[6pt]&{d_1},{d_2} \in (1,D).\end{split}$ | (11) |
式(11)中,M为粒子的个数;D为粒子的维数;r为[0, 1]上的均匀分布随机数;
由于不同维的上下限往往不同,所以纵向交叉之前需要对粒子的各维进行归一化处理,纵向交叉结束后还需要对所产生的中庸解进行反归一化处理. 一般算法在迭代过程中某些维容易陷入局部最优而停止更新,但不同的维一般都有差异. 纵横交叉算法正是观察到这种现象,使用纵向交叉在不同维进行算术交叉,可以有效地帮组陷入局部最优的维跳出困境,而且每次交叉只产生一个子代,在保持种群多样性的同时而不破坏有可能比较好的维. 相比于其他搜索算法,纵向交叉是纵横交叉算法的一个明显的特征.
根据前面的阐述可知,CSO是连续线性的群体智能搜索算法,不利于求解机组状态优化的离散问题,因此有必要对CSO进行二进制化. 本文采用Sigmiod函数对交叉后的中庸解进行转换,公式为
| $\left\{ \begin{array}{l}{B_{id}} = 1{\rm{ if }}R < S({\rm{M}}{{\rm{S}}_{id}}),\\[6pt]{B_{id}} = 0{\rm{ if }}R \geqslant S({\rm{M}}{{\rm{S}}_{id}}).\end{array} \right.$ | (12) |
式(12)中,R为[0, 1]上的均匀分布随机数;Bid为二进制化结果;S(x)为Sigmoid函数,可表示为式(13)
| $S\left( x \right) = 1/[1 + \exp \left( { - x} \right)].$ | (13) |
在机组组合问题中,约束条件的处理是一个难点,一般采用的是罚函数法,给不满足约束的粒子设定一个惩罚系数,使其朝着可行解的方向进化. 这种方法使得收敛速度变慢,而且收敛得到的解很难绝对的满足约束条件,使得求解精度降低. 本文采用启发式的策略代替罚函数法修正约束条件,提高求解的速度和精度.
(1) 最小开停机时间约束. 离散CSO在每次交叉之后产生的解一般不满足最小开停机时间约束,所以每次离散交叉之后都需要检查机组状态是否满足最小开停机时间约束. 对于不满足约束的解,一般有3个调整的方向,即:调整违背约束时段之前的机组状态、调整违背约束时段之后的状态、调整违背约束时段的机组状态. 本文根据违背约束时段的开停机时间与最小开停机时间的比值确定机组状态的调整方向,这一概率选择机制可以产生更多的机组组合策略,增加种群的多样性,保证算法的全局收敛能力. 以违背最小开机时间约束为例,不同方向的调整方法如式(14)所示.
| $\left\{ \begin{array}{l}{\rm{if\;rand}}1 \leqslant \displaystyle\frac{{{\rm{to}}{{\rm{n}}_{it}}}}{{{\rm{MU}}{{\rm{T}}_i}}}{\rm{\& \;rand}}2 \leqslant {\rm{0}}{\rm{.5}}\\[11pt]{\rm{ \& \;tof}}{f_{i,t - ({\rm{MU}}{{\rm{T}}_i} - {\rm{to}}{{\rm{n}}_i})}}{\rm{ > MD}}{{\rm{T}}_i}{\rm{, }}\text{向前调整};\\[11pt]{\rm{if\;rand}}1{\rm{ }} \leqslant \displaystyle\frac{{{\rm{to}}{{\rm{n}}_{it}}}}{{{\rm{MU}}{{\rm{T}}_i}}}{\rm{\& \;rand}}2{\rm{ > 0}}{\rm{.5, }}\text{向后调整};\\[11pt]{\rm{if\;rand}}1{\rm{ > }}\displaystyle\frac{{{\rm{to}}{{\rm{n}}_{it}}}}{{{\rm{MU}}{{\rm{T}}_i}}}{\rm{, }}\text{调整违背约束的时段}.\end{array} \right.$ | (14) |
(2) 旋转备用约束. 根据“上大压小”的原则,优先开启大容量的机组满足选择备用约束,之后还要检查最小开停机时间约束是否满足. 当这两项约束都满足之后,检查是否有冗余的机组. 冗余的机组会增加运行的成本,在满足约束的情况下尽可能地关闭冗余机组.
(3) 功率平衡约束. 根据式(4),功率的不平衡量可以表示为
| $\Delta P = {\rm{Loa}}{{\rm{d}}_t} - \sum\limits_{i = 1}^N {({P_{it}}{u_{it}})} .$ | (15) |
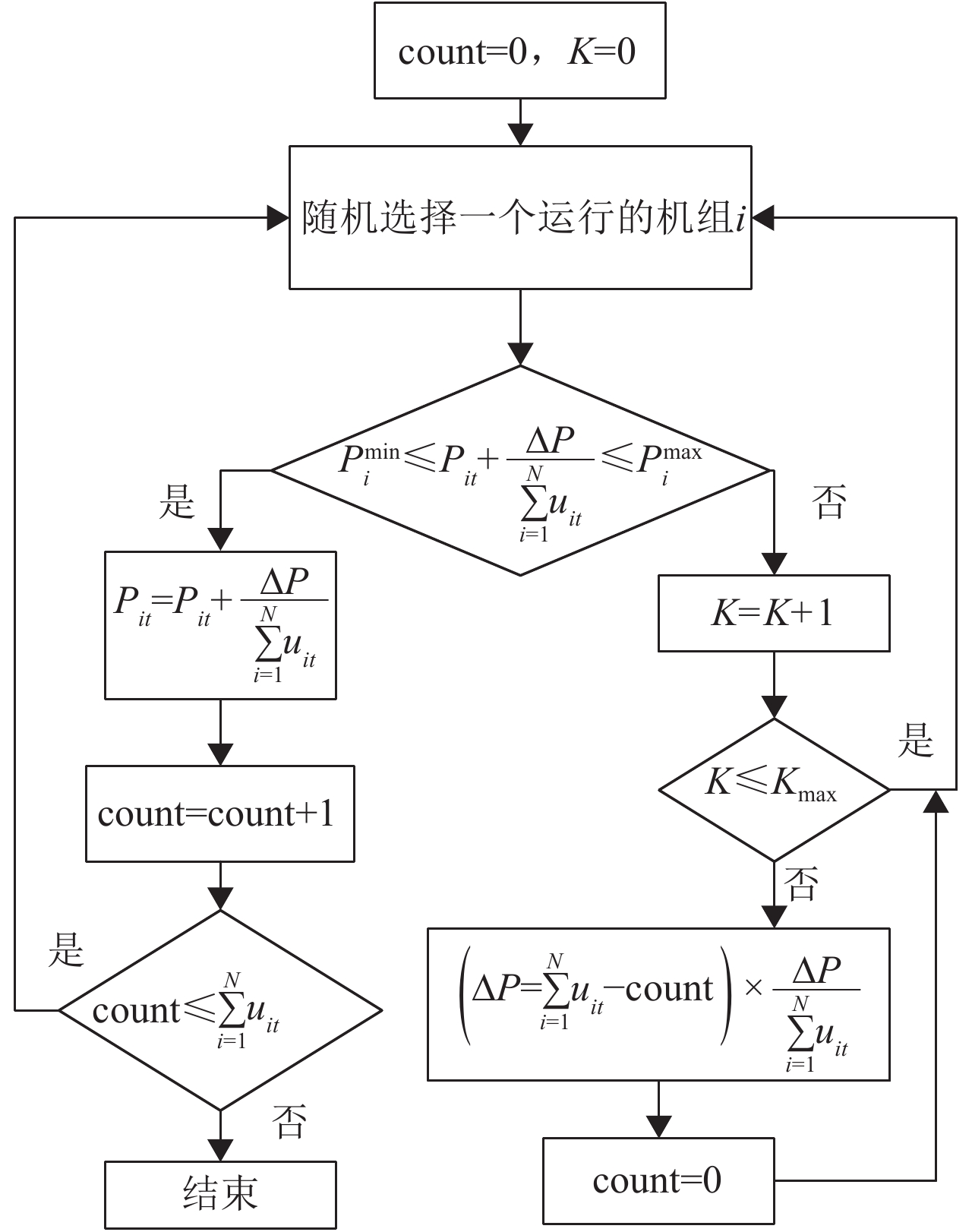
这些不平衡量需要分配到运行的机组出力上以满足功率平衡约束. 本文将不平衡量平均分成对应时段所开机组数目的等份,然后随机地分配到一些机组之上,使得功率平衡能够很好地满足. 具体流程如图1所示.
|
图 1 功率平衡修正流程图 Figure 1 Flow chart of power balance correction |
结合机组组合问题的数学模型和混合纵横交叉算法的原理,混合纵横交叉算法应用到机组组合问题主要包括以下步骤:
(1) 设置参数,初始化种群;
(2) 修正约束,计算粒子的适应度值;
(3) 离散CSO和连续CSO分别对机组状态变量和机组出力变量交叉产生子代;
(4) 每一次交叉之后修正子代的约束并计算适应度值与父代进行比较,适应度好的解保留到占优解里作为下一次交叉的父代;
(5) 判断是否达到最大迭代次数,如果是,输出最优解,否则转到步骤(3).
4 算例分析本文首先对10机24 h的系统进行机组组合优化分析,机组参数和负荷数据参见文献[3]. 种群规模为20,迭代次数为100次.
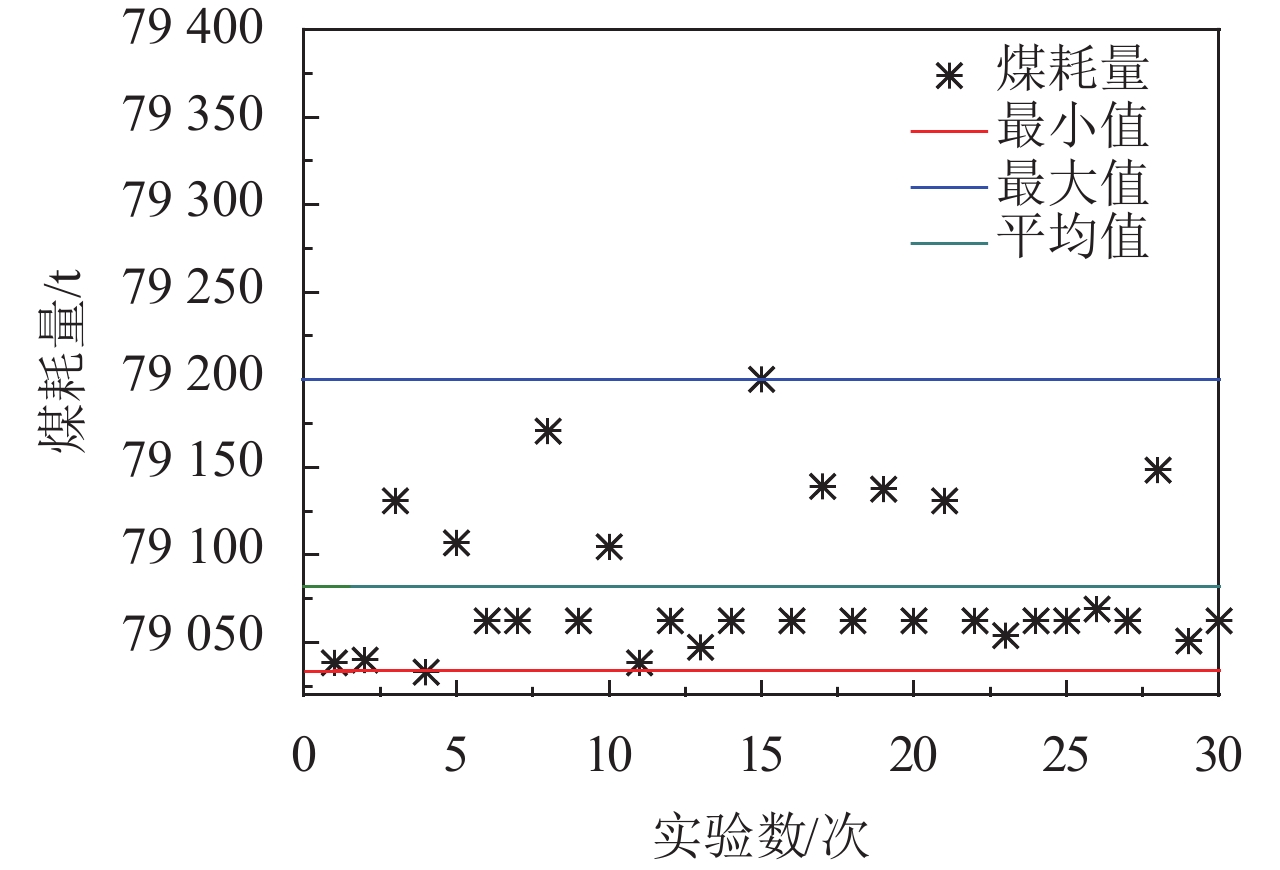
由于搜索算法的随机性,为了减少统计误差,本文对测试系统进行30次独立的实验,结果分布如图2所示. 30次独立重复实验的最小值、平均值和最大值分别为79 033.7 t、79 081.8 t和79 200.2 t. 最大值和和最小值相差为166.5 t,相对于最小值的偏差仅为0.21%,而且由图2可以看出,大部分解都分布在平均值以下,证明了混合纵横交叉算法在求解机组组合问题时具有良好的寻优能力和鲁棒性.
|
图 2 实验结果分布图 Figure 2 Distribution chart of experiment results |
为了进一步验证本文算法的有效性,将本文的煤耗量与其他算法的结果相比较,统计结果如表1所示.
| 表 1 10机系统结果比较1) Table 1 Comparison of results for 10-unit system |
本文所提混合纵横交叉算法总的煤耗量为79 033.2 t,其中启动费用为267.3 t. 系统优化过后的机组出力表如表2所示,出力为0表示机组停机,不为0表示机组运行. 从表1可以计算出,与Hopfield模拟退火混合算法、双重粒子群算法、遗传算法的煤耗量相比,本文算法的煤耗量分别节省81.4 t、632.6 t、773.8 t,分别降低了0.1%、0.79%、0.97%. 虽然本文算法煤耗量略高于文献[8]和[14]的所得结果,但是本文采用启发式的策略修正约束条件,使得约束条件能够很好的满足. 从文献[14]给出的机组出力分布表可以看出,系统在第17时段的机组出力比负荷需求少17 MW,没能满足机组的功率平衡约束. 文献[8]采用罚函数法处理约束条件,很难得到质量很高的解,而且根据文献中所提供的机组出力分布计算得到的煤耗量为79 307.3 t,比文献中给出的煤耗量结果要高. 从表2可以看出,本文的优化结果符合“上大压小”的原则,优先开启大容量的机组,这样既可以节约煤耗成本,又符合节能减排的目的和实际工程需求.
| 表 2 10机系统机组状态及功率分配 Table 2 Unit status and power dispatch of 10-unit system |
另外,为了验证本文算法在处理大规模系统时的全局收敛能力,对40机24 h的系统进行机组组合优化分析,机组参数和负荷数据参见文献[11]. 随着系统规模的增大,机组的启动状态数目会呈指数增加,一般算法很容易陷入局部最优,使得求解更加困难. 根据研究发现[15],大部分算法在陷入局部最优时都是某些维停滞了更新. 本文算法的纵向交叉是对不同的维进行交叉,能够很好地帮组停滞的维跳出困境,然后通过横向交叉将信息扩散至整个种群. 不同算法的收敛结果如表3所示. 从表3可以看出,本文算法的优化结果不仅优于改进的算法,而且还优于混合的算法,证明了本文算法在求解大规模机组组合系统时良好的全局寻优能力.
| 表 3 40机系统结果比较 Table 3 Comparison of results for 40-unit system |
本文提出了一种新型的混合纵横交叉算法求解机组组合问题,该算法分别采用离散CSO和连续CSO处理机组状态更新和负荷出力更新. 进化过程中横向交叉和纵向交叉交替进行,不仅加快了算法的收敛速度,而且可以保证算法的全局收敛能力. 在处理约束问题时,采用启发式的策略修正约束,避免了使用罚函数法处理约束时机组出力小于负荷需求的现象. 通过2个算例的仿真可以看出,本文算法能够很好地用于机组组合问题,在机组数目增多时,能够克服维数灾难,取得满意的收敛结果.
| [1] | SENJYU T, SHIMABUKURO K, UEZATO K, et al. A fast technique for unit commitment problem by extended priority list[J]. IEEE Transactions on Power Systems, 2003, 18(2): 882-888. DOI: 10.1109/TPWRS.2003.811000. |
| [2] |
白晓民, 于尔铿. 用动态规划法进行电力系统机组组合最优化[J].
中国电机工程学报, 1984, 4(1): 13-21.
BAI X M, YU E K. Optimization for unit commitment of electric power system by dynamic programming[J]. Proceedings of the CSEE, 1984, 4(1): 13-21. |
| [3] |
韩学山, 柳焯. 考虑发电机组输出功率速度限制的最优机组组合[J].
电网技术, 1994, 18(06): 11-16.
HAN X S, LIU Z. Optimal unit commitment considering unit's ramp-rate limits[J]. Power System Technology, 1994, 18(06): 11-16. |
| [4] | DATTA D. Unit commitment problem with ramp rate constraint using a binary-real-coded genetic algorithm[J]. Applied Soft Computing, 2013, 13(9): 3873-3883. DOI: 10.1016/j.asoc.2013.05.002. |
| [5] |
蔡超豪, 蔡元宇. 机组优化组合的遗传算法[J].
电网技术, 1997, 21(1): 44-47.
CAI C H, CAI Y Y. Optimization of units commitment by genetic algorithm[J]. Power System Technology, 1997, 21(1): 44-47. |
| [6] | 周俊. 机会约束规划下含风电场的机组组合优化[D]. 广州: 广东工业大学自动化学院, 2014. |
| [7] | DATTA D, DUTTA S. A binary-real-coded differential evolution for unit commitment problem[J]. International Journal of Electrical Power & Energy Systems, 2012, 42(1): 517-524. |
| [8] |
张炯, 刘天琪, 苏鹏, 等. 基于遗传粒子群混合算法的机组组合优化[J].
电力系统保护与控制, 2009, 37(9): 25-29.
ZHANG J, LIU Q T, SHU P, et al. Unit commitment optimization based on genetic algorithm and particle swarm optimization hybrid algorithm[J]. Power System Protection and Control, 2009, 37(9): 25-29. |
| [9] | TRIVEDI A, SRINIVASAN D, BISWAS S, et al. A genetic algorithm-differential evolution based hybrid framework: Case study on unit commitment scheduling problem[J]. Information Sciences, 2016, 354: 275-300. DOI: 10.1016/j.ins.2016.03.023. |
| [10] |
陈璟华, 梁丽丽, 丁林军, 等. 计及风电场并网的机会约束规划的机组组合优化[J].
广东工业大学学报, 2017, 34(1): 50-54.
CHEN J H, LIANG L L, DING L J, et al. Unit commitment optimization based on chance-constrained programming in wind power integrated system[J]. Journal of Guangdong University of Technology, 2017, 34(1): 50-54. |
| [11] | YUAN X, JI B, ZHANG S, et al. A new approach for unit commitment problem via binary gravitational search algorithm[J]. Applied Soft Computing, 2014, 22(5): 249-260. |
| [12] | MORADI S, KHANMOHAMMA S, HAGH M T, et al. A semi-analytical non-iterative primary approach based on priority list to solve unit commitment problem[J]. Energy, 2015, 88: 244-259. DOI: 10.1016/j.energy.2015.04.102. |
| [13] |
李整, 谭文, 秦金磊. 一种用于机组组合问题的改进双重粒子群算法[J].
中国电机工程学报, 2012, 32(25): 189-195.
LI Z, TAN W, QIN J L. An improved dual particle swarm optimization algorithm for unit commitment problem[J]. Proceedings of the CSEE, 2012, 32(25): 189-195. |
| [14] |
陈海良, 郭瑞鹏. 基于改进离散粒子群算法的电力系统机组组合问题[J].
电网技术, 2011, 35(12): 94-99.
CHEN H L, GUO R P. Unit commitment based on improved discrete particle swarm optimization[J]. Power System Technology, 2011, 35(12): 94-99. |
| [15] | MENG A, CHEN Y, YIN H, et al. Crisscross optimization algorithm and its application[J]. Knowledge-based Systems, 2014, 67(4): 218-229. |
| [16] |
吴金华, 吴耀武, 熊信艮. 机组组合问题的扩展Hopfield神经网络算法[J].
电力系统自动化, 2003, 27(7): 41-44.
WU J H, WU Y W, XIONG X Y. Optimization of unit commitment by improved Hopfield neural network algorithm[J]. Automation of Electric Power Systems, 2003, 27(7): 41-44. |
| [17] | YUAN X, NIE H, SU A, et al. An improved binary particle swarm optimization for unit commitment problem[J]. Expert Systems with Applications, 2009, 36(4): 8049-8055. DOI: 10.1016/j.eswa.2008.10.047. |
| [18] | JEONG Y, PARK J, SHIN J, et al. A thermal unit commitment approach using an improved quantum evolutionary algorithm[J]. Electric Power Components & Systems, 2009, 37(7): 770-786. |
 2017, Vol. 34
2017, Vol. 34