随着经济的发展,人们的生活发生了极大的变化,为了节省时间成本,很多人选择了驾车出行. 驾车出行人数的增加,且我国多数城市人口密度大,使得停车位越来越紧凑,准确将车倒入车位或者说准确将车停好已经成为每个驾驶员所必须具备的技能. 但是,在倒车过程中往往会存在视角盲区,这使得驾驶员在倒车过程中会出现刮碰的情况. 为了解决这一问题,很多车辆配备了车辆辅助安全倒车系统[1],以将车辆周围的环境信息和车辆的位置信息以俯视图的方式反馈到车内的显示屏上,驾驶员根据显示屏的提示进行安全准确的倒车和停车.
但是,目前车辆的辅助安全倒车系统的显示屏并不能很好地显示车辆四周的环境信息,这是由于辅助安全倒车系统往往会将同一场景的至少两张图像进行融合,形成一幅大场景图像. 传统的渐入渐出算法[2]只实现了单个方向上的平滑过渡而没有实现整个区域的平滑过渡,导致重叠区域过渡不够均匀,使得图像拼接过程后仍然存在缝隙. 这使得车辆辅助安全倒车系统的显示屏不能很好地呈现车辆四周的环境信息,不能给用户以良好的视觉效果. 而人类所获取的信息中有70%~80%来源于视觉. 现在,人们已不满足于当前泊车系统的图像拼接效果,因而需要实现更平滑的过渡效果.
本文提出的图像拼接技术[3]是将同一场景的两张或者多张有重叠区域的图像通过图像配准和图像融合技术拼接成一幅大场景,拼接后的全新图像包含拼接前全部图像的所有信息. 本实验的图像拼接主要有4个步骤:图像的几何校正、图像预处理、图像配准和图像融合,如图1所示. 本文中,主要论述了:图像配准原理、图像融合中权重函数的设计,在论文后期还对图像拼接质量进行评估. 图像质量评价技术[4-5]是为了对图像拼接的图像处理技术的性能进行衡量,反映了图像拼接的效果. 结果表明,文中提出的图像融合中的权重设计方法是确实可行的. 此外,文中论述的权重设计方法主要是图像重叠区域出现两个不连续点的情况下,图像拼接过程中权重的设计方案. 对于图像重叠区域有多个不连续点的情况,权重的设计思路也可按照文中重叠区域只有两个不连续点的情况进行处理. 实验中算法的设计主要包括:(1) 找到两幅图像的交点并判断哪些点是连续点或不连续点;(2) 构造图像重合区域的连续映射;(3) 设计权重函数.图像拼接技术的研究在航天领域[6]、大地测绘[7]、医学影像的合成方面[8]以及虚拟现实[9-10]、日常生活中都具有广泛的应用.

|
图 1 图像拼接的步骤 Figure 1 Steps of image mosaic |
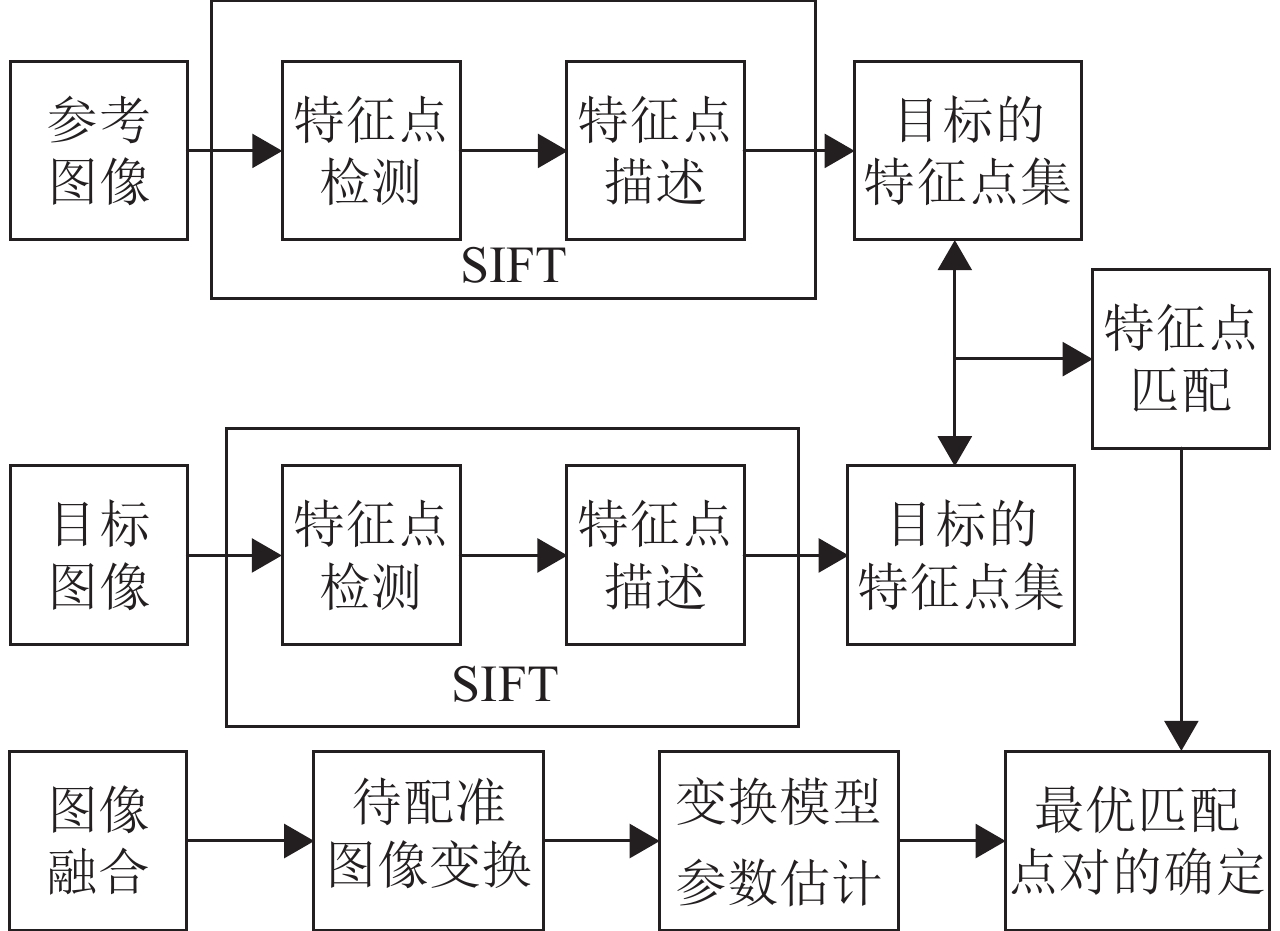
图像经过精确的配准后可以避免图像在融合时期出现的重影现象. 因此,在图像融合步骤之前必须经过图像配准这一环节. 图像拼接实验中,图像配准采用的技术是SIFT[11] 算法,该算法的流程如图2所示. SIFT算法由David G. Lowe[12]在1999年首次提出,并在2004年加以完善. 该算法是一种通过在尺度空间中寻找极值点,并提取位置、尺度、旋转不变量来检测图像中的局部性特征的计算机视觉算法. 算法提取图像特征的步骤为:(1) 尺度空间极值检测:在所有尺度和图像位置上进行搜索,对于尺度和旋转不变的潜在兴趣点,SIFT算法是通过使用一个高斯微分函数有效地进行识别;(2) 关键点定位:对于每个候选的位置来说,一个详细的模型决定位置和尺寸,关键点是基于它们的稳定性来进行选择;(3) 方向确定:分配给每个关键点位置的一个或多个方向是基于图像局部梯度方向确定的,相对于每一个指定了方向、尺度和位置的特征,所有后面的操作都是在变换过的图像数据上进行,因此提供了这些变换的不变性;(4) 关键点描述:局部图像梯度是在选择的每一个关键点周围区域里进行测量,这些图像局部的梯度被变换成一种允许较大局部形状的变形和光照变化的表示.
|
图 2 SIFT算法流程 Figure 2 Flow of SIFT algorithm |
SIFT特征匹配算法包括两个阶段:第一阶段是SIFT特征的生成,第二阶段是SIFT特征向量的匹配. 取一幅图像中的某个关键点,并找出其与另一个图像中欧氏距离最近的前两个关键点,在这两个关键点中,如果最近的距离除以次近的距离少于某个比例阈值,则接受这一对匹配点. 降低这个比例阈值,SIFT匹配点数目会减少,但更加稳定. 图3表示的是基于SIFT的特征及其匹配的效果.

|
图 3 图像匹配过程 Figure 3 Process of image matching |
直接平均值法中,设f12(x, y)为图像融合后的像素值,融合后图像的像素值的计算公式为:
| ${f_{12}}(x,y) = \left\{ \begin{array}{l}{f_1}(x,y),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(x,y) \in {S_{10}};\\[5pt]\displaystyle\frac{1}{2}\left[ {{f_1}(x,y) + {f_2}(x,y)} \right],\;\;\;\;\;(x,y) \in S;\;\\[11pt]{f_2}(x,y),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(x,y) \in {S_{20}}.\end{array} \right.$ | (1) |
式(1)中f1(x, y)、f2(x, y)为待融合的两幅图像,S10表示参考图像f1(x, y)中未与待匹配图像f2(x, y)重叠的区域,S20表示待匹配图像f2(x, y)中未与参考图像f1(x, y)重叠的区域,S表示两幅图像f1(x, y),f2(x, y)的重叠区域. 该算法对图像进行融合后的效果如图4(c)所示. 其中,红色圈出来的部分表示缝隙出现的位置. 融合后的图像其左下脚和右上角图片有部分显示为黑色,这是因为计算机在处理拼接后没有像素的图片时,将图片显示为黑色. 由实验结果可知,平均值法的图像融合只是对重叠区域的像素求平均,使其像素值不至于骤变,但是这种方法并不能使图像进行平滑过渡.

|
图 4 平均值法图像融合效果图 Figure 4 Image fusion effect of average method |
渐入渐出算法的原理是将相邻视角图像的颜色值进行加权,然后得到重叠区每一个像素点的颜色值. 其中,像素点到图像重叠区域两边缘的距离是融合权重. 渐入渐出算法融合原理的数学表示如图5所示.

|
图 5 渐入渐出融合数学模型 Figure 5 The mathematical model of fade-in and fade-out |
图5中的T表示的是融合过渡区,W表示的是权重,Wl表示原图像a的权重系数,Wr表示原图像b的权重系数. 在进入过渡区之前,原图像a的权重系数为1到0线性递减,原图像b的权重系数由0到1线性递增. 因此融合后图像的颜色值表示为
| $\begin{split}&I{(x,y)_{}} = {W_l}{I_l}(x,y) + {W_r}{I_r}(x,y) = \\&d{I_l}(x,y) + (1 - d){I_r}(x,y).\end{split}$ | (2) |
式(2)中,Il(x, y)、Ir(x, y)表示图像a、b在重叠区域任意一点Xi的像素值. d表示当前坐标点Xi到右边界X2的距离与图形相交区域的宽度的比值. 并且
| ${W_l} = d = \frac{{{X_2} - {X_i}}}{{{X_2} - {X_1}}},\;\;\;{W_r} = 1 - d = \frac{{{X_i} - {X_1}}}{{{X_2} - {X_1}}}.$ |
过渡区的权重系数在每一点满足:Wl+Wr=1. 其中,X1<Xi<X2. 该算法对图像进行融合后的效果如图6所示,其中红色圈出来的部分表示缝隙出现的位置. 融合后的图像其左下脚和右上角图片有部分显示为黑色,这是因为计算机在处理拼接后没有像素的图片时因图片没有像素,将其显示为黑色.

|
图 6 渐入渐出法图像融合效果图 Figure 6 Effect of image fusion of the gradually fading algorithm |
由实验结果可知,渐入渐出算法在图像融合后只在水平方向上产生了拼接缝隙. 这是因为渐入渐出算法在设计权重时只考虑了单方向的像素值平滑过渡,而没有考虑整个区域的像素的平滑过渡. 该算法相比平均值法来说解决了重叠区域像素平滑过渡的问题,但是其融合效果并没有达到最优. 自然地,寻找整个重叠区域的平滑过渡成了本文要解决的重要问题.
2.2 改进的权重处理渐入渐出算法实现了权重系数的线性化过渡,因此在整个视觉上解决了左右方向出现的拼接缝隙. 然而在上下两个方向的拼接缝隙缺依旧还在. 基于渐入渐出法在重叠的垂直方向设计权值函数的思想,本文提出一种在整个图像的重叠区域设计一个连续权重函数的方法,该方法可以将水平方向和垂直方向的拼接缝隙都消除. 假设实验处理后图像的像素值为h(x, y),那么h(x, y)可以表示为
| $h(x,y) = a(x,y){f_1}(x,y) + b(x,y){f_2}(x,y),$ | (3) |
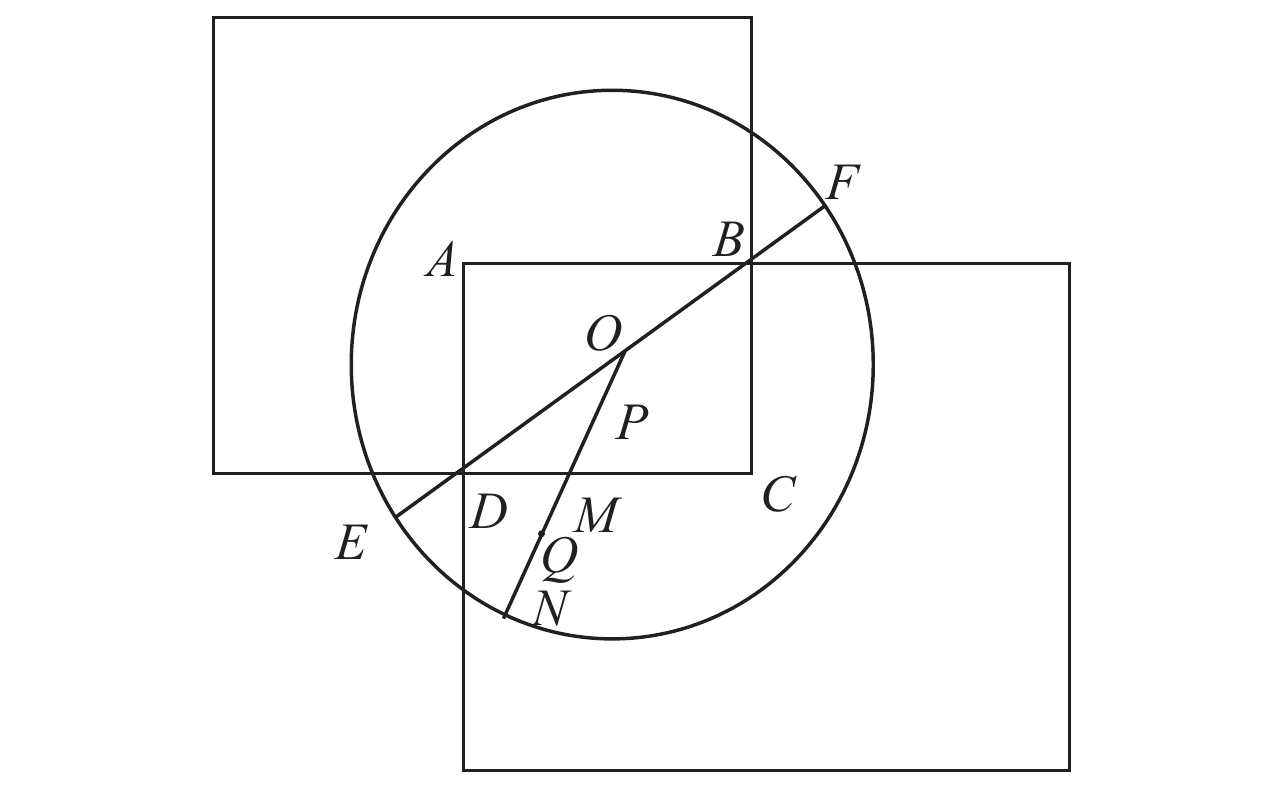
其中a(x, y)+b(x, y)=1,并且f1(x, y)、f2(x, y)分别为原图像a、b的像素值. 图7为原图像的数学模型.
|
图 7 图像融合的数学模型 Figure 7 Mathematical model of image fusion |
从图7中可以看出缝隙可能出现在左右(AD和BC)两边或上下(AB和CD)两边,本实验重叠区域的权重函数用a(x, y)表示. 如果采用前文所述的渐入渐出法消除左右两边的缝隙后,再用渐入渐出法消除上下的缝隙,则会导致a(x, y)在左右两边再次变得不连续,从而左右两边的缝隙又会再次出现.
实验表明,缝隙出现的位置即为函数a(x, y)不连续的位置,也就是说如果a(x, y)不连续点构成了一条曲线,那么该曲线将会是一条缝隙. 因此,消除缝隙的一种很自然的方法是构造全图像上的连续函数a(x, y),从函数f12(x, y)中可以看到要a(x, y)在全图像上连续那么在边界AD和AB的取值必须为1,在BC和CD上的取值必须为0,这将使权重函数a(x, y)在B和D两点必然是不连续的,但只要不连续点不构成一条曲线那么从视觉上来看就看不出缝隙. 因此,构造一个在全图像上(除去B和D点)的连续函数就可以消除掉所有缝隙了.
实验中,假定相交的区域为一个矩形,则其权重函数a(x, y)的构造思路如下:
(1) 构造ABCD围成的矩形区域到闭圆盘上的连续映射,f:ABCD→△,△表示的是一个闭圆盘. 连接BD,取BD的中点O,以O为圆心作半径为r的圆. 其中f的定义方法为:对于ABCD内部一个非O的一点P,连接OP交ABCD的边界于M,交圆的边界于N,在ON上取一点Q使得OP/OM=OQ/ON.因此,按照上述规则定义f(P)=Q为矩形区域到圆形的映射,容易验证这样定义的f是连续的,设P点的坐标为(x, y),Q点的坐标为(u, v),已知f(P)=Q函数连续,所以可以构造了2个连续函数u=u(x, y)和v=v(x, y).
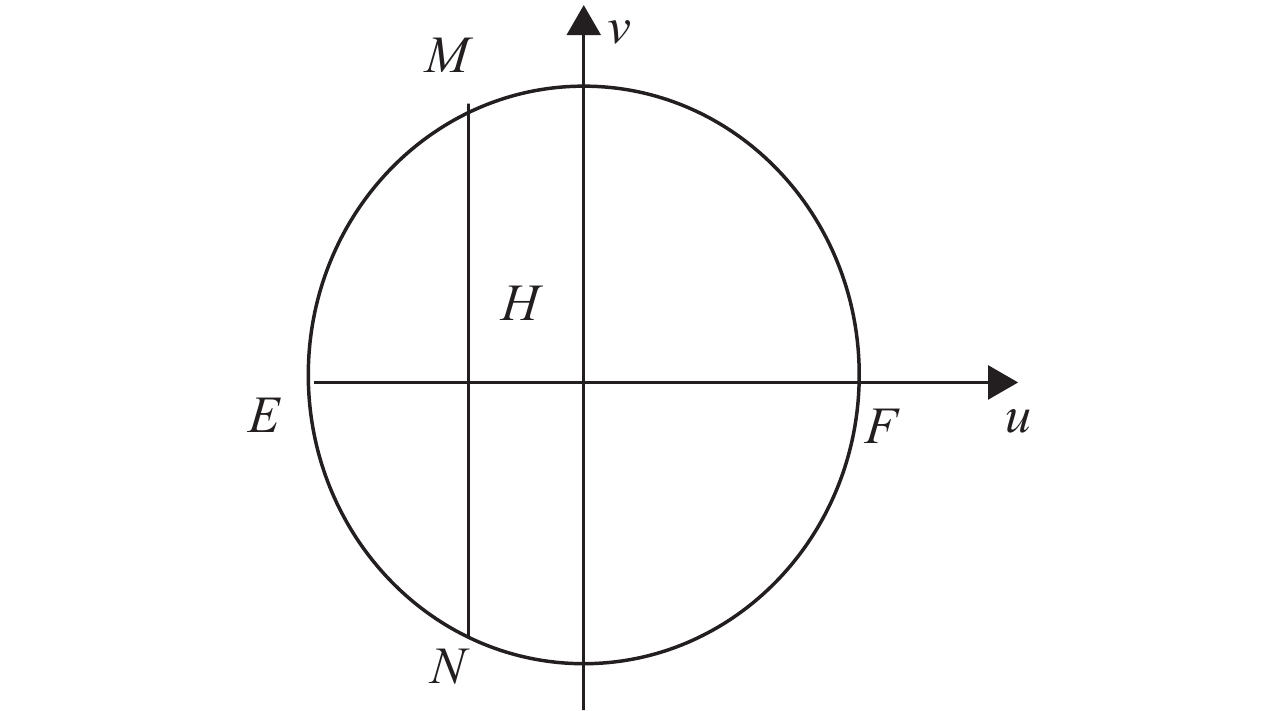
(2) 构造圆上的连续函数. 见图8 ,B和D通过f对应到了E和F. 本文构造的连续函数的定义域是不包括E和F两点,对圆内任意一点H(u, v),作u轴的垂线交上半圆和下半圆分别为M和N,定义函数,容易得到z(u, v)是关于u和v的连续函数,且z(u, v)=HN/MN函数z在上半圆的取值为1,在下半圆的取值为0,易得函数的解析表达式为
| $z(u,v) = \frac{1}{2} (1 + \frac{v}{{\sqrt {0.25 - {u^2}} }}).$ | (4) |
式(4)中,取圆的半径为1/2. 因此,这里得到了重叠区域ABCD(除两点)边界及内部的连续函数
| $z(x,y) = \frac{1}{2} (1 + \frac{{v(x,y)}}{{\sqrt {0.25 - {u^2}(x,y)} }}).$ |
|
图 8 映射图形 Figure 8 Map of the graph |
该算法对图像进行融合后的效果如图9所示. 由图9中可知本文设计的算法解决了平均值法和渐入渐出算法中出现的图像拼接缝隙,在视觉上达到了良好的视觉效果,在整个图像重叠区域实现了像素的平滑均匀过渡.
3 实验结果与分析本实验的软件环境为VS2010配置opencv2.4.9,并且在64位的PC机上进行了仿真测试,测试采用的图像是640×480的24位RGB图像. 图像经过几何校正和预处理后,在特征点提取阶段,首先检测两幅图像的所有特征点,然后对第1幅图像的特征点建立一个KD树,找到第2幅图中各个特征点到最近邻和次近邻的距离,进而通过距离比值的方法筛选匹配点. 最后计算两幅图像的变换矩阵得到两幅图像的共同区域. 之后,采用本文描述的改进方法对重合区域设计权重,进行重叠区域的融合. 融合之后的效果如图9(c)所示.
图像质量的好坏在很大程度上取决于人眼获取图像信息后大脑的主观反应,这属于偏主观的一个概念. 因此,为验证文中提出的改进的权重设计方法在图像融合效果中的好坏,需要对文中提出的融合方法进行评价,本文采用基于相似度的图像融合质量评估方法(Structural Similarity, SSIM)[13-15]以及采用边缘差分谱评价算法(difference of edge map, DoEM)[16]对图9进行评价. 融合实验结果见表1.

|
图 9 改进算法的融合效果 Figure 9 Effect of image fusion of improved algorithm |
| 表 1 图像融合评价结果 Table 1 Evaluation results of image fusion |
本文的基于相似度的图像融合质量评估方法SSIM方法是通过熵加权因子对融合图像和源图像的相似度(分别从亮度、对比度、结构三方面度量)进行计算来评价图像. SSIM取值范围[0, 1],值越大,表示图像融合效果越好;边缘差分谱评价法DoEM方法是通过对待评价图像进行边缘提取,然后利用拼接前后图像的边缘轮廓信息,综合图像像素误差信息和结构信息,对图像进行评价. DoEM取值范围[0, 1],值越大,表示图像融合效果越好.
4 结论将本文提出的改进权重函数算法和经典的平均值法、渐入渐出算法相比较,本文提出的改进权重函数算法解决了平均值法和渐入渐出算法中出现的图像拼接缝隙,在视觉上达到了良好的视觉效果,在整个图像重叠区域实现了像素的平滑均匀过渡. 该算法在实际应用中具有普适性,平滑清晰的全景图像有着显著的现实价值. 因此,文中提出的权重设计方案是可行的.
| [1] | ZHANG X R. Research on car reversing warning system based on CAN bus[J]. Applied Mechanics & Materials, 2014, 686(8): 119-121. |
| [2] | CAO H. Mosaic method for CCD images[J]. Tool Engineering, 2010, 18(1): 32-47. |
| [3] |
吴黎明, 蔡文. 图像拼接技术在大尺寸物体测量中的应用[J].
自动化与信息工程, 2014, 35(6): 36-39.
WU L M, CAI W. Application of image stitching technology in the measurement of large-size objects[J]. School of Information Engineering, 2014, 35(6): 36-39. |
| [4] | JIANG G Y. Overview on image quality assessment methods[J]. Journal of Electronics & Information Technology, 2010, 32(1): 219-226. |
| [5] |
周武杰, 郁梅, 李福翠, 等. 基于小波图像融合的非对称失真立体图像质量评价方法[J].
光电工程, 2011, 38(11): 100-105.
ZHOU W J, YU M, LI F C, et al. Quality assessment method for asymmetric distortion of stereoscopic image based on wavelet image fusion[J]. Opto Electronic Engineering, 2011, 38(11): 100-105. |
| [6] |
梁健, 刘召芹, 邸凯昌. 一种行星探测应用的可量测虚拟现实环境构建方法[J].
航天器工程, 2012, 21(3): 28-34.
LIANG J, LIU Z Q, DI K C. Construction of a 3D measurable virtual reality environment for planetary exploration applications[J]. Spacecraft Engineering, 2012, 21(3): 28-34. |
| [7] |
郭虎. 关于扫描地形图图像拼接方法的探讨[J].
大地纵横, 2001(4): 25-27.
GUO H. Discussions about the ways of scanning topographic map image combining[J]. Surveying and Mapping In Shanxi, 2001(4): 25-27. |
| [8] |
孙韬, 葛亮, 王伟, 等. 基于MIP图像拼接系统的大型古生物化石数字化应用研究[J].
古生物学报, 2016(2): 244-253.
SUN T, GE L, WANG W, et al. Large fossil digitalization based on the mosaic of image program(MIP)[J]. Acta Palaeontologica Sinica, 2016(2): 244-253. |
| [9] | SHUM H Y, NG K T, CHAN S C. A virtual reality system using the concentric mosaic: construction, rendering, and data compression[J]. IEEE Transactions on Multimedia, 2005, 7(1): 85-95. DOI: 10.1109/TMM.2004.840591. |
| [10] | WANG Z, CHEN Y, ZHU Z, et al. An automatic panoramic image mosaic method based on graph model[J]. Multimedia Tools and Applications, 2016, 75(5): 2725-2740. DOI: 10.1007/s11042-015-2619-0. |
| [11] | CHEUNG W, HAMARNEH G. $n$-SIFT: $n$-dimensional scale invariant feature transform[J]. IEEE Transactions on Image Processing, 2009, 18(9): 2012-2021. DOI: 10.1109/TIP.2009.2024578. |
| [12] | LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. DOI: 10.1023/B:VISI.0000029664.99615.94. |
| [13] | YANG C, ZHANG J Q, WANG X R, et al. A novel similarity based quality metric for image fusion[J]. Information Fusion, 2008, 9(2): 156-160. DOI: 10.1016/j.inffus.2006.09.001. |
| [14] | WANG Z, BOVIK A C, SHEIKH H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. DOI: 10.1109/TIP.2003.819861. |
| [15] |
李红蕾, 凌捷, 徐少强. 关于图象质量评价指标PSNR的注记[J].
广东工业大学学报, 2004, 21(3): 74-78.
LI H L, LING J, XU S Q. The exegesis of the quality assessment PSNR of images[J]. Journal of Guangdong University of Technology, 2004, 21(3): 74-78. |
| [16] |
万国挺, 王俊平, 李锦, 等. 图像拼接质量评价方法[J].
通信学报, 2013, 34(8): 76-81.
WAN G T, WANG J P, LI J, et al. Method for quality assessment of image mosaic[J]. Journal on Communications, 2013, 34(8): 76-81. |
 2017, Vol. 34
2017, Vol. 34

