近年来,图像特征点匹配受到了人们广泛关注,图像特征点匹配技术是计算机视觉领域的一个重要课题,在许多领域内有着广泛而实际的应用. 如图像拼接、目标追踪、三维重建、模式识别、自动导航、医学诊断、遥感影像处理等[1]. 因此,对图像匹配做进一步深入的研究有着非常重要的意义. 但是由于拍摄环境、拍摄角度、传感器的缺陷,使得图像不仅受噪声的影响,而且可能存在图像变形等影响. 传统的基于灰度的图像匹配方法无法适应这些变化和实时性要求较高的场合. 因此,基于局部特征的图像匹配方法被广泛应用于图像匹配的领域. 其中,图像特征点匹配方法主要分为3个步骤:特征点检测、特征点描述子和特征点匹配[2].
经过国内外学者的努力,已经有大量的局部特征匹配算法被广泛应用. 其中,传统的角点检测算法有Moravec算子[3]、Harris算子[4]、SUSAN算子[5]、FAST算子[6]. 另外,Lowe等[7]于2004年提出SIFT算法在尺度、旋转、视角和光照等条件下具有较强的稳定性,但是计算量大,运算时间长. 为此,Bay等[8]于2006年提出SURF算法,利用积分图像和盒状滤波来近似高斯滤波缩短了计算时间,但是需要大量时间去构建局部特征描述符,难以满足实时性要求.
近年来,不断有新的局部特征描述子被提出来,Calonder等[9]于2010年提出BRIEF描述符,BRIEF算法不使用传统的梯度直方图来描述特征点,改用检测随机响应的方式,大大提高了描述子的生成和匹配速度,但是对噪声敏感,不具备旋转不变性和尺度不变性. Rublee等[10]于2011年提出ORB描述符,该算法运算速度快,缺点是在图像发生尺度变化时,特征点匹配的准确度会降低. Leutenegger等[11]于2011年提出BRISK描述符,该算法具有尺度不变性和旋转不变性,而且运算速度快,在对有较大模糊的图像配准时,BRISK算法表现最为出色. Alahi等[12]于2012 年提出FREAK描述符,通过利用模拟人类视网膜的特性来进行采样点的选择,但是不具备尺度不变性,在图像尺度发生变化的情况下,特征点的匹配准确度会降低. 根据以上分析,本文提出了一种改进的FREAK算法来解决FREAK算法的缺陷,并且对图像存在尺度变化的情况也具有较强的鲁棒性.
1 FREAK特征点匹配算法 1.1 FAST特征点检测FREAK算法是利用FAST算法来检测图像的特征点,如图1所示,这里考虑以像素点p为圆心,半径为3的离散化的圆,这个圆的边界上有16个像素.

|
图 1 FAST特征点检测 Figure 1 FAST feature points detection |
FSAT的基本原理是:如果在这个大小为16个像素的圆上有N(一般N取9或12)个连续的像素点,它们的像素值要么都比I(p)+εd大,要么都比I(p)-εd小,那么p就是一个特征点. 如下式所示:
| $N = \sum\limits_{x\forall ({\rm{circle}}(p))} {\left| {I(x) - I(p)} \right| > {\varepsilon _d}}. $ | (1) |
其中,I(x)表示圆环模板上任意一点的像素灰度值,I(p)为中心像素点的灰度值,εd为设定的阈值.
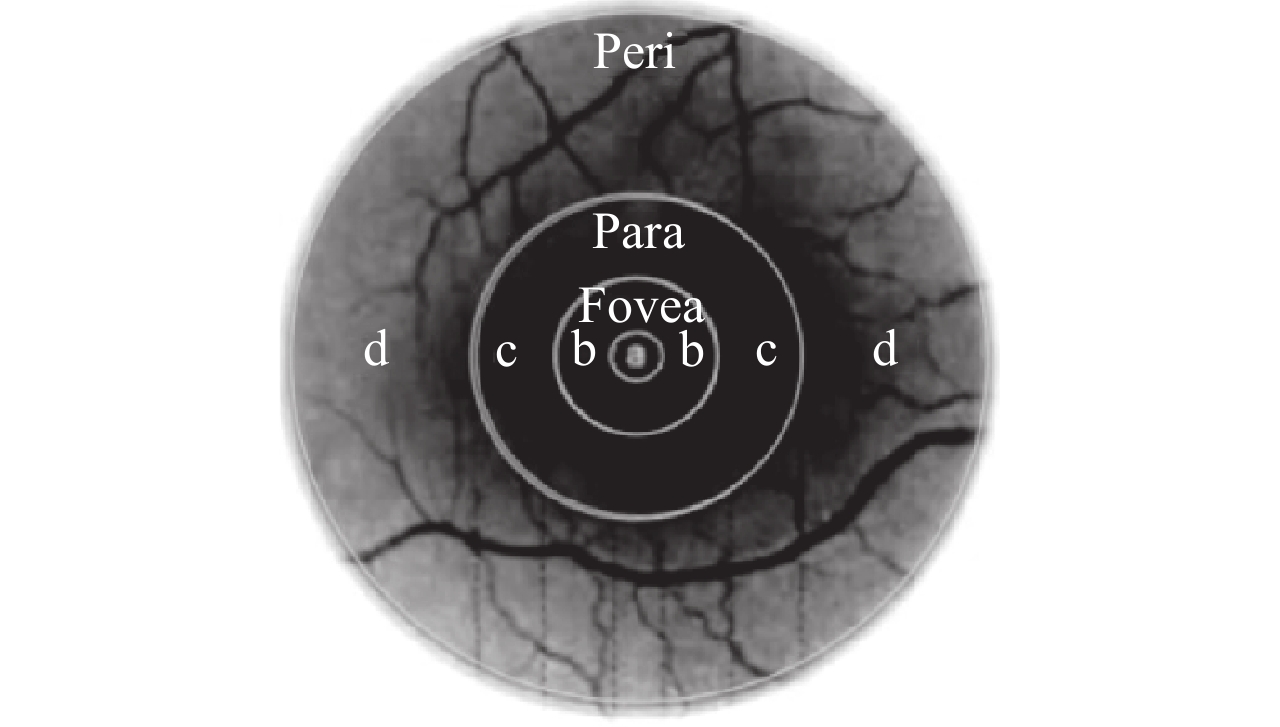
1.2 FREAK特征点描述 1.2.1 人眼视网膜研究表明,在人眼的视网膜区域中,感受光线的细胞的密度是不相同的. 如图2所示,人眼的视网膜根据感光细胞的密度分成了4个区域:foveola、fovea、parafoveal、perifoveal. 与foveola的距离越大,感受域中的神经节细胞的密度和枝状结构的密度越小. 其中,foveola区域是接受高分辨率的图像,低分辨率的图像是在周边区域获得. FREAK描述符正是模拟人类视网膜的结构而提出的算法,如图3所示.
|
图 2 人眼视网膜结构 Figure 2 The structure of the human retina |
|
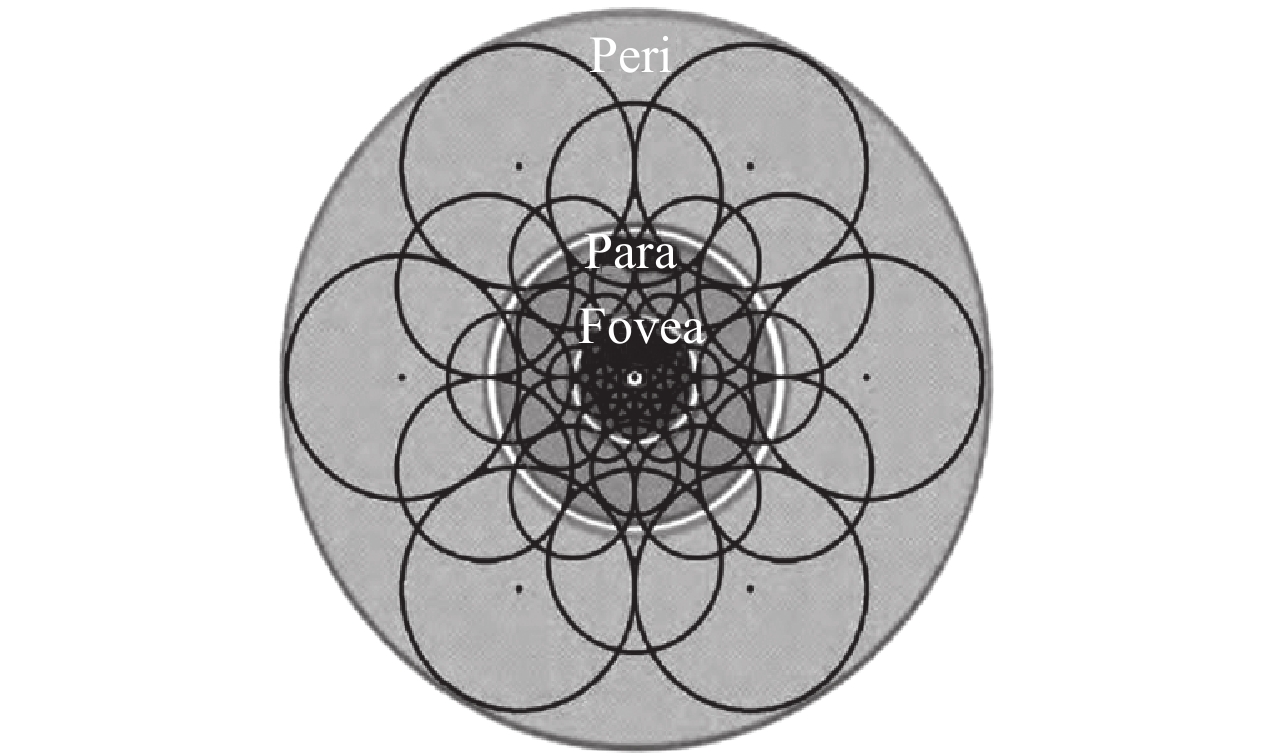
图 3 FREAK采样模式 Figure 3 FREAK sampling mode |
FREAK算法采取了更接近人眼视觉系统接收图像信息的采样模型. 如图3所示,该采样模式以特征点为中心,由7层同心圆环构成,每层圆环均匀取6个采样点. 圆与圆之间有重叠的部分,是为了获取足够多的图像信息. 并且采样点离特征点的距离越近,采样点圆的半径越小,即采样点越密集,离特征点的距离越远,采样点圆的半径越大,即采样点越稀疏. 为了降低噪声的影响,需要对每个采样点进行高斯平滑处理,每个圆圈的半径表示了高斯模糊的标准差.
1.2.3 FREAK描述子FREAK描述子由采样点对的强度比较结果级联组成,形成二进制位串描述子. 这里用F表示,则有
| $F = \sum\limits_{0 \leqslant a < N} {{2^a}} T({P_a}).$ | (2) |
| $T({P_a}) = \left\{ \begin{array}{l}1,\begin{array}{*{20}{c}}{}&{(I({P_a}^{r1}) - I(P_a^{r2}) > 0);}\end{array}\\[3pt]0,\begin{array}{*{20}{c}}{}&{{\rm{otherwise}}{\rm{.}}}\end{array}\end{array} \right.$ | (3) |
其中,Pα是一个采样点对,
假设一个特征点取M个采样点,那么就有
(1) 首先,构建一个矩阵D, D的每一行表示一个特征点二进制描述子,每一行有
(2) 对D的每一列计算均值,由于D中的元素都是0/1分布,均值越接近0.5,说明该列具有更大的方差,方差越大表示该列携带的信息量越多;
(3) 将各列的方差按从大到小的顺序排列;
(4) 选取该矩阵的前k列作为最终的二进制描述子,这里k取512.
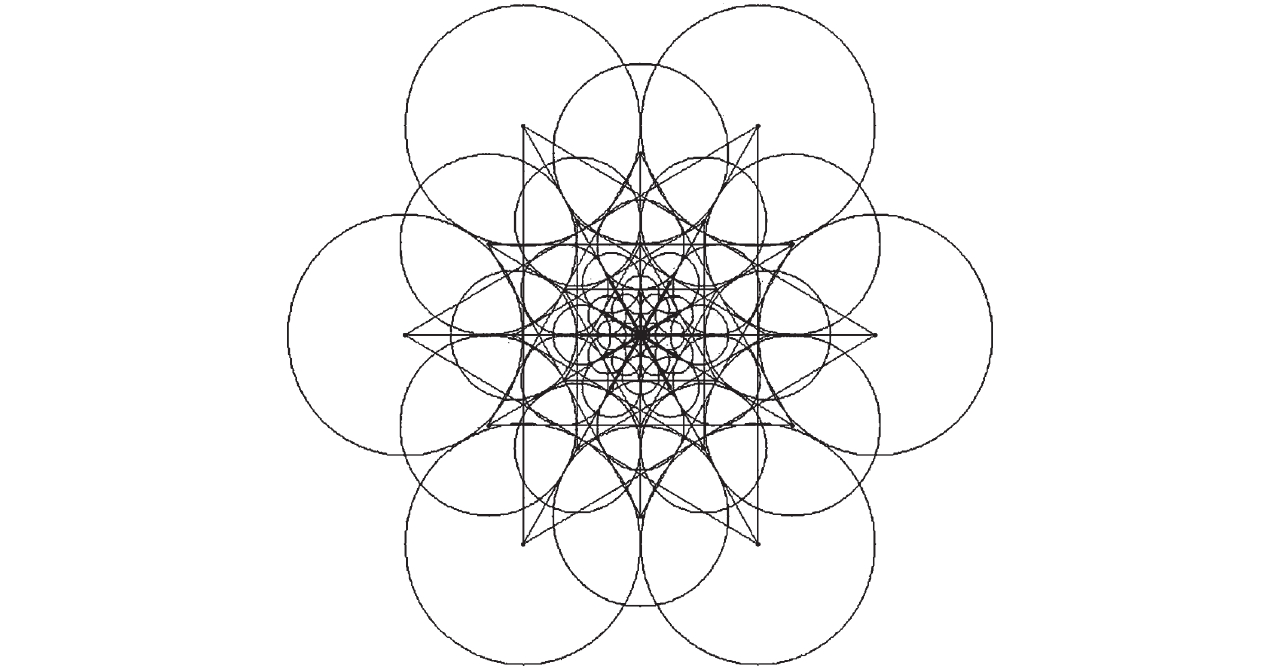
为保证FREAK算法具有旋转不变性,需要为每一个特征点增加方向的信息. FREAK算法采用45个距离长的、对称的采样点计算其梯度,如图4所示.
|
图 4 中心对称采样点对 Figure 4 Center symmetric sampling point |
其特征点方向计算公式为
| $O = \frac{1}{M}\sum\limits_{{P_o} \in G} {(I(P_o^{r1}) - I(P_o^{r2}))} \frac{{P_o^{r1} - P_o^{r2}}}{{\left\| {P_o^{r1} - P_o^{r2}} \right\|}}.$ | (4) |
其中,G表示特征点对比点对的集合,M表示G中点对的数量,
由于FREAK算法得到的是0和1组成的512位二进制描述子,所以通过异或运算计算两个二进制描述子的汉明距离. 汉明距离[13]的定义为
| ${D_{hm}}({H_1},{H_2}) = \sum\limits_{i = 1}^{512} {({x_i} \oplus {y_i})} .$ | (5) |
其中,H1,H2是两特征点描述子,且
由于FREAK算法中采用FAST算子进行特征点检测,虽然具有计算简单、速度较快的优势,当图像尺度发生变化时,特征点不具备尺度不变性,在后续的特征点匹配中会出现了大量的误匹配. 另外,在特征匹配阶段只是利用汉明距离进行匹配,不可避免存在少量错误的匹配点,算法没有对错误匹配点进一步剔除. 以上两个原因导致匹配效果不理想,造成算法的匹配准确度不高. 因此,要解决FREAK不具备尺度不变性的缺陷,就是要求特征点检测阶段检测出来的特征点需要具有尺度不变性,从而生成的特征描述符含有尺度不变性. 鉴于此,本文提出两点改进:(1) 在特征点检测阶段,利用SIFT算法的多尺度空间理论来检测出具有尺度不变性的特征点;(2) 在特征点匹配阶段采用由粗到细的匹配策略,在粗匹配的基础上结合RANSAC算法剔除误匹配点,提高了匹配的准确度.
2.1 SIFT特征点检测算法 2.1.1 构建尺度空间一幅二维图像的尺度空间定义为
| $L(x,y,\sigma ) = G(x,y,\sigma ) \cdot I(x,y).$ | (6) |
| $G(x,y,\sigma ) = \frac{1}{{2{{π}} {\sigma ^2}}}{\rm{e}} - ({x^2} + {y^2})/2{\sigma ^2}.$ | (7) |
其中,
利用不同尺度因子的高斯差分函数与图像卷积生成高斯差分尺度空间,在尺度空间检测稳定的极值点.
| $\begin{aligned}D(x,y,\sigma ) = & \left[ {G(x,y,k\sigma ) - G(x,y,\sigma )} \right] \cdot I(x,y) = \\& L(x,y,k\sigma ) - L(x,y,\sigma ).\end{aligned}$ | (8) |
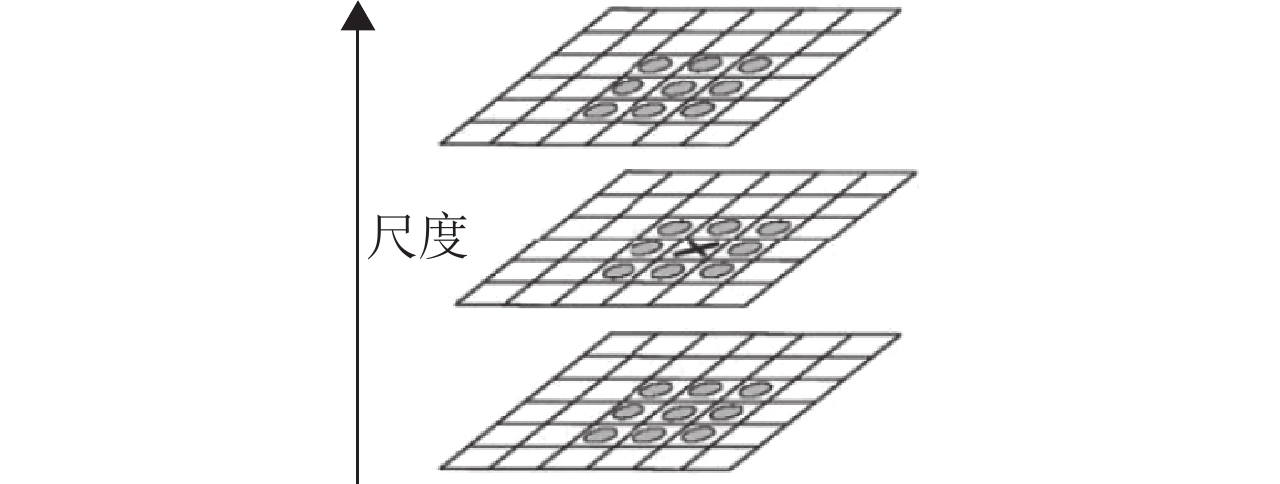
特征点是由DoG空间的局部极值点组成的,特征点的初步探查是通过同一组内各DoG相邻两层图像之间比较完成的. 如图5所示,一个点如果在DoG尺度空间同一尺度的8个点以及上下相邻尺度的18个点(2×9=18),共26个点中是最大或最小值时,那么该点是图像在该尺度下的一个特征点[14].
|
图 5 DoG空间极值点检测 Figure 5 DoG space extreme point detection |
为了提高所检测出的特征点的精度,以下利用拟合三维二次函数来精确定位特征点的位置和尺度. 首先,在某极值点处对
| $D(X) = D + \frac{{\partial {D^{\rm{T}}}}}{{\partial X}}X + \frac{1}{2}{X^{\rm{T}}}\frac{{{\partial ^2}D}}{{\partial {X^2}}}X.$ | (9) |
对X求偏导,并令导函数为零,可以得到极值点偏移量
| $\hat X = - \frac{{{\partial ^2}{D^{ - 1}}}}{{\partial {X^2}}}\frac{{\partial D}}{{\partial X}}.$ | (10) |
对应的方程值为
| $D(\hat X) = D + \frac{1}{2}\frac{{\partial {D^{\rm{T}}}}}{{\partial X}}\hat X.$ | (11) |
若
另外,由于图像的边缘容易受噪声的影响,为了提高匹配的稳定性,可以利用主曲率与特征值的关系来去除这些不稳定的边缘响应点. 其中,主曲率通过一个2×2的Hessian矩阵求出.
| $\mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}}{{D_{xx}}}&{{D_{xy}}}\\{{D_{xy}}}&{{D_{yy}}}\end{array}} \right].$ | (12) |
假设α是较大的特征值,β是较小的特征值,可得
| ${{\rm{Tr}}}(\mathit{\boldsymbol{{{H}}}}) = {{{D}}_{xx}} + {{{D}}_{yy}} = \alpha + \beta .$ | (13) |
| ${{\rm{Det}}}(\mathit{\boldsymbol{{{H}}}}) = {{{D}}_{xx}}{{{D}}_{yy}} - {({D_{xy}})^2} = \alpha \beta .$ | (14) |
令
| $\frac{{\rm{Tr}{{(\mathit{\boldsymbol{{{H}}}})}^2}}}{{{\rm{Det}}(\mathit{\boldsymbol{H}})}} = \frac{{{{(\alpha + \beta )}^2}}}{{\alpha \beta }} = \frac{{{{(r\beta + \beta )}^2}}}{{r{\beta ^2}}} = \frac{{{{(r + 1)}^2}}}{r}.$ | (15) |
r的值越大,式(15)的比值也越大. 因此,为了检测主曲率是否在某一阈值r下,只需要判断下式:
| $\frac{{{\rm{Tr}}{{(\mathit{\boldsymbol{H}})}^2}}}{{{\rm{Det}}(\mathit{\boldsymbol{H}})}} < \frac{{{{(r + 1)}^2}}}{r}.$ | (16) |
若成立,则保留该极值点,反之剔除,从而去除边缘响应点,这里r取10.
2.2 RANSAC剔除误匹配点图像经过汉明距离匹配后,不可避免存在少量错误的匹配点,本文选用RANSAC[15]算法来剔除错误的匹配点对. RANSAC算法作为一种模型假设检验方法,它利用较少的初始数据集来构建模型,进而对全部数据进行正确的筛选. 重要的是,RANSAC算法计算过程稳定、容错能力强且对噪声和误匹配特征点有较强的鲁棒性,能很好地剔除误匹配点对,从而获得稳定的最佳匹配点对集.
RANSAC算法目的是找到最优的单应性矩阵H,采用迭代法来估计该矩阵的8个参数,使得满足该矩阵的内点个数最多. 由于参考图像与待匹配图像存在平移、旋转、尺度等变换,可用单应性矩阵H来描述2幅图像点坐标之间的变换关系,即B'=HB. 变换如式(17)所示:
| $\left[ \begin{array}{l}x'\\[3pt]y'\\[3pt]1\end{array} \right] = \left[ {\begin{array}{*{20}{c}}{{h_{11}}}&{{h_{12}}}&{{h_{13}}}\\[3pt]{{h_{21}}}&{{h_{22}}}&{{h_{23}}}\\[3pt]{{h_{31}}}&{{h_{32}}}&1\end{array}} \right]\left[ {\begin{array}{*{20}{c}}x\\[3pt]y\\[3pt]1\end{array}} \right].$ | (17) |
其中,(x′, y′)是参考图像的点,(x, y)是待匹配图像中与(x′, y′)相对应的点.
RANSAC算法基本步骤[16]如下:
(1) 首先将汉明距离匹配后得到的S个待匹配点对的集合,记作集合P.
(2) 然后从S个待匹配点对的集合中随机抽出4个匹配点对,求出矩阵H中的8个参数值.
(3) 利用估计的参数对待匹配点对的集合剩下的S-4个匹配点对进行判断,若点(x, y)经过变换矩阵H后的点与(x′, y′)的欧氏距离小于设定的阈值,则该待匹配视为内点,反之为外点.
(4) 重复步骤(2)和(3)k次后转入(5),并统计每次内点的数量.
(5) 选择内点数最多的变换矩阵参数作为最终的变换参数,与此对应内点集合为最终的匹配点集.
其中,迭代次数k在不大于最大迭代次数的情况下,是在不断更新而不是固定的.
| $k = \frac{{\log (1 - p)}}{{\log (1 - {\omega ^m})}}.$ | (18) |
其中,p表示置信度,一般取0.995;ω表示内点的比例;m表示计算模型所需要的最少样本数,m一般取4.
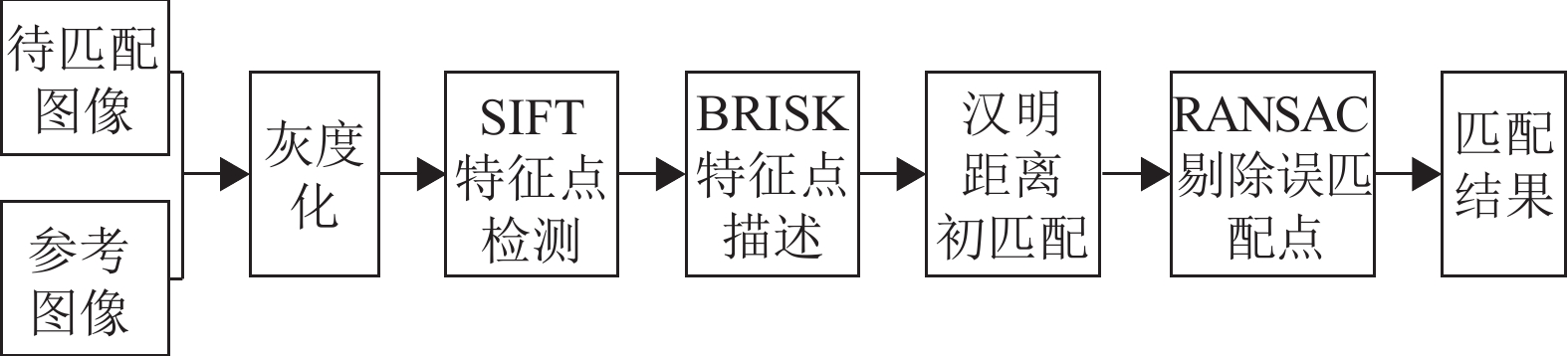
本文SFREAK算法流程图如图6所示:
|
图 6 SFREAK算法流程图 Figure 6 Flow chart of SFREAK algorithm |
首先,借鉴SIFT算法中的多尺度空间理论,生成多尺度空间图像,并在多尺度空间里检测出具有尺度不变性的特征点;然后,利用FREAK描述符对特征点进行描述,得到具有旋转不变性的二进制位串描述子;最后,在汉明距离进行初始匹配的基础上结合RANSAC剔除错误匹配点,完成图像间的特征点匹配. 这样,本文改进的算法既解决了FREAK算法特征点检测阶段不具备尺度不变性的缺陷,同时也解决了匹配结果中存在较多错误匹配点的问题.
3 实验对比与结果分析本文进行了仿真实验对比分析,实验硬件平台:Intel(R) Core(TM) i5-4590 CPU 3.30GHz,8G内存;实验软件平台:Windows7 64位操作系统,Visual Studio 2012,OpenCV 2.4.9.
3.1 尺度不同对比实验为了验证本文提出的SFREAK算法既能解决尺度不变性的缺陷,也能解决匹配结果存在较多错误匹配点的问题,选择以尺度发生变化的4组图像为实验对象进行对比实验. 实验图像来自于文献[17],FREAK、SIFT和SFREAK3种算法的4组实验匹配结果如图7所示.

|
图 7 图像匹配结果 Figure 7 Matching results of images |
从实验结果来看,FREAK算法由于采用FAST算法进行特征点检测,虽然检测出较多的特征点,但是也因为其不具备尺度不变性导致匹配结果出现错误匹配点多,匹配效果不理想. SFREAK算法由于借鉴SIFT算法尺度空间理论,解决了FREAK不具备尺度不变性的问题. 另外,针对特征点匹配策略单一,仅采用简单的汉明距离进行匹配导致匹配效果不理想的问题,本文在特征点匹配阶段加入RANSAC算法匹配点进行提纯,匹配效果有较大的提高.
为了更加直观比较在图像发生尺度变化的情况下,FREAK、SIFT和SFREAK特征点匹配的准确度差异,统计了以上4组实验数据结果如表1所示.
| 表 1 算法匹配准确度对比 Table 1 Comparison of algorithm matching accuracy |
为减少实验的误差,取4组实验匹配准确度的平均值. 从表1可知,特征点匹配准确度从大到小分别为SFREAK、SIFT和FREAK. SFREAK的特征点匹配准确度为95.7%,比FRREAK提高约61.9%. 实验结果表明,SFREAK算法克服了FREAK算法不具备尺度不变性的缺陷,并且较优于SIFT算法,从而可说明本文所提出的改进方法的可行性.
3.2 算法运行时间对比为了分析算法的运行效率,同样对FREAK、SIFT、SFREAK算法进行比较分析,3种算法的具体用时如表2所示.
| 表 2 算法匹配时间对比 Table 2 Comparison of algorithm matching time |
算法耗时从小到大分别为FREAK、SFREAK和SIFT,本文提出的SFREAK算法耗时约为356.9 ms,经典SIFT算法是它的3.4倍,FREAK算法耗时约为164.4 ms. FREAK较快的原因有两方面:(1) 特征点提取过程中使用FAST角点检测算法,而SFREAK是基于SIFT尺度空间理论提取出具有尺度不变性的特征点;(2) 在特征点匹配阶段,FREAK仅仅是采用简单的汉明距离匹配,而SFREAK匹配过程较FREAK多了RANSAC算法的检验筛选的环节.
从实验结果不难发现,虽然FREAK算法具有运算速度快和存储内存小的优越性,但是不足之处是匹配准确度过低,匹配结果误匹配点较多,难以满足实用性的要求. 所以,本文权衡运行速度和匹配准确率之间的关系,增加RANSAC算法剔除误匹配点,具有较好的鲁棒性的同时匹配准确度也有极大的提高.
4 结束语本文针对FREAK算法特征点不具备尺度不变性以及特征匹配策略单一的缺陷,对FREAK算法进行改进. 结合SIFT算法使开始检测到的特征点具有尺度不变性,并且匹配阶段使用RANSAC算法剔除误匹配点. 该改进算法很好解决了FREAK算法不具备尺度不变性的缺陷以及图像匹配效果不理想的问题. 经过对比实验分析,本文提出的SFREAK算法较SIFT、FREAK算法在尺度发生变化的情况下优势明显,具有良好的鲁棒性. 当然,本文也存在不足的地方,如何进一步提高算法的实时性和匹配准确度,将是我们未来研究的方向.
| [1] |
付偲, 邓丽, 卢根, 等. 基于快速视网膜关键点算法改进的图像匹配方法[J].
计算机工程与应用, 2016, 52(19): 208-212.
FU C, DENG L, LU G, et al. Improved image matching based on fast retina keypoint algorithm[J]. Computer Engineering and Applications, 2016, 52(19): 208-212. DOI: 10.3778/j.issn.1002-8331.1412-0291. |
| [2] |
谢红, 王石川, 解武. 基于改进的FREAK算法的图像特征点匹配[J].
应用科技, 2016, 43(4): 35-40.
XIE H, WANG S C, XIE W. Feature points matching in images based on improved FREAK[J]. Applied Science and Technology, 2016, 43(4): 35-40. |
| [3] | MORAVEC H P. Rover visual obstacle avoidance[C]//International joint conference on artificial intelligence.[S.l.]: Morgan Kaufmann Publishers Inc. 1981: 785-790. |
| [4] | HARRIS C G, STEPHENS M J. A combined corner and edge detector[C]//Alvey Vision Conference.[S.l.]: [s.n.] 1988: 147-151. |
| [5] | SMITH S M, BRADY J M. SUSAN—A new approach to low level image processing[J]. International Journal of Computer Vision, 1997, 23(1): 45-78. DOI: 10.1023/A:1007963824710. |
| [6] | ROSTEN E, DRUMMOND T. Machine learning for high-speed corner detection[M]//Computer Vision-ECCV 2006. Berlin: Springer Heidelberg, 2006: 430-443. |
| [7] | LOWE D G. Distinctive image features from scale-invariant key points[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. DOI: 10.1023/B:VISI.0000029664.99615.94. |
| [8] | BAY H, ESS A, TUYTELAARS T, et al. Speeded-up robust features (SURF)[J]. Computer Vision and Image Understanding, 2008, 110(3): 346-359. DOI: 10.1016/j.cviu.2007.09.014. |
| [9] | CALONDER M, LEPTIT V, STRECDA C, et al. BRIEF: Binary robust independent elementary features[C]//European Conference on Computer Vision.[s.n.]: Springer-Verlag, 2010: 778-792. |
| [10] | RUBLEE E, RABAUD V, KONOLIGE K, et al. ORB: An efficient alternative to SIFT or SURF[C]//IEEE International Conference on Computer Vision.[S.l.]: IEEE, 2012: 2564-2571. |
| [11] | LEUTENEGGER S, CHLI M, SIEGWART R Y. BRISK: Binary robust invariant scalable keypoints[C]//International Conference on Computer Vision.[S.l.]:IEEE Computer Society, 2011: 2548-2555. |
| [12] | ORTIZ R. FREAK: Fast retina keypoint[C]//Computer Vision and Pattern Recognition.[S.l.]: IEEE, 2012: 510-517. |
| [13] |
杨永奎. BRISK特征点检测匹配算法的探究[J].
建设机械技术与管理, 2016(5): 77-80.
YANG Y K. Research on detection and matching algorithm of the BRISK feature point[J]. Product & Technology, 2016(5): 77-80. |
| [14] |
鹿煜炜, 胡峻. 基于SIFT和SURF的医学图像特征匹配研究[J].
中国医疗设备, 2016, 31(4): 40-44.
LU Y W, HU J. Research on medical image matching based on SIFT and SURF features[J]. China Medical Devices, 2016, 31(4): 40-44. |
| [15] |
李德隆, 刘伟. 基于改进的SIFT特征点的双目定位[J].
广东工业大学学报, 2017, 34(1): 90-94.
LI D L, LIU W. Object location for binocular stereo vision based on improved[J]. Journal of Guangdong University of Technology, 2017, 34(1): 90-94. |
| [16] |
王灿进, 孙涛, 陈娟. 基于FREAK特征的快速景象匹配[J].
电子测量与仪器学报, 2015(2): 204-212.
WANG C J, SUN T, CHEN J. Rapid scene matching based on FREAK descriptor[J]. Journal of Electronic Measurement and Instrumentation, 2015(2): 204-212. |
| [17] |
陈天华, 王福龙, 张彬彬. 基于改进ORB和对称匹配的图像特征点匹配[J].
计算机系统应用, 2016, 25(5): 147-152.
CHEN T H, WANG F L, ZHANG B B. Image keypoints matching based on improved ORB and symmetrical match[J]. Computer Systems Applications, 2016, 25(5): 147-152. |
 2017, Vol. 34
2017, Vol. 34
