随着机器人技术研究的不断发展,飞行机器人在许多领域获得应用. 而其自主定位能力是实现高精度导航的关键. 目前大多数飞行机器人都配备了GPS和惯性导航系统,但是GPS本身存在精度不高、数据跳变等缺陷,尤其是在室内环境下,常常无法获得GPS信号. 天气条件、云层的厚度也会影响GPS信号的接收. 而惯性导航系统则是通过加速度计和陀螺仪实现自我定位,其定位精度较差,且会产生累积误差. 随着计算机视觉技术的不断提高,基于视觉里程计的定位问题已经成为机器人领域的研究热点. 自从Nister[1]提出以来,基于视觉里程计的视觉slam算法引起学者的普遍关注,计算机视觉在机器人定位方面得到越来越多的应用[2-3],尤其是基于室内环境的视觉定位,即在未知环境中基于视觉里程计进行机器人的自我定位[4]. 视觉里程计的定位方法主要是通过获得的视觉信息,将连续的前后两帧的数据进行匹配获得机器人的相对位姿,具有体积小,功耗低等优点.
考虑到基于视觉里程计的方法不会产生累积误差,但存在由机器人速度较快或转动较快等原因引起视觉里程计方法相邻两帧难以匹配的问题,为了解决在室内环境下进行飞行机器人的自主定位方法的鲁棒性,有学者提出将视觉信息和IMU数据相结合的方法(VIO)[5-7]. 由于单目的局限性,一个新检测到的特征点的深度信息具有高度的不确定性[8]. 为了提高新检测的特征点深度信息估计的精确度,Civera等[9]提出了反向深度方法,开创了新的深度估计方法,较传统的方法有明显的优势. 由于特征点信息量较大,Audras[10]将基于图像像素的直接法与RGB-D相机相结合,提高了视觉slam的计算速度;Kim提出了半稠密法[11],Kerl和Engel分别将稀疏法的运动估计应用于RGB-D[12]和单目相机[13].
本文提出一种基于BA(Bundle Adjustment)的改进视觉/惯性融合定位算法,融合单目视觉[14]和惯性单元信息,通过获得的视觉信息修正惯性单元因漂移而产生的误差,结合反向深度法和直接法,提高了特征点的深度估计精度和算法的计算速度,然后对局部用光束平差法进一步优化位姿估计的误差,从而提高了无人机飞行过程中的定位精度.
1 视觉/惯性融合模型 1.1 状态参数根据Michael Bloesch的直接法[7],将IMU和相机模型的状态向量描述为
| $\mathit{\boldsymbol{x}} = (\mathit{\boldsymbol{r}},\mathit{\boldsymbol{v}},\mathit{\boldsymbol{q}},{\mathit{\boldsymbol{b}}_f},{\mathit{\boldsymbol{b}}_w},\mathit{\boldsymbol{c}},\mathit{\boldsymbol{z}},{\mathit{\boldsymbol{\mu }}_0},\cdots,{\mathit{\boldsymbol{\mu }}_N},{\rho _0},\cdots,{\rho _N}).$ | (1) |
其中x表示状态向量,向量中各元素代表的含义为:r为IMU的中心位置,v为IMU的速度,q为IMU坐标系相对于世界坐标系的姿态,bf为加速度计的噪声,bw为陀螺仪的噪声,c为IMU对相机的外参中的平移向量,z为IMU对相机的外参中的旋转向量,μi表示特征点i的方向向量,ρi表示特征点i的距离参数,其中ρi为反向深度,假设特征点i的距离用di表示,则有:di=1/ρi. 由于切面空间比较容易计算,所以将三维空间中的向量都投影到二维切面子空间中计算,最后得到三维空间中的单位向量. 用方向向量和距离参数表示,可以在滤波过程中较实时初始化检测到的特征点. 关于距离的初始值可以用一个固定值,如果收敛也可以用当前估计场景的平均值作为特征点的距离初始值,相对应的协方差则设置为无穷大.
1.2 过程模型假设加速度为
| $\mathit{\boldsymbol{\tilde r}} = - {{\rm{ }}\mathit{\boldsymbol{\hat w}}}\times \mathit{\boldsymbol{r}} + \mathit{\boldsymbol{v}} + {\mathit{\boldsymbol{w}}_r},$ | (2) |
| $\mathit{\boldsymbol{\tilde v}} = - \mathit{\boldsymbol{\hat w}}\times \mathit{\boldsymbol{v}} + \mathit{\boldsymbol{\hat f}}+ {\mathit{\boldsymbol{q}}^{ - 1}}\left( g \right),$ | (3) |
| $\mathit{\boldsymbol{\tilde q}} = - \mathit{\boldsymbol{q}}\left( {\mathit{\boldsymbol{\hat w}}} \right),$ | (4) |
| ${\mathit{\boldsymbol{\tilde b}}_f} = {\mathit{\boldsymbol{w}}_{{\mathit{\boldsymbol{b}}}_f}},$ | (5) |
| ${\mathit{\boldsymbol{\tilde b}}_w} = {\mathit{\boldsymbol{w}}_{{\mathit{\boldsymbol{b}}}_w}},$ | (6) |
| $\mathit{\boldsymbol{\tilde c}} = {\mathit{\boldsymbol{w}}_c},$ | (7) |
| $\mathit{\boldsymbol{\tilde z}} = {\mathit{\boldsymbol{w}}_{\mathit{\boldsymbol{z}}}},$ | (8) |
| $\mathit{\boldsymbol{\tilde \mu }} = {\mathit{\boldsymbol{N}}^{\rm{T}}}({\mathit{\boldsymbol{\mu }}_i}){\mathit{\boldsymbol{\hat w}} _v} - \left[ {\begin{array}{*{20}{c}}0&1\\[3pt]{ - 1}&0\end{array}} \right]{\mathit{\boldsymbol{N}}^{\rm{T}}}\left( {{\mathit{\boldsymbol{\mu }}_i}} \right)\frac{{{{\mathit{\boldsymbol{\hat v}}_v}}}}{{d\left( {{\rho _i}} \right)}} + {\mathit{\boldsymbol{w}}_{u,i}},$ | (9) |
| ${\mathit{\boldsymbol{\tilde \rho }}_i} = - \mathit{\boldsymbol{\mu }}_i^{\rm{T}}/{\mathit{\boldsymbol{d}}'}\left( {{\rho _i}} \right) + {\mathit{\boldsymbol{w}}_{\rho ,i}}.$ | (10) |
其中
| $\mathit{\boldsymbol{\hat f}} = \mathit{\boldsymbol{\tilde f}} - {\mathit{\boldsymbol{b}}_f} - {\mathit{\boldsymbol{w}}_f},$ | (11) |
| $\mathit{\boldsymbol{\hat w}} = \mathit{\boldsymbol{\tilde w}} - {\mathit{\boldsymbol{b}}_w} - {\mathit{\boldsymbol{w}}_w}.$ | (12) |
相机的线速度和角速度为
| ${{\mathit{\boldsymbol{\hat v}}_v}} = {\mathit{\boldsymbol{z}}}\left( {\mathit{\boldsymbol{v}} + \mathit{\boldsymbol{\tilde w}} \times {\mathit{\boldsymbol{c}}}} \right),$ | (13) |
| ${{\mathit{\boldsymbol{\hat w}}_v}} = \mathit{\boldsymbol{z}}(\mathit{\boldsymbol{\tilde w}} ).$ | (14) |
由于单目视觉运动参数估计中需要给定先验尺度信息,而在摄像机运动过程中这个信息可能会产生漂移,从而引入一定的误差. 假设P为相机坐标系中的坐标,相机旋转矩阵为R,平移矩阵为t, 含焦距的矩阵为F,畸变参数为k1,k2,rp(p)为比例因子,p为像素坐标则将世界坐标系下坐标为X的3D点投影到相机坐标系的公式为
| $\mathit{\boldsymbol{P}} = \mathit{\boldsymbol{R}} \times {X} + \mathit{\boldsymbol{t}}\mathit{\boldsymbol{.}}$ | (15) |
转换到像素坐标系,
其中,
当有多组点对应时,可以用最小二乘法由(15)式求解出摄像机的运动参数.
以上采用最小二乘法解算出相机的运动参数,由于在图像定位过程中存在一定的误差,采用一定的优化准则对所得结果进行迭代优化,从而提高其定位的精确度. 一般采用最小二乘法的结果作为初始值,在本文中采用图像和X点之间重投影误差来优化摄像机的相对运动参数.
2.1 运动估计对于每一张捕获的图片,都进行一次状态更新,假设相机的内参是已知的,则可以计算向量μ在相应的图像坐标系下的投影为p=π(μ). 每一个特征点i对应一个方向向量
| ${\mathit{\boldsymbol{e}}_{l,j}} = {\mathit{\boldsymbol{P}}_l}({\mathit{\boldsymbol{p}}_j}) - {I_l}(\mathit{\boldsymbol{p}}{s_l} + W{\mathit{\boldsymbol{p}}_j}) - \bar m,$ | (16) |
| ${\mathit{\boldsymbol{y}}_i} = {\mathit{\boldsymbol{b}}_i}(\pi ({\mathit{\boldsymbol{\hat \mu }}_i})) + {n_i},$ | (17) |
| ${\mathit{\boldsymbol{H}}_i} = {A_i}(\pi ({\mathit{\boldsymbol{\hat \mu }}_i}))\frac{{{\rm{d}}\pi }}{{{\rm{d}}\mu }}(\mathit{\boldsymbol{\hat \mu }}_i^{}).$ | (18) |
其中,Il表示l层金字塔图像,Pl为以坐标P为中心的图像区域,el, j为强度误差,sl为尺度,
从图1可以看到,在摄像机运动过程中相邻帧图像可以观测到共同的三维路标点. 即存在重叠区域,将这些重叠区域进行分块. 再将每块的首帧中图像的特征的三维点数据作为初始值,采用投影关系对运动参数和空间三维点坐标同时进行优化. 通过最小化前后两帧图像重投影误差[15],求得最优的运动参数. 即求式(18)的最小值,
| $\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{d^2}\left( {{{Q}_{ji}}\mathit{\boldsymbol{,}}{{X}_{ij}}} \right)} } .$ | (19) |
n表示3D点数;m表示帧数;Xij表示图像j上第i个点的坐标;Qji表示点i在图像j上的预测值;d(x, y)表示向量x,y的欧氏距离. 由式(15)知道,可以通过使式(19)最小来优化矩阵R和t.
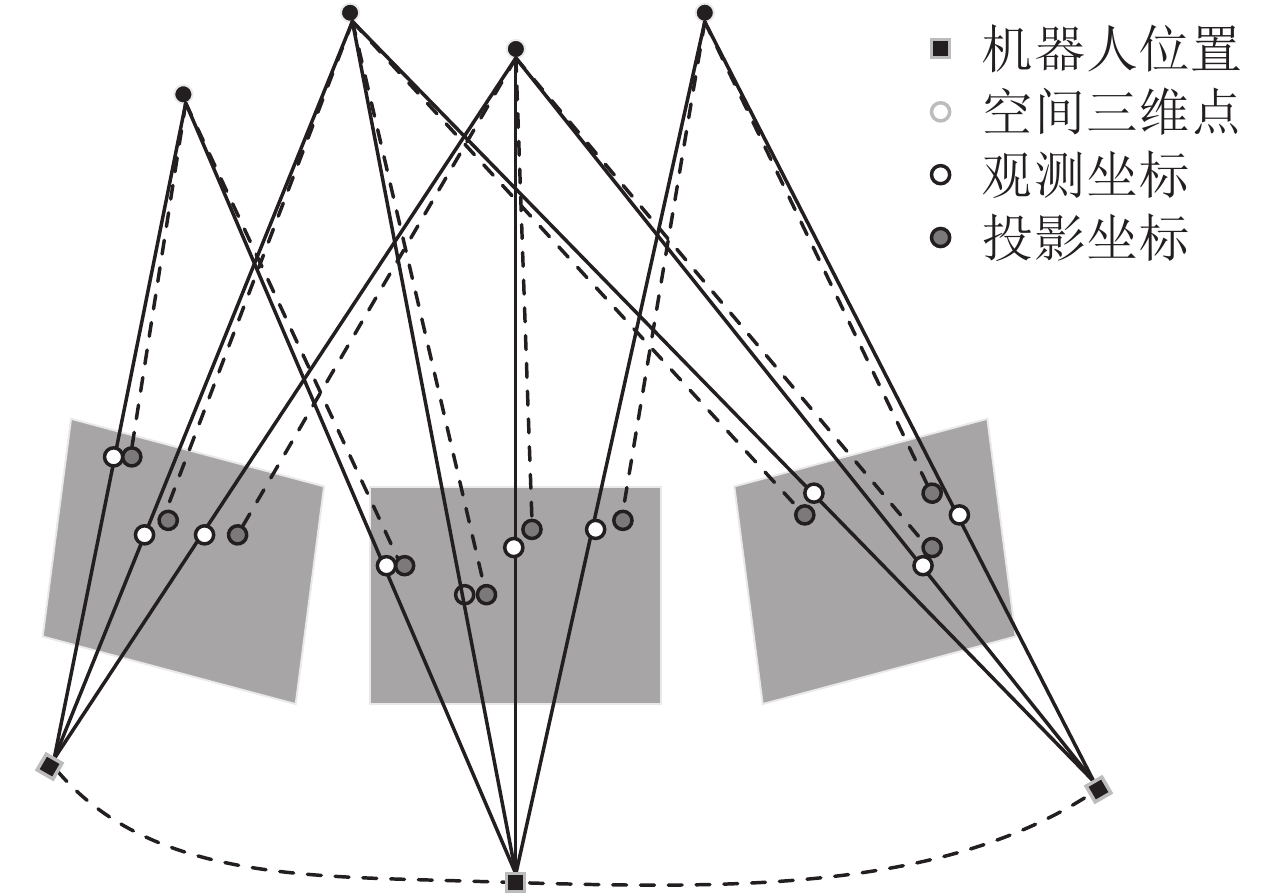
|
图 1 视觉里程计定位示意图 Figure 1 The map of visual odometer positioning |
在图像帧数较多时,采用BA方法进行优化,可以提高计算效率. 在本文中,特征点用
| $\lambda _i^j\left[ {\begin{array}{*{20}{c}}{y_i^j}\\[5pt]1\end{array}} \right] = \mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{R}}X_i^j + {\mathit{\boldsymbol{t}}}} \right).$ | (20) |
为了使整个运动过程中,每个观测位置获得的观测值和预测值之间的误差和最小,得到式(21),从而使得参数最优.
| $ \mathop {\min }\limits_{X_i^j,R,t} \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{{\left\| {\frac{1}{{\lambda _i^j}}C\left( {RX_i^j + t} \right) - \left[ {\begin{array}{*{20}{c}} {y_i^j}&1 \end{array}} \right]} \right\|}^2}.} } $ | (21) |
其中m表示机器人的观测位置总数,n表示观测到的3D路标点总数,用
本文所用数据为瑞士联邦理工学院计算机视觉团队的EuRoC MAV验证数据集[16].
所有实验均运行在配置为i7处理器,主频3.40 GHz, 内存为8G的电脑上,系统为Ubuntu14.04. 实验记录了不同场景下VIO算法和本文算法通过计算得出的不同运动轨迹和该轨迹的真实值的曲线.
EuRoc数据集不但提供了无人机在运行过程中的视觉信息和惯性单元的信息,还提供了无人机的真实轨迹信息,本文利用该数据集及其对比工具对所提位姿估计算法进行验证.
分别使用VIO方法和本文方法对数据集进行实验,图2为两组实验及真实轨迹的对比结果. 其中Ground Truth表示实际的轨迹.
3.2 绝对轨迹误差ATE绝对轨迹误差用于比较估计帧的轨迹与真实轨迹帧之间的绝对距离. 通过刚体转换操作S,将轨迹对齐,则第i帧的绝对位姿误差为
其中惯性单元相对于相机的外参数初始值设为0,反向深度参数ρi的初始值设为0.5 m–1, 标准协方差参数设置为1 m–1.
3.3 实验结果及分析图2中的5幅图是本文算法和VIO算法基于5组数据进行实验得到的结果对比图,其中黑色实线、红色虚线和蓝色虚线分别表示的是飞行机器人的真实轨迹以及VIO算法和本文算法估计的机器人的轨迹.
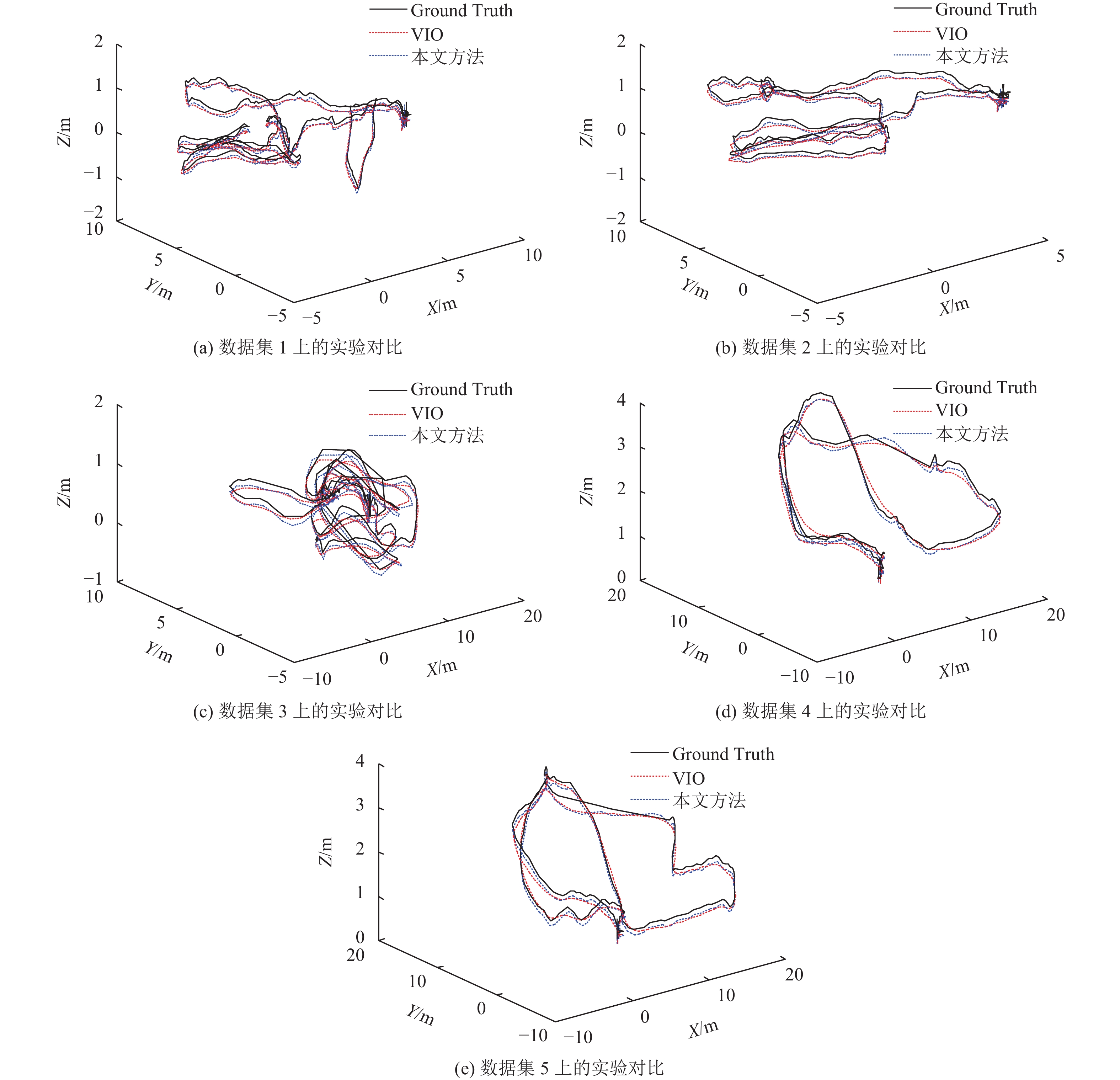
|
图 2 VIO算法和本文算法的实验结果对比 Figure 2 Comparing the results of VIO methods and proposed algorithm |
将两种方法的轨迹根均值平方误差(ATE.RMSE)以及两种方法的处理每帧图形的时间进行对比,结果如表1所示. 通过表1可以看出,本文方法的定位精度要优于VIO方法的定位精度,证明了该算法的有效性. 此外,从处理时间上来看,虽然本文算法较VIO算法的处理时间有所增加,但也可以实时计算出相对位置.
| 表 1 数据集对比实验表 Table 1 Contrast experiments based on datasets |
视觉里程计和惯性系统在定位方面各有自己的优缺点,本文提出基于BA的改进视觉/惯性融合定位算法, 通过将视觉信息和惯性信息融合定位,使得两种方式可以互相弥补单一方法的不足;采用反向深度法进行距离估计,用直接法加快计算速度,计算无人机的运动轨迹,最后用光束平差法进行优化,有效提高了飞行机器人的定位精度. 通过对瑞士联邦理工学院计算机视觉团队的EuRoC MAV验证数据的测试表明,该算法有较强的鲁棒性,是一种有效的视觉/惯性融合新方法.
| [1] | NISTER D, NARODITSKY O, BERGEN J. Visual odometry[C]//Computer vision and pattern recognition, 2004. CVPR 2004. Proceedings of the 2004 IEEE Computer Society Conference on. [s.l.]: IEEE, 2004, 1(1): 652-659. |
| [2] |
李力, 王耀南, 刘洪剑, 等. 旋翼飞行机器人视觉定位方法及系统[J].
机器人, 2016, 38(1): 8-16.
LI L, WANG Y N, LIU H J, et al. Visual positioning method and system for rotor flying robot[J]. Robot, 2016, 38(1): 8-16. |
| [3] |
曾碧, 林展鹏, 邓杰航. 自主移动机器人走廊识别算法研究与改进[J].
广东工业大学学报, 2016, 33(5): 9-14.
ZENG B, LIN Z P, DENG J H. Algorithm research on recognition and improvement for corridor of autonomous mobile robot[J]. Journal of Guangdong University of Technology, 2016, 33(5): 9-14. |
| [4] |
刘斯亮, 程良伦. 大曲率船体外板水火加工机器人运动轨迹优化研究[J].
广东工业大学学报, 2017, 34(1): 84-89.
LIU S L, CHENG L L. A research of motion trajectory optimization for large curvature of ship hull plate processing line robot[J]. Journal of Guangdong University of Technology, 2017, 34(1): 84-89. |
| [5] | WEISS S, ACHTELIK M W, LYNEN S, et al. Monocular vision for long-term micro aerial vehicle state estimation: A Compendium[J]. Journal of Field Robotics, 2013, 30(5): 803-831. DOI: 10.1002/rob.2013.30.issue-5. |
| [6] | MARTINELLI A. Closed-form solution of visual- inertial structure from motion[J]. International Journal of Computer Vision, 2014, 106(2): 138-152. DOI: 10.1007/s11263-013-0647-7. |
| [7] | GUI J, GU D, WANG S, et al. A review of visual inertial odometry from filtering and optimisation perspectives[J]. Advanced Robotics, 2015, 29(20): 1-13. |
| [8] |
李德隆, 刘伟. 基于改进的SIFT特征点的双目定位[J].
广东工业大学学报, 2017, 34(1): 90-94.
LI D L, LIU W. Object Location for binocular stereo vision based on improved sift feature[J]. Journal of Guangdong University of Technology, 2017, 34(1): 90-94. |
| [9] |
张朝飞, 罗建军, 龚柏春, 等. 一种复杂多介质环境下的视觉/惯性自适应组合导航方法[J].
中国惯性技术学报, 2016, 24(2): 190-195.
ZHANG C F, LUO J J, GONG B C, et al. Adaptive integrated navigation method of visual positioning/INS in complex multi-medium environment[J]. Journal of Chinese Inertial Technology, 2016, 24(2): 190-195. |
| [10] | WHELAN T, KAESS M, JOHANNSSON H, et al. Real-time large-scale dense rgb-d slam with volumetric fusion[J]. International Journal of Robotics Research, 2014, 34(4-5): 598-626. |
| [11] | KIM J H, CADENA C, REID I. Direct semi-dense slam for rolling shutter cameras[C]//IEEE International Conference on Robotics and Automation. Stockholm: IEEE, 2016: 1308-1315. |
| [12] | KERL C, STRUM J, CREMERS D. Robust odometry estimation for rgb-d cameras[C]//IEEE International Conference on Robotics and Automation. Karlsruhe: IEEE, 2013: 3748-3754. |
| [13] | ENGEL J, SCHOPS T, CREMERS D. Lsd-slam: large-scale direct monocular slam[C]//European Conference on Computer Vision. Berlin: Springer International Publishing, 2014: 834- 849. |
| [14] | MUR-ARTAL R, MONTIEL J M M, TARDOS J D. ORB-SLAM: A versatile and accurate monocular slam system[J]. IEEE Transactions on Robotics, 2015, 31(5): 1147-1163. DOI: 10.1109/TRO.2015.2463671. |
| [15] | VANDERPLAATS G N. Efficient algorithm for numerical optimization[J]. Journal of Aircraft, 2015, 16(16): 842-847. |
| [16] | BURRI M, NIKOLIC J, GOHL P, et al. The EuRoC micro aerial vehicle datasets[J]. International Journal of Robotics Research, 2016, 35(10): 1157-1163. DOI: 10.1177/0278364915620033. |
 2017, Vol. 34
2017, Vol. 34