动态规划是一种逆向计算方法,必须在时间上逆向求解最优控制序列. 虽然动态规划能精确求解哈密顿-雅可比-贝尔曼方程,但会导致计算量和存储量随着控制序列的长度也即解的时间维度的增加而急剧增长,也即“维数灾”问题[1]. 由Werbos提出的自适应动态规划通过迭代计算求解哈密顿-雅可比-贝尔曼方程[2-5],迭代控制策略和迭代性能指标函数逐渐逼近最优控制策略和最优性能指标函数,避免了“维数灾”问题. 自适应动态规划有4种基本的实现结构:启发式动态规划(HDP)、二次启发式规划(DHP)、执行依赖启发式动态规划(ADHDP)和执行依赖二次启发式规划(ADDHP)[2-3]. 文献[6]提出了全新的自适应动态规划实现结构:全局二次启发式规划(GDHP)和执行依赖全局二次启发式规划(ADGDHP).
值迭代是自适应动态规划的一种迭代方式,需要初始化迭代性能指标函数[7-8]. Al-Tamimi等[9]给出了一种应用于离散时间仿射非线性系统的值迭代,首次指出迭代性能指标函数初始化为零可保证迭代收敛到最优,并给出了数学证明. Zhang等[10]研究了离散仿射非线性系统的最优跟踪控制问题,并给出了值迭代的收敛性和最优性证明. Wang等[11]给出了应用于离散时间非仿射非线性系统的值迭代的收敛性和最优性证明. 文献[9-11]要求迭代性能指标函数初始化为零. Wei等[12]给出一种保证迭代控制策略是稳定控制策略的迭代性能指标函数的初始化方法,并给出了收敛性证明. 文献[13-14]证明了迭代性能指标函数初始化为半正定函数可保证值迭代收敛到最优,极大地放松了值迭代对迭代性能指标函数的初始化要求.
文献[9-14]指出,如果值迭代的迭代次数趋向无穷,那么迭代性能指标函数和迭代控制策略分别等于最优性能指标函数和最优控制策略. 无穷次迭代是无法实现的,有限次迭代所得的迭代性能指标函数和迭代控制策略是含有残差的近似最优性能指标函数和近似最优控制策略. 如果为迭代计算给定一个收敛精度,则可通过多次迭代让残差达到收敛精度的要求. 由于放松了对迭代次数的要求,自适应动态规划的实时性将无法得到保证. 如果给定迭代次数,则不能保证残差达到收敛精度的要求.
值迭代的残差大小与初始的迭代性能指标函数有关. 初始的迭代性能指标函数影响着迭代次数和收敛精度. 本文根据文献[13-14]的证明结果,研究了一种在有限迭代次数下保证收敛精度的快速自适应动态规划算法.
1 问题描述本文所描述的离散时间非仿射非线性系统如下:
| ${{\mathit{\boldsymbol{x}}}_{k + 1}} = F({{\mathit{\boldsymbol{x}}}_k},{{\mathit{\boldsymbol{u}}}_k}),\;\;k = 0,1,2, \cdots .$ | (1) |
其中
优化目标是寻找控制序列
| $J({{\mathit{\boldsymbol{x}}}_k},{\underline {\mathit{\boldsymbol{u}}} _k}) = \sum\limits_{t = k}^\infty {U({{\mathit{\boldsymbol{x}}}_t},{{\mathit{\boldsymbol{u}}}_t})} .$ | (2) |
其中
根据Bellman最优定理,最优性能指标函数满足如下哈密顿-雅可比-贝尔曼方程:
| ${J^*}({{\mathit{\boldsymbol{x}}}_k}) = \mathop {\min }\limits_{u({{\mathit{\boldsymbol{x}}}_k})} \{ U({{\mathit{\boldsymbol{x}}}_k},u({{\mathit{\boldsymbol{x}}}_k})) + {J^*}({{\mathit{\boldsymbol{x}}}_{k + 1}})\} .$ | (3) |
式(3)也可表示为
| ${J^*}({{\mathit{\boldsymbol{x}}}_k}) = U({{\mathit{\boldsymbol{x}}}_k},{u^*}({{\mathit{\boldsymbol{x}}}_k})) + {J^*}({{\mathit{\boldsymbol{x}}}_{k + 1}}).$ | (4) |
其中
| ${u^*}({{\mathit{\boldsymbol{x}}}_k}) = \mathop {\arg \min }\limits_{u({{\mathit{\boldsymbol{x}}}_k})} \{ U({{\mathit{\boldsymbol{x}}}_k},u({{\mathit{\boldsymbol{x}}}_k})) + {J^*}({{\mathit{\boldsymbol{x}}}_{k + 1}})\} .$ | (5) |
即
| ${u^*}({{\mathit{\boldsymbol{x}}}_k}) = = \mathop {\arg \min }\limits_{u({{\mathit{\boldsymbol{x}}}_k})} \{ U({{\mathit{\boldsymbol{x}}}_k},u({{\mathit{\boldsymbol{x}}}_k})) + {J^*}({{\mathit{\boldsymbol{x}}}_{k + 1}})\} .$ | (6) |
设
| ${u_i}({{\mathit{\boldsymbol{x}}}_k}) = \mathop {\arg \min }\limits_{u({{\mathit{\boldsymbol{x}}}_k})} \{ U({{\mathit{\boldsymbol{x}}}_k},u({{\mathit{\boldsymbol{x}}}_k})) + {J_i}({{\mathit{\boldsymbol{x}}}_{k + 1}})\} .$ | (7) |
| ${J_{i + 1}}({{\mathit{\boldsymbol{x}}}_k}) = \mathop {\rm{min}}\limits_{u({{\mathit{\boldsymbol{x}}}_k})} \{ U({{\mathit{\boldsymbol{x}}}_k},u({{\mathit{\boldsymbol{x}}}_k})) + {J_i}({{\mathit{\boldsymbol{x}}}_{k + 1}})\}.$ | (8) |
文献[13-14]证明了若
粒子群算法会初始化多个携带不同可行解的粒子,各粒子在迭代过程中通过其他粒子的解来更新自己的解. 参考粒子群算法,本节提出了基于自适应动态规划的协同优化算法(Cooperative Optimization Based on Adaptive Dynamic Programming,COADP). COADP会创建多个值迭代“粒子”. 在每一次迭代里,COADP根据所有“粒子”的迭代性能指标函数来重新构建各“粒子”的迭代性能指标函数.
设一个进程(或智能体、粒子等)运行一个值迭代. 设A是进程的数量,
(1) COADP的初始化.
由于迭代性能指标函数可初始化为任意半正定函数,COADP将首先初始化A个进程及A个互不相同的半正定函数
(2) COADP的迭代.
命名
| $u_i^{(a)}({{\mathit{\boldsymbol{x}}}_k}) = \mathop {\arg \min }\limits_{u({{\mathit{\boldsymbol{x}}}_k})} \{ U({{\mathit{\boldsymbol{x}}}_k},u({{\mathit{\boldsymbol{x}}}_k})) + J_i^{(a)}({\mathit{\boldsymbol{x}}}_{k + 1}^{})\} .$ | (9) |
| $V_{i + 1}^{(a)}({{\mathit{\boldsymbol{x}}}_k}) = U({{\mathit{\boldsymbol{x}}}_k},u_i^{(a)}({{\mathit{\boldsymbol{x}}}_k})) + J_i^{(a)}({\mathit{\boldsymbol{x}}}_{k + 1}^{}).$ | (10) |
与式(8)不同的是,式(10)没有立刻更新
(3) COADP的更新.
设第
若
| ${B_{i + 1}} = \mathop {\arg \min }\limits_a \left\{ {\left\| {\frac{{V_{i + 1}^{(a)}({{\mathit{\boldsymbol{x}}}_k}) - J_i^{(a)}({{\mathit{\boldsymbol{x}}}_k})}}{{V_{i + 1}^{(a)}({{\mathit{\boldsymbol{x}}}_k})}}} \right\|} \right\}.$ | (11) |
为了实现可比性,式(11)中采用的是相对变化率. 在重新构建
| $J_{i + 1}^{(a)}({\mathit{\boldsymbol{x}}_k}) = \left\{\!\!\!\! \begin{array}{l}V_{i + 1}^{({B_{i + 1}})}({{\mathit{\boldsymbol{x}}}_k}),{{ }}a = {B_{i + 1}};\\[8pt]\!\max \left\{ {V_{i + 1}^{({B_{i + 1}})}({{\mathit{\boldsymbol{x}}}_k}) + Ra_{i + 1}^{(a)} \!\!\cdot \!\!D\! \cdot \!\!V_{i + 1}^{({B_{i + 1}})}({{\mathit{\boldsymbol{x}}}_k}),0} \right\},\\[8pt]\quad{{ }}a \ne {B_{i + 1}}.\end{array} \right.$ | (12) |
其中
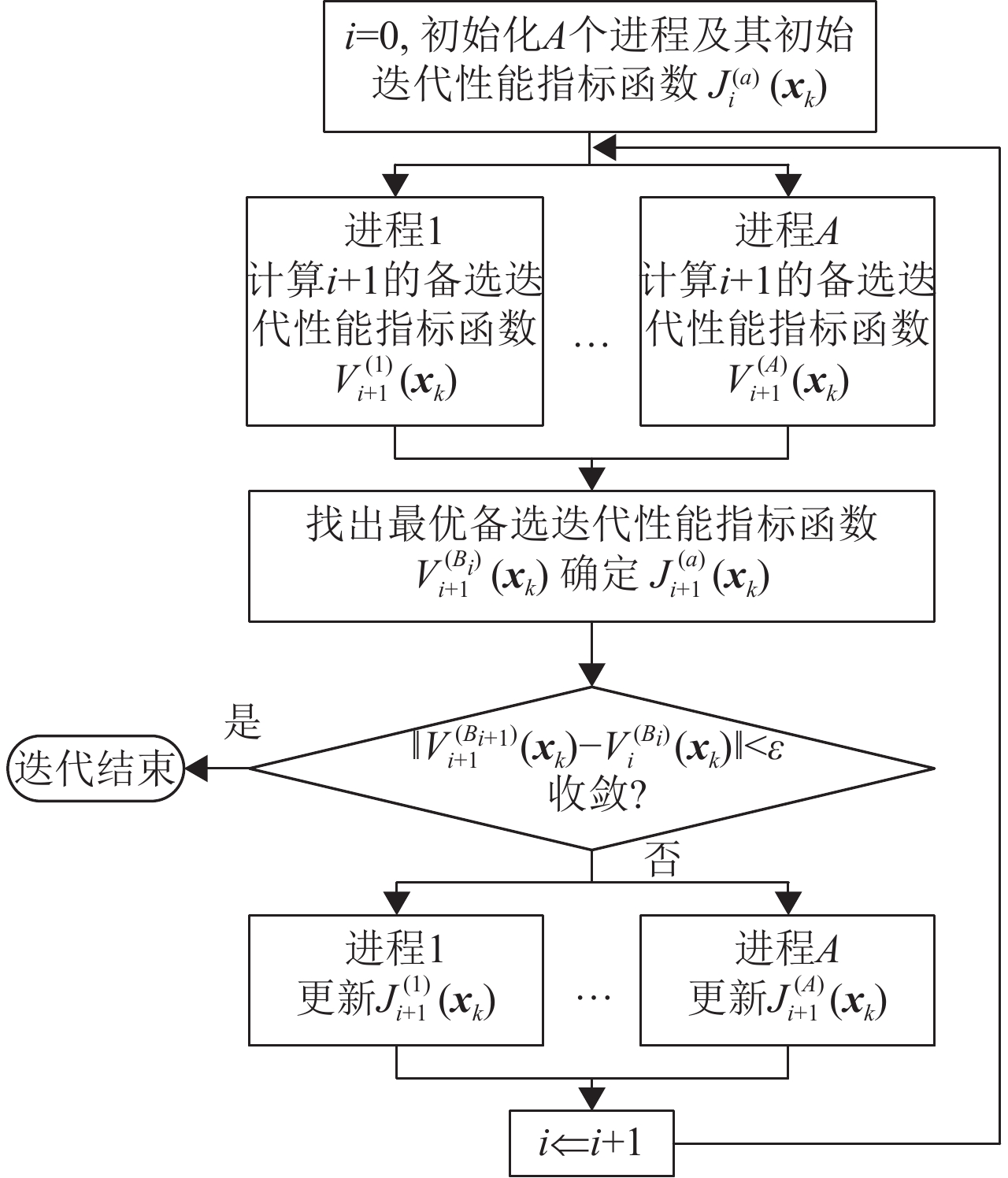
图1是COADP的流程图. 当
|
图 1 COADP算法的流程图 Figure 1 Flow chart of COADP |
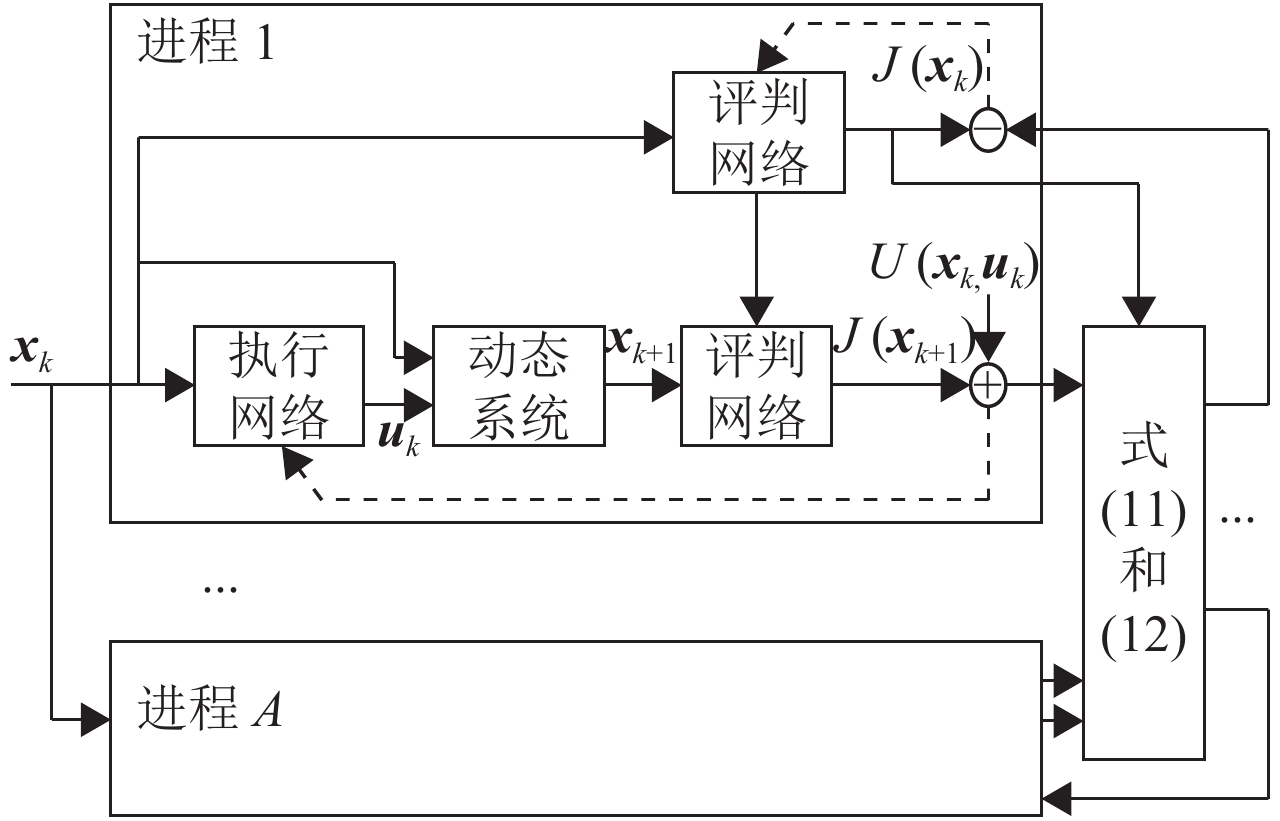
图2是COADP的结构图,其中每个进程均采用HDP结构. 采用三层BP神经网络近似
|
图 2 COADP算法的结构图 Figure 2 Scheme of COADP |
例1:非仿射非线性系统为
| ${{\mathit{\boldsymbol{x}}}_{k + 1}} = {{\mathit{\boldsymbol{x}}}_k} + \sin ({{\mathit{\boldsymbol{x}}}_k} + {{\mathit{\boldsymbol{u}}}_k}).$ | (13) |
其中
首先令进程数量A=3,初始化各进程的评判网络为:
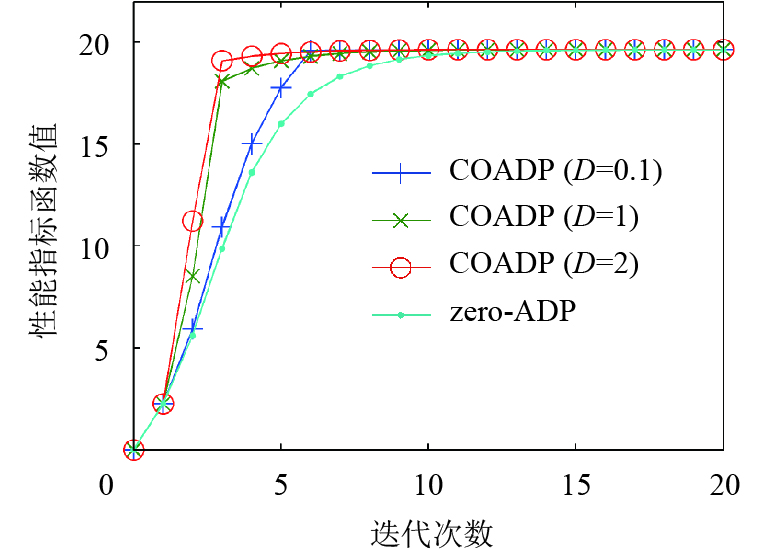
修改进程数量A=7,新增的4个进程的评判网络初始化为
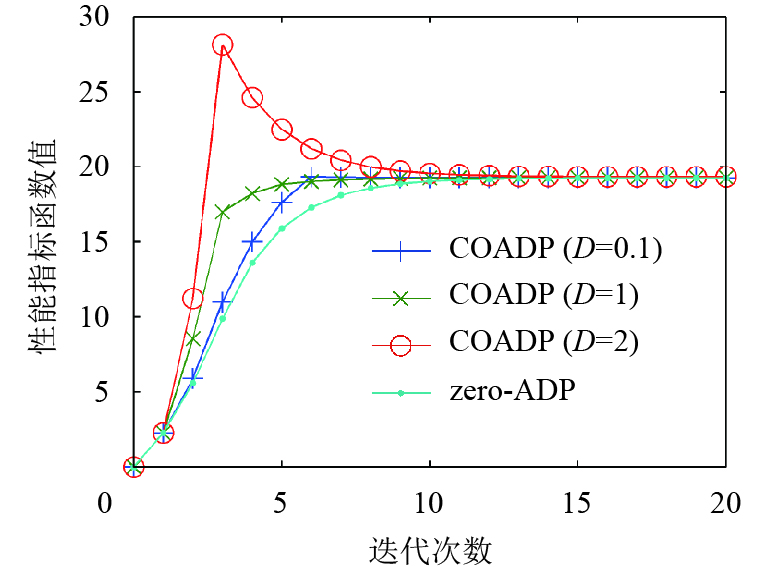
若D足够大,则通过式(12)更新所得的某一
|
图 3 例1的最优备选迭代性能指标函数收敛过程(A=3) Figure 3 Convergence of the best optional iterative performance index function for Example 1 (A=3) |
|
图 4 例1的最优备选迭代性能指标函数收敛过程(A=7) Figure 4 Convergence of the best optional iterative performance index function for Example 1 (A=7) |
例2: 非仿射非线性系统为
| ${{\mathit{\boldsymbol{x}}}_{k + 1}} = \left[ {\begin{array}{*{20}{c}}{ - {{\mathit{\boldsymbol{x}}}_{1k}}{{\mathit{\boldsymbol{x}}}_{2k}}}\\[7pt]{1.5{{\mathit{\boldsymbol{x}}}_{2k}} + \sin ({\mathit{\boldsymbol{x}}}_{2k}^2 + {{\mathit{\boldsymbol{u}}}_k})}\end{array}} \right].$ | (14) |
其中
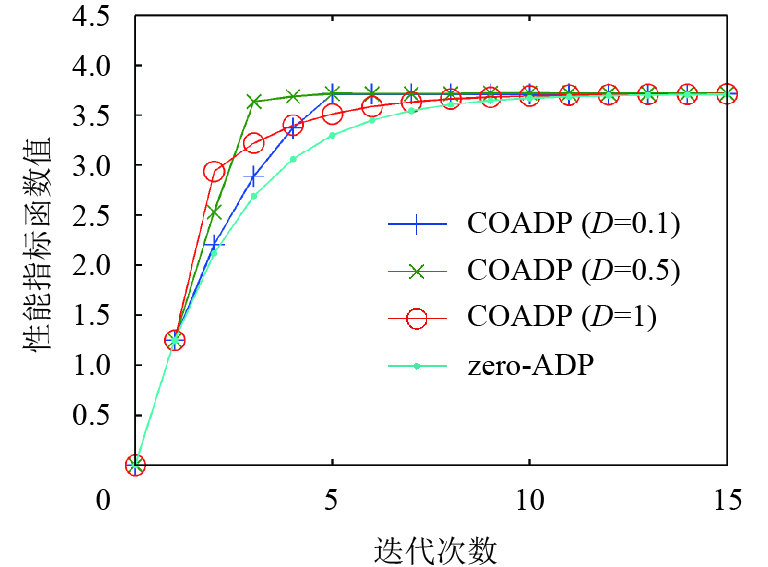
|
图 5 例2的最优备选迭代性能指标函数收敛过程(A=3) Figure 5 Convergence of the best optional iterative performance index function for Example 2 (A=3) |
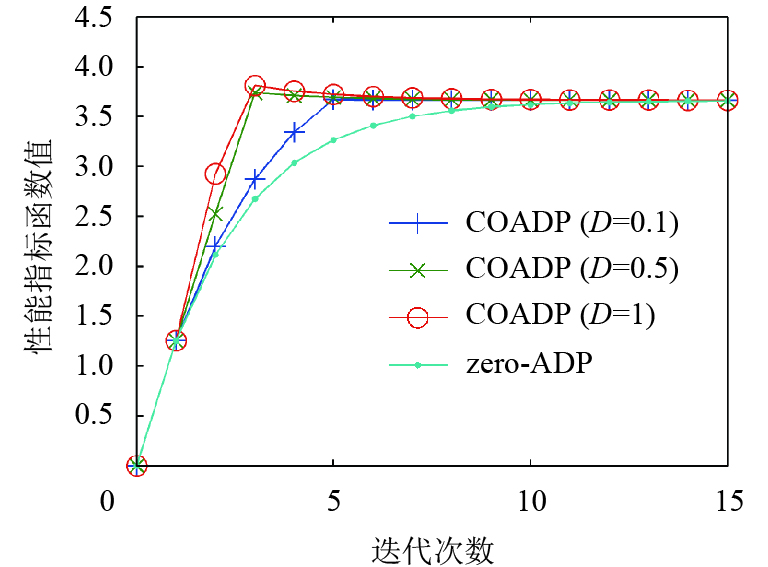
|
图 6 例2的最优备选迭代性能指标函数收敛过程(A=7) Figure 6 Convergence of the best optional iterative performance index function for Example 2 (A=7) |
例3:仿射非线性系统为
| ${{\mathit{\boldsymbol{x}}}_{k + 1}} = \left[ \begin{array}{l}({\mathit{\boldsymbol{x}}}_{1k}^2 + {\mathit{\boldsymbol{x}}}_{2k}^2 + {{\mathit{\boldsymbol{u}}}_k})\cos ({{\mathit{\boldsymbol{x}}}_{2k}})\\[6pt]({\mathit{\boldsymbol{x}}}_{1k}^2 + {\mathit{\boldsymbol{x}}}_{2k}^2 + {{\mathit{\boldsymbol{u}}}_k})\sin ({{\mathit{\boldsymbol{x}}}_{2k}})\end{array} \right].$ | (15) |
其中
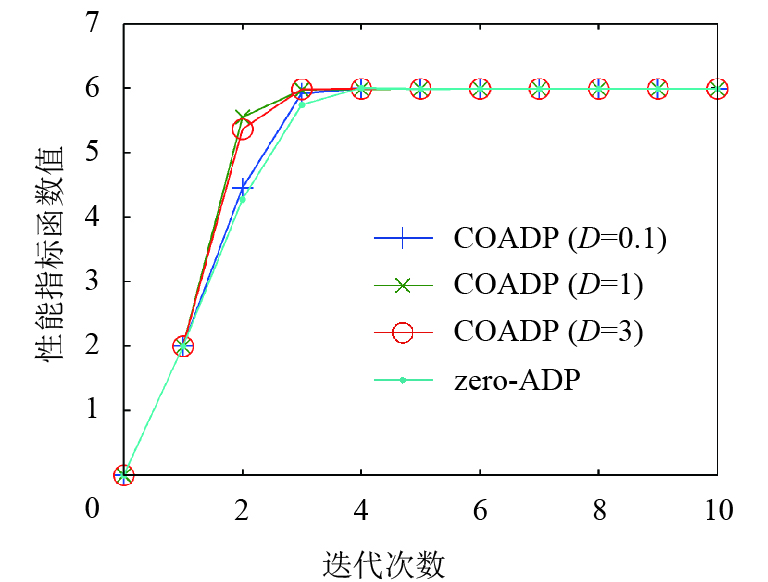
|
图 7 例3的最优备选迭代性能指标函数收敛过程(A=3) Figure 7 Convergence of the best optional iterative performance index function for Example 3 (A=3) |
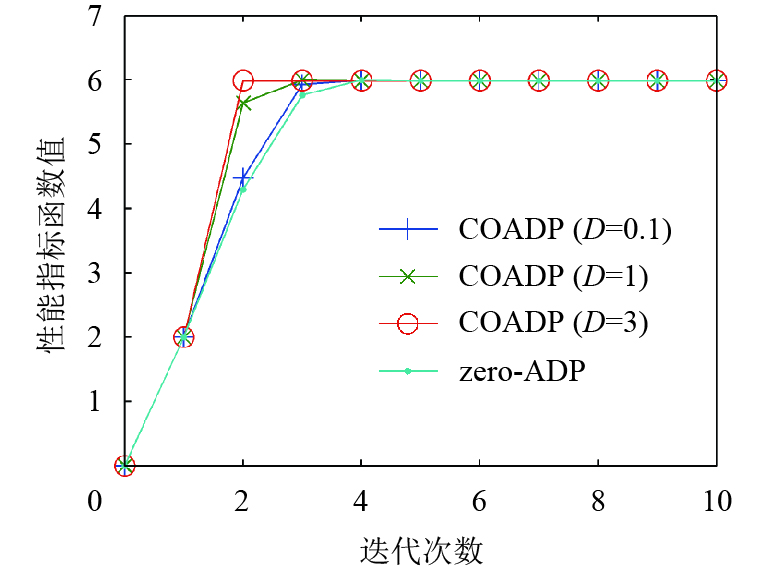
|
图 8 例3的最优备选迭代性能指标函数收敛过程(A=7) Figure 8 Convergence of the best optional iterative performance index function for Example 3 (A=7) |
以上3个例子的仿真结果表明,如果D过小,或者如果D过大而A过小,则COADP算法的效果与zero-ADP的效果相若,COADP算法不能显著加快残差减小的速度. 在实际应用中,对于不同的系统,A和D的恰当取值是难以确定的. 为了充分发挥COADP算法的优势,应把A和D设置为较大的数值.
4 总结本文研究了一种在有限迭代次数下保证收敛精度的快速自适应动态规划算法. 本文提出的协同优化算法能令残差快速减小,令自适应动态规划更为实用.
| [1] | BELLMAN R E. Dynamic Programming[M]. Princeton: Princeton University Press, 1957. |
| [2] | WERBOS P J. Advanced forecasting methods for global crisis warning and models of intelligence[J]. General Systems Yearbook, 1977, 22(6): 25-38. |
| [3] | WERBOS P J. Approximate Dynamic Programming for Real-time Control and Neural Modeling, in Handbook of Intelligent Control[M]. New York: Van Nostrand Reinhold, 1992. |
| [4] | MILLER W T, SUTTON R S, WERBOS P J. A Menu of Designs for Reinforcement Learning Over Time, in Neural Networks for Control[M]. Cambridge: MIT Press, 1991. |
| [5] | MURRAY J J, COX C J, LENDARIS G G, SAEKS R. Adaptive dynamic programming[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C, 2002, 32(2): 140-153. DOI: 10.1109/TSMCC.2002.801727. |
| [6] | PROKHOROV D V, WUNSCH D C. Adaptive critic designs[J]. IEEE Transactions on Neural Networks, 1997, 8(5): 997-1007. DOI: 10.1109/72.623201. |
| [7] | LEWIS F L, LIU D. Reinforcement learning and adaptive dynamic programming for feedback control[J]. IEEE Circuits & Systems Magazine, 2009, 9(3): 32-50. |
| [8] | LEWIS F L, VRABIE D, VAMVOUDAKIS K G. Reinforcement learning and feedback control: using natural decision methods to design optimal adaptive controllers[J]. IEEE Control Systems, 2012, 32(6): 76-105. DOI: 10.1109/MCS.2012.2214134. |
| [9] | AL-TAMIMI A, LEWIS F L, ABU-KHALAF M. Discrete-time nonlinear HJB solution using approximate dynamic programming: convergence proof[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetices, 2008, 38(4): 943-949. DOI: 10.1109/TSMCB.2008.926614. |
| [10] | ZHANG H, WEI Q, LUO Y. A novel infinite-time optimal tracking control scheme for a class of discrete-time nonlinear systems via the greedy HDP iteration algorithm[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetices, 2008, 38(4): 937-942. DOI: 10.1109/TSMCB.2008.920269. |
| [11] | WANG D, LIU D, WEI Q, ZHAO D, JIN N. Optimal control of unknown nonaffine nonlinear discrete-time systems based on adaptive dynamic programming[J]. Automatica, 2012, 48(8): 1825-1832. DOI: 10.1016/j.automatica.2012.05.049. |
| [12] | WEI Q, LIU D. A novel iterative θ-adaptive dynamic programming for discrete-time nonlinear systems[J]. IEEE Transactions on Automation Science and Engineering, 2014, 11(4): 1176-1190. DOI: 10.1109/TASE.2013.2280974. |
| [13] | WEI Q, LIU D, LIN H. Value iteration adaptive dynamic programming for optimal control of discrete-time nonlinear systems[J]. IEEE Transactions on Cybernetics, 2016, 46(3): 840-853. DOI: 10.1109/TCYB.2015.2492242. |
| [14] |
刘毅, 章云. 基于值迭代的自适应动态规划的收敛条件[J].
广东工业大学学报, 2017, 34(5): 10-14.
LIU Y, ZHANG Y. A convergence condition of value-iteration based adaptive dynamic programming[J]. Journal of Guangdong University of Technology, 2017, 34(5): 10-14. |
| [15] | NAVARRO-LOPEZ E M. Local feedback passivation of nonlinear discrete-time systems through the speed-gradient algorithm[J]. Automatica, 2007, 43(7): 1302-1306. DOI: 10.1016/j.automatica.2006.12.017. |
| [16] | SIRA-RAMIREZ H. Non-linear discrete variable structure systems in quasi-sliding mode[J]. International Journal of Control, 1991, 54(5): 1171-1187. DOI: 10.1080/00207179108934203. |
 2017, Vol. 34
2017, Vol. 34

