变式是我国传统理科教学的一种特色[1]. 变式是教师通过特征的变换,让学生从不同背景条件、不同维度角度,进行多方位理解同一事物,得以归纳该事物的特征属性,使学生区分出事物的本质特征与非本质特征,最终形成概念,被认为是一种能够使学习者掌握并合理运用概念的方法[2]. 将变式应用于教学中即称为“变式教学”[3]. 随着变式教学研究的开展,已经被越来越多地运用到不同学科课程的教学当中.
实验课程教学是开展探究性学习,培养学生实践操作能力,进行创新人才培养不可忽视的重要教学环节[4-6]. 在实验课程教学中开展变式教学,有助于实施实验探索,丰富实验教学内容、培养学生思维灵活性[7].
然而,在变式教学的教学实施过程中,存在着一个问题:很多教师使用变式时往往是出于灵感和无计划性的[3]. 那么,是否有作为指导教师进行特征变式处理的方法呢?
可拓学是1983年由中国学者提出的一门原创性的横断学科,它综合了形式逻辑和辩证逻辑的长处,探索问题的变换和推理,构建了连接自然科学与社会科学的桥梁,辅助人们进行创新活动,构建自主创新模型,提高平民化创新的能力[8-10]. 因此,本文提出了将可拓学理论作为特征变式的指导方法,介绍基于可拓学的特征变式处理过程,以高校电工电子实验课程教学为例,对基于可拓学的特征变式进行实践尝试.
1 可拓学的简介可拓学包括了基元理论、可拓集理论和可拓逻辑等内容. 本文采用可拓学中的基元理论对变式教学设计进行研究. 基元理论包含了基元的可拓变换和基元的拓展分析等内容.
基元是将物、动作与关系等特征表达在一个三元组中,形式化地描述事、物和关系,是定性与定量相结合的特征表示模型,为知识表示提供了新的形式化工具. 基元的形式为一个有序三元组M=(O, c, v),其中O为事物、动作或事物间关系的名称,c为关于事物、动作或事物间关系O相应的特征,v为关于特征c的量值. 往往事物、动作或关系具有多维的特征,因此可变式为
| $M = \left( {O,c,v} \right) = \left[ {\begin{array}{*{20}{c}}{O,}&{{c_1},}&{{v_1}}\\[5pt]{}&{{c_2},}&{{v_2}}\\[5pt]{}& \vdots & \vdots \\[5pt]{}&{{c_n},}&{{v_n}}\end{array}} \right].$ |
基元的可拓变换是把一个对象变为另一个对象或分解为若干对象. 通常采用对基元进行如置换、分解、增加、删减、扩大或缩小等变换处理方法,使事物的特征或量值发生了变化.
基元的拓展分析是把事物和事物间的关系看成可以拓展的,分析和变换问题条件,使目标得以实现. 基元的拓展分析包含了由事物特征量值发散性的发散分析、事物之间特征量值相关性的相关分析、事物之间特征量值蕴含性的蕴含分析、事物之间特征量值可扩性的可扩分析.
2 基于可拓学的特征变式教学设计变式教学可从瑞典教育学家F·Marton的变易学习理论(Variation Theory of Learning,有的文献翻译为变异学习理论)中获得理论基础[11]. 变易学习理论认为:人对事物的了解,关键在于他所聚焦事物的特征;必须促进他把未被他关注或辨识的特征分辨出来;而要把某种事物的关键特征从众多背景和多个事物中分辨出来,需要透过变易的处理方法[12]. 因此,教师在备课时,可以从学习内容中分拣出相关的关键特征进行变式处理,在此基础上形成教学策略,以提高教学效果.
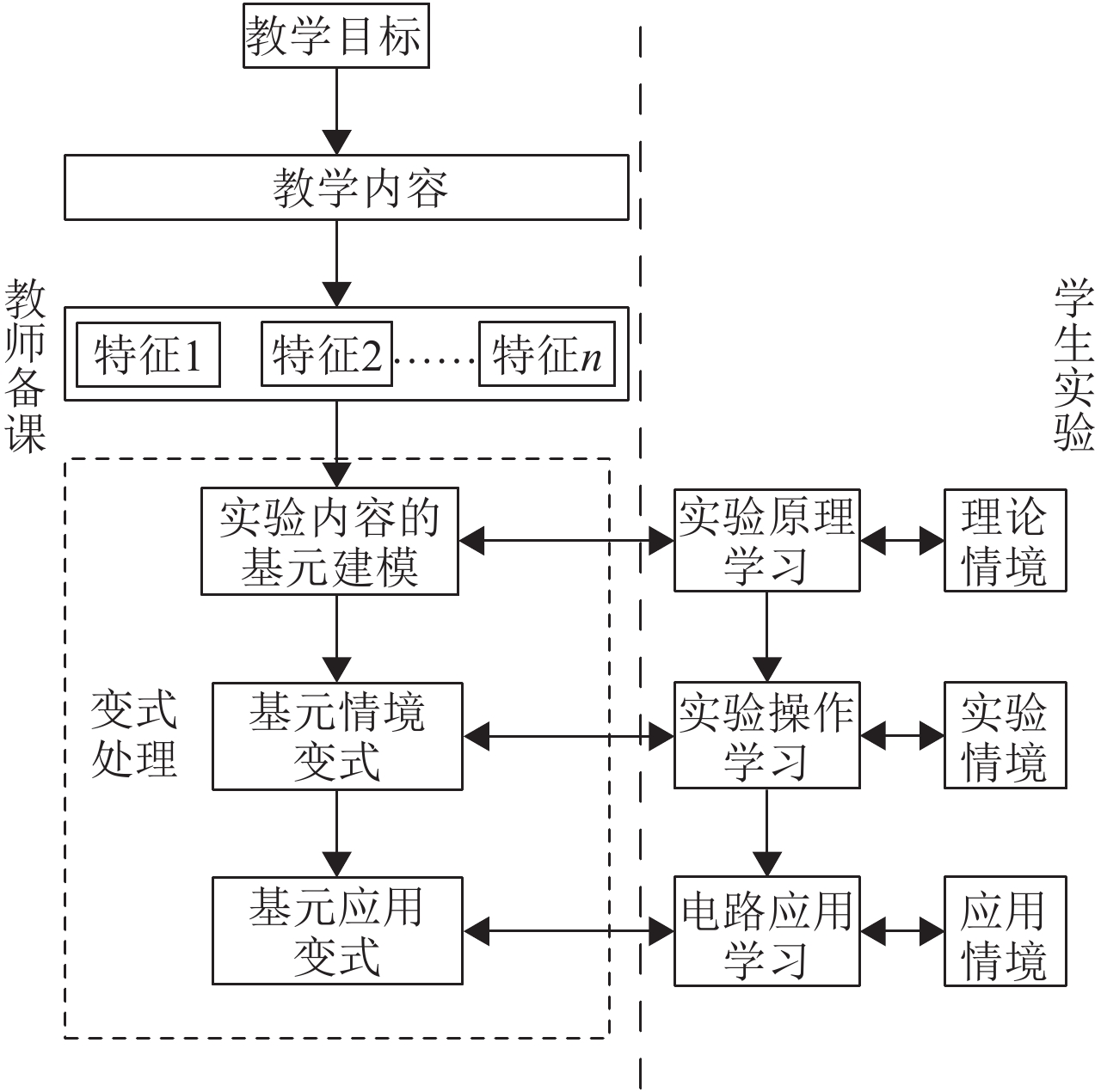
而可拓学的基元理论突出了对事物及其特征量值的形式化定量化表示,以及这些要素的变换和拓展,以达到解决问题的目的. 为此,可利用可拓学的有关内容作为进行特征变式教学设计的指导方法,其过程如图1所示.
|
图 1 基于可拓学的特征变式教学设计 Figure 1 The model of variation teaching based on Extenics |
传统的实验教学包含了教师实验原理讲解和学生实验操作两个环节,分别对应“理论情境”和“实验情境”的学习. 为了促进学生理论联系实际,促进学生知识的迁移,增加了应用学习的环节,即“应用情境”的学习,丰富和拓展了实验教学的空间和内容,克服传统实验教学仅局限于验证理论知识的短板.
教师首先根据教学目标确定教学内容,再从教学内容中将有关概念、知识点的特征抽取出来. 在此基础上,进行基于可拓学的变式处理.
基于可拓学的变式处理过程可分为3部分:(1) 实验内容的基元建模;(2) 基元情境变式;(3) 基元应用变式.
(1) 实验内容的基元建模.
在备课时,教师需要在预设的学习内容中将关键特征挖掘出来,评估它们是否容易被学生关注和分辨,将它们由背景变成前景,引导学生加以关注和分析. 在此可以用基元来描述实验项目的有关概念、实验原理、操作方法以及概念之间的关系,由基元表达式进行教学内容的特征建模. 教师通过基元呈现教学内容的特征,辨析在实验原理授课环节中教学内容的重点和难点,并进行“理论情境”的教学设计.
(2) 基元情境变式.
再由知识点的基元表达式中的特征及其特征量值去寻找进行情境变式的要素,利用诸如置换、分解、增加、删减、扩大和缩小等可拓变换方法进行变式处理,进行“实验情境”的教学设计. 设计的实验教学内容中通过改变实验条件引起实验现象特征的变化,制造特征情境变式,引导学生观察不同实验现象之间的差异,关注和分辩其关键特征,思考产生差异的原因,从而领会关键特征的本质,以及关键特征之间的关联,促进学生对实验原理或规律的掌握.
(3) 基元应用变式.
从各个知识点的基元表示中提取有关的特征,以及从实验情境的有关实验现象中提取特征信息,利用基元的拓展分析,对教学内容中的特征及其量值寻求在实际应用中的关联,进行特征应用变式,拓展出具有与实验原理相同特征的原理应用例子,进行“应用情境”教学设计. 通过特征应用变式,得到与实验原理相关联的实际案例,将它融入到学生学习中,促进学生将掌握的理论原理与应用相结合,扩大学生认知的深度和广度,加强学生对教学内容现实意义的认同.
3 基于可拓学的特征变式教学实践以高校电工电子实验课程《RC一阶动态电路响应》为例,说明基于可拓学的变式教学设计.
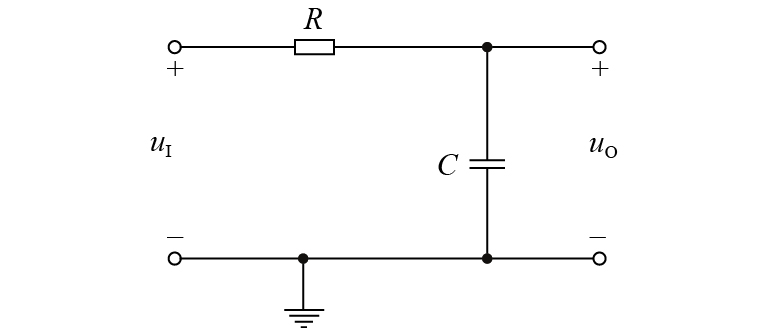
该实验项目一个重要的教学目标是:研究RC一阶动态电路的方波响应[13]. 教学内容涉及了如图2所示RC一阶动态电路,实验过程中需要研究和讨论电路的响应,并由实验现象测量电路的时间常数.
|
图 2 RC一阶动态电路 Figure 2 A RC first-order dynamic circuit |
(1) 基元建模.
主要的教学内容可分别用如式(1)~(5)所示进行基元表示. 根据式(1)~(5),找出教学内容的关键特征,重点设计如何讲解零输入响应与零状态响应、时间常数的概念特征和测量过程方法.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
(2) 基元情境变式.
由式(4)和式(5)可知,RC一阶电路中,电路的时间常数τ=RC,实验的前提条件为“时间常数τ远小于输入方波周期”. 则有
| (6) |
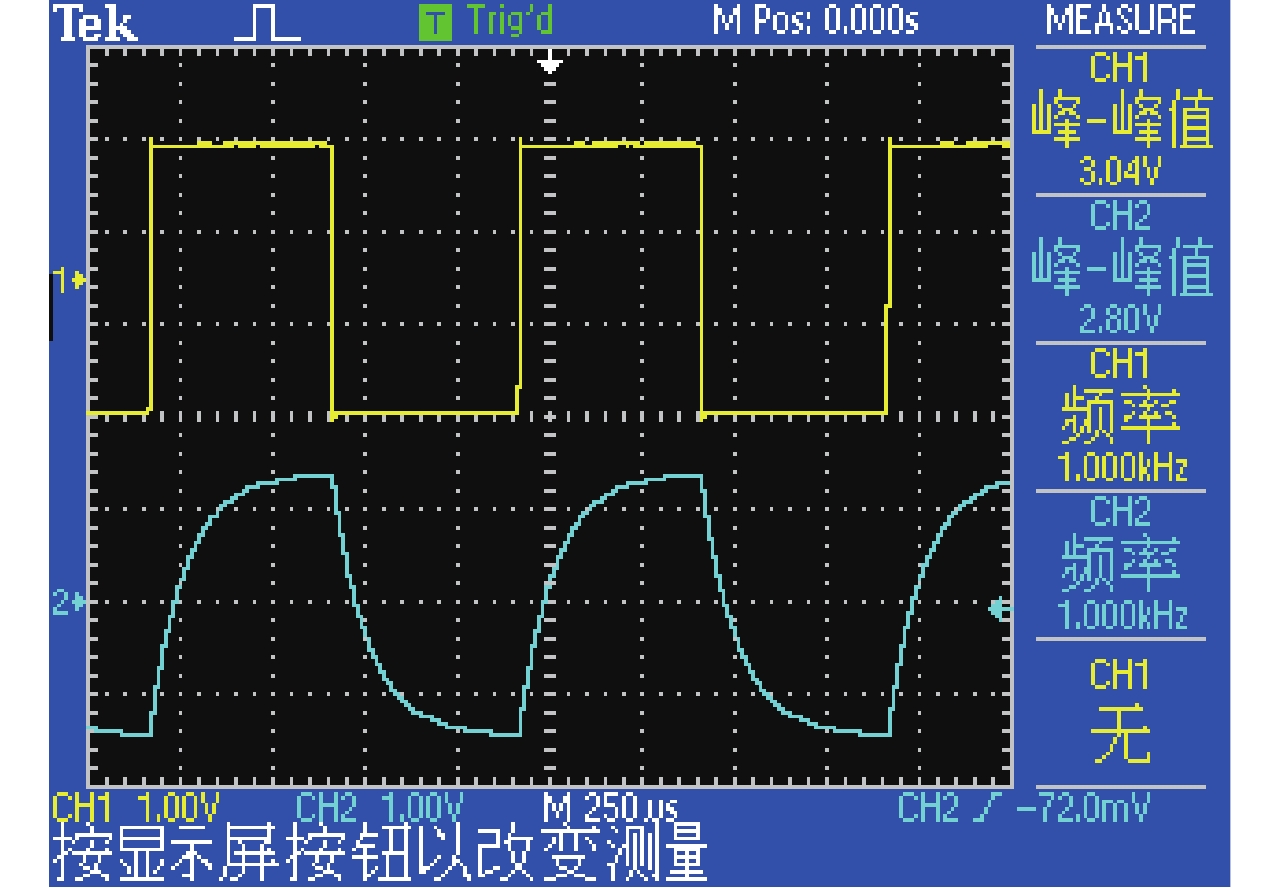
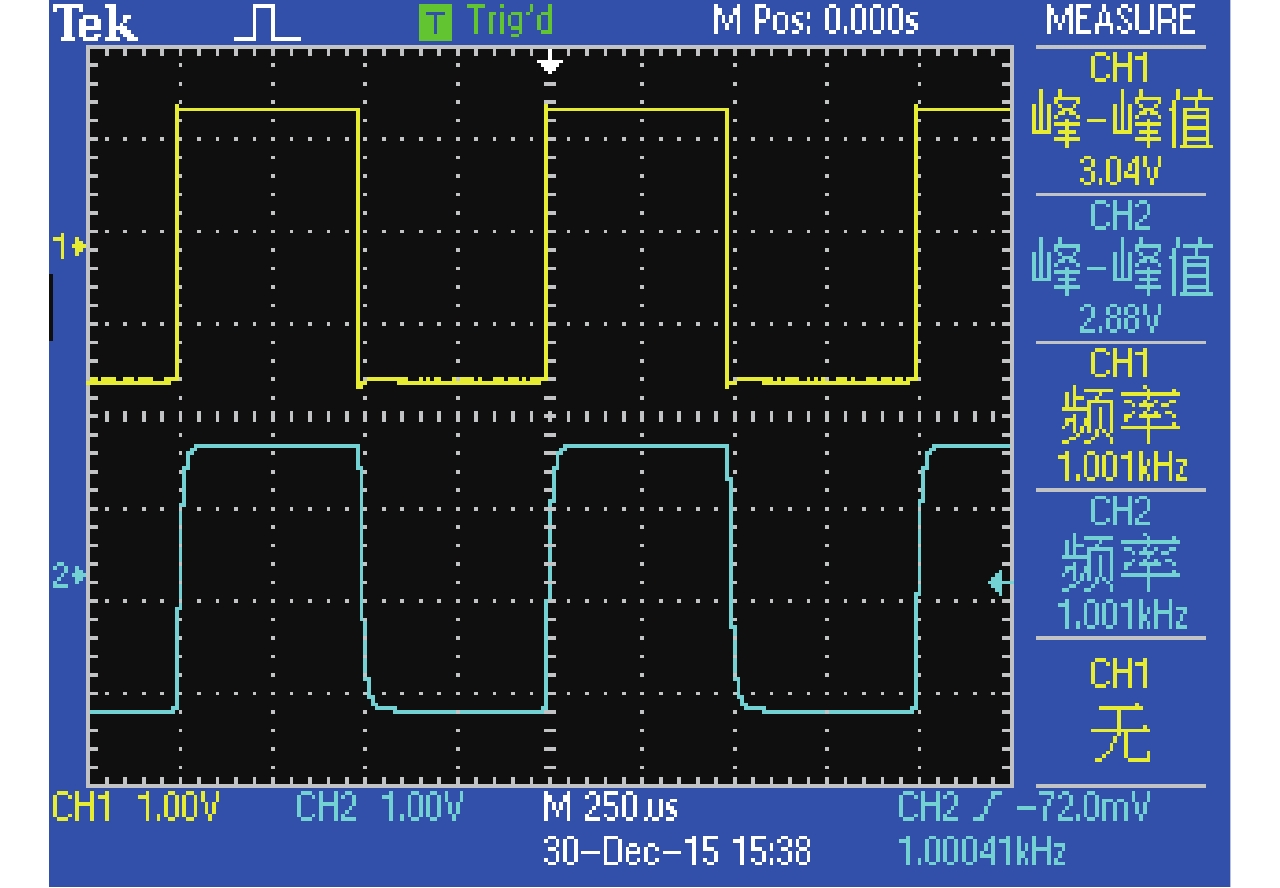
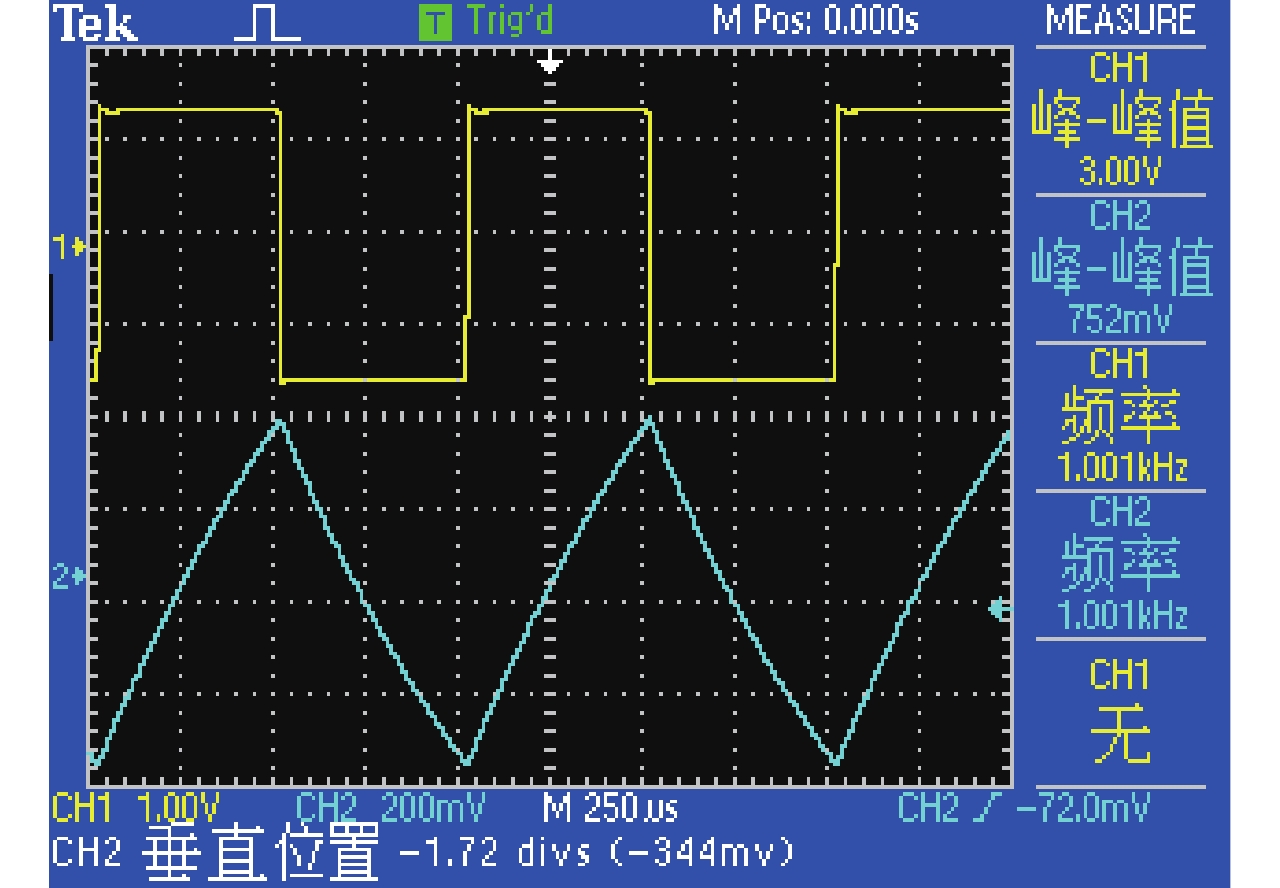
因此可以用可拓变换将实验的前提条件进行变式. 由τ =RC,增大电阻值或电容值,将“时间常数τ远小于输入方波周期”变式为“时间常数τ大于输入方波周期”,要求学生观察其实验现象特征的变化并分析其原因. 例如:在如图2所示电路中,令R=10 kΩ,C=10 nF,输入f =1 kHz方波信号,其输出响应波形如图3所示;在此基础上,令式(6)中,0<n <1,减小电路的电阻值或电容值,降低电路时间常数,电路的输出响应波形如 图4所示;另外令式(6)中,n >1,增大电路的电阻值或电容值,提高电路的时间常数,使实验的前提条件“时间常数 τ远小于输入方波周期”发生变化,出现如图5所示的实验现象;要求学生观察图3~5中波形的特征并分析特征变化的原因.
|
图 3 RC一阶动态电路输出响应波形1 Figure 3 An output waveform of RC first-order dynamic circuit |
|
图 4 RC一阶动态电路输出响应波形2 Figure 4 An output waveform of RC first-order dynamic circuit |
|
图 5 RC一阶动态电路输出响应波形3 Figure 5 An output waveform of RC first-order dynamic circuit |
由式(2)和式(5)可知,电路的一个特征是以电容为输出端口,输出信号为电路中电容两端的电压信号UC,通过可拓变换,有
| (7) |
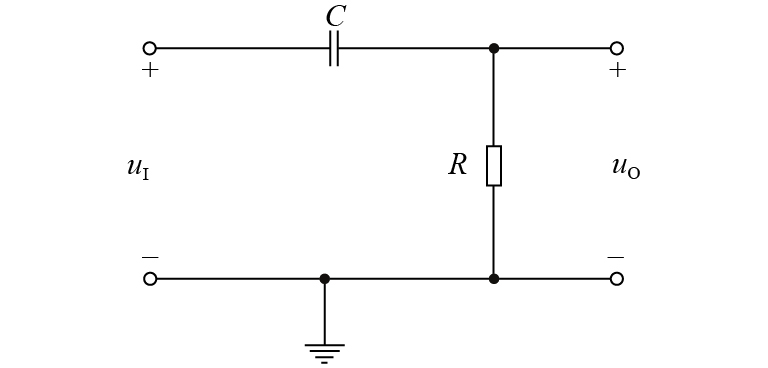
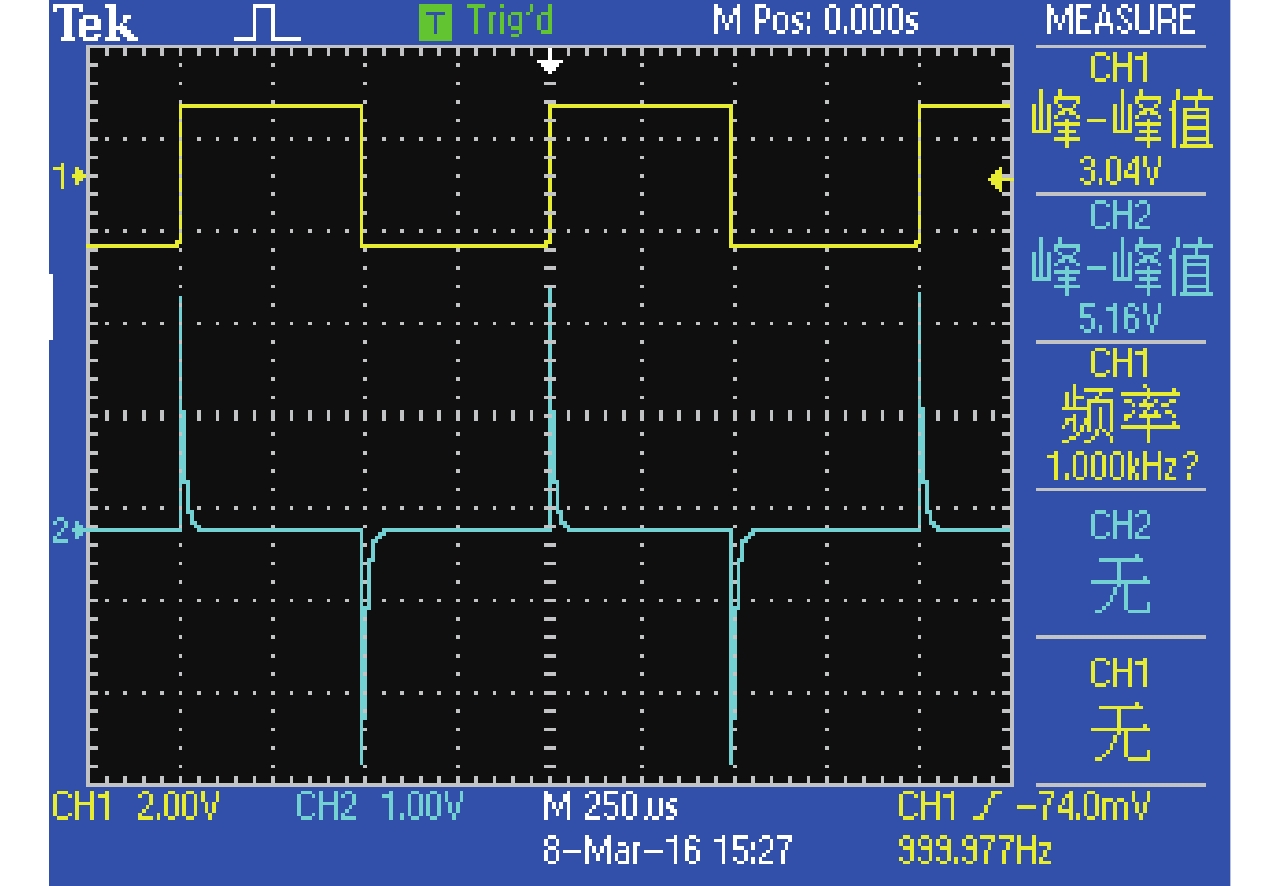
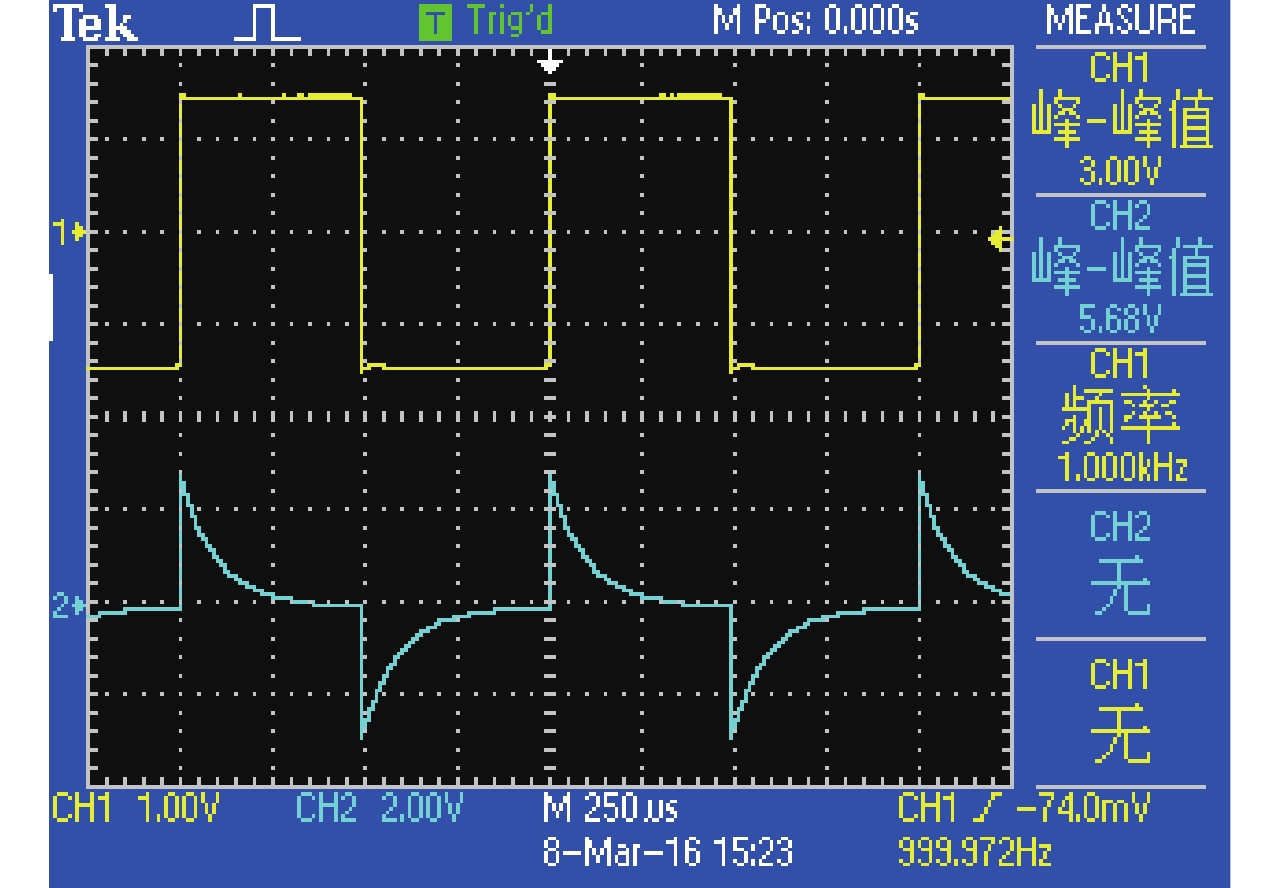
将输出端口变式为电阻器,输出信号变式为以电路中的电阻两端的电压信号UR为输出信号,变式后的电路如图6所示,要求学生观察输出信号波形的特征,对比图2和图6两种电路输出信号波形特征的不同并分析其原因. 例如:令图6电路中R=10 kΩ,C为1 nF,输入f =1 kHz方波信号,输出响应波形如图7所示;图8~9所示为改变电路时间常数得到的输出响应波形;要求学生观察图7~9中波形的特征并分析特征变化的原因.
|
图 6 进行变式的RC一阶电路 Figure 6 A RC first-order dynamic circuit by variation |
|
图 7 RC一阶电路进行变式后响应波形1 Figure 7 An output waveform of RC first-order dynamic circuit by variation |
|
图 8 RC一阶电路进行变式后响应波形2 Figure 8 An output waveform of RC first-order dynamic circuit by variation |
|
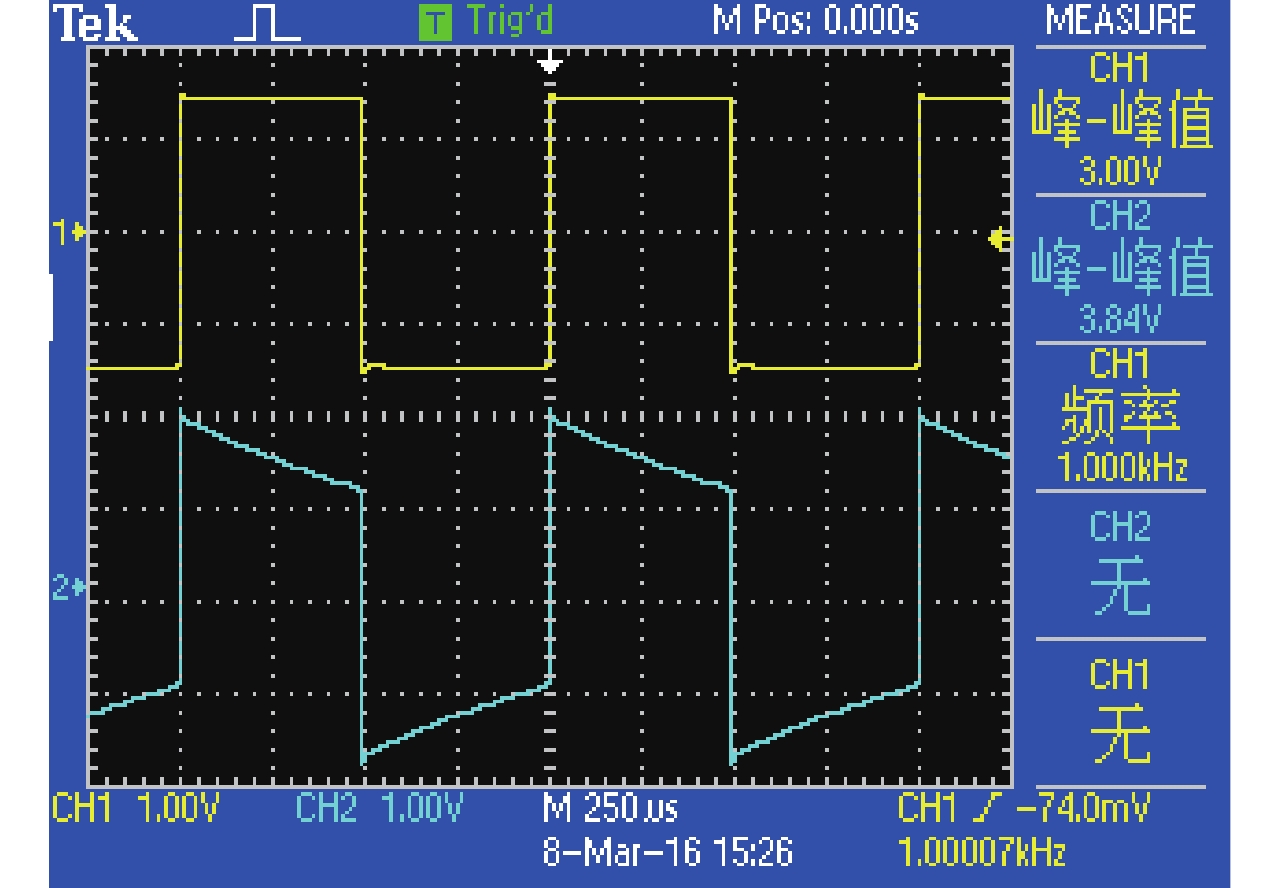
图 9 RC一阶电路进行变式后响应波形3 Figure 9 An output waveform of RC first-order dynamic circuit by variation |
(3) 基元应用变式.
由拓展分析尝试将电路原理的特征与实际应用相联系. 比如从式(4)、式(6)、图3~5波形曲线的特征变化,可知电路时间常数的大小与电容充放电速度的快慢之间存在相关性,同时电容充放电速度的快慢与控制时间长短之间存在相关性. 由拓展分析,有
| (8) |
| ((9)) |
如式(9)所示,可以联系到定时控制电路,如由调节电路时间常数来控制LED忽明忽暗速度的呼吸灯电路,将其作为学生“应用情境”学习的案例.
在教学实践中由于实验学时的限制,将学生的“应用情境”学习嵌入到《电工与电子技术实训》课程的电子工艺教学环节中,形成实验课程与实训课程相融合的教学模式[14]. 图10所示为学生完成的呼吸灯电路作品.

|
图 10 学生完成的呼吸灯电路 Figure 10 A breathing light made by a student |
(1) 设计变式的着眼点.
教师常常会这样假设:只要教师给学生讲清教学内容,学生对知识内容的理解就会和教师的理解一样. 事实上却并非如此[15]. 由于知识背景等原因,学生在加工、理解教师传递过来的信息时会存在一些困难或障碍.
因此,教师需要以学生已有的知识基础为“固定点”展开变式,为学生学习搭建“脚手架”。在进行基元建模,设计理论情境教学时,教师需要确定哪些教学内容的特征不容易被学生理解;在进行基元情境变式,设计实验情境教学时,教师需要思考如何让学生在循序渐进地完成实验的过程中,观察和分析实验现象关键特征的变易;在进行基元应用变式,设计应用情境教学时,教师需要考虑选取的应用案例的难易程度是否能为学生所接受。
(2) 可拓学的应用形式.
可拓学在变式教学中的使用主要体现在教师备课阶段,即作为指导教师进行的教学内容变式处理的方法,教师在教学中可不需将可拓学具体的有关内容透露给学生.
另外,本文以电工电子基础实验为例进行可拓学在特征变式的应用研究,由于电工电子实验教学的实际情况,仅仅采用了可拓学理论的部分内容. 教师若是将可拓学应用到其他课程的变式教学中,建议先阅读可拓学的有关文献,选择与本课程相关的内容,以便能更好地将可拓学理论结合到本课程的变式教学中.
5 结语变式是由重复学习向理解学习转化的实现途径,有助于学生对知识特征的理解,并促进学生的生产性学习. 教师在备课时,可以思考采用适当的变式进行教学. 由于可拓学研究了事物变换、拓展的可能性,这为可拓学指导教师如何进行教学内容的变式提供了可能.
变式是我国传统教育的一种特色,顾泠沅先生率先进行了研究,并将传统的变式教学进行恢复和整理[16],而可拓学是我国学者提出一门原创性学科,将可拓学理论应用到变式教学中,开展教学实践和研究,是对发展传统教学方法的一种尝试.
| [1] | 胡扬洋, 陈清梅, 邢红军. 中国物理变式教学研究: 传统与发展[J]. 教育导刊, 2014(2): 76-79. |
| [2] | 顾明远. 教育大辞典(简编本)[M]. 上海: 上海教育出版社, 1999. |
| [3] | 聂必凯. 数学变式教学的探索性研究[D]. 上海: 华东师范大学, 2004. http://cdmd.cnki.com.cn/article/cdmd-10269-2004087307.htm |
| [4] |
安永磊, 高淑贞, 刘娜, 等. 开放性创新实验教学模式优化与实践[J].
实验技术与管理, 2016, 33(8): 21-23, 27.
AN Y L, GAO S Z, LIU N, et al. Optimization and practice on teaching mode of open innovative experiments[J]. Experimental Technology and Management, 2016, 33(8): 21-23, 27. |
| [5] |
邓锂强, 朱伟玲. 把测量性实验改进为探究性实验[J].
实验技术与管理, 2015, 32(8): 170-172, 175.
DENG L Q, ZHU W L. Improving measurement experiments to exploration experiments[J]. Experimental Technology and Management, 2015, 32(8): 170-172, 175. |
| [6] |
蔡佩君, 王晓萍, 王立强, 等. 构建以效果和能力培养为主导的实验教学模式[J].
实验室研究与探索, 2016, 35(4): 186-189.
CAI P J, WANG X P, WANG L Q, et al. Construction of effect-and-ability-oriented experimental teaching model[J]. Research and Exploration in Laboratory, 2016, 35(4): 186-189. |
| [7] | 李韶卿. 高中生物教学应注重培养学生的思维品质[J]. 教育理论与实践, 2016, 31(5): 57-59. |
| [8] | 杨春燕, 蔡文.可拓工程[M]. 北京: 科学出版社, 2007. |
| [9] |
陈爱玲, 刘玮, 李兴森. 多方法协同提升顿悟能力的机制研究[J].
广东工业大学学报, 2015, 32(3): 18-22.
CHEN A L, LIU W, LI X S. Research on the coordinating methods to enhance the epiphany ability of university students[J]. Journal of Guangdong University of Technology, 2015, 32(3): 18-22. |
| [10] |
周志丹, 李兴森. 企业自主创新的可拓创新模型构建与应用研究[J].
科学学研究, 2010, 28(5): 769-776.
ZHOU Z D, LI X S. Research on extenics-based innovation model construction and application of enterprise independent innovation[J]. Studies in Science of Science, 2010, 28(5): 769-776. |
| [11] | 陈红兵. 变式理论与变异理论———两个教学理论的比较与关系探析[J]. 教育科学研究, 2013(8): 22-26. |
| [12] | 卢敏玲. 变易理论和优化课堂教学[M]. 合肥: 安徽教育出版社, 2011. |
| [13] | 彭端. 电工与电子技术实验教学[M]. 武汉: 武汉大学出版社, 2011. |
| [14] |
郭萍, 张园如, 任青莲. 基于三课一体的电子技术教学模式[J].
山西电子技术, 2013(6): 26-27.
GUO P, ZHANG Y R, REN Q L. Electronic technology teaching mode based on a system of three classes[J]. Shanxi Electronic Technology, 2013(6): 26-27. |
| [15] | 孟扬, 朱月华. 变异教学理论(上)[J]. 中国教师, 2014(9): 89-92, 95. |
| [16] |
李静, 王秀兰. 本原性问题驱动下的高等数学变式教学[J].
数学教育学报, 2013, 22(6): 94-97.
LI J, WANG X L. Teaching Higher Mathematics with variation under primitive ideas driving[J]. Journal of Mathematics Education, 2013, 22(6): 94-97. |
 2017, Vol. 34
2017, Vol. 34
