双种群烟花算法

引用本文

徐焕芬, 刘伟, 谢月珊. 双种群烟花算法[J]. 广东工业大学学报, 2017, 34(5): 65-72. DOI: 10.12052/gdutxb.160124.

Xu Huan-fen, Liu Wei, Xie Yue-shan. Fireworks Algorithm Based on Dual Population for Optimization Problems[J]. JOURNAL OF GUANGDONG UNIVERSITY OF TECHNOLOGY, 2017, 34(5): 65-72. DOI: 10.12052/gdutxb.160124. 复制到剪切板

基金项目:

国家自然科学基金资助项目(61202269)

作者简介:

徐焕芬(1992–)，女，硕士研究生，主要研究方向为智能计算。

文章历史

收稿日期：2016-10-10

Contents Abstract Full text Figures/Tables PDF

双种群烟花算法

徐焕芬, 刘伟, 谢月珊

广东工业大学　应用数学学院，广东　广州 510520

收稿日期：2016-10-10

基金项目：国家自然科学基金资助项目(61202269)

作者简介：徐焕芬(1992–)，女，硕士研究生，主要研究方向为智能计算。

摘要: 为了克服烟花算法收敛速度慢、种群多样性不足的缺陷, 提出一种基于双种群策略的烟花算法. 该算法两个种群并行独立运算, 进化过程中两种群交叉执行爬山算子与协作算子; 爬山算子有利于加强算法的局部搜索能力, 协作算子促使两种群信息交换, 维持种群多样性, 避免陷入局部最优解; 同时算法改进了最大爆炸半径的设置方法, 采用锦标赛选择策略以提高算法的收敛速率. 实验对比说明, 新算法是一个有效的稳定算法, 具有更高的求解精度和更快的收敛速度.

关键词: 烟花算法双种群协作算子爬山算子

Fireworks Algorithm Based on Dual Population for Optimization Problems

Xu Huan-fen, Liu Wei, Xie Yue-shan

School of Applied Mathematics, Guangdong University of Technology, Guangzhou 510520, China

Abstract: A fireworks algorithm based on dual population is proposed to solve optimization problems. A dual population strategy is used to amend the shortcomings, i.e. slow convergence and bad population diversity of the existing fireworks algorithms. Each of two populations is running independently. Meanwhile, they alternately perform the hill-climbing and collaborative operator during the evolution process. Therein, the hill-climbing operator can enhance the local search performance of the proposed algorithm. And the collaborative operator is utilized to maintain the population diversity, avoiding getting stuck in local optimal regions. Furthermore, the proposed algorithm improves the setting of the maximum amplitude of the explosion and uses the tournament selection strategy to improve the convergence rate. The experimental results indicate that the proposed algorithm is superior to the compared algorithms in terms of the stabilization and reliability for most of test problems. It has higher accuracy lever and faster convergence rate.

Key words: fireworks algorithm dual population collaborative operator hill-climbing operator

Ying Tan在2010年受烟花爆炸的启发，提出了烟花算法. 该算法的寻优能力强，得到广大研究者的青睐. 烟花算法主要由爆炸算子，变异算子和选择策略组成，具有对质量较好的烟花进行局部搜索和对较差的烟花进行全局搜索的能力. 传统烟花算法存在以下3个不足之处：(1) 受烟花爆炸半径的影响，后期烟花爆炸半径大于最优峰值所在的区域，以致陷入局部最优；(2) 若搜索区域很小，高斯变异作用被弱化；(3) 传统烟花算法所使用的轮盘赌选择策略，随机性较大，不能保证留下较多的优质的烟花，从而降低了算法的收敛速度.

为此，许多学者提出多种对烟花算法的爆炸半径、变异算子、烟花爆炸策略等的改进^[1-11]. 文献[1]提出基于定向变异的烟花算法，该算法根据烟花爆炸信息确定变异方向与变异步长，定向变异产生的潜在解添加到种群，有利于提高种群的多样性与质量；文献[2]提出基于差分进化操作的烟花算法，该算法引入了交叉算子和变异算子，通过增加种群多样达到跳出局部最优的目的；文献[3]通过独立选择操作和避免拥挤的合作策略，动态修改爆炸半径方法来提高种群多样性，但该文所用的固定搜索空间方法可能导致算法效率不高；文献[4]对每个烟花采用动态爆炸半径，若找到更优值则爆炸半径将增大，否则爆炸半径减小，此方法有利于提高算法的局部搜索能力；文献[5]引入自适应转换函数，利用自适应转换函数产生烟花爆炸的数量和爆炸的幅度，能够产生质量高的解；文献[6]提出的改进的烟花爆炸优化算法，该论文采用精英策略，每一代的每个烟花按一定的概率与最好的个体进行交叉操作，可丰富烟花种群的多样性，使之跳出局部最优值，但后期存在交叉变异失效的情况；文献[7]将烟花算法与差分算法相结合，通过模型结构的改进和参数的学习，从而扩大搜索范围，避免过早陷入局部最优，但该算法使用保留较优个体进入下一轮迭代的选择策略，使得算法前期收敛速度快而后期收敛速度慢；文献[8]针对种群初始化出现的个体分布不均匀的情况，提出自适应反向学习算子，可加快算法的收敛速度，但易陷入局部最优；文献[9-10]分别针对高斯变异存在的缺点提出协方差变异和差分变异，可以弥补高斯变异的不足，使其具有跳出局部最优的能力，但协方差变异计算代价较高，差分变异则易陷入局部最优值；文献[11]提出改进烟花爆炸半径的方法，保证算法前期搜索半径较大，后期接近最优值时爆炸半径较小，有利于增强算法局部搜索与全局搜索能力，但是该算法的优化效果不明显，找到的最优值与精确值有一定的误差.

本文利用爬山算子和协作算子与烟花算法相结合，提出了一种双种群烟花算法. 该算法采用双种群结构，两个种群独立进化，算法在一定条件下通过信息互换，增加种群多样性. 数据实验分析表明，新算法具有较快收敛速度和较高的求解精度.

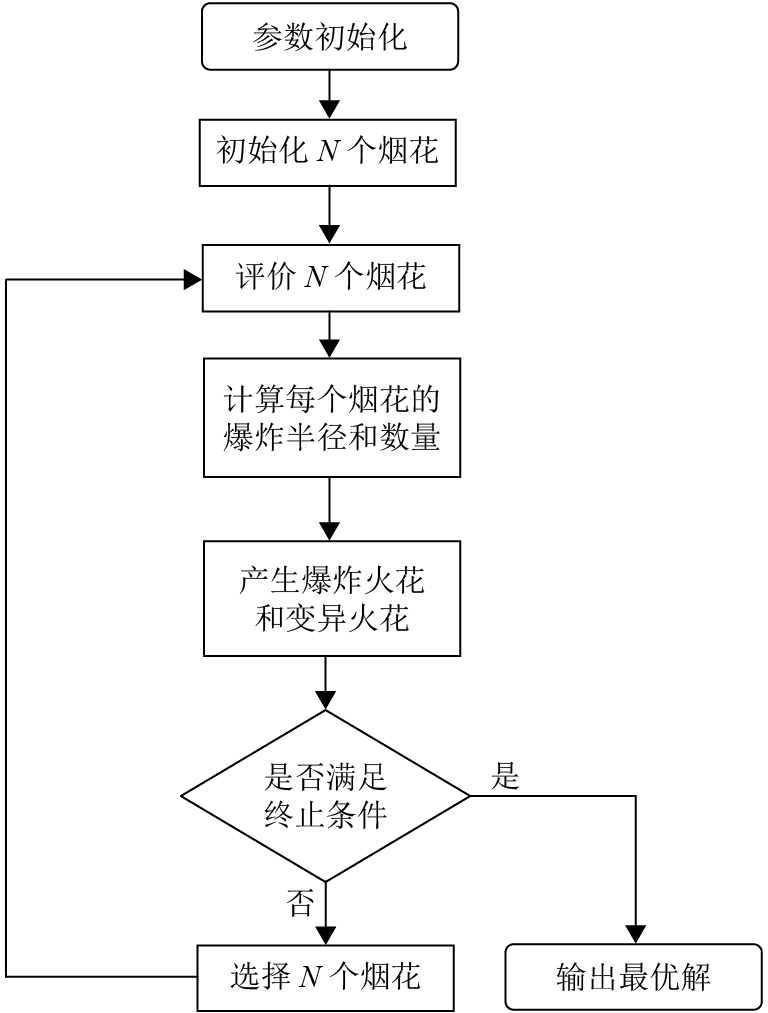
1 烟花算法

烟花算法是受实际生活中烟花爆炸产生火花的启发而提出的一种智能优化算法^[12-13]，在这里烟花被视为可行域内的一个解向量，烟花爆炸产生火花的过程即解在其领域内的搜索过程. 烟花算法的寻优性能主要是由爆炸算子、变异算子和选择策略决定，烟花算法其程序框图如图1所示.

图 1 烟花算法流程图 Figure 1 Flowchart of fireworks algorithm

1.1 烟花初始化

在烟花算法中，假设求解的问题为n维函数的无约束优化问题

$\min f\left( X \right) \in {\bf{R}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} X \in {\bf{\Omega }} \subset {{\bf{R}}^n}.$

(1)

其中 ${\bf{\Omega }}$ 为可行域，在可行域内随机产生N个烟花，第i个烟花的位置为 ${X_i} = \left( {x_{_i}^1,x_{_i}^2, \cdots ,x_{_i}^n} \right)$ ， $\left( {i = 1,2, \cdots ,N} \right)$ , 并计算该烟花的适应值f_i.

1.2 烟花爆炸操作

烟花爆炸操作，先评价可行域内产生的烟花的适应值. 为了保证较优烟花进行局部搜索，较差烟花进行全局搜索的目的，对烟花爆炸的半径和爆炸数量进行设计.

根据式(2)和(3)计算第i个烟花的爆炸半径A_i，爆炸数量S_i.

${A_i} = A \times \frac{{f\left( {{X_i}} \right) - {y_{{\rm{min}}}} + \varepsilon }}{{\sum\limits_{i = 1}^N {\left( {f\left( {{X_i}} \right) - {y_{{\rm{min}}}}} \right)} + \varepsilon }},$

(2)

${S_i} = S \times \frac{{{y_{{\rm{max}}}} - f\left( {{X_i}} \right) + \varepsilon }}{{\sum\limits_{i = 1}^N {\left( {{y_{{\rm{max}}}} - f\left( {{X_i}} \right)} \right) + \varepsilon } }}.$

(3)

其中， ${y_{{\rm{min}}}} = \min \left\{ {f\left( {{X_1}} \right),f\left( {{X_2}} \right), \cdots ,f\left( {{X_N}} \right)} \right\}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} $ 代表N个烟花中适应值最小值； ${y_{{\rm{max}}}} = \max \left\{ {f\left( {{X_1}} \right),{\left( {{X_2}} \right), \cdots ,}} \right.$ $\left. {f\left( {{X_N}} \right)} \right\}$ 代表N个烟花中适应值最大值；A为最大爆炸半径；S代表最大爆炸数量； $\varepsilon $ 代表一个非常小的数；式(2)说明较优烟花的搜索半径较小，执行局部搜索行为，较差的烟花执行全局搜索行为；式(3)说明每一轮迭代质量较好的烟花可爆炸产生更多数量的火花，获得较多优质烟花.

烟花爆炸需要确定每个烟花的爆炸半径和爆炸产生火花数量. 第i个烟花产生第j个火花 ${x_{\left( {i,j} \right)}}$ 的方式为：随机选取第i个烟花的Z维坐标按式(4)更新.

$x_{\left( {i,j} \right)}^k = x_i^k + {A_i} \times {\rm{rand}}\left( { - 1,1} \right),1 \leqslant k \leqslant Z.$

(4)

为了保证烟花爆炸后产生的火花在可行域内，利用式(5)进行越界处理.

$\left\{ \begin{array}{l}{B^k_{\rm{u}}} - {\rm{rand}}\left( 1 \right) \times \left( {x_i^k - {B^k_{\rm{u}}}} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_i}^k > {B^k_{\rm{u}}};\\[9pt]{B^k_{\rm{d}}} + {\rm{rand}}\left( 1 \right) \times \left( {{B{^k_{\rm{d}}}} - x_i^k} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_i}^k < {B^k_{\rm{d}}}.\end{array} \right.$

(5)

其中， $x_{\left( {i,j} \right)}^k$ 代表第i个烟花产生的第j个火花的第k维的坐标， ${B_{\rm{u}}}^k$ 代表第k维坐标的上界， ${B_{\rm{d}}}^k$ 代表第k维坐标的下界， ${\rm{rand}}\left( 1 \right)$ 代表[0, 1]的随机数， ${\rm{rand}}\left( { - 1,1} \right)$ 代表[–1, 1]的随机数.

1.3 烟花变异操作

烟花变异过程是按高斯分布产生m个变异火花以增加种群多样性的目的，避免陷入局部最优. 烟花种群中随机选择m个烟花，每个烟花随机选择z维坐标进行高斯变异操作，第i个烟花的第 $k,\left( {k = 1,2, \cdots ,z} \right)$ 维的坐标按式(6)更新.

$\dot x_i^k = x_i^k \times {\rm{Gaussian}}\left( {1,1} \right).$

(6)

其中， ${\rm{Gaussian}}\left( {1,1} \right)$ 表示均值和方差均为1的高斯分布随机数， $\dot x_i^k$ 表示第i个变异火花的第k维坐标，若变异火花为不可行解，则按式(5)进行越界处理.

1.4 烟花选择策略

经过烟花爆炸和变异后产生的烟花与火花总数为 $K = N + S + m$ ，选择N个烟花（火花）组成下一代种群. 传统烟花算法使用轮盘赌策略，该策略在保存最优个体的前提下使用轮盘赌选择N-l个个体生成烟花种群.

2 双种群烟花算法

双种群^[14]是维持种群多样的一种有效方法. 新算法的两个种群并行独立运算，交替执行爬山算子和协作算子；爬山算子有利于种群进行局部搜索，协作算子通过两个种群间信息共享，有利于种群进行全局搜索.

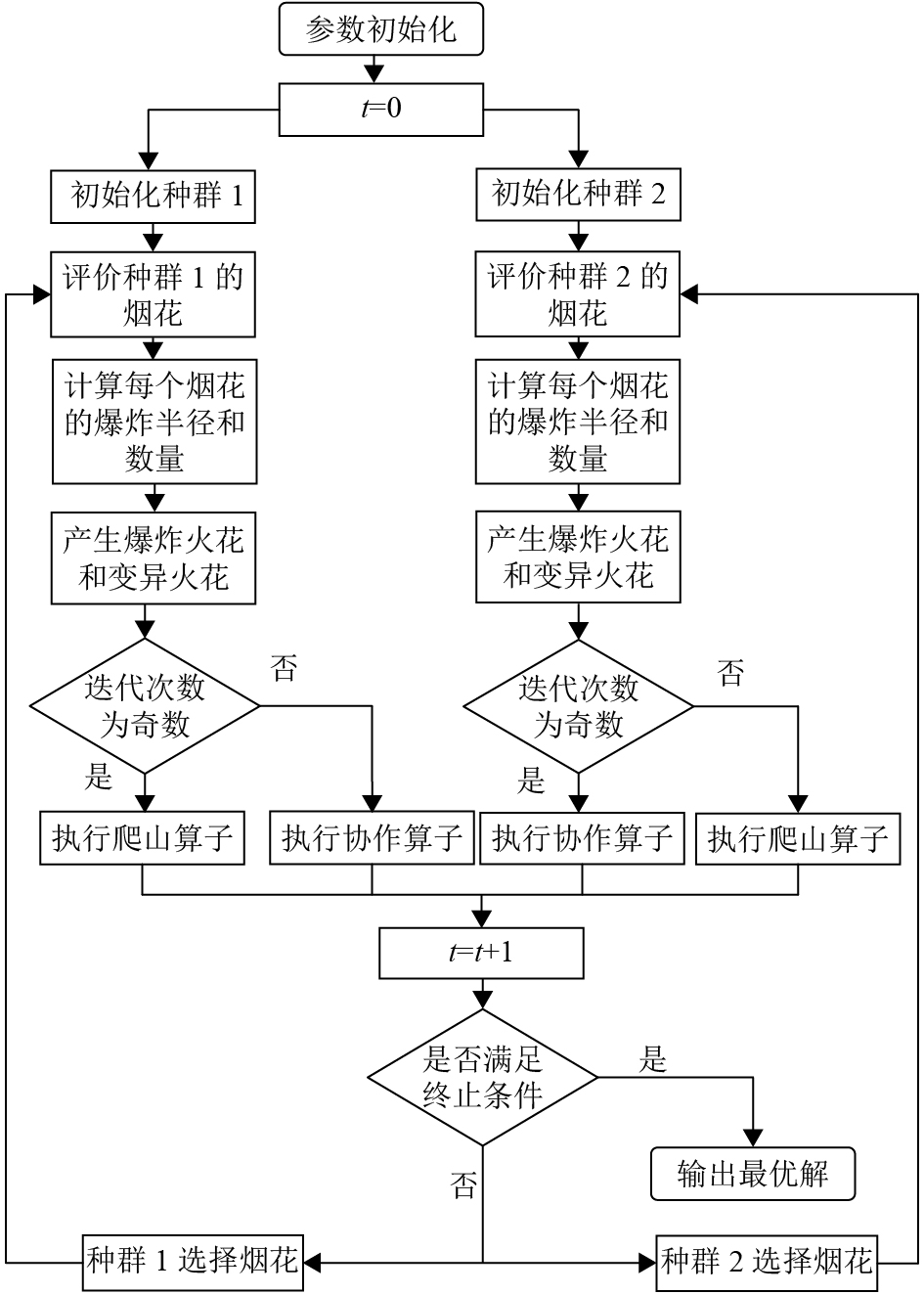
双种群烟花算法的流程图如图2所示.

图 2 双种群烟花算法流程图 Figure 2 Flowchart of dual population fireworks algorithm

2.1 最大爆炸半径的设置

传统烟花算法中最大爆炸半径设为常数，这使得算法后期精细搜索能力被弱化，导致算法精度不高. 根据动态搜索的思想，最大爆炸半径呈非线性递减的变化，有利于算法前期侧重全局搜索，后期侧重局部搜索，以达到加快算法收敛速度的效果.

$A = {A_{{\rm{init}}}} - \left( {{A_{{\rm{init}}}} - {A_{{\rm{final}}}}} \right)\frac{{\sqrt {\left( {2{\rm{MaxIter}} - {\rm{curIter}}} \right) \times {\rm{curIter}}} }}{{{\rm{MaxIter}}}},$

(7)

其中， ${\rm{MaxIter}}$ 表示最大迭代次数； ${\rm{curIter}}$ 表示当前迭代次数；A表示当前迭代中最大的爆炸半径； ${A_{{\rm{init}}}}$ 表示算法初始爆炸半径； ${A_{{\rm{final}}}}$ 表示算法结束时爆炸半径.

2.2 爬山算子

爬山算子^[15-16]是对个体进行局部寻优的一种操作. 首先随机生成一个搜索方向D, 个体 ${X_i}$ 沿D的正方向搜索，计算出步长为 $\lambda $ 的新个体，若新个体优于原个体，则步长不变，并替换原个体 ${X_i}$ ，否则将步长减半，重新搜索，一直重复l次，对个体进行局部寻优.

定义　若个体 ${X_i} = \left( {x_i^1,x_i^2, \cdots ,x_i^n} \right)$ ，搜索方向 $D = \left( {{d_1},{d_2}, \cdots ,{d_j}, \cdots ,{d_n}} \right)$ , 其中d_j为[0, 1]的随机数， $j = 1,2, \cdots ,n$ ，令 $\lambda = 1$ ， $l = 10$ .

步骤1：P=1；

步骤2： ${X_i}$ 沿D的正方向搜索，得到个体 $X_i'$

$X_i' = {X_i} + \lambda D;$

(8)

步骤3: 若新个体优于原个体，则步长不变，并替换个体 ${X_i}$ ，否则令 $\lambda = \displaystyle\frac{\lambda }{2}$ ；

步骤4:若 $P \leqslant l$ , 则 $P = P + 1$ , 返回步骤2；否则算法结束.

2.3 协作算子

协作算子^[17-19]有算术交叉算子和两点交叉算子两种形式，由交叉概率 $p_c$ 控制决定，如果满足 ${\rm{rand}}\left( {0,1} \right) < p_c$ ，则执行算术交叉操作，否则执行两点交叉操作. 协作算子通过个体间信息共享，既可维持种群多样性，也可优化个体.

2.3.1 算术交叉操作

双种群烟花算法中，若种群1中个体 ${X_i}$ 执行算术交叉操作，则从种群2中选择当前最优个体 ${X_j}$ ，按以下方式产生新个体：

$X_i' = r \cdot {X_i} + \left( {1 - r} \right) \cdot {X_j},$

(9)

$X_i{''} = \left( {1 - r} \right) \cdot {X_i} + r \cdot {X_j}.$

(10)

其中r表示算术交叉因子， $X_i'$ 、 $X_i^{''}$ 分别表示产生的新个体，若新个体优于 ${X_i}$ ，则更新 ${X_i}$ . 通过个体与其他种群的优质个体交叉交换信息产生了两个新的个体，可有效保持种群的多样性，有利于种群的进化.

2.3.2 两点交叉算子

双种群烟花算法中，若种群1中个体 ${X_i}$ 执行两点交叉操作，则从种群2中随机选择优个体 ${X_j}$ ，随机产生两个交叉点位置a，b，将交叉点所夹的片段进行交换产生新个体：

$X_i' = \left( {x_i^1,x_i^2, \cdots ,x_j^a,x_j^{a + 1}, \cdots ,x_j^b, \cdots x_i^n} \right){\kern 1pt} {\kern 1pt} ,$

(11)

$X_i^{''} = \left( {x_j^1,x_j^2, \cdots ,x_i^a,x_i^{a + 1}, \cdots ,x_i^b, \cdots x_j^n} \right){\kern 1pt} {\kern 1pt} .$

(12)

其中 $1 \leqslant a \leqslant b \leqslant n$ , $X_i'$ 、 $X_i^{''}$ 分别表示产生的新个体，若新个体优于 ${X_i}$ ，则更新 ${X_i}$ ，否则以小概率p保留新个体，一般 $p \leqslant 0.01$ .该算子能提高算法的收敛速度，一定程度上又维持了种群的多样性.

2.4 选择策略

为了尽可能多地将优秀个体保留到下一代种群中，新算法采用锦标赛选择策略^[20].

双种群烟花算法中，每个种群独立选择生成下一代种群，选择方式为先使用最优保存策略保留最优烟花，然后采用锦标赛选择策略选择N-l个烟花组成下一代种群. 锦标赛选择策略规模c=10.

2.5 双种群并行搜索策略

由图2可知, 双种群烟花算法中种群1与种群2是两个相互独立进化的种群，两个种群共享同一参数t（进化代数），两个种群搜索都由t控制；在同一次进化迭代中，两个种群各自执行爆炸算子、变异算子、爬山算子或协作算子、种群选择与评价，实现双种群的独立搜索优化，完成双种群并行搜索策略.

3 数值仿真

为测试本文所提出算法的性能，如表1选取CEC2013测试集^[21]中5个测试函数(F₁、F₂、F₆、F₇、F₈)和CEC2014测试集^[22]中的3个测试函数(F₃、F₄、F₅)，将新算法(记为DPFA)分别与同类型算法如反向烟花算法(记为OBLFA)^[8]、混沌烟花算法(记为CPAFA)^[23]、遗传算法(记为DECGA)^[24]和微分进化算法(记为DE)^[25]进行比较.

表 1 测试函数 Table 1 Test Function

函数名	测试函数	搜索空间	最优值	维数
Sphere	${F_1} = \sum\limits_{i = 1}^n {x_i^2} $	[–10, 10]	0	50
Rastrigin	${F_2} = \sum\limits_{i = 1}^n {\left( {x_i^2 - 10\cos \left( {2{\rm{\pi }}{\kern 1pt} {x_i}} \right) + 10} \right)} $	[–10, 10]	0	30
Bent Cigar	${F_3} = x_{_1}^2 + {10^6}\sum\limits_{i = 2}^n {x_i^2} $	[–100, 100]	0	50
Ackyey	$\begin{array}{l}{F_4} = - 20{\rm{exp}}\left( { - 0.2\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {x_i^2} } } \right) - \exp \left( {\frac{1}{n}\sum\limits_{i = 1}^n {\cos 2{\rm{\pi }}{x_i}} } \right)\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + 20 + e\end{array}$	[–32, 32]	0	100
HGBat	$\begin{array}{l}{F_5} = {\left\| {{{\left( {\sum\limits_{i = 1}^n {x_i^2} } \right)}^2} - {{\left( {\sum\limits_{i = 1}^n {{x_i}} } \right)}^2}} \right\|^{\frac{1}{n}}} + \left( {0.5\sum\limits_{i = 1}^n {x_i^2} + \sum\limits_{i = 1}^n {{x_i}} } \right)/n\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + 0.5\end{array}$	[–100, 100]	0	100
Rosenbrock	${F_6} = \sum\limits_{i = 1}^{n - 1} {\left[ {100{{\left( {x_i^2 - {x_{i + 1}}} \right)}^2} + {{\left( {{x_i} - 1} \right)}^2}} \right]} $	[–10, 10]	0	5
Griewank	${F_7} = {\displaystyle\frac{1}{{4\;000}}}\sum\limits_{i = 1}^5 {x_i^2} - \prod\limits_{i = 1}^5 {\cos (\frac{{{x_i}}}{{\sqrt i }})} + 1$	[–600, 600]	0	30
Trid6	${F_8} = \sum\limits_{i = 1}^n {{{\left( {{x_i} - 1} \right)}^2} - \sum\limits_{i = 2}^n {{x_i}{x_{i - 1}}} } $	[–36, 36]	–50	6

表 1 测试函数 Table 1 Test Function

数值实验运用MATLAB编程，为了比较的有效性，3种算法采用相同的参数设置，种群规模为100，最大迭代次数为100，同一条件下独立运行50次，记录实验结果的最优值、最差值、均值和标准差.

3.1 交叉概率p_c和算术交叉因子r参数灵敏度分析

选取测试函数F₁，给出了新算法对交叉概率p_c和算术交叉因子r的灵敏度分析，如表2所示.

表 2 F₁交叉概率p_c和算术交叉因子r的参数灵敏度分析 Table 2 F₁ sensitivity analysis in parameter of p_c and r

表2给出了不同p_c和r情况下，测试函数F₁实验所求的最优值. 由表2知，F₁的最优值为1.54×10^–20，从而确定测试函数F₁参数值选择为r=0.9，p_c=0.1.

本文通过多个测试函数，若干组p_c和r组合进行数值实验，比较优化效果，给出了p_c和r的选择参考范围，建议r的取值范围为[0.5, 1]，p_c的取值范围为[0.1, 0.7]. 其他7个测试函数是在p_c和r的选择参考范围内，经过类似参数灵敏度分析方法确定p_c和r参数值，如表3所示.

3.2 种群多样性评价

种群熵^[26]是常用的评价种群多样性的方法之一，种群熵的定义如下：若第t代种群有Q个子集： ${S_{t1}}, $ ${S_{t2}},\; \cdots ,\;\; $ ${S_{tQ}},\;$ 各子集包含的个体数目记为 $\left| {{S_{t1}}} \right|$ ， $\left| {{S_{t2}}} \right|,\; \cdots ,\; $ $\left| {{S_{tQ}}} \right|$ ，且对任意 $p,q \in \left\{ {1,2, \cdots ,Q} \right\}$ ， ${S_{tp}} \cap {S_{tq}} = \emptyset $ ， $\mathop \cup \limits_{q = 1}^Q {S_{tq}} = {A_t}$ ， ${A_t}$ 为第t代解群的集合，则第t代种群的熵计算公式为

${E_t} = - \sum\limits_{j = 1}^Q {{P_j}\lg \left( {{P_j}} \right)} ,$

(13)

${P_j} = \frac{{\left| {{S_{tj}}} \right|}}{N}.$

(14)

其中，N为解群中个体的数目，当解群中个体都相同时，Q=1，种群熵取最小值 ${E_{\min }} = 0$ ，当解群中个体均不相同时，Q=N，种群熵取最大值 ${E_{\max }} = \lg \left( N \right)$ .

表4为3种算法对同一测试函数F₁数值实验在不同迭代次数时计算所得种群熵值，对比分析可知：本文算法早期(前30代)种群熵较大，后期(50代后)种群熵较小；说明新算法早期种群多样好，利于算法全局搜索，后期种群集中利于局部搜索，从而提高算法优化性能.

表 3 F₁-F₈优化计算结果 Table 3 Optimum results of F₁-F₈

函数	算法	参数值	最差值	最优值	均值	标准差
F₁	OBLFA	p_c=0.1r=0.9	0.312 6	1.82×10^–10	0.006 7	0.044 2
	CPAFA		6.11×10^–6	2.13×10^–9	5.29×10^–7	1.01×10^–6
	DPFA		2.42×10^–14	2.74×10^–19	7.07×10^–16	3.39×10^–15
F₂	OBLFA	p_c=0.6r=0.8	0.891 0	3.64×10^–12	0.072 5	0.170 9
	CPAFA		0.008 5	3.76×10^–10	0.000 2	0.002 3
	DPFA		0.405 272	0	0.008 1	0.056 7
F₃	OBLFA	p_c=0.1r=0.9	0.559 7	9.57×10^–5	0.088 7	0.142 9
	CPAFA		0.895 5	1.02×10^–3	0.176 0	0.223 2
	DPFA		1.53×10^–7	4.47×10^–14	4.71×10^–9	2.15×10^–8
F₄	OBLFA	p_c=0.6r=0.8	0.677 2	1.31×10^–3	0.109 9	0.160 7
	CPAFA		0.168 6	9.69×10^–3	0.049 0	0.029 3
	DPFA		0.017 2	8.88×10^–16	0.002 8	0.002 9
F₅	OBLFA	p_c=0.2r=0.8	0.863 8	0.421 8	0.565 1	0.097 5
	CPAFA		0.662 0	0.439 3	0.505 7	0.054 1
	DPFA		0.908 0	0.412 5	0.629 0	0.177 6
F₆	DECGA	p_c=0.1r=0.9	0.730 2	4.67×10^–4	0.259 6	0.235 1
	DE		0.773 8	0.025	0.232 2	0.104 0
	DPFA		9.58×10^–12	7.90×10^–28	1.93×10^–13	1.34×10^–12
F₇	DECGA	p_c=0.6r=0.8	0.006 5	1.68×10^–9	7.62×10^–4	1.51×10^–3
	DE		0.278 5	8.7×10^–3	0.027 6	0.040 1
	DPFA		6.63×10^–11	0	1.50×10^–12	8.91×10^–12
F₈	DECGA	p_c=0.2r=0.8	–47.928 7	–49.999 4	–49.500 3	0.429 2
	DE		–45.048 9	–49.756 9	–47.633 5	1.118 3
	DPFA		–49.999 9	–50	–49.999 9	1.03×10^–13

表 3 F₁-F₈优化计算结果 Table 3 Optimum results of F₁-F₈

3.3 实验结果比较分析

表 4 种群多样性评价 Table 4 Population diversity

由表3可知，F₁、F₃、F₄、F₆、F₇、F₈测试函数，新算法的最差值、最优值、均值、标准差均优于反向烟花算(OBLFA)和混沌烟花算法(CPAFA).

对于F₂，新算法求出函数最优解，相对于F₁，F₃，F₄新算法精度分别为10^–19、10^–14、10^–16，说明新算法有较高的求解精度；与反向烟花算法与混沌烟花算法比较，新算法的实验数据大部分标准差均最小，说明新算法的稳定性较高.

对于函数F₇，F₈，新算法找到理论最优值，对于F₆，新算法求解的最优值为7.90×10^–28，说明新算法寻优能力优于遗传算法(DECGA)和微分进化算法(DE)；新算法的实验数据的均值，标准差均最小，说明新算法的稳定性高于遗传算法和微分进化算法.

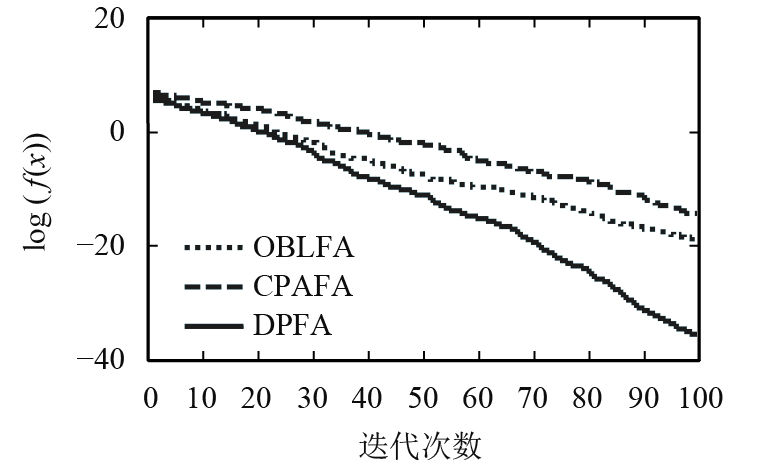
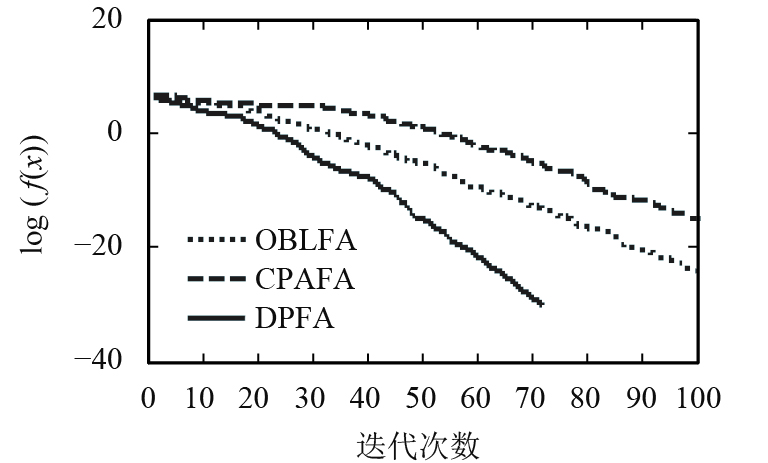
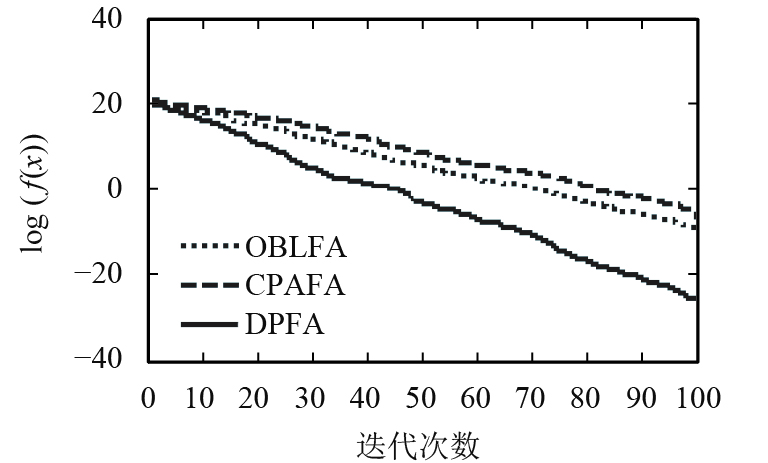
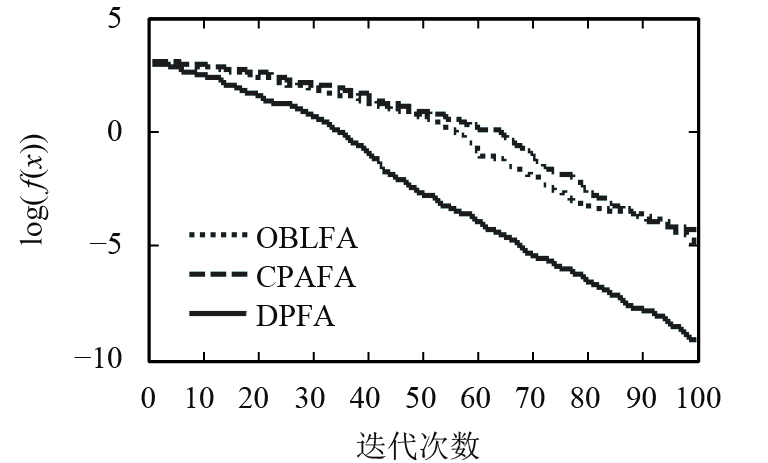
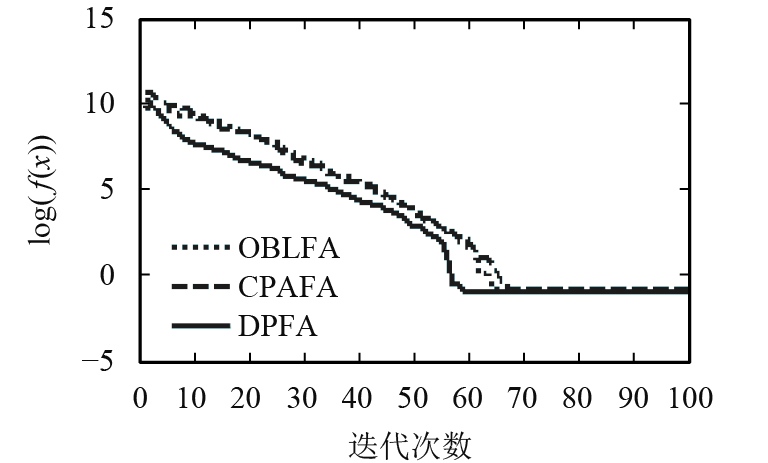
测试函数的进化曲线图如图3~10所示. 由图3~7可以看出，新算法收敛速度均优于反向烟花算(OBLFA)和混沌烟花算法(CPAFA).新算法引入爬山算子，增强了算法局部搜索能力，具有不断寻优的能力，从而提高算法收敛速度；新算法两种群独立并行搜索，在每次迭代中，通过协作算子实现信息交流共享；新算法中的协作算子能够提高种群多样性与种群质量，加强了算法的全局搜索能力.

图 3 F₁进化曲线 Figure 3 F₁ convergence curve

图 4 F₂进化曲线 Figure 4 F₂ convergence curve

图 5 F₃进化曲线 Figure 5 F₃ convergence curve

图 6 F₄进化曲线 Figure 6 F₄ convergence curve

图 7 F₅进化曲线 Figure 7 F₅ convergence curve

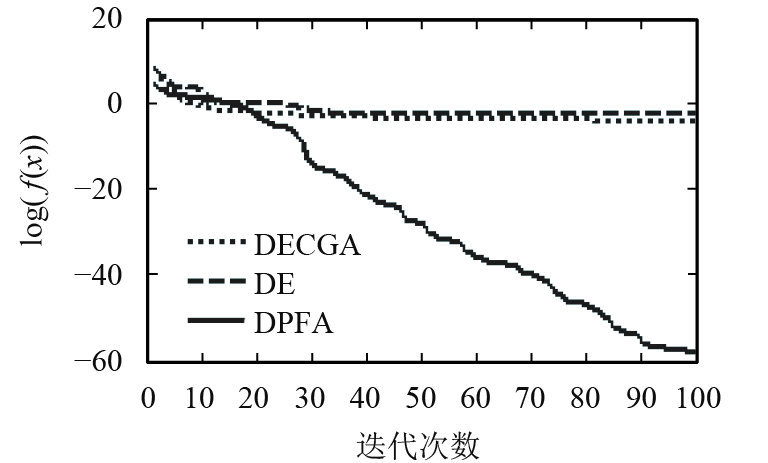
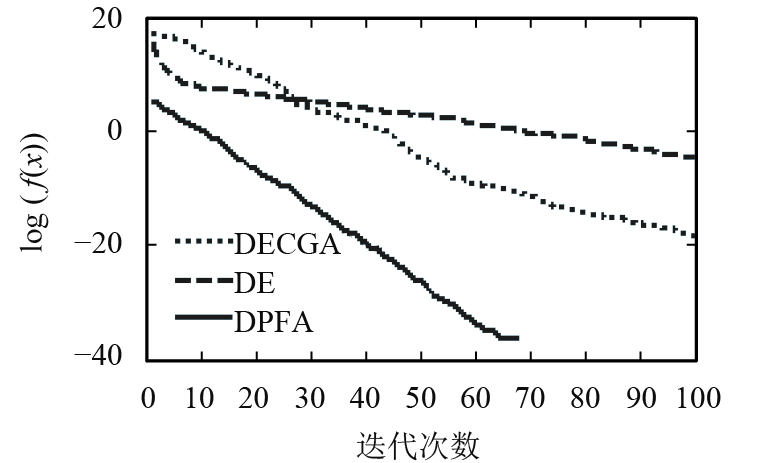
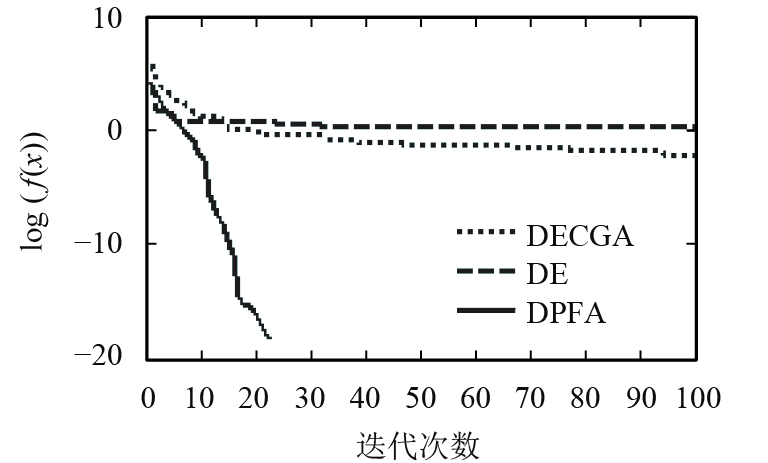
由图8~10可知，新算法收敛速度优于遗传算法(DECGA)和微分进化算法(DE). 对于F₇，新算法70次迭代找到最优值，对于F₈，新算法25次迭代找到最优解；由于爬山算子加强了算法局部搜索能力，协作算子通过双种群信息交流，提高了种群多样性与种群质量，增强新算法全局搜索能力，因而整体上优化了算法性能.

图 8 F₆进化曲线 Figure 8 F₆ convergence curve

图 9 F₇进化曲线 Figure 9 F₇ convergence curve

图 10 F₈进化曲线 Figure 10 F₈ convergence curve

双种群烟花算法通过两种群间的信息交换，维持了种群的多样性，种群交替执行爬山算子和协作算子，有利于全局优化与局部优化有效结合，加快算法收敛速度，提高算法精度.

4 结语

本文提出新的双种群烟花算法，新算法引入了爬山算子和协作算子，将局部搜索和全局搜索有效结合在一起，增加了种群多样性，有效平衡传统烟花算法全局搜索和搜索速度慢的矛盾，使其比传统算法有更高的求解精度和更快的收敛速度. 数值实验表明新算法拥有更强的寻优能力，使用范围更广，是一种稳健的求解无约束优化问题的新算法.

参考文献

[1]	LI J Z, TAN Y. Orienting mutation based fireworks algorithm [C]//2015 IEEE Congress on Evolutionary Computa- tion(CEC). [s.n.]: IEEE, 2015: 1265-1271. DOI: 10.1109/ CEC.2015.7257034.
[2]	ZHENG Y J, XU X L, LING H F, et al. A hybrid fireworks optimization method with differential evolution operators[J]. Neurocomputing, 2015, 148: 75-82. DOI: 10.1016/j.neucom.2012.08.075.
[3]	ZHENG S Q, LI J Z, JANECEK A, et al. A cooperative framework for fireworks algorithm [C]//IEEE/ACM Transactions on Computational Biology and Bioinformatics. [s.n.]: IEEE, 2016, 14(1): 27-41. DOI: 10.1109/TCBB. 2015.2497227.
[4]	ZHENG S Q, JANECEK A, LI J Z, et al. Dynamic search in fireworks algorithm [C]//2014 IEEE Congress on Evolutionary Computation(CEC). [s.n.]: IEEE, 2014: 3222-3229. DOI: 10.1109/CEC.2014.6900485.
[5]	SI T, GHOSH R. Explosion sparks generation using adaptive transfer function in firework Algorithm [C]//2015 Third International Conference on Signal Processing, Communication and Networking(ICSCN). [s.n.]: IEEE, 2015, 14(1): 1-9. DOI: 10.1109/ICSCN.2015.7219917.
[6]	曹炬, 季艳芳. 改进的烟花爆炸优化算法及其收敛性分析[J]. 计算机工程与科学, 2012, 31(1): 90-93. CAO G, JI Y F. An improved fireworks explosion optimization algorithm. An improved fireworks explosion optimization algorithm and its convergence Analysis[J]. Computer Engineer & Science, 2012, 31(1): 90-93.
[7]	朱晓东, 刘冲, 郭雅默. 基于烟花算法与差分进化算法的模糊分类系统设计[J]. 郑州大学学报(工学版), 2015, 36(6): 47-51. ZHU X D, LIU C, GUO Y M. Design of fuzzy classification system based on fireworks optimization and differential evolution algorithm[J]. Journal of Zhengzhou University (Engineering Science), 2015, 36(6): 47-51.
[8]	李浩, 柏鹏, 张辉, 等. 反向烟花算法及其应用研究[J]. 西安交通大学学报, 2015, 49(11): 82-87. LI H, BAI P, ZHANG H, et al. Backward fireworks algorithm and application research[J]. Journal of Xi’an Jiaotong University, 2015, 49(11): 82-87. DOI: 10.7652/xjtuxb201511014.
[9]	CHAO Y, YING T. Fireworks algorithm with covariance mutation [C]//2015 IEEE Congress on Evolutionary Computation (CEC). [s.n.]: IEEE, 2015: 1250-1256. DOI: 10.1109/CEC.2015.7257032.
[10]	YU C, LI J Z, TAN Y. Improve enhanced fireworks algorithm with differential mutation [C]//2014 IEEE International Conference on Systems, Man, and Cybernetics(SMC). [s.n.]: IEEE, 2014: 264-269. DOI: 10.1109/SMC. 2014.6973918.
[11]	杜振鑫. 烟花算法中烟花爆炸半径的改进研究[J]. 计算机时代, 2013, 1(1): 28-29. DU Z X. Study on improvement of explosion radius in fireworks algorithm[J]. Computer Era, 2013, 1(1): 28-29.
[12]	谭营, 郑少秋. 烟花算法研究进展[J]. 智能系统学报, 2014(5): 515-528. TAN Y, ZHENG S Q. Recent advances in fireworks algorithm[J]. CAAI Transactions on Intelligent Systems, 2014(5): 515-528.
[13]	YAN P, ZHENG S Q, TAN Y, et al. An empirical study on influence of approximation approaches on enhancing fireworks algorithm [C]//2012 IEEE International Conference on Systems, Man, and Cybernetics (SMC). [s.n.]: IEEE, 2012: 1322-1327. DOI: 10.1109/ICSMC.2012. 6377916.
[14]	谭跃, 谭冠政, 叶勇, 等. 具有混沌局部搜索策略的双种群遗传算法[J]. 计算机应用研究, 2011, 28(2): 469-471. TAN Y, TAN G Z, YE Y, et al. Dual population genetic algorithm with chaotic local search strategy[J]. Application Research of Computers, 2011, 28(2): 469-471.
[15]	柴岩, 周艳钊. 遗传算法的爬山法改进[J]. 辽宁工程技术大学学报(自然科学版), 2014, 33(7): 996-999. CHAI Y, ZHOU Y Z. Improved genetic algorithm based on climbing[J]. Journal of Liaoning Technical University (Natural Science), 2014, 33(7): 996-999.
[16]	梁瑞仕, 姜云飞, 杨会志. 基于有序爬山法的前向启发式搜索规划[J]. 电子科技大学学报, 2013, 42(3): 464-468. LIANG R S, JIANG Y F, YANG H Z. Forward heuristic search planning based on ordered hill climbing algorithm[J]. Journal of University of Electronic Science and Technology of China, 2013, 42(3): 464-468.
[17]	慕彩红, 焦李成, 刘逸. M-精英协同进化数值优化算法[J]. 软件学报, 2009, 20(11): 2925-2938. MU C H, JIAO L C, LIU Y. M-elite coevolutionary algorithm for numerical optimization[J]. Journal of Software, 2009, 20(11): 2925-2938.
[18]	慕彩红, 焦李成, 刘逸. 求解约束优化问题M-精英协同进化算法[J]. 西安电子科技大学学报(自然科学版), 2010, 37(5): 854-861. MU C H, JIAO L C, LIU Y. M-elite coevolutionary algorithm for constrained optimization[J]. Journal of Xidian University, 2010, 37(5): 854-861.
[19]	李松芳, 刘伟. 基于万有引力思想的遗传算子[J]. 广东工业大学学报, 2015, 32(1): 121-127. LI S F, LIU W. Genetic operator based on the idea of universal gravitation[J]. Journal of Guangdong University of Technology, 2015, 32(1): 121-127.
[20]	夏桂梅, 曾建潮. 基于锦标赛选择遗传算法的随机微粒群算法[J]. 计算机工程与应用, 2007, 43(4): 51-53. XIA G M, ZENG J C. Stochastic particle swarm optimization algorithm based on genetic algorithm of tournament selection[J]. Computer Engineering and Applications, 2007, 43(4): 51-53.
[21]	LIANG J, SUGANTHAN P N, HERNANDEZ-DIAZ A G. Problem definitions and evaluation criteria for the cec2013 special session on real-parameter optimization [R/OL]. (2016-10-21) [2016-10-23]. http://www.ntu.edu.sg/ home/EPNSugan/index_files/CEC2013/CEC2013.htm.
[22]	LIANG J J, QU B Y, SUGANTHAN P N. Problem definitions and evaluation criteria for the cec2014 special session and competition on single objective real-parameter numerical optimization [R/OL]. (2016-10-21) [2016-10-23]. http://www.ntu.edu.sg/home/EPNSugan/index_files/CEC2014/CEC2014.htm.
[23]	王培崇, 李丽荣. 改进的混合混沌烟花爆炸搜索算法[J]. 微电子学与计算机, 2014, 31(11): 69-73. WANG P C, LI L R. Improved hybrid chaos and fireworks explosion search algorithm[J]. Microelectronics & Computer, 2014, 31(11): 69-73.
[24]	刘全, 王晓燕, 傅启明, 等. 双精英协同进化遗传算法[J]. 软件学报, 2012, 23(4): 765-775. LIU Q, WANG X Y, FU Q M, et al. Double elite coevolutionary genetic algorithm[J]. Journal of Software, 2012, 23(4): 765-775.
[25]	LEI S, LIU W. A differential evolution algorithm based on self-adapting mountain-climbing operator[J]. Applied Mechanics and Materials, 2012, 266: 2332-2338.
[26]	崔逊学, 多目标进化算法及其应用[M]. 北京: 国防工业出版社, 2006: 93-94.