数字保序匹配问题是检测相似度和预测趋势领域的研究重点. 目前，字符串匹配技术应用已逐步扩展到股票预测分析，基金走势，气象预报等众多领域^[1]. 给出一个长度为n的文本T及长度为m的段落P；T，P都属于有限集合Z，所谓字符串匹配是从P中找到所有的变化趋势与T相同的子字符串. 随着对字符串匹配问题的不断研究，特别是数字字符匹配在日常生活中变得越来越重要，如每日股票的成交量及每股的股值动态趋势变化，日常的天气温度、湿度等的趋势变化都是相应的数值变化^[2-6]. 假设数字字符P=(10，22，15，30，20，18，27)，T=(22，85，79，24，42，27，62，40，32，47，69，55，25)，那么就可以得出T中与P有关联顺序的子串u=(24，42，27，62，40，32，47).

KMP方法首先是由Kubica等^[4]提出，该算法最先是在计算顺序边缘表上使用，Kubica等人通过研究发现从文本中找出所有与段落中的关联关系表所耗时是线性的. 因此，表明总时间复杂度是线性的. Kim等^[3]基于前缀表示方法改进了KMP. 而前缀表示方法又是基于查找前缀中的每个数的秩的方法. 这种方法的时间复杂度为O(nlogm). Cho等^[5]基于坏字符规则提出BMH方法在q-grams问题中使用，这种方法在文本中查找时因为每当遇到一个坏字符就会跳过大段的字符，所以算法的平均复杂度是亚线性的. 在最坏的情况下时间复杂度为O(mn). Cho等人提出了一种基于时间复杂度为线性的改进版本^[6]，这种版本结合了KMP方法.

对于保序匹配的问题，有学者提出了离线处理方法^[2]和在线处理方法^{[3-5, 7-8]}. Kubica与Kim等^[3-4]提出了一种基于Knuth-Morris-Pratt (KMP)算法的处理方法. Cho等^[5-6]给出了一种基于坏字符探索的亚线性算法（Boyer-Moore算法^[9]），Belazzougui等^[7]提出了一种改进的亚线性算法来处理保序匹配问题. 本文提出一种新的基于二进制转换与编码的保序匹配算法. 该算法有效提高了数字字符匹配效率和保序匹配质量，且具有线性时间复杂度.

1 相关工作

为了方便后面的论述，这里给出顺序同构及其相关的定义和证明.

定义1　两个字符串 $u\!=\!u_1, u_2, \cdots , u_m , v\!=\!v, v_2, \cdots ,v_m$ 在字符集中有相同的长度，称之为顺序同构^[3-4]，如果

${u_i} \leqslant {u_j} \Leftrightarrow {v_i} \leqslant {v_j}\left( {1 \leqslant i,j \leqslant m} \right),$

则可表示为u≈v.

定义2　对字符串x的前缀表达式u_x：

${u_x}\left[ i \right] = \left| {\left\{ {j:x\left[ j \right] \leqslant x\left[ i \right],0 \leqslant j \leqslant i} \right\}} \right|.$

引理1　对于两个字符串x和y，

若x≈y，则u_x≈u_y.

证明　假设x ≈ y， $x\left[ i \right] \leqslant x\left[ j \right] \Leftrightarrow y\left[ i \right] \leqslant y\left[ j \right]$ ， $0 \leqslant i < j < \left| x \right|$ . 因此，u_x=u_y.

引理2　假如 $x\left[ {0 \cdot \cdot t} \right] \approx y\left[ {0 \cdot \cdot t} \right]$ . 且 $0 \leqslant i,j \leqslant t$ ，若 $x\left[ i \right] < $ $x\left[ j \right]$ ，则 $y\left[ i \right] < y\left[ j \right]$ ，若 $x\left[ i \right] = x\left[ j \right]$ ，则 $y\left[ i \right] = y\left[ j \right]$ .

证明　首先证明第一种情形：(1) 当 $x\left[ i \right] < x\left[ j \right]$ ；假如 $y\left[ i \right] \geqslant y\left[ j \right]$ ，则由定义1可知 $x\left[ i \right] \geqslant x\left[ j \right]$ ，这与假设 $x\left[ i \right] < x\left[ j \right]$ 矛盾. (2) 当 $x\left[ i \right] = x\left[ j \right]$ ；由定义1知 $x\left[ i \right] \leqslant x\left[ j \right]$ ， $y\left[ i \right] \leqslant y\left[ j \right]$ ，同样可由顺序同构知，若 $y\left[ i \right] \leqslant y\left[ j \right]$ 且 $y\left[ j \right] \leqslant y\left[ i \right]$ ， $y\left[ i \right] = y\left[ j \right]$ ，则 $x\left[ j \right] \leqslant x\left[ i \right]$ ， $y\left[ j \right] \leqslant y\left[ i \right]$ .

在本文所研究的问题中，研究的目的是从 $T=t_1t_2 \cdots t_n $ 中找出所有的顺序同构字串 $P=p_1 p_2 \cdots p_m $ .首先把数字字符转换成二进制字符，即 $P=p_1 p_2 \cdots p_m $ 转换成 $P^*=b_1 b_2 \cdots b_{m-1} $ . 转换的规则如式(1)：

${t_i} = \left\{ \begin{array}{l}1,\;\;\;\;\;{t_{i - 1}} < {t_i};\\[5pt]0,\;\;\;\;\;{\text{其他}}.\end{array} \right.\;\;\;\;{p_i} = \left\{ \begin{array}{l}1,\;\;\;\;\;{p_{i - 1}} < {p_i};\\[5pt]0,\;\;\;\;\;{\text{其他}}.\end{array} \right.$

(1)

若 ${p_i} < {p_{i + 1}}$ ，则b_i为1，否则b_i为0. 在对文本T、P进行处理时，会有以下几种特殊情况. 这里采用二进制向量E表示；如果 ${p_{r\left[ i \right]}} < {p_{r\left[ {i + 1} \right]}},{\rm{i}} < j$ ，则E[i]=1；若 ${p_{r\left[ i \right]}} = {p_{r\left[ {i + 1} \right]}}$ 或者 ${p_{r\left[ i \right]}} > {p_{r\left[ {i + 1} \right]}}$ ，则E[i]=0；因此在以下情况下本文是不做研究的.

${t_{j - 1 + r\left[ i \right]}} > {t_{j - 1 + r\left[ {i + 1} \right]}}$

(2)

${t_{j - 1 + r\left[ i \right]}} = {t_{j - 1 + r\left[ {i + 1} \right]}},{E}\left[ i \right] = 0$

(3)

${t_{j - 1 + r\left[ i \right]}} < {t_{j - 1 + r\left[ {i + 1} \right]}},{E}\left[ i \right] = 1$

(4)

这里t_j表示在T中的字符.

2 算法介绍与复杂度分析 2.1 KMP算法

本文中介绍的是基于前缀表达式改进的KMP算法. 算法匹配的过程中如果遇到T、P不匹配时则进行两个部分操作. (1) 计算模式串移动next[j]后末字符在文本中的位置；(2) 比较文本和模式串在该位置的字符是否匹配，算法描述：

1. input into n

2. JUDGE：

3. while i<n

4. if T[i] == P[i]

5. if j == m–1

6. find and count++;

7. i++，j = 0

8. goto JUDGE;

9. else i++，j++;

10. goto JUDGE;

11. end if

12. else p=p→next[j]

13. if End==P[i]

14. j = next[j];

15. goto JUDGE;

16. else i=i+2;

17. j=0;

18. goto JUDGE;

19. end

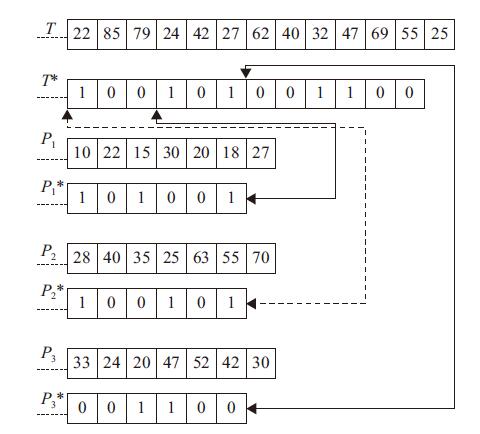
该算法的优点是：当目标串与源串匹配时，如果源串出现不匹配的字符时，该目标串直接与源串的下一个字符开始匹配. 图1是本文提出的基于二进制编码后的3次匹配过程演示. 其中T是源串，3次匹配的源串都不变. 而P₁、P₂、P₃各表示第1次，第2次，第3次匹配的目标串；这里 $T^* $ 、 $P_1^* $ 、 $P_2^* $ 、 $P_3^* $ 分别表示二进制编码后的串.

2.2 复杂度分析

本文将验证如果使用任何亚线性算法对数字字符进行二进制转换，那么该处理方法在任何情况下其平均时间复杂度是亚线性的.

假设P、T数字字符都满足这样的条件：P中的数值与T中数值都是相互独立的、均匀的、离散的整数. $P^* $ 、 $T^*$ 是转换后的集合，c表示集合中整数出现的次数，由于在 $P^* $ 、 $T^*$ 中有c²个整数对跟c个等式，那么在 $P^* $ 、 $T^*$ 中整数出现在任意一个位置的概率就为

$\displaystyle g = \frac{{\frac{{{c^2}}}{2} - \frac{c}{2}}}{{{c^2}}} = \frac{{c - 1}}{{2c}},$

(5)

因此，一个数值字符匹配的概率h为

$\begin{array}{l}\displaystyle h = {g^2} + {\left( {1 - g} \right)^2} = 2g\left( {g - 1} \right) + 1 = \displaystyle \frac{1}{2} + \frac{1}{{2{c^2}}}.\end{array}$

(6)

在 $P^*=b_1b_2 \cdots b_{m-1}$ 及 $ T^*$ 中内部相邻的位置其实并不是独立的，考虑段落的宽松匹配 $P^{**}=b_1\$ b_3 b_5\cdots \$ b_s $ ， $P^{**}$ 中包含了 $P^{*}$ 中的0、1与其他任何的字符，其中 $s = 2\left\lfloor {m/2} \right\rfloor - 1$ . 那么 $P^{**}$ 与 $T^{*}$ 匹配的概率要小于h^(m-1)/2，随着m的逐渐增大，概率会趋向为0，当c=2时， $P^{*}$ 匹配的概率同样小于 $P^{**}$ 匹配的概率. 表明本文中提出的处理方法在任何情况，如果转换成二进制形式的时间复杂度为线性的，则总的时间复杂度是线性的. 本文也考虑了最坏的情况，如果 $P^{*}$ 为1^m-1且 $T^{*}$ 为1^n-1，则总的时间复杂度则为O(nm).

3 实验与结果分析

本文测试了4种保序匹配算法. 有两种基于BNDM算法^[1]，分别是SBNDM2、SBNDM4. 在BNDM算法中，每一个对齐窗口的处理方式都跟Boyer-Moore算法一样是从右向左进行处理的. 第3种算法为Fast Shift-Or (FSO)^[10]. 这里之所以选择该算法是因为这种算法处理二进制文本速度非常快. 第4种算法为KMP算法^{[8, 10-12]}；SBNDM2与SBNDM4算法时间复杂度是亚线性的，FSO与KMP算法时间复杂度是线性的. 为了提升过滤效率本文选用了基于误配q-gram过滤器^[13]. 这里把长度为x的q-gram和模式长度为m的P定义成： ${l_x} = \max \left\{ {i{\rm{|}}{u_{p\left[ {i - q + 1..i} \right]}} = {u_x},q - 1 \leqslant i < m - 1} \right\}$ . 这里，l_x表示在P中上次的位置. 通过引理1知，若 ${u_{p\left[ {i - q + 1..i} \right]}} \ne {u_x}$ ，则 $p\left[ {i - q + 1..i} \right]! \approx x$ ，因此不会漏掉任何一个匹配位置，所以匹配移动的窗口D定义为： $D\left[ {f\left( x \right)} \right] = $ $ \min\left( {m - q + 1,m - {l_x} - 1} \right)$ ，f(x)使用前缀表达式来表示为

$f\left( x \right) = \mathop \sum \limits_{k = 0}^{q - 1} {u_x}\left[ k \right]*k!.$

(7)

注意：若前缀表达式从0至q!–1都映射，则D需要O(q!)空间. 实验环境配置采用的是2.70 GHz的CPU，16 GB的内存，操作系统为Ubuntu 12.10版本.

实验数据是随机产生的，数据的范围是0至2³⁰的整数，数据集长度为1 000 000. 在总数据集中随机选取匹配库长度为n=1 000. 待匹配的长度取4种情况：m分别为5、10、15、20. 表1为实验测试的4种算法的平均执行时间的对比，本文中分别对4种算法进行了80次实验，表1中的SBNDM2、SBNDM4、FSO、KMP是未改进的算法；SBNDM2(1)、SBNDM4(1)、FSO(1)、KMP(1)算法是基于二进制编码改进后的的算法.

表1中的实验结果可以用来做一个性能比较，不难发现以下规律：(1) 当m=5时，SBNDM2算法与SBNDM4算法匹配速度是比较快的，KMP算法匹配速度是最慢的；(2) m=10时，FSO算法匹配速度是最快的，KMP算法匹配速度是最慢的；(3) m=15或20时，SBNDM4算法匹配速度是最快的，KMP算法匹配速度是最慢的；(4) 特别的是SBNDM2算法与SBNDM4算法两者的匹配速度是很接近的；(5) 随着m取值的增加，匹配时间有减少的趋势; (6) 所取的4种值不管为何值时，KMP算法匹配速度总是最慢的; (7) 改进后的算法提高了匹配效率.

4 结束语

本文针对数值保序匹配问题提出了一种基于二进制编码处理方法. 在研究中使用了SBNDM2、SBNDM4、FSO、KMP 4种算法来实现并且对提出的新的处理方式进行了实验测试对比. 理论分析和实验结果表明：基于二进制编码^[14]的处理方法，能够进行正确有效的匹配，并且具有较低的空间和时间复杂度；提高了数字字符匹配的计算效率；有效降低了数字字符匹配的时间消耗；有较大的理论与应用价值. 当然本文中的方法在预处理上会有时间消耗，但其时间复杂度是线性的，且总体的匹配计算时间会大大减少，如何使总体匹配时间进一步的减少将是后续研究的重点.