广东工业大学学报  2017, Vol. 34Issue (5): 52-55.  DOI: 10.12052/gdutxb.160179.
0

引用本文 

郑永敏, 鲍鸿, 张晶. 基于维纳–小波分析的语音去噪新方法[J]. 广东工业大学学报, 2017, 34(5): 52-55. DOI: 10.12052/gdutxb.160179.
Zheng Yong-min, Bao Hong, Zhang Jing. A New Speech Denoising Method Based on Wiener Filtering and Wavelet Analysis[J]. JOURNAL OF GUANGDONG UNIVERSITY OF TECHNOLOGY, 2017, 34(5): 52-55. DOI: 10.12052/gdutxb.160179.

基金项目:

广东省科技计划资助项目(2013B040401015)

作者简介:

郑永敏(1991–)，男，硕士研究生，主要研究方向为声音去噪与识别。

通信作者

张晶(1977–)，女，副教授，主要研究方向为语音识别. E-mail：ha_go@163.com

文章历史

收稿日期：2016-12-19
Contents              Abstract              Full text              Figures/Tables              PDF
基于维纳–小波分析的语音去噪新方法
郑永敏1, 鲍鸿1, 张晶2     
1. 广东工业大学　自动化学院，广东　广州  510006;
2. 广东外语外贸大学　信息科学技术学院，广东　广州  510420
收稿日期：2016-12-19
基金项目：广东省科技计划资助项目(2013B040401015)
作者简介：郑永敏(1991–)，男，硕士研究生，主要研究方向为声音去噪与识别。
通信作者：张晶(1977–)，女，副教授，主要研究方向为语音识别. E-mail：ha_go@163.com
摘要: 小波分析具备多分辨性、低熵性和灵活选择基底的特性, 是目前较常用的语音去噪技术之一. 但是由于在小波分析去噪中需要设定合适的阈值消除含有噪声信号的小波系数, 这会过滤部分有用的语音信号, 降低去噪后的语音质量. 为了解决这个问题, 提出了一种将维纳滤波和小波分析进行结合的去噪新方法. 该方法根据维纳滤波具备最小均方误差的特点, 可以先过滤掉大部分噪声信号, 再进行小波分析二次去噪. 仿真实验结果表明, 该新方法较小波分析去噪在信噪比和整体质量方面得到较大提升.
关键词: 维纳滤波    小波分析    阈值函数    去噪    
A New Speech Denoising Method Based on Wiener Filtering and Wavelet Analysis
Zheng Yong-min1, Bao Hong1, Zhang Jing2     
1. School of Automation, Guangdong University of Technology, Guangzhou 510006, China;
2. Institute of Information Science and Technology, Guangdong University of Foreign Studies, Guangzhou 510420, China
Abstract: Denoising in wavelet analysis sets the threshold to eliminate the wavelet coefficients of the noise, which filters some useful speech signals and reduces voice quality. In order to resolve the problem, a new speech denoising method based on Wiener filter and wavelet analysis is proposed. According to the characteristic of the least mean square error of the Wiener filter, the method filters out most of the noise signal, and then denoises it by the wavelet analysis. Experiments is carried out in simulation, and the results reveal that the method is more improved than wavelet analysis in terms of signal-to-noise ratio (SNR) and speech quality.
Key words: Wiener filtering    wavelet analysis    threshold function    denoising    

小波分析是由外国学者MEYER Y、MALLAT S及DAUBECHIES I等人自1986年以来的研究而快速发展的一门新学科[1]，目前广泛运用在图像信号去噪、语音信号去噪、数字水印技术和机械故障检测等领域. 小波分析在频域分析和时域分析两方面都拥有较好的局部化功能，能够在不同尺度分辨率上进行信号分解，尤其是针对噪声语音这种短时平稳信号进行分解. 目前使用小波分析法进行语音去噪最为广泛，但是小波分解对噪声语音信号进行处理时，需要将信号分解成高频系数和低频系数两部分，有用信号主要保存在低频系数中，噪声信号和少量的有用信号保存在高频系数中，为保证过滤噪声信号，通常设定阈值较大，这也过滤掉部分有用信号，导致去噪后的语音质量较差，甚至出现失真. 为了防止去噪过程中有用信号的丢失，本文将采用维纳滤波法对噪声信号进行初步去噪，再用小波分析方法，对带噪语音进行第二次去噪.

1 维纳滤波的基本原理

维纳(Wiener)滤波是用来解决从噪声语音中提取有用信号的一种滤波方法[2]. 设带噪语音为

${y}(n) = {s}(n) + {d}(n),$ (1)

其中s(n)为纯语音信号，d(n)为噪声信号. 维纳滤波方法要设计一个数字滤波器h(n)，当输入信号为y(n)时，滤波器的输出S(n)为

${S}(n) = {y}(n) {h}(n) = \sum\limits_{m = - \infty }^{ + \infty } {{y}(n - m)} {h}(m).$ (2)

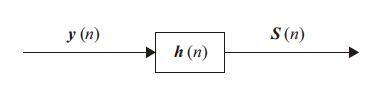
维纳滤波器的输入输出关系框图可用图1表示. 根据维纳滤波最小均方误差原则[3]，通过设计传递函数h(n)使得语音信号s(n)和输出信号S(n)的均方误差最小. 当均方误差 ${\varepsilon } = {E}[{\{ {s}(n) - {S}(n)\} ^2}]$ 取到最小值时，可以最大程度地消除噪声信号d(n)，因此维纳滤波器被称为最佳线性过滤器.

图 1 维纳滤波框图 Figure 1 Flow chart of wiener filtering
2 小波分析原理 2.1 小波分解与重构

小波分解与重构的基本原理[4]：(1) 首先选取恰当的小波基和分解次数对带噪语音信号Y进行分解，获得该带噪语音信号的低频系数a1和高频系数b1；在第二次分解中，将低频系数a1分解成低频系数a2和高频系数b2；在第三次分解中，继续对低频系数a2进行分解，以此类推，进行N次的分解，N是分解层数. (2) 根据选定的阈值函数和阈值规则对分解得到的高频系数 ${b_1},{b_2}, \cdots ,{b_N}$ 进行阈值化，得到阈 ${b'_1},{b'_2}, \cdots ,{b'_N}$ ，这里 ${b'_1},{b'_2}, \cdots ,{b'_N}$ 表示阈值化的高频系数. (3) 将阈值化的高频系数和最后一次分解得到的低频系数aN进行小波重构[5]，就可以得到去噪后的新语音信号Y1，此时 ${{Y}_1} = {b'_1} + {b'_2} + \cdots + {b'_{N}} +{a'_N}$ .

2.2 阈值函数的选择

在小波分析中，软阈值和硬阈值是最常用的两类阈值函数[6]. 在软阈值函数的定义中，对大于设定阈值的小波系数，软阈值函数采取向小波系数幅度值减少的方向共同收缩一个单位阈值的方法，对其他系数的值全置零，因此软阈值处理相对比较平滑[7]. 硬阈值函数的优点是能够将语音信号中的一些突变信号保留下来，伴随的缺点产生新的间断点[8]，这会导致去噪后的结果出现较大的方差误差. 因此，本文对噪声语音选用软阈值函数进行去噪处理.

2.3 小波阈值的估计

在去噪过程中如何对阈值进行量化尤为重要，由于噪声是一种随机信号，其信号的方差是未知的，实际去噪过程中必须对阈值进行估计[9]. 若选择的阈值过小，阈值化后会残留多余的噪声信息；相反，则会滤掉部分有用信号分量，利用小波重构后的语音信号会产生一定的失真. 阈值规则一般有如下4种阈值[10-11]：固定阈值(sqtwolog)、硬SURE阈值(rigrsure)、启发式阈值(heursure)和极大极小阈值(minimaxi). 4种阈值规则各有优缺点，其中rigrsure阈值规则比较保守，当有极少部分高频信息处于噪声范围内时，能够提取出微小的有用信号，而其他三种阈值规则的缺点是会把这种弱小的有用信号当做噪声信号过滤掉，因此本文选取硬SURE阈值规则来处理噪声信号.

3 维纳–小波分析新方法

在单独使用小波分析法进行噪声语音信号去噪过程中，为保证过滤噪声信号，通常需要设定较大的阈值[12]，而同时这也过滤掉部分有用信号，导致出现部分有用信号丢失的情况，甚至去噪后的语音语音会出现失真的现象.

维纳滤波的最大特点是具备最小均方误差，在对噪声信号的处理中，通过数字滤波器h(n)能够使输入信号和输出信号两者的均方误差值达到最小，利用维纳滤波这种特点，将维纳滤波法和小波分析法相结合进行去噪能够很好地弥补单独使用小波分析进行去噪产生语音失真的缺点. 维纳–小波分析法的流程图如图2所示，具体步骤如下.

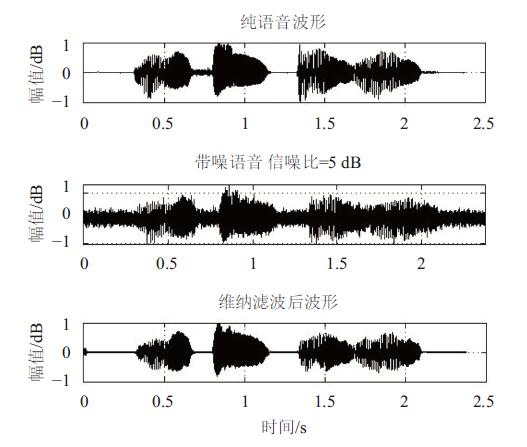
(1) 对噪声语音信号进行维纳滤波去噪，除去绝大部分的无用信号，此时噪声语音信号大幅减少；实验结果如图3所示.

(2) 选择恰当的小波基和分解次数对已经进行维纳滤波的语音信号进行小波分解[13]，分解成低频系数和高频系数两部分. 参考文献[14]可知，sym6小波基具备较好的对称性和正则性，对强噪声和弱噪声的去噪都有比较好的效果；选取的层数最好不超过3层，过高会导致边缘信息的丢失，因此本实验采用sym6小波基和分解层数为3层进行去噪处理.

(3) 采用rigrsure阈值规则对分解后的高频系数阈值化，保留大于设定阈值的信号，小于设定阈值的信号则过滤[15].

(4) 采用小波重构对低频系数和阈值处理后的高频系数进行重构，就可以得到去噪后的语音信号.

图 2 维纳–小波分析法流程 Figure 2 The procedure of Wiener filtering and wavelet analysis
图 3 维纳滤波去噪波形图 Figure 3 The oscillogram of wiener filtering
4 仿真实验与结果

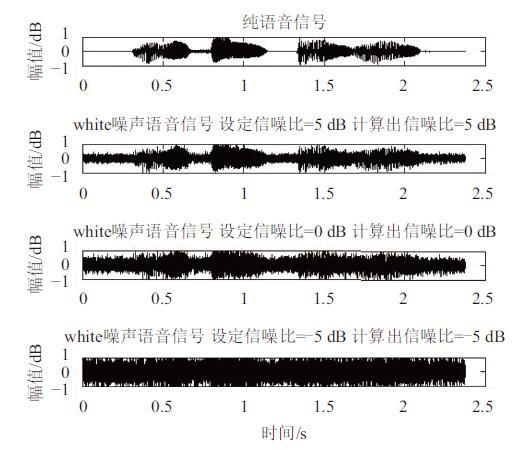
在MATLAB中用小波分析方法和维纳-小波分析方法进行仿真比较，对一段纯净语音bluesky信号，内容为“蓝天，白云”，分别叠加了5 dB、0 dB和-5dB信噪比的白噪声，以对比两种方法的效果，图4为叠加不同信噪比的白噪声语音波形图.

图 4 噪声语音波形图 Figure 4 The oscillogram of noisy speech

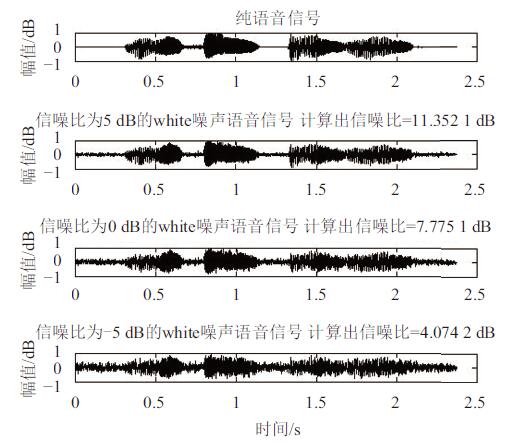
实验一，使用MATLAB对叠加了5 dB、0 dB和-5 dB信噪比的白噪声语音信号采用小波分析去噪，去噪效果如图5所示. 实验二，在MATLAB中调用WienerScalart96m_2函数对叠加了不同信噪比的噪声语音信号进行经维纳滤波去噪，对所得到的信号进行小波分析去噪，得到的去噪效果如图6所示. 在这里，用信噪比(Signal Noise Ratio, SNR)这个信号评价指标来评价两种方法的效果[16]，用SNRin表示输入的信噪比.

图 5 小波分析法去噪效果 Figure 5 Denoising effect of wavelet analysis
图 6 维纳–小波分析法去噪效果 Figure 6 Denoising effect of wiener filtering and wavelet analysis

从图5和图6可以看出，小波分析法去噪后的语音波形图丢失了部分有用信号，而维纳–小波分析法将大部分噪声信号过滤掉，得到的语音信号质量也明显较好. 两种去噪方法的去噪后语音信噪比如表1所示，维纳–小波分析去噪法在对叠加不同信噪比的白噪声语音信号进行去噪的情况下，信噪比增大，去噪效果比小波分析去噪法更好.

表 1 两种去噪方法的信噪比 Table 1 SNR of two denoising methods
5 结论

本文根据小波分析法在语音去噪中遇到的问题进行了研究与分析，提出了维纳–小波分析去噪法，将维纳滤波法和小波分析法相结合进行去噪. 本文从信噪比方面进行对比实验，实验分析表明，维纳–小波分析去噪法比小波分析去噪法具有更好的去噪效果，不仅能够大幅减少噪声信号，保留原有有用语音信号，同时能够提高去噪后语音的信噪比和改善语音质量.

参考文献
[1] Mallat S. A theory for multiresolution signal decomposition: the wavelet representation[J]. IEEE Trans On Pattern Analysis and Machine Intelligence, 1989, 11(7): 674-693. DOI: 10.1109/34.192463.
[2] 宋知用. MATLAB在语音信号分析与合成中的应用[M]. 北京: 北京航空航天大学出版社, 2013: 195-199.
[3] 李战明, 尚丰. 一种基于语音端点检测的维纳滤波语音增强算法[J]. 电子设计工程, 2016, 24(2): 42-44.
LI Z M, SHANG F. A wiener filtering speech enhancement algorithm based on speech endpoint detection[J]. Electronic Design Engineering, 2016, 24(2): 42-44.
[4] 张植奎. 基于LabVIEW的语音信号小波去噪分析[D]. 天津: 南开大学生物物理学院, 2009.
[5] 朱宗明, 姜占才. 小波递归最小二乘语音自适应增强[J]. 电子设计工程, 2016, 24(1): 69-72.
ZHU Z M, JIANG Z C. Algorithm for speech adaptive enhancement of wavelet recursive least square[J]. Electronic Design Engineering, 2016, 24(1): 69-72.
[6] ZHOU Y, LAI S, LIU L, et al. An improved approach to threshold function de-noising of mobile image in CL2 Multi-wavelet transform domain [C]//Mobile Technology, Applications and Systems, 2005 2nd International Conference, [S.l.]: [s.n.], 2005: 1-4.
[7] 刘凤山, 吕钊, 张超, 等. 改进小波阈值函数的语音增强算法研究[J]. 信号处理, 2016, 32(2): 203-213.
LIU F S, LYU Z, ZHANG C, et al. Research on speech enhancement algorithm based on modified wavelet threshold function[J]. Journal of Signal Processing, 2016, 32(2): 203-213.
[8] 林颖, 常永贵, 李文举, 等. 基于一种新阈值函数的小波阈值去噪研究[J]. 噪声与振动控制, 2008, 1(1): 79-81.
LIN Y, CHANG Y G, LI W J, et al. A de-nosing algorithm of wavelet threshold based on a new thresholding function[J]. Noise and Vibration Control, 2008, 1(1): 79-81.
[9] 何文. 基于小波变换与模糊理论的医学超声图像增强与去噪方法研究[J]. 电子设计工程, 2015, 23(12): 101-104.
HE W. Enhancement and denoising method of medical ultrasound image based on wavelet transform and fuzzy theory[J]. Electronic Design Engineering, 2015, 23(12): 101-104. DOI: 10.3969/j.issn.1674-6236.2015.12.031.
[10] TUFEKCI Z, GOWDY J N. Feature extraction using discrete wavelet transform for speech recognition[J]. Department of Electrical and Computer Engineering, 2000, 4(7-9): 116-123.
[11] DANIEL V, DAVID O, JEFERSON S, et al. Comparison analysis between rigrsure, sqtwolog , heursure and minimaxi techniques using hard and soft thresholding methods[J]. IEEE Program of Electronics Engineering, 2016, 1(16): 01-05.
[12] 陆真, 裴东兴. 基于连续小波阈值函数的语音增强技术[J]. 山西电子技术, 2016, 1(1): 40-42, 57.
LU Z, PEI D X. The algorithm of image denoising based on the optimized wavelet thresholding function[J]. Shanxi Electronic Technology, 2016, 1(1): 40-42, 57.
[13] 秦叶, 陈新度, 冯文贤. 小波基的选择与振动信号分析[J]. 广东工业大学学报, 1997, 14(4): 61-64.
QIN Y, CHEN X D, FENG W X. Selection of wavelet basis and analysis of vibration signal[J]. Journal of Guangdong University of Technology, 1997, 14(4): 61-64.
[14] 韦力强. 基于小波变换的信号去噪研究[D]. 长沙: 湖南大学电气与信息工程学院, 2007.
[15] 雷鸣. 基于小波神经网络的车辆发动机故障诊断[J]. 制造业自动化, 2012, 34(6): 24-26.
LEI M. The fault diagnosis of vehicle engine based on wavelet neural network[J]. Manufacturing automation, 2012, 34(6): 24-26.
[16] 袁野, 王夏天, 张子辰, 等. 基于小波变换和改进的瞬态独立成分分析融合算法的心电信号降噪方法[J]. 中国医学物理学杂志, 2016, 33(4): 415-422.
YUAN Y, WANG X T, ZHANG Z C, et al. Electrocardiogram noise reduction based on fused algorithm of wavelet transform and improved independent component analysis[J]. Chinese Journal of Medical Physics, 2016, 33(4): 415-422.