实时估计移动机器人姿态是机器人导航技术中的关键问题，也是长期以来不断探索的一个方向. 在传统的里程计技术中，移动机器人行进时碰到障碍物打滑或者倾斜，光电码盘、测速电机等无法准确测定机器人的相对位移^[1]，无法准确获取机器人的定位信息. 在机器人学与计算机视觉领域，视觉里程计是一个通过分析相关图像序列来确定机器人姿态的过程. 视觉里程计能克服传统里程计的不足，更加精准^[2]，能运用在GPS无法覆盖的机器人室内行走、星际探索和宇航员行走导航等任务^[3-5].

视觉运动估计方法分为两类，第一种是基于特征方法^{[2, 6]}：提取一系列稀疏的图像特征点，在连续图像帧中使用特征描述算子匹配特征点，使用对极几何恢复相机运动结构，通过重投影误差恢复相机姿态结构. 基于特征方法依赖检测和匹配的阈值，需要高鲁棒的取样估计技术处理错误的匹配点. 第二种是直接法：基于灰度不变假设，根据图像的像素信息来计算相机运动，可以完全不用计算关键点和描述子，避免了特征计算时间和特征缺失情况^[7]. 直接法使用光度测量误差的计算相比使用重投影误差的计算更密集，能够处理弯曲和大型图像区域.

2004年，Nister等^[8]定义了视觉里程计术语，并提出了一种单目视觉里程计的实现途径和流程. Henry等^[9]使用RGB-D相机获取连续帧的彩色和深度信息，通过SIFT特征点提取与匹配，RANSAC算法排除错误匹配点的干扰，完成相机的运动估计，但计算量较大，实时性较差. 文献[10]利用单目相机获取地面信息，采用光流法跟踪特征点，基于平面单应性关系进行位姿估计，但无法排除非地面信息，环境适应性差. 文献[11]通过改进SURF算法提高特征匹配的正确率和鲁棒性，但特征点的提取和描述子的计算耗时较多，缺乏明显纹理信息时导致没有足够特征点而无法估计相机运动.

针对上述研究现状，本文提出结合特征法的稀疏性与直接法的正确率实现移动机器人的单目视觉里程计. 当关键帧被用于确定初始位置时需要提取特征点，使用金字塔KLT算法跟踪下一帧的特征点. 相机运动估计需要处理连续帧，不再是采用较耗时特征检测和匹配，本文采用最小化光度测量误差的方法对特征点图像块进行直接匹配，提高每一帧图像的处理速度，利用g2o库优化局部连续的运动位姿信息，提高运动估计的鲁棒性.

1 特征检测与跟踪 1.1 特征检测

对于经典特征提取SIFT、SURF等算法在执行效率上较为欠缺，本文使用FAST(Features from Accelerated Segment Test)特征提取算法^[12]. 如图1所示，点p是待检测点，计算点p周围的16个点与点p灰度值的差值是否足够大，如果16个灰度差值大于某个阈值的个数足够多，则认为点p为一个特征点，如式（1）所示.

$N{\rm{ = }}\sum\limits_{1 \leqslant i \leqslant 16} {|I({x_{\rm{i}}}) - I(p)|} > m.$

(1)

满足判定条件的像素点个数N，I(p)为待检测点p的灰度值，I(x_i)为圆周上像素点的灰度值，m为设定的阈值，N一般为12或9. 为了提高检测效率，先检查点p垂直水平方向上的4个点（即图1中1, 5, 9, 13），这4个点中至少有3个点与候选点灰度值的差值足够大，否则不用计算其他点，认为该候选点不是特征点.

本文采用SSE2指令和Shi-Tomasi算法对FAST特征检测的角点进行筛选，确保角点的稳定性，实现效率较高. 最后通过四叉树的方式^[13]对提取的特征点进行划分，以保证特征点均匀化.

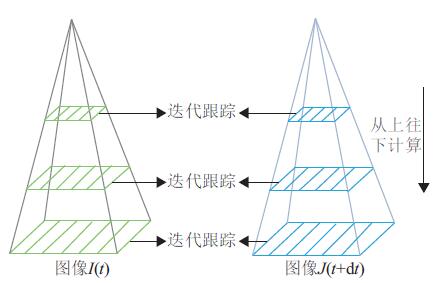
1.2 特征跟踪

由于计算和匹配描述算子比较耗时，本文采用金字塔KLT跟踪算法^[14]来预测下一帧的特征点. 如图2所示，从图像金字塔的最高一层开始计算光流和仿射变换矩阵，将上一层的光流和仿射变换矩阵作为下一层的初始值，计算出下一层的光流和仿射变换矩阵，重复这个过程直到金字塔的原始图像层，这样解决了运动范围过大及不连贯导致易丢失跟踪点的情况，实现更快和更长的运动跟踪.

在每一图像层中，相邻两帧I、J在某局部窗口w上是一样的，在假设亮度恒定情况下，在窗口w内有： $I(x,y,t) = J({x'},{y'},t + {\rm{d}}t)$ . 在窗口w上，所有 $(x,y)$ 都往一个方向移动了 $({\rm{d}}x,{\rm{d}}y)$ ，从而得到 $({x'},{y'})$ ，即t时刻的 $(x,y)$ 点在 $t + {\rm{d}}t$ 时刻为 $(x + {\rm{d}}x,y + {\rm{d}}y)$ ，所以求解跟踪匹配问题即是求解最小二乘法公式（2）问题，通过高斯牛顿迭代法收敛得稳定解^[15]. 跟踪效果如图3所示，以左图为参考帧，使用金字塔KLT算法跟踪右图当前帧的特征点.

$ \begin{split}\in (d) = & \in ({\rm{d}}x,{\rm{d}}y) = \\ & \sum\limits_{x = {u_x} - {w_x}}^{{u_x} + {w_x}} {\sum\limits_{y = {u_y} - {w_y}}^{{u_y} + {w_y}} {{{(I(x,y) - J(x + {\rm{d}}x,y + {\rm{d}}y))}^2}{\rm{ }}} } .\end{split}$

(2)

2 确定初始位置

确保初始位置的准确有利于减少累计误差. 利用金字塔KLT算法确定对应特征点，通过归一化直接线性变换DLT算法根据两帧之间对应特征点计算单应矩阵几何模型，并从相关位姿中进行重构. 对单应矩阵进行奇异值分解，计算出两帧之间的旋转和平移.

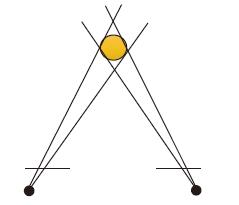
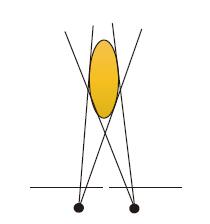
为了更好地确定初始位置和下一帧的特征跟踪，选择检测到的特征数大于100的图像作为第一帧. 通过金字塔KLT算法确定下一帧特征的估计位置和估计特征的单位向量，如果两帧之间像素差值的中值小于50，则认为跟踪的帧不是关键帧，不进行深度估计，避免两帧的距离过近影响3D点的准确度. 图4表示测得正常的3D点. 图5表示由于距离过近测得的3D点变成椭圆形.

2.1 单应矩阵

将一帧图像中的点集X_i映射到另一帧图像中的点集X_i′的射影变换叫做单应性^[16]. 随机选取8组对应点 $\left\{ {{X_i} \leftrightarrow X_i'} \right\}$ ，单应矩阵H满足变换方程：

$X_i' = {{H}}{X_i}\;\text{,即}\;X_i' \times {{H}}{X_i} = 0.$

(3)

设 $X_i' = {(x_i',y_i',w_i')^{\rm{T}}}$ ，则上式可变成

$\begin{split}X_i' \times &{{H}}{X_i} = \left( {\begin{array}{*{20}{c}}{y_i'{{{h}}^{3{\rm{T}}}}{X_i} - w_i'{{{h}}^{2{\rm{T}}}}{X_i}}\\[6pt]{w_i'{{{h}}^{1{\rm{T}}}}{X_i} - x_i'{{{h}}^{3{\rm{T}}}}{X_i}}\\[6pt]{x_i'{{{h}}^{2{\rm{T}}}}{X_i} - y_i'{{{h}}^{1{\rm{T}}}}{X_i}}\end{array}} \right) = \\ &\left[ {\begin{array}{*{20}{c}}{{0^{\rm{T}}}}&{ - w_i'X_i^{\rm{T}}}&{y_i'X_i^{\rm{T}}}\\[6pt]{w_i'X_i^{\rm{T}}}&{{0^{\rm{T}}}}&{ - x_i'X_i^{\rm{T}}}\end{array}} \right]\left( {\begin{array}{*{20}{c}}{{{{h}}^1}}\\[6pt]{{{{h}}^2}}\\[6pt]{{{{h}}^3}}\end{array}} \right) = 0.\end{split}$

(4)

其中， ${{{A}}_i} = \left[ {\begin{array}{*{20}{c}}\!\! {{{\rm{0}}^{\rm{T}}}}&{ - w_i'X_i^{\rm{T}}}&{y_i'X_i^{\rm{T}}} \!\! \\[5pt]\!\! {w_i'X_i^{\rm{T}}}&{{{\rm{0}}^{\rm{T}}}}&{ - x_i'X_i^{\rm{T}}} \!\! \end{array}} \right]$ ， ${{h}} = \left( {\begin{array}{*{20}{c}}\!\! {{{{h}}^1}} \!\! \\\!\! {{{{h}}^2}} \!\! \\\!\! {{{{h}}^3}} \!\!\end{array}} \right)$ ，h是由矩阵H的元素组成的9维矢量.

对点集 $\left\{ {{X_i} \leftrightarrow X_i'} \right\}$ 进行归一化处理，计算包括位移和缩放的相似变换T，将点集X_i变到新点集X_ii，使得点集X_ii的形心位于原点 ${(0,0)^{\rm{T}}}$ ，到原点的平均距离是 $\sqrt 2 $ . 针对第二帧图像上的点集，计算相似变换 ${{T}}'$ 将点集 $X_i'$ 变换到 $X_{ii}'$ . 根据每组对应点 ${X_{ii}} \leftrightarrow X_{ii}'$ ，由式（4）计算矩阵A_i，将8个2×9的矩阵A_i组合成一个16×9的矩阵A. 利用SVD算法对矩阵A进行分解求得矩阵H′. 通过式（5）解除归一化，求得单应矩阵H.

${{H}} = {{{T}}^{' - 1}}{{{H}}'}{{T}}.$

(5)

2.2 旋转矩阵R和平移向量t的最优解

根据文献[16]的方法分解单应矩阵H，得到8组相机运动R和t的理论解. 通过对符合单应矩阵H的特征点进行验证得到R和t的最优解. 根据特征点在相机前面，参考平面的法向量与相机光线方向的夹角小于90°，以及尺度比值的判断条件，筛选出最优姿态解R和t.

2.3 线性三角形法计算3D点

根据两帧图像的点坐标 $X = {(u,v,1)^{\rm{T}}}$ ， ${X'} = {({u'},{v'},1)^{\rm{T}}}$ 和投影矩阵 ${{M}} = \left[ {{{R}}|{{t}}} \right]$ ， ${{{M}}'} = \left[ {{{{R}}'}|{{{t}}'}} \right]$ 计算3D点 $P = {(x,y,z,1)^{\rm{T}}}$ ，投影变换关系：

$X = {{M}}P,{X'} = {{{M}}'}P.$

(6)

展开得到关于点P的4个线性方程组：

$\left\{\begin{array}{l}u({{{M}}^{3{\rm{T}}}}P) - ({{{M}}^{1{\rm{T}}}}P) = 0,\\[4pt]v({{{M}}^{3{\rm{T}}}}P) - ({{{M}}^{2{\rm{T}}}}P) = 0,\\[4pt]{u'}({{{M}}^{'3{\rm{T}}}}P) - ({{{M}}^{'1{\rm{T}}}}P) = 0,\\[4pt]{v'}({{{M}}^{'3{\rm{T}}}}P) - ({{{M}}^{'2{\rm{T}}}}P) = 0.\end{array}\right.$

(7)

即 ${{A}}P = 0$ ，

其中 ${{{M}}^{i{\rm{T}}}}$ 是M的行， ${{A}} = \left[ {\begin{array}{*{20}{c}}{u{{{M}}^{3{\rm{T}}}} - {{{M}}^{1{\rm{T}}}}}\\{v{{{M}}^{3{\rm{T}}}} - {{{M}}^{2{\rm{T}}}}}\\{{u'}{{{M}}^{'3{\rm{T}}}} - {{{M}}^{'1{\rm{T}}}}}\\{{v'}{{{M}}^{'3{\rm{T}}}} - {{{M}}^{'2{\rm{T}}}}}\end{array}} \right].$

利用SVD算法对矩阵A进行分解求得3D点P. 将两个关联特征对应的3D点进行重投影，通过阈值对重投影误差的关系确定内外点，并确保内点数大于40.

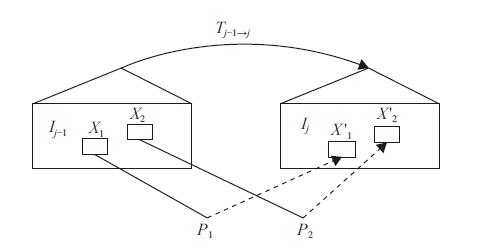
3 相机运动估计

本文采用最小化光度测量误差的直接法处理连续帧来估计相机运动. 如图6所示，第j-1帧图像 ${I_{j - 1}}$ 的特征点X_i通过投影矩阵投影到三维空间点 ${P_{j - 1}}$ ，将点 ${P_{j - 1}}$ 通过位姿转换 ${{{{T}}}_{j - 1 \to j}}[{{R}}|{{t}}]$ 得到在当前图像 ${I_j}$ 坐标系下的点 ${P_j}$ . 点 ${P_j}$ 通过相机内参K投影到图像 ${I_j}$ 平面得到 $X_i'$ . 由于重投影的点存在误差，导致X_i和 $X_i'$ 的亮度值不相等，通过迭代优化位姿 ${{{{T}}}_{j - 1 \to j}}[{{R}}|{{t}}]$ 使得亮度值残差最小，如式（8）所示. 可见，此为非线性最小二乘问题，通过高斯牛顿迭代法^[15]求解得到位姿转换 ${{{{T}}}_{j - 1 \to j}}[{{R}}|{{t}}]$ .

$\begin{split} \arg \mathop {\min }\limits_{{{T}_{j - 1 \to j}}} \frac{1}{2}{\sum\limits_{i \in \Re } {||{{I}_j}({{M}}({{{{{\rm{T}}}}}_{j - 1 \to j}} \cdot {{M}}} ^{ - 1}}({X_i},{Z_{{X_i}}}))) -\\ {{I}_{j - 1}}({X_i})|{|^2} = 0.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\end{split}$

(8)

其中， $\Re $ 表示一个区域，M表示投影矩阵，X_i表示像素坐标，I(·)表示对应的灰度值.

由于相连两帧估计位姿的方式造成累计误差，出现漂移的现象，因此需要通过重投影找到多个关键帧与当前帧有共同视角，对这些帧进行约束，采用文献[17]提出的用于图优化算法的g2o库对局部连续关键帧进行优化.

4 结果与分析

TurtleBot移动机器人是一款基于ROS机器人操作系统的移动机器人^[18]. 如图7所示，移动机器人采用韩国Yujin Kobuki移动底盘和华硕Xtion pro live摄像头，NVIDIA Jetson TK1主控平台片上系统(SOC)搭载了包含192个CUDA核心的NVIDIA Kepler GPU和四核Cortex-A15架构的ARM CPU，功耗低并满足本次实验需求. 在Ubuntu系统中的Qt Creator集成环境下进行软件开发，其中利用了机器人操作系统框架ROS、便于实现图优化算法的g2o库以及用于图像处理的OpenCV库等.

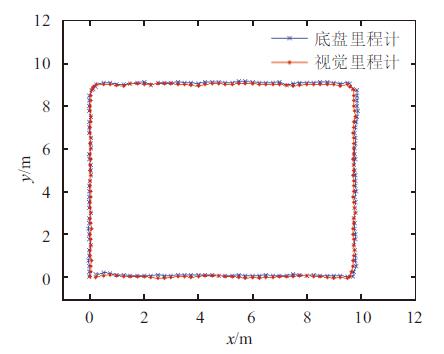
移动机器人以0~0.3 m/s的速度环绕约10 m×9 m的矩形行驶，将Kobuki移动底盘的里程计获取到的二维坐标和行驶距离视为标准值，视觉里程计计算得到的运动轨迹与底盘里程计的运动轨迹作比较，如图8所示. 底盘里程计计算移动机器人行走约37.54 m，视觉里程计计算得到约37.88 m，两者误差为0.9%. 可见，两者运动轨迹基本一致，误差不大.

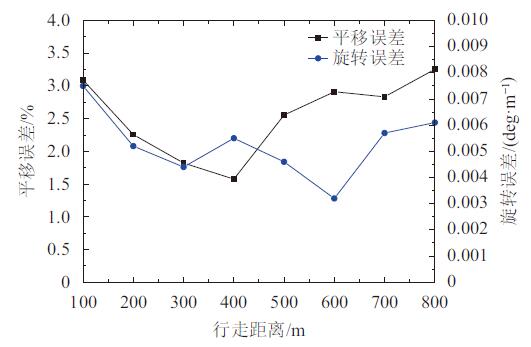
利用KITTI数据集^[19]测试本文设计的单目视觉里程计，将运动估计得到的平移值和旋转值与真实轨迹实际值作比较，计算得到平移误差和旋转误差，如图9所示. 可见，平移误差控制在5%之内，旋转误差控制在0.008 deg/m之内，行走距离为400 m时平移误差最小，行走距离为600 m时旋转误差是最小的，测试行走路径越长，平移误差和旋转误差都有所增加.

5 结论

本文提出一种结合特征法的稀疏性与直接法的正确率实现移动机器人的单目视觉里程计. 采用Shi-Tomasi算法和四叉树方式确保了FAST检测的特征点的稳定性和均匀化，确定初始位置时利用金字塔KLT跟踪算法预测下一帧的特征点并根据两帧之间对应特征点计算单应矩阵模型，有利于减少累计误差. 采用最小化光度测量误差的直接法和图优化算法处理连续帧来估计相机运动. 视觉里程计与底盘里程计的测试对比结果，以及KITTI数据集的测试结果证明了本文设计的单目视觉里程计的有效性和实用性.