地球上的城市人口已经超过了农村人口，占世界人口的54%. 城市人口的数量从1950年的7.46亿，急剧增长到2014年的39亿. 在持续的人口增长和城市化的影响下，预计到了2050年，城市人口会增加25亿^[1]. 由于城市人口的快速增长，城市蔓生现象发生，城市人口从市中心开始向低人口密度的郊区转移，城市形态呈现出分散、低密度、区域功能单一和依赖汽车交通的特点^[2]. 城市蔓生造成大量的土地浪费，严重影响了自然环境，浪费大量的社会公共资源，不利于经济可持续发展^[3].

为持续发展经济和保护生态环境，美国政府在20世纪90年代提出一种减缓城市郊区化发展的城市发展计划，被称为精明增长^[4]. 精明增长遵守可持续发展的土地开发理论，是一种有计划、全面的发展方式，其拥有10个基本原则^[5]，且围绕着3个核心，即经济繁荣(Economically Prosperous)、社会公平(Socially Equitable)、环境可持续(Environmentally Sustainable)，简称3个E. 精明增长被提出之后，在美国得到了社会各方面专家的支持，包括城市规划师、建筑学家、开发商和社会学家等^[6].

为了有效地衡量精明发展的程度，本文建立了一个基于主成分分析法和支持向量回归的评估模型. 提出的模型以精明增长的3个E作为参考，选用了经济因素、社会因素和环境因素作为3个分量。而每个因素都由几个指标构成，因此可以将模型拆分成多个指标构成，以方便预测未来某个城市的精明增长程度.

1 度量精明增长模型的建立 1.1 综合评价模型的建立

建立一个衡量城市精明增长的模型，称为精明增长评价函数(total metric of smart growth, SGTM)，由经济因素、社会因素和环境因素影响，分别设此3个因素为ECF、SOF和ENF. 定义如式(1)所示.

${\rm{SGTM}} = \frac{{{\rm{ECF}} + \alpha {\rm{SOF}} + \beta {\rm{ENF}}}}{{1 + \alpha + \beta }}.$

(1)

其中，α和β分别是相对经济因素的社会因素和环境因素对总指标的影响权重，其数值视不同城市的发展程度而定. 当α=β=1时，表明3个因素对总指标有同等的贡献，视不同城市的发展程度而定.

1.2 评价指标的选取

评价指标的选取应遵循以下原则：(1) 经济繁荣(Economically Prosperous)；(2) 社会公平(Socially Equitable)；(3) 环境可持续(Environmentally Sustainable).

1.3 反映经济因素的指标

估计房价中间值(Estimated Median House or Condo Value，EMH)、失业率(Unemployment Rate，UR)和家庭收入中间值(Median Household Income，MHI)等. 在当代现代化城市进程中，最直接最准确衡量居民经济的无疑就是房价和家庭收入. 而对于一个城市而言，就业率是重要指标，高就业率是经济稳定的保证^[7]. 因此，选取了EMH、UR和MHI作为反映经济因素的评价指标.

1.4 反映社会因素的指标

教育基尼指数(Education Gini Index，EGI)、健康饮食率(Healthy Diet Rate，HDR)和犯罪率(Crime Index，CI). 从教育、健康和安全3个维度去考虑以保证社会公平. 其中，教育基尼指数是一个衡量教育公平的指标，该指数越低说明教育越公平^[8]. 饮食健康是居民社会生活的基础，犯罪率是社会稳定安全的最直观的指标. 这3个评价指标可以综合反映各个城市的社会因素.

1.5 反映环境因素的指标

空气质量指标(Air Quality Index，AQI)和燃气使用率(Utility Gas Rate，UGR). 在现代化城市中，市民最关注的环境问题就是空气污染. 空气质量的好坏极大地影响了的生活. 因此选用AQI和UGR去评估环境因素. AQI主要通过计算4种主要污染物（地面臭氧、颗粒物污染、一氧化碳和二氧化硫）的含量指数得到^[9]. UGR反映能量消耗比例.

1.6 主成分分析

主成分分析是非常有效的综合评测方法，主要利用了降维思想，在损失很少信息的前提下把多个指标转化为几个综合指标的多元统计方法^[10]. 本文使用主成分分析法对3个因素（即经济、社会和环境因素）分别建立评价模型. 主要步骤如下.

1) 数据预处理.

由于每个指标的属性不同，有些指标是效益型指标（如家庭收入和健康饮食率等），这类指标通常数值越高越好，有些指标是成本型指标（如失业率和犯罪率），这类指标通常数值越低越好. 不同评价指标往往具有不同的量纲和量纲单位，为了消除由此带来的不可公度性，应将各评价指标作无量纲化处理^[11]. 因此，对数据进行预处理，把数据归一化，且统一转化为效益型指标.

对于效益型指标，有

$\tilde a = \frac{{a - {a_{{\rm{min}}}}}}{{{a_{{\rm{max}}}} - {a_{{\rm{min}}}}}}.$

(2)

其中， $\tilde a$ 和a分别是归一化后和归一化前的变量，a_max和a_min分别是变量a的最大值与最小值.

对于成本型指标，有

$\tilde b = \frac{{{b_{{\rm{max}}}} - b}}{{{b_{{\rm{max}}}} - {b_{{\rm{min}}}}}}.$

(3)

其中， $\tilde b$ 和b分别是归一化后和归一化前的变量，b_max和b_min分别是变量b的最大值与最小值.

2) 计算相关系数矩阵R.

${R} = {\left( {{r_{ij}}} \right)_{m \times m}}.$

(4)

${r_{ij}} = \frac{{\mathop \sum \nolimits_{k = 1}^n {{\tilde a}_{ki}} \cdot {{\tilde a}_{kj}}}}{{n - 1}},\;i,j = 1,2, \cdots ,m.$

(5)

其中，r_ij是第i个指标和第j个指标的相关系数，r_ii=1，r_ij=r_ji.

3) 计算相关系数矩阵R的特征值和特征向量. 设其特征值 ${\lambda _1} \geqslant {\lambda _2} \geqslant \cdots \geqslant {\lambda _m} \geqslant 0$ ，对应的特征向量 ${{{u}}_1} , {{{u}}_2}, \cdots , {{{u}}_{{m}}} \geqslant 0$ ，这里， ${{{u}}_j}= \left[{{{{{u}}}}_{1j}},{{{{{u}}}}_{2j}} \cdots , {{{{{u}}}}_{{{mj}}}}\right]^{\rm{T}} \geqslant 0$ 包含m个新指标变量的特征向量.

$\begin{array}{l}{y_1} = {{{u}}_{11}}{{\tilde x}_1} + {{{u}}_{21}}{{\tilde x}_2} + \cdots + {{{u}}_{m1}}{{\tilde x}_m},\\{y_2} = {{{u}}_{12}}{{\tilde x}_1} + {{{u}}_{22}}{{\tilde x}_2} + \cdots + {{{u}}_{m2}}{{\tilde x}_m},\\[5pt]\;\;\; \cdots \\{y_m} = {{{u}}_{1m}}{{\tilde x}_1} + {{{u}}_{2m}}{{\tilde x}_2} + \cdots + {{{u}}_{mm}}{{\tilde x}_m}.\end{array}$

特征值分解求解式如下

${{A}}={{U}} {{\varLambda}} {{U}}^{\rm{T}}.$

(6)

其中， ${U} = \left[ {{{u}_1},{{u}_2} \cdots ,{{u}_{{m}}}} \right]$ ，矩阵U的列向量便是矩阵A的特征向量， $ {\varLambda } = {\rm{diag}}\left( {{\lambda _1},{\lambda _2}, \cdots ,{\lambda }}_m \right)$ 为特征值对角矩阵，其中diag(·)表示对角矩阵操作.

4) 选择p( $p \leqslant m$ )个主成分，并计算综合评分.

(1) 计算每个主成分的信息贡献率b_j和累积贡献率α_p.

${b_j} = \frac{{{\lambda _j}}}{{\mathop \sum \nolimits_{k = 1}^m {\lambda _k}}}.$

(7)

${\alpha _p} = \frac{{\mathop \sum \nolimits_{k = 1}^p {\lambda _k}}}{{\mathop \sum \nolimits_{k = 1}^m {\lambda _k}}}.$

(8)

当α_p接近于1时，选择的p个新变量 ${y_1},{y_2}, \cdots ,{y_p}$ 就可以代替原来的m个指标变量. 一般地，当第p个主成分的累积贡献率大于80%时，余下的主成分可以舍弃.

(2) 计算综合得分.

$Z = \mathop \sum \limits_{j = 1}^p {b_j}{y_j}.$

(9)

其中，b_j是第j个主成分的信息贡献率. 最终，建立的分别评价3个因素的模型如下所示.

对于经济因素，有

${\rm{ECF}} = 0.629\;0{y_{_{{\rm{ECF}}1}}} + 0.278\;5{y_{_{{\rm{ECF}}2}}}.$

其中，

$\begin{array}{l}{y_{_{{\rm{ECF}}1}}} = 0.669\;5{{\tilde x}_1} + 0.045\;9{{\tilde x}_2} + 0.741\;4{{\tilde x}_3},\\[5pt]{y_{_{{\rm{ECF}}2}}} = 0.488\;0{{\tilde x}_1} + 0.779\;7{{\tilde x}_2} - 0.392\;4{{\tilde x}_3}.\end{array}$

${{\tilde x}_1}$ ， ${{\tilde x}_2}$ ， ${{\tilde x}_3}$ 分别表示估计房价中间值(EMH)、失业率(UR)和家庭收入中间值(MHI).

对于社会因素，有

${\rm{SOF}} = 0.409\;6{y_{_{{\rm{SOF}}1}}} + 0.331\;0{y_{_{{\rm{SOF}}2}}} + 0.262\;1{y_{_{{\rm{SOF}}3}}}.$

其中，

$\begin{array}{l}{y_{_{{\rm{SOF}}1}}} = 0.701\;3{{\tilde x}_4} - 0.009\;1{{\tilde x}_5} + 0.741\;4{{\tilde x}_6},\\[5pt]{y_{_{{\rm{SOF}}2}}} = 0.563\;8{{\tilde x}_4} - 0.604\;8{{\tilde x}_5} + 0.562\;4{{\tilde x}_6},\\[5pt]{y_{_{{\rm{SOF}}3}}} = 0.436\;2{{\tilde x}_4} + 0.796\;4{{\tilde x}_5} + 0.419\;0{{\tilde x}_6}.\end{array}$

${{\tilde x}_4}$ ， ${{\tilde x}_5}$ ， ${{\tilde x}_6}$ 分别表示教育基尼指数(EGI)、健康饮食率(HDR)和犯罪率(CI).

对于环境因素，有

${\rm{ENF}} = 0.718\;2{y_{_{{\rm{ENF}}1}}} + 0.281\;8{y_{_{{\rm{ENF}}2}}}.$

其中，

$\begin{array}{l}{y_{_{{\rm{ENF}}1}}} = 0.707\;1{{\tilde x}_7} - 0.707\;1{{\tilde x}_8},\\[6pt]{y_{_{{\rm{ENF}}2}}} = 0.707\;1{{\tilde x}_7} + 0.707\;1{{\tilde x}_8}.\end{array}$

${{\tilde x}_7}$ ， ${{\tilde x}_8}$ 分别表示空气质量指标(AQI)和燃气使用率(UGR).

5) 分值归一化.

经过主成分分析提取出评价模型后，仍不能计算出SGTM，这是因为3个因素的分值量纲不同. 因此，需要将每个因素的得分进行归一化.

$\tilde c = \frac{{c - {c_{{\rm{min}}}}}}{{{c_{{\rm{max}}}} - {c_{{\rm{min}}}}}}.$

(10)

6) 模型的验证.

使用从网上收集来的数据（数据源：http:// www.city-data.com），利用提出的SGTM模型分析一些城市的精明增长程度.并通过预测一些指标的发展趋势，计算未来城市的精明发展程度. 2013年部分城市的SGTM值如表1所示.

如前所述，SGTM由经济因素、社会因素和环境因素等综合影响，且每个因素又受到多个评价指标影响，因此SGTM能够通过多个维度综合有效地评估城市精明增长程度.

由表1可以看出，像纽约和洛杉矶等大城市的SGTM并没有火奴鲁鲁的高. 虽然火奴鲁鲁是一个旅游城市，却拥有最高的SGTM，证明火奴鲁鲁拥有较高的发展潜力和精明增长. 而一些繁荣的大城市，虽然经济因素得分比火奴鲁鲁高了很多，但其社会因素和环境因素的得分却不如火奴鲁鲁，因此其SGTM值反而低于火奴鲁鲁. 这很好地验证了模型可以有效地评估城市精明增长程度.

2 精明增长的预测

本文将支持向量回归(Support Vector Regression，SVR)应用于精明增长的预测当中. 支持向量回归是支持向量机(Support Vector Machine)的一种，是建立在统计学习理论基础上的学习方法，其学习策略是间隔最大化. 由于其具有优异的预测能力、泛化能力及良好的鲁棒性，且适用于小样本学习，因此它成为非常受欢迎的机器学习算法. 支持向量回归可描述成凸优化问题，这里，使用其对偶及核函数形式. 假设给定一个训练集 $\{ \left( {{x_1},{y_1}} \right), \cdots , $ $\left( {{x_l},{y_l}} \right) \} \subset $ X $\times {{\mathbb{R}}^d}$ ，其中X表示输入空间 ${{\mathbb{R}}^d}$ 中的实例. SVR的目标是找到一个决策函数f(x)，这个函数的预测误差不大于ε^[12]. 问题可描述如下.

$\begin{array}{l}{\rm{max}}\;\;\;\;\; - \displaystyle\frac{1}{2}\mathop \sum \limits_{i,j = 1}^l \left( {{\alpha _i} - \alpha _i^*} \right)\left( {{\alpha _j} - \alpha _j^*} \right)K\left( {{x_i},{x_j}} \right)-\\[6pt]\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \varepsilon \mathop \sum \limits_{i = 1}^l \left( {{\alpha _i} + \alpha _i^*} \right)+ \mathop \sum \limits_{i = 1}^l {y_i}\left( {{\alpha _i} - \alpha _i^*} \right).\\[6pt]{\rm{s.}}\;{\rm{t.}}\;\;\;\;\;\;\;\;\left\{ {\begin{array}{*{20}{c}}{\mathop \sum \limits_{i = 1}^l \left( {{\alpha _i} - \alpha _i^*} \right) = 0},\\[6pt]{{\alpha _i},\alpha _i^* \in \left[ {0,C} \right].}\end{array}} \right.\end{array}$

其中， $K\left( {{x_i},x} \right) = {\rm{exp}}\left( { - \displaystyle\frac{\left\| {{{x_i} - {x}}} \right\|^2}{{2{\sigma ^2}}}} \right)$ 是径向基核函数，表示将输入从输入空间映射到特征空间得到的特征向量之间的内积^[13]. ${\alpha _i},\alpha _i^{\rm{*}},{\eta _i},\eta _i^{\rm{*}}$ 是拉格朗日乘子变量；常数C >0称为惩罚参数，用来权衡间隔最大化及误差大于ε的样本数量尽可能少. 在Matlab中使用libsvm工具箱可以快速地求解这个问题，从而求解得决策函数为

$f\left( x \right) = \mathop \sum \limits_{i = 1}^l \left( {\alpha _i^{\rm{*}} - {\alpha _i}} \right)K\left( {{x_i},x} \right) + b.$

(11)

3 案例研究

林肯市(Lincoln)是内布拉斯加州的首府，成立于1856年，是相当典型的美国中型城市，大多数经济活动是来自服务业和制造业. 20世纪70年代，林肯市被美国国务院指定为“难民友好”的城市. 由于大量难民的到来，林肯市的劳动力丰富且相对廉价，但是犯罪率增高，社会不稳定^[14]. 此外，人口的增长还给林肯市带来严重的负担. 过多的人口，导致原本教育资源丰富的林肯市缺乏足够的学校.

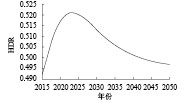
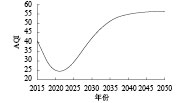
假设林肯市符合经济增长原则，利用2010~2014年的原始评价指标数据进行训练，预测未来林肯市的精明增长SGTM值. 表2展示了每10年的SGTM预测值。为了显示出制定城市规划的有效性，需要计算一组SGTM的参考值。这组参考值的计算建立在经济社会完全理想化发展的基础假设上，所有评价指标都按照原来的趋势变化。在2010～2014年的原始数据的基础上，如果某一指标的原始趋势是逐年增长的，则使用线性回归拟合该指标的增长趋势；反之，如果某一指标的原始趋势是逐年下降的，则使用对数衰减函数拟合该指标的下降趋势，这是出于防止指标值下降至负值的考虑。通过一系列趋势拟合，可以预测所有指标在未来各年份的数值，然后利用式(1) 计算得到未来各年份的SGTM参考值。规划1的内容是增加居民健康计划预算投入，评估方式是通过SVR预测HDR指标（见图1），其中SVR的自变量是人口及居民健康计划预算投入。规划2的内容是增加城市环境治理预算投入，评估方式是通过SVR预测AQI指标（见图2），其中SVR的自变量是人口及城市环境治理预算投入。

对比表2的分析可以得到以下结论：规划1得到的SGTM值与参考值非常接近，这意味着该规划在前期是比较成功的，这是因为HDR的预测值在前期（2025年之前）非常接近原始数据的线性增长趋势。但是，2025年之后，虽然仍然在持续增加居民健康计划预算投入，但是HDR值反而逐渐降低，预测SGTM值略小于参考值（因有效位数因素，表2中的预测SGTM等于参考值）。这意味着仅仅增加居民健康计划预算投入不能长期保证精明增长，因为预算投入远远跟不上人口的增长，且带来的经济成本是非常巨大的。规划2得到的SGTM值相比参考值下降明显更快。这是因为随着时间的推移，预测到AQI值趋向饱和，偏离原来理想化的变化趋势。这说明仅增加环境治理预算并不能保证环境长期良性发展，且带来更大的资源浪费。综上所述，仅增加财政预算投入是不能长期保证精明增长的，还需考虑其他因素（如人口素质和经济结构等）。

4 结论

综上所述，本文建立了一个名为SGTM的模型去评估精明增长. SGTM包含3个关键因素，分别反映经济繁荣、社会公平和环境可持续. 在每一个因素中分别选取几个指标，通过PCA来确定指标与因素之间的关系. 选取了美国的20个城市进行了初步的分析，计算出它们的SGTM值以评估模型针对不同城市的有效性. 同时就林肯市进行了深入的案例分析. 实验结果表明，SGTM模型可以对城市实际的发展计划进行评估和预测，使得城市的计划更加科学合理，在人口增长的背景下，更加符合精明增长.