最优潮流是当系统的结构参数及负荷给定时,通过对控制变量的寻优选择,找到满足所有运行约束条件,并使系统的某一性能指标或目标函数达到最优时的潮流分布[1].
最优潮流问题是一个典型的大规模有约束非线性多峰值的非凸规划问题. 针对这类问题的求解,国内外众多学者提出了各种不同的优化算法. 传统的经典解算法如:简化梯度法[2]、牛顿法[3-4]、二次规划法、解耦法和内点法[5-6]等,这类算法本质上都是利用目标函数对控制变量一阶或二阶梯度求解,具有收敛速度快、过程清晰等优点. 但是,此类算法对初值非常敏感且对优化目标及约束条件有一定的要求. 鉴于此类算法的不足,许多学者提出了另一类求解最优潮流问题的算法,即现代人工智能算法. 这些算法包括混沌优化方法、粒子群优化算法[7]、差分进化算法[8]、引力搜索算法[9]、模拟退火算法和遗传算法[10]等. 此类算法与导数无关,克服了经典算法对初值敏感的缺点,具有内在并行性,能处理非连续的、非光滑的、高度非线性解空间的复杂优化问题,是一种具有很好全局收敛性能的优化算法,已经广泛运用于求解各种电力系统优化问题[11-13].
1995年美国普渡大学的Kennedy和Eberhart首次提出模拟鸟群觅食行为的粒子群优化算法. 此算法所依赖的参数少,前期具有较快的收敛速度,但后期由于所有粒子都向最优粒子靠近,种群因丧失多样性而容易陷入局部最优. 鉴于差分进化算法中变异、交叉和选择操作能使种群跳出局部最优解的优势,本文将差分进化算法融合到粒子群优化算法中,提出一种改进差分进化粒子群优化算法. 采用双种群进化策略,通过信息分享机制,使两个种群在寻优过程中协同进化. 提出一种老化机制和精英改选机制,改善了粒子群算法易陷入局部最优的缺陷.
1 最优潮流问题的一般模型最优潮流是一种典型的多变量多约束非线性的组合优化问题. 本文以系统总发电费用最小为目标函数, 通过优化发电机的有功出力和机端电压等, 使系统的发电费用最优. 其数学模型为
|
${\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\begin{array}{*{20}{c}}{\min f({{u}},{{x}})}.\\[6pt]\;\;\;\;\;{\left\{ \begin{array}{l}g({{u}},{{x}}) = 0;\\[6pt]h({{u}},{{x}})\leqslant 0.\end{array} \right.}\end{array}$
|
(1) |
式中,f是目标函数,如发电煤耗或发电成本;u是控制变量,包括发电机有功、机端电压和变压器变比;x为状态变量,包括PQ节点电压、发电机无功出力等;g为基本潮流方程等式约束;h为不等式约束,包括发电机有功PG约束、发电机无功QG约束、节点电压约束和线路潮流约束等.
1.1 目标函数本文采用发电费用最小为目标函数,建立以二次函数近似表示机组发电成本的最优潮流模型:
|
$\min {F_C} = \sum\limits_{i = 1}^{{N_G}} {({a_i}{{P}_{Gi}}^2 + {b_i}{{P}_{Gi}} + {c_i})} ,$
|
(2) |
式中,FC为发电成本;NG为系统中发电机台数;PGi为第i台发电机有功出力;ai、bi、ci为第i台发电机的成本系数.
1.2 约束条件 1.2.1 等式约束最优潮流的优化必须满足基本的潮流方程式,其等式约束为
|
$\left. \begin{array}{l}\displaystyle\Delta {{P}_i} = {{P}_{Gi}} - {{P}_{Li}} = \sum\limits_{j = 1}^N {{{V}_i}} {{V}_j}({{G}_{ij}}\cos {\delta _{ij}} + {{B}_{ij}}\sin {\delta _{ij}})\\\displaystyle\Delta {{Q}_i} = {{Q}_{Gi}} - {{Q}_{Li}} = \sum\limits_{j = 1}^N {{{V}_i}} {{V}_j}({{G}_{ij}}\sin {\delta _{ij}} - {{B}_{ij}}\cos {\delta _{ij}})\end{array} \right\}.$
|
(3) |
式中,N为系统中的节点数;Vi、Vj分别是第i节点和第j节点电压幅值;PGi、QGi分别为第i台发电机有功出力和无功出力;PLi、QLi分别为第i节点有功功率负荷和无功功率负荷;
不等式约束中包含发电机有功上下限值约束、无功上下限值约束、节点电压约束和线路潮流约束.
|
$\left. \begin{array}{l}{{P}_{Gi}}^{\min } \leqslant {{P}_{Gi}} \leqslant {{P}_{Gi}}^{\max }\\[6pt]{{Q}_{Gi}}^{\min } \leqslant {{Q}_{Gi}} \leqslant {{Q}_{Gi}}^{\max }\\[6pt]{{V}_i}^{\min } \leqslant {{V}_i} \leqslant {{V}_i}^{\max }\\[6pt]{{S}_{Li}} \leqslant {{S}_{Li}}^{\max }\end{array} \right\},$
|
(4) |
式中,PGimin、PGimax为第i台发电机出力下限值和上限值,QGimin、QGimax为第i台发电机无功出力上限值和下限值,Vimin、Vimax为节点电压下限值和上限值.
1.3 不等式约束处理对于优化过程中变量越限的处理,目前研究中还缺乏统一的比较高效的处理机制. 当前研究工作中主要通过建立罚函数,将约束条件引入到目标函数中形成一个新的目标函数,将原来有约束优化问题转化为无约束优化问题,通过惩罚因子对越限数值进行处理,但缺点是惩罚因子的选取对最终优化结果有比较大的影响. 惩罚因子选取过大容易导致算法陷入局部最优,惩罚因子选取得较小则算法很难收敛到比较满意的最优解. 本文在众多专家学者的研究基础之上,决定采用自适应调整罚因子,使罚因子根据变量越限量的大小动态改变,数学表述为
|
$\begin{split}\displaystyle\min {F_C} = \sum\limits_{i = 1}^{{N_G}} {{F_i}} ({{P}_{Gi}}) + {K_V}\sum\limits_{i = 1}^{{N_{PQ}}} {({{V}_i}} - {{V}_i}^{\lim }{)^2} +\\ \displaystyle{K_Q}\sum\limits_{i = 1}^{{N_G}} {{{({{Q}_{Gi}} - {{Q}_{Gi}}^{\lim })}^2}} + {K_P}\sum\limits_{i = 1}^{{N_G}} ( {{P}_{1G}} - {{P}^{\lim }}{)^2}.\end{split}$
|
(5) |
式中,Vilim为越限节点电压限值,若越上限值则取上限值Vimax,若越下限值则取下限值Vimin;QGilim为发电机无功出力限值,若越上限值则取上限值QGimax,若越下限值则取下限值QGimin;Plim为平衡节点有功出力限值,同上. KV、KQ、KP分别为对应惩罚项的惩罚系数.
2 基于老化机制和精英改选机制的差分进化和粒子群混合算法原理 2.1 差分进化算法差分进化算法(Differential Evolution,DE)是由Storn和price于1995年提出,是一种连续空间全局优化启发式算法. 差分进化算法原理简单,易于实现,与遗传算法一样,都具有变异、交叉和选择操作,区别在于差分进化算法利用当前种群个体间的差异先进行变异和交叉操作,然后采用贪婪选择策略对种群中的个体进行选择操作产生新一代种群. 定义D维空间内的个体
1) 变异操作.
在变异操作中任一变异个体
|
${{Q}_i}^{t + 1} = {{X}_{s1}} + G({{X}_{s2}}^t - {{X}_{s3}}^t).$
|
(6) |
式中,s1、s2、s3是属于[1, N]且不同于i的整数,G为变异因子,用来控制向量差的大小,t为当前代,Xs1、Xs2、Xs3为当前代中随机选取的个体.
由于变异操作中G的大小对算法收敛速度和精度都有比较大的影响,本文采用自适应变异因子策略,当迭代后期粒子趋于一致时,增大变异因子,保持种群的多样性;当粒子差异较大时,减小变异因子,使算法寻优速度得到加强. 其数学表达式为
|
${G_i} = \left\{ \begin{array}{l}1,{\rm{if(fi}}{{\rm{t}}_{{\rm{worst}}}}{\rm{ = fi}}{{\rm{t}}_{{\rm{best}}}}{\rm{)}};\\[6pt]\displaystyle {\rm{1 - }}\frac{{{\rm{fi}}{{\rm{t}}_{{\rm{worst}}}}{\rm{ - fi}}{{\rm{t}}_i}}}{{{\rm{fi}}{{\rm{t}}_{{\rm{worst}}}}{\rm{ - fi}}{{\rm{t}}_{{\rm{best}}}}}}{\rm{,otherwise}}.\end{array} \right.$
|
(7) |
式中,fiti为第i个粒子的适应度值,fitworst为粒子适应度最差值,fitbest为粒子适应度最优值.
2) 交叉操作.
父代个体和变异个体根据交叉概率按式(8)产生新个体
|
${u_{ij}}^{t + 1} = \left\{ \begin{array}{l}{q_{ij}}^{t + 1},{\rm{if(rand < CR)or}}(j = {j_{{\rm{rand}}}});\\[6pt]{x_{ij}}^t,{\rm{otherwise}}.\end{array} \right.$
|
(8) |
式中,rand是(0, 1)之间均匀分布的随机数,
|
${\rm{CR}} = {\rm{C}}{{\rm{R}}_{\rm{0}}} \times {2^{{{\rm{e}}^{(1 - \frac{{{T_{\max }}}}{{t + 1}})}}}}.$
|
(9) |
式中,CR0是初始交叉因子,本文选取CR0=0.8,Tmax为最大迭代次数,t为当前迭代次数.
3) 选择操作
选择操作中采用贪婪策略,其依据是根据适应度函数来决定交叉后的个体是否取代父代个体,并选择适应度更优的个体进入下一次更新迭代,即
|
${{X}_i}^{t + 1} = \left\{ \begin{array}{l}{{U}_i}^{t + 1},{\rm{if}}({F_C}({{U}_i}^{t + 1}) < {F_C}({{X}_i}^t));\\[6pt]{{X}_i}^t,{\rm{otherwise}}.\end{array} \right.$
|
(10) |
式中,FC为优化的目标函数值,Xit+1为下一代的第i个个体.
2.2 粒子群优化算法粒子群优化算法(Particle Swarm Optimization,PSO)是源于对鸟群觅食群集行为的研究而总结出的一种群体智能优化算法. 收敛速度和精度是衡量群体智能优化算法优劣的两大关键因素. 粒子群优化算法以其收敛速度快、依赖参数少、对初值不敏感的特点而被广泛运用于各种优化问题的求解. PSO算法中,以速度、位置、适应度3项指标表征,通过不断跟踪个体最优值Pbest(到目前迭代为止,所找到的粒子本身最优值)以及种群最优极值Gbest(到目前迭代为止,整个种群中所找到的最优值),不断地更新粒子的速度及位置,直到达到最大迭代次数或找到满足精度的最优解. 假设在D维的搜索空间中,n个粒子组成一个种群
|
${{V}_{id}}^{t + 1} = \omega {{V}_{id}}^t + {c_1}{r_1}({{P}_{id}}^t - {{X}_{id}}^t) + {c_2}{r_2}({g_{id}}^t - {{X}_{id}}^t),$
|
(11) |
|
${{X}_{id}}^{t + 1} = {{X}_{id}}^t + {{V}_{id}}^{t + 1}.$
|
(12) |
式中,
|
$\omega = {\omega _{\max }} - ({\omega _{\max }} - {\omega _{\min }}) \times \frac{t}{{{T_{\max }}}}.$
|
(13) |
式(13)中,
虽然粒子群优化算法具有快速收敛性能,但其在优化的整个过程中都以Gbest作为引导,在前期其收敛速度会比较快,但后期如果Gbest陷入局部最优解,则整个种群将陷入“早熟”,使优化问题不能得到全局最优解. 为了改善PSO算法的这一缺点,本文提出一种“老化机制”,引入到粒子群的寻优迭代过程中,在Gbest陷入局部最优时,引入新的粒子与其竞争,增强种群的多样性,提高算法的全局寻优能力. 改进粒子群优化算法的具体流程图如图1所示.
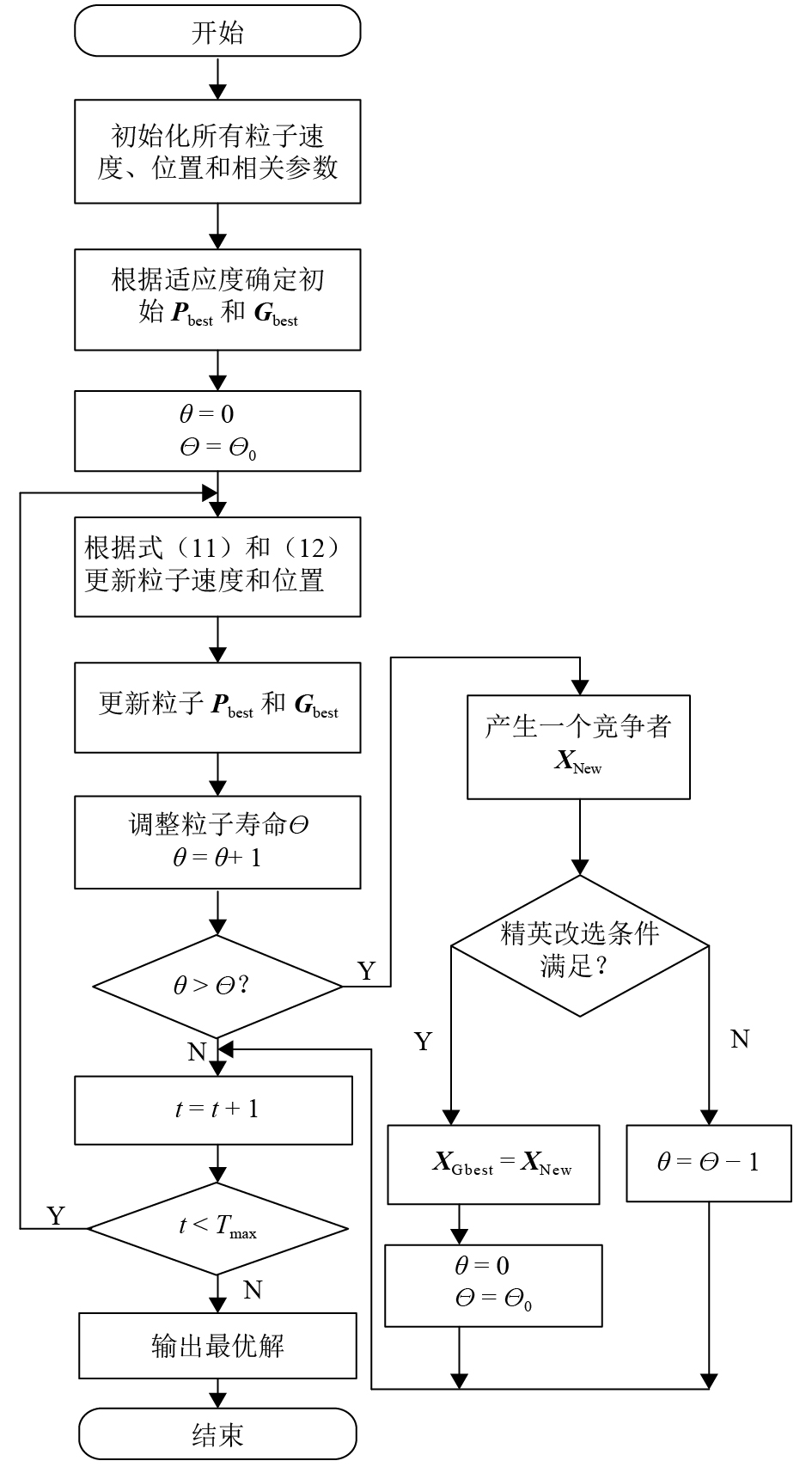
|
图 1 改进粒子群优化算法流程图 Figure 1 Flow chart of improved particle swarm optimization algorithm |
假设最优粒子寿命为
策略1:if
策略2:if
策略3:if
其中,
|
${\delta _{{X_{G_{\rm{best}}}}}}(t) = f({{X}_{G_{\rm{best}}}}(t)) - f({{X}_{G_{\rm{best}}}}(t - 1)),$
|
(14) |
|
$\sum\limits_{i = 1}^n {{\delta _{{X_{{{P}}_{\rm{best}}{_i}}}}}(t) = } f({{X}_{{{P}}_{\rm{best}}{_i}}}(t)) - \sum\limits_{i = 1}^n {f({{X}_{{{P}}_{\rm{best}}{_i}}}(t - 1))} .$
|
(15) |
式(14)和(15)分别表示当前代种群个体极值联合优化和群体极值优化程度,其值越大则种群全局最优个体的引导能力越强,反之则越弱,容易陷入局部最优解. 本文竞争个体的产生办法和精英改选机制如图2所示.
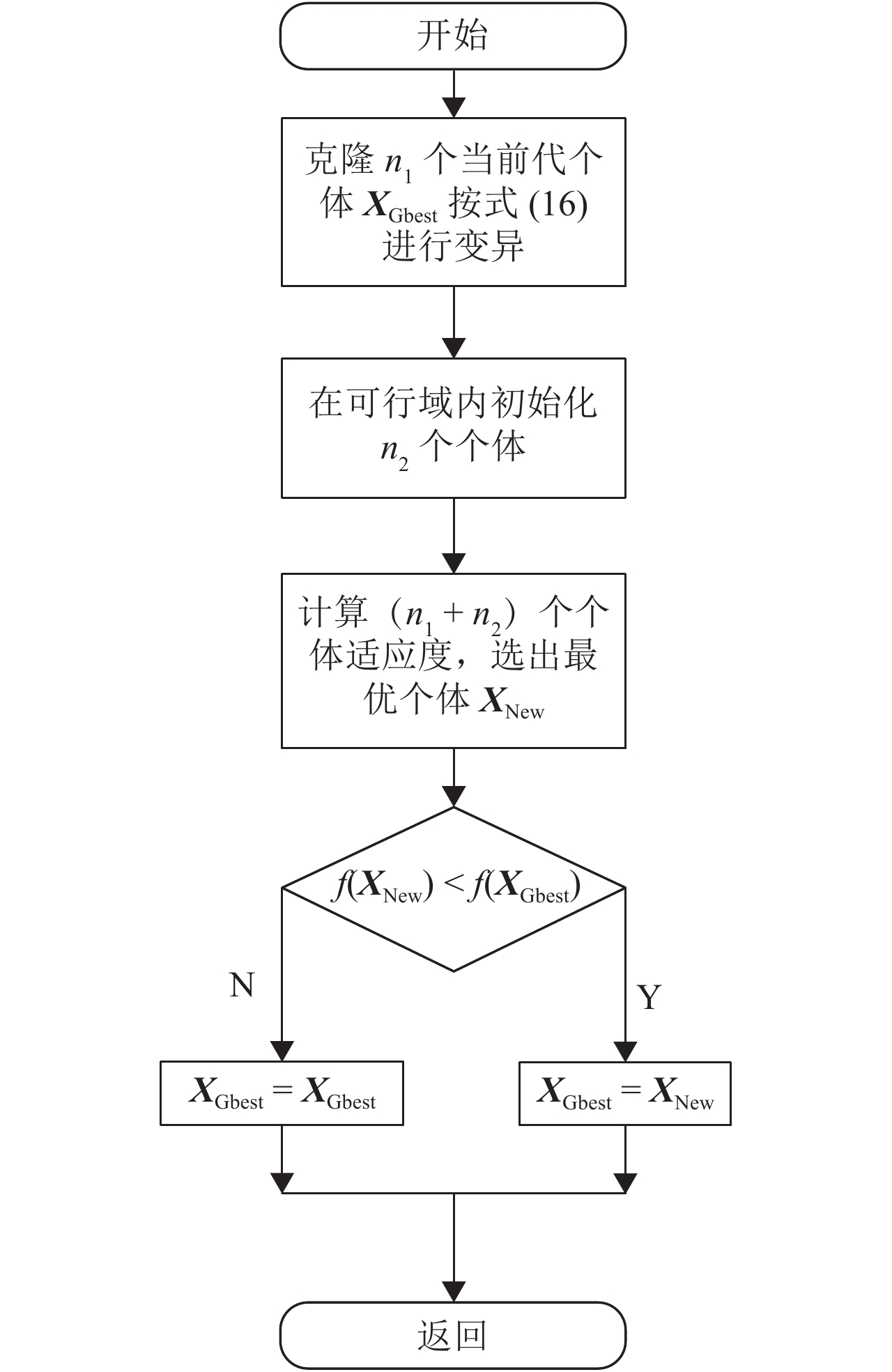
|
图 2 精英改选流程图 Figure 2 Flow chart of elite re-election |
利用文献[15]中介绍的多项式变异策略,以克隆个体为父代p,对每个p按式(16)生成子代c:
|
${c_k} = {p_k} + ({x_k}^u - {x_k}^l){\delta _k}.$
|
(16) |
式中,ck、pk为c、p的第k个分量,
|
${\delta _k} = \left\{ \begin{array}{l}{(2{r_k})^{\frac{1}{{{\eta _m} + 1}}}} - 1,0 \leqslant {r_k} \leqslant 0.5;\\[6pt]1 - {[2(1 - {r_k})]^{\frac{1}{{{\eta _m} + 1}}}},0.5 \leqslant {r_k} \leqslant 1.\end{array} \right.$
|
(17) |
式中,rk是均匀分布于[0, 1]上的随机数;
本文取PSO算法得到的最优个体与DE算法得到的最优个体进行比较,将适应度更优的个体作为下一代进化的依据,将PSO算法与DE算法相结合,既可以保持PSO算法的快速收敛特性,又利用DE算法中变异、交叉、选择操作增强粒子的多样性,使得混合算法的寻优能力大大提高.
3 基于改进差分进化和粒子群混合算法(DEPSO)的电力系统最优潮流计算运用本文提出的DEPSO算法进行最优潮流计算的具体步骤如下:
(1) 确定算法各项初始参数,如:初始交叉因子CR0,种群规模NP,粒子维数D,惯性权重
(2) 采用双种群策略,将种群均匀地分成PSO种群和DE种群,随机初始化在不同的区域;
(3) 根据式(11)和(12)对PSO种群中的粒子进行速度与位置更新,潮流计算得到各个粒子的适应度,更新
(4) 根据式(6)、(8)、(10)对DE种群进行变异、交叉和选择操作,通过潮流计算得到子代个体适应度,选出最优个体
(5) 比较两个种群产生的最优个体
(6) 判断迭代次数是否达到最大迭代次数
以改进IEEE30节点系统作为测试算例,并将传统粒子群算法(PSO)、差分进化算法(DE)和本文算法(DEPSO)进行对比,利用MATLAB R2016a编程对所提出的算法进行验证.
IEEE30节点系统含6台发电机(节点1、2、5、8、11、13),4台可调变压器,41条线路,假设在10、12、15、17、20、21、23、24和29节点接入无功补偿装置,系统详细参数请见文献[16-17]. 负荷节点电压限值设为0.95~1.05p.u,基准容量为100MVA. 表1给出了算法基本参数信息,表2给出了IEEE30节点系统发电机参数信息.
| 表 1 算法基本参数 Table 1 Basic parameters of the algorithm |
| 表 2 常规发电机组参数 Table 2 Parameters of conventional generators |
在初始条件相同的情况下,表3和表4给出了不同算法的优化结果. 从表中可以看出,PSO算法发电费用为801.882 6 $/h,DE算法发电费用为800.347 0 $/h,DEPSO算法发电费用为799.779 7 $/h,同时与文献[18-19]所提算法计算进行比较,DEPSO算法的优化结果均有明显优势.
| 表 3 不同算法优化结果比较 Table 3 Comparison of different algorithm optimization results |
| 表 4 不同算法变量优化结果比较 Table 4 Comparison of variables optimization results of different algorithms |
群体智能优化算法在初始化过程中具有一定的随机性,表5给出了PSO算法、DE算法、DEPSO算法、文献[18-19]连续计算40次的最大值、平均值和最小值的结果对比. 从结果中可以看出,DEPSO不依赖于初值的选取,在任意初值条件下,DEPSO算法都能收敛到全局最优值,避免“早熟”现象出现.
| 表 5 不同算法发电费用 Table 5 Cost of power generation by different algorithms |
| 表 6 不同算法最终优化结果比较 Table 6 Comparison of the final optimization results of different algorithms |
表6给出了PSO、DE和DEPSO算法最终寻优结果的对比. 优化前的发电费用为900.76 $/h,从中可以看出DEPSO算法收敛到最优解的迭代次数明显比其他两种算法少,且优化率比PSO算法高0.23%,比DE算法高0.07%,比文献[18]高0.29%,比文献[19]高0.12%. 因此该算法收敛速度更快,精度更高. 图3为3种算法的收敛曲线,由此可知,DEPSO算法前期初始点与PSO算法和DE算法基本相同,但其收敛速度非常快,达到相同精度的迭代次数明显少于其他两种算法. 另外该算法收敛过程较为平缓,显示了其良好的鲁棒性能,且迭代至第26代时就收敛到较为满意的解,寻找到的最优解要优于PSO算法和DE算法,显示其跳出局部最优解的能力更强.
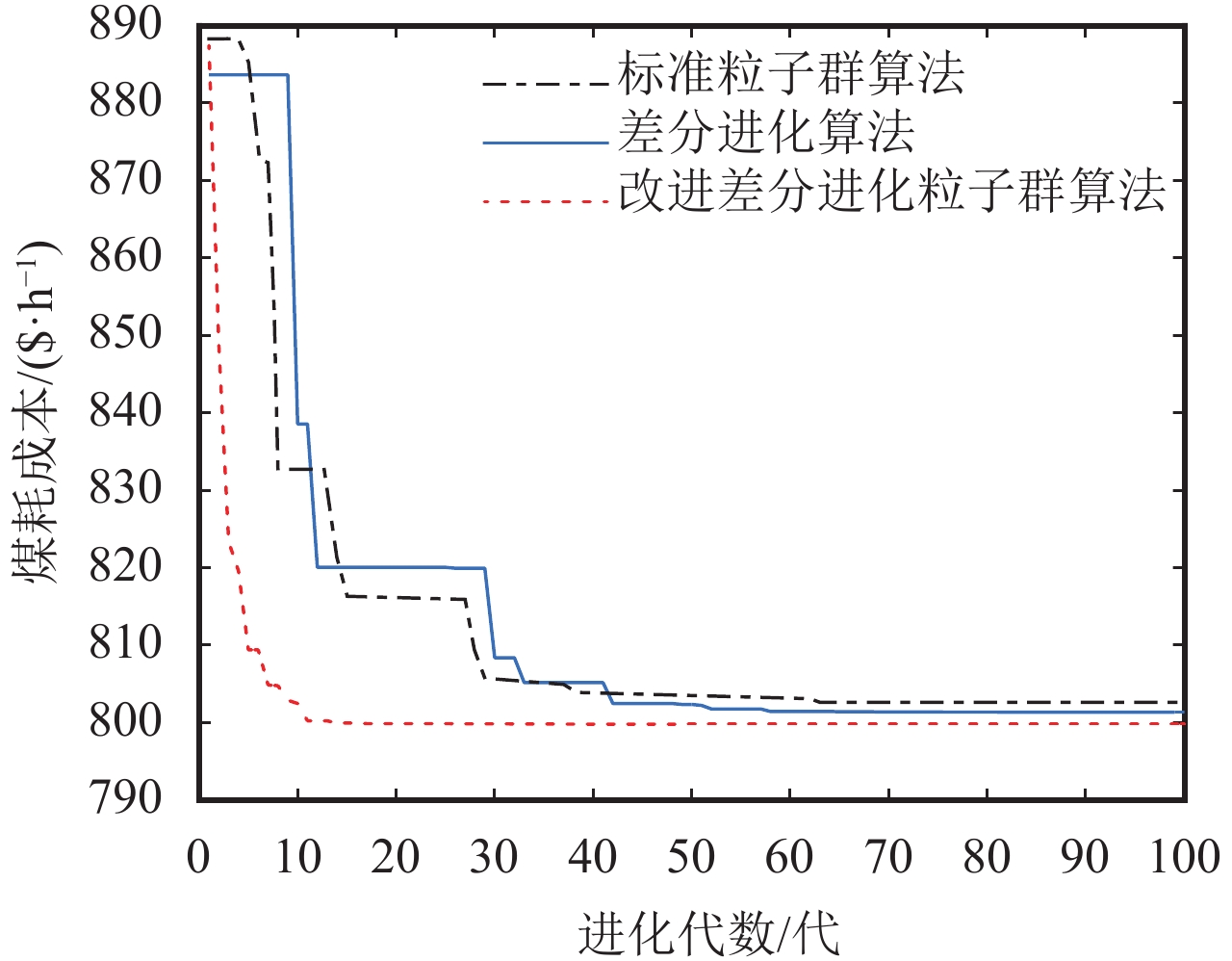
|
图 3 3种算法的收敛曲线 Figure 3 Convergence curves of the three algorithms |
本文提出一种基于改进差分进化和粒子群的电力系统最优潮流混合优化算法,以发电费用最小为目标函数,在算法寻优过程中引入老化机制和精英改选机制,根据最优粒子的引导能力动态调整其寿命,增强了种群的多样性,避免“早熟”现象出现. IEEE30节点系统仿真测试结果表明,所提算法具有更快的收敛速度和更高的收敛精度,迭代次数少,跳出局部最优解的能力显著增强,为解决电力系统最优潮流计算问题提供了一种新的思路和方法.
| [1] |
俞俊霞, 赵波. 基于改进粒子群优化算法的最优潮流计算[J].
电力系统及其自动化学报, 2005, 17(4): 83-88.
YU J X, ZHAO B. Improved particle swam optimization algorithm for optimal power flow problems[J]. Proceedings of the CSU-EPSA, 2005, 17(4): 83-88. |
| [2] | DOMMEL H W, TINNEY W F. Optimal power flow solutions[J]. IEEE Trans on Power Apparatus and Systems, 1968, 87(10): 1866-1876. |
| [3] |
陈恳. 直角坐标牛顿-拉夫逊法潮流计算新解法[J].
电力系统及其自动化学报, 1999, 11(4): 66-69.
CHEN K. New power flow solution for rectangular coordinate Newton-Raphson[J]. Proceedings of the CSU-EPSA, 1999, 11(4): 66-69. |
| [4] |
杨跃光, 刘璇. 一种改进的Newton算法在电力系统潮流计算中的研究与应用[J].
陕西电力, 2011, 39(10): 4-6.
YANG Y G, LIU X. Research and application of improved newton algorithm for power flow calculation in power system[J]. Shaanxi Electric Power, 2011, 39(10): 4-6. DOI: 10.3969/j.issn.1673-7598.2011.10.003. |
| [5] |
候芳, 吴政球, 王良缘. 基于内点法的快速解耦最优潮流算法[J].
电力系统及其自动化学报, 2001, 13(6): 8-12.
HOU F, WU Z Q, WANG L Y. Optimal power solution based on fast decouple interior point algorithm[J]. Proceedings of the CSU-EPSA, 2001, 13(6): 8-12. |
| [6] |
蔡广林, 韦化. 基于非线性互补方法的内点最优潮流算法[J].
电网技术, 2005, 29(21): 21-26.
CAI G L, WEI H. An interior point optimal power flow algorithm based on nonlinear complementarity method[J]. Power System Technology, 2005, 29(21): 21-26. DOI: 10.3321/j.issn:1000-3673.2005.21.005. |
| [7] |
李鑫滨, 朱庆军. 一种改进粒子群优化算法在多目标无功优化中的应用[J].
电工技术学报, 2010, 25(7): 137-143.
LI X B, ZHU Q J. Application of improved particle swarm optimization algorithm to multi-objective reactive power optimization[J]. Transactions of China Electric Technical Society, 2010, 25(7): 137-143. |
| [8] | PRICE K, STORN R. Differential evolution: a simple evolution strategy for fast optimization[J]. Software Tools, 1997, 22(4): 18-24. |
| [9] |
罗萍, 刘伟, 周述波. 自适应混沌变异的万有引力搜索算法[J].
广东工业大学学报, 2016, 33(01): 57-61.
LUO P, LIU W, ZHOU S B. Gravitational search algorithm of adaptive chaos mutation[J]. Journal of Guangdong University of Technology, 2016, 33(01): 57-61. DOI: 10.3969/j.issn.1007-7162.2016.01.011. |
| [10] |
乐秀璠, 覃振成, 尹峰. 基于自适应模拟退火遗传算法的多目标最优潮流[J].
继电器, 2005, 33(7): 10-15.
LIE X F, QIN Z C, YIN F. Multi-objective optimal power flow based on adaptive simulated annealing genetic algorithm[J]. Relay, 2005, 33(7): 10-15. |
| [11] |
陈璟华, 梁丽丽, 丁林军, 等. 计及风电场并网的机会约束规划的机组组合优化[J].
广东工业大学学报, 2017, 34(01): 50-54, 64.
CHEN J H, LIANG L L, DING L J, et al. Unit commitment optimization based on chance-constrained programming in wind power integrated system[J]. Journal of Guangdong University of Technology, 2017, 34(01): 50-54, 64. DOI: 10.12052/gdutxb.160087. |
| [12] |
马玲, 于青, 刘刚, 等. 基于量子差分进化算法的电力系统无功优化[J].
电力系统保护与控制, 2013, 41(17): 39-43.
MA L, YU Q, LIU G, et al. Power system reactive power optimization based on quantum DE algorithm[J]. Power System Protection and Control, 2013, 41(17): 39-43. DOI: 10.7667/j.issn.1674-3415.2013.17.006. |
| [13] |
郭经韬, 陈璟华, 周俊, 等. 基于组合混沌序列动态粒子群算法的电力系统无功优化[J].
广东工业大学学报, 2014, 31(2): 85-89.
GUO J T, CHEN J H, ZHOU J, et al. Reactive power optimization based on combined chaotic dynamic particle swarm optimization algorithm[J]. Journal of Guangdong University of Technology, 2014, 31(2): 85-89. |
| [14] |
阳春华, 钱晓山, 桂卫华. 一种混沌差分进化和粒子群优化混合算法[J].
计算机应用研究, 2011, 28(2): 439-441.
YANG C H, QIAN X S, GUI W H. Hybrid algorithm of chaotic differential evolution and particle swarm optimization[J]. Application Research of Computers, 2011, 28(2): 439-441. |
| [15] | DEB K. Multi-objective Optimization Using Evolutionary Algorithms [M]. New Jersey: John Wiley & Sons, Inc, 2001. |
| [16] | ALSAC O, STOTT B. Optimal load flow with steady-state security[J]. IEEE transactions on power apparatus and systems, 1974(3): 745-751. |
| [17] | YURYEVICH J, WONG K P. Evolutionary programming based optimal power flow algorithm[J]. IEEE Transactions on Power Systems, 1999, 14(4): 1245-1250. DOI: 10.1109/59.801880. |
| [18] | SAYAH S, ZEHAR K. Modified differential evolution algorithm for optimal power flow with non-smooth cost functions[J]. Energy conversion and Management, 2008, 49(11): 3036-3042. DOI: 10.1016/j.enconman.2008.06.014. |
| [19] | LAI L L, MA J T, YOKOYAMA R, et al. Improved genetic algorithms for optimal power flow under both normal and contingent operation states[J]. International Journal of Electrical Power & Energy Systems, 1997, 19(5): 287-292. |
 2017, Vol. 34
2017, Vol. 34