随着基于位置的服务的需求日益增大,无线定位技术成为了当前研究的热点. 在室外环境,全球定位系统、北斗卫星导航系统和蜂窝定位技术能满足大多数的定位需求. 在室内环境中,无线信号传播受到建筑构造,物体阻隔和人员走动的影响,容易造成无线信号的强度严重衰减,出现的无线屏蔽和阻隔效应导致定位精度低甚至不能完成定位.
无线信号定位方法分为基于测距(Range-based)的定位和基于非测距(Rang-free)的定位. 基于测距的定位方法如AOA、TOA和TDOA是通过无线信号传播衰减模型计算信号接收器的位置,但是受多径散射影响,定位精度偏低且误差较大. 基于非测距的定位方法如信号强度指纹匹配定位、室内图像定位和机器学习定位等,因为不需要计算无线信号模型的参数,能有效地克服室内多径环境的影响,提高定位精度[1-2].
目前,Wi-Fi在室内分布广泛,不需刻意部署,成本较低,利用室内Wi-Fi定位是较好的选择,但Wi-Fi信号容易受复杂的室内环境影响,接收信号强度指示(Received Signal Strength Indication, RSSI)值容易出现波动、偏差和缺失. 常见的室内Wi-Fi定位方法有k近邻(k Nearest Neighbor, KNN),加权k近邻(Weight k Nearest Neighbor, WKNN),SVM和单层神经网络等[3]. 但KNN与WKNN对大规模的指纹数据库计算量较大,在样本不平衡时将导致定位结果产生较大的偏差,支持向量机(Support Vector Machine, SVM )对缺失的RSSI信号比较敏感,对于高维数据的映射解释力不强,单层神经网络对指纹数据库的训练速度较慢且容易陷入过拟合. 由于上述算法是利用浅层结构进行非线性特征变换的机器学习方法,其建模和表达能力有限,在一些数据更复杂的情况时就会遇到各种困难[4-5]. 随着深度学习概念的提出,文献[6-7]分别采用信道状态信息(Channel State Information, CSI)和超宽带(UWB)信号结合深度学习用于室内定位中,但采集CSI和UWB信号依赖硬件设备,成本较大且难以采集.
深度学习网络具有良好的泛化能力,能从复杂的室内环境中的RSSI信号提取有效的特征,学习和构建室内无线信号模型. 由于Wi-Fi普遍存在,文献[8-9]将室内采集的RSSI信号组成指纹数据库,并使用深度学习网络对其进行训练和学习,能达到较好的定位效果,但是文献只关注了定位的准确率而没有考虑信号的特征提取和算法运行效率.
为了提高定位的准确率和效率,本文提出一种基于深度学习网络的堆叠去噪自编码器(Stacked Denoising Auto Encoder, SDAE),通过ReliefF约简指纹数据库RSSI信号的室内定位算法(ReliefF Fingerprint Based Stacked Denoising Auto Encoder, RFB-SDAE),文中算法通过ReliefF[10]约简指纹采集中的冗余信息,减少无关数据对深度学习网络特征学习的影响. 利用SDAE的多层隐含层预训练约简后的指纹数据库,并使用误差反向传播调整,使重构误差最小化,增强模型的泛化能力,减少指纹数据库的训练时间和分类时间. 通过标准数据库UJIIndoorLoc[11]进行实验验证,本文所提出的算法有更好的定位效果.
1 指纹匹配定位算法在众多室内定位算法中,指纹匹配定位算法是较为常用的定位算法. 其中,在室内定位中起决定性作用的信号强度信息为信号特征,室内指纹匹配定位算法包括离线阶段和在线阶段.
离线阶段主要是建立指纹数据库. 在室内的指纹数据库中,有多个参考点(Reference Point, RP)的RSSI信号,表示为
|
${{{r}}_i} = ({\rm{RSS}}{{\rm{I}}_{i1}},{\rm{RSS}}{{\rm{I}}_{i2}}, \cdots ,{\rm{RSS}}{{\rm{I}}_{ij}}, \cdots ,{\rm{RSS}}{{\rm{I}}_{iN}}).$
|
(1) |
其中i=1, 2, …, M, M是所有参考点的总数,N(j=1, 2, …, N)表示室内环境中存在N个Wi-Fi接入点(Access Point, AP),RSSIij表示在第i个参考点所接收到第j个AP的信号强度值. 由M个RP的RSSI信号所组成的指纹数据库为
|
$S = \{ ({{{r}}_1},{m_1}),({{{r}}_2},{m_2}), \cdots ,({{{r}}_i},{m_i}), \cdots ,({{{r}}_M},{m_M})\} .$
|
(2) |
在线定位阶段主要是计算待定位点的位置. 在某待定位点s在线采集的RSSI信号为
|
${{\hat{ r}}_s} = ({\rm{RSS}}{{\rm{I}}_{s1}},{\rm{RSS}}{{\rm{I}}_{s2}}, \cdots ,{\rm{RSS}}{{\rm{I}}_{sj}}, \cdots ,{\rm{RSS}}{{\rm{I}}_{sN}}).$
|
(3) |
根据指纹匹配定位算法,通过式(3)与离线阶段的指纹数据库中记录的RSSI信号进行匹配,通过式(4)得到s的区域ms,从而确定待定位点所在区域mi.
|
${\hat {{r}}_s} \to S \to {m_s} \to {{m}} \to {m_i}.$
|
(4) |
其中,
对大量RSSI信号统计和分析可知,RSSI信号在不同的室内环境下所表现出来的分布总是难以统一于同一个模型,在众多的室内定位算法中,大部分是以高斯函数拟合RSSI信号分布曲线,但是高斯拟合模型不能完全表征室内区域信号分布的规律[12]. 采用一般的指纹匹配定位算法难以准确地构建室内信号模型,因此所得到的定位准确率难以满足现实需求.
2 堆叠式去噪自编码器深度学习网络通过多层非线性结构的隐含层将低层的数据输出作为高层的输入,从大量的训练输入数据中学习得到各分层级的特征,对深度学习网络结构模型每一个隐含层的输入数据都有相对应的特征表示,将原始输入的数据通过非线性变换,转换为具有不变性和鉴别性的特征[13].
堆叠式自编码器(Stacked Auto Encoder, SAE)是由多个自编码器(Auto Encoder, AE)堆叠所组成的深度学习神经网络,是深度学习常用方法之一[14-15]. 自编码器通过给定的无标签数据,用非监督学习学习输入数据中的特征,尽可能复现原输入数据. 去噪自编码器(Denoising Auto Encoder, DAE)则是在自编码器的基础上,对训练数据随机加入噪声,自编码器自主从含随机噪声的数据中学习并重构原始的输入数据. 堆叠式去噪自编码器是将多个DAE堆叠在一起组成的深度架构,SDAE从初始的输入的数据中自主学习并提取有效的特征,经过无监督训练的特征学习,分别得到各层的参数. 深度学习利用具有层次结构的人工神经网络的特点,在一个假设给定输出与输入相同的神经网络中,通过重构误差自顶向下传输,调整网络中每层的参数,输出每一个隐含层的权重和偏置,从而得到输入数据的模型结构.
虽然SDAE深度学习相比于单层神经网络有更强的表达复杂目标函数的能力,但是能否从指纹数据库的RSSI信号中提取有效和重要的判别信息对深度学习的泛化性能有很大的影响,是造成深度学习在训练过程中陷入学习困难,难以构建起一个准确模型的原因. 因此对于SDAE深度学习而言,约简输入数据的冗余信息,优化指纹数据库,通过预训练得到各层的网络参数,及稀疏性约束隐含层神经元数目将对SDAE网络模型的构建起到重要的作用.
3 RFB-SDAE室内定位算法由于现有的室内定位算法大部分是以浅层结构的机器学习方法为主,难以构建合适的室内信号模型,在构建的指纹数据库中,所采集的RSSI信号存在高维度,多噪声等问题,在室内定位的研究中存在局部区域的“维数灾难”. 冗余信息是影响利用RSSI信号定位所导致的运行效率和定位准确率不高的主要原因[16]. 因此本文提出基于SDAE深度学习的RFB-SDAE室内定位算法. 该算法通过约简及预处理去除指纹数据库中的冗余信息,预训练及稀疏化SDAE网络,优化求解各层参数,获得较为精确的室内信号模型,并利用该模型实现室内的区域定位.
3.1 RSSI信号约简与预处理由于AP在室内的位置相对是固定的,在同一区域内的RSSI信号较为相似,在不同区域内的RSSI信号存在比较大的差异性. ReliefF算法在处理室内定位的区域多分类问题时,对各区域采集的RSSI信号进行约简,每次从指纹数据库S的中随机取出一组RSSI信号ri,并在其中寻找与ri相似与不相似的各k个近邻RSSI信号,通过式(5),更新室内每个区域RSSI信号的AP权重.
|
$\begin{array}{l}W({\rm{RSSI}}) = W({\rm{RSSI}}) - \sum\limits_{g = 1}^k {{\rm{diff}}({\rm{RSSI}},{{{r}}_i},{{{H}}_g})} /(nk) + \\\sum\limits_{ m_i \notin {\rm{Class}}{{({r}}_i,m_i})} \!\!\!{[\frac{{p({m_i})}}{{1 - p({{\rm{Class}}({r}}_i,m_i))}\!\!}\sum\limits_{g = 1}^k {{\rm{diff}}({\rm{RSSI}},{{{r}}_i},{{{M}}_g}({m_i}))} ]} /(nk).\end{array}$
|
(5) |
在式(5)中,diff(RSSI, ri, Hg)、diff(RSSI, ri, Mg(mi))分别表示ri与Hg、Mg(mi)在RSSI信号上的差异值,其中,Hg表示相似室内区域的最近邻RSSI信号,Mg(mi)表示不相似室内区域mi中的第g个最近邻RSSI信号,n表示样本抽样的次数. P(mi)表示区域mi在训练集中所占比例,p(Class(ri, mi))表示随机选取的信号组合(ri, mi)的比例.
对RSSI信号约简后得到RSSI样本
|
${{{r}}_i}{\! '} = ({\rm{RSS}}{{\rm{I}}_{i1}},{\rm{RSS}}{{\rm{I}}_{i2}}, \cdots ,{\rm{RSS}}{{\rm{I}}_{ij}}, \cdots ,{\rm{RSS}}{{\rm{I}}_{iN'}}).$
|
(6) |
其中,N′(j=1, 2, …, N′)表示室内环境中约简后存在N′个接入点. 则由M个RP的RSSI指纹样本组成新的指纹数据库为
|
$S' = \{ ({{{r}}_1}{\!\!\! '},{m_1}),({{{r}}_2}{\!\!\! '},{m_2}),\cdots,({{{r}}_i}{\!\! '},{m_i}),\cdots,({{{r}}_M}{\!\!\!\!\! '} \; ,{m_M})\} .$
|
(7) |
同时,为减少指纹数据库训练过程中的计算量,降低RSSI指纹样本之间的差异性对深度学习网络模型的影响,适应SDAE深度学习网络的要求,需要对约简后的RSSI样本的指纹数据库S′作归一化预处理.
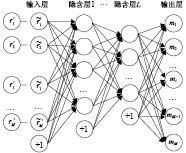
3.2 RFB-SDAE预训练如图1所示,基于RFB-SDAE深度学习的指纹匹配定位方法中,在输入的RSSI样本
|
${{{h}}^{(l)}} = {f_\theta }({{\tilde{ r}}_i}') = {\rm{sigm}}({{{W}}^{(l)}}{{\tilde{ r}}_i}' + {{{b}}^{(l)}}).$
|
(8) |
其中,参数θ={W(l), b(l)},W(l),b(l)分别表示第l隐含层的RSSI样本的权重和偏置,sigm(z)=1/(1+exp(-z))表示sigmoid函数,h(l)表示当前隐含层l的编码输出.
在解码过程中,第l隐含层的编码输出作为第l+1隐含层重构输入.
|
${{{h}}^{(l + 1)}} = {{\rm{g}}_{_{\theta '}}}({{{h}}^{(l)}}) = {\rm{sigm}}({{{W}^{(l + 1)}}{{{h}}^{(l)}} + {{b}}^{(l + 1)}}).$
|
(9) |
其中,参数θ′={W(l+1), b(l+1)},W(l+1),b(l+1)分别表示第l+1隐含层中RSSI样本的重构权重和偏置,h(l+1)表示当前隐含层l+1的重构解码输出. 两者之间的重构误差表示为
|
$L{\rm{(}}{{{h}}^{(l)}}{\rm{,}}{{{h}}^{(l + 1)}}{\rm{)}} = {\rm{||}}{{{h}}^{(l)}}{\rm{ - }}{{{h}}^{{\rm{(}}l + {\rm{1)}}}}{\rm{|}}{{\rm{|}}^{\rm{2}}}.$
|
(10) |
经过RFB-SDAE的各隐含层对RSSI样本的映射编码与重构解码后,定义一个损失函数J(W(l), b(l))表示输入RSSI样本与输出定位区域之间的重构误差损失为
|
$\begin{array}{c}J({{{W}}^{(l)}},{{{b}}^{(l)}}) = \left[ {\displaystyle\frac{1}{T}\sum\limits_{u = 1}^T {\displaystyle\frac{1}{2}||{{{h}}_{{{W,b}}}}({{{\tilde{ r}}}_i}) - {m_i}{\rm{|}}{{\rm{|}}^{\rm{2}}}} } \right] + \displaystyle\frac{\lambda }{2}||{{W}}_u^{(l)}|{|^2}.\end{array}$
|
(11) |
式(11)中第一项为每批次训练的RSSI样本损失函数的平均值,第二项为权重惩罚项. 其中,T为每批输入训练的RSSI样本数目,λ是惩罚系数,hW, b(·)表示样本对应的网络输出,
|
图 1 SAE的结构框架 Figure 1 The structure of the SAE framework |
约简处理后的RSSI样本作为RFB-SDAE网络输入层,经过各隐含层神经元计算得到输出的权重和偏置,若隐含层设置的神经元数目过多,容易出现“恒等情况”,丧失自动学习RSSI样本的能力,因此需要在RFB-SDAE中进行稀疏化,稀疏性限制隐含层大部分的神经元,使之处于非激活状态,得到的室内信号模型能更好地表示RSSI样本.
通过对RFB-SDAE各隐含层的稀疏化可以得到有效的输出特征表示,定义稀疏去噪自编码器的损失函数为
|
$\hat J({{{W}}^{(l)}},{{{b}}^{(l)}}) = J({{{W}}^{(l)}},{{{b}}^{(l)}}) + \beta \sum\limits_{u = 1}^v {{\rm{KL}}(\rho ||{\rho _u})}.$
|
(12) |
其中,β为稀疏限制项权重,v为隐含层神经元个数,ρ为稀疏系数,ρu为隐含层单个节点输出的平均值,KL为相对熵衡量准则.
对RSSI信号约简后,指纹数据库S′的RSSI样本作为网络的输入数据,经过预训练及稀疏化过程,得到网络隐含层的输出权重W(L)和偏置b(L). 训练完成后的网络输出RSSI样本对应的特征表示,得到关于RSSI特征的室内信号模型.
将在线采集的RSSI信号
|
${{{m}}} = {\rm{sigm}}({{{W}}^{(L)}}{{{h}}^{(L{\rm{ - }}1)}} + {{{b}}^{(L)}}).$
|
(13) |
如图2所示,RFB-SDAE算法由指纹数据库S和S′、深度学习网络、在线采集信号和定位区域预测等部分所组成. 整体上包括模型训练和定位输出两个部分.

|
图 2 RFB-SDAE算法框架 Figure 2 RFB-SDAE algorithm framework |
步骤1:在室内环境中采集的RSSI信号组成深度学习的原始训练集;
步骤2:约简指纹数据库S的RSSI信号,去除RSSI信号中包含的冗余信息,处理后的RSSI信号组成RSSI样本的指纹数据库S′,并预处理以适应深度学习网络的数据要求;
步骤3:处理后的指纹数据库S′输入深度学习网络中进行预训练,RFB-SDAE逐层对RSSI样本编码,提取特征数据;
步骤4:对RSSI样本的编码数据稀疏化处理,求解重构解码之后输出的特征与输入样本的重构误差;
步骤5:逐层训练并调整网络参数,使得输出特征的重构误差最小,训练结束后得到关于RSSI特征的室内无线信号模型.
3.4.2 定位输出步骤1:预处理在线阶段采集的RSSI信号,作为定位的目标数据输入;
步骤2:在训练后的RFB-SDAE深度学习网络加入分类器,将网络最后一层输出的特征输入分类器;
步骤3:确定在线阶段采集的RSSI信号所对应的室内区域mi.
4 结果与分析在现阶段关于室内定位的研究中,大部分均是采用自行收集的RSSI数据库进行研究,不同的实验环境和收集设备各有不同的差异性,用于验证提出的算法的有效性和准确率有着很大的不确定性. 因此使用统一的数据库去验证研究定位算法的准确率和有效性,将对提高研究效率有很大的现实意义.
4.1 实验环境在UCI机器学习数据库中提供了Universitat Jaume I大学建筑所采集的用于室内定位研究的Wi-Fi标准指纹数据UJIIndoorLoc,将采用该数据库在Matlab2015a平台上进行仿真验证与测试.
对UJIIndoorLoc指纹数据库中的目标定位楼层划分为多个网格区域,对建筑内各采集点的位置区域进行标号,标记的位置标号mi作为输出的目标定位区域. 实验指标中,综合准确率指经过训练学习后的目标定位区域在以预测区域为中心,预测区域周围一个划分单元格以内的区域的准确率;完全准确率指经过训练学习后的目标定位区域与预测区域完全一致的准确率.
设定指纹数据库中没采集到AP的空缺RSSI值为-200dBm,用以区别采集数据. 设定ReliefF的k近邻样本数为10,约简指纹数据库,约简后的AP数为N′,并对约简后的指纹数据库归一化.
实验采用N′-L-M堆叠式去噪自编码器的多层网络结构,其中,N′(j=1, 2, …, N′)表示室内环境中存在N′个约简后的AP数量,即指纹数据库对RFB-SDAE的输入维度,L表示RFB-SDAE隐含层的层数及神经元数目,M(i=1, 2, …, M)表示室内所有RP的总数,即输出定位区域的维度. RFB-SDAE的学习率设定为1,随机置零概率设为0.5,隐含层的稀疏系数设为0.01.
4.2 参数选择参数设置对深度学习网络的训练和学习有较大的影响,为在RFB-SDAE网络中获得较好的效果,需要对其中的隐含层以及各隐含层中的神经元数目进行选择. 根据文献[17]及相关经验可得,在各隐含层中层逐渐降低神经元的数目,可得到一个较好的参数设置.
如表1所示,实验设置了不同的隐含层层数及各隐含层所含的神经元数目,测试在相同的较少迭代次数的情况下,得到不同参数选择下的结果.
| 表 1 隐含层及神经元数目选择 Table 1 Hidden layer and neurons number selection |
随着隐含层及神经元数目增加,定位效果能到达了一个最优结果. 由于指纹数据库中的样本有限,在样本不足的情况下,使得深度学习网络梯度下降困难,若随意增加网络深度,运行时间将增多且会降低定位准确率. 因此,结合本节实验的结果与消耗时间,实验采用具有4层隐含(200-150-100-50)的网络结构.
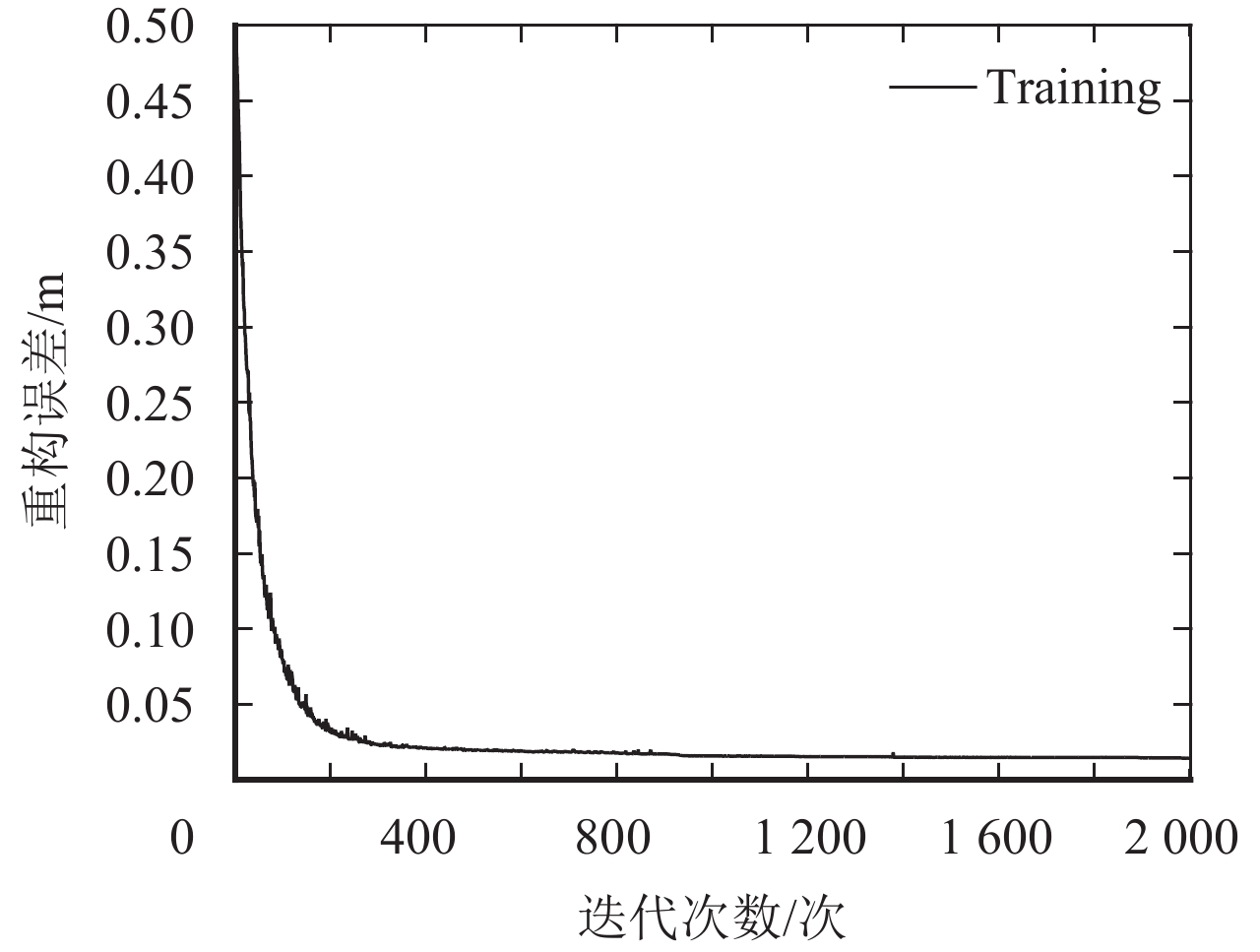
4.3 误差收敛分析实验为RSSI样本的指纹数据库在深度学习网络下经过编码与解码之后的重构误差的收敛性分析,设定迭代次数为2 000次的训练,如图3所示,对比在不同迭代次数下RFB-SDAE的重构误差的变化情况.
|
图 3 不同迭代次数下的重构误差 Figure 3 Reconstruction error per epoch |
由图3可以看出,RFB-SDAE编码与解码后重构误差随迭代次数的增加而减小. 在迭代次数开始至300次左右时,输入的RSSI样本经过各隐含层的映射编码与重构解码,通过反向传播训练和调整隐含层的输出权值和偏置,重构误差变化比较明显. 在之后的迭代过程中,重构后的特征数据接近于输入数据的表示形式,因此各隐含层输出特征的重构误差逐渐趋于平整,收敛于一个稳定的误差值. 考虑到实验的效率与结果,结合迭代次数与重构误差的变化情况,可以根据具体的应用情况选择合适的迭代次数.
4.4 定位准确率分析实验验证不同迭代次数下对室内定位准确率的实验效果,设定固定的隐含层数以及各隐含层的神经元数目,对比在不同迭代次数下RFB-SDAE的综合准确率和完全准确率的变化情况.
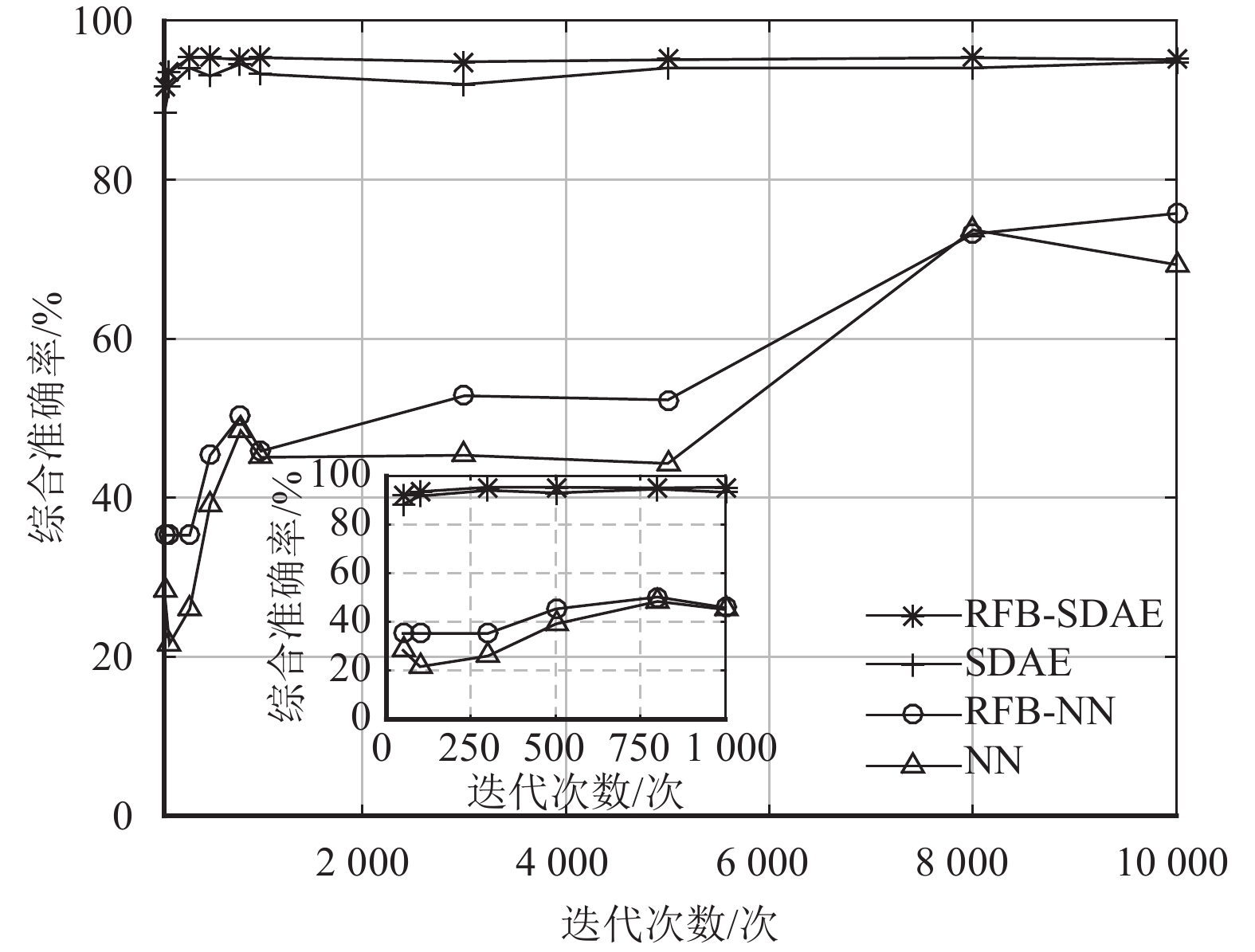
如图4所示,随着迭代次数的增加,RFB-SDAE、SDAE、RFB-NN和NN算法的综合准确率都有提升. 其中,RFB-SDAE算法和RFB-NN算法的综合准确率较SDAE算法和NN算法有小幅度的提升,这是因为ReliefF算法在约简过程中去除了RSSI信号中冗余信息,能一定程度上提升综合准确率. RFB-SDAE和SDAE是基于自编码器的网络结构,在图4中可以看出RFB-SDAE和SDAE算法都有较好的综合准确率. 而基于SDAE深度学习网络的综合准确率较单层神经网络有明显的提升,说明经过多层隐含层的神经网络的学习与训练,SDAE深度学习网络更适用于室内复杂环境中的定位.
|
图 4 不同迭代次数下的综合准确率 Figure 4 Comprehensive accuracy per epoch |
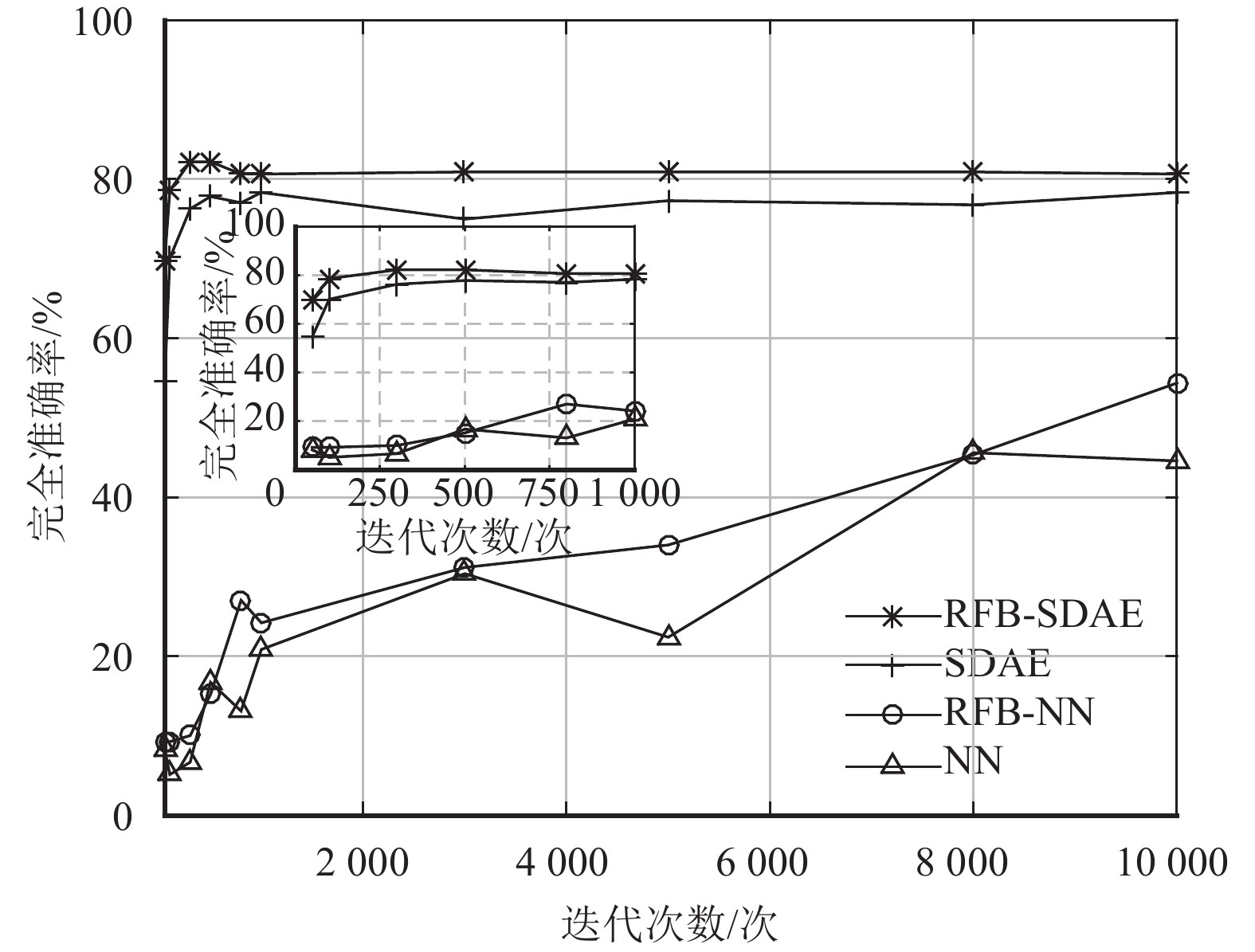
如图5所示,RFB-SDAE算法的完全准确率在迭代次数较多的情况下能达到80%,较SDAE算法有较大幅度的提升,且无论是SDAE深度学习网络还是单层神经网络,经过ReliefF对RSSI信号约简后,RFB-SDAE和RFB-NN的完全准确率都高于没经过预处理的算法,原因在于指纹数据库中的冗余信息对于进行训练与学习时的神经网络有弱化学习能力的影响,因此对RSSI信号进行了筛选与过滤,将不满足条件的信号排除,从而能提高算法定位的完全准确率.
|
图 5 不同迭代次数下的完全准确率 Figure 5 Complete accuracy per epoch |
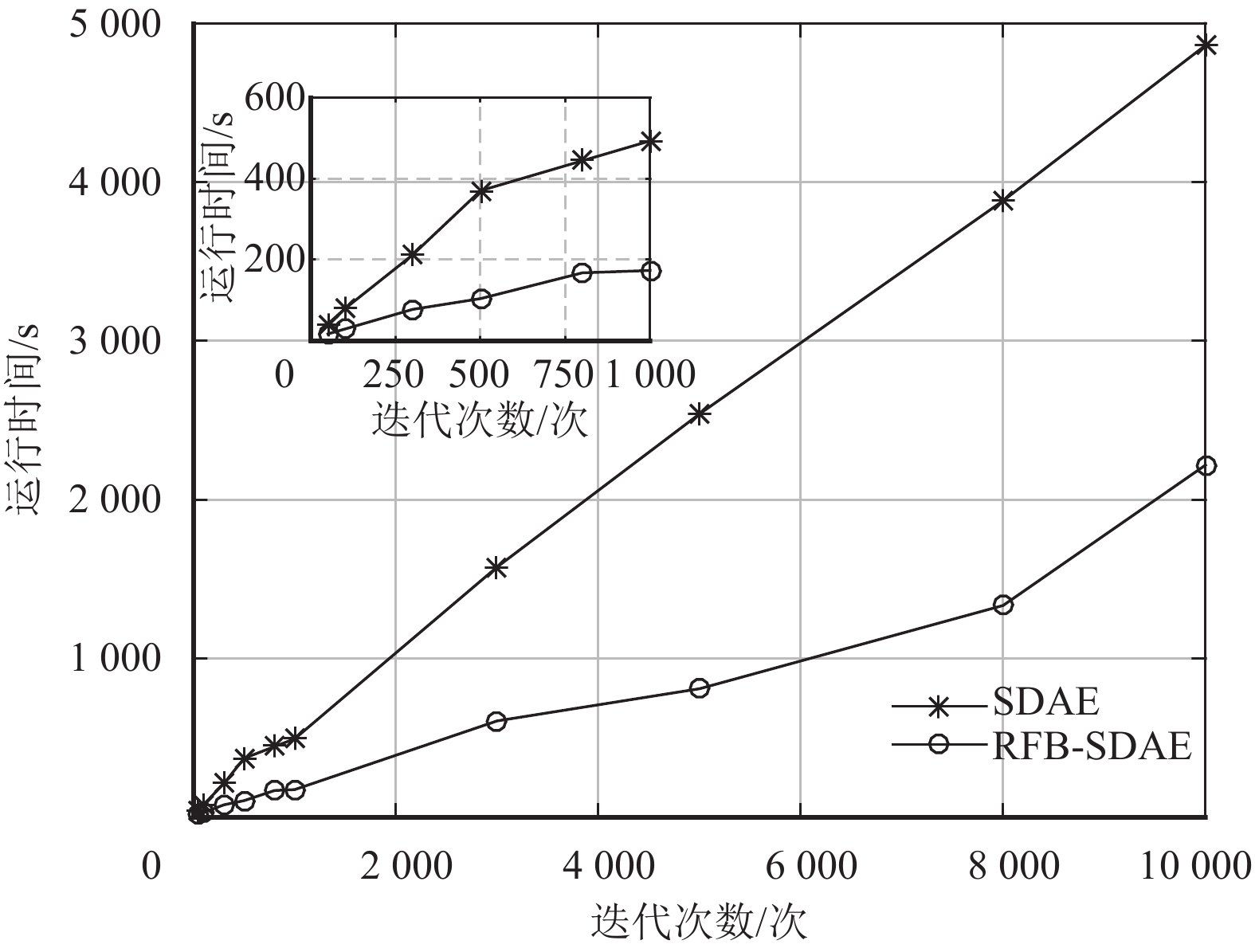
图6对RFB-SDAE和SDAE方法的运行时间进行比较,分析采用ReliefF方法约简后对执行效率的影响. 设定每批相同的训练神经元数目,对比在不同迭代次数下经过约简处理的RFB-SDAE和SDAE在运行时间上的变化情况.
由图6可以看出,经过ReliefF算法进行RSSI信号约简后的程序运行时间较没经过约简的数据有较大幅度减少,在不影响定位准确率的情况下,程序运行的效率提高了54%以上,由于经过约简去除与室内定位无关的RSSI信号后,并提取与其相关的RSSI样本,将减少SDAE每个隐含层的程序消耗时间,因此说明指纹数据库的RSSI信号经过ReliefF算法约简后,再进行训练和学习,并以此实现室内区域定位的RFB-SDAE算法将提高算法执行效率,从而更高效率地实现室内无线定位.
|
图 6 运行时间比较 Figure 6 Comparison of running time |
本文提出了基于深度学习网络的指纹匹配定位的RFB-SDAE算法. 本方法将目标定位楼层划分为多个网格区域,结合ReliefF算法约简及预处理RSSI信号,采用SDAE深度学习框架,通过多层神经网络非线性变化,重构输入的RSSI信号. 利用训练好的室内信号定位模型结合分类器对在线采集的RSSI信号分类处理,从而确定所对应的室内定位区域. 实验结果表明,该算法相比于SDAE和单层神经网络提高了综合定位准确率和完全定位准确率,相比于SDAE,有更高效的算法运行效率和更好的定位效果. 下一步的工作主要是在不同的室内环境采集AP的RSSI信号,研究该算法在不同环境下的定位效果,以及进一步提高该算法的定位准确率.
| [1] | LIU H, DARABI H, BANERJEE P, et al. Survey of wireless indoor positioning techniques and systems[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2007, 37(6): 1067-1080. DOI: 10.1109/TSMCC.2007.905750. |
| [2] |
黄婷婷, 刘广聪, 陈海南. 无线传感器网络自定位算法的研究[J].
广东工业大学学报, 2015, 32(4): 127-131.
HUANG T T, LIU G C, CHEN H N. Self-localization algorithm of wireless sensors networks[J]. Journal of Guangdong University of Technology, 2015, 32(4): 127-131. |
| [3] | FARID Z, NORDIN R, ISMAIL M. Recent advances in wireless indoor localization techniques and system[J]. Journal of Computer Networks & Communications, 2013, 2013(42): 15-15. |
| [4] | KIM R, LIM H, HWANG S N, et al. Robust indoor localization based on hybrid Bayesian graphical models [C]// IEEE GLOBECOM. Austin: IEEE. 2014: 423-429. |
| [5] | YU F, JIANG M H, LIANG J, et al. An indoor localization of wifi based on support vector machines[J]. Advanced Materials Research, 2014, 926-930(5): 2438-2441. |
| [6] | WANG X, GAO L, MAO S, et al. DeepFi: Deep learning for indoor fingerprinting using channel state information [C]// Wireless Communications and Networking Conference. New Orleans: IEEE, 2015: 1666-1671. |
| [7] | LUO J, GAO H. Deep belief networks for fingerprinting indoor localization using ultrawide band technology[J]. International Journal of Distributed Sensor Networks, 2016, 2016: 1-8. |
| [8] | GU Y, CHEN Y, LIU J, et al. Semi-supervised deep extreme learning machine for Wi-Fi based localization[J]. Neurocomputing, 2015, 166(C): 282-293. |
| [9] | ZHANG W, LIU K, ZHANG W, et al. Deep neural networks for wireless localization in indoor and outdoor environments[J]. Neurocomputing, 2016, 194(C): 279-287. |
| [10] | SPOLAÔR N, CHERMAN E A, MONARD M C, et al. ReliefF for multi-label feature selection[C]//Intelligent Systems (BRACIS), 2013 Brazilian Conference on Fortaleza. Brazil: IEEE, 2013: 6-11. |
| [11] | TORRES-SOSPEDRA J, MONTOLIU R, MARTINEZ-USO A, et al. UJIIndoorLoc: A new multi-building and multi-floor database for WLAN fingerprint-based indoor localization problems [C]// International Conference on Indoor Positioning and Indoor Navigation. Busan: IEEE, 2014: 261-270. |
| [12] | 陈丽娜. WLAN位置指纹室内定位关键技术研究[D]. 上海: 华东师范大学信息科学技术学院. |
| [13] | O'CONNOR P, NEIL D, LIU S C, et al. Real-time classification and sensor fusion with a spiking deep belief network[J]. Frontiers in Neuroscience, 2013, 7: 178. |
| [14] | VINCENT P, LAROCHELLE H, LAJOIE I, et al. Stacked denoising autoencoders: learning useful representations in a deep network with a local denoising criterion[J]. Journal of Machine Learning Research, 2010, 11(12): 3371-3408. |
| [15] | SCHMIDHUBER J. Deep learning in neural networks: An overview[J]. Neural Networks, 2014, 61: 85. |
| [16] | DOUGHERTY E R. Small sample issues for microarray-based classification[J]. Comparative & Functional Genomics, 2001, 2(2): 28-34. |
| [17] | FÉLIX G, SILLER M, ÁLVAREZ E N. A fingerprinting indoor localization algorithm based deep learning [C]//Ubiquitous and Future Networks (ICUFN), 2016 Eighth International Conference on . Vienna: IEEE, 2016: 1006-1011. |
 2017, Vol. 34
2017, Vol. 34

