近些年,多智能体系统的协同控制研究获得了更多的关注. 编队控制作为协同控制的一个重要研究方向,在飞行器[1]、无人机[2]和自主水下机器人[3-4]等领域得到了广泛的应用[5-6]. 在多智能体系统的编队控制中,最重要的一个问题是基于邻居节点的局部信息来设计分布式编队控制协议,使得多智能体系统在资源紧缺、通讯拓扑结构变化、信息交互间断和时滞等情况下,实现并保持期待的编队队形[7].
学者提出了多种方法来解决多智能体系统的编队控制问题,如基于行为的策略[8],虚拟结构方法[9]和领导跟随方法[10],并得到了许多重要的成果[11-23]. 文献[11]考虑一阶多智能体系统在有限时间下的动态编队问题,文献[12]研究二阶多智能体系统的时变组编队控制,可是这些文献都没有考虑时延的影响.
由于信息的传递和数据处理的速度限制,智能体间的通讯不可避免地存在时延. 为此,文献[13]提出存在位置通讯常时延的二阶多智能体在固定拓扑结构下的编队方法,文献[14]研究了具有位置通讯小时变时延的二阶多智能体系统在固定拓扑结构下的一致性及编队控制,文献[15]在文献[13-14]基础上考虑了智能体间存在速度通讯时延并设计编队控制算法,文献[16]则在非线性的外部干扰时下考虑的多智能体系统编队控制问题.
在实际生活中,多智能体网络间的通信拓扑结构会因资源受限和外界干扰等因素而发生变化,因此要同时考虑通讯时延和切换的通讯拓扑结构对系统的影响. 不同于多数文献要求系统的通讯拓扑结构在每个时刻都要连通,联合连通拓扑结构的系统仅需要在一个时间段内所有的拓扑结构图的联合是连通的。这在很大程度上解决了资源受限、通讯网络突然间断和切换等问题. 文献[17]在联合连通拓扑结构下研究具有通讯常时延的二阶多智能体系统的一致性,文献[18]在此基础上考虑了存在通讯时变时延的系统有限时间的一致性,文献[10]在联合连通拓扑结构下研究了不均衡系统的一致性,文献[19]则在联合连通拓扑结构下,针对具有常时延的多智能体系统设计编队控制协议.
受以上文献启发,本文将文献[13]的结果扩展到带有切换的联合连通的拓扑结构下的二阶多智能体系统,首次考虑存在多时变时延的系统的编队控制问题. 利用局部邻居节点信息,设计分布式编队控制协议. 通过模型变换,利用Lyapunov-Krasovskii理论分析系统编队控制的稳定性,并以线性矩阵不等式的形式给出了多智能体系统实现编队稳定的充分条件,最后给出了环形联合连通拓扑结构对于解决智能体间通讯间断问题的优越性. 与文献[13-15]相比,本文考虑的是切换的联合连通的通信拓扑结构而非固定拓扑结构,与文献[14-15, 19]相比,本文研究的是多时变时延并考虑了大时变和未知时变的影响,而非小时变时延或常时延.
1 问题描述 1.1 图论[20]记
引理1[21] 对于连通的无向图G,其Laplacian矩阵L满足:
(1) 0是矩阵L的单一的特征值,特征值0所对应的特征向量为1n,即
(2) 其余的n-1个特征值均为正实数.
引理2[22] 对于对称矩阵
引理3[23] 对任意可微的实向量函数
| $\begin{array}{l}1/h{[x(t) - x(t - \tau (t))]^{\rm T}}{Q}[x(t) - x(t - \tau (t))] \leqslant \\[6pt]\;\;\int_{t - \tau (t)}^t {{{\dot x}^{\rm T}}(s){Q}\dot x(s)} {\rm{d}}s,\;\;\;t \geqslant 0,\;\;\;\;h > 0.\end{array}$ |
引理4[23] 对于仅包含一生成树的有向图或连通的无向图G,其Laplacian矩阵L满足:
假设多智能体系统由n个智能体组成,在每个时刻点t,每个智能体通过接受来自邻居智能体的信息来更新当前的状态. 在无向图中,每个智能体视为一个点,边
假设两个通信无向图间的切换时间大于正常数T2. 考虑一个无穷的递增序列tr,
考虑由n个智能体组成的系统,第i个智能体的动态方程为
| $\left\{ \begin{array}{l}{{\dot x}_i}(t) = {v_i}(t),\\[6pt]{{\dot v}_i}(t) = {u_i}(t),\;\;\;\;i = 1,2, \cdots ,n.\end{array} \right.$ | (1) |
其中xi(t)、vi(t)、ui(t)分别为智能体i的位置信息,速度信息和控制协议.
在二维平面上,第i个飞行器航迹角
基于一致性的理论,设计如下的控制协议:
| $\begin{split}{u_i}(t) = & - k({v_i}(t) - {v_0}) - \displaystyle\sum\limits_{j \in {N_i}(t)} {{a_{ij}}(t)[{x_i}(t - {\tau _{ij}}) - } \\ & {x_j}(t - {\tau _{ij}}) - {d_{ij}}].\end{split}$ | (2) |
其中k为多智能体速度反馈增益,v0、dij为多智能体系统达到理想编队队形结构时的速度、智能体i到智能体j的距离.
备注:与文献[13, 18]的协议相比,本文提出的协议不需要测量邻居智能体的速度.
假设1 在每一个时间区间
假设2 通讯时滞
假设3 通讯时滞
令
| $\left\{ {\begin{aligned}& {{{\bar x}_i}(t) = {x_i}(t) - {x_0}(t) - {d_i} = {d_i}(t) - {d_i},}\\& {{{\bar v}_i}(t) = {v_i}(t) - {v_0},}\end{aligned}} \right.$ | (3) |
其中x0(t)、v0为虚拟领导者的位置信息、速度信息,并且满足
| ${\dot x_{\rm{0}}}(t) = {v_0},$ | (4) |
其中
| ${u_i}(t) = - k \cdot {\bar v_i}(t) - \sum\limits_{j \in {N_i}(t)} {{a_{ij}}(t)[{{\bar x}_i}(t - {\tau _{ij}}) - } {\bar x_j}(t - {\tau _{ij}})].$ | (5) |
对上面方程作如下模型变换. 令
| $\left\{ \begin{aligned}& {{\tilde v}_i}(t) = 2{{\bar v}_i}(t)/k + {{\bar x}_i}(t),\\& y(t) = [{{\bar x}_1}(t),{{\tilde v}_1}(t), \cdots {{\bar x}_n}(t),{{\tilde v}_n}(t)],\\& {{A}} = \left[ {\begin{array}{*{20}{c}}{ - k/2}&{k/2}\\[6pt]{k/2}&{ - k/2}\end{array}} \right]\;,\;{{B}} = \left[ {\begin{array}{*{20}{c}}0&0\\[6pt]{2/k}&0\end{array}} \right]\;.\end{aligned} \right.$ | (6) |
则对于控制协议(2),系统的动态可描述为
| ${{\dot y}}(t) = ({{I}_n} \otimes {A})y(t) - \sum\limits_{m = 1}^r {({{L}_{\sigma m}}} \otimes {B})y(t - {\tau _m}),$ | (7) |
其中
| ${l_{mij}} = \left\{ \begin{array}{l} - {a_{ij}},\;j \ne i,\;{\tau _m}\left( \cdot \right) = {\tau _{ij}}\left( \cdot \right);\\[6pt] - \displaystyle\sum\limits_{m = 1}^n {{l_{mij}},\;} j = i;\\[6pt]0,\;j = i,\;{\tau _m}\left( \cdot \right) \ne {\tau _{ij}}\left( \cdot \right).\end{array} \right.$ |
当
| $\left\{ \begin{array}{l}\mathop {\lim }\limits_{t \to \infty } [{x_i}(t){\rm{ - }}{x_j}(t)] = {d_{ij}},\\[6pt]\mathop {\lim }\limits_{t \to \infty } {v_i}(t) = {v_0}.\end{array} \right.$ | (8) |
所以多智能体系统能达到预期的编队和速度.
2 主要结果假设时不变通讯图Gσ在每个子区间
| ${U}_\sigma ^{\rm T}{{L}_\sigma }{{U}_\sigma } = {\rm{diag}}\{ {L}_\sigma ^1,{L}_\sigma ^2, \cdots ,{L}_\sigma ^{{l_\sigma }}\} ,$ | (9) |
| ${y^{\rm T}}(t){{U}_\sigma } = [y{_\sigma ^1}^{\rm T}(t),y{_\sigma ^2}^{\rm T}(t), \cdots ,y{_\sigma ^{{l_\sigma }}}^{\rm T}(t)].$ | (10) |
其中
| ${\dot y}_\sigma ^i(t) = ({{I}_{d_\sigma ^i}} \otimes {A})y_\sigma ^i(t) - \sum\limits_{m = 1}^r {({L}_{\sigma m}^i \otimes {B})} y_\sigma ^i(t - {\tau _m}).$ | (11) |
其中,
令
| $\begin{split}\dot y_\sigma ^i(t) = & [({{I}_{d_\sigma ^i}} \otimes {A}) - {L}_{\sigma m}^i \otimes {B}]y_\sigma ^i(t) + \\& \sum\limits_{m = 1}^r {({L}_{\sigma m}^i \otimes {B}} )\xi _{\sigma m}^i(t).\end{split}$ | (12) |
对于子区间
其中
| $\begin{array}{l}G(t) = {[{\varPhi }_\sigma ^i\;{L}_{\sigma 1}^i \otimes {B}, \cdots ,{L}_{\sigma r}^i \otimes {B}]^{\rm T}},\\[6pt]{{\varXi }_{11}} = {\bar \varPhi }_\sigma ^i + \beta \sum\limits_{m = 1}^r {{d_m}{I}} ,\;\bar {{\varPhi}} _\sigma ^i = \alpha ({\varPhi }_\sigma ^i + {\varPhi }{_\sigma ^i}^{\rm T}),\\[6pt]{{\varXi }_{12}} = [\alpha ({L}_{\sigma 1}^i \otimes {B}) + \beta (1 - {d_1}){I}, \cdots ,\\[6pt]\;\;\;\;\;\;\;\;\;\alpha ({L}_{\sigma r}^i \otimes {B}) + \beta (1 - {d_r}){I}],\\[6pt]{{\varXi }_{22}} = {\rm{diag}}\{ - \frac{{\rho (1 - {d_1})}}{{{h_1}}}{I} - \beta (1 - {d_1}){I}, \cdots , - \\[6pt]\;\;\;\;\;\;\;\;\;\;\frac{{\rho (1 - {d_r})}}{{{h_r}}}{I} - \beta (1 - {d_r}){I}\} .\end{array}$ |
同样,对于在子区间
其中
| $\begin{array}{l}{{\varPsi }_{11}} = \alpha ({\varPhi }_\sigma ^i + {\varPhi }{_\sigma ^i}^{\rm T}),\;{{\varPsi }_{22}} = {\rm{diag}}\{ - \frac{\rho }{{{h_1}}}{I}, \cdots , - \frac{\rho }{{{h_r}}}{I}\} ,\\[6pt]{{\varPsi }_{12}} = [\alpha ({L}_{\sigma 1}^i \otimes {B}), \cdots ,\alpha ({L}_{\sigma r}^i \otimes {B})].\end{array}$ |
定理1 考虑由动态方程(1)和(4)描述的具有多时变时延和切换拓扑结构的多智能体系统满足假设1、2、3.对于所有可能的σ和
| ${{W}^{\rm T}}{\varXi }_\sigma ^i{W} < 0.$ | (13) |
其中
证明 根据引理2,式(13)成立等价于
| $\begin{split}& \left[ \!\!\! {\begin{array}{*{20}{c}}{{{E}^{\rm T}}{\bar \varPhi }_\sigma ^i{E}} & {\alpha {{E}^{\rm T}}({L}_{\sigma 1}^i \otimes {B}){E}} & \cdots & {\alpha {{E}^{\rm T}}({L}_{\sigma r}^i \otimes {B}){E}}\\[6pt] \!\!\! \!\!\! * & { - \displaystyle\frac{{\rho (1 - {d_1})}}{{{h_1}}}{{E}^{\rm T}}{E}} & 0 & 0\\ \!\!\! \!\!\! * & * & \ddots & 0\\ [6pt] \!\!\! \!\!\! * & * & * & { - \displaystyle\frac{{\rho (1 - {d_r})}}{{{h_r}}}{{E}^{\rm T}}{E}}\end{array}} \!\!\! \right]+\\& \beta \left[ \!\!\! {\begin{array}{*{20}{c}}{\displaystyle\sum\limits_{m = 1}^r {{d_m}} {{E}^{\rm T}}{E}} & {(1 - {d_1}){{E}^{\rm T}}{E}} & \cdots & {(1 - {d_r}){{E}^{\rm T}}{E}}\\ \!\!\!\!\!\! * & {({d_1} - 1){{E}^{\rm T}}{E}} & 0 & 0\\ \!\!\!\!\!\! * & * & \ddots & 0\\[6pt] \!\!\! \!\!\! * & * & * & {({d_r} - 1){{E}^{\rm T}}{E}}\end{array}} \!\!\! \right]+\\& \rho \sum\limits_{m = 1}^r {{h_m}} {G^{\rm T}}(t)G(t) < 0.\end{split}$ | (14) |
选取合适的α,β,ρ以及较小的hm,则不等式(14)成立等价于
| ${{E}^{\rm T}}(\alpha {\varPhi }_\sigma ^i + \alpha {\varPhi }{_\sigma ^i}^{\rm T}){E} < 0.$ | (15) |
其中
| $- {{E}^{\rm T}}({\varPhi }_\sigma ^i + {\varPhi }{_\sigma ^i}^{\rm T}){E} > 0.$ | (16) |
因此,在假设1、2和3条件下,可选合适α,β,ρ和hm使式(13)恒成立.
下面证明系统在控制协议(2)下能形成预期的稳定的编队并达到理想的速度.
选取如下的Lyapunov-Krasovskii函数:
| $\begin{array}{l}V(t) = \alpha {y^{\rm T}}(t)y(t) + \beta \sum\limits_{m = 1}^r {\int_{t - {\tau _m}(t)}^t {{y^{\rm T}}(s)y(s)} {\rm{d}}s}+ \\\; \; \; \; \; \; \rho \sum\limits_{m = 1}^r {\int_{ - {\tau _m}(t)}^0 {\int_{t + \theta }^t {{{\dot y}^{\rm T}}(s)\dot y(s)} } {\rm{d}}s{\rm{d}}\theta } .\end{array}$ |
根据式(12),V(t)可改写为
| $\begin{array}{l}V(t) = \sum\limits_{i = 1}^{{l_\sigma }} {\left\{ {\alpha y{{_\sigma ^i}^{\rm T}}(t)y_\sigma ^i(t) + \beta \sum\limits_{m = 1}^r {\int_{t - {\tau _m}(t)}^t {y{{_\sigma ^i}^{\rm T}}(s)y_\sigma ^i(s)} {\rm{d}}s} } \right.}+ \\[6pt]\; \; \; \; \; \; \left. { \rho \sum\limits_{m = 1}^r {\int_{ - {\tau _m}(t)}^0 {\int_{t + \theta }^t {\dot y{{_\sigma ^i}^{\rm T}}(s)\dot y_\sigma ^i(s)} } } {\rm{d}}s{\rm{d}}\theta } \right\}.\end{array}$ |
由式(14)计算
| $\begin{array}{l}\dot V(t) \leqslant \sum\limits_{i = 1}^l {y{{_\sigma ^i}^{\rm T}}(t)(\alpha {\varPhi }_\sigma ^i + \alpha {\varPhi }{{_\sigma ^i}^{\rm T}})y_\sigma ^i(t)}+ \\\;\;\;\; \beta \sum\limits_{m = 1}^r {y{{_\sigma ^i}^{\rm T}}(t)y_\sigma ^i(t)} + 2\alpha y{_\sigma ^i}^{\rm T}(t)\sum\limits_{m = 1}^r {({L}_{\sigma m}^i \otimes {B})\xi _{\sigma m}^i(t)}+ \\\;\;\;\; \beta \sum\limits_{m = 1}^r {({d_m} - 1)y{{_\sigma ^i}^{\rm T}}(t - {\tau _m})y_\sigma ^i(t - {\tau _m})}+ \\\;\;\;\; \left( {1 - {{\dot \tau }_m}\left( t \right)} \right)\sum\limits_{m = 1}^r {\int\limits_{t - {\tau _m}(t)}^t {\dot y{{_\sigma ^i}^{\rm T}}(s)\dot y_\sigma ^i(s)} {\rm{d}}s} \} .\end{array}$ |
再由引理3得
| $\begin{array}{l}\dot V(t) \leqslant \sum\limits_{i = 1}^{{l_\sigma }} {\{ y{{_\sigma ^i}^{\rm T}}(t)(\alpha {\varPhi }_\sigma ^i + \alpha {\varPhi }{{_\sigma ^i}^{\rm T}} + \beta \sum\limits_{m = 1}^r {{d_m}} {I})y_\sigma ^i(t)}+ \\[6pt] 2y{_\sigma ^i}^{\rm T}(t)[\alpha \sum\limits_{m = 1}^r {({L}_{\sigma m}^i \otimes {B}) - \beta \sum\limits_{m = 1}^r {({d_m} - 1){I}]} \xi _{\sigma m}^i(t)}+ \\[6pt] \rho \sum\limits_{m = 1}^r {{h_m}[{\varPhi }_\sigma ^iy_\sigma ^i(t) + \sum\limits_{m = 1}^r {({L}_{\sigma m}^i} \otimes {B})\xi _{\sigma m}^i(t){]^{\rm T}} \cdot } \\[6pt]\;\;\;\;\;\;\;\;\;[{\varPhi }_\sigma ^iy_\sigma ^i(t) + \sum\limits_{m = 1}^r {({L}_{\sigma m}^i} \otimes {B})\xi _{\sigma m}^i(t)]-\\[6pt] \sum\limits_{m = 1}^r {(\rho (1 - {d_m})/{h_m} + \beta (1 - {d_m}))\xi {{_{\sigma m}^i}^{\rm T}}(t)\xi _{\sigma m}^i(t)} \} \\[6pt] = \sum\limits_{i = 1}^{{l_\sigma }} {z{{_\sigma ^i}^{\rm T}}(t){{\varXi}} _\sigma ^iz_\sigma ^i(t)} .\end{array}$ | (17) |
因
| $\dot V(t) \leqslant \sum\limits_{i = 1}^{{l_\sigma }} {z{{_\sigma ^i}^{\rm T}}(t){{W}^{\rm T}}{\tilde \varXi }_\sigma ^i{W}z_\sigma ^i(t)} .$ | (18) |
其中,
| $\begin{array}{l}\tilde y_\sigma ^i(t) = [y_{\sigma 1}^i(t),y_{\sigma 2}^i(t), \cdots ,y_{\sigma (r - 1)}^i(t)],\\[6pt]\tilde z{_\sigma ^i}^{\rm T}(t) = [\tilde y_\sigma ^i(t),\tilde \xi _{\sigma 1}^i(t), \cdots ,\tilde \xi _{\sigma {\rm{r}}}^i(t)],\\[6pt]\tilde \xi _{\sigma m}^i(t) = \tilde y_\sigma ^i(t) - \tilde y_\sigma ^i(t - {\tau _m}(t)).\end{array}$ |
再由式(16)可得
| $\dot V\left( t \right) \leqslant \sum\limits_{i = 1}^{{l_\sigma }} { - {\lambda _i}{{\left\| {\tilde y{{_\sigma ^i}^{\rm{T}}}\left( t \right)} \right\|}^2}} \leqslant - {\lambda _m}/n{\left\| {y{{_\sigma ^i}^{\rm{T}}}\left( t \right)} \right\|^2} < 0.$ |
由文献[24]定理2.1可知,系统在区间
定理2 考虑由动态方程(1)和(4)描述的具有多时变时延和切换拓扑结构的多智能体系统满足假设1和假设2. 对于所有可能的σ和
| ${{W}^{\rm T}}{\varPsi }_\sigma ^i{W} < 0.$ | (19) |
其中
证明 选取Lyapunov-Krasovskii函数
| $V(t) = \alpha {y^{\rm T}}(t)y(t) + \rho \sum\limits_{m = 1}^r {\int_{t - {h_m}}^t {(s - t + {h_m}){{\dot y}^{\rm T}}(s)\dot y(s)} {\rm{d}}s} ,$ |
其他部分的证明与定理1证明过程类似,此处省略.
因此,当式(13)或式(14)成立时,多智能体系统在通讯时延
推论1 具有无向的环形联合连通的通讯拓扑结构的多智能体系统在多个智能失联时,保持通讯联系的智能体组成的多智能体系统仍能在定理1和定理2的条件下实现稳定的理想编队和速度.
证明 在这种情况下,保持通讯联系的智能体组成的多智能体系统的通讯拓扑结构为联合连通,对各个具有联合连通的部分分别应用定理1或定理2即可证明,此略.
3 仿真实验此部分通过Matlab仿真实验来验证本文所提出的理论方案的正确性和有效性.
实验一 在切换的通讯拓扑结构下,考虑由4个飞行器组成的二阶多智能体系统共有G1,G2两个不连通拓扑图,并按
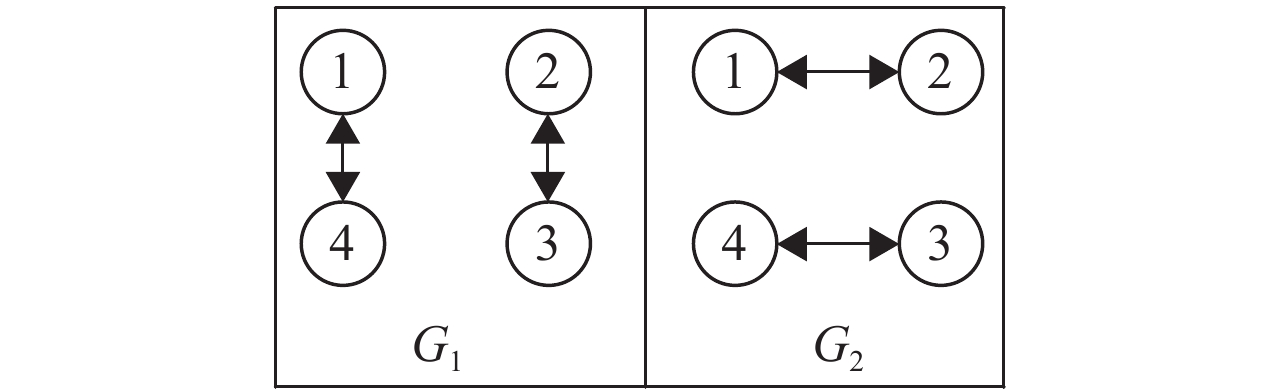
|
图 1 实验一和实验二的系统通信拓扑结构图 Figure 1 Possible interaction topologies of MAS in experiments |
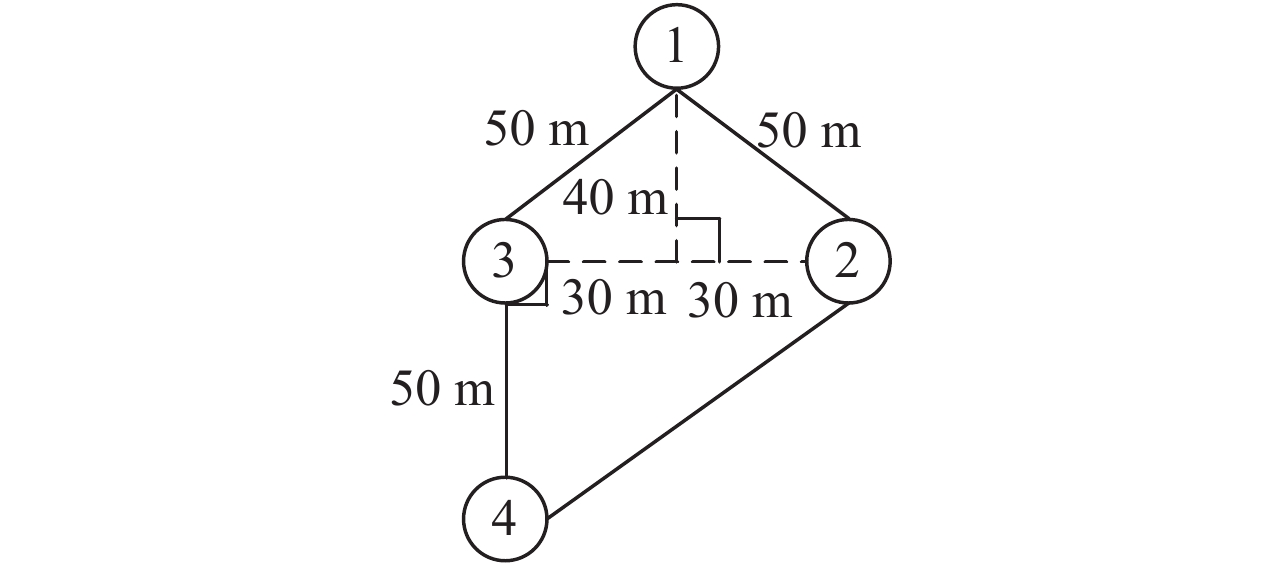
|
图 2 飞行器系统理想的编队队形结构 Figure 2 Desired formation of the multi-aircraft systems |
| 表 1 多智能体系统的初始状态 Table 1 Initial states of the multi-agent systems |
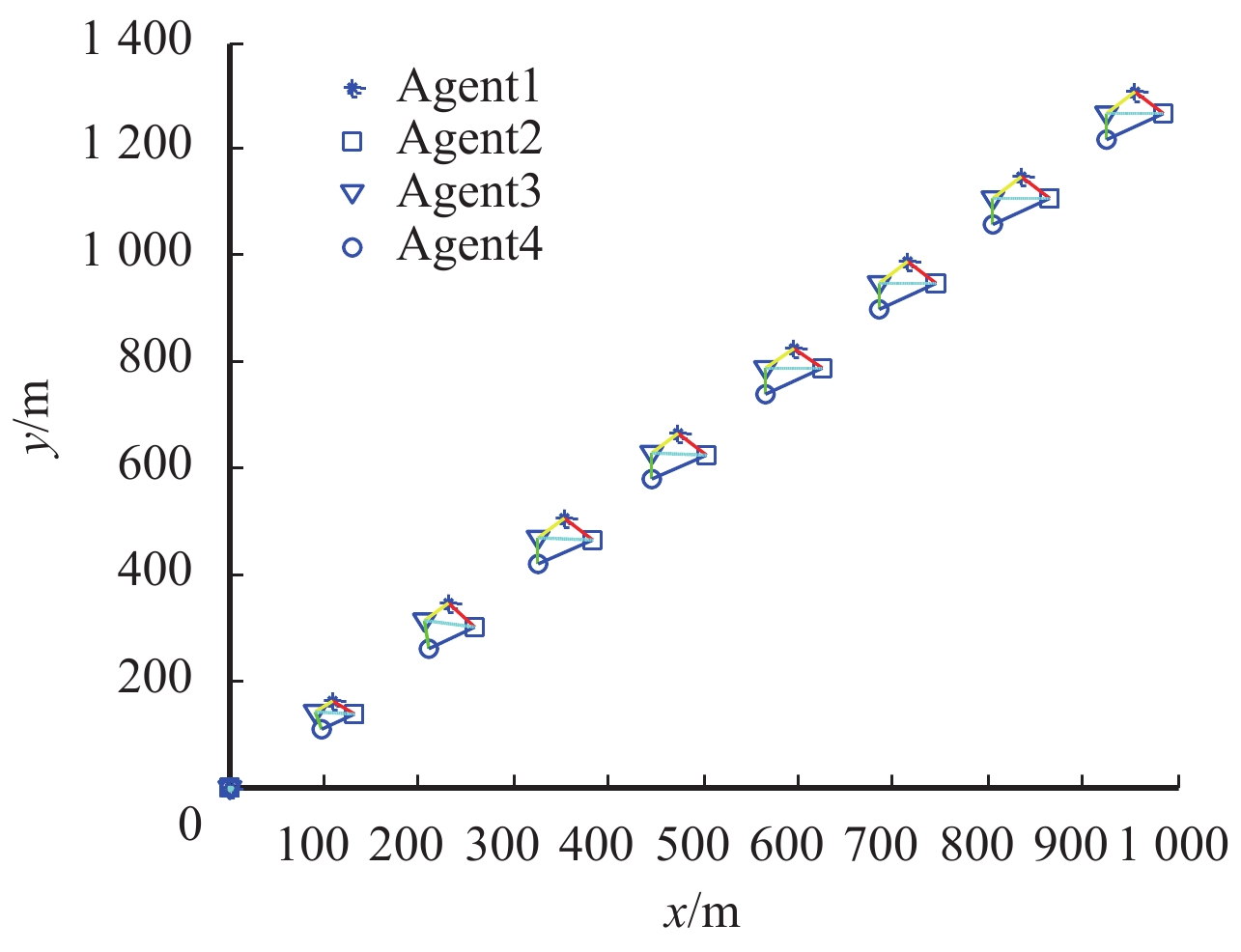
|
图 3 飞行器位置变化曲线 Figure 3 Position trajectories of multi-aircraft systems |
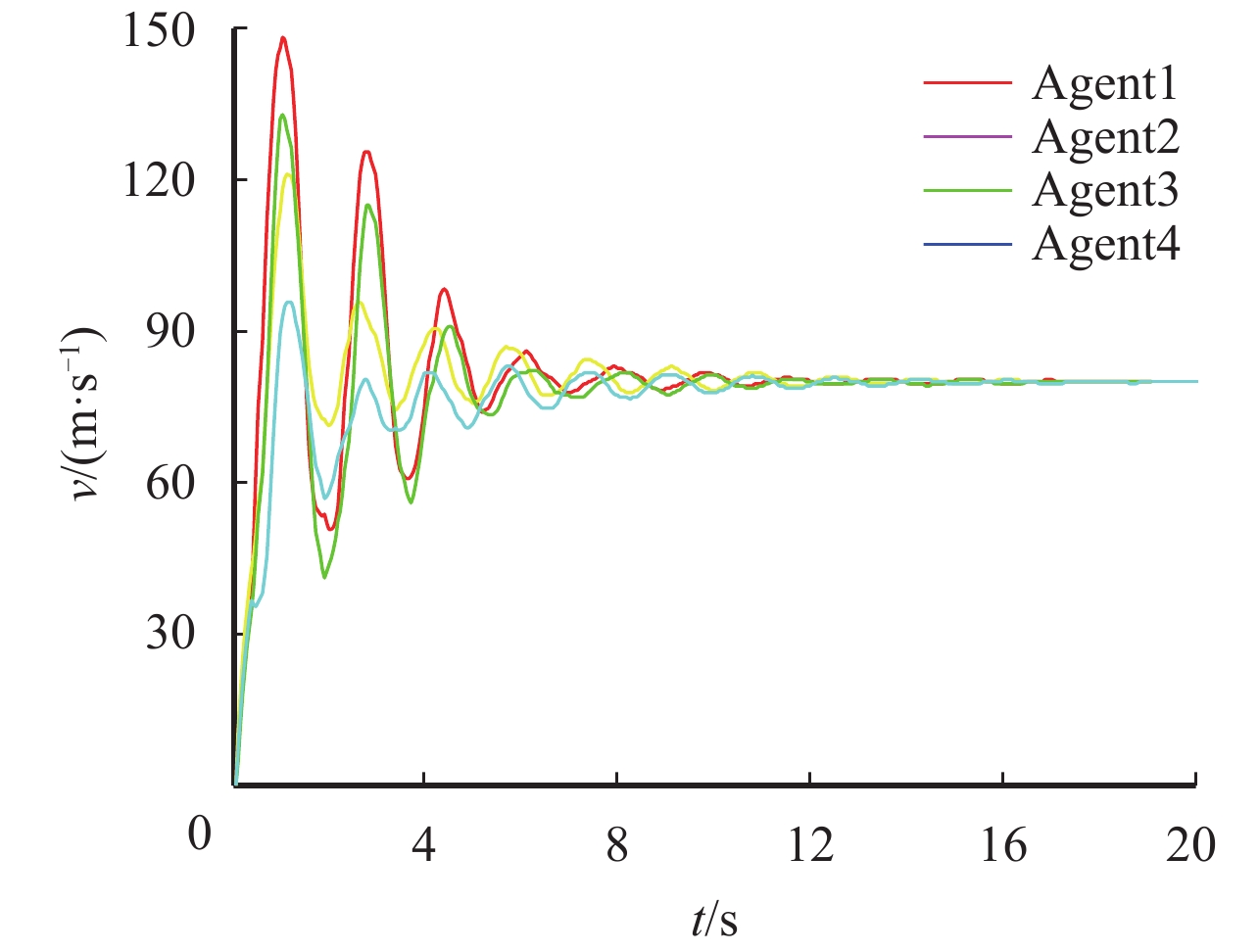
|
图 4 飞行器速度变化曲线 Figure 4 Velocity change among multi-aircraft systems |
|
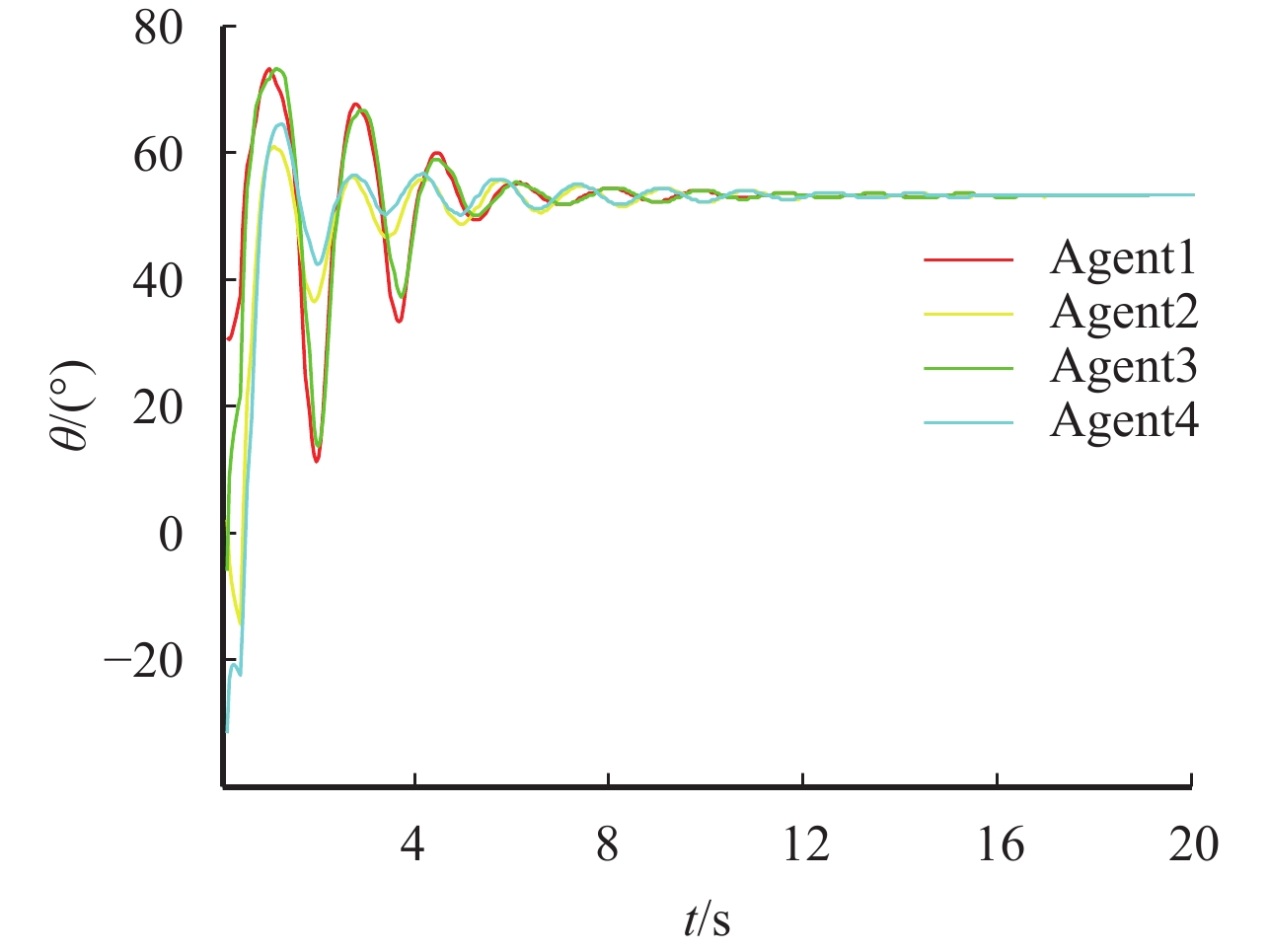
图 5 飞行器航迹角变化曲线 Figure 5 Flight path angle trajectories of multi-aircraft systems |
注:当取时延的变化率为零时,求解式(13)也可得到0.39 s允许的通讯时延,而文献[19]的最大的时延为0.3 s. 因为本文引入新颖Lyapunov-Krasovskii泛函以及应用更广泛的不等式(13),使得飞行器系统能允许更长的通讯时延.
实验二 考虑由4架飞机组成的二阶多智能体系统,在切换的通讯拓扑结构、切换的理想编队和理想速度,并且通信存在时变时滞甚至间断条件下的编队问题. 系统通讯拓扑结构由两个不连通的拓扑图组成,如图1所示,并按
| $\begin{split}& {u_i}(t) = - k({v_i}(t - {\tau _i}) - {v_0}) - \sum\limits_{j \in {N_i}(t)} {{a_{ij}}(t)[{x_i}(t - {\tau _{ij}}) - } \\& {x_j}(t - {\tau _{ij}}) - {d_{ij}}].\end{split}$ | (22) |
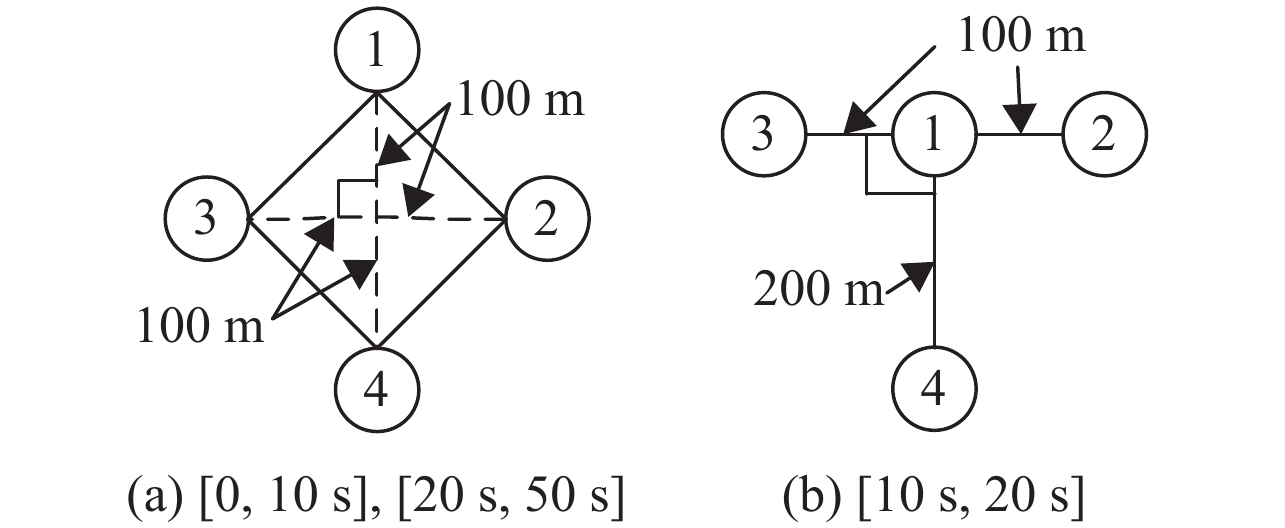
实验的8个时延值由范围为[0,0.4 s]、分度值为0.05 s的随机函数产生. 本文期待的飞机系统的编队队形如图6所示,但受飞行环境的影响和战略的需要[25],理想的编队队形和速度会在飞行时间10 s、20 s时刻进行切换,假设图6(a)编队结构适用于时间范围[0,10 s)和[20 s,50 s],图6(b)编队结构适用于时间范围[10 s,20 s). 在[0,50 s]系统的理想编队队形的切换顺序为
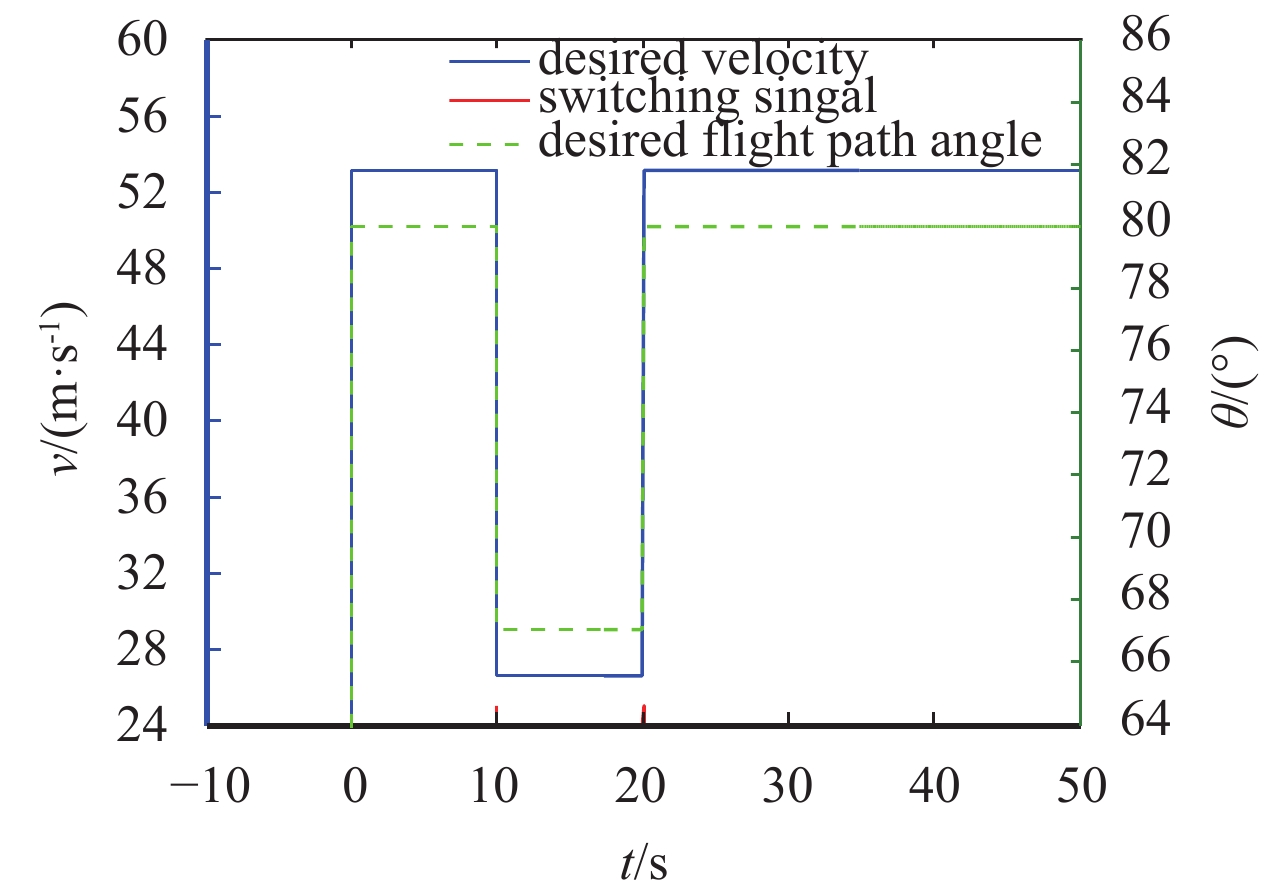
选取k=2.55,求解式(19)可得一个可行解:α=0.255 3,ρ=0.134 3. 图8~图12给出了4架飞机的位置、速度和航迹角的变化曲线.
|
图 6 理想的飞机系统编队队形 Figure 6 Desired formation of the multi-airplane systems |
|
图 7 理想的飞行速度和航迹角变化曲线 Figure 7 Desired velocity and flight path angle curves |
|
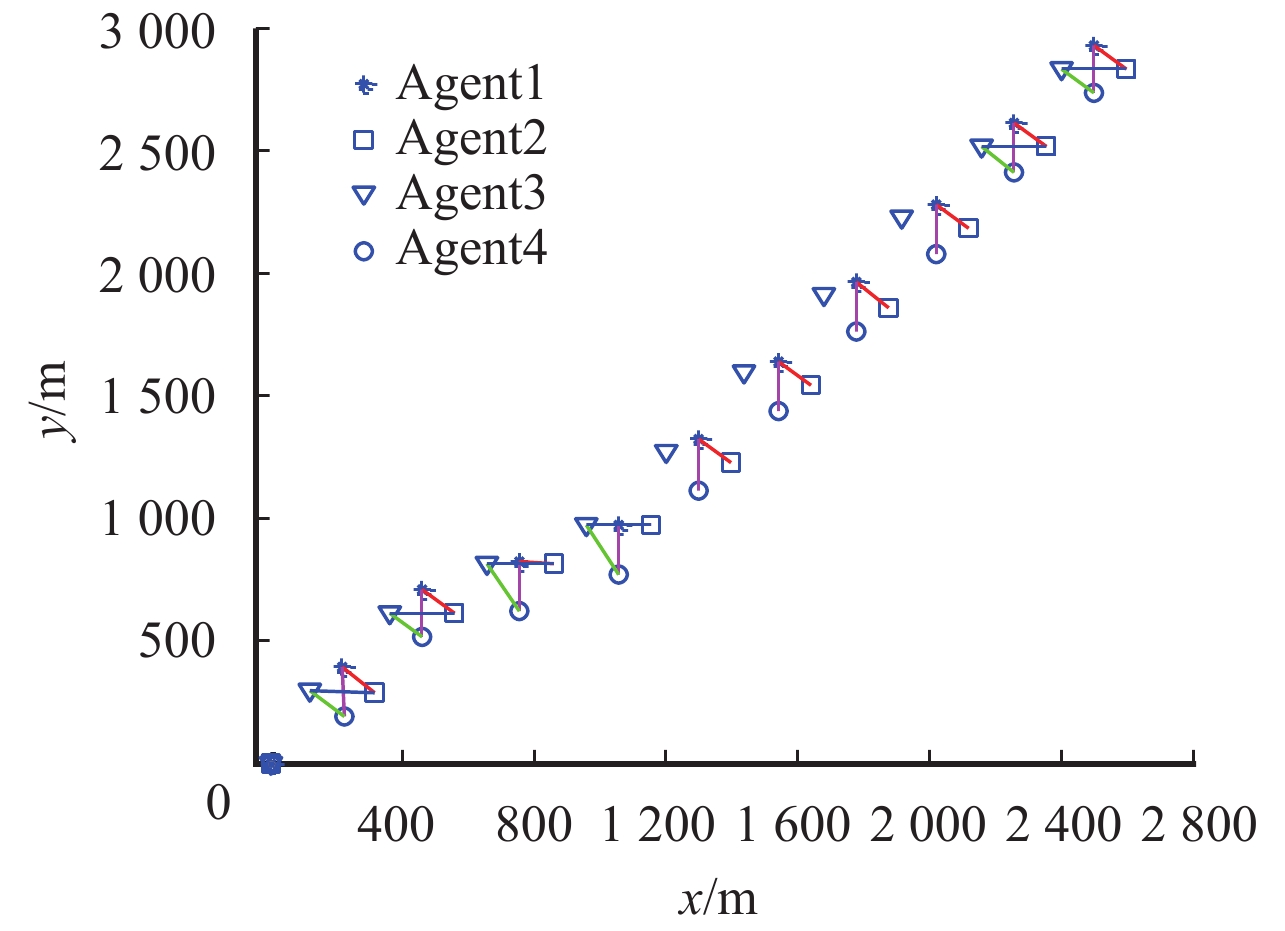
图 8 飞机位置变化曲线 Figure 8 Position trajectories of multi-airplane systems |
|
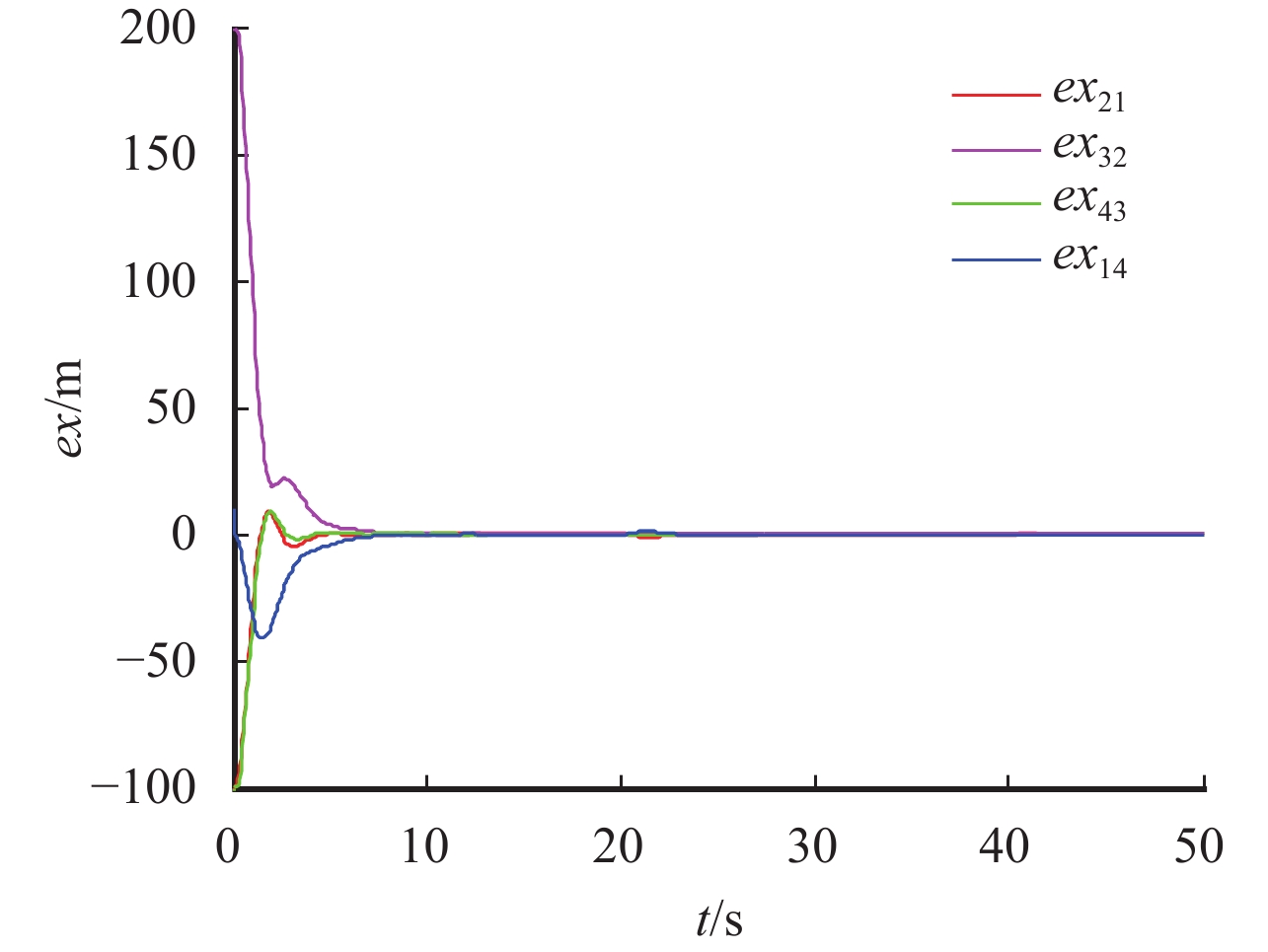
图 9 飞机的位置沿X轴方向变化曲线 Figure 9 Distance error change on X-axis between airplanes |
|
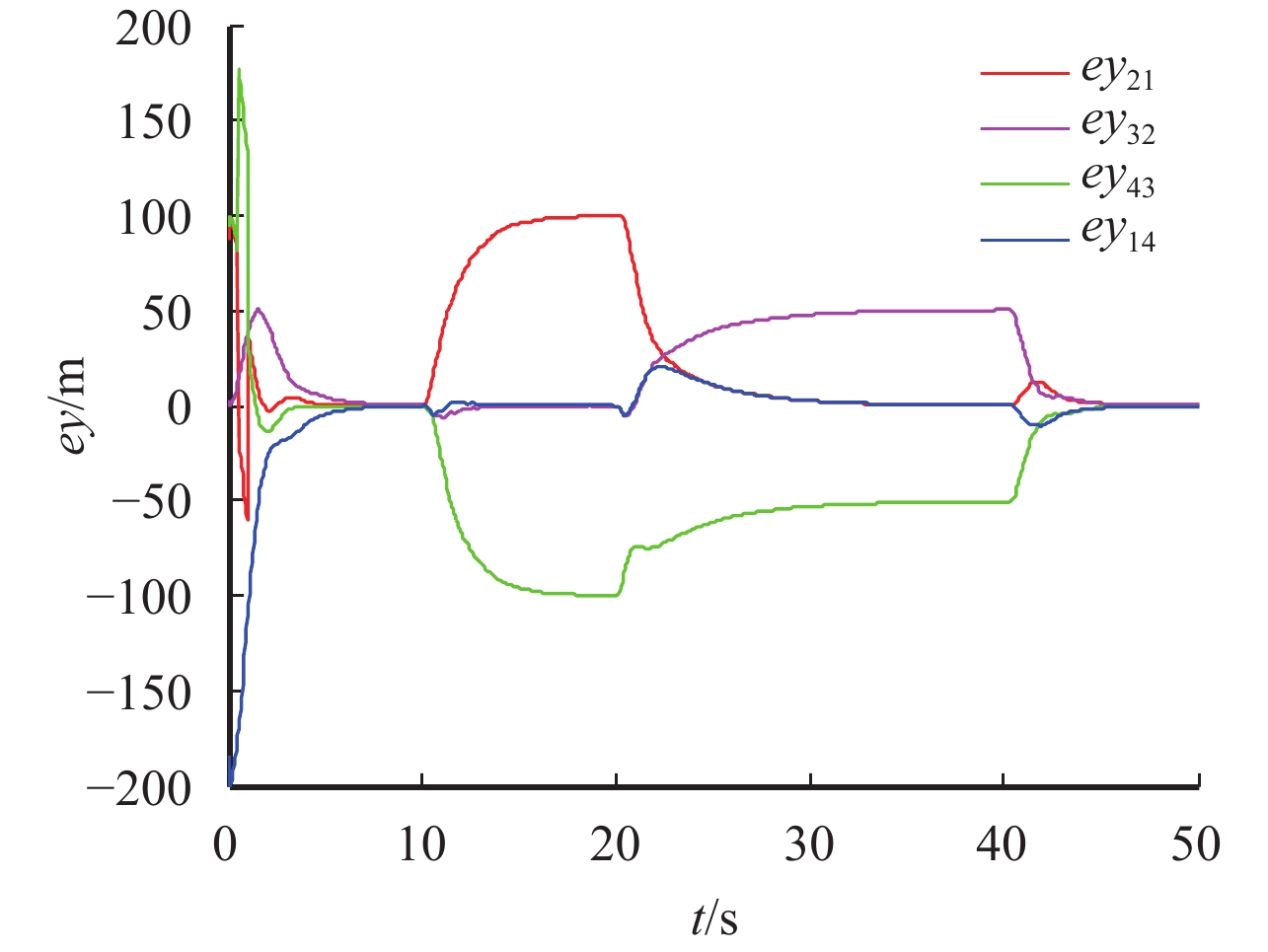
图 10 飞机的位置沿Y轴方向变化曲线 Figure 10 Distance error change on Y-axis between airplanes |
从图8可以看到飞机系统在控制协议下能完成理想队形的切换. 在3号飞机失联时,其他飞机仍然实现按预期的编队目标,而在与3号飞机恢复通信后整个飞机系统能继续实现理想编队.
|
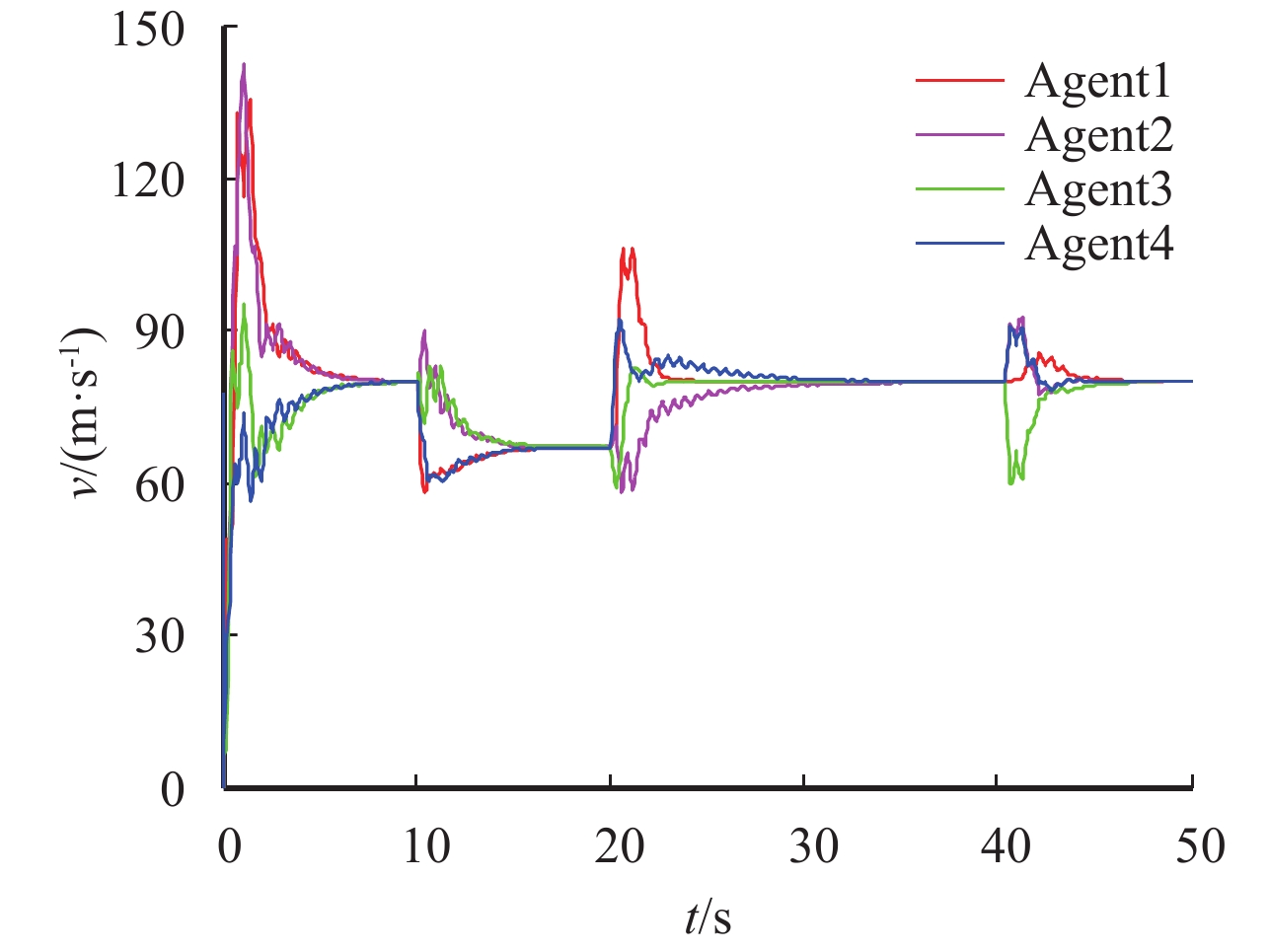
图 11 飞机速度变化曲线 Figure 11 Velocity change among multil-airplane systems |
|
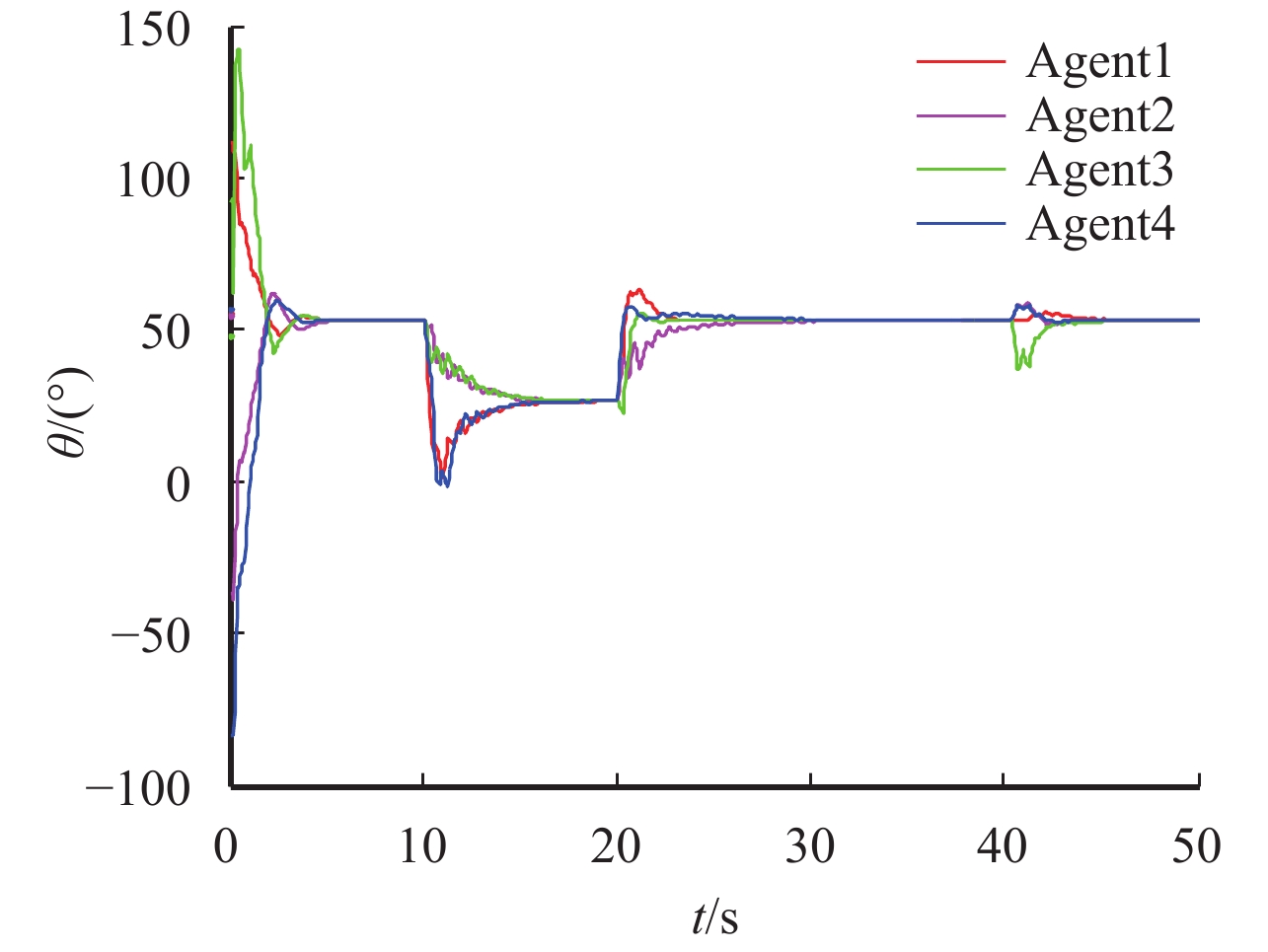
图 12 飞机航迹角变化曲线 Figure 12 Flight path angle trajectories of multi-airplane systems |
由图9~图12可知,在理想编队队形结构切换瞬间,飞机的位置、速度和航迹角变化大. 而图中出现多个不同的时刻的波峰是因为各部飞机的时延值不同.
在[60 s,100 s),3号飞机失联后,因引入速度负反馈,所以在图11~图12中3号飞机仍能逐渐实现理想的编队速度和航迹角并到达稳定的位置,并出现图9~图10中稳定的编队位置偏差现象. 而其他飞机组成的系统具有非环形的联合连通的通信拓扑结构,仍然能实现目标编队队形,但相对在[0,30 s)环形联合连通的通讯拓扑结构来说,这个阶段形成目标队形的时间较长,而在与3号飞机恢复通讯后,整个飞机系统形成环形联合连通的通信拓扑,所以用较短的时间就能实现预期的编队队形结构.
综上分析可得,当飞机间存在多时变且变化率未知的通讯时延,本实验采用的控制协议在式(2)的基础上允许速度存在多时变自时延,相对于文献[19]固定常时延的控制协议,应用范围更广. 多飞机系统在协议(2)和满足定理条件的前提下能实现切换的理想的编队队形结构和速度,并保持稳定,从而验证了定理1和定理2. 3号飞机失联后,系统仍能实现理想速度,而其余的飞机仍能完成预期的目标并保持稳定的队形,从而验证了推论1.
4 结论本文研究了在虚拟领导者下的具有多时变时延的二阶多智能体系统在通讯拓扑结构为联合连通下的编队控制问题. 首先设计编队控制算法,然后利用模型变换方法和Lyapunov-Krasovskii理论来分析系统的稳定性,并用LMIs的形式给出了在小时延变化率和未知时延变化率两种情况下,多智能体系统实现稳定编队和速度的充分条件,接着推导出联合连通拓扑结构具有解决编队过程中智能体失联问题的优越性. 最后的仿真实验在本文研究通讯时延基础上增加了速度自时延,实验结果也有效地验证了算法的正确性和有效性.
| [1] | YAN W S, FANG X P, LI J B. Formation optimization for AUV localization with range-dependent measurements noise[J]. IEEE Communications Letters, 2014, 18(9): 1579-1582. DOI: 10.1109/LCOMM.2014.2344033. |
| [2] | DONG X W, YU B C, SHI Z Y, et al. Time-varying formation control for unmanned aerial vehicles theories and applications[J]. IEEE Transactions on Control System. Technology, 2015, 23(1): 340-348. DOI: 10.1109/TCST.2014.2314460. |
| [3] | OIKAWA R, TAKIMOTO M, KAMBAYASHI Y. Distributed formation control for swarm robots using mobile agents [C]// 2015 10th Jubilee IEEE International Symposium on Applied Computational Intelligence and Informatics (SACI): IEEE, 2015: 111-16. |
| [4] | OIKAWA R, TAKIMOTO M, KAMBAYASHI Y. Composing swarm robot formations based on their distributions using mobile agents[J]. Lecture Notes in Computer Science, 2016(9571): 108-120. |
| [5] |
唐平, 杨宜民. 多智能体系统与足球机器人系统体系结构研究[J].
广东工业大学学报, 2001, 18(4): 1-4.
TANG P, YANG Y M. Study on multi-agent system and the structure of soccer game system[J]. Journal of Guangdong University of Technology, 2001, 18(4): 1-4. |
| [6] |
陈璟华, 陈少华, 杨宜民, 等. 电力系统二级电压的多智 能体协调控制[J].
广东工业大学学报, 2003, 20(1): 28-31.
CHEN J H, CHEN S H, YANG Y M, et al. Multi-agent Based on secondary voltage coordination control in power system[J]. Journal of Guangdong University of Technology, 2003, 20(1): 28-31. |
| [7] | OH K K, PARK M C, AHN H S. A survey of multi-agent formation control[J]. Automatica, 2015(53): 424-440. |
| [8] | BALCH T, ARKIN R C. Behavior-based formation control for multirobot teams[J]. IEEE Transactions on Robotics and Automation, 1998, 14(6): 926-939. DOI: 10.1109/70.736776. |
| [9] | LEWIS M A, TAN K H. High precision formation control of mobile robots using virtual structures[J]. Autonomous Robots, 1997, 4(4): 387-403. DOI: 10.1023/A:1008814708459. |
| [10] | MO L P, NIU Y G, PAN T T. Consensus of heterogeneous multi-agent systems with switching jointly-connected interconnection[J]. Physica A, 2015(427): 132-140. |
| [11] | MA L B, HE F H, SUN C P, et al. Finite time dynamical formation control of multi-agent systems [C]// Proceedings of the 34th Chinese Control Conference. [s.n.]: Hangzhou, China, 2015: 7398-7403. |
| [12] | DONG X W, LIN Q D, ZHAO Q L, et al. Time-varying group formation analysis and design for second-order multi-agent systems with directed topologies[J]. Neurocomputing, 2016(205): 367-374. |
| [13] | LUO X Y, HAN N N, GUAN X P. Leader-following consensus protocols for formation control of multi-agent network[J]. Journal of Systems Engineering and Electronics, 2011, 22(6): 991-997. DOI: 10.3969/j.issn.1004-4132.2011.06.016. |
| [14] | XIA H, HUANG T Z, SHAO J L, et al. Formation control of second-order multiagent systems with time-varying delays[J]. Mathematical Problems in Engineering, 2014(2014): 1-8. |
| [15] | LU X Q, AUSTIN F, CHEN SH. Formation control for second-order multi-agent systems with time-varying delays under directed topology[J]. Commun Nonlinear Sci Numer Simulat, 2012(17): 1382-1391. |
| [16] | LI W X, CHEN Z Q, LIU Z X. Leader-following formation control for second-order multiagent systems with time-varying delay and nonlinear dynamics[J]. Nonlinear Dyn, 2013(72): 803-812. |
| [17] | LIN P, JIA Y M. Consensus of a class of second-order multi-agent systems with time-delay and jointly-connected topologies[J]. IEEE Transactions on Automatic Control, 2010, 55(3): 778-785. DOI: 10.1109/TAC.2010.2040500. |
| [18] | WANG F, CHEN X, HE Y. Finite-time consensus of second-order multi-agent systems with jointly-connected topologies [C]// Proceedings of the 33rd Chinese Control Conference.[s.n.]: Nanjing, China, 2014: 1662-1667. |
| [19] |
薛瑞彬, 宋建梅, 张民强. 具有时延及联合连通拓扑的多飞行器分布式协同编队飞行控制研究[J].
兵工学报, 2015, 36(3): 493-502.
XUE R B, SONG J M, ZHANG M Q. Research on distributed multi-vehicle coordinated formation flight control with coupling time-delay and jointly-connected topologies[J]. Acta Armamentarii, 2015, 36(3): 493-502. |
| [20] | LIN P, JIA Y M. Multi-agent consensus with diverse time-delays and jointly-connected topologies[J]. Automatica, 2011, 47(4): 848-856. DOI: 10.1016/j.automatica.2011.01.053. |
| [21] | GODSIL C, ROYLE G. Algebraic Graph Theory [M]. New York: Springer-Verlag, 1997: 163-187. |
| [22] | BOYD B, GHAOUI L E, FERON E, et al. Linear Matrix Inequalities in System and Control Theory [M]. Philadelphia: SIAM, 1994: 28-29. |
| [23] | SUN Y, WANG L, XIE G. Average consensus in networks of dynamic agents with switching topologies and multiple time-varying delays[J]. Systems & Control Letters, 2008, 57(2): 175-183. |
| [24] | HALE J K, VERDUYN LUNEL S M. Introduction to Functional Differential Equations [M]. New York: Springer, 1993: 99-115. |
| [25] |
樊琼剑, 杨忠, 方挺, 等. 多无人机协同编队飞行控制的研究现状[J].
航空学报, 2009, 30(4): 684-693.
FAN Q J, YANG Z, FANG T, et al. Research status of coordinated formation flight control for multi-UAVs[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(4): 684-693. |
 2017, Vol. 34
2017, Vol. 34
