近年来,神经网络被广泛地应用到各个领域,并在机器人、航空、通信、模式识别、图像处理、联想记忆、信号处理以及组合优化等各方面有巨大的应用前景[1]. 根据是否遭受外界噪声干扰,神经网络被简单分为确定性神经网络和随机神经网络. 通常来说,确定性神经网络用常微分方程来描述,而随机神经网络则是通过随机微分方程来描述,当不遭受外界干扰时确定性神经网络能准确地描述实际系统. 但是,当系统遭受外界扰动时,确定性神经网络则无法描述. 所以在带外界扰动的情况下,随机神经网络被用来描述实际系统. 然而随着科学技术的高速发展,实际系统变得越来越复杂,且经常会遭受不确定的外界扰动,我们把它看作随机扰动. 同时,由于随机神经网络系统的震荡、发散,甚至不确定性因素使得系统存在时滞问题,硬件设施因有限的切换速度使得时滞问题在滤波和信息处理中大量存在. 因此研究随机时滞神经网络的稳定性问题十分重要. 另一方面,实际系统常常受到各类因素的干扰,如控制上的变化和传感器噪声等,它们能显著影响系统的稳定性. 因此只考虑系统的渐近稳定性是不够的,还需考虑系统在扰动存在情况下的暂态特性,即系统的输入状态稳定性(ISS). Lyapunov稳定性理论主要分析系统无外部扰动时的稳定性. Lyapunov稳定指系统从任何初始状态下出发都可以回到固有的平衡点. 然而,Lyapunov稳定性理论不适用于分析和处理系统在带外部扰动时状态响应是否控制在预设区域里面. 当系统不存在外部扰动时,输入状态稳定也就意味着系统是Lyapunov意义下的渐近稳定,同时输入状态稳定也意味着带有界输入时系统响应有界. 因此,提出系统的输入状态稳定变得十分必要. 据我们所知,随机时滞神经网络的稳定性已有了许多的研究,而对于随机时滞神经网络输入状态稳定性的研究却很少. 因此,更深层次的研究随机时滞神经网络输入状态稳定也有很重要的意义[2-3].
目前已经有大量关于随机滞后神经网络稳定性的研究以及关于输入状态稳定性问题的研究.比如文献[4-6]研究了不确定随机神经网络系统微分方程模型以及微分系统的全局渐近稳定性,文献[3]中提出关于系统的输入状态稳定问题,文献[7-10]中深入研究输入状态稳定性问题并给出了各自适当的ISS-Lyapunov方程. 文献[11-12]利用LMI方法研究随机时滞神经网络的稳定性问题,文献[2, 13]利用代数不等式研究一类随机神经网络的均方随机输入状态稳定问题.
尽管Riccati方程的处理方法在文献[9]中研究系统输入状态稳定性时有很多优势,但是只能得到满足某一个方面性能指标参数最优值,而不能得到满足多方面性能指标参数最优值,并且在求解时往往需要依赖于参数的调整,这给分析和综合结果带来了很大的保守性. 为了弥补其不足,有学者提出了用线性矩阵不等式[14](LMI)来研究时滞系统的鲁棒控制问题. 目前的研究主要是如何选用合适Lyapunov-Krasovskii函数,采用适当的不等式变换得到一个或者多个线性矩阵不等式判据来判断系统的稳定性. LMI方法比较容易利用计算机求出结果,同时减少随机神经网络系统稳定性结果的保守性. 据本文作者所知,LMI方法较少用在随机神经网络的输入状态稳定的研究中,基于以上考虑. 本文用LMI方法研究Hopfiled随机时滞神经网络的随机输入状态稳定性(SISS)问题.
1 系统模型以及预备知识本文中,随机时滞Hopfield型神经网络模型:
| $\left\{ {\begin{split}& {\rm{d}}{{x}}(t) = \left[ { - {{D}}x(t) + {{A}}f({{x}}(t) + {{B}}f({{x}}(t - \tau (t))) + } \right.\\[3pt]& \;\;\;\;\;\;\;\;\;\;\;\;\; \left. {u(t)} \right]{\rm{d}}t{ + {\sigma }(t,{x}(t),{x}(t - \tau (t))){\rm{d}}{\omega }(t),}\\[3pt]& {{x}(t) = {\psi }(t),t \in [ - \tau ,0].}\end{split}} \right.$ | (1) |
其中x(t)为状态向量,
假设1[15] 存在正数Ii使得
| $0 \leqslant \frac{{{f_i}({x_i})}}{{{x_i}}} \leqslant {l_i},\;\;\;{f_i}(0) = 0.$ | (2) |
假设2[12] 存在常矩阵C1,C2和P>0,使得
| $\begin{split}& {{\sigma }^{\rm T}}(t,{x}(t),{x}(t - \tau (t))){P\sigma }(t,{x}(t),{x}(t - \tau (t))) \leqslant \\& \;\;\;\;\;{{x}^{\rm T}}(t){{C}_1}{x}(t) + {{x}^{\rm T}}(t - \tau (t)){{C}_2}{x}(t - \tau (t)).\end{split}$ | (3) |
定义1[16] 对于系统(1),如果存在
| $\varepsilon (\left\| x \right\|) < \beta ({\left\| {{x_0}} \right\|_\tau },t) + \gamma (\left| u \right|),\forall t \geqslant 0,{x}(0) = {x_0},$ | (4) |
则系统为输入状态稳定.
定义2[16] 考虑系统(1),给出一个Lyapunov-Krasovskii函数
| ${\alpha _1}(\left\| x \right\|) \leqslant {{V}}(x,t) \leqslant {\alpha _2}(\left\| x \right\|),$ | (5) |
| ${LV} \leqslant - {\alpha _3}(\left\| x \right\|) + {\alpha _4}(\left| u \right|).$ | (6) |
对于
| $\begin{array}{l}{LV} = {{V}_t}(t,x) + {{V}_x}(t,x){f} + \frac{1}{2}{\rm{tr}}[{{h}^{\rm T}}{{V}_{xx}}(t,x){h}],\\[6pt]{f} = - {Dx}(t) + {A}f({x}(t)) + {B}f({x}(t - \tau (t))) + {u}(t),\\[6pt]{h} = {\sigma }(t,{x}(t),({x}(t - \tau (t))).\end{array}$ |
那么
引理1[15]
| $\begin{split}& {[{{\varTheta }_1} + {{\varTheta }_2}{{\varTheta }_3}]^{\rm T}}{\varDelta }[{{\varTheta }_1} + {{\varTheta }_2}{{\varTheta }_3}]\leqslant\\& {\varTheta }_1^{\rm T}{[{{\varDelta }^{ - 1}} - {\phi ^{ - 1}}{{\varTheta }_2}{\varTheta }_2^{\rm T}]^{ - 1}}{{\varTheta }_1} + \phi {\varTheta }_3^{\rm T}{{\varTheta }_3}.\end{split}$ | (7) |
引理2[15] 如果系统(1)存在随机输入状态稳定(SISS)Lyapunov方程,则系统为随机输入状态稳定.
2 主要结果定理1 考虑系统(1),如果存在常数μ>0且存在5个正定对角矩阵
| $\left[ {\begin{array}{*{20}{c}}{\tilde{ S}}&\!\!\!{{PA}}&\!\!\!{{PI}}&\!\!\!0&\!\!\!{{PB}}&\!\!\!0&\!\!\!{ - {\tau ^2}{{D}^{\rm T}}{R}}&\!\!\!0\\[6pt]*&\!\!\!{{{Q}_2} - {S}}&\!\!\!0&\!\!\!0&\!\!\!0&\!\!\!0&\!\!\!{{\tau ^2}{{A}^{\rm T}}{R}}&\!\!\!0\\[6pt]*&\!\!\!*&\!\!\!{ - \rho {I}}&\!\!\!0&\!\!\!0&\!\!\!0&\!\!\!{{\tau ^2}{{I}^{\rm T}}{R}}&\!\!\!0\\[6pt]*&\!\!\!*&\!\!\!*&\!\!\!{{{\varXi }_1}}&\!\!\!0&\!\!\!0&\!\!\!0&\!\!\!0\\[6pt]*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!{{{\varXi }_2}}&\!\!\!0&\!\!\!0&\!\!\!0\\[6pt]*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!{ - {R}}&\!\!\!0&\!\!\!0\\[6pt]*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!{ - {\tau ^2}{R}}&\!\!\!{{\tau ^2}{BR}}\\[6pt]*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!{ - {I}}\end{array}} \right] < 0$ | (8) |
成立,其中
| $\begin{array}{l}\tilde {{S}} = 2{{P}}D + {{{Q}}_1} + {{{C}}_1} + {{{L}}^{\rm{T}}}{{SL}} + {{G}},\\[6pt]{{{\varXi}} _1} = - (1 - \mu ){{{Q}}_1} + {C_2},\\[6pt]{{{\varXi}} _2} = - (1 - \mu ){{{Q}}_2} + {{I}}.\\[6pt]{{L}} = {\rm{diag}}\{ {l_1},{l_2}, \cdots ,{{\mathop{l}\nolimits} _n}\} ,\end{array}$ |
则系统(1)是随机输入状态稳定的.
证明 构建如下的Lyapunov泛函:
| $\begin{split}& {V}(x,t) = {{x}^{\rm T}}(t){Px}(t) + \int_{t - \tau (t)}^t {{{x}^{\rm T}}(s){{Q}_1}{x}(s)} {\rm{d}}s+\\& \;\;\;\;\;\;\;\;\;\;\;\;\; \int_{t - \tau (t)}^t {{{f}^{\rm T}}({x}(s)){{Q}_1}f(x(s))} {\rm{d}}s+\\& \;\;\;\;\;\;\;\;\;\;\;\;\; \tau \int_{ - \tau }^0 {\int_{t + \theta }^t {{{\bar{ y}}^{\rm T}}(s){R} {\bar { y}}(s){\rm{d}}s} {\rm{d}}\theta } .\end{split}$ | (9) |
其中
| $\bar{ y}(s) = - {Dx}(t) + {A}f({x}(t) + {B}f({x}(t - \tau (t))) + {u}(t).$ |
令
存在
| $\begin{array}{l}\underline \sigma ({P}){\left\| {{x}(t)} \right\|^2} \leqslant {{x}^{\rm T}}(t){Px}(t) \leqslant \underline \sigma ({P}){\left\| {{x}(t)} \right\|^2},\\[6pt]0 \leqslant \int_{t - \tau (t)}^t {{{x}^{\rm T}}(s){{Q}_1}} {x}(s){\rm{d}}s \leqslant \tau (t)\bar \sigma ({{Q}_1}){\left\| {{x}(t)} \right\|^2},\\[6pt]0 \leqslant \int_{t - \tau (t)}^t {{{f}^{\rm T}}({x}(s)){{Q}_2}} {f}(x(s)){\rm{d}}s \leqslant \tau (t)\bar \sigma ({{Q}_2}){\left\| {{f}(x(t))} \right\|^2}\\[6pt]\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \leqslant \tau (t)\bar \sigma ({{L}^{\rm T}}{{Q}_2}{L}){\left\| {{x}(t)} \right\|^2},\\[6pt]0 \leqslant \tau \int_{ - \tau }^0 {\int_{t + \theta }^t {{{\bar{ y}}^{\rm T}}(s) {R} {\bar { y}}(s){\rm{d}}s} {\rm{d}}\theta } \leqslant \varpi \bar \sigma ({R}){\left\| {{x}(t)} \right\|^2}.\end{array}$ |
易知
| $\begin{array}{l}\underline \sigma ({P}){\left\| {{x}(t)} \right\|^2} \leqslant {V}(x,t)\leqslant\\[6pt] (\bar \sigma ({P})) + \tau (t)\bar \sigma ({{Q}_1}) + \tau (t)\bar \sigma ({{L}^{\rm T}}{{Q}_2}{L}) + \varpi \bar \sigma ({R})){\left\| {{x}(t)} \right\|^2}.\end{array}$ |
根据Itô's公式,对
| $\begin{array}{l}{LV}(x,t) \leqslant \\[6pt]\;\;\;\;\;\;\;\;\;\;\; - 2{{x}^{\rm T}}(t){PDx}(t) + 2{{x}^{\rm T}}(t){PA}f({x}(t))+ \\[6pt]\;\;\;\;\;\;\;\;\;\;\; 2{{x}^{\rm T}}(t){PB}f({x}(t - \tau (t))) + 2{{x}^{\rm T}}(t){Pu}(t)+\\[6pt]\;\;\;\;\;\;\;\;\;\;\; {{f}^{\rm T}}({x}(t){{Q}_2}{f}(x(t)) + {{x}^{\rm T}}(t){{Q}_1}{x}(t)-\\[6pt]\;\;\;\;\;\;\;\;\;\;\; (1 - \tau '(t)){{x}^{\rm T}}(t - \tau (t)){{Q}_1}{x}(t - \tau (t))-\\[6pt]\;\;\;\;\;\;\;\;\;\;\; (1 - \tau '(t)){{f}^{\rm T}}({x}(t - \tau (t)){{Q}_2}{f}({x}(t - \tau (t)))+\\[6pt]\;\;\;\;\;\;\;\;\;\;\; {{\sigma }^{\rm T}}(t,{x}(t),{x}(t - \tau (t))){P\sigma }(t,{x}(t),{x}(t - \tau (t)))+\\[6pt]\;\;\;\;\;\;\;\;\;\;\; {\tau ^2}{{\bar{ y}}^{\rm T}}(t) {R} {\bar { y}}(t) - \tau \int_{t - \tau }^t {{{\bar{ y}}^{\rm T}}(s) {R} {\bar { y}}(s){\rm{d}}s} .\end{array}$ | (10) |
根据引理1
| $\begin{split}& {\tau ^2}{{\bar{ y}}^{\rm T}}(t){R} {\bar { y}}(t)\\& = {\tau ^2}[ - {Dx}(t) + {A}f{({x}(t) + {B}f({x}(t - \tau (t))) + {u}(t)]^{\rm T}} \times\\& \;\;\; {R}[ - {Dx}(t) + {A}f({x}(t) + {B}f({x}(t - \tau (t))) + {u}(t)]\leqslant\\& [ - {Dx}(t) + {A}f{({x}(t) + {u}(t)]^{\rm T}}{({({\tau ^2}{R})^{ - 1}} - {B}{{B}^{\rm T}})^{{\rm{ - }}1}}\times\\& \;\;\; [ - {Dx}(t) + {A}f({x}(t) + {u}(t)]+\\& \;\;\; {{f}^{\rm T}}({x}(t - \tau (t))){f}({x}(t - \tau (t)).\end{split}$ | (11) |
此外
| $- \tau \int_{t - \tau }^t {{{\bar{ y}}^{\rm T}}(s){R}} \bar{ y}(s) \leqslant - \int_{t - \tau }^t {{{\bar{ y}}^{\rm T}}(s){\rm{d}}s{R}} \int_{t - \tau }^t {{{\bar{ y}}^{\rm T}}(s)} {\rm{d}}s.$ | (12) |
根据假设1
| ${{x}^{\rm T}}(t){{L}^{\rm T}}{SLx}(t) \geqslant {{f}^{\rm T}}({x}(t)){S}f({x}(t)).$ | (13) |
据式(10)-(13)
| $\begin{array}{l}{LV}(x,t) \leqslant {{\varPi }_1}\left[ {\begin{array}{*{20}{c}}{\tilde{ S}} & {{PA}} & {{PI}} & 0 & {{PB}} & 0\\[5pt]* & {{{Q}_2} - {S}} & 0 & 0 & 0 & 0\\[5pt]* & * & { - \rho {I}} & 0 & 0 & 0\\[5pt]* & * & * & {{{\varXi }_1}} & 0 & 0\\[5pt]* & * & * & * & {{{\varXi }_1}} & 0\\[5pt]* & * & * & * & * & { - {R}}\end{array}} \right]{\varPi }_1^{\rm T}\\[35pt]\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + {{\varPi }_2}{{\varPi }_3}{[{({\tau ^2}{R})^{ - 1}} - {B}{{B}^{\rm T}}]^{ - 1}}{{\varPi }_4}{\varPi }_2^{\rm T}-\\[5pt]\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; {{x}^{\rm T}}(t){Gx}(t) + \rho {{u}^{\rm T}}(t){u}(t).\end{array}$ | (14) |
其中
| $\begin{array}{l}\tilde {{S}} = - 2{{PD}} + {{{Q}}_1} + {{{C}}_1} + {{{L}}^{\rm{T}}}{{SL}} + {{G}},\\[6pt]{{{\varPi}} _1} = \left[ {{{x}}(t){{f}}(x(t)){{u}}(t){{x}}(t - \tau (t))} f({{x}}(t -\right.\\[6pt]\;\;\;\;\;\;\;\;\; { \tau (t))) int_ - {\tau } {{{\bar {{y}}}^{\rm{T}}}(s){\rm{d}}s} } ],\\[6pt]{{\varPi} _2} = [ {{{x}}(t){{f}}({{x}}(t)){{u}}(t)} ],\\[6pt]{{\varPi} _3} = {[ { - {{{D}}^{\rm{T}}}{{{A}}^{\rm{T}}}{{{I}}^{\rm{T}}}} ]^{\rm{T}}},\\[6pt]{{{\varPi}} _4} = \left[ - {{D}}{{A}}{{I}} \right],\\[6pt]{{C}} = {{{G}}^{\rm{T}}},\\[6pt]\rho > 0.\end{array}$ |
若不等式
| $\left[ {\begin{array}{*{20}{c}}{\tilde{ S}}&\!\!\!{{PA}}&\!\!\!{{PI}}&\!\!\!0&\!\!\!{{PB}}&\!\!\!0&\!\!\!{ - {{D}^{\rm T}}}\\[5pt]*&\!\!\!{{{Q}_2} - {S}}&\!\!\!0&\!\!\!0&\!\!\!0&\!\!\!0&\!\!\!{{{A}^{\rm T}}}\\[5pt]*&\!\!\!*&\!\!\!{ - \rho {I}}&\!\!\!0&\!\!\!0&\!\!\!0&\!\!\!{{{I}^{\rm T}}}\\[5pt]*&\!\!\!*&\!\!\!*&\!\!\!{{{\varXi }_1}}&\!\!\!0&\!\!\!0&\!\!\!0\\[5pt]*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!{{{\varXi }_2}}&\!\!\!0&\!\!\!0\\[5pt]*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!{ - {R}}&\!\!\!0\\[5pt]*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!{{{({\tau ^2}{R})}^{ - 1}} - {B}{{B}^{\rm T}}}\end{array}} \right] < 0$ | (15) |
成立,则
| $\begin{array}{l}{LV} \leqslant - {{x}^{\rm T}}(t){Gx}(t) + \rho {{u}^{\rm T}}(t){u}(t) \leqslant \\[6pt]\;\;\;\;\;\;\;\;\;\;\; - {\lambda _{\min }}({G}){\left\| {{x}(t)} \right\|^2} + \rho {\left| {{u}(t)} \right|^2} = \\[6pt]\;\;\;\;\;\;\;\;\;\;\; - \sigma ({G}){\left\| {{x}(t)} \right\|^2} + \rho {\left| {{u}(t)} \right|^2}.\end{array}$ |
定义函数:
| $\begin{array}{l}{\kappa _1}(s) = \underline {{\sigma}} ({{P}}){s^2},\\[5pt]{\kappa _2}(s) = (\underline {{\sigma}} ({{P}}) + \tau (t)\overline {{\sigma}} ({{{Q}}_1})+\\[5pt] \;\;\;\;\;\;\;\;\;\;\;\;\; \tau (t)\overline {{\sigma}} ({{{L}}^T}{{{Q}}_2}L) + \varpi \overline {{\sigma }}({{R}})){s^2},\\[5pt]{\kappa _3}(s) = \underline {{\sigma}} ({{P}}){s^2},\\[5pt]{\kappa _4}(s) = \rho {s^2}.\end{array}$ |
明显:
| $\begin{array}{l}{\kappa _1}(\left\| x \right\|) = \underline {{\sigma}} ({{P}}){\left\| x \right\|^2},\\[5pt]{\kappa _2}(\left\| x \right\|) = (\underline {{\sigma}} ({{P}}) + \tau (t)\overline {{\sigma}} ({{{Q}}_1})+\\[5pt] \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \tau (t)\overline {{\sigma}} ({{{L}}^{\rm{T}}}{{{Q}}_2}{{L}}) + \varpi \overline {{\sigma}} ({{R}}){\left\| x \right\|^2},\\[5pt]{\kappa _3}(\left\| x \right\|) = \underline {{\sigma}} ({{P}}){\left\| x \right\|^2},{\kappa _4}(\left\| x \right\|) = \rho {\left\| x \right\|^2},\end{array}$ |
满足定义2中的条件(5),(6),则系统为随机输入状态稳定. 另一方面利用Schur补引理,不等式(15)等价于
| $\left[ {\begin{array}{*{20}{c}}{\tilde{ S}}&\!\!\!{{PA}}&\!\!\!{{PI}}&\!\!\!0&\!\!\!{{PB}}&\!\!\!0&\!\!\!{ - {{D}^{\rm T}}}&\!\!\!0\\[5pt]*&\!\!\!{{{Q}_2} - {S}}&\!\!\!0&\!\!\!0&\!\!\!0&\!\!\!0&\!\!\!{{{A}^{\rm T}}}&\!\!\!0\\[5pt]*&\!\!\!*&\!\!\!{ - \rho {I}}&\!\!\!0&\!\!\!0&\!\!\!0&\!\!\!{{{I}^{\rm T}}}&\!\!\!0\\[5pt]*&\!\!\!*&\!\!\!*&\!\!\!{{{\varXi }_1}}&\!\!\!0&\!\!\!0&\!\!\!0&\!\!\!0\\[5pt]*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!{{{\varXi }_2}}&\!\!\!0&\!\!\!0&\!\!\!0\\[5pt]*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!{ - {R}}&\!\!\!0&\!\!\!0\\[5pt]*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!{ - {{({\tau ^2}{R})}^{ - 1}}}&\!\!\!{B}\\[5pt]*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!*&\!\!\!{ - {I}}\end{array}} \right] < 0.$ | (16) |
式(16)左右乘
给出随机Hopfield时滞神经网络输入状态稳定的算例并进行数值模拟,验证结果的有效性:
例1:首先考虑一个二维的随机Hopfield时滞神经网络(1),其中
| $\begin{array}{l}{D} = \left[ {\begin{array}{*{20}{c}}5 & 0\\[5pt]0 & 5\end{array}} \right],{A} = \left[ {\begin{array}{*{20}{c}}{ - 0.8} & {1.4}\\[5pt]{0.5} & { - 1.3}\end{array}} \right],\\[10pt]{B} = \left[ {\begin{array}{*{20}{c}}{0.9} & {0.8}\\[5pt]{0.4} & {1.4}\end{array}} \right],{I} = \left[ {\begin{array}{*{20}{c}}1 & 0\\[5pt]0 & 1\end{array}} \right],\\[10pt]{L} = \left[ {\begin{array}{*{20}{c}}1 & 0\\[5pt]0 & 1\end{array}} \right],\\[10pt]\mu = 0.3,\;\;\;\;\;{{C}_1} = {{C}_2} = {\rm{0}}{\rm{.06}} {I}.\end{array}$ |
通过MATLAB(LMI)工具箱,可得以下可行解
| $\begin{array}{l}{P} = \left[ {\begin{array}{*{20}{c}}{53.9833} & { - 0.5465}\\[5pt]{ - 0.5465} & {55.7584}\end{array}} \right],\\[10pt]{{Q}_1} = \left[ {\begin{array}{*{20}{c}}{81.7224} & {2.1168}\\[5pt]{2.1168} & {70.4753}\end{array}} \right],\\[10pt]{{Q}_2} = \left[ {\begin{array}{*{20}{c}}{91.4172} & {22.9171}\\[5pt]{22.9171} & {112.0736}\end{array}} \right],\\[10pt]{G} = \left[ {\begin{array}{*{20}{c}}{58.2584} & {2.0484}\\[5pt]{2.0484} & {47.4454}\end{array}} \right],\\[10pt]{S} = \left[ {\begin{array}{*{20}{c}}{151.8478} & { - 2.0451}\\[5pt]{ - 2.0451} & {206.2091}\end{array}} \right].\end{array}$ |
假定
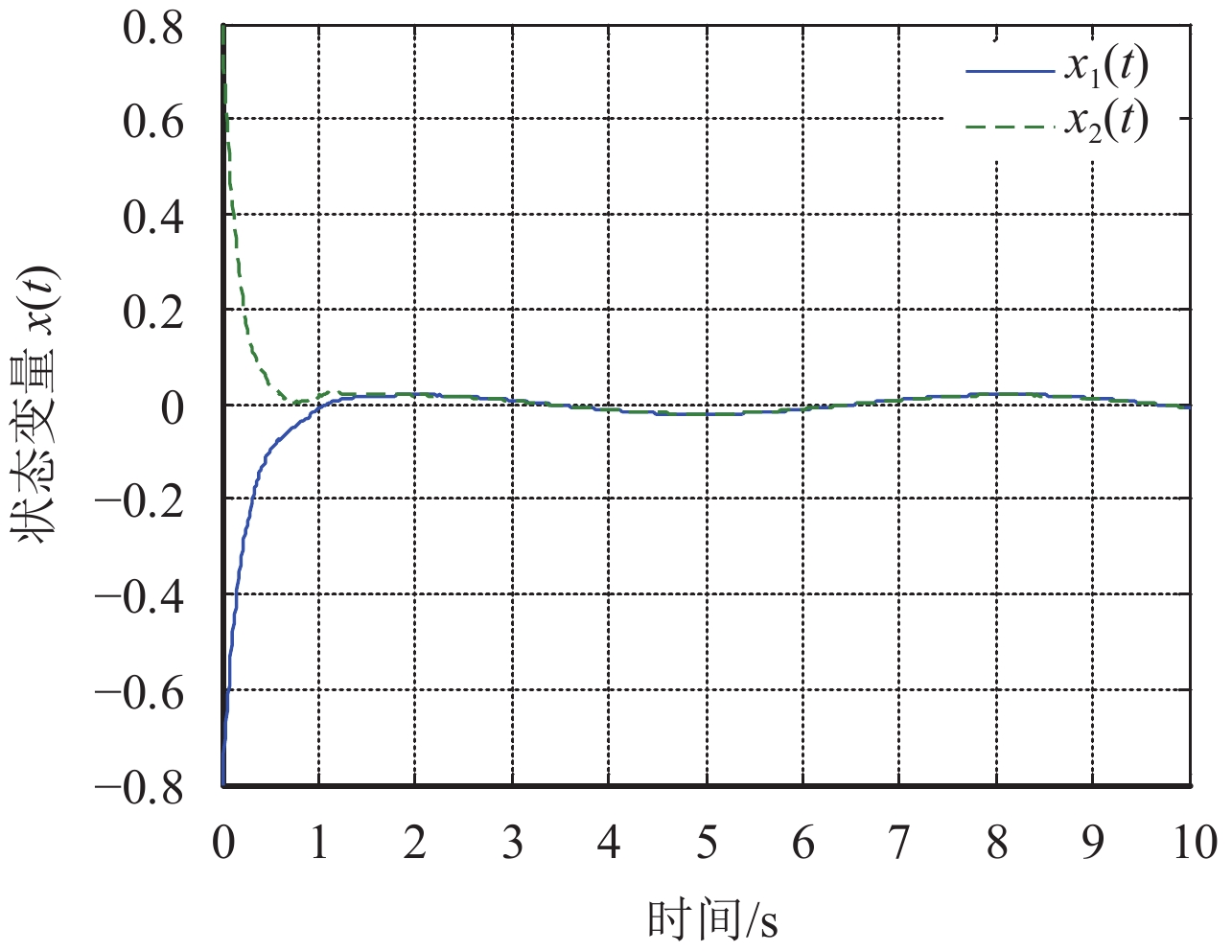
|
图 1 系统(1)状态响应x1(t),x2(t) Figure 1 The state response x1(t), x2(t) of system (1) |
根据图形以及LMI仿真结果,可轻易得出时滞神经网络状态方程满足随机时滞输入状态稳定.
例2:考虑一个三维的随机Hopfield时滞神经网络(1)其中
| $\begin{array}{l}{D} = \left[ {\begin{array}{*{20}{c}}5 & 0 & 0\\[5pt]0 & 4 & 0\\[5pt]0 & 0 & 5\end{array}} \right],{A} = \left[ {\begin{array}{*{20}{c}}{{\rm{ - }}0.3} & {0.4} & {{\rm{ - }}0.3}\\[5pt]{0.2} & {0.4} & 0\\[5pt]0 & {0.1} & {{\rm{ - }}0.3}\end{array}} \right],\\[15pt]{B} = \left[ {\begin{array}{*{20}{c}}0 & {0.2} & {{\rm{ - }}0.2}\\[5pt]{0.5} & 0 & {0.2}\\[5pt]{{\rm{ - }}0.2} & {0.2} & 0\end{array}} \right],{I} = \left[ {\begin{array}{*{20}{c}}1 & 0 & 0\\[5pt]0 & 1 & 0\\[5pt]0 & 0 & 1\end{array}} \right],\\[15pt]{L} = {I},\;\;\;\mu = 0.3,\;\;\;{{C}_1} = {{C}_2} = {\rm{0}}{\rm{.05}}{I}.\end{array}$ |
通过MATLAB(LMI)工具箱,可得以下可行解
| $\begin{array}{l}{P} = \left[ {\begin{array}{*{20}{c}}{44.4944} & {1.0467} & {{\rm{ - }}3.4243}\\[6pt]{1.0467} & {473020} & {{\rm{ - }}3.4002}\\[6pt]{{\rm{ - }}3.4243} & {{\rm{ - }}3.4002} & {51.8041}\end{array}} \right],\\[16pt]{{Q}_1} = \left[ {\begin{array}{*{20}{c}}{72.2520} & { - 0.2189} & {{\rm{ - }}3.7149}\\[6pt]{ - 0.2189} & {67.2283} & {3.4882}\\[6pt]{{\rm{ - }}3.7149} & {3.4882} & {65.6609}\end{array}} \right],\\[16pt]{{Q}_2} = \left[ {\begin{array}{*{20}{c}}{61.6316} & {0.3150} & {{\rm{ - }}0.{\rm{4052}}}\\[6pt]{0.3150} & {83.7859} & {7.1819}\\[6pt]{{\rm{ - }}0.{\rm{4052}}} & {7.1819} & {58.7869}\end{array}} \right],\\[16pt]{G} = \left[ {\begin{array}{*{20}{c}}{59.3963} & { - 0.4084} & {{\rm{ - 4}}{\rm{.7762}}}\\[6pt]{ - 0.4084} & {83.7859} & {4.2919}\\[6pt]{{\rm{ - 4}}{\rm{.7762}}} & {4.2919} & {51.0797}\end{array}} \right],\\[16pt]{S} = \left[ {\begin{array}{*{20}{c}}{106.6178} & {0.6701} & {{\rm{ - 2}}{\rm{.6846}}}\\[6pt]{0.6701} & {127.2291} & {6.5557}\\[6pt]{{\rm{ - 2}}{\rm{.6846}}} & {6.5557} & {98.7177}\end{array}} \right].\end{array}$ |
假定
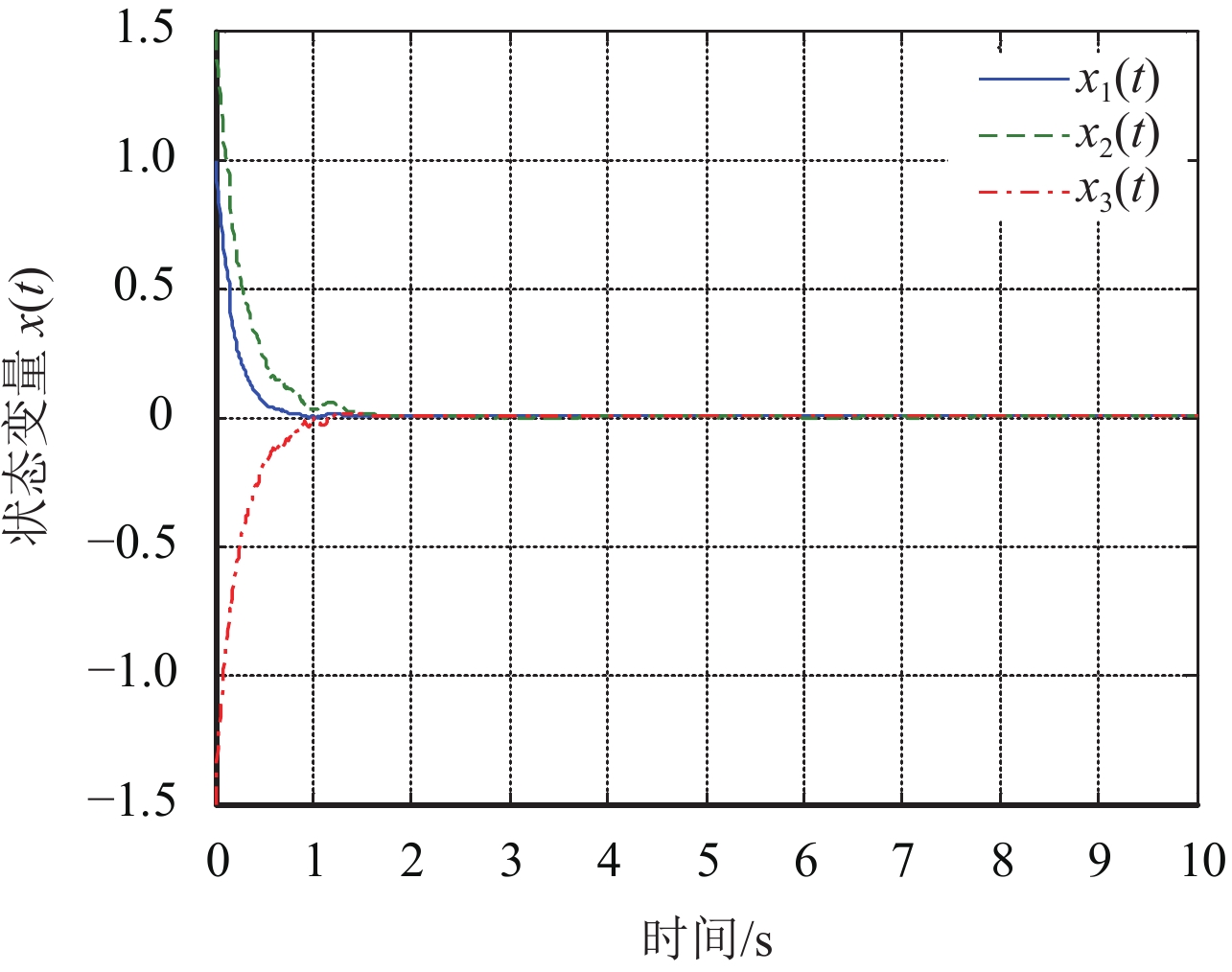
|
图 2 系统(1)状态响应x1(t),x2(t)和x3(t) Figure 2 The state response x1(t), x2(t) and x3(t) of system (1) |
本文针对Hopfield随机神经网络的输入状态稳定性问题,采用Lyapunov-Krasovskii泛函、Itô公式以及随机分析理论,得到了系统(1)随机输入状态稳定的结果. 实例验证所得结果的有效性.
| [1] |
刘勇健, 刘义建. 人工神经用于岩体工程的方法改进[J].
广东工业大学学报, 2002, 19(1): 21-25.
LIU Y J, LIU Y J. The improving methods of artificial neural network in Geo-techn-ical engineering[J]. Journal of Guangdong University and Technology, 2002, 19(1): 21-25. |
| [2] | ZHU Q X, CAO J D. Mean-square exponential input-to-state stability of stochastic delayed neural networks[J]. Neurocomputing, 2014, 131(0): 157-163. |
| [3] | SONTAG E D. Smooth stabilization implies coprime factorization[J]. IEEE Trans. Autom. Control, 1989, 34(4): 435-443. DOI: 10.1109/9.28018. |
| [4] | BLYTHE S, MAO X R, LIAO X L. Stability of stochastic delay neural networks[J]. Journal of the Franklin Institute, 2001, 338(0): 481-495. |
| [5] | 胡宣达. 随机微分方程稳定性理论[M]. 南京:南京大学出版社, 1990. |
| [6] | MAO X R. Exponential Stability of Stochastic Differential Equations [M]. New York: Marcel Dekker Inc, 1994. |
| [7] | GRUNE L. Input-to-state dynamical stability and its Lyapunov function characterization[J]. Automatic Control, IEEE Transactions on, 2002, 47(9): 1499-1504. DOI: 10.1109/TAC.2002.802761. |
| [8] | TAI Z. Input-to-state stability for Lur’e stochastic distributed parameter control systems[J]. Applied Mathematics Letters, 2012, 25(4): 706-711. DOI: 10.1016/j.aml.2011.09.057. |
| [9] | AHN C K. Passive learning and input-to-state stability of switched Hopfield neural networks with time-delay[J]. Information Sciences, 2010, 180(23): 4582-4594. DOI: 10.1016/j.ins.2010.08.014. |
| [10] | ALWAN MOHAMAD S, LIU Z, XIE W C. On design of robust reliable control and input-to-state stabilization of uncertain stochastic systems with state delay[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(4): 1047-1056. DOI: 10.1016/j.cnsns.2012.08.029. |
| [11] | HUANG H Y, DU Q S, KANG X B. Global exponential stability of neutral high-order stochastic Hopfield neural networks with Markovian jump parameters and mixed time delays[J]. ISA Transactions, 2013, 52(6): 759-767. DOI: 10.1016/j.isatra.2013.07.016. |
| [12] |
江明辉, 廖晓昕. 变时滞随机微分方程的指数稳定性[J].
数学物理学报, 2006, 6(6): 254-258.
JIANG M H, LIAO X X. Exponential stability of stochastic differential equations with variable delays[J]. Journal of Mathematical Physics, 2006, 6(6): 254-258. |
| [13] | ZHU Q X, CAO J D, RAKKIYAPPAN R. Exponential input-to-state stability of stochastic Cohen–Grossberg neural networks with mixed delays[J]. Nonlinear Dynamics, 2015, 79(2): 1085-1098. DOI: 10.1007/s11071-014-1725-2. |
| [14] | ZHOU D M, YU S H, ZHANG Z Q. New LMI-based conditions for global exponential stability to a class of Cohen–Grossberg BAM networks with delays[J]. Neurocomputing, 2013, 121(18): 512-522. |
| [15] | LI X L, WANG M R. Novel robust stability criteria for stochastic hopfield neural network with time-varying delays [M]. Neural Information Processing. Springer Berlin Heidelberg, 2012: 474-479. |
| [16] | ZHAO F, ZHANG Q L, YAN X G, et al. Stochastic input-to-state stability and H∞ filtering for a class of stochastic nonlinear systems[J]. Applied Mathematics & Computation, 2014, 227: 672-686. |
 2017, Vol. 34
2017, Vol. 34