粒子群算法[1]是由Eberhart和Kennedy于1995年提出的一种全局搜索算法,同时它也是一种模拟自然界的生物活动以及群体智能的随机搜索算法. 算法是作者通过对鸟群觅食活动的规律性的观察,将社会心理学上的个体认知经验、社会经验、种群智慧等思想融合到组织性和规律性很强的群体行为中,进而转变为优化问题求解过程中可行解迭代时向局部最优和全局最优靠拢,最终产生优化问题的全局最优解. 但由于粒子群优化算法是一种有针对性的随机的启发式算法,在解决复杂优化问题时,对全局最优粒子进行粒子靠拢和追逐,最终粒子会趋向统一化而缺少多样性,每次求解的结果可能不同,也有可能找不到全局最优解. 该算法存在容易在局部最优点停止、进化后期收敛速度慢、鲁棒性差等缺陷[2]. 针对以上问题,本文就远离最差解的思想在粒子群算法中引入2个因子:全局最差解和局部最差解,并分别测试全局最差解和局部最差解对粒子群优化算法的影响.
1 标准粒子群算法及其改进 1.1 标准粒子群算法在可行解空间随机产生一群粒子,每个粒子都无质量和体积信息,将每个粒子作为可行解空间中的一个可行解,适应度函数即为目标函数. 迭代过程中,每个粒子都在可行解空间中进行位置变化,粒子的位置更新由粒子的速度确定. 通常粒子将追逐当前的最优粒子而运动,并经过逐代更新搜索,最后得到全局最优解. 每次迭代过程中,粒子都将向2个最优值靠拢:一个是粒子本身历史的最优解,即局部最优解;另一个是整个粒子群群体当前找到的最优解,即全局最优解.
假设种群规模popsize为n的粒子群在d维的搜索空间中按照一定的速度进行飞行. 粒子i在t时刻的状态设置如下.
粒子的位置:
| $\begin{array}{*{20}{l}}{{{X}_i}(t) = ({{x}_{i1}}(t),{{x}_{i2}}(t), \cdot \cdot \cdot ,{{x}_{id}}(t)),}\\[6pt]{{{x}_{id}}(t) \in [{L_d},{U_d}],}\end{array}$ |
其中,Ld为搜索空间的下限,Ud为搜索空间的上限;
粒子的速度:
| $\begin{array}{l}{{v}_i}(t) = ({{v}_{i1}},{{v}_{i2}}, \cdot \cdot \cdot ,{{v}_{id}}),\\[6pt]{{v}_{id}}(t) \in [{{v}_{\min }},{{v}_{\max }}],\end{array}$ |
其中,vmin为最小速度,vmax为最大速度;
个体最优位置:
| ${{P}_{{\rm{best}}}}_i(t) = ({{p}_{i1}}(t),{p}{}_{i2}(t), \cdot \cdot \cdot ,{{p}_{id}}(t));$ |
全局最优值位置:
| ${{G}_{{\rm{best}}}}(t) = ({{p}_{g1}}(t),{{p}_{g2}}(t), \cdot \cdot \cdot ,{{p}_{gd}}(t)),$ |
其中,
那么粒子在t+1时刻的位置更新公式如下:
| $\begin{split}& {{v}_{id}}(t + 1) = w \times {{v}_{id}}(t) + {c_1} \times {r_1} \times ({{P}_{{\rm{best}}}}_i(t) - \\& \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; {{x}_{id}}(t)) +{c_1} \times {r_2} \times ({{G}_{{\rm{best}}}}(t) - {{x}_{id}}(t)),\\& {{x}_{id}}(t + 1) = {{x}_{id}}(t) + {{v}_{id}}(t + 1),\end{split}$ | (1) |
式(1)中,r1、r2均为在(0, 1)区间均匀分布的随机数;c1、c2为学习因子,一般取2.
1.2 已有的粒子群改进算法根据已有文献,目前粒子群算法已有的改进一般从以下几个方面进行:
(1) 惯性权重模型:惯性权重w是前一速度的惯性控制量. 一般设置为从0.9线性递减到0.4[3-5],即
| $w = {w_{\max }} - \frac{{{w_{\max }} - {w_{\min }}}}{{{\rm{ite}}{{\rm{r}}_{\max }}}} \times {\rm{iter,}}$ | (2) |
其中,wmax为惯性权重最大值,一般经验设为0.9,wmin为惯性权重最小值,一般经验设为0.4;itermax为迭代最大次数,iter为当前迭代次数.
(2) 学习因子模型:代表了粒子向局部最优点Pbest和全局最优点Gbest靠拢的加速权重. c1、c2一般取2.0,代表着对2个引导方向的同等重视[6]. 也有一些c1、c2不相等的设置,但其范围都在0~4之间,比如将c1线性减小,c2线性增大的设置能动态平衡算法的多样性和收敛性[7-8].
(3) 拓扑结构:不同的拓扑结构会影响算法的全局搜索和局部搜索的能力. Kennedy在进化计算国际会议CEC上发表了文章[9-10],提出了例如星型结构、环型结构、齿形结构、金字塔结构、冯·诺依曼结构等等不同的拓扑结构,并且比较了它们在PSO中的性能. 国内的一些学者也提出了一些新的拓扑设计准则, 如菱形十二面的拓扑结构[11]、层次环形结构的拓扑结构[12]、基于加权有向的拓扑结构[13], 并证明了其改进效果.
(4) 与其他算法结合:自粒子群算法提出之后,很多学者就不断地将PSO算法和其他搜索算法或者思想技术相结合,形成了许多PSO算法和其他算法混合的算法的改进版本. 这些算法有些融合了传统进化计算中的算子[14-15],例如选择算子、交叉算子、变异算子等,有些直接与其他算法相结合,例如模拟退火算法、免疫算法、差分进化算法、人工鱼群算法等[16-17].
2 本文改进的粒子群算法针对标准粒子群优化算法容易陷入局部最优、寻优精度低及后期搜索速度慢等缺陷,本文提出一种基于全局最差解(Gworst)和局部最差解(Pworst)的改进粒子群算法(LWPSO),并针对同时改进Gworst和Pworst、只改进Gworst、只改进Pworst这3种情况进行仿真实验.
本文算法参数设定:
惯性权重:
| ${w_{\max }} = 0.9, \;\; {w_{\min }} = 0.4.$ |
学习因子:c1、c2=2;
粒子更新公式:
| $\begin{array}{l}{{v}_{id}}(t + 1) = w {{v}_{id}}(t) + {c_1} {r_1} ({{P}_{{\rm{best}}}}_i(t) - {{x}_{id}}(t)) + \\[6pt]{c_1} {r_2} \times ({{G}_{{\rm{best}}}}(t) - {{x}_{id}}(t)) - {\rm{ }}{r_3} ({{P}_{{\rm{worst}}}}_i(t) - {{x}_{id}}(t)),\\[6pt]{{x}_{id}}(t + 1) = {{x}_{id}}(t) + {{v}_{id}}(t + 1),\end{array}$ | (3) |
其中,Pworsti(t)为i粒子t时刻局部最差粒子位置,即个体最差位置;r1、r2、r3为均匀分布在0到1之间的随机数;同时改进时加入Gworst的影响,Gworst为全局最差粒子位置.
2.1 算法流程如下
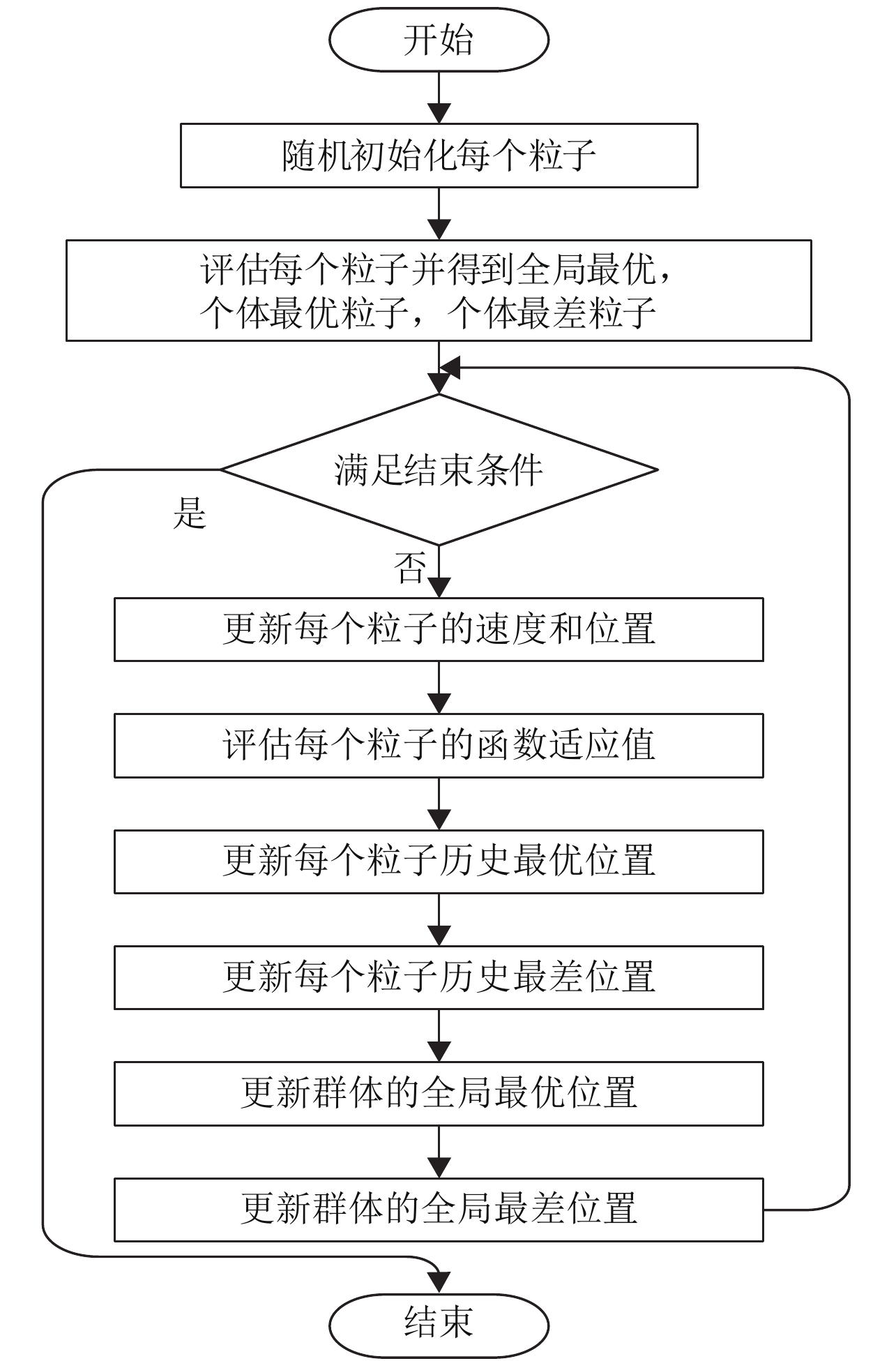
|
图 1 算法流程图 Figure 1 Flow diagram of algorithm |
(1) 按种群规模初始化粒子位置和速度,用目标函数计算粒子的适应度值,将个体的历史最优(Pbest)和历史最差(Pworst)设为当前位置,种群中最优个体位置作为当前全局最优(Gbest).
(2) 按照式(3)进行粒子位置和速度更新,然后计算粒子的适应度值.
(3) 如果该粒子当前的适应度值优于历史最优值,那么历史最优被当前值取代.
(4) 如果该粒子当前的适应度值优于全局最优值,那么全局最优被当前值取代.
(5) 如果该粒子当前的适应度值差于历史最差值,那么历史最差被当前值取代.
(6) 如果满足结束条件,则结束并输出Gbest;否则转至(2).
3 仿真实验及分析 3.1 测试函数测试函数如表1所示.
| 表 1 测试函数 Table 1 Test Functions |
为了验证本文算法的有效性,和惯性权重w线性改变的粒子群算法[3]基于上述测试函数进行仿真实验比较. 图2~7中LWPSO是本文算法,PSO是惯性权重w线性减少,c1、c2=2的粒子群算法[3]. popsize取20,维度为30,最大迭代次数为100. 测试采用MATLAB 2013a版本,CPU为E5200,频率2.5 GHz,测试环境Win10下进行,以下为测试结果.
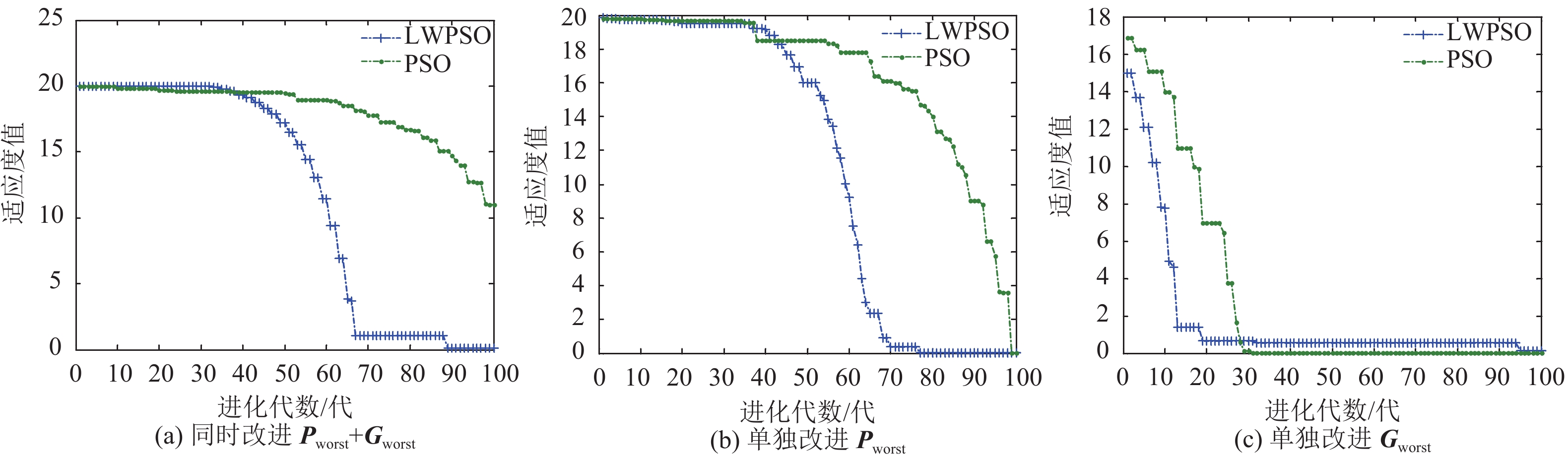
|
图 2 Ackley函数优化曲线 Figure 2 Convergence curves of Ackley function |
Ackley函数测试结果:粒子更新公式单独改进Pworst和二者同时改进之后效果明显,收敛速度有所提高;而单独改进Gworst的影响反而效果不好或和原有算法差不多.
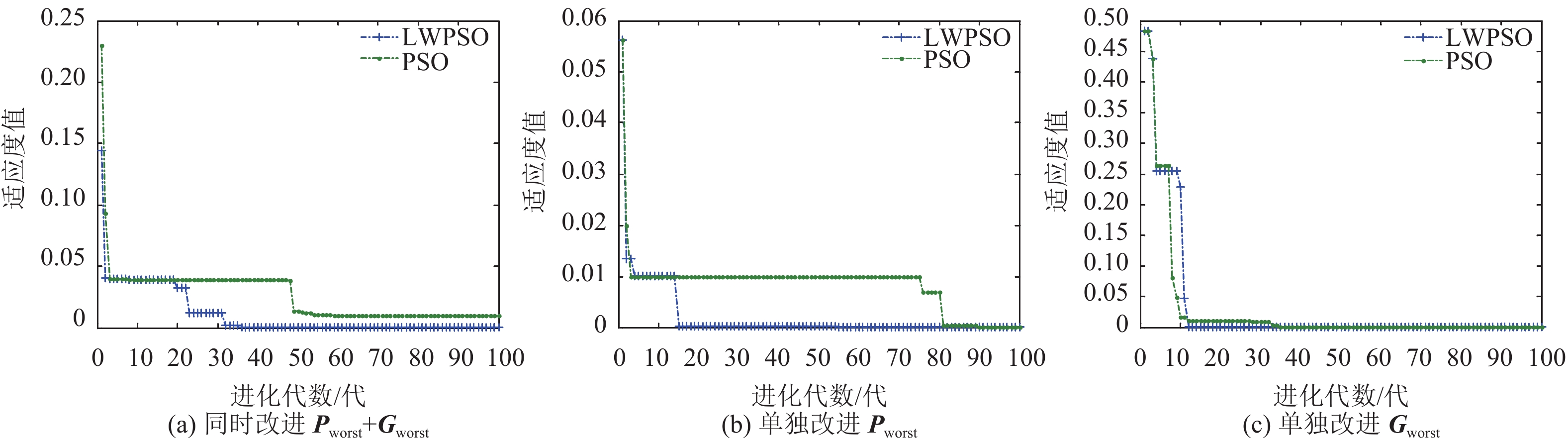
|
图 3 Griewank函数优化曲线 Figure 3 Convergence curves of Griewank function |
Griewank函数测试结果:Griewank函数的测试结果都不错,Pworst和Gworst都同时改进的效果比初值相同的PSO效果较好;而单独改进了Gworst虽然最后达到最优,但是不如PSO速度快;单独改进了Pworst的效果很明显,能够更快速的收敛.
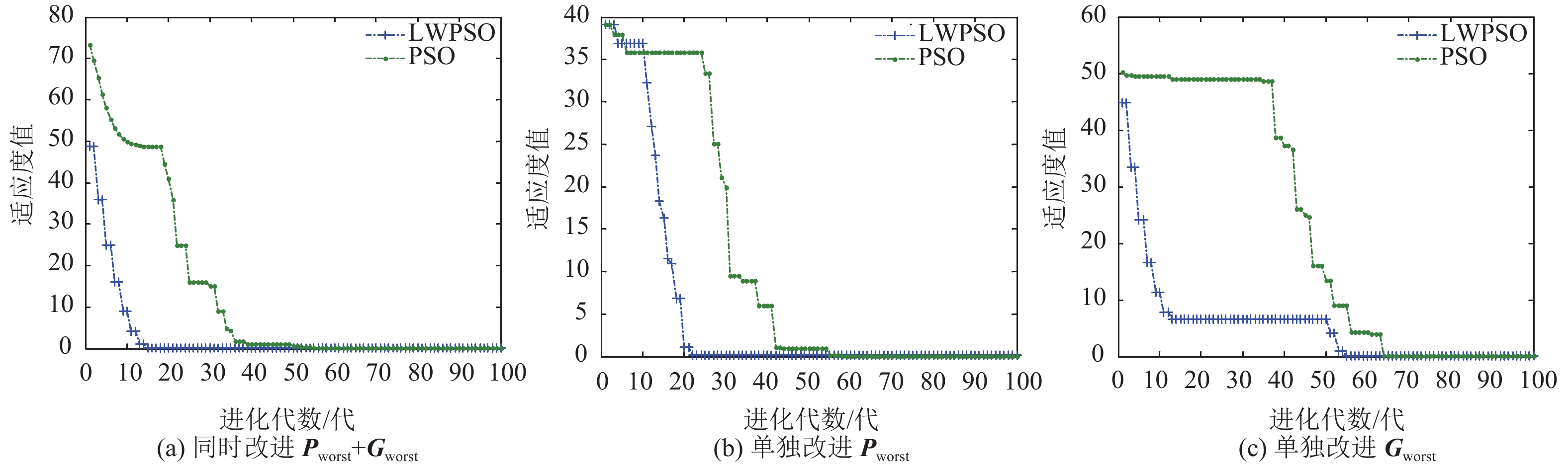
|
图 4 Rastrigin函数优化曲线 Figure 4 Convergence curves of Rastrigin function |
Rastrigin函数测试结果:3种改进效果均比较理想,其中同时改进和单独改进Pworst效果最好,收敛速度较快.
|
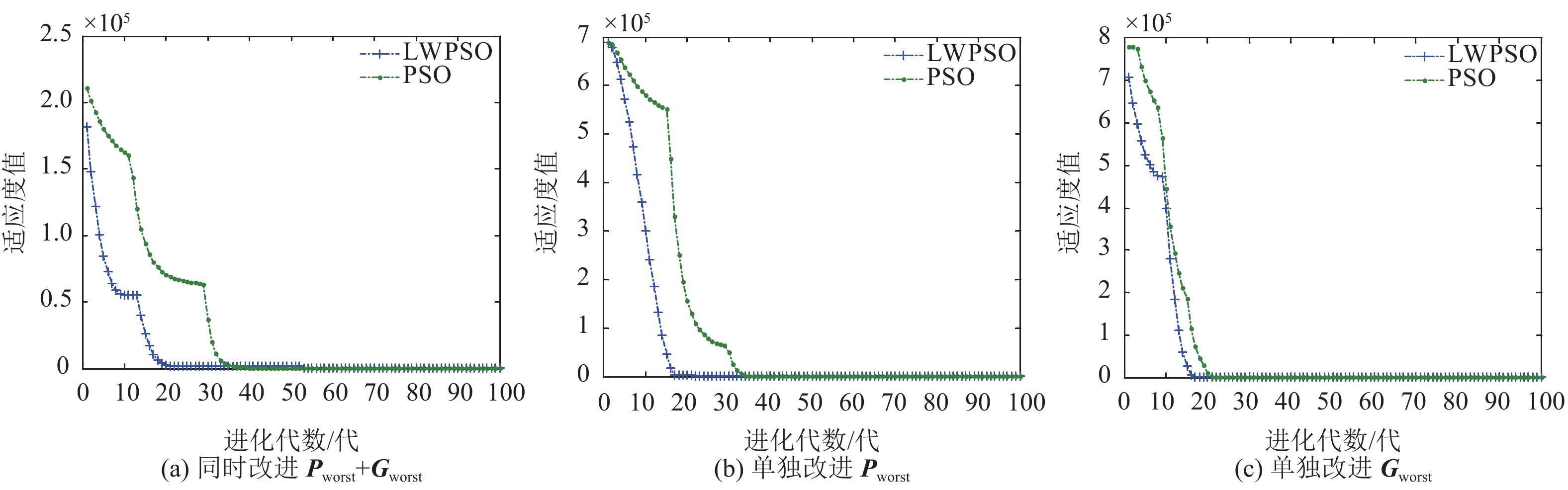
图 5 Rosenbrock函数优化曲线 Figure 5 Convergence curves of Rosenbrock function |
Rosenbrock函数测试结果:3种改进之后的收敛速度均有所提高,其中二者同时改进和单独改进Pworst效果更好.
|
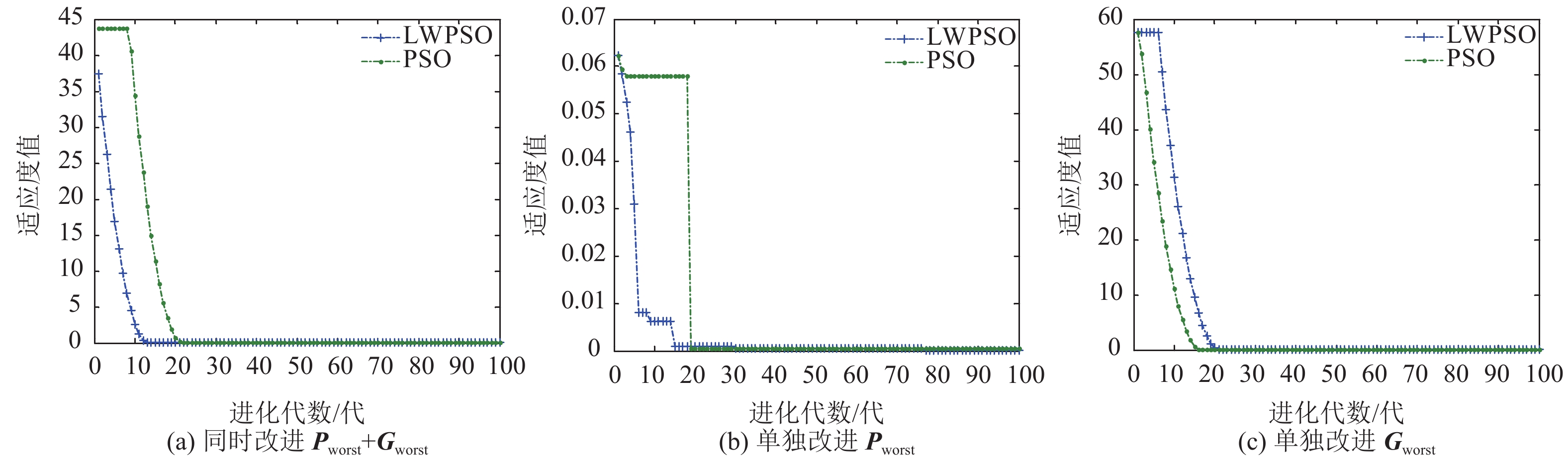
图 6 Sphere函数优化曲线 Figure 6 Convergence curves of Sphere function |
Sphere函数测试结果:二者同时改进和单独改进Pworst之后的收敛速度有所提高,而单独改进Gworst之后的收敛速度有所下降.

|
图 7 Matyas函数优化曲线 Figure 7 Convergence curves of Matyas function |
Matyas函数测试结果:可以看出PSO有时易陷入局部最优,但3种改进之后的算法均能到达最优值,其中单独改进Pworst的效果最好,收敛速度最快.
综上,单独改进Pworst的LWPSO在各个函数的表现都很出色,收敛速度均有所提高,算法改进的有效性得到验证.
表2为上述2种算法求解对应函数精度对比,算法分别独立运行30次取平均值(最大迭代次数为1 000,维度为30,种群规模20),加粗部分为精度高的算法. 从表2中可以看出,除了Sphere函数的精度2种算法差不多之外,其他函数的求解精度LWPSO均明显优于PSO.
| 表 2 函数最优值精度对比 Table 2 The accuracy comparison of functions optimization |
本文针对标准粒子群优化算法容易早熟收敛和易陷入局部最优的缺点,提出一种基于全局最差解(Gworst)和局部最差解(Pworst)的改进粒子群算法,并分别针对同时改进Gworst和Pworst、只改进Gworst、只改进Pworst进行仿真. 实验结果显示:Gworst改进之后的结果则和粒子群算法(本文的粒子群算法指的是惯性权重和学习因子改进之后的粒子群算法)效果差不多,二者同时改进和单独改进Pworst的效果较好,收敛速度和精度有所提高;其中单独改进Pworst的效果最好,在几个测试函数中都得到了体现. 如果把个体最优和全局最优对粒子的影响比喻成向量的形式,Pbest和Gbest影响之后的向量方向是趋向Gbest的. 当粒子群后期,Gbest无变化时,Pbest等于Gbest,这时速度靠拢方向向量为零,粒子前进的方向只有自身惯性,而我们加入了Pworst和Gworst之后的算法显然能够避免这一点. 在算法前期,远离Pworst和Gworst的方向向量相当于在趋向Gbest的方向的加速,所以收敛速度较快;算法后期当Gbest无变化时,Gworst和Pworst又能够使粒子的前进方向不仅受自身惯性的影响,而且可以继续的寻优,从而找到全局最优.
| [1] | KENNEDY J, EBERHART R C. Particle swarm optimization[J]. Proc IEEE Int Conf Neural Networks, 1995, 4(8): 1942-1948. |
| [2] | SCHMITT M, WANKA R. Particle swarm optimization almost surely finds local optima[J]. Theoretical Computer Science, 2014, 561: 57-72. |
| [3] | SHI Y, EBERHART R. Modified particle swarm optimizer [C]// IEEE International Conference on Evolutionary Computation Proceedings. Anchorage, Alaska, USA: IEEE Service Center. 1998: 69-73. |
| [4] |
赵志刚, 黄树运, 王伟倩. 基于随机惯性权重的简化粒子群优化算法[J].
计算机应用研究, 2014, 31(2): 361-363.
ZHAO Z G, HUANG S Y, WANG W Q. Simplified particle swarm optimization algorithm based on stochastic inertia weight[J]. Application Research of Computers, 2014, 31(2): 361-363. |
| [5] |
张选平, 杜玉平, 秦国强, 等. 一种动态改变惯性权的自适应粒子群算法[J].
西安交通大学学报, 2005, 39(10): 1039-1042.
ZHANG X P, DU Y P, QIN G Q, et al. Adaptive particle swarm algorithm with dynamically changing inertia weight[J]. Journal of Xi’an Jiaotong University, 2005, 39(10): 1039-1042. DOI: 10.3321/j.issn:0253-987X.2005.10.001. |
| [6] | RATNAWEERA A, HALGAMUGE S K, WATSON H C. Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 240-255. DOI: 10.1109/TEVC.2004.826071. |
| [7] | P N SUGANTHAN. Particle swarm optimizer with neighborhood operator [C]// Evolutionary Computation. Washington DC, US: Procc IEEE Congr Evol Comput. 1999: 1958-1962. |
| [8] |
任凤鸣, 李丽娟. 改进的PSO算法中学习因子(c1, c2)取值的实验与分析
[J].
广东工业大学学报, 2008, 25(1): 86-89.
REN F M, LI L J. Experiment and analysis of the value selection of acceleration coefficients (c1, c2) in PSO method [J]. Journal of Guangdong University of Technology, 2008, 25(1): 86-89. |
| [9] | KENNEDY J, MENDES R. Population structure and particle swarm performance [C]// Evolutionary Computation, CEC’02. Hawaii, US: Congress on Evolutionary Computation. 2002: 1671-1676. |
| [10] | KENNEDY J, MENDES R. Neighborhood topologies in fully informed and best-of-neighborhood particle swarms[J]. IEEE Transactions on Systems Man & Cybernetics Part C, 2006, 36(4): 515-519. |
| [11] |
马胜蓝, 叶东毅, 杨玲玲. 一种新的粒子群拓扑设计准则[J].
计算机工程, 2015, 41(1): 200-206.
MA S L, YE D Y, YANG L L. A new design criteria of particle swarm topology[J]. Computer Engineering, 2015, 41(1): 200-206. |
| [12] |
石松, 陈云. 层次环形拓扑结构的动态粒子群算法[J].
计算机工程与应用, 2013, 49(8): 1-5.
SHI S, CHEN Y. Dynamic particle swarm optimization algorithm with hierarchical ring topology[J]. Computer Engineering and Applications, 2013, 49(8): 1-5. |
| [13] |
方峻, 唐普英, 任诚. 一种基于加权有向拓扑的改进粒子群算法[J].
计算机技术与发展, 2006, 16(8): 62-65.
FANG J, TANG P Y, REN C. A modified particle swarm optimization based on directional weighting Topology[J]. Computer Technology and Development, 2006, 16(8): 62-65. |
| [14] | CHEN Y, PENG W C, JIAN M C. Particle swarm optimization with recombination and dynamic linkage discovery[J]. IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics A Publication of the IEEE Systems Man & Cybernetics Society, 2007, 37(6): 1460-1470. |
| [15] | ANDREWS P S. An investigation into mutation operators for particle swarm optimization [C]// Evolutionary Computation. Vancouver, Canada: IEEE Congress on Evolutionary Computation. 2006: 1044-1051. |
| [16] |
张创业, 莫愿斌. 基于协同进化思想的人工鱼和粒子群混合优化算法[J].
广西民族大学学报: 自然科学版, 2009, 15(1): 74-77.
ZHANG C Y, MO Y B. AFSA and PSO hybrid algorithm based on collaborative evolution[J]. Journal of Guangxi University for Nationalities (Natural Science Edition), 2009, 15(1): 74-77. |
| [17] |
周玉光, 曾碧, 叶林锋. 改进粒子群优化算法及其在4G网络基站选址中的应用[J].
广东工业大学学报, 2015, 32(2): 64-68.
ZHOU Y G, ZENG B, YE L F. Improved particle swarm optimization and its application in 4G network base station location[J]. Journal of Guangdong University of Technology, 2015, 32(2): 64-68. |
 2017, Vol. 34
2017, Vol. 34

