我国水资源非常丰富,国家根据各地水资源的特点陆续建立了多处梯级水电站以使水资源得到更加充分的利用. 流域梯级开发的日益推进,使得梯级水库群的优化调度问题受到越来越多的关注,其优化求解成为一个具有重要价值的研究课题. 梯级水库优化调度是一个强约束、非线性、多变量的复杂规划问题[1],需要考虑上下游水库之间的水力、电力联系以及处理各种约束问题[2],其中关键问题有两方面,一是建立水库优化调度的数学模型,二是选择求解该数学模型的最优化方法. 目前,梯级水库优化调度传统方法主要包括:线性规划[3]、非线性规划[4]和动态规划[5]等. 这些传统方法主要存在结果收敛不稳定、计算程度复杂以及无法避免“维数灾”等问题[6]. 而群智能算法譬如遗传算法(DE)[7]、免疫算法[8]、改进差分进化算法[9]和蚁群算法(ACO)[10-11]有容易实现、原理简单、搜索寻优能力强等优点,为梯级水库优化调度提供了新的方向和思路.
纵横交叉算法(CSO)是一种全新的群智能优化算法[12],由广东工业大学的孟安波副教授等人于2014年提出,创造性地引入横向交叉和纵向交叉两种算子,能较好地解决一般智能算法存在的局部最优问题[13-16].
本文以清江流域梯级电站为研究背景,建立水布垭—隔河岩联合梯级水库调度模型. 根据梯级水库的运行特点,引入惩罚项处理约束变量,应用纵横交叉算法(CSO)进行仿真计算. 将仿真结果与其他经典算法进行了对比,验证了纵横交叉算法(CSO)求解梯级水库优化调度问题上的高效性和适用性.
1 纵横交叉算法纵横交叉算法在整体流程框架上与粒子群算法相似,通过一系列的操作(主要有横向交叉、纵向交叉、竞争算子)来实现种群的迭代进化过程,最终求得最优解.
CSO的流程如下:
步骤1:初始化种群;
步骤2:执行横向交叉后进入竞争算子;
步骤3:执行纵向交叉后进入竞争算子;
步骤4:终止条件:如果达到设定的最大迭代次数,算法结束,否则转入步骤2.
下面分别介绍横向交叉、纵向交叉和竞争算子的具体操作流程. 为后文叙述简便,纵横交叉算法涉及的变量含义如表1所示.
| 表 1 纵横交叉算法参数及其含义 Table 1 Parameters and implications of CSO |
横向交叉是在种群中两个不同个体粒子的所有维之间进行一种算术交叉;假设父代个体粒子和的第d维进行横向交叉,则它们繁殖的子代粒子为
| $\begin{split}M{S_{hc}}(i,d) =\; &{r_1} \times X(i,d) + (1 - {r_1}) \times X(j,d) + \\ &{c_1} \times (X(i,d) - X(j,d)).\end{split}$ | (8) |
| $\begin{split}M{S_{hc}}(j,d) = \; &{r_2} \times X(j,d) + (1 - {r_2}) \times X(i,d) + \\& {c_2} \times (X(j,d) - X(i,d)).\end{split}$ | (9) |
其中,d=
横向交叉得到中庸解MShc,通过竞争机制与父代种群DSvc进行比较,适应度更好的粒子才会被保留下来,更新的结果保存在矩阵DShc中.
1.2 纵向交叉纵向交叉是在个体粒子不同维之间进行的一种算术交叉. 由于各维度代表的物理意义不尽相同,交叉前需对不同维之间进行归一化处理. 纵向交叉的结果只产生一个子代,目的是使陷入局部最优的维有机会摆脱出来且不破坏其他正常维. 使用交叉概率pv来控制当前种群参与纵向交叉的维的数量规模. 父代个体粒子通过式(3)将第d1维和第d2维进行纵向交叉产生第d1维后代.
| $\begin{split}M{S_{vc}}(i,{d_1}) = r \times X(i,{d_1}) + (1 - r) \times X(i,{d_2}),\\[3pt]\;\;\;\;\;\;\;\;i \in (1,M),{d_1},{d_2} \in (1,N).\end{split}$ | (10) |
其中,
在实际工程中,绝大部分群智能算法的局部最优问题往往是由于种群的某些维停滞不前,称之为维局部最优. 所以,纵横交叉算法的纵向交叉是通过种群中不同维进行算术交叉实现的,根据纵向交叉概率pv(通常取0.8)进行交叉操作不仅能使陷入停滞不前的维有机会摆脱出来,同时它的变异方式能较好地维持种群的多样性. 交叉后同样进入竞争机制,与其父代粒子进行比较,择优保留在DSvc中.
2 梯级水库优化调度模型梯级水库作为一个整体联合运行,具有库容、水文以及电力方面的补偿效益. 本文建立了梯级电站总发电量最大模型,已知年调度期内各水库初始水位、期望月末水位以及各区间内来水情况,综合考虑水位、下泄流量和出力等多种约束条件,确定水库群的水位最优运行轨迹,使得年调度期内梯级电站总发电量最大.
2.1 目标函数以年最大发电量为目标,建立梯级水电站年最大发电量的优化调度模型,其目标函数为
| $\max E = \sum\limits_{i = 1}^n {\sum\limits_{t = 1}^T {N_t^i} } \cdot \Delta t.$ | (1) |
式中,E为调度期内梯级总发电量;
梯级水库优化调度中的约束条件主要分为等式约束和不等式约束. 等式约束包括水量平衡约束和流量平衡约束;不等式约束包括出力约束、水位约束和下泄流量约束.
(1) 流量平衡约束:
| $V_{t + 1}^i = V_t^i + [I_t^i - Q_t^i - W_t^i] \times \Delta t.$ | (2) |
式中,
(2) 其他约束.
流量平衡约束:
| $I_t^{i + 1} = Q_t^i + q_t^i.$ | (3) |
下泄流量约束:
| $Q_{t\min }^i \leqslant Q_t^i \leqslant Q_{t\max }^i.$ | (4) |
水位上下限约束:
| $Z_{t\min }^i \leqslant Z_t^i \leqslant Z_{t\max }^i.$ | (5) |
电站出力约束:
| $N_{t\min }^i \leqslant N_t^i \leqslant N_{t\max }^i.$ | (6) |
水位边界约束:
| $Z_1^i = Z_b^i,Z_{m + 1}^i = Z_e^i.$ | (7) |
式中,
(1) 初始化策略.
设定种群大小为X,纵向交叉概率为pv,最大迭代次数为m代. 群搜索算法的初始种群会对算法迭代方向有一定的影响. 种群中的每个粒子表示一个解,第i个粒子可表示为
| $X(i) = [H_{i1}^a, \cdots ,H_{i{N_p}}^a,H_{i1}^b, \cdots ,H_{i{N_p}}^b].$ | (11) |
X(i)是一个一维向量,每一维表示水库群不同时段末的水库水位. 根据各个水库的正常水位、死水位以及汛限水位,设定每一维的上下限. 随机产生一个符合各维大小限制的初始种群.
(2) 约束机制和计算适应度.
采用适应度函数来识别每个粒子的优劣. 本文中梯级水库优化调度模型属于极大值优化问题,采用梯级电站总发电量的正值作为适应度值. 违背过机流量和出力约束的解属于不可行解,故当水电机组的出力越限时,引入惩罚项(
| ${\rm{fit}} = \sum\limits_{i = 1}^n {\sum\limits_{t = 1}^T {\left[ {N_t^i + \delta \cdot \left( {N_t^i - {N_{\max }}} \right) \cdot {N_{{\rm{penish}}}}}. \right]} } \cdot \Delta t.$ | (12) |
其中
| $\delta = \left\{ \begin{array}{l}1,N_t^i > {N_{\max }},\\[6pt]0,0 \leqslant N_t^i \leqslant {N_{\max }}.\end{array} \right.$ | (13) |
式中,
计算种群每个粒子的适应度,适应度最好的粒子,记作gbest.
(3) 横向交叉.
设X(i)和X(j)两个粒子配对,依式(1)和式(2)产生两个中庸解
(4) 纵向交叉.
设粒子
(5) 保存全局最优.
计算新种群每个粒子的适应度,保留适应度最好的粒子,记作gbest. 判断是否达到最大迭代次数m,若没有则进行步骤(2),继续迭代;若达到最大迭代次数,则输出gbest,得到最终优化结果.
计算流程图如图1所示.
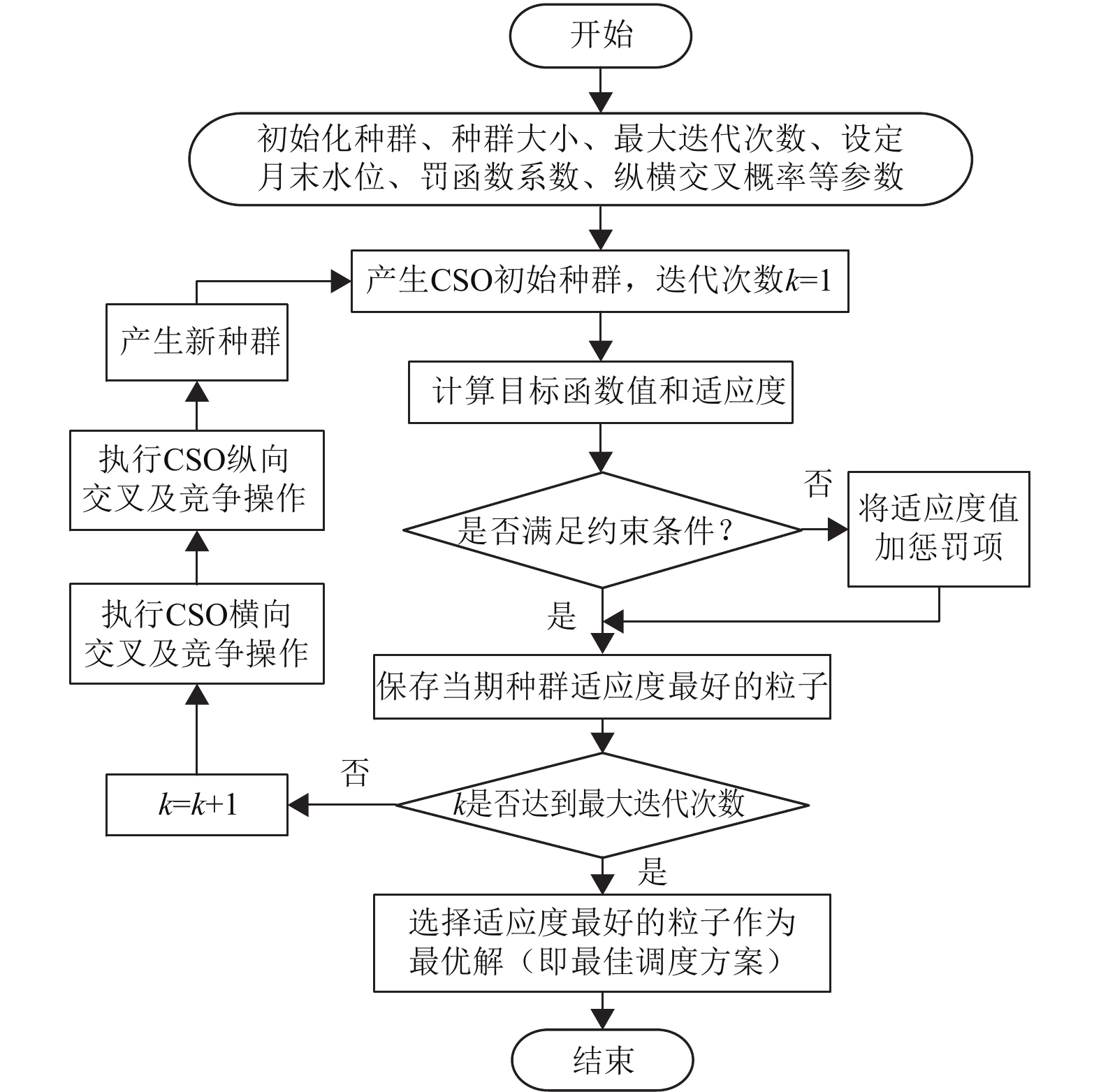
|
图 1 CSO算法流程示意图 Figure 1 Flowchart of the CSO algorithm |
以清江流域两座主要水库的长期优化调度为例对本文算法进行验证,采用该流域典型年资料进行计算仿真. 清江是三峡以下长江中游第二大支流,干流全长423 km,流域面积1.7万km2,总落差1 430 m, 水力资源丰富,可开发装机330万kW,开发电能105亿kW·h. 清江干流自上而下采用水布垭—隔河岩—高坝洲的三级梯级开发方案,其中水布垭为多年调节,隔河岩为年调节,高坝洲为日调节,形成以发电为主,兼顾防洪、航运的梯级水利枢纽工程.
本文选取水布垭-隔河岩梯级调度模型进行仿真计算. 水布垭水库位于隔河岩水库的上游,清江梯级调度期为每年5月至次年4月,主汛期为7月和8月. 水布垭、隔河岩水电站水库参数见表2.
| 表 2 水布垭、隔河岩水电站水库参数 Table 2 Parameters setting for hydropower plants Shuibuya and Geheyan |
采用CSO算法对调度模型进行求解,采用该流域典型年径流量资料进行计算. 算法参数设定如下:种群粒子数量为50;最大迭代次数为300;横向交叉和纵向交叉的概率分别为1、0.8. 其中,CSO算法中只需设置一个参数pv(纵向交叉概率), pv通过试算选取最适值,区间取值范围为[0.1,0.9],如图2所示,在不同pv下各运行CSO实验程序20次,取平均值作比较,确定本算例中纵向交叉概率的最佳参数为0.8. 鉴于CSO、PSO、EM、GA均属于随机搜索算法,为减少随机性对结果的影响,将各算法程序独立运行50次,取总发电量平均值进行对比.
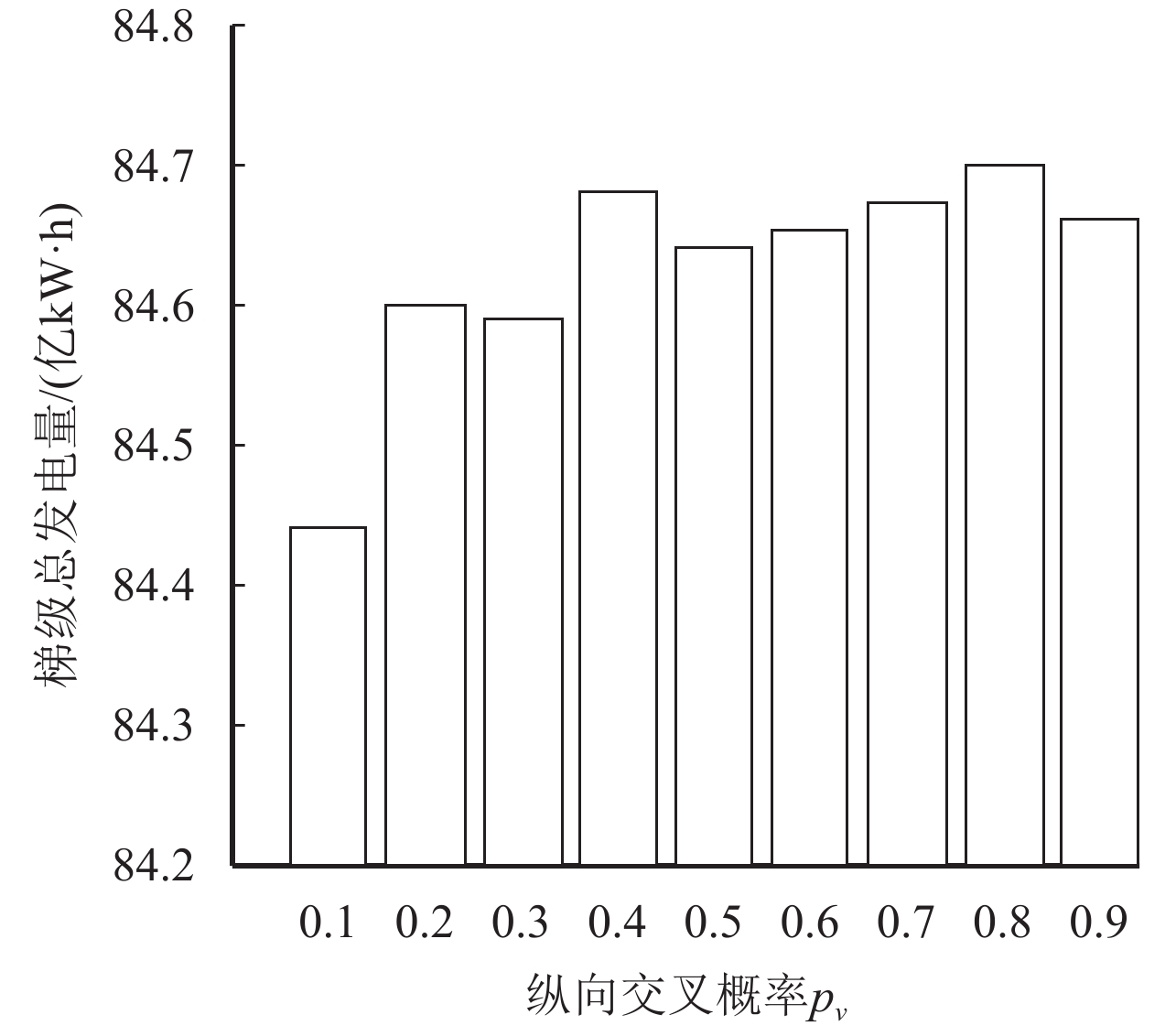
|
图 2 CSO不同pv值时的最优值 Figure 2 The optimal value with different pv by CSO algorithm |
由表3可以看出,经CSO算法优化后的梯级电站总发电量平均值为84.71亿kW·h,相较于PSO算法、EM算法和GA算法,分别提高了3.87%、5.64%和8.34%. 对比寻优时间,CSO寻优时间比PSO略长, 优于EM和GA. 对比寻优相对时间,即CSO算法在取得GA, EM, PSO各算法总发电量平均值时所用的时间,分别只用了1.97 s、2.26 s和2.74 s, 显示出CSO极快的寻优收敛速度.
| 表 3 不同算法优化总发电量对比 Table 3 Total generation obtained by different methods |
从算法优化结果稳定来看,CSO优化结果的标准差为0.21,远低于另外3种算法.
如图3所示,在迭代300次后,CSO某单次运行结果中50个种群最优结果的标准差为0.02,大部分种群最优结果处于平均值和最大值之间. 结合表3,对比显示出CSO极强的寻优稳定性. CSO优化总发电量最大,稳定性最强,在寻优时间相仿的情况下具有很强的竞争力.
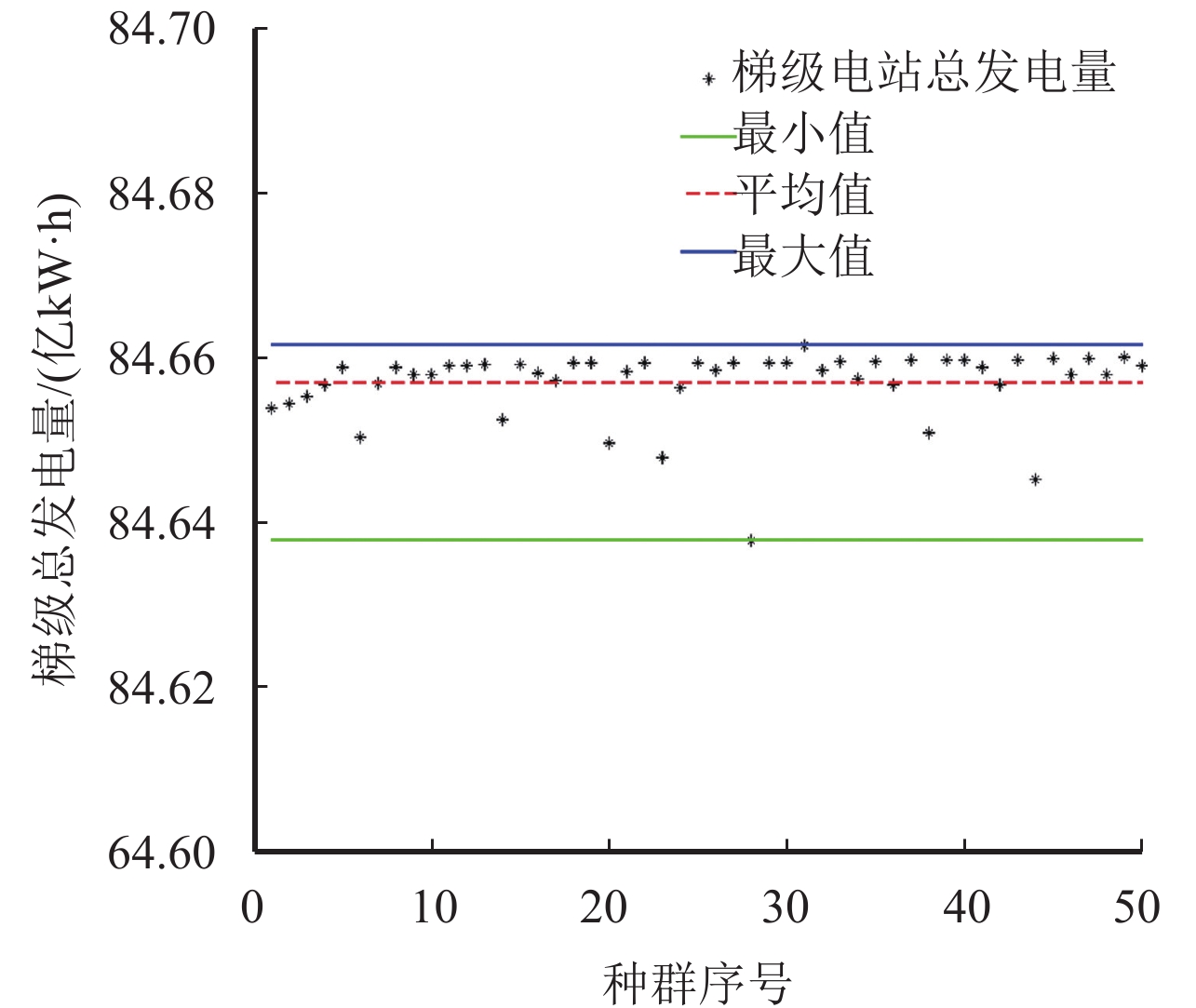
|
图 3 单次运行种群最优结果散点图 Figure 3 Total generation obtained by different populations |
为取得更好的寻优结果,智能算法一般通过增加迭代次数或增大种群规模的方式来实现,但弊端是导致计算机占用内存过多以及寻优时间的延长. 算法搜索的高效性体现在可以在小的种群规模下经过一定的迭代次数即可收敛到全局最优解. 设定不同的种群规模进行优化计算,来进一步展现CSO搜索能力的高效性.
由图4可以看出,在种群规模越大的情况下,CSO算法收敛越快. 在迭代到1 000次时,不同种群规模下的收敛值非常接近. 表明CSO在小的种群规模下通过一定的迭代次数就可以得到优异的收敛结果. 表3的结果中,在种群规模为50,迭代次数为300次的情况下,GA、EM、PSO优化得到的最大发电值分别为79.30亿kW·h、82.31亿kW·h以及82.86亿kW·h,而CSO在同等情况下的最大优化值达到85.04亿kW·h,这表明GA、EM、PSO在不同程度上陷入了局部最优解,而CSO则可以有效地从局部最优解中摆脱出来顺利收敛到全局最优解或准全局最优解. 这种优异的表现得益于CSO算法中的纵向交叉机制,它能使陷入局部最优的维有机会摆脱出来,并且通过它的变异方式维持了种群的多样性,进而使整个种群迅速摆脱了局部最优解.
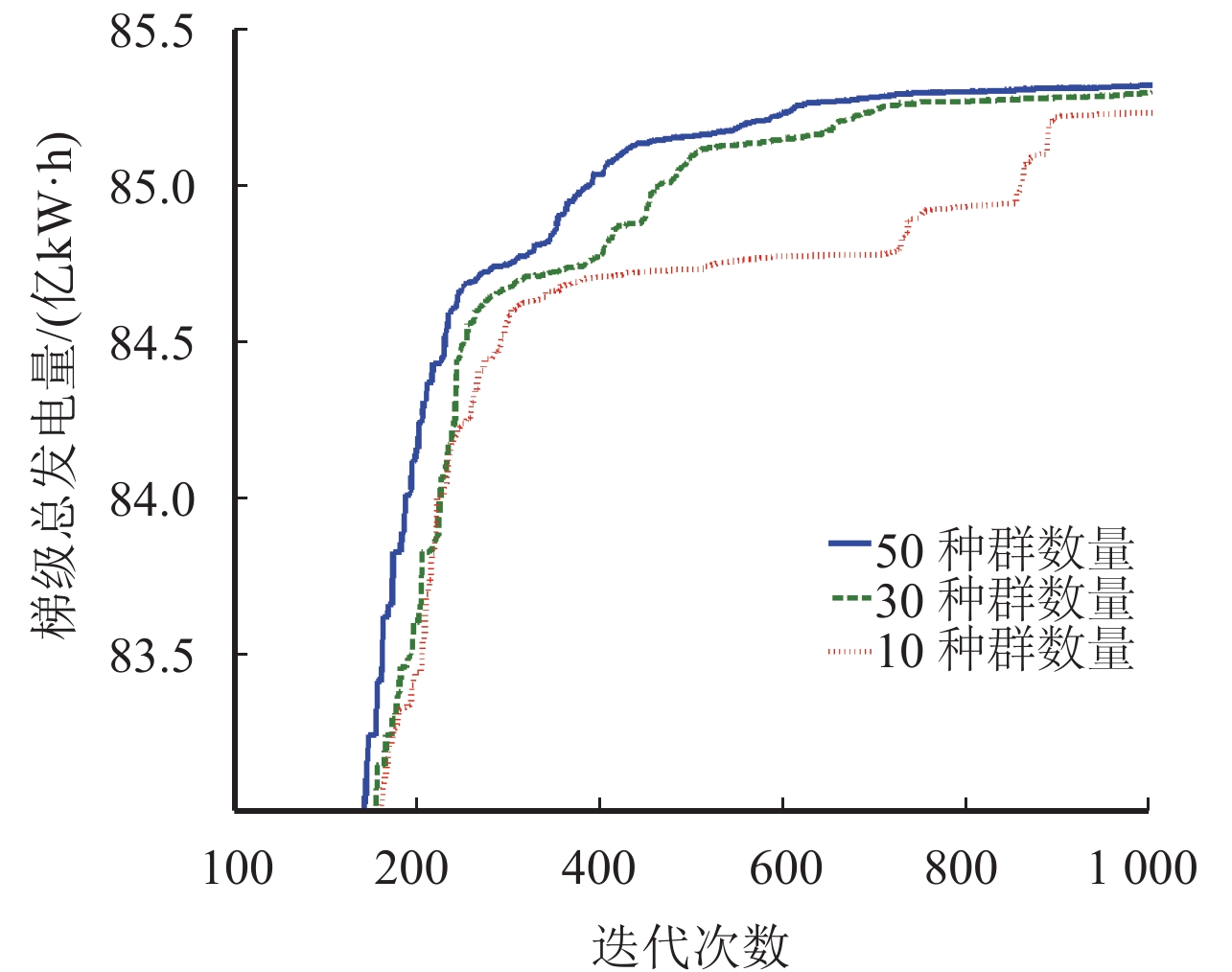
|
图 4 CSO不同种群规模收敛图 Figure 4 Total generation obtained by different populations |
由表4可以看到,CSO调度结果满足梯级电站群的各项约束条件,水布垭水库(多年调节型)在蓄水期抬高水位充分蓄水,枯水期水位逐渐回落进行补偿以满足梯级最小出力需求;隔河岩水库(年调节型)汛前降低水位,汛后逐渐抬高至最高水位,保持高水头发电运行以增加梯级总发电量. 同时在该典型年资料下无弃水产生,做到了对水力资源的充分利用. 调度结果可靠、合理,表明CSO算法在梯级水库调度中具有可行性和适用性.
| 表 4 CSO单次调度结果 Table 4 One scheduling result optimized by CSO |
本文针对梯级水库优化调度的求解问题,给出了满足水库运行的各项约束条件以及引入惩罚项的优化调度模型,结合纵横交叉算法进行了实例计算,得出该梯级水库年调度的最优调度方案. 作为一种新颖的群智能算法,纵横交叉算法只有纵向交叉一个设置参数,同时具有寻优结果稳定、搜索能力高效等优点. 实验结果验证了其在水库优化调度中的有效性和实用性,为梯级水库优化调度提供了一条新的途径. 本文仅对纵横交叉算法应用于梯级水库优化调度做了初步的探讨和验证,完善其搜索机制并将其高效的搜索机制运用于水库多目标优化调度将作为下一步的研究方向.
| [1] |
郭生练, 陈炯宏, 刘攀, 等. 水库群联合优化调度研究进展与展望[J].
水科学进展, 2010(4): 496-503.
GUO S L, CHEN J H, LIU P, et al. State-of-the-art review of joint operation for multi-reservoir systems[J]. Advances in Water Science, 2010(4): 496-503. |
| [2] |
明波, 黄强, 王义民, 等. 基于改进布谷鸟算法的梯级水库优化调度研究[J].
水利学报, 2015(3): 341-349.
MING B, HUANG Q, WANG Y M, et al. Cascade reservoir operation optimization based-on improved cuckoo search[J]. Journal of Hydraulic Engineering, 2015(3): 341-349. |
| [3] |
吴杰康, 郭壮志, 秦砺寒, 等. 基于连续线性规划的梯级水电站优化调度[J].
电网技术, 2009(08): 24-29.
WU J K, GUO Z Z, QIN L H, et al. Successive linear programming based optimal scheduling of cascade hydropower station[J]. Power System Technology, 2009(08): 24-29. |
| [4] | MAHMOUD M, DUTTON K, DENMAN M. Design and simu- lation of a nonlinear fuzzy controller for a hydropower plant[J]. Electric Power Systems Research, 2005, 73(2): 87-99. DOI: 10.1016/j.epsr.2004.05.006. |
| [5] |
冯仲恺, 廖胜利, 牛文静, 等. 梯级水电站群中长期优化调度的正交离散微分动态规划方法[J].
中国电机工程学报, 2015(18): 4635-4644.
FENG Z K, LIAO S L, NIU W J, et al. Orthogonal discrete differential dynamic programming for mid-long term optimal operation of cascade hydropower system[J]. Proceedings of the CSEE, 2015(18): 4635-4644. |
| [6] |
冯仲恺, 廖胜利, 程春田, 等. 库群长期优化调度的正交逐步优化算[J].
水利学报, 2014(08): 903-911.
FENG Z K, LIAO S L, CHENG C T, et al. Orthogonal progressive optimality algorithm for long-term optimal operation of multi-reservoir system[J]. Journal of Hydraulic Engineering, 2014(08): 903-911. |
| [7] |
李梅, 梁慧冰. 遗传算法在供水系统优化调度中的应用[J].
广东工业大学学报, 2000, 17(1): 33-36.
LI M, LIANG H B. The application of genetic algorithm to the optimal dispatch of water supply system[J]. Journal of Guangdong University of Technology, 2000, 17(1): 33-36. |
| [8] | LI A, WANG L, LI J, et al. Application of immune algorithm-based particle swarm optimization for optimized load distribution among cascade hydropower stations[J]. Computers & Mathematics with Applications, 2009, 57(6): 1785-1791. |
| [9] |
郑慧涛, 梅亚东, 胡挺, 等. 改进差分进化算法在梯级水库优化调度中的应用[J].
武汉大学学报(工学版), 2013, 46(1): 57-61.
ZHENG H T, MEI Y D, HU T, et al. Improved differential evolution algorithm and its application to optimal operation of cascade reservoirs[J]. Engineering Journal of Wuhan University, 2013, 46(1): 57-61. |
| [10] |
白涛, 黄强. 蜂群遗传算法及在水库群优化调度中的应用[J].
水电自动化与大坝监测, 2009(1): 1-4.
BAI T, HUANG Q. Bee-swarm genetic algorithm and its application in optimal operation of group reservoirs[J]. Hydropower Automation and Dam Monitoring, 2009(1): 1-4. |
| [11] |
师凯, 蔡延光, 邹谷山, 等. 分段蚁群算法在运输调度问题中的应用[J].
广东工业大学学报, 2006, 23(01): 71-76.
SHI K, CAI Y G, ZOU G S, et al. Application of subsection ant colony algorithm to vehicle routing problems[J]. Journal of Guangdong University of Technology, 2006, 23(01): 71-76. DOI: 10.3969/j.issn.1007-7162.2006.01.015. |
| [12] | MENG A B, CHEN Y, YIN H, et al. Crisscross optimization algorithm and its application[J]. Knowledge-based Systems, 2014, 67: 218-229. DOI: 10.1016/j.knosys.2014.05.004. |
| [13] | MENG A B, HU H W, YIN H, et al. Crisscross optimization algorithm for large-scale dynamic economic dispatch problem with valve-point effects[J]. Energy, 2015, 93(2): 2175-2190. |
| [14] | MENG A B, LI Z, YIN H, et al. Accelerating particle swarm optimization using crisscross search[J]. Information Sciences, 2016, 329: 52-72. DOI: 10.1016/j.ins.2015.08.018. |
| [15] |
彭显刚, 林利祥, 刘艺, 等. 基于纵横交叉-拉丁超立方采样蒙特卡洛模拟法的分布式电源优化配置[J].
中国电机工程学报, 2015(16): 4077-4085.
PENG X G, LIN L X, LIU Y, et al. Optimal distributed generator allocation method based on correlation latin hypercube sampling monte carlo simulation embedded crisscross optimization algorithm[J]. Proceedings of the CSEE, 2015(16): 4077-4085. |
| [16] |
孟安波, 卢海明, 胡函武, 等. 混合小波包与纵横交叉算法的风电预测神经网络模型[J].
太阳能学报, 2015(7): 1645-1651.
MENG A B, LU H M, HU H W, et al. Hybrid wavelet packet-CSO-ENN approach for short-term wind power forecasting[J]. Acta Energiae Solaris Sinica, 2015(7): 1645-1651. |
 2017, Vol. 34
2017, Vol. 34
