最近几年，我国网络购物保持着迅猛发展的势头. 2016年8月CNNIC发出报告，称中国网民规模已达7.10 亿，其中网购用户有4.47 亿^[1]；在2016年上半年的全国社会消费品零售总额中，网上零售额22 367 亿元，同比增长28.2%. 由此可见，网络购物已成为网民购物的重要渠道. 然而，假冒伪劣现象一直在制约着网购的进一步发展，根据国家网络监管司发布的2014年下半年网络交易商品监测结果显示，抽查了淘宝网、京东商城、天猫等平台共92个批次的样品采样，正品率却仅有58.7%. 同时，中新网联合数字100市场研究公司发起的调查显示，超过60%的受访者表示网购过假货. 在电商售假原因方面，41.4%的受访者认为是电商平台监管不严导致假货泛滥.

然而，目前学术上关于网购市场中假冒伪劣现象的研究并不多. 张理智^[2]认为，导致假冒伪劣产品泛滥的原因，是市场经济中理性经济人追求利益最大化；Henry Stewart^[3]认为网络购物平台电子化、虚拟化、自动化、开放性等特性为假货销售提供了一个最理想的平台；杜宏^[4]提出制约我国电子商务健康发展的主要障碍是商家的诚信问题，应该通过健全法律法规、加大惩罚力度以及提高失信成本等宏观手段去建立并完善电子商务的诚信体系；徐琳^[5]运用4个博弈模型来说明在不同情况下欺诈行为产生的原因，认为商家的不良行为会导致网络市场的萎缩，进而危及到整个行业的利益.

上述文献对假冒伪劣现象的原因等方面有所研究，但存在以下不足：一是站在理性人角度，忽视了网购市场主体的价值感受；二是孤立考虑单个市场主体的收益与成本，忽视了主体之间的利益相关性；三是在解决问题方面一般以惩罚为主，较少考虑适当的奖金激励；四是已有文献主要从道德角度来进行定性分析，较少定量分析电商平台与其他市场主体之间进行策略交换的行为规律. 因此，本文用累积前景理论改进了演化博弈方法，构建出电商平台和线上商家的收益感知矩阵；进而考虑电商平台与线上商家之间利益相关性，探讨正面奖励对线上商家的销售行为的具体影响和适用条件.

1 概念界定 1.1 累积前景理论概念

研究表明，在不确定的情况下人们的决策行为通常是有限理性的，Tversky和Kahneman在Quiggin^[6]的研究上进行拓展，提出了“累积前景理论”^[7]. 比起前景理论，新理论的优势在于：(1) 预先设置参照点. 人们在决策时会根据此参照点来衡量得失. (2) 风险偏好. 在收益时人们倾向于风险厌恶，反之人们倾向于风险追求^[8-9]. 决策权重函数 $\pi \left( {{p_i}} \right)$ 及价值函数 $v\left( {\Delta x} \right)$ 如下：

$\pi \left( p \right) = \frac{{{p^r}}}{{{{\left[ {{p^r} + {{\left( {1 - p} \right)}^r}} \right]}^{\frac{1}{r}}}}},$

(1)

$v\left( {\Delta x} \right) = \left\{ \begin{array}{l}{(\Delta x)^\alpha },\Delta x \geqslant 0,\\ - \lambda {\left( { - \Delta x} \right)^\beta },\Delta x < 0,\end{array} \right.$

(2)

其中，在决策函数中，p_i表示事件i发生的概率；决策权重 $\pi \left( {{p_i}} \right)$ 为主观概率p_i的函数，具有 $0 \leqslant \pi ({{\rm{p}}_i}) \leqslant 1$ 的特征； $r \in (0,1)$ ，r越小函数越弯曲.

在价值函数中， $\Delta {x_i}$ 为事件i发生后所得的实际收益与参照点(x₀)的差，即 $\Delta {x_i}{\rm{ \;=\; }}{x_i} - {x_0}$ . α，β( $\alpha ,\beta \in $ $\left( {0,1} \right)$ )为风险偏好系数. λ表示损失规避系数，λ $\geqslant$ 1则代表博弈主体对损失更加敏感.

1.2 演化博弈论

演化博弈论最初产生于生物学领域，然后被引入经济学领域. 它将生物体视为有限理性的当局者，在相互竞争的同时完成自身的演化^[10]. John Maynard Smith^[11-12]等提出演化稳定策略(Evolutionary Stable Strategy, ESS)之后，不同领域的学者对之进行了广泛的研究以及应用，多被使用于供应链的研究，如从政府补贴背景下研究制造商与供应商R&D合作与竞争策略选择的演化博弈^[13]，这些研究都使得理论体系日益完善.

电商平台与线上商家的过程也可以看做一个演化博弈. 一方面，线上商家根据电商平台的规定等采取相应的行动，决定是否在该电商平台诚信销售；另一方面，电商平台根据线上商家的行为、判断网络经济未来发展趋势等，对现有规定做出相应的调整.

2 模型假设 2.1 构建收益矩阵

在不考虑系统外部影响的情况下，线上商家通过自身和电商平台的反复博弈结果，来选择销售策略. 基于此，可以做如下前提假设：

假设1：博弈过程中只存在线上商家与电商平台，且均为有限理性，策略选择是基于他们对策略得失值的心理感受（即前景价值），而不是策略本身的直接利益得失. 本文中，前景价值V包含决策权重函数 $\pi \left( {{p_i}} \right)$ 和价值函数 $v\left( {\Delta x} \right)$ ，即 $V{\rm{ = }}\sum\limits_i {\pi \left( {{p_i}} \right)} {{v}}\left( {\Delta {x_i}} \right)$ .

假设2：线上商家具有典型的异质性，通常既追求个体利益又考虑社会利益. 将线上商家的销售策略设为{诚信销售A₁，违法销售A₂}，电商平台的策略集合为{积极监管B₁，消极监管B₂}. 设电商平台积极监管的实际成本为m>0，相应前景价值为M；线上商家诚信销售时需要耗费的实际成本为n>0，相应前景价值为N. 线上商家违法销售时，获取非法收益g>0，同时受到实际处罚额度为f₁>0，相应前景价值为F₁；采取违法行为时需要承担的名誉和经济等损失的风险总和为f₂>0，扣除g之后相应的前景值为F₂. 采取策略组合(A₂, B₂)的概率为p₂.

假设3：博弈双方承受的经济损失成本线性相关，当一方出现问题时，另一方需要承担连带责任. 当线上商家违法销售时，存在着商品安全等潜在的风险损失，进一步影响到电商平台，风险传递系数为U $\geqslant$ 0；当只有线上商家一方坚持采取诚信销售时，由于此时电商平台采取的策略是消极监管，电商平台的不监管加上其他商人受到自身利益的驱使，导致平台上存在着大量假冒伪劣商品，这会给采取A₁策略的线上商家以及电商平台自身带来损失，双方所承担的经济损失成传递系数为 ${Q_2} \in \left( {0,1} \right]$ ；只有电商平台积极监管时，双方所需要承担的经济损失传递系数 ${Q_1} \in \left( {0,1} \right]$ .

基于上述假设，构建博弈双方的收益矩阵如表1所示.

结合累积前景理论和上述假设，即可有以下分析：

(1) 当博弈双方策略组合为(A₁, B₁)时，此时诚信销售的概率p₁=1. 根据假设1可知，

$\begin{array}{l}{m} = \pi \left( {{p_1}} \right)v\left( m \right) + \pi \left( {1 - {p_1}} \right)v\left( 0 \right) = v\left( m \right);\\[4pt]{N} = \pi \left( {{p_1}} \right)v\left( n \right) + \pi \left( {1 - {p_1}} \right)v\left( 0 \right) = v\left( n \right).\end{array}$

(2) 当博弈双方策略组合为(A₂, B₂)时，线上商家的违法行为风险成本为F₂，电商平台需承担连带责任损失UF₂. 线上商家违法销售概率为p₂，故 ${{F}_2} = \pi \left( {{p_2}} \right)v\left( {{f_2} - g} \right)$ .

(3) 当博弈双方策略组合为(A₂, B₁)时，线上商家受到电商平台处罚F₁，以及承担违法行为带来的风险损失Q₁F₂；而电商平台需要承担积极监管成本M和被转嫁的连带责任损失UQ₁F₂. 设线上商家违法销售时被发现的实际概率为p₃，被发现后实际处罚为f₁，若没有被发现则处罚为0. 由假设l可知， ${{F}_2} \! = \! \pi \left( {{p_2}} \right)v\left( {{f_2} - g} \right) + \pi \left( {1 - {p_2}} \right)v\left( 0 \right) \! = \! \pi \left( {{p_2}} \right)v\left( {{f_2} - g} \right).$

(4) 当博弈双方策略组合为(A₁, B₂)时，线上商家需要付出实际成本N，并承担经济损失风险感知Q₂F₂；而电商平台需支付连带责任损失UQ₂F₂.

2.2 演化稳定策略

设：电商平台选择积极监管的比例是y，选择消极监管的比例是(1–y)；线上商家诚信销售的比例是x，选择违法销售的比例是(1–x).

电商平台选择“积极监管”行为的适应度

${U_m} = y \left( - {{M}} \right) + \left( 1 - y \right) \left( {{{F}}_1} - {{M}} - U{{Q}}_1 {{{F}}_2} \right),$

电商平台选择“消极监管”行为的适应度

${U'_m} = y( - U{{Q}}_2 {{F}_2}) + (1 - y)( - U {{F}_2}),$

则平均适应度为

${\overline U _m} = x{U_m} + (1 - x){U'_m}.$

根据Malthusian方程，电商平台采取积极监管策略时数量的增长率等于其适应度U_m减去平均适应度 ${\overline U _m}$ ，t为时间，可得复制动态方程为

$\begin{array}{l}\dot x = \frac{\displaystyle{{d_x}}}{{\displaystyle{d_t}}} = x({U_m} - {\bar U_m}) = x(1 - x)\left[ {{{F}_1} - {M} +} \right.\\[9pt]\left. {\left( {1 - {{Q}_1}} \right){U}{{F}_2} - {{F}_1}y + ({{Q}_1} + {{Q}_2} - 1){U}{{F}_2}y} \right].\end{array}$

同理，

$\begin{array}{l}\dot y = \frac{{\displaystyle{d_y}}}{{\displaystyle{d_t}}} = y({U_n} - {\bar U_n}) = y(1 - y)[{{{F}}_1}x + ({{{Q}}_1} + \\[9pt]{{{Q}}_2} - 1){{{F}}_2}{{x}} + {{{F}}_2} - {{N}} - {{{Q}}_2}{{{F}}_2}],\end{array}$

对应的雅克比矩阵为

${{J}} = \left( {\begin{array}{*{20}{c}}{\left( {1 \! - \! 2{x}} \right)\left[ {{{F}_1} \! - \! {M} \! + \! \left( {1 \! - \! {{Q}_1}} \right){{{U}}}{{F}_2} \! - \! {{F}_1}{y} \! + \! ({{Q}_1} \! + \! {{Q}_2} \! - \! 1){U}{{F}_2}{y}} \right]} \! & \! {{x}\left( {1 \! - \! {x}} \right)\left[ {({{Q}_1} + {{Q}_2} - 1){U}{{F}_2} - {{F}_1}} \right]}\\[8pt]{{y}\left( {1 - {y}} \right)\left[ {{{F}_1} + \left( {{{Q}_1} + {{Q}_2} - 1} \right){{F}_2}} \right]} \! & \! {\left( {1 \! - \! 2{y}} \right)\left[ {{{F}_1}{x} \! + \! \left( {{{Q}_1} \! + \! {{Q}_2} \! - \! 1} \right){{F}_2}{x} \! + \! {{F}_2} \! - \! {N} \! - \! {{Q}_2}{{F}_2}} \right]}\end{array}} \right).$

3 模型分析及结果 3.1 模型分析

根据表2，只有当行列式的符号呈现正且迹的符号呈现负时，所得到的平衡点才是稳定的，即演化稳定策略；若两者都为正，则这个点是不稳定的平衡点.

通过上面的分析，可以知道，在这4个点中，只有C(1, 1)是稳定的，此时满足这4个条件：

$\begin{array}{*{20}{c}} {{N} \leqslant {{F}_1} + {{Q}_1}{{F}_2},} & {{N} \leqslant {{F}_2} - {{Q}_2}{{F}_2}},\\ {{M} \leqslant {{F}_1} + (1 - {{Q}_1}){U}{{F}_2}.} & {{M} \leqslant {{Q}_2}{U}{{F}_2}.} \end{array}$

3.2 结果讨论

以上分析可知，当

$\begin{array}{*{20}{c}} {{N} \leqslant {{F}_1} + {{Q}_1}{{F}_2},} & {{N} \leqslant {{F}_2} - {{Q}_2}{{F}_2}},\\ {{M} \leqslant {{F}_1} + (1 - {{Q}_1}){U}{{F}_2},} & {{M} \leqslant {{Q}_2}{U}{{F}_2}}. \end{array}$

这4个条件同时满足时，即电商平台和线上商家均重视商品质量，系统达到最优程度. 事实上保证线上商家诚信销售只要满足 ${N} \leqslant {{F}_1} + {{Q}_1}{{F}_2}$ ， ${N} \leqslant {{F}_2} - {{Q}_2}{{F}_2}$ 这两个条件即可. 即，线上商家诚信销售所付出的成本要小于所感知到的处罚风险与在被积极监管条件下的风险之和，同时也要小于在电商平台消极监管的条件下，线上商家诚信销售给其自身带来的绩效.

然而，在现实中，系统往往难以达到最优点C(1, 1). 具体分析如下.

(1) 网络市场环境的影响. 电商平台集客能力强、辐射覆盖面广，2015年，淘宝集市店已有600多万个卖家. 面对过于庞大且充满不确定性的市场，电商平台难以做到不间断、不留死角的全面监控，因此，会出现电商平台监管积极时诚信销售、电商平台监管松懈时违法销售的现象，最终导致监管成本m增加和违法行为被发现的概率p₂降低，导致条件式不平衡.

(2) 消费者的需求刺激. 2006年，央视《东方时空》推出一项网络调查，在问题“如果你买过假名牌，是有意还是无意当中购买？”中，有24.42%的调查者选择了有意购买. 部分消费者的有意购假意愿及行为，不仅强化线上商家的造假动机，满足了商家的追逐超利润心理，还会增加线上商家的非法收益g，从而降低F₂，导致等式失去平衡.

(3) 侥幸心理的影响. 学者李海东定义侥幸心理：行为人明知自己的行为可能发生危害社会的结果，却寄希望于偶然不发生这种危害结果的一种心理状态^[14]. 这种心理导致了人们常常利用管理上的制度空缺来进行违法或者擦边的行为. 线上商家往往会低估违法行为被发现的概率和事故发生的概率，即 $\pi \left( {{p_2}} \right) < {p_2},\pi \left( {{p_3}} \right) < {p_3}$ ，这会导致上述条件式失去平衡.

(4) 认知超载与认知惰性的影响. 认知超载是指由于认知资源不足而导致决策效果不佳，认知惰性则制约认知资源从而导致决策质量降低^[15-16]. 由于这两种心理的存在，部分决策主体将违法带来的痛苦与平时生活中遭遇的普通罚款等痛苦归纳为一类，从而低估违法行为造成的损失，即 $v\left( {{f_2} - g} \right) < ({f_2} - g)$ .

(5) 行为经济学的前景理论认为，当损失确定时，有限理性的决策主体倾向于风险追求. 具体分析如表3所示.

综合以上因素，不良行为必然会在网购市场中不断发生.

4 讨论“奖金激励”造成的影响分析

目前，当发现线上商家的违法销售行为时，电商平台往往是以惩罚为主，如淘宝网的处理措施一般为扣分、限制买家行为、关闭店铺、公示警告和查封账户等. 但这并不能有效制止违法行为，线上商家会继续演变利用更先进的技术及手段来避免受到惩罚. 因此，本文从新的角度来寻找方法：电商平台除了严厉的监管惩罚，可以适当地加入奖金激励，激发商家诚信销售的积极性，促使人们自觉维护网络购物的秩序^[17].

4.1 引入“奖金激励”因子分析

在上述博弈模型的基础上引入奖金因子，这里主要是指电商平台给予生产或销售正品的商家的激励. 设奖金收入为t，参照点实际收入为t₀，违法行为收入为g，一旦被发现（概率为p₂）将按照每单位违法行为收入予以惩罚k. 惩罚k是伴随着违法行为而存在的心理、声誉等贴现损失的总和. 因此，违法行为发生后若未被发现实际收入为： ${T_1} = g + t - {t_0}$ ；被发现将会受到处罚，实际收入为： ${T_2} = t - {t_0} - kg$ . 结合累积前景理论，建立奖金激励机制下线上商家销售策略的模型为

$\begin{array}{l}{\rm{max}}V\left( g \right) = \pi \left( {1 - {p_2}} \right)v\left( {{T_1}} \right) + \pi \left( {{p_2}} \right)v({T_2}),\\[6pt]{\rm{s}}{\rm{.t}}{\rm{.}}\left\{ \begin{array}{l}V(g) \geqslant 0,\\g \geqslant 0.\end{array} \right.\end{array}$

(3)

设： ${T_1}\!\! -\!\! {T_2} \!\!=\! \left( {1 \!+ \!k} \right)g \!=\! \xi $ . 若使式子 $V\left( g \right)\! = \!\pi \left( {1 \!\!-\!\! {p_2}} \right)$ × $v\left( {{T_1}} \right) + \pi \left( {{p_2}} \right)v({T_2})$ 达到最优，可取全微分化简得

$\frac{{{\rm{d}}{T_1}}}{{{\rm{d}}{T_2}}} \! = \! - \! \frac{{\pi \left( {{p_2}} \right)v'\left( {{T_2}} \right)}}{{\pi \left( {1 \! - \! {p_2}} \right)v'\left( {{T_1}} \right)}} \! = \! - \! \frac{{\pi \left( {{p_2}} \right)v'\left( {{T_2}} \right)}}{{\pi \left( {1 \! - \! {p_2}} \right)v'\left( {{T_2} \! + \! \xi } \right)}} \! = \! K\left( {{T_2}} \right),$

所以

$\begin{array}{c}\! \! \displaystyle \frac{{{\rm{d}}K}}{{{\rm{d}}{T_2}}} \! \! = \! \! - \! \frac{{\pi \left( {{p_2}} \right)}}{{\pi \left( {1 - {p_2}} \right)}} \! \times \! \left[\!{- \! \frac{{v' \! \left( {{T_2} \! + \! \xi } \right)v'' \! \left( {{T_2}} \right) \! - \! v'' \! \left( {{T_2} \! + \! \xi } \right)v' \! \left( {{T_2}} \right)}}{{{{[v' \! \left( {{T_2} \! + \! \xi } \right)]}^2}}} \!} \right] \!\! = \! \! \! \\[10pt]\displaystyle \frac{{\pi \left( {{p_2}} \right)}}{{\pi \left( {1 - {p_2}} \right)}} \! \times \! \frac{{v'({T_2})}}{{v'({T_1})}} \! \times \! \left[ {\frac{{v''\left( {{T_1}} \right)}}{{v'\left( {{T_1}} \right)}} - \frac{{v''\left( {{T_2}} \right)}}{{v'\left( {{T_2}} \right)}}} \right].\end{array}$

设S(T) $=-\frac{\displaystyle{v''(T)}}{\displaystyle{v'(T)}}$ ，则S(T)为线上商家在收入水平为T时的绝对风险规避系数. 通常情况下，绝对风险规避系数越大，则将越趋向于风险回避.

因为 $\frac{\displaystyle{\pi \left( {{p_2}} \right)}}{\displaystyle{\pi \left( {1 - {p_2}} \right)}} \times \frac{\displaystyle{v'({T_2})}}{\displaystyle{v'({T_1})}} > 0$ ，因此， $\frac{{\displaystyle{\rm{d}}K}}{{\displaystyle{\rm{d}}{T_2}}}$ 的取值取决于 $S\left( {{T_2}} \right) - S({T_1})$ .

当 ${T_1} > {T_2} > 0$ 时， $S({T_2}) - S({T_1}) > 0$ ，则 $\frac{{\displaystyle{\rm{d}}K}}{{\displaystyle{\rm{d}}{T_2}}} > 0$ ，此时线上商家是风险爱好者. 随着奖金增加，线上商家将会设法谋取更多非法收益，奖金激励并不能有效地抑制商家的违法行为的发生.

当 ${T_1} > 0$ 、T₂ < 0时， $S({T_2}) - S({T_1}) < 0$ ，则 $\frac{{\displaystyle{\rm{d}}K}}{{\displaystyle{\rm{d}}{T_2}}} < 0$ ，线上商家是风险回避者. 随着奖金的增加，违法行为被发现时心理感知损失就越大，线上商家逐渐倾向于风险规避.

当 $0 > {T_1} > {T_2}$ 时， $S({T_2}) - S({T_1}) > 0$ ，则 $\frac{{\displaystyle{\rm{d}}K}}{{\displaystyle{\rm{d}}{T_2}}} > 0$ ，此时线上商家是风险爱好者，逐渐倾向于风险追求.

综上所述，当满足 ${T_1} > 0,{T_2} < 0$ 时，违法行为被发现时心理感知损失会随着奖金的增加而增加，线上商家倾向于诚信销售. 此时，电商平台应该采用奖金激励政策，促使更多的线上商家倾向于风险规避，减少违法行为的发生概率.

4.2 SD仿真检验结果 4.2.1 SD流图模型建立

结合上述分析，采用Vensim PLE Version 6.0建立电商平台监管的SD博弈模型如图1所示.

该模型主要由2个流位变量、2个流率变量、10个外部变量和4个中间变量构成. 2个流位变量用来表示电商平台积极监管的概率和线上商家诚信销售的概率；2个流率变量表示电商平台积极监管的变化率和诚信销售的线上商家的变化率；10个外部变量分别对应上述博弈支付矩阵中的参数，它们的假设值为：电商平台监管成本M和线上商家销售成本N均为1；线上商家违法销售时，受到实际处罚F₁为0.5，名誉等损失F₂为1；经济损失传递系数Q₁与Q₂分别为0.5和0.3；风险传递系数U和违法收益g均为1；惩罚系数k和奖金收入t均为2.

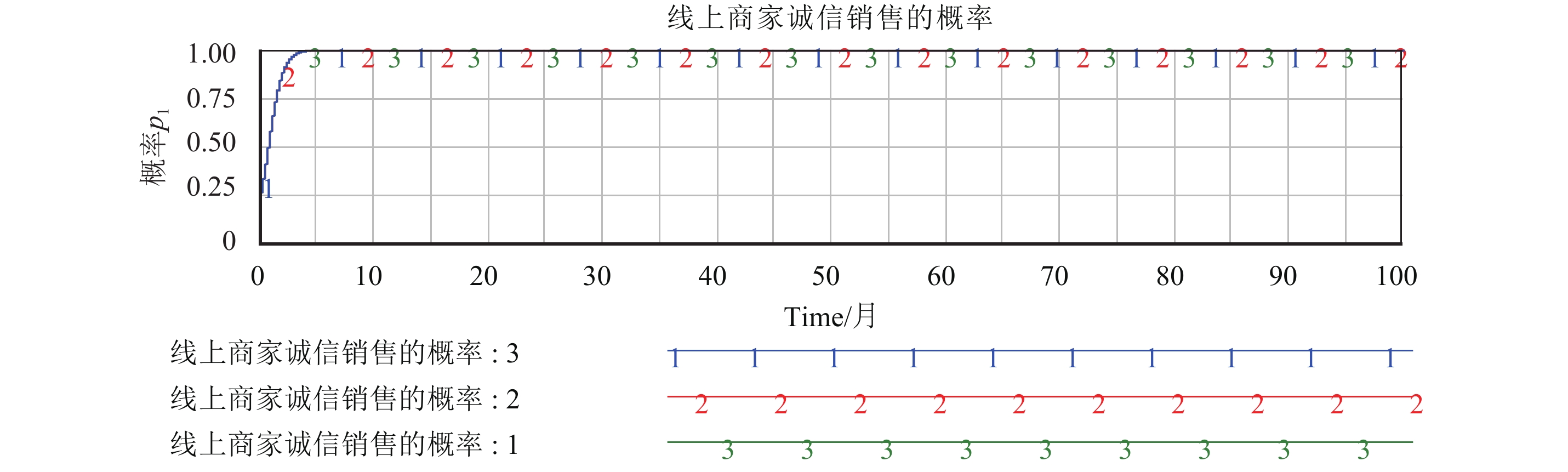
4.2.2 SD仿真分析奖金激励的变化对演化结果影响

模型初始值假设为：仿真起始时间INITIAL TIME=0，仿真结束时间FINAL TIME=100，仿真步长TIME STEP=0.007 812 5. 图2是当 ${T_1} > 0,{T_2} < 0$ 时，随着奖金收入的变化，线上商家诚信销售概率p₁的变化曲线.

图2中曲线l、2、3所表示含义分别是奖酬t=2、t=3、t=4时线上商家诚信销售的概率. 从图2中可以看出，随着奖金的增加，线上商家整体倾向于风险规避. 此时电商平台应该加大奖酬鼓励，更进一步地促进线上商家诚信销售.

SD仿真结果与建立的奖金变化对线上商家销售行为影响模型结果一致. 可见电商平台在适宜的时候( ${T_1} > 0,\; {T_2} < 0$ )，可以通过提高奖金来进一步促使线上商家诚信销售.

5 结论

本文主要研究结论如下：

(1) 经过累积前景理论改进的演化博弈方法，对有限理性人的博弈分析具有显著适用性，更好地体现了博弈主体在决策过程中存在的有限理性特点，也使得博弈现象和预测结果更合理.

(2) 4项条件在现实生活中难以得到满足，是因为博弈主体在决策过程中受到双重影响：一边受到侥幸、认知惰性等内部因素的影响，同时又受到网络市场的虚拟性、范围广等来自外部因素的影响. 这些都使得博弈双方倾向于低估处罚风险损失及违法风险损失，于是在面临损失时更容易风险追求，导致最优策略难以实现.

(3) 合理运用奖金激励以及惩罚进行双向控制，有助于网购健康发展. 本文提出由电商平台对线上商家进行奖金激励，可以发现，首先，奖金激励在一定条件下是可以适用的：当 ${T_1} > 0,{T_2} < 0$ 时，加大奖金力度可以有效激励线上商家诚信销售的积极性，更好地减少不良行为的发生. 然而，有时候还需要惩罚机制的配合：当 ${T_1} > {T_2} > 0$ 与 $0 > {T_1} > {T_2}$ 时，电商平台可以加大惩罚力度，加强销售过程的管理与外部监督，给线上商家心理上一个强有力的威慑效应，在合理的水平上抑制违法行为的发生. 最后，电商平台和线上商家必须充分认识到外界监督的重要性以及惩罚的严厉性，形成正确的诚信销售与惩罚成本的心理感知.