土体孔隙对土的工程性质有重大影响. 前人研究表明,土体结构(含孔隙)的形成过程与分形构造过程十分相似[1-3],由于分形具有自相似对称性,人们往往采用分维数来描述其特征,但对于不同类型问题其分维数定义有所不同,目前也并无通用的分维数定义来适合所有的分形结构.
本文基于Sierpinski模型对珠江三角洲地区软土ESEM图片进行微观结构分形研究,研究土体的微观孔隙大小、排列、形状以及分布等相关孔隙特征参数,形成一个能够综合反映土体孔隙微观结构变化的参数——孔隙结构影响因子,并通过大量实验数据揭示参数与土体宏观参数之间的联系,对工程实践具有一定的指导意义.
1 基于Sierpinski模型的软土孔隙分布分维在研究土孔隙微观结构的大量文献中,Sierpinski分形模型是采用较多的一种理论[4-6]. 该模型是一种类似于地毯图形的分形图形,其地毯空心面积为式(1)所示.
| $A({\delta _i}) = {N_i}\delta _i^2 = C\delta _i^{2 -D},$ | (1) |
式(1)中,D为分维数,C为常数.
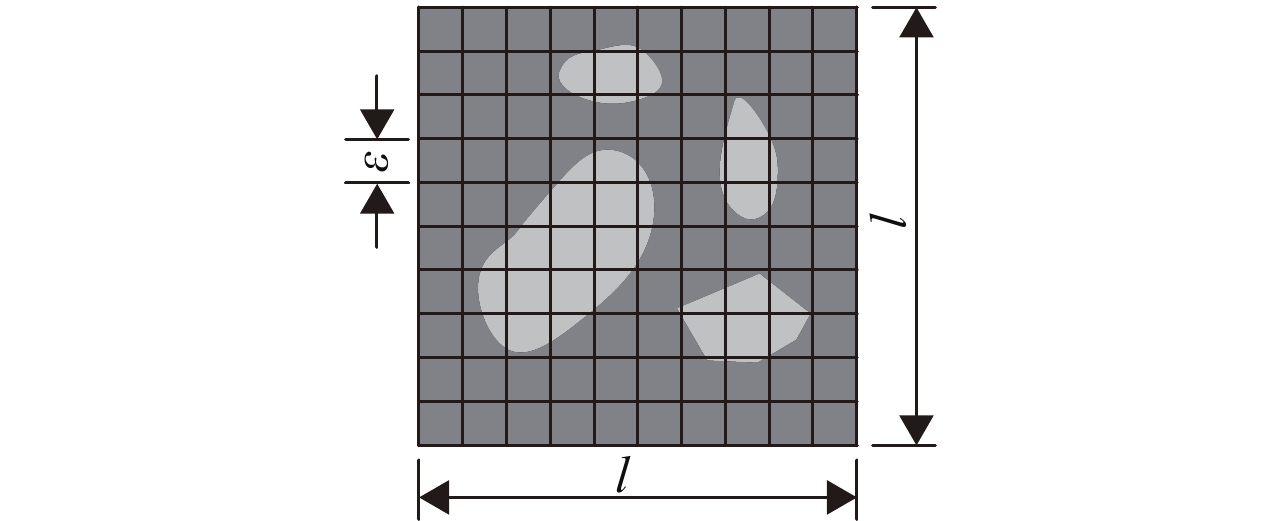
在土的微观研究中,使用Sierpinski分形模型的分维数来描述土的孔隙结构. 孔隙分维数的获取方法为:首先使用显微镜拍摄土体微观孔隙图片并选取部分图片进行图像处理,得到边长为l的正方形图片(如图1所示),孔隙用浅灰色来表示.
|
图 1 土体孔隙分布分维的算法 Figure 1 Algorithm of soil pore distribution fractal dimension |
然后将图片划分为边长为ε的正交网格,统计处于浅灰色孔隙中的网格个数N(ε);改变网格单元尺寸ε, 分别得到不同的ε1, ε2, ε3
| $D = -\mathop {\lim }\limits_{\varepsilon \to 0} \frac{{\ln N(\varepsilon )}}{{\ln \varepsilon }} = -K。$ | (2) |
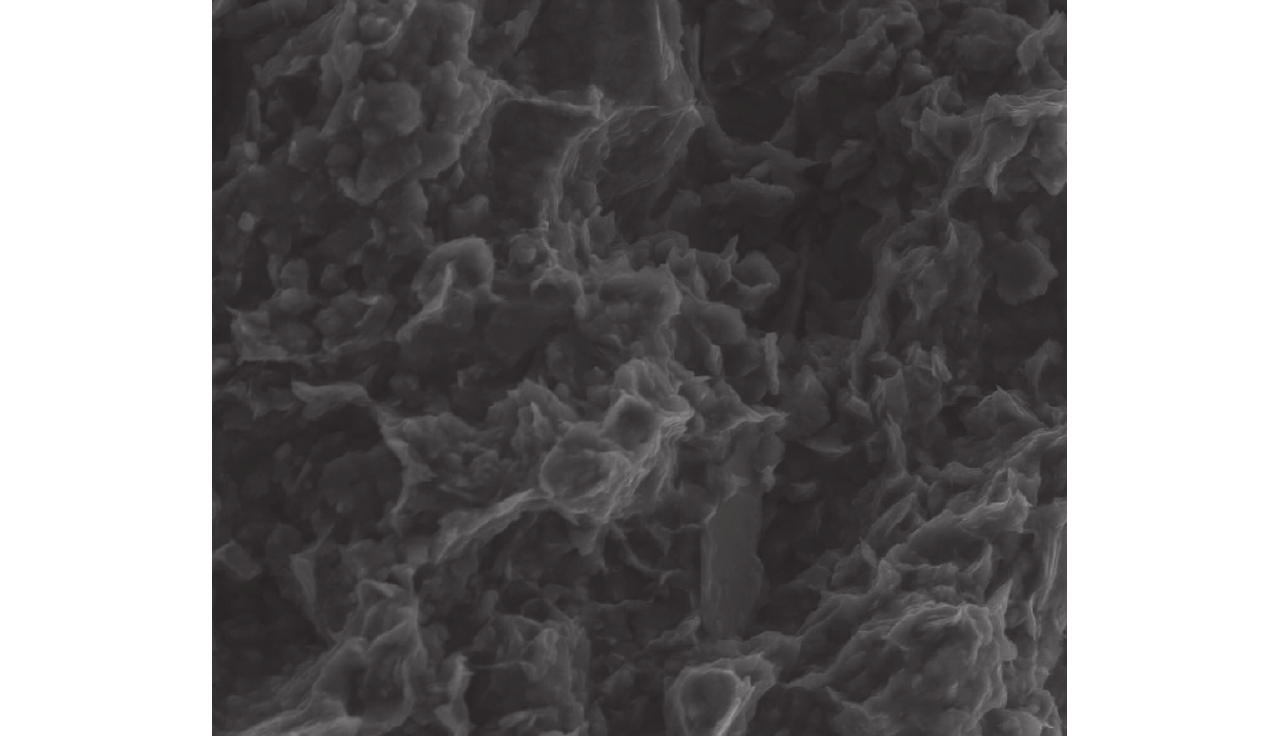
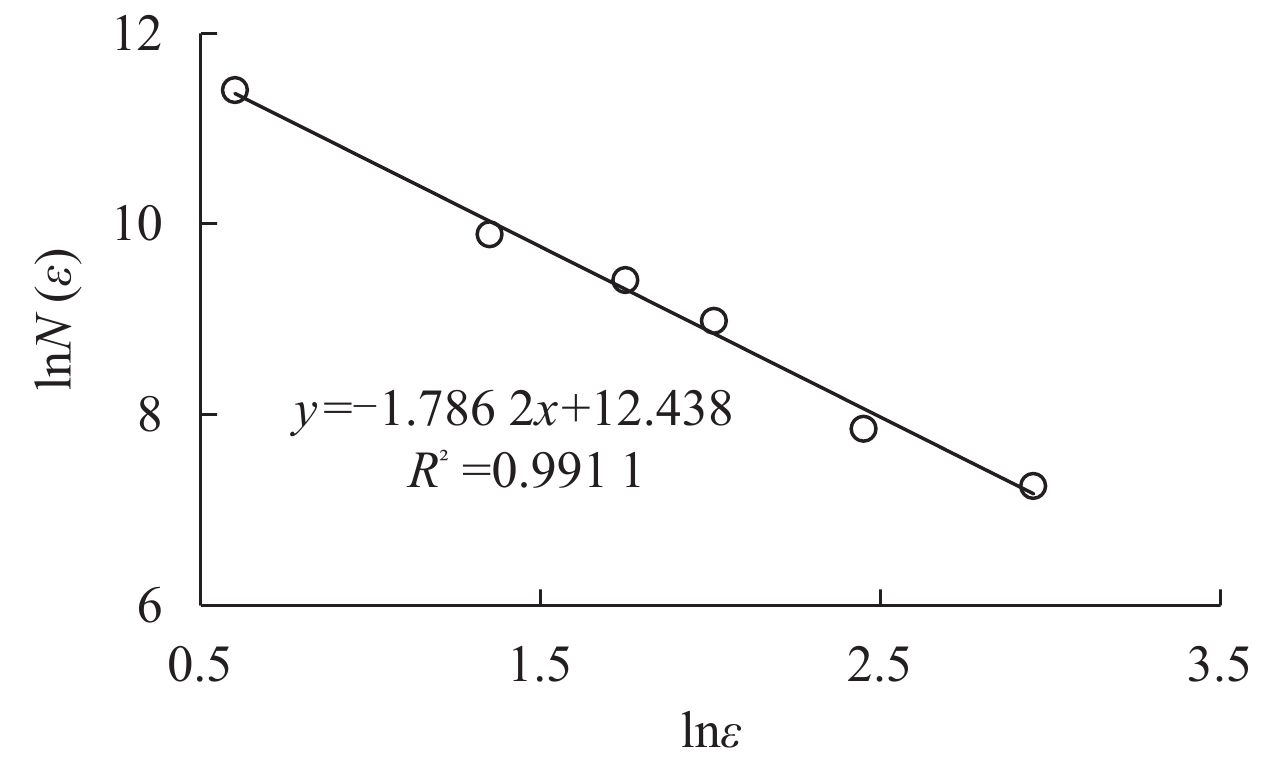
本文以珠江三角洲地区几种软土为研究对象,其物理力学指标见表1. 其中,广州金沙洲地区软土[8]的ESEM图像(见图2)的孔隙分布分维散点图如图3所示,可以看出其lnN(ε)-lnε关系曲线具有十分明显的线性特征,其斜率即为ρnN(ε)-ρn(ε)孔隙分布分维值Dbd.
| 表 1 珠江三角洲典型软土主要物理力学指标 Table 1 Main physical and mechanical indexes of typical soft soil in the PRD |
|
图 2 JSZ软土的ESEM图片(×2 000) Figure 2 ESEM images of JSZ soft soil (×2 000) |
|
图 3 孔隙分布分维散点图(JSZ软土) Figure 3 Scatter gram of pore distribution fractal dimension (JSZ soft soil) |
土体受到荷载作用时,其孔隙会发生明显的变化[9-10]. 本文使用分形模型对珠江三角洲软土微观结构进行研究,引入综合参数——孔隙结构影响因子Fs来反映软土孔隙结构的变化,考虑软土的孔隙形状与大小、排列的定向性以及分布的综合影响,如式(3)所示.
| $F{}_{\rm{s}} = {D_{{\rm{bd}}}}\overline D {H_{\rm{m}}}/(RF),$ | (3) |
式(3)中,Dbd为孔隙分布分维值;
表2为不同固结荷载作用下,珠江三角洲几种代表性软土的孔隙分布分维值Dbd;利用Quanta 200环境扫描电子显微镜拍摄得到不同固结荷载作用下土样竖直切面的显微照片后,采用PCAS图像处理技术[14-16]分析得到的等效孔径
| 表 2 不同固结压力下软土竖直切面孔隙的分布分维值Dbd1) Table 2 Pore distribution fractal dimension of soft soil vertical plane under different consolidation pressure (Dbd) |
|
表 3 各软土样的等效孔径
|
| 表 4 软土样的孔隙平均形状系数F Table 4 The average pore shape factor of soft soil samples (F) |

|
图 4 不同固结压力下软土的孔隙概率熵Hm Figure 4 Hm of soft soil under different consolidation pressure |
根据表2~表4及图4的结果,由式(3)计算可得不同固结荷载p作用下几种典型珠江三角洲软土的孔隙结构因子参数,结果详见表5.
| 表 5 不同压力下软土竖直切面的Fs Table 5 Soft soil’s vertical section Fs under different pressure |
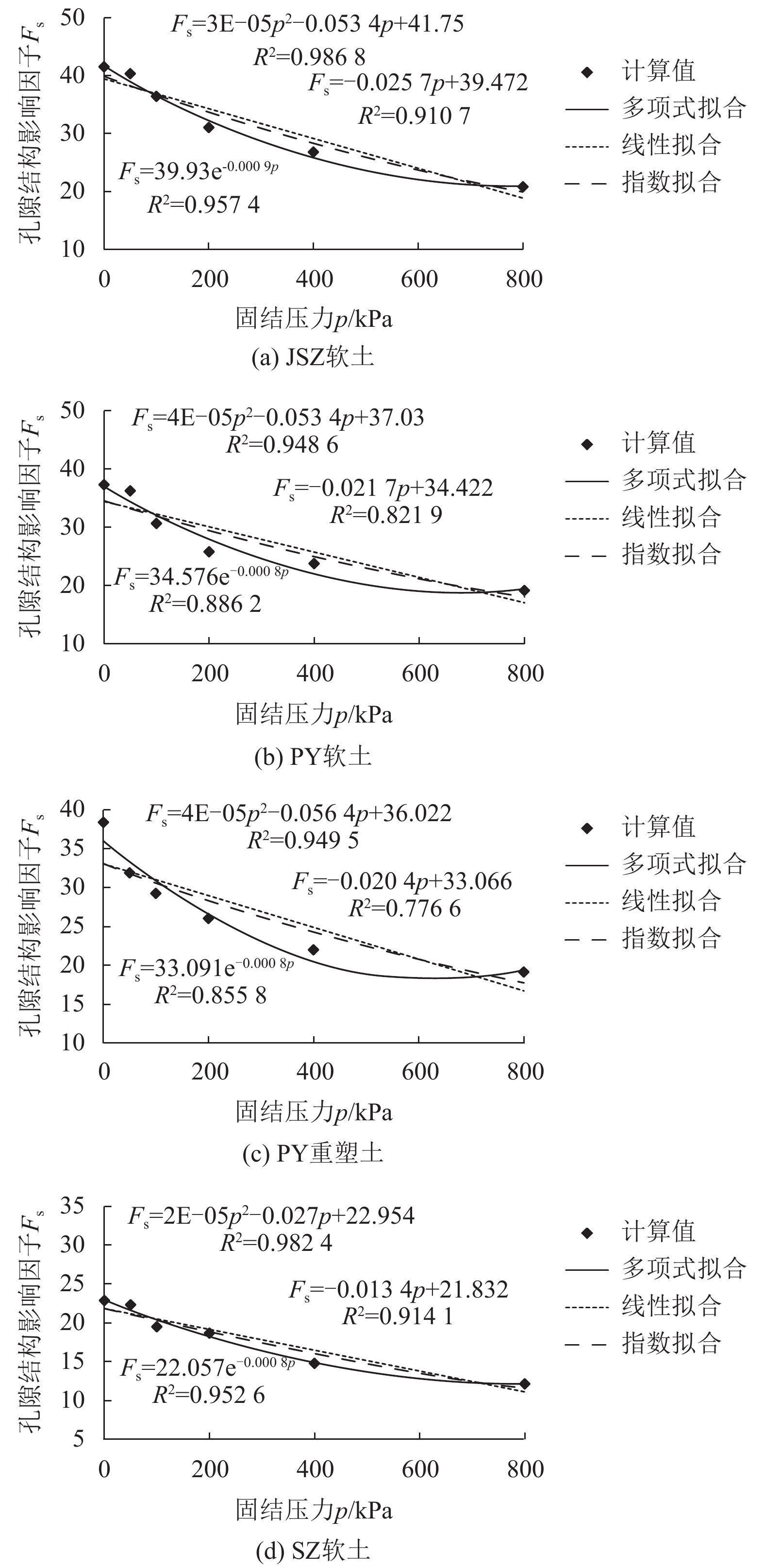
根据表5可绘制出如图5所示的珠江三角洲典型软土的孔隙结构影响因子参数Fs与固结压力p的关系曲线(Fs-p曲线),并对Fs-p曲线进行拟合. 由表5和图5可得如下结论:
|
图 5 软土竖直切面的Fs-p曲线 Figure 5 Fs-p curves of the vertical section of soft soil |
(1) 原状软土的Fs-p关系曲线,使用多项式拟合、指数拟合与线性拟合时,其相关性均较好,其R值介于0.907~0.993之间,而重塑土的相关性略差,其相关系数R值介于0.881~0.974之间;
(2) 软土的Fs-p曲线各种拟合中,多项式拟合相关性最好,其R值大于0.974,相关性最差的是线性拟合,其R值大于0.881,指数拟合相关性介于上述两者中间,其R值大于0.925.
根据以上数据及分析可以得到如下结论:
(1) 孔隙结构影响因子Fs是一个能够反映软土孔隙微观大小、排列方向性、形状以及分布的参数,数据处理表明,此参数与固结荷载具有较大的相关性,并且Fs随着固结荷载p的增大而减小.
(2) 比较这几种典型的珠江三角洲地区软土的孔隙结构影响因子,表明在初始状态下JSZ软土的孔隙结构影响因子最大,PY软土次之,SZ软土最小. 在固结初期(p<50 kPa),原状土的孔隙结构影响因子变化较小,随着荷载增大,软土结构达到屈服状态,孔隙结构影响因子加速减小,随后,当软土孔隙由大、中孔隙向小、微甚至难以压缩的超微孔隙转化后,孔隙结构影响因子大小趋于稳定状态. 当荷载达到800 kPa时,软土的地区差异性变得模糊,其孔隙结构影响因子均值稳定在18左右.
(3) 比较重塑土与原状土的Fs-p曲线可知,在相同固结荷载作用下,原状土的孔隙结构影响因子参数大小比重塑土的大. 认为重塑土的原始结构遭到破坏,颗粒间的接触较弱,结构强度遭到损失,因此导致了重塑土的孔隙结构影响因子较小,并且在固结初期(p<100 kPa)时重塑土的Fs-p曲线出现了急降段. 在固结后期,无论是原状土还是重塑土,其孔隙均为小、微孔隙,较难再压缩,因此两者的孔隙结构影响因子减缓变慢,趋于一致.
3 孔隙结构影响因子与软土宏观工程特性的关联性研究孔隙结构影响因子是一个能反映孔隙大小、排列定向性、分布和形态的综合性参数,必然导致土体的宏观参数发生改变,对于指导软土工程具有重要的意义. 以番禺软土和深圳软土作为研究对象,试探讨孔隙结构影响因子和渗流系数与压缩系数的关联性.
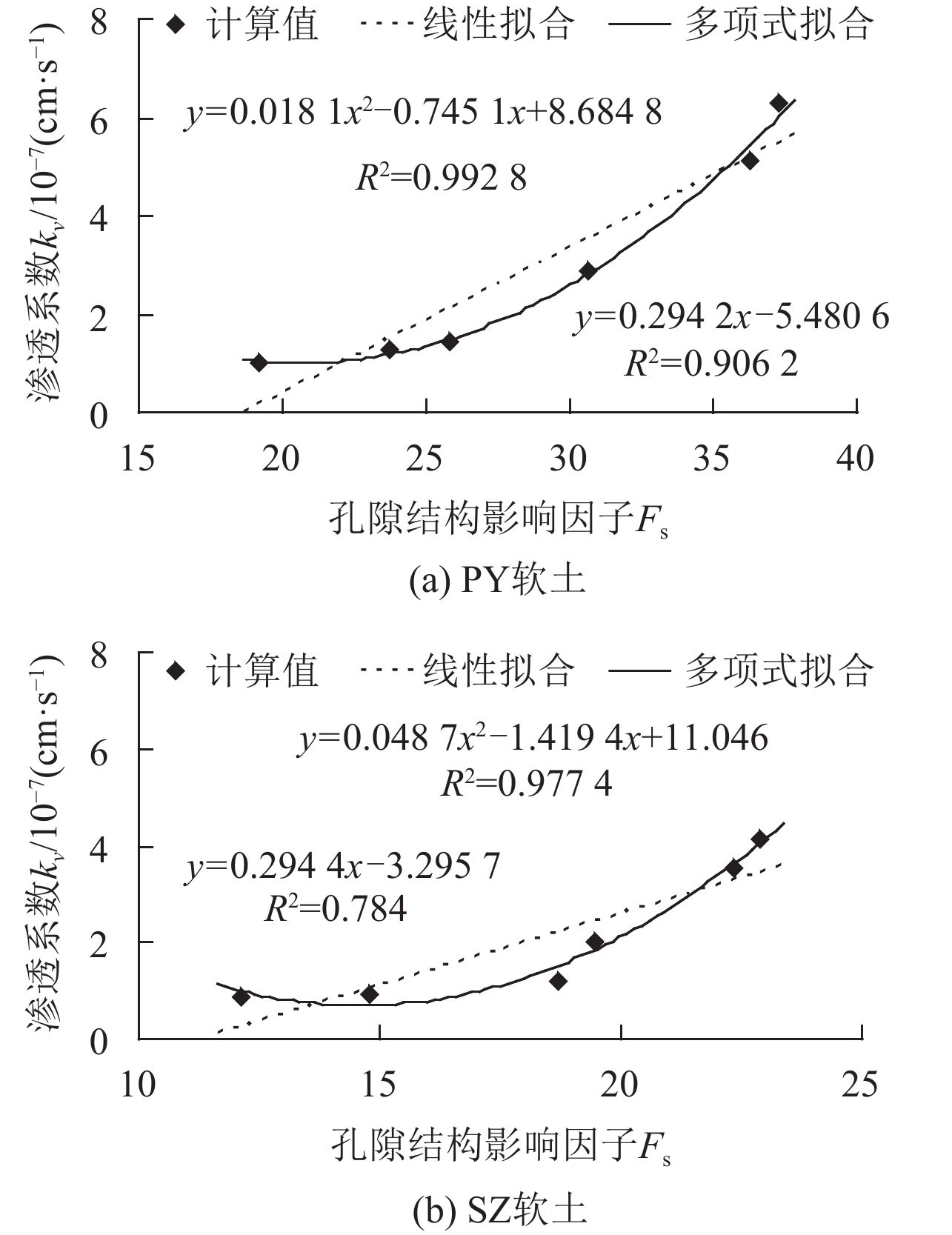
3.1 孔隙结构影响因子与土的渗透性关系分析通过实验测得不同固结荷载下的孔隙结构影响因子所对应的渗透系数,详见表6,可得到两者的关系曲线kv-Fs,并对曲线进行了线性拟合和多项式拟合,详见图6. 由图6可知,两个地区的软土渗透系数均随着孔隙结构影响因子的减小而减小.
| 表 6 软土固结过程中的Fs及kv1) Table 6 Soft soil’s Fs&kv in the process of consolidation |
|
图 6 软土的kV-Fs关系曲线 Figure 6 kV-Fsrelationship curves of soft clay |
由前文可知,在固结过程中,孔隙结构影响因子呈现减小趋势,此时软土中的孔隙孔径减小、排列发生改变、孔径分布变得均匀并且向小、微甚至超微孔隙发展,这些因素都会导致软土的渗透性能降低. 分析表明了软土的渗透性随着孔隙结构影响因子这一微观参数的变化而变化. 分析结果表明,kv-Fs关系曲线的多项式拟合较线性拟合的相关性要好. 当孔隙结构影响因子较大时,其对渗透系数的影响较大,表现为曲线较为陡峭;当孔隙结构影响因子较小时,kv-Fs关系曲线较为平缓,说明此时孔隙结构影响因子对渗透系数的影响较小. 分析认为,在固结后期,软土孔隙以小、微甚至超微孔隙为主,水在微孔隙中流动会产生滑移边界等“微尺度效应”现象[17],导致孔隙结构影响因子对渗透系数影响减弱,表现为kv随Fs减小的趋势变缓,因此导致线性拟合效果不如多项式拟合效果.
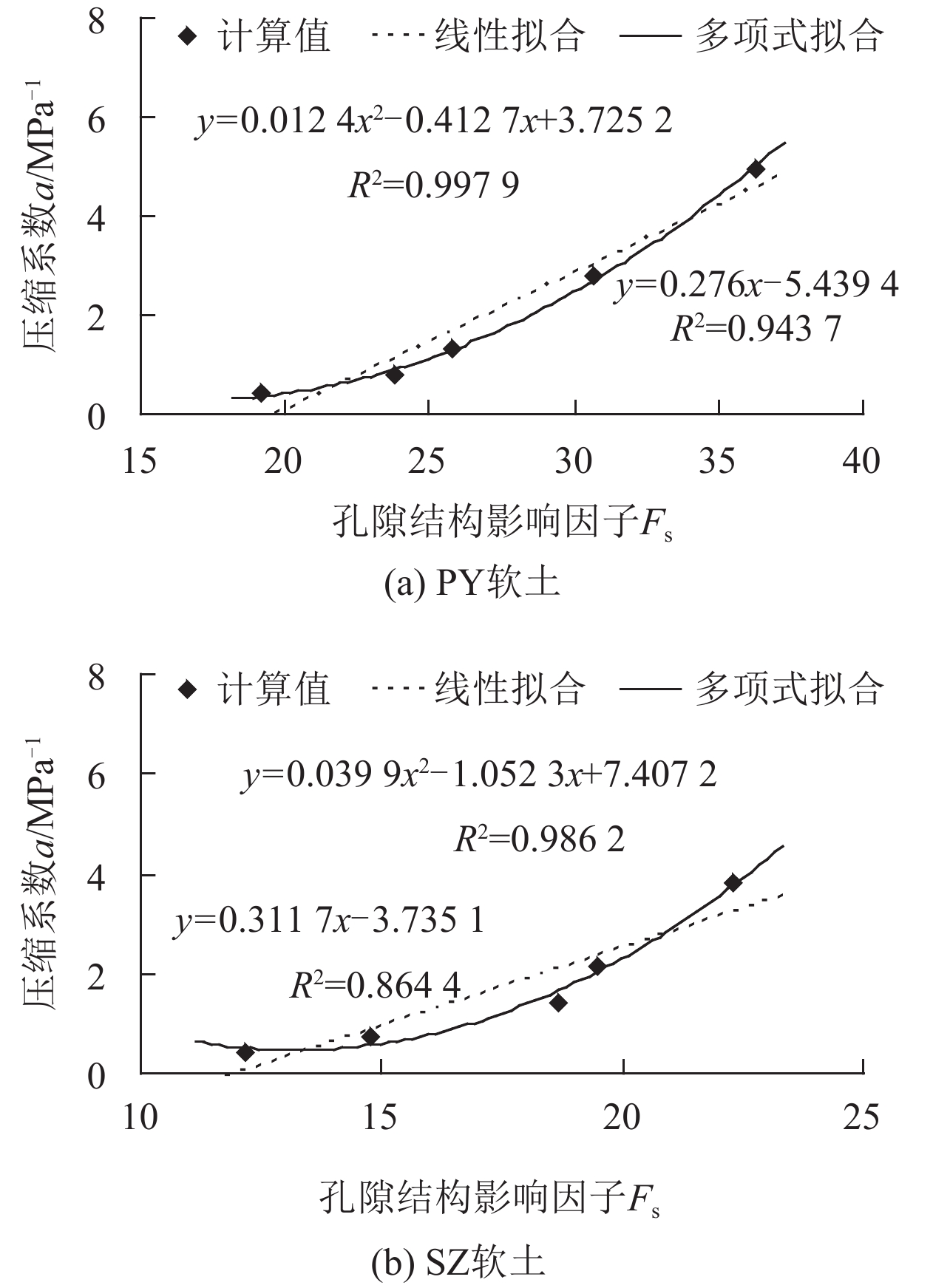
3.2 孔隙结构影响因子与土的压缩性关系分析根据压缩试验得到不同固结荷载作用下的压缩系数(a=-de/dp),结合表5所对应的孔隙结构影响因子计算值,得到表7中数据,其a-Fs曲线如图7所示,由图可知,压缩系数与孔隙结构影响因子关系曲线的多项式拟合与线性拟合的相关性均较为理想.
| 表 7 软土固结过程中的Fs及a1) Table 7 Soft soil’s Fs&a in the process of consolidation |
|
图 7 软土的a-Fs关系曲线 Figure 7 a-Fs relationship curves of soft clay |
由此可知,固结过程中,随着大孔隙数量的湮灭、小孔隙的增长,孔隙结构影响因子降低、软土压缩系数明显下降,两者之间存在较为显著的线性正相关性,说明宏观的压缩系数a是微观的孔隙结构影响因子Fs的宏观体现和映证,两者之间可以利用拟合方程进行相互换算.
4 结论本文研究了软土固结过程中的孔隙微观特征变化,定义了一个能够反映软土孔隙的大小、形状、分布以及排列定向性的微观参数——孔隙结构影响因子Fs,并研究了孔隙结构影响因子对软土宏观参数的相关性,得到以下结论:
(1) 孔隙结构影响因子Fs是一个能够综合反映软土微观孔隙大小、排列定向性、分布以及形态的参数,能够描述软土固结过程中的孔隙变化特征. 研究表明当软土的孔隙越小,孔隙结构影响因子Fs也就越小,结构越稳定,其受荷载的影响也越小.
(2) Fs-p曲线的二次多项式拟合相关性明显,且孔隙结构影响因子随着固结荷载的增大而减小,进而趋于稳定. 研究表明,当固结荷载达到一定程度时,孔隙结构影响因子的地区差异性减弱,重塑土与原状土的差异性减弱,各土样的孔隙结构影响因子趋于一致,数值大小均在18左右.
(3) 微观参数——孔隙结构影响因子Fs与软土的渗透系数、压缩系数等宏观参数之间存在明显的正相关性. 其中,kv-Fs、a-Fs曲线的多项式拟合相关性较好,宏观参数kv和a是微观参数Fs的宏观体现和映证,可以利用拟合方程进行相互换算.
| [1] | 周晖. 珠江三角洲软土显微结构与渗流固结机理研究[D]. 广州: 华南理工大学土木与交通学院, 2013. |
| [2] | BARTOLI F, PHILIPPY R, DOIRISSE M, et al. Structure and self-similarity in silty and sandy soils: The fractal approach[J]. Journal of Soil Science, 1991, 42(2): 167-185. DOI: 10.1111/ejs.1991.42.issue-2. |
| [3] |
王大鹏, 王秋兵, 韩春兰, 等. 辽宁省古红土颗粒分形特征研究[J].
安徽农业科学, 2007, 35(20): 6186-6189.
WANG D P, WANG Q B, HAN C L, et al. Study of fractal features of paleosol in Liaoning Province[J]. Journal of Anhui Agricultural Sciences, 2007, 35(20): 6186-6189. DOI: 10.3969/j.issn.0517-6611.2007.20.093. |
| [4] |
伍丢峰. 土颗粒粒径分维值与土的粘聚力的关系[J].
湖南水利水电, 2007(2): 23-24.
WU D F. Soil particle size fractal value and the cohesive soil[J]. Hunan Hydropower, 2007(2): 23-24. |
| [5] |
张佑林, 夏家华, 黎国华, 等. 粉体颗粒的形状与分维[J].
武汉工业大学学报, 1996, 18(4): 53-56.
ZHANG Y L, XIA J H, LI G H, et al. The particle shape and fractal dimension[J]. Journal of Wuhan University of Technology, 1996, 18(4): 53-56. |
| [6] | 谢和平, 薛秀谦. 分形应用中的数学基础与方法[M]. 北京: 科学出版社, 1997: 68-79. |
| [7] | 蔡建超, 胡祥云. 多孔介质分形理论与应用[M]. 北京: 科学出版社, 2016: 55-80. |
| [8] | ZHOU H, YAN W F. Sierpinski Fractal Characteristics of Consolidation of Soft Characteristics[J]. The Electronic Journal of Geotechnical Engineering, 2016, 21(11): 4111-4119. |
| [9] |
刘勇健, 刘湘秋, 刘雅恒, 等. 珠江三角洲软土物理力学性质对比分析[J].
广东工业大学学报, 2013, 30(3): 30-36.
LIU Y J, LIU X Q, LIU Y H, et al. A contrastive analysis of the physico-mechanical properties of soft soils in the Pearl River Delta[J]. Journal of Guangdong University of Technology, 2013, 30(3): 30-36. |
| [10] |
刘勇健, 符纳, 陈创鑫, 等. 三轴冲击荷载作用前后软黏土的微观结构变化研究[J].
广东工业大学学报, 2015, 32(2): 23-27.
LIU Y J, FU N, CHEN C X, et al. Study on microstructure changes of soft clay before and after triaxial impact load[J]. Journal of Guangdong University of Technology, 2015, 32(2): 23-27. |
| [11] |
施斌. 粘性土微观结构定向性的定量研究[J].
地质学报, 1997, 71(1): 36-44.
SHI B. Quantitative research on the orientation of microstructure of clayey soil[J]. Acta Geologica Sinica, 1997, 71(1): 36-44. |
| [12] | ZHOU H, FANG Y G, GU R G, et al. Microscopic analysis of saturated soft clay in Pearl River Delta[J]. Journal of Central South University of Technology, 2011, 18(2): 504-510. DOI: 10.1007/s11771-011-0724-4. |
| [13] |
周晖, 李勇. 珠江三角洲区域软土的物理力学指标研究与分析[J].
矿产与地质, 2015, 29(6): 116-119.
ZHOU H, LI Y. Analysis on physical mechanic indexes of soft soil in Pearl River Delta Region[J]. Mineral Resources and Geology, 2015, 29(6): 116-119. |
| [14] |
刘春, 王宝军, 施斌, 等. 基于数字图像识别的岩土体裂隙形态参数分析方法[J].
岩土工程学报, 2008, 30(9): 1383-1388.
LIU C, WANG B J, SHI B, et al. Analytic method of morphological parameters of cracks for rock and soil based on image processing and recognition[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(9): 1383-1388. |
| [15] | ZHOU H, FANG Y G, GU R G. Modified consolidation model and calculation of soft soil based on microcosmic test[J]. The Electronic Journal of Geotechnical Engineering, 2015, 20(17): 9725-9734. |
| [16] | ZHOU H, FANG Y G, LIANG J W, et al. Renguo Gu*. Influence of Mineral Constituents for Fine Clay’s Strength Characteristics[J]. The Electronic Journal of Geotechnical Engineering, 2015, 20(17): 9717-9724. |
| [17] |
周晖, 房营光, 梁健伟, 等. 微电场效应对土体渗透特性的影响研究[J].
桂林理工大学学报, 2015, 35(4): 845-849.
ZHOU H, FANG Y G, LIANG J W, et al. The research of the micro electric field effect on the soil permeability characteristics[J]. Journal of Guilin University of Technology, 2015, 35(4): 845-849. |
 2017, Vol. 34
2017, Vol. 34