在工程活动中总会遇到各种各样的矛盾问题^[1-4]，而且很多矛盾问题常常是相互影响并交织在一起的，这就形成了复杂矛盾问题. 解决复杂矛盾问题，既要考虑包含其中的单个矛盾问题的处理，也要考虑矛盾问题之间的相互联系以及由此可能引发的传导矛盾问题. 处理复杂矛盾问题时极易引发传导矛盾问题，传导矛盾问题的分析与处理是复杂矛盾问题处理中的关键问题.

传导矛盾问题是由原矛盾问题的解变换对另一与其相关问题的目标元或条件元的传导变换造成的. 文献[5-6]指出了传导矛盾问题的由来，并将传导矛盾问题分成两类：一类是由原问题的相关问题导致的；另一类是由原问题的共轭问题导致的. 文献[7]给出了传导变换发生时，定量研究传导变换的重要指标——传导效应的计算方法；文献[8]则在此基础上特别说明了同对象信息元传导特征的传导度的概念及从数据库中获取传导知识的步骤. 但上述文献都没有涉及传导矛盾问题的成因分析，也没有给出任何传导矛盾问题的解决方法. 文献[9]在前述文献研究的基础上，通过引入传导相关度对传导矛盾问题的成因进行了分析，并给出了传导矛盾问题的解决思路，这为复杂矛盾问题系统中传导矛盾问题的分析和解决提供了参考依据. 但文献[9]对复杂矛盾问题中的传导作用的研究还不够深人，对传导矛盾问题的成因剖析也过于简单，具体表现在：(1) 文中传导相关度的定义存在缺陷，它的取值符号的确定需要经过一个模糊的人为判定过程；(2) 未对复杂矛盾问题中遇到的各种形式的传导矛盾问题进行分类的细化研究；(3) 对传导矛盾问题的成因剖析时，没有把传导矛盾问题放入到复杂矛盾问题中去考虑. 所以，该文的研究成果在实际的传导矛盾问题分析和处理过程中还不能很好地发挥其理论指导的作用.

为此，本文在文献[9]研究的基础上，对复杂矛盾问题中的传导矛盾问题进行了分类，并给出了严格的形式化定义；然后重新修正了传导相关度的定义并从复杂矛盾问题系统的角度对分类后传导矛盾问题的成因进行了深入剖析.

1 传导矛盾问题的分类及定义

假设有一个矛盾问题，它有多个目标 ${D_1},{D_2},\cdots,$ ${D_n}$ ，也有多个条件 ${C_1},{C_2},\cdots,{C_n}$ ，若将其分解为若干个子问题 ${P_1},{P_2},\cdots,{P_l}$ ，这些子问题有的是矛盾问题，有的是相容问题，且它们之间还存在相关关系，这样就形成一个矛盾问题网，称其为复杂矛盾问题^{[3, 10]}，表示为Ps，

$Ps = \hat g*\hat l.$

(1)

这里 $\hat g = ({D_1} \circ {D_2} \circ \cdots \circ {D_n})$ ， $\hat l = ({C_1} \circ {C_2} \circ \cdots \circ {C_n})$ .（注： $ \circ $ 符号表示合成，可以是 $ \wedge $ （与）， $ \vee $ （或）， $\neg $ （非）这些符号或它们的连接）.

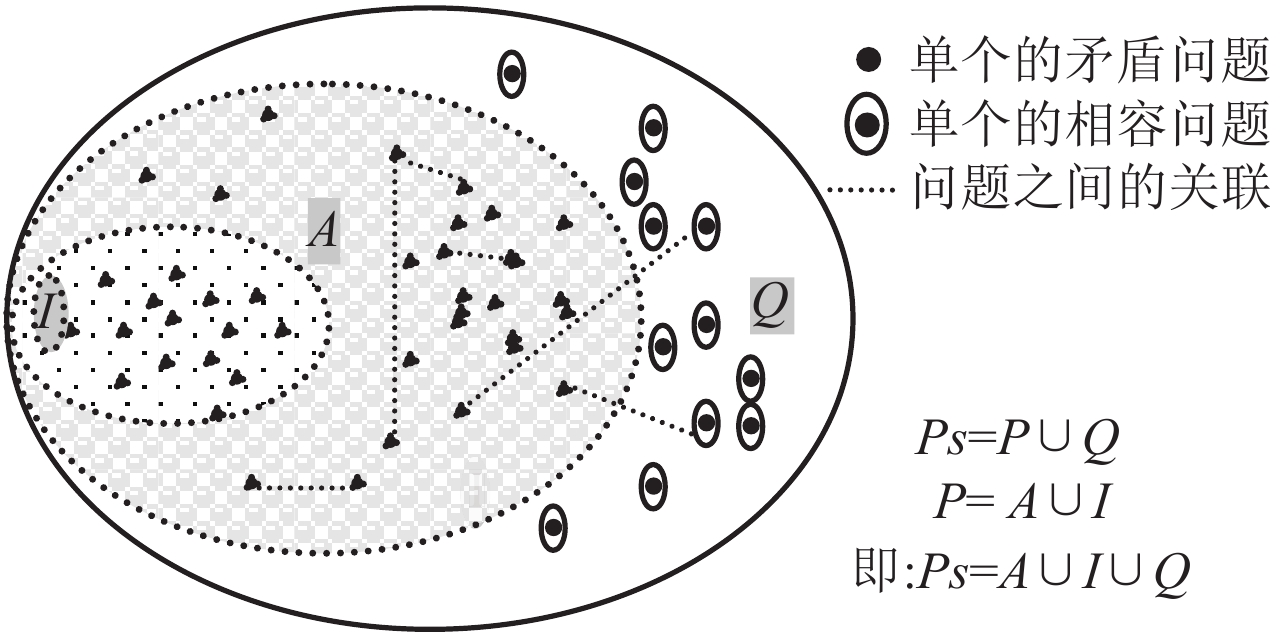
Ps中既包含矛盾问题也包含和矛盾问题相关的非矛盾（相容）问题，所以可以认为Ps是一个问题集合. 如图1所示，如果用P表示其中的矛盾问题集合，用Q表示相容问题集合，显然有： $Ps = P \cup Q$ ；而矛盾问题当中既有关联矛盾问题也有独立矛盾问题^[10]，即： $P = A \cup I$ .

集合A中的矛盾问题相互之间是有一定关联的，简称关联矛盾问题集. 处理关联矛盾问题集中的某一矛盾问题时，有可能由于传导作用使得和它相关联的矛盾问题的矛盾程度更加严重. 这种情形的传导矛盾称之为强化传导矛盾问题.

定义1　设有一个矛盾问题 ${P_m} = {D_m}*{C_m}$ $\left( {{P_m} \in A} \right)$ ， ${T_{{P_m}}} = ({T_{{D_m}}},{T_{{C_m}}})$ 为P_m的解变换. 若在关联矛盾集A中存在另一个矛盾问题 ${P_l} = {D_l}*{C_l}$ 且 ${P_l} \sim {P_m}$ ，按照传导变换规则： ${T_{{P_m}}}{ \Rightarrow _{{P_m}}}{T_{{P_l}}}$ ， $_{{P_m}}{T_{{P_l}}} =$ ${(_{{D_m}}}{T_{{D_l}}}{,_{{C_m}}}{T_{{C_l}}})$ ， ${(_{{D_m}}}{T_{{D_l}}}{D_l})*{(_{{C_m}}}{T_{{C_l}}}{C_l}) = {D'_l}*{C'_l} = {P'_l}$ ，变换后 ${N'_l} > {N_l}$ （注： ${N'_l}$ 为 ${P_l}^\prime $ 的矛盾度^[10]；N_l为P_l的矛盾度），则称 ${P'_l}$ 为 ${T_{{P_m}}}$ 关于P_l的强化传导矛盾问题.

此外，由于P和Q都是复杂矛盾问题Ps中的集合，因此包含在它们中的问题也可能存在某种关联，使得处理它们时会发生相互影响. 比如，在处理P中的矛盾问题时，有可能会使Q中和它相关联的一个相容问题转变成为一个新的矛盾问题. 这种情形的传导矛盾，称之为质变传导矛盾问题.

定义2　设有一个矛盾问题 ${P_m} = {D_m}*{C_m}$ $\left( {{P_m} \in P} \right)$ ， ${T_{{P_m}}} = ({T_{{D_m}}},{T_{{C_m}}})$ 为P_m的解变换. 若存在另一个相容问题 ${P_0} = {D_0}*{C_0}({P_0} \in Q,{\text{即}}{N_0} \leqslant 0)$ 且 ${P_0} \sim {P_m}$ ，按照传导变换规则： ${T_{{P_m}}}{ \Rightarrow _{{P_m}}}{T_{{P_0}}}{,_{{P_m}}}{T_{{P_0}}} =$ ${(_{{D_m}}}{T_{{D_0}}}{,_{{C_m}}}{T_{{C_0}}})$ ， ${(_{{D_m}}}{T_{{D_0}}}{D_0})*{(_{{C_m}}}{T_{{C_0}}}{C_0}) = {D'_0}*{C'_0} = {P'_0}$ ，变换后 ${N'_0} > 0$ （即， ${P'_0} \in P$ ）（注： ${N'_0}$ 为 ${P_0}^\prime $ 的矛盾度；N₀为P₀的矛盾度），则称 ${P'_0}$ 为 ${T_{{P_m}}}$ 关于P₀的质变传导矛盾问题.

2 传导矛盾问题的成因分析

定义3　设在t₀时刻有两个条件基元C₁和C₂： ${C_{\rm{1}}}({t_0}) = ({N_1}({t_0}),{c_1},{v_1}({t_0}))$ ， ${C_2}({t_0}) = ({N_2}({t_0}),{c_2},{v_2}({t_0}))$ . 若在t时刻对条件基元C₁进行主动变换φ： $\varphi {C_{\rm{1}}}({t_0}) = {C_{\rm{1}}}(t){\rm{ = }}({N_{\rm{1}}}(t),{c_{\rm{1}}},{v_{\rm{1}}}(t))$ （ $t > {t_0}$ ，且 ${v_1}(t) \ne $ $ {v_1}({t_0})$ ），φ的传导变换 $_\varphi T$ ： $_\varphi T{C_2}({t_0}) = {C_2}(t) =$ $ ({N_2}(t),{c_2},{v_2}(t))$ ，则称γ为C₁，C₂在传导变换中的相关度.

$\gamma = \frac{{{v_2}(t) - {v_2}({t_0})}}{{{v_1}(t) - {v_1}({t_0})}}.$

(2)

(1) 当γ=0，说明C₁，C₂两个条件基元不相关联. 不相关联的条件基元在可拓的变换过程中不会发生传导变换；

(2) 当γ≠0，说明C₁，C₂两个条件基元相关联. 相关联的条件基元在可拓变换过程中会发生传导变换. 比如，C₁特征量值的变化可带动C₂特征量值的改变.

定义4　设{B₁}是矛盾问题P₁的条件基元集，{B₂}是矛盾问题P₂的条件基元集，如果对 $\forall {B_1} \in \{ {B_1}\} $ ，至少存在一个 ${B_2} \in \{ {B_2}\} $ 使得B₁与B₂对应，即 $\{ {B_1}\} \sim \{ {B_2}\} $ ，则P₁与P₂也相关，并称P₁和P₂为关联矛盾，记作

${P_1} \sim {P_2}.$

(3)

定义5　设矛盾问题 ${P_i},{P_j} \in P$ 且 ${P_i} \sim {P_j}$ . 如果P_i的化解对P_j的影响是正面的，即P_i的化解使P_i和P_j的矛盾度均变小，则称P_i和P_j正相关，记作

${P_i} + \sim {P_j}.$

(4)

定义6　设 ${P_i},{P_j} \in P$ 且 ${P_i} \sim {P_j}$ . 若P_i的化解对P_j的影响是负面的，即P_i的化解使P_i矛盾度变小而使P_j的矛盾度变大，则称P_i和P_j负相关，记作

${P_i} - \sim {P_j}.$

(5)

例1：假设有一个复杂矛盾问题 $P = P \cup Q$ ，其中 ${P_1},{P_2},{P_3} \in P$ ， ${P_0} \in Q$ （即， ${P_1},{P_2},{P_3}$ 是矛盾问题，而P₀是相容问题）并且： ${P_0} = {D_0} \uparrow {C_0}$ ， ${P_1} = {D_1} \uparrow {C_1}$ ， ${P_2} = {D_2} \uparrow {C_2}$ ， ${P_3} = {D_3} \uparrow {C_3}$ .

下面先来分析强化传导矛盾问题的成因.

设 ${P_{\rm{1}}} = {D_{\rm{1}}}*{C_{\rm{1}}}$ ， ${P_{\rm{2}}} = {D_{\rm{2}}}*{C_{\rm{2}}}$ ，且条件基元C₁，C₂之间存在着关联关系（即， ${C_1} \sim {C_2}$ ），那么由定义4可知 ${P_1} \sim {P_2}$ .

对于矛盾问题P₁，C₁对应的特征值增大（即 $({v_1}(t) - {v_1}(t0)) > 0$ ，用 $ \mapsto $ 表示）有利于其解决，则易知： ${S_1}({V_c},{V_d}) > 0$ （P₁的矛盾符号函数^[10]取正值）；对于矛盾问题P₂，C₂对应的特征值减小（即 $({v_2}(t) - {v_2}(t0)) < 0$ ，用 表示）有利于其解决，则易知 ${S_2}({V_c},{V_d}) < 0$ （即，P₂的矛盾符号函数取负值）. C₁和C₂的相关度γ可按式(2)求得，易知γ<0.

如果C₁特征值的增大刚好使得C₂的特征值减小，表示为

$ {C_1} \mapsto \Rightarrow {C_2}.$

(6)

这种情况就是通过增大C₁的特征值来化解P₁矛盾问题的同时也导致了矛盾问题P₂的部分解决. 具体分两种情形详细说明：

(1) 如果C₁特征值的增大不仅使得矛盾问题P₁完全解决，而且使得C₂的特征值向着减小的方向变化，这种变化又弱化了矛盾问题P₂的矛盾程度.

(2) 如果C₁特征值的增大不仅使得矛盾问题P₁完全解决，而且又使得矛盾问题P₂也完全解决.

上面的两种情形均是非常理想的，即P₁和P₂正相关，表示为： ${P_1} + \sim {P_2}$ .

如果C₁特征值的增大恰好使得C₂的特征值也增大（即 $({v_2}(t) - {v_2}(t0)) > 0$ ），这时根据式(2)易知γ>0. 这种情况是很不理想的，因为对矛盾问题P₁的化解引发了矛盾问题P₂矛盾程度的加剧. 即，P₁和P₂负相关，表示为： ${P_1} - \sim {P_2}$ （负相关）.

结合上述两种情况，再考虑P₁和P₂两矛盾问题中条件基元特征值在不同时刻的变化，就可得到P₁和P₂的相关情况分析表1.

由表1可得出如下内容.

如果矛盾问题P₁的矛盾符号函数 ${S_1}({V_c},{V_d})$ 和矛盾问题P₂的矛盾符号函数 ${S_2}({V_c},{V_d})$ 异号，则

$\gamma < 0 \Rightarrow {P_1} + \sim {P_2}.$

(7)

$\gamma > 0 \Rightarrow {P_1} - \sim {P_2}.$

(8)

如果矛盾问题P₁的矛盾符号函数 ${S_1}({V_c},{V_d})$ 和矛盾问题P₂的矛盾符号函数 ${S_2}({V_c},{V_d})$ 同号，则

$\gamma > 0 \Rightarrow {P_1} + \sim {P_2}.$

(9)

$\gamma < 0 \Rightarrow {P_1} - \sim {P_2}.$

(10)

定义7　设C₁和C₂是矛盾问题P₁和P₂的条件基元， ${S_1}({V_c},{V_d})$ 和 ${S_2}({V_c},{V_d})$ 是矛盾问题P₁和P₂的矛盾符号函数. 若在传导变换中C₁和C₂相关联（即γ≠0），则称η为条件基元C₁，C₂在传导变换中的传导相关度.

$\eta = {S_1}({V_c},{V_d}) * {S_2}({V_c},{V_d}) * \gamma .$

(11)

如果C₁和C₂是线性相关的，设∆v₁为C₁特征量的取值变化，∆v₂为C₂特征量的取值变化，那么容易求出C₁和C₂的线性回归系数b， $b = \frac{\displaystyle{\Delta {v_1}}}{\displaystyle{\Delta {v_2}}}$ . 又因为 $\gamma = \frac{\displaystyle{{v_2}(t) - {v_2}(t0)}}{\displaystyle{{v_1}(t) - {v_1}(t0)}} = \frac{\displaystyle{\Delta {v_1}}}{\displaystyle{\Delta {v_2}}}$ . 所以，在实际应用中可用线性回归系数b来取代相关度γ直接计算出传导相关度η的值，即

$\eta \approx {S_1}({V_c},{V_d}) * {S_2}({V_c},{V_d}) * b.$

(12)

分析传导相关度η和矛盾问题P₁和P₂的相关情况，可得到表2.

定义8　如果两个条件基元的传导相关度η>0，那么由此引发的传导变换称为正传导变换.

定义9　如果两个条件基元的传导相关度η<0，那么由此引发的传导变换称为负传导变换.

由表2，可知：

(1) 如果η>0，则P₁和P₂正相关，这时发生的传导变换就是正传导变换. 并且η的绝对值越大，P₁和P₂的正相关的程度越大，越有利于两个矛盾问题的解决.

(2) 如果η<0，则P₁和P₂负相关，这时发生的传导变换称为负传导变换. 并且η的绝对值越大，P₁和P₂的负相关程度越大. 这种情况，在可拓变换过程中，极易引发传导矛盾问题.

通过上面的分析可知，定义1所定义的强化传导矛盾问题是由于两个矛盾问题的条件基元所对应的传导相关度η<0而造成的.

接下来考虑定义2所定义的质变传导矛盾问题的成因.

仍以例1的复杂矛盾问题为例来说明.

已知： ${P_0} = {D_0} \uparrow {C_0}$ 是复杂矛盾问题Ps中的一个相容问题； ${P_{\rm{3}}} = {D_{\rm{3}}} \uparrow {C_3}$ 是复杂矛盾问题Ps中的一个矛盾问题.

如果为了解决矛盾问题P₃需要增大条件基元C₃所对应的特征值，而C₃特征值的增大正好促使C₀的特征值也发生了变化（变为 ${C'_0} $ ），而C₀特征值的变化使得相容问题P₀变成了一个矛盾问题( ${P_0} \notin Q$ )，即产生了新的矛盾问题，表示为 ${P'_0}$ .

${P'_0} = {D_0} \uparrow {C'_0} ({P'_0} \in P).$

(13)

设η表示条件基元C₃和C₀的传导相关度，通过分析易知：

当η=0时，C₃，C₀是不会发生传导变换的；

当η>0时，C₃，C₀之间的传导变换不会引发出新的矛盾问题；

当η<0时，C₃，C₀之间的传导变换会直接诱发新的矛盾问题的产生.

由上可知，定义2所定义的质变传导矛盾问题也是由于两个矛盾问题的条件基元间的传导相关度η<0而造成的.

结合上述两种情形的分析，可以得出结论：由于复杂矛盾系统中很多矛盾问题相互关联，所以在解决其中的某一矛盾问题时，可能会发生传导变换，而如果在传导变换过程中存在着不同矛盾问题的条件基元传导相关度η<0的情况，就会诱发传导矛盾问题. 根据文献[10]，知道传导相关度小于零实质是由复杂矛盾问题中显化或潜在的技术矛盾所导致，所以传导矛盾问题可以尝试转化为技术系统中的技术矛盾，然后通过使用TRIZ矛盾矩阵表中的创新原理来解决^[11-12].

3 应用实例

假设在一个城市交通复杂矛盾问题 $Ps = P \cup Q$ 中： ${P_0} = {D_0} \uparrow {C_0}$ ； ${P_1} = {D_1} \uparrow {C_1}$ ； ${P_2} = {D_2} \uparrow {C_2}$ ； ${P_3} = {D_3} \uparrow {C_3}$ ；并且 ${P_1},{P_2},{P_3} \in P$ ， ${P_0} \in Q$ （即， ${P_1},{P_2},{P_3}$ 是矛盾问题，而P₀是相容问题）.

若D₁=（出行，打车，易），C₁=（出租车，数量 ${v_1}({t_0})$ ，少），则 ${P_1} = {D_1}*{C_1}$ 是一个矛盾问题（即， ${N_1} > 0$ ）. 也就是说，现有的出租车数量不能满足人们日常的出行需要，使得出行打车容易的局面难于实现. 对于矛盾问题P₁，显然C₁往增大的方向变化有利于其解决，所以P₁的矛盾符号函数取正值，即： ${S_1}({V_c},{V_d}) > 0$ .

若D₂=（路面，拥堵程度，无），C₂=（机动车，数量 ${v_2}({t_0})$ ，较多），则 ${P_2} = {D_2}*{C_2}$ 也是一个矛盾问题（即， ${N_2} > 0$ ）. 也就是说，在现有机动车数量较多的情况下，要想实现路面畅通无阻不拥堵是不太可能的. 对于矛盾问题P₂，显然C₂往减小的方向变化有利于其解决，所以P₂的矛盾符号函数取负值，即： ${S_{\rm{2}}}({V_c},{V_d}) < 0$ .

现在，为了解决矛盾问题P₁，作变换 ${T_{{P_{\rm{1}}}}} = (e,{T_{{C_{\rm{1}}}}})$ ： ${T_{{C_{\rm{1}}}}}{C_{\rm{1}}}$ =（出租车，数量 ${v_1}(t)$ ，多）. 即增加出租车数量来解决出行打车难的问题，使 ${N_1} \leqslant 0$ . 但是，知道： ${C_1} \sim {C_2}$ ，所以出租车数量的增加会导致路面机动车数量的增多，即由传导规则： ${T_{{P_1}}} = > {}_{{P_1}}{T_{{P_2}}}$ ， ${}_{{P_1}}{T_{{P_2}}} = (e,{}_{{C_1}}{T_{{C_2}}})$ ， ${}_{{C_1}}{T_{{C_2}}}{C_2}$ =（机动车，数量 ${v_2}(t)$ ，很多）= ${C'_2} $ . 由此可知 $\gamma = \frac{\displaystyle{{v_2}(t) - {v_2}(t0)}}{\displaystyle{{v_1}(t) - {v_1}(t0)}} > 0$ ，又因为 ${S_1}({V_c},{V_d}) > 0$ ， ${S_2}({V_c},{V_d}) < 0$ ，所以

$\eta = {S_1}({V_c},{V_d}) * {S_2}({V_c},{V_d}) * \gamma < 0.$

(14)

因此， ${P_1} - \sim {P_2}$ . $e{D_2} = {D_2}$ ，记 ${P'_2} = {D_2}*{C_2}^\prime $ ，显然有 ${N_2}^\prime > {N_2}$ （注， ${N'_2}$ 为 ${P_2}^\prime $ 的矛盾度；N₂为P₂的矛盾度），这时称 ${P'_2}$ 为 ${T_{{P_1}}}$ 关于P₂的强化传导矛盾问题. 即，由于出租车数量的增加导致了路面机动车数量的增多，而机动车数量的增多又会直接导致路面拥堵程度加剧. 也就是说，在城市交通这个复杂矛盾问题中对矛盾问题P₁的解决，导致了矛盾问题P₂矛盾程度的加剧或者说是强化，这就是在定义1中给出的强化传导矛盾问题.

若D₃=（交通事故，发生率，低），C₃=（摩托车及电动自行车 ${v_3}({t_0})$ ，路面通行数量，多），则 ${P_3} = {D_3}*{C_3}$ 是一个矛盾问题（即， ${N_3} > 0$ ）. 也就是说：如果路面通行的摩托车及电动自行车数量多的话，是不太可能降低交通事故发生率的. 对于矛盾问题P₃，显然C₃往减小的方向变化有利于其解决，所以P₃的矛盾符号函数取负值，即： ${S_3}({V_c},{V_d}) < 0$ .

若D₀=（快递，收取速度，快），C₀=（电动自行车，允许通行路段 ${v_0}({t_0})$ ，较多），则 ${P_0} = {D_0}*{C_0}$ 是一个相容问题，（即， ${N_0} \leqslant {\rm{0}}$ ）. 也就是说：有了电动自行车的最后一公里送达，快递的收取速度加快不少. 对于相容问题P₀，显然C₀往增多的方向变化更有利于目标的达成，所以可以认为P₀的矛盾符号函数取正值，即： ${S_0}({V_c},{V_d}) > 0$ .

现在，为了解决矛盾问题P₃，作变换 ${T_{{P_3}}} = (e,{T_{{C_3}}})$ ： ${T_{{C_3}}}{C_3}$ =（摩托车及电动自行车，路面通行数量 ${v_3}(t)$ ，少）. 即通过对摩托车及电动自行车实施路面限行来控制其通行数量，以此解决交通事故频发问题，使 ${N_1} \geqslant 0$ . 但是，知道： ${C_{\rm{3}}} \sim {C_{\rm{0}}}$ ，所以对路面摩托车及电动自行车的限行也会导致允许电动自行车通行路段的减少，即由传导规则： ${T_{{P_3}}} = > {}_{{P_3}}{T_{{P_0}}}$ ， ${}_{{P_3}}{T_{{P_0}}} = (e,{}_{{C_3}}{T_{{C_0}}})$ ， ${}_{{C_3}}{T_{{C_0}}}{C_0}$ =（电动自行车，允许通行路段 ${v_0}(t)$ ，少）= ${C_0}^\prime $ . 由此可知 $\gamma = \frac{\displaystyle{{v_3}(t) - {v_3}(t0)}}{\displaystyle{{v_0}(t) - {v_0}(t0)}} > 0$ ，又因为 ${S_3}({V_c},{V_d}) < 0$ ， ${S_0}({V_c},{V_d}) > 0$ ，所以

$\eta = {S_3}({V_c},{V_d}) * {S_0}({V_c},{V_d}) * \gamma < 0.$

(15)

因此， ${P_3} - \sim {P_0}$ . $e{D_2} = {D_2}$ ，记： ${P_0}^\prime = {D_0}*{C_0}^\prime $ ，显然， ${N_0}^\prime > 0$ （注： ${N'_0}$ 为 ${P_0}^\prime $ 的矛盾度；N₀为P₀的矛盾度），这时称 ${P'_0}$ 为 ${T_{{P_3}}}$ 关于P₀的变性传导矛盾问题. 即，由于对摩托车及电动自行车进行路面限行导致了允许电动自行车通行路段的减少，而允许电动自行车通行路段的减少又会直接导致快递不能在最后一公里及时送到客户手中. 也就是说，在城市交通这个复杂矛盾问题中对矛盾问题P₃的解决，导致了相容问题P₀变成了一个矛盾问题 ${P_0}^\prime $ ，这就是在定义2中定义的变性传导矛盾问题.

4 结束语

本文通过引入传导相关度、正相关、负相关等反映传导变换本质和内涵的一些重要概念，深入剖析了复杂矛盾问题系统中由原问题的相关问题导致的这一类传导矛盾问题的成因，并通过实例进行了验证. 研究成果为复杂矛盾问题系统中传导矛盾问题的智能化分析提供了一定的理论依据. 但实际的复杂矛盾问题系统中，不仅存在着由原问题的相关问题导致的传导矛盾问题，也存在着由原问题的共轭问题导致的传导矛盾问题，而且这些问题相互联系，构成一个错综复杂的网状关系，一个矛盾问题的解决往往会连带影响很多矛盾问题. 所以这样的复杂矛盾问题系统的分析还有待进一步地研究和探讨.