随着计算机科学技术的发展,数据量呈现爆炸式增长,这些数据中隐藏着许多有用的信息. 聚类分析作为数据挖掘中一种重要的手段,在机器学习、模式识别、电信、生物信息等等领域有着广泛的应用[1],其原理在于通过计算数据之间的相似度,将数据划分成若干个簇.
常见的聚类方法包括:划分法、层次法、基于密度的方法等等. DBSCAN算法[2]属于基于密度聚类的一种算法,其原理是:对于聚类中的每个对象,在给定的半径邻域内的数据对象必须超过某个阀值. 算法简洁,对噪声点不敏感,而且可以发现任意形状的簇. DBSCAN算法在现实世界中有着许多应用,对此国内外学者有着许多研究,文献[3]通过卫星云图热点数据与DBSCAN算法相结合,来提前防止森林火灾. 文献[4]提出一种核DBSCAN算法,实现了对民航客户行为的分析. 文献[5]通过将DBSCAN算法与无线传感技术相结合,以去除噪声点来提高定位的准确性,等等.
DBSCAN算法的不足之处在于以下两点:
(1) 由于需要在整个数据空间构建树,算法需要很大的IO开销,这也是限制算法发展的重要瓶颈之一.
(2) 算法输入参数没有一个很完美的科学标准来作为参考,这就使得人为干扰的因素变得很大,参数选取略有偏差对于聚类的效果有时会呈现出完全不同的效果.
针对DBSCAN算法以上的两个缺点,国内外有许多学者都做了很深入的研究. 在IO开销方面VIJAYALAKSMI S和PUNITHAVALLI M[6]提出了一种以k-dimensional树来代替R树使得算法时间复杂度明显降低;李双庆和慕升弟[7]在基于隐马尔科夫模型的流量背景下,改进了DBSCAN算法,并应用在网络流量的大规模数据,改进后的算法聚类的时间相比传统DBSCAN有着明显的改善. 随着大数据技术的发展,越来越多的学者将DBSCAN算法与云平台相结合,采用并行计算,来降低算法的时间效率;Woong-Kee Loh等[8]提出了一种利用GPU来划分数据,对每个子区域进行聚类.
针对DBSCAN算法在密度不均匀的区域聚类效果不理想的缺点,WANG S M等[9]提出了一种MDBSCAN算法,该算法根据统计学方法来产生两个密度参数以解决DBSCAN算法在密度分布不均匀的数据集聚类效果差问题;文献[10]在OPTICS算法[11]的基础上提出了一种ICA算法对可达距离方面进行改进,改进后的算法可用于处理动态数据集;Campello[12]提出了一种HDBSCAN算法,该算法是DBSCAN算法与基于层次聚类算法相结合而来的,是对OPTICS算法的一种改进,但对于边界点的处理方面效果却不是很理想;Dockhorn[13]针对HDBSCAN算法的缺点提出了m pts-HDBSCAN算法,该算法克服了HDBSCAN算法边界点聚类效果差的问题,但是由于使用的是核心点数量m pts作为全局参数,当数据密度分布相差较大时,聚类的效果不理想.
本文针对m pts-HDBSCAN算法在密度分布不均匀的数据集聚类效果不理想的情况,提出了一种数据分区算法,然后对分区后的子数据集采用m pts-HDBSCAN进行聚类,最后对每一个分区聚类结果进行合并.
1 m pts-HDBSCAN算法介绍m pts-HDBSCAN算法是由DBSCAN算法改进的,算法通过固定参数m pts,然后通过遍历所有可能的数值来自动选择一个合适的ε值. 以下为DBSCAN算法单调性证明:
定义1 dis(x, y),表示两点之间的距离.
定义2
| ${{\rm{N}}_\varepsilon }{\rm{(}}p{\rm{)}} = {\rm{\{ }}q \in D{\rm{|dist(}}p,q{\rm{)}} \leqslant \varepsilon {\rm{\} }}.$ | (1) |
定义3 以半径为ε,最小阈值点为m pts范围内,核心点的数目.
| ${\rm{core}}{{\rm{s}}_{\varepsilon ,{m_{{\rm{pts}}}}}} = {\rm{\{ }}p \in D{\rm{|}}{m_{{\rm{pts}}}} \leqslant \left| {{{\rm{N}}_\varepsilon }{\rm{(}}p{\rm{)}}} \right|{\rm{\} }}.$ | (2) |
证明:对于数据点
| $\left| {{{\rm{N}}_{\varepsilon 1}}{\rm{(}}p{\rm{)}}} \right| \geqslant \left| {{{\rm{N}}_{\varepsilon 2}}{\rm{(}}p{\rm{)}}} \right|$ | (3) |
成立.
由式(3)可知,通过增加ε可以影响核心点数目。
令m pts为一固定值,可得出
| $\left| {{\rm{\{ }}p \in D{\rm{|}}{m_{{\rm{pts}}}} \leqslant \left| {{{\rm{N}}_{\varepsilon 1}}{\rm{(}}p{\rm{)}}} \right|{\rm{\} }}} \right| \geqslant \left| {{\rm{\{ }}p \in D{\rm{|}}{m_{{\rm{pts}}}} \leqslant \left| {{{\rm{N}}_{\varepsilon 2}}{\rm{(}}p{\rm{)}}} \right|{\rm{\} }}} \right|,$ |
即
| $\left| {{\rm{cor}}{{\rm{e}}_{\varepsilon 1,{m_{{\rm{pts}}}}}}} \right| \geqslant \left| {{\rm{cor}}{{\rm{e}}_{\varepsilon 2,{m_{{\rm{pts}}}}}}} \right|.$ | (4) |
由以上的分析可得出,在参数m pts固定的情况下,核心的数量随着聚类半径ε的增大而增多,固定其中的参数m pts,遍历找到最佳匹配参数ε,从而降低多个参数带来的影响.
文献[9]最后通过在多种数据集下进行聚类来证明算法的有效性,但算法只局限在数据密度分布相对均匀的情况下才能取得较好的效果. 由于算法使用一个全局参数m pts进行聚类,当数据的密度分布差异较大时,算法的聚类效果就显得差强人意.
2 m pts-HDBSCAN改进针对m pts-HDBSCAN算法的缺点,本文提出了一种数据分区算法,根据分区阈值这个标准来判定是否将数据进行分区,然后再将划分后的每一个子数据集运用m pts-HDBSCAN算法进行聚类.
对数据进行划分有以下两个好处.
(1) m pts-HDBSCAN算法是以固定一个参数,通过算法的单调性来选取另一个参数,由于使用全局参数,在数据的密度差异性较大时,如果依据密度较大的区域来选取m pts,密度较小的区域会标记为噪声点,反之,密度较大的区域会划分成许多子类;采用数据分区,对密度差异较大的一些区域进行数据划分,对每个区域进行单独聚类就可以很好地解决全局参数带来的误差问题.
(2) 密度相差比较多的区域,数据之间没有多少相关性,对每一个区域的数据进行聚类也可以从侧面解决m pts-HDBSCAN算法的IO开销问题.
在只考虑二维数据的情况下,算法改进分为4大步:
(1) 利用关系型数据库系统中的聚集函数进行数据分布特性的统计.
(2) 根据数据密度差异不同划分成若干个子数据区.
(3) 对每一部分用m pts-HDBSCAN算法进行聚类.
(4) 将最终的数据合并输出.
2.1 数据分区首先将数据库中的数据映射到二维平面上,使用直方图来表示密度分布情况,在画直方图之前首先要确定分组的数目x,一般情形下:
如图1所示,通过平滑曲线依次连直方图中心点,便可得知数据密度的大致情况.
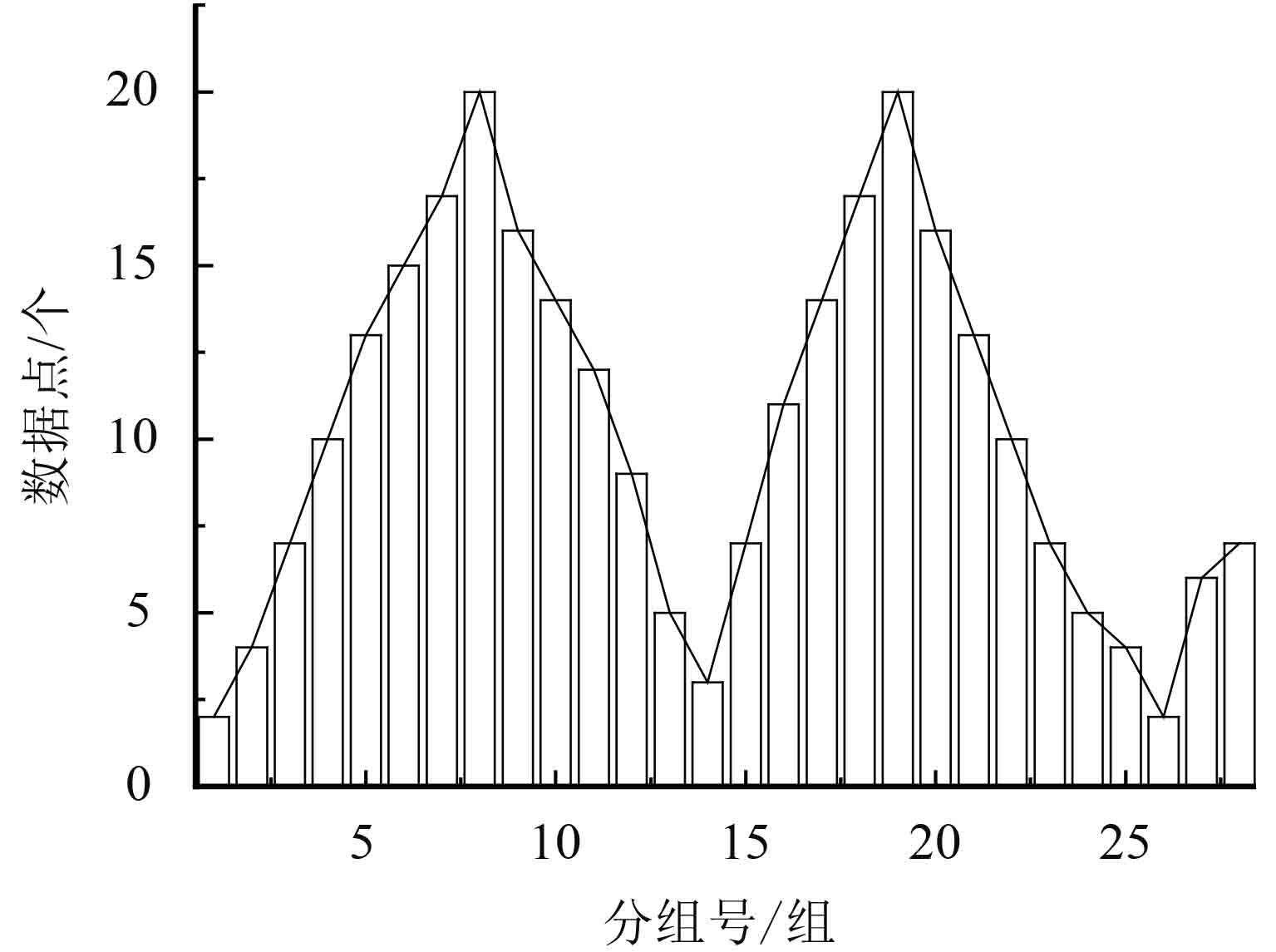
|
图 1 分组密度数据 Figure 1 The density with data of the group |
对于数据分区,国内外学者提出过一些算法,其中大多数与Hadoop等大数据平台有关[15-16],文献[14]没有考虑波峰与波谷之间密度相差不大的情况,对数据进行划分时就会显得意义不大;文献[17]没有考虑在数据连续时要用怎样的标准对数据进行划分.
如图2所示,组号为20、24分别处于波谷,如果按照文献[14]进行划分的话,数据将划分成3个子集. 这样处理显然是不合理的.
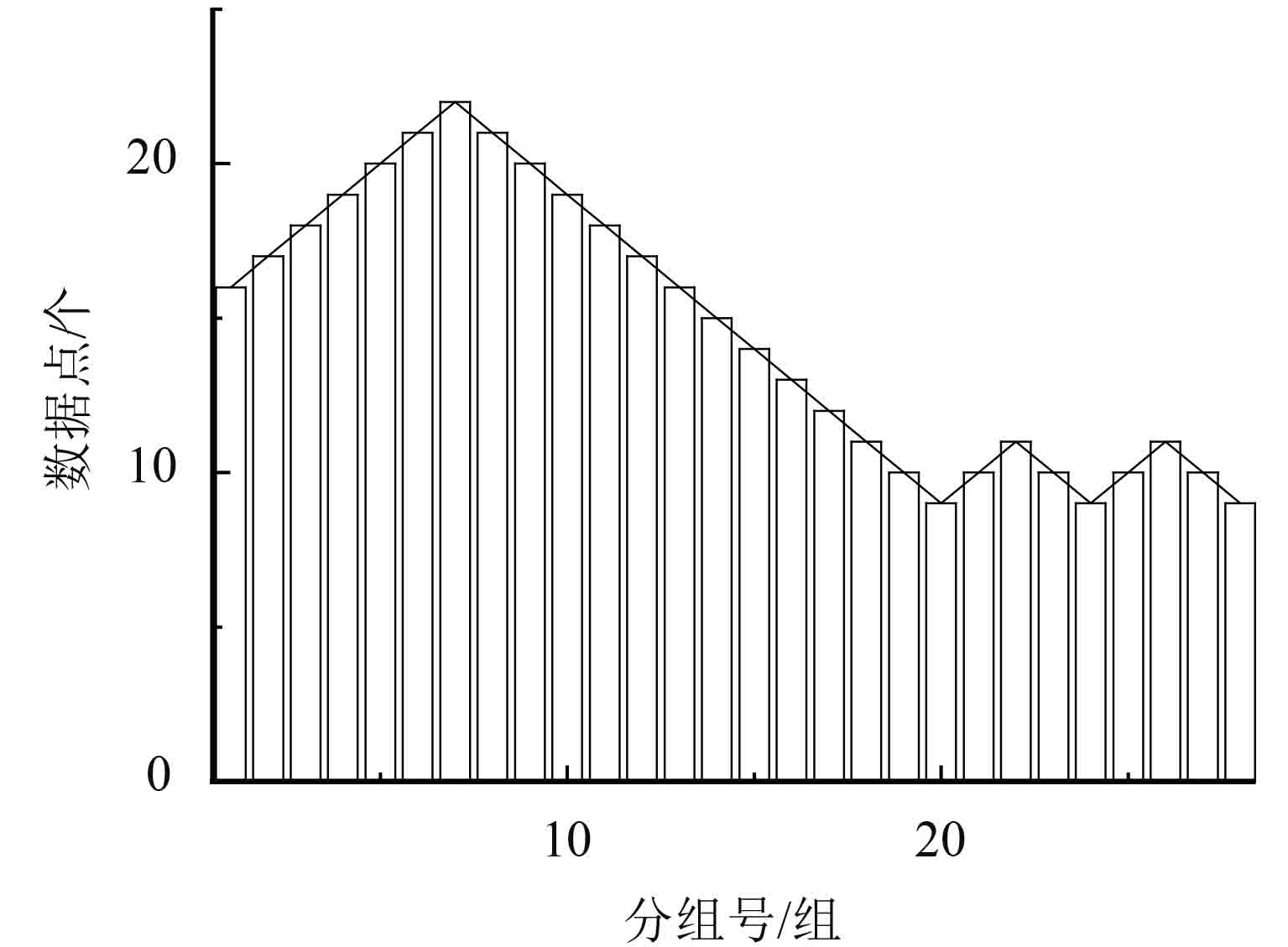
|
图 2 密度变化不大的数据 Figure 2 Density of the data varies little |
为此,本文提出了另一种分区算法,当相邻的波峰与波谷之间的密度差值超过某一阈值(本文称之为分区阈值)时,便在波谷处进行分区处理. 假设第i处的数据密度值用ρ i 来表示. 为了表示方便,本文给出几个定义.
定义1 波峰值peak
i
,表示数据密度为ρ
i
处恰好处于波峰位置,峰值密度为peak
i
. 即
定义2 波谷值though
j
,表示数据密度为ρ
i
处恰好处于波谷位置,波谷密度为though
j
. 即though
j
定义3 分区阈值∆ρ,若相邻波峰与波谷之间的密度差值大于∆ρ时,进行数据划分.
即
其中peak i ,though j 为相邻的波峰波谷.
算法1:Partitioning
2.2 聚类与合并通过数据分区后形成数据子集D
1, D
2, D
3
| $D = {D_1} \cup {D_2} \cup {D_3},\cdots,{D_n}.$ |
且
算法2:Clustering
分区聚类后的子类在进行合并时,要注意两点:
(1) 两个相邻的簇,进行聚类时所取的参数值如果相同,要考虑是不是合并成一个簇,本文提出的判断依据如下所示.
如果
(2) 如果边界点在相邻类的范围内,要考虑是否将其合并,这里根据的依据是公式
同理,ε j 为m pts-HDBSCAN算法生成的最佳聚类半径. 如果符合上式,则合并边界点到该类簇.
算法3:Merging
3 实验验证在本节,取密度分布不均匀数据集,分别用m pts-HDBSCAN算法与改进算法进行对比,从聚类效果来验证改进算法的有效性.
为了增强实验的对比性,本文选取了如图3所示的数据集. 用改进后的算法与原m pts-HDBSCAN算法同时进行聚类.
为了方便起见,本文采用符号“×”来代表噪声点,其他不同的类用不同符号来表示.
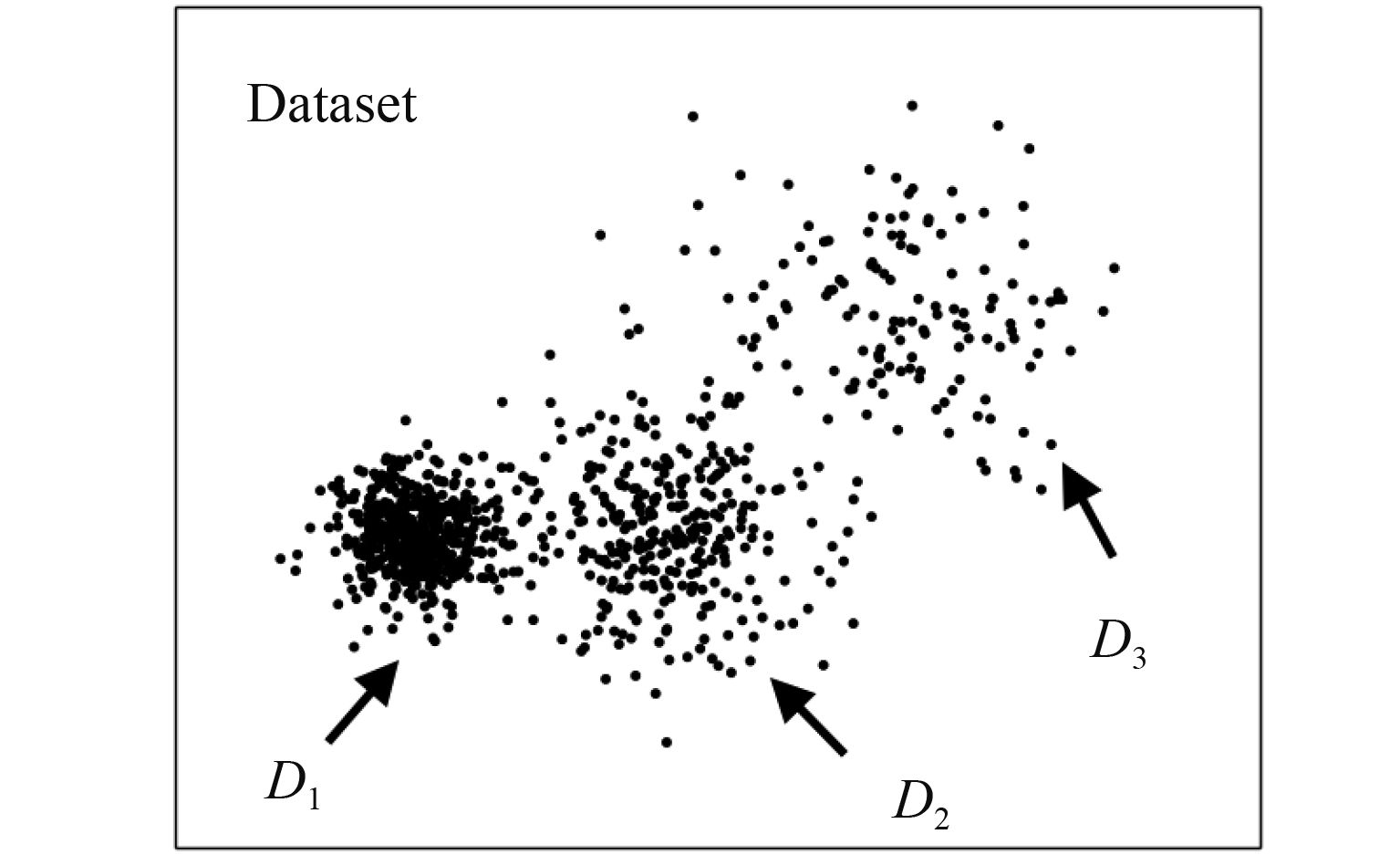
|
图 3 实验数据集 Figure 3 Experimental dataset |
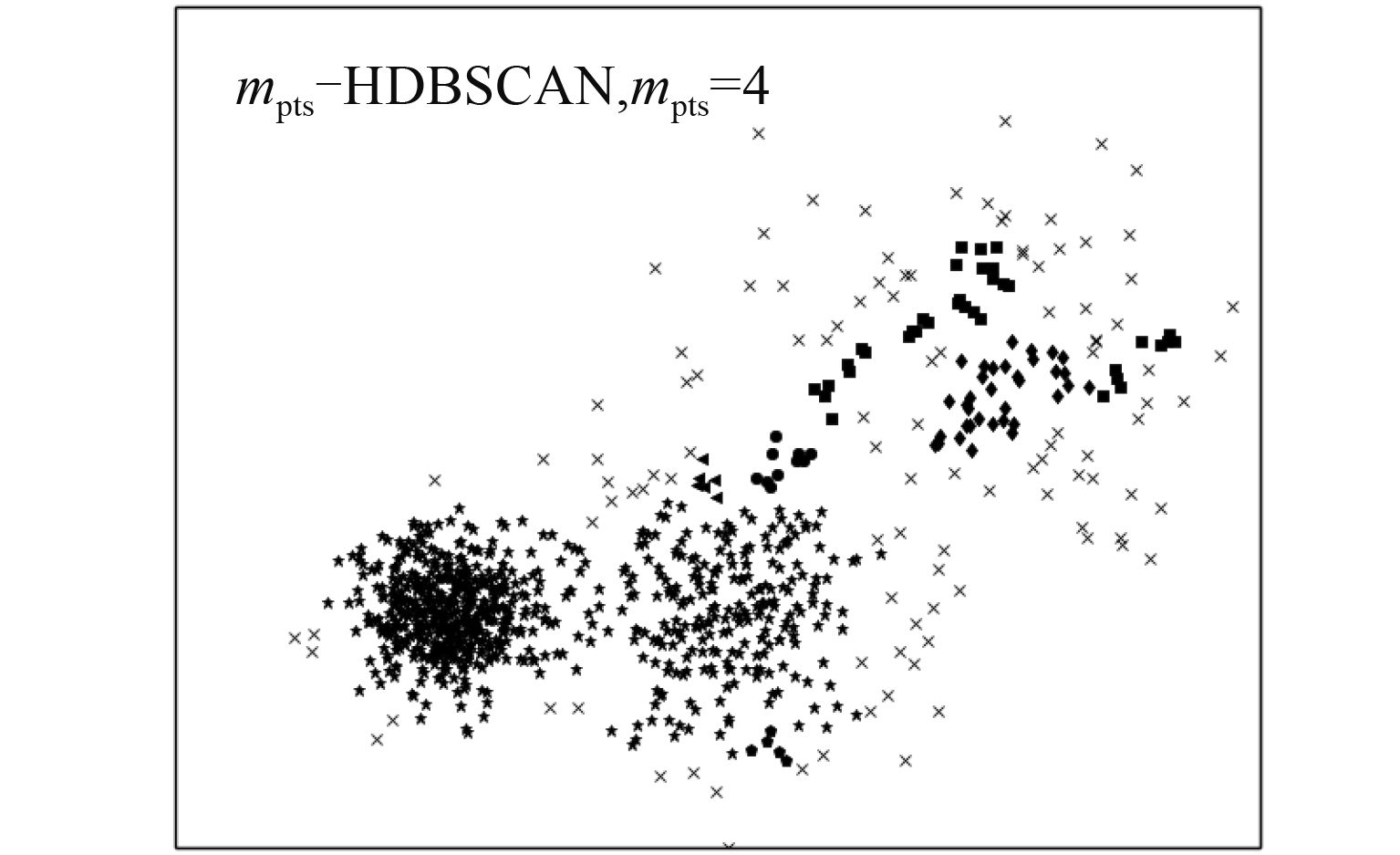
|
图 4 m pts-HDBSCAN算法聚类结果,m pts=4 Figure 4 m pts-HDBSCAN clustering result, m pts=4 |

|
图 5 m pts-HDBSCAN算法聚类结果,m pts=3 Figure 5 m pts-HDBSCAN clustering result, m pts=3 |

|
图 6 改进m pts-HDBSCAN聚类结果 Figure 6 Improved m pts-HDBSCAN clustering result |
通过实验对比后,对于如图3所示的数据集,当m pts的值为3或者4时,m pts-HDBSCAN算法聚类结果如图4与图5所示. 可以发现图3中D 1与D 2两个不同的类将会合并在一起,与此同时数据较稀疏的区域将会划分成多个区域. 最后通过对m pts取不同的值,m pts-HDBSCAN算法都很难得到正确的聚类结果,其原因在于m pts-HDBSCAN算法使用了全局参数来进行聚类,如果按照密度较稠密的区域确定参数值,密度较稀疏的类很容易被认为是边界点,而按照密度较稀疏的区域来确定参数值时,图3中的D 1与D 2将会合并成一个类. 而根据密度的差异预先对数据分区,根据波峰波谷差值是否大于分区阈值,对数据进行划分预处理. 然后对每个子数据分别取不同参数值进行聚类,就可以避免以上问题。改进的m pts-HDBSCAN算法聚类的结果如图6所示,实验结果很明显,改进后的算法聚类的效果要比m pts-HDBSCAN更加理想.
4 结束语本文提出了一种新的数据分区算法来克服m pts-HDBSCAN算法因参数固定对密度分布不均匀的数据聚类效果不理想的缺点. 对划分后的子数据运用m pts-HDBSCAN算法进行聚类,聚类的质量显著提升.
未来的工作将在两个方面展开. (1) 分区算法与固定聚类半径ε时的ε-HDBSCAN算法是否同样具有有效性. (2) 将该算法改进运用到Spark大数据平台上,用于大数据处理.
| [1] |
滕少华, 吴昊, 李日贵, 等. 可调多趟聚类挖掘在电信数据分析中的应用[J].
广东工业大学学报, 2014, 31(3): 1-7.
TENG S H, WU H, LI R G, et al. The application of the adjustable multi-time clustering algorithm in telecom data[J]. Journal of Guangdong University of Technology, 2014, 31(3): 1-7. |
| [2] | HINNEBURG A, KEIM D. An efficient approach to clustering large muiti-media databases with noise[C]//Proceedings of the4th ACM SIGKDD, American Association for Artificial Intelligence. New York: KDD, 1998: 58-65. |
| [3] | NISA K K, ANDRIANTO H A, Mardhiyyah R. Hotspot clustering using DBSCAN algorithm and shiny web framework [C]//Advanced Computer Science and Information Systems (ICACSIS), 2014 International Conference on. [S.l.]: IEEE, 2014: 129-132. |
| [4] |
潘玲玲, 张育平, 徐涛. 核DBSCAN算法在民航客户细分中的应用[J].
计算机工程, 2012, 38(10): 70-73.
PAN L L, ZHANG Y P, XU T. Application of kernel DBSCAN algorithm in civil aviation customer segmentation[J]. Computer Engineering, 2012, 38(10): 70-73. DOI: 10.3969/j.issn.1000-3428.2012.10.020. |
| [5] |
朱烜璋. 基于DBSCAN的无线传感网定位方法[J].
计算机工程与应用, 2013, 49(11): 80-83.
ZHU X Z. Location method based on DBSCAN in wireless sensor networks[J]. Computer Engineering and Applications, 2013, 49(11): 80-83. DOI: 10.3778/j.issn.1002-8331.1210-0189. |
| [6] | VIJAYALAKSMI S, PUNITHAVALLI M. A fast approach to clustering datasets using DBSCAN and pruning algorithms[J]. International Journal of Computer Applications, 2012, 60(14): 1-7. |
| [7] |
李双庆, 慕升弟. 一种改进的DBSCAN算法及其应用[J].
计算机工程与应用, 2014, 50(8): 72-76.
Li S Q, MU S D. Improved DBSCAN algorithm and its application[J]. Computer Engineering and Applications, 2014, 50(8): 72-76. |
| [8] | LOH W K, YU H. Fast density-based clustering through dataset partition using graphics processing units[J]. Information Sciences, 2015, 308(7): 94-112. |
| [9] | WANG S M, LIU Y, SHEN B. MDBSCAN: Multi-level density based spatial clustering of applications with noise [C]//Proceedings of the The 11th International Knowledge Management in Organizations Conference on The changing face of Knowledge Management Impacting Society. Hagen, Germany: ACM, 2016: 21-27. |
| [10] | FU J S, LIU Y, CHAO H C. ICA: An incremental clustering algorithm based on OPTICS[J]. Wireless Personal Communications, 2015, 84(3): 2151-2170. DOI: 10.1007/s11277-015-2517-9. |
| [11] | ANKERST M, BREUNIG M M, KRIEGEL H P, et al. OPTICS: ordering points to identify the clustering structure[J]. ACM, 1999, 28(2): 49-60. |
| [12] | CAMPELLO R J G B, MOULAVI D, SANDER J. Density-based clustering based on hierarchical density estimates[C]//Pacific-Asia Conference on Knowledge Discovery and Data Mining. Berlin Heidelberg: Springer, 2013: 160-172. |
| [13] | DOCKHORN A, BRAUNE C, KRUSE R. An alternating optimization approach based on hierarchical adaptations of DBSCAN [C]//Computational Intelligence, 2015 IEEE Symposium Series on. [S.l.]: IEEE, 2015: 749-755. |
| [14] |
冯少荣, 肖文俊. DBSCAN聚类算法的研究与改进[J].
中国矿业大学学报, 2008, 37(1): 105-111.
FENG S R, XIAO W J. An improved DBSCAN clustering algorithm[J]. Journal of China University of Mining & Technology, 2008, 37(1): 105-111. |
| [15] | HE Y B, TAN H Y, LUO W M, et al. MR-DBSCAN: a scalable map reduce-based DBSCAN algorithm for heavily skewed data[J]. Frontiers of Computer Science, 2014, 8(1): 83-99. DOI: 10.1007/s11704-013-3158-3. |
| [16] | DAI B R, LIN I C. Efficient map/reduce-based dbscan algorithm with optimized data partition [C]//Cloud Computing (CLOUD), 2012 IEEE 5th International Conference on. [S.l.]: IEEE, 2012: 59-66. |
| [17] |
周水庚, 周傲英, 曹晶, 等. 基于数据分区的DBSCAN算法[J].
计算机研究与发展, 2000, 37(10): 1153-1159.
ZHOU S G, ZHOU A Y, CAO J. A data-partitioning-based dbscan algorithm[J]. Journal of Computer Research & Development, 2000, 37(10): 1153-1159. |
 2017, Vol. 34
2017, Vol. 34