随着互联网的迅速发展，网上聚集了海量的数据信息，然而，用户却很难迅速从中找到其需要的信息，出现了“信息过载”现象. 推荐系统是一种解决信息过载的有效方法. 协同过滤算法因其高效和便捷性被广泛地应用在推荐系统中，其核心是找到与用户具有相似兴趣的用户群，然后利用这些用户对物品的评分推测目标用户对物品的感兴趣程度. 协同过滤算法具有较好的推荐效果，但其推荐准确率受限于数据稀疏性问题和冷启动问题. 数据稀疏性问题指的是在用户物品评分矩阵中用户和物品的数量十分庞大而用户对物品的评分数较少，通过这样的稀疏矩阵计算得到的相似度不准确，最终会影响推荐的质量；而冷启动问题指的是对于新加入的用户或物品，由于评分记录不存在从而不能为该用户进行个性化推荐和无法将该物品推荐给对其感兴趣的用户.

矩阵分解技术(Matrix Factorization，简称MF)是一种解决数据稀疏和冷启动问题的有效方法. 传统的矩阵分解技术包括：奇异值分解(singular value decomposition, SVD)算法^[1]、概率矩阵分解(probabilistic matrix factorization, PMF)算法^[2]和非负矩阵分解(non-negative matrix factorization, NMF)算法^[3]等. 这些算法都是将一个高维矩阵通过降维的方法分解为两个或多个低维矩阵，通过低维空间研究高维空间的性质，这在一定程度上缓解了数据稀疏和冷启动问题.

随着社交网络的发展，研究人员将信任关系引入推荐系统，以此缓解数据稀疏和冷启动问题. Yang等^[4]提出的TrustMF模型对引入的用户信任网络信息进行细分，从信任和被信任的角度进行混合推荐；Jamali等^[5]提出的SocialMF方法考虑了信任在社交网络中的传播特性；刘英南等^[6]提出的推荐模型考虑了信任和不信任在社会网络中的传递和动态演化；肖晓丽等^[7]提出了一种融合用户兴趣和信任信息的聚类推荐算法；杜永萍等^[8]通过构建用户声望信任和局部信任的信任网络进行混合推荐. 社交网络信任关系的引入，一定程度上缓解了数据稀疏和冷启动问题，并提高了推荐准确率. 然而，由于目前大多数基于信任的推荐算法引入的都是用户的显式信任关系，显式信任信息需要用户明确指定，考虑到安全和隐私问题，通常较难获取，而且在存在大量用户的推荐系统中，只有少部分用户会明确给出其信任信息，所以显式信任也存在着数据稀疏的问题. 为此，本文提出一种融合隐式信任关系的矩阵分解推荐算法，将从历史数据中挖掘出的隐式信任数据引入推荐系统，以此提高推荐准确率.

1 相关工作 1.1 信任的定义

Guo^[9]给出了信任在推荐系统中的定义，信任被定义为一个人对他人提供有价值评分的能力的信赖程度. 根据文献[10]，信任具有如下特征：(1) 非对称性，比如用户u信任用户v，但并不代表用户v同样也信任用户u；(2) 传递性，传递性是在基于信任的推荐系统中的一个非常重要的特性，它表示如果用户u信任用户v，同时用户v也信任用户p，那么在一定程度上可以认为用户u也信任用户p；(3) 动态性，信任不是一成不变的，它会随着时间而不断变化；(4) 上下文相关性，在不同的上下文环境下，用户的信任值是不同的，如一个用户在电影方面值得信任，但不代表他在其他方面也值得信任.

根据信任数据来源不同，可将信任分为显式信任和隐式信任. 显示信任指的是用户明确给出对其他用户的信任值，范围一般在[0, 1]之间. 在公开的数据集中信任值一般都用0和1表示，其中0表示不信任，1表示信任；隐式信任通常是利用用户的历史评分数据来挖掘出用户间的信任关系. 在关于隐式信任的研究中，O’Donovan^[11]提出了两种信任：Profile-level信任和Item-level信任.

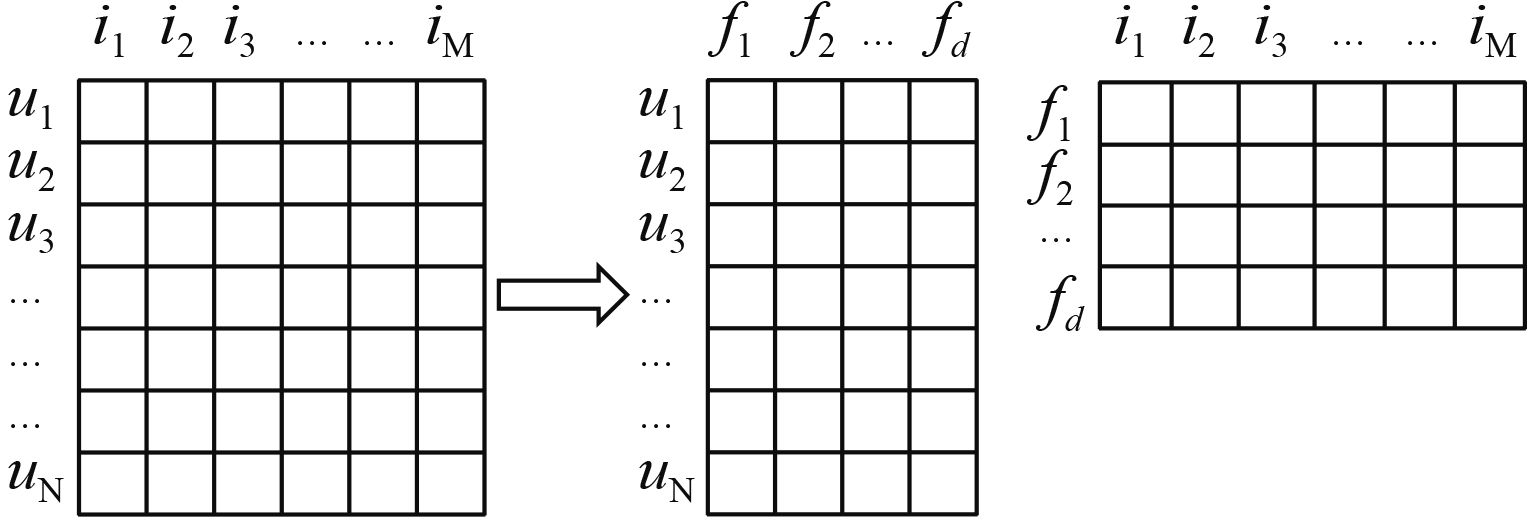
1.2 矩阵分解算法

矩阵分解算法的基本原理是将一个用户–物品评分矩阵 R^N×M分解成两个低阶矩阵，即用户特征矩阵 P^d×N和物品特征矩阵 Q^d×M，其中d为特征数，则 R ≈ P ^T Q ，如图1所示.

基于图1所给的用户–物品评分矩阵分解，可以得到用户u对物品j的预测评分 ${\widehat r_{u,j}}$ ，如式(1)所示.

${\widehat r_{u,j}} = {{q}}_j^{\rm{T}}{{{p}}_u} = \sum\limits_{k = 1}^d {{q_{j,k}}} {p_{u,k}}.$

(1)

其中向量 p _u 为用户特征矩阵 P 中每个用户所对应的向量，向量 q _j 为物品特征矩阵 Q 中每个物品所对应的向量，p _u,k 表示用户u在第k个特征的兴趣度，q _j,k 表示物品j拥有第k个特征的程度. 另外由于在用户评分矩阵中，每个用户存在着不同的评分标准，即有些用户的评分比较严格，导致某些物品的评分较低，而有些用户的评分比较宽松，导致某些物品的评分较高. 为了解决这个问题，Koren Y^[12]提出基准偏移量b _u,j ，更新后的评分预测模型为

${\widehat r_{u,j}} = {b_{u,j}} + {{q}}_j^{\rm{T}}{{{p}}_u}.$

(2)

其中 ${b_{u,j}} = {b_u} + {b_j} + \mu $ ；b _u 、b _j 分别代表用户u和物品j的评分偏置；μ表示全局平均评分.

用户–物品评分矩阵中不仅包含用户对物品的评分，还包含一些额外的用户隐式反馈信息，这些隐式反馈信息告诉我们用户对哪些物品进行了评分，它反映了用户的偏好，从中可挖掘出用户对某个特征的喜好程度. 通过使用这些隐式反馈信息，可以更好地探索用户的行为，能有效缓解数据稀疏和冷启动问题，提高推荐的准确度. 为此，SVD++算法^[12]在SVD算法的基础上，引入了用户隐式反馈信息，通过增加另一个物品特征集合，即对每一个物品i，都有一个与之相关联的d维特征向量 y _i ∈ R^d，其评分预测模型为

${\widehat r_{u,j}} = {b_{u,j}} + {{q}}_j^{\rm{T}}({{{p}}_u} + |{I_u}{|^{ - \frac{1}{2}}}\sum\limits_{i \in {I_u}} {{{{y}}_i}} ).$

(3)

其中I _u 为用户u评分过的物品集， ${{{p}}_u} + |{I_u}{|^{ - \frac{1}{2}}}\sum\limits_{i \in {I_u}} {{{{y}}_i}} $ 表示用户u的特征偏好程度.

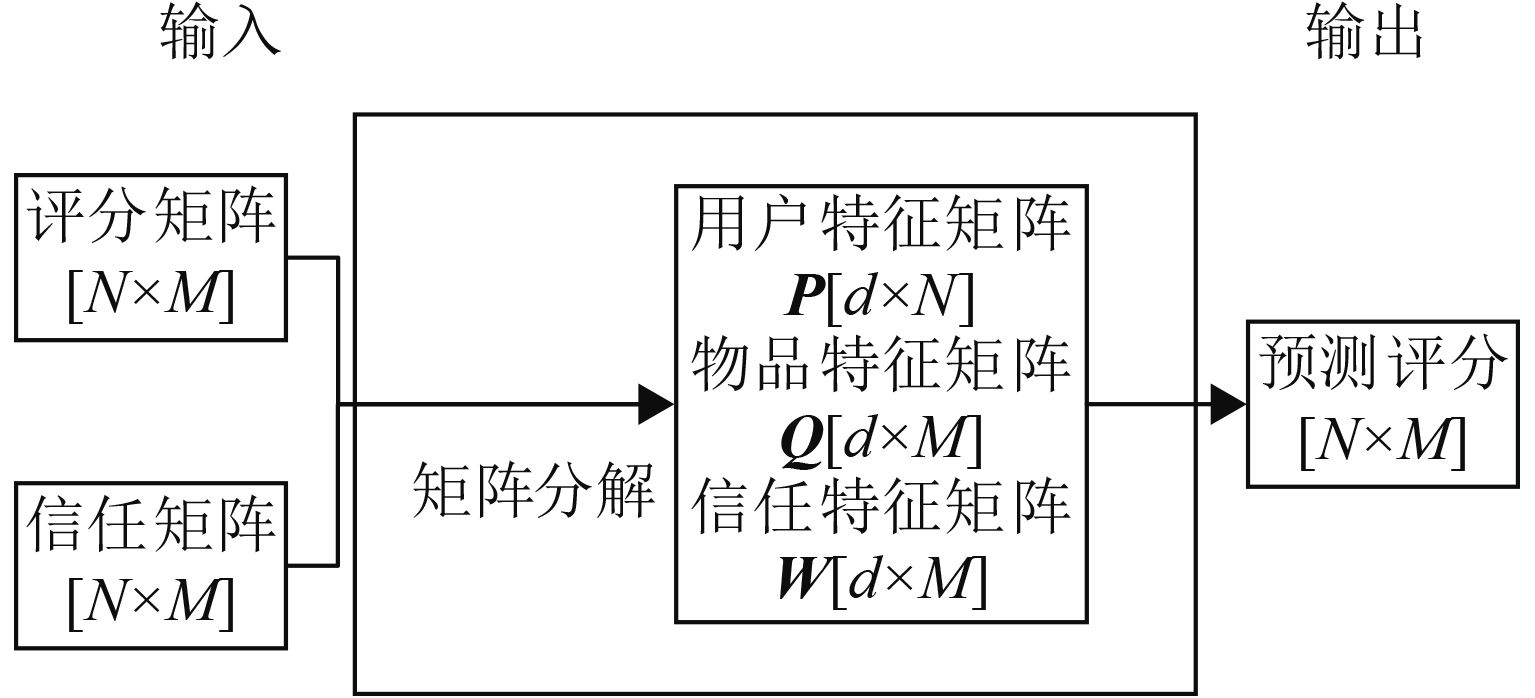
为了进一步缓解数据稀疏和冷启动问题，提高推荐准确率，信任关系被引入了推荐系统. TrustSVD^[13]在SVD++算法的基础上引入用户间的显式信任关系，其基本原理是认为用户更倾向于喜欢他们信任的用户的推荐，在评分上表现为用户的评分更受其信任用户的影响，TrustSVD将这种影响引入用户的评分预测中. 算法的基本流程如图2所示.

通过对用户评分矩阵 R 和信任矩阵 T 进行矩阵分解，即 R ≈ P ^T Q ， T ≈ P ^T W ， ${\widehat t_{u,v}} = {{w}}_v^{\rm{T}}{{{p}}_u}$ ，其评分预测模型为

${\widehat r_{u,j}} = {b_{u,j}} + {{q}}_j^{\rm{T}}({{{p}}_u} + |{I_u}{|^{ - \frac{1}{2}}}\sum\limits_{i \in {I_u}} {{{{y}}_i}} + |{T_u}{|^{ - \frac{1}{2}}}\sum\limits_{v \in {T_u}} {{{{w}}_v}} ).$

(4)

其中 w _v 为信任特征矩阵 W 中每个被信任者所对应的向量， q _j ^T w _v 可解释为用户u受其信任用户v对其在物品j上的评分的影响，T _u 表示用户u的显式信任集合.

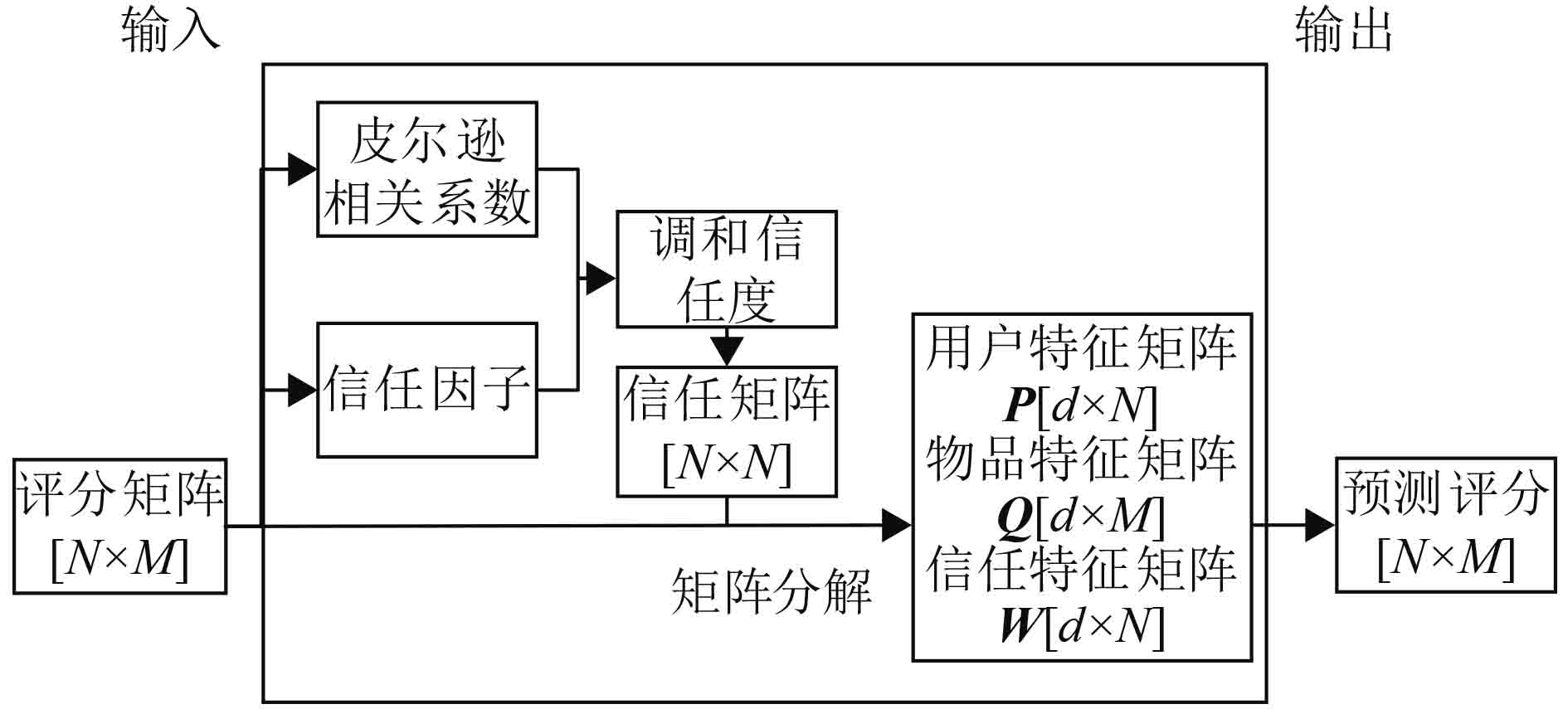
2 融合隐式信任的矩阵分解推荐算法

由于在TrustSVD算法中引入的信任关系是显式信任关系，而显式信任存在着较难获取和数据稀疏的问题，为此，本文提出一种融合隐式信任关系的矩阵分解推荐算法，在SVD++算法的基础上引入从用户的历史数据中挖掘出的隐式信任信息来提高推荐准确率. 该算法的基本流程如图3所示，整个流程可分为两个部分，其中第一部分是隐式信任度的计算，主要是根据用户–物品评分矩阵计算用户间的皮尔逊相关系数和每个用户在整个推荐系统中的信任因子^[14]，然后通过调和信任度得到用户间的隐式信任度，最终形成隐式信任矩阵；第二部分是对评分矩阵和信任矩阵进行矩阵分解，最终得到用户特征矩阵、物品特征矩阵和信任特征矩阵.

2.1 隐式信任的度量 2.1.1 皮尔逊相关系数

在传统的推荐算法中，皮尔逊相关系数是计算用户相似度的一种经典算法，其相关公式为

${S_{u,v}} = \frac{{\sum\nolimits_i {({r_{u,i}} - \overline {{r_u}} )({r_{v,i}} - \overline {{r_v}} )} }}{{\sqrt {\sum\nolimits_i {{{({r_{u,i}} - \overline {{r_u}} )}^2}} } \sqrt {\sum\nolimits_i {{{({r_{v,i}} - \overline {{r_v}} )}^2}} } }}.$

(5)

其中，r _u,j 和r _v,j 分别表示用户u和用户v对项目i的评分， $\overline {{r_u}} $ 和 $\overline {{r_v}} $ 表示用户u和用户v的总体评分的平均值.

Papagelis M等^[15] 通过皮尔逊相关系数来度量用户间的信任值. 对于给定阈值，当皮尔逊相关系数大于它时，则认为该值为用户间的信任值，否则为0.

$T_{u,v}' = \left\{ {\begin{array}{*{20}{l}}{{S_{u,v}},、\;\;\;\;{\rm{if }}\; {{\rm{S}}_{u,v}} > {\theta _s},|{I_{u,v}}|{\rm{ > }}{\theta _I};}\\{0,\;\;\;\;{\rm{ otherwise}}{\rm{.}}}\end{array}} \right.$

(6)

其中 ${\theta _s}$ 表示用户相似度的阈值，I _u,v 表示用户u和用户v的共同评分项目数， ${\theta _I}$ 表示共同评分项目数阈值. Sotos等^[16]通过实验证明只有当 ${\theta _s}$ =0.707时，即S _u,v >0.707，该信任值才具有传递性，因此取 ${\theta _s}$ =0.707. 另外取 ${\theta _I}$ =2，表示当用户共同评分数大于2时，该相关系数才有意义.

2.1.2 信任因子

信任因子^[14]可以用来表示用户在整个推荐系统中被其他用户信任的程度，其取值范围在[0, 1]之间，信任因子越大，则表示该用户越值得信任.

在实际生活中，新人往往倾向于向别人提出咨询. 对于在系统中积极评价的用户，其信任值要高于消极评价的用户的信任值. 假设f _u 为用户u对项目的评价个数，当f _u 的值越高时，则说明用户u越受其他用户信任；反之，当f _u 的值越低时，则说明用户u受其他用户的信任程度也越低. 设q _u 为用户u对其他用户的最近邻次数，次数越多，表明越受其他用户信任；反之，则说明该用户越不受其他用户信任.

设T _u 为用户u的信任因子，其计算公式可表示为

${T_u} = \frac{{2(1 - 1/\ln {f_u})(1 - 1/\ln ({q_u} + 3))}}{{2 - 1/\ln {f_u} - 1/\ln ({q_u} + 3)}}.$

(7)

2.1.3 调和信任度

本文的调和信任度同时考虑皮尔逊相关系数和信任因子两方面对权重的影响，采用调和平均数公式，其计算公式为

${T_{u,v}} = \frac{{2T_{u,v}' \times {T_v}}}{{T_{u,v}' + {T_v}}}.$

(8)

其中，T _u,v 表示用户u对用户v的调和信任度，T’ _u,v 表示用户u和用户v的皮尔逊相关系数，T _v 表示用户v的信任因子. 隐式信任度计算算法的具体描述如下所示.

算法1　隐式信任度计算算法

输入：用户物品评分矩阵 R 输出：隐式信任度1 根据公式(1)计算用户u和用户v的相似sim(u, v)2 if sim(u, v)> ${\theta _s}$ 3 trust1(u, v)=sim(u, v)4 else5 trust1(u, v)=06 计算用户v的评分项目数count7 q=neighbourTimes[v] //用户v作为其它用户的最近邻次数8 trust2(v)=2*(1-1 /log(count))*(1-1/log(q+3))/(2-1/log(count)-1/log(q+3))9 trust(u, v)=2*trust1(u, v)* trust2(v)/(trust1(u, v)+trust2(v))

2.2 评分预测

本文提出的算法的评分预测模型为

${\widehat r_{u,j}} = {b_{u,j}} + {{q}}_j^{\rm{T}}({{{p}}_u} + |{I_u}{|^{ - \frac{1}{2}}}\sum\limits_{i \in {I_u}} {{{{y}}_i}} + |T_u^I{|^{ - \frac{1}{2}}}\sum\limits_{v \in T_u^I} {{{w}}_v^I} ).$

(9)

其中T _u^I表示用户u的隐式信任集合； q _j ^T、 w _v^I可解释为用户u受其隐式信任用户v对其在物品j的评分的影响.

为了避免拟合问题，该模型的损失函数将采用TrustSVD算法的正则化策略，即给予评分数较多的用户和流行物品更小的惩罚，给予冷启动用户和物品更大的规范，得到的目标函数为

$\begin{aligned}& L = \frac{1}{2}\sum\limits_u {\sum\limits_{j \in I{}_u} {{{({{\widehat r}_{u,j}} - {r_{u,j}})}^2} + \frac{{\lambda _t^I}}{2}\sum\limits_u {\sum\limits_{v \in T_u'} {{{({{\widehat t}_{u,v}} - t_{u,v}^I)}^2}} } } }+ \\ &{\rm{ }}\frac{\lambda }{2}\sum\limits_u {|{I_u}{|^{ - \frac{1}{2}}}b_u^2 + } \frac{\lambda }{2}\sum\limits_j {|{U_j}{|^{ - \frac{1}{2}}}b_j^2}+ \\ &{\rm{ }} \sum\limits_u {(\frac{\lambda }{2}|{I_u}{|^{ - \frac{1}{2}}} + \frac{{\lambda _t^I}}{2}|T_u^I{|^{ - \frac{1}{2}}})} ||{{{p}}_u}||_F^2+\\ &{\rm{ }}\frac{\lambda }{2}\sum\limits_j {|{U_j}{|^{ - \frac{1}{2}}}||{{{q}}_j}||_F^2 + } \frac{\lambda }{2}\sum\limits_i {|{U_i}{|^{ - \frac{1}{2}}}||{{{y}}_i}||_F^2} +\\ &{\rm{ }}\frac{\lambda }{2}|T_v^{I + }{|^{ - \frac{1}{2}}}||{{w}}_v^I||_F^2.\end{aligned}$

(10)

其中，U _i 、U _j 分别为对物品i和物品j评过分的用户集合；T _v ^I+为隐式信任用户v的用户集合.

为了得到损失函数在最小值情况下的 P 、 Q 和 W ，采用随机梯度下降法进行求解，算法的具体描述如下所示.

算法2　融合隐式算法的矩阵分解推荐算法.输入：用户–物品评分矩阵 R ，隐式信任矩阵 T ，学习率α，最大迭代次数K输出：潜在特征矩阵 P 、 Q 、 W 1 初始化 P ， Q ， W ，b _u ，b _j 2 for iter= $\displaystyle 1, 2, \cdots ,$ Kdo3 for each<u, j>∈ R , each<u, v>∈ T 4 根据公式(9)计算用户u对物品j的预测评 ${\widehat r_{u,j}}$ 5 计算预测评分和实际评分的差值 ${e_{u,j}} = {\widehat r_{u,j}} - {r_{u,j}}$ 6 计算预测信任和实际信任的差值 ${e_{u,v}} = {\widehat t_{u,v}} - t_{u,v}^I$ 7 ${b_u} \leftarrow {b_u} - \alpha ({e_{u,j}} + \lambda |{I_u}{|^{ - \frac{1}{2}}}{b_u})$ 8 ${b_j} \leftarrow {b_j} - \alpha ({e_{u,j}} + \lambda |{U_j}{|^{ - \frac{1}{2}}}{b_j})$ 9 $\begin{array}{l}{{{p}}_u} \leftarrow {{{p}}_u} - \alpha ({e_{u,j}}{q_j} + \lambda _t^I{e_{u,v}}{{w}}_v^I{\rm{ + }}(\lambda |{I_u}{|^{ - \frac{1}{2}}}+\end{array}$ 　 $\begin{array}{l}{\rm{ }} {\lambda _t}|T_u^I{|^{ - \frac{1}{2}}}){{{p}}_u})\end{array}$ 10 $\begin{array}{l}{{{q}}_j} \leftarrow {{{q}}_j} - \alpha ({e_{u,j}}({{{p}}_u} + |{I_u}{|^{ - \frac{1}{2}}}\sum\limits_{i \in {I_u}} {{{{y}}_i}} +\end{array}$ 　 $\begin{array}{l}{\rm{ }}|T_u^I{|^{ - \frac{1}{2}}}\sum\limits_{v \in T_u^I} {{{w}}_v^I} + \lambda |{U_j}{|^{ - \frac{1}{2}}}{{{q}}_j}))\end{array}$ 11 $\forall i \in {I_u}:{{{y}}_i} \leftarrow {{{y}}_i} - \alpha ({e_{u,j}}|{I_u}{|^{ - \frac{1}{2}}}{{{q}}_j} + \lambda |{U_i}{|^{ - \frac{1}{2}}}{{{y}}_i})$ 12 $\begin{array}{l} \forall v \in T_u^I:{{w}}_v^I \leftarrow {{w}}_v^I - \alpha ({e_{u,j}}|{T_u}{|^{ - \frac{1}{2}}}{{{q}}_j}+\end{array}$ 　 $\begin{array}{l}{\rm{ }} \lambda _t^I{e_{u,v}}{{{p}}_u} + \lambda |T_v^{I + }{|^{ - \frac{1}{2}}}{{w}}_v^I)\end{array}$ 13 根据上面所计算出的值更新潜在特征矩阵 P 、 Q 、 W 14 end for 15 end for

3 实验结果及分析 3.1 数据集

本实验所采用的数据集是FilmTrust^[17]，表1给出了该数据集的具体信息.

3.2 评价标准

本文采用平均绝对偏差MAE和均方根误差RMSE作为度量标准，当MAE或者RMSE越小时，则表明推荐准确率越高. 设预测的用户评分集合为 $\{ {P_1},{P_2},\cdots,{P_N}\} $ ，实际的用户评分集合为 $\{ {R_1},{R_2},\cdots,{R_N}\} $ ，则计算公式为

${\rm{MAE}} = \frac{{\sum\nolimits_{i = 1}^N {|{P_i} - {R_i}|} }}{N},$

(11)

${\rm{RMSE}} = \sqrt {\frac{{{{\sum\nolimits_{i = 1}^N {({P_i} - {R_i})} }^2}}}{N}} .$

(12)

3.3 实验结果及分析

为了验证本文推荐算法ITrustSVD的效果，本实验将与SocialMF方法、TrustMF方法、SVD++方法和TrustSVD方法进行比较. 本文的推荐算法ITrustSVD的参数设置如下：λ=0.9，λ _t =0.8，学习率设为0.01，迭代次数100次，特征数d分别取值5和10. 另外对于其他方法的参数设置如下：对于SocialMF方法，λ _u =λ _v =0.001，λ _t =1；对于TrustMF方法，λ=0.001，λ _t =1；对于SVD++方法，λ=0.1；对于TrustSVD方法，λ=1.2，λ _t =0.9. 本实验采用5折交叉验证，每次试验随机选取80%的数据作为训练集，并将剩下的20%的数据作为测试集，实验结果如表2所示.

由实验结果可知，在不同的特征数下，算法ITrustSVD相比其它算法在MAE和RMSE都有一定的提升，特别是与传统的加入隐式反馈信息的SVD++算法和基于显式信任的TrustSVD算法相比，算法ITrustSVD都稍优于上述两种算法. 分析原因可知，本文的隐式信任关系是由皮尔逊相关系数和用户在整个推荐系统中的信任度共同推断得出的，它与用户的偏好和用户在推荐系统中让人信赖的程度有关. 在显式信任较难获取和存在数据稀疏的情况下，引入用户的隐式信任关系对提升整体推荐效果有积极的作用，能在一定程度上提高推荐的准确率.

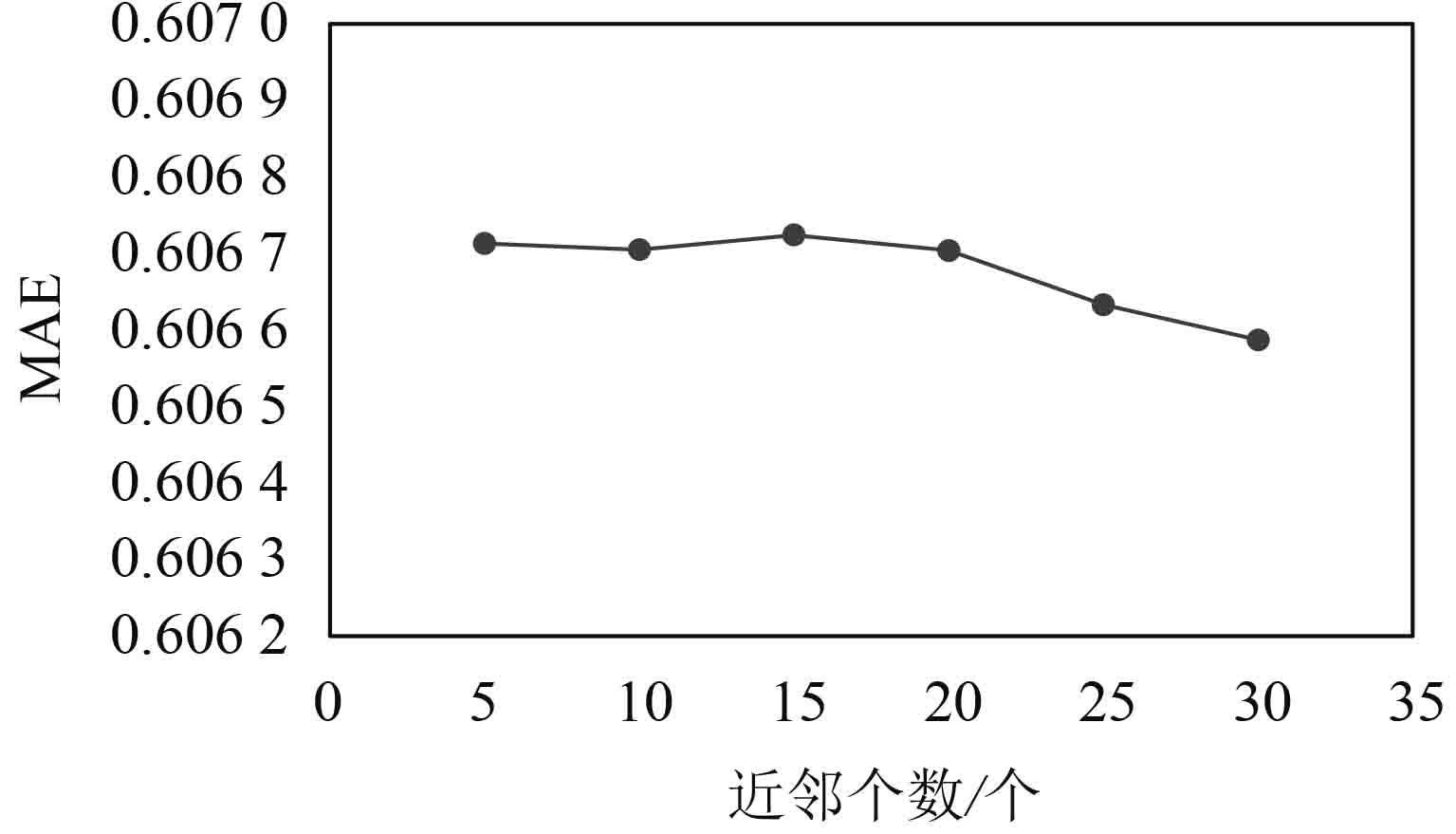
3.4 近邻个数对推荐结果的影响

本文的隐式信任值由皮尔逊相关系数和信任因子两部分构成，而信任因子的影响因素包含用户对项目的评价个数和用户作为其他用户的最近邻次数，不同的近邻个数会导致最近邻次数的不同，最终影响信任因子的结果. 在实验中分别选择近邻个数在5、10、15、20、25、30的情况下，对MAE进行计算分析，实验结果如图4所示. 当近邻个数为30时，MAE的值最低，因此在实验中将近邻个数的值设为30.

4 结束语

本文提出一种融合用户隐式信任关系的矩阵分解推荐算法，通过由皮尔逊相关系数和信任因子计算得到的调和信任度来度量用户之间的隐式信任关系，在一定程度上缓解显式信任较难获取和数据稀疏的缺点. 实验结果表明该算法能提高推荐结果准确率，能更好地为用户做出推荐. 然而，随着数据规模的扩大、迭代次数的增加，算法所需的计算时间也不断增加，因此下一步的工作重点是对算法进行分布式实现.