2. 广东省审计厅 计算机审计中心, 广东 广州 510630
2. Computer Audit Center, Guangdong Audit Office, Guangzhou 510360, China
在线社区使用户更易获取资源和资源共享,也极大地改变了人们之间的交流方式. 好友推荐功能作为社交网络中流行且实用的个性化服务,能让用户结识一些志趣相投的好友,从而提高在线社交网络的用户活跃度,繁荣社区. 然而,单纯为增加用户数及绑定用户关系的过于频繁的推荐方式会让用户产生厌烦. 在好友推荐数受限的情况下,精准推荐已成为当前推荐机制研究的重要问题[1]. 社交网络中因信息过载而面临的过度推荐问题与受限推荐解决方式已成为工业界与学术界关注热点[2].
从好友推荐的用户相似度矩阵可知,一个好友可以推荐给多个好友,而多个好友可以推荐给同一个好友,因此好友推荐是一种多对多关系. 进而受限推荐问题可转换为一类多对多指派问题,即在推荐数与接纳数等资源受限的情况下,通过指派实现精准推荐. 据此,本文以大型教学与科研协作平台学者网为研究背景,引入基于角色的协同模型E-CARGO对推荐机制进行建模[3-6],将好友推荐转化为多对多指派问题,使用带回溯的Kuhn-Munkres算法(KM B)对推荐受限情况下最优推荐指派进行了研究与解决.
1 相关工作分析推荐系统被广泛接受的概念和定义是Resnick和Varian在1997年给出的:它利用电子商务网站向客户提供商品信息和建议,帮助用户完成决定应该购买什么产品,模拟销售人员帮助客户完成购买过程[7]. 对于在线社交网络,好友推荐是其研究与重点之一.
如高灵渲等[8]提出新的基于CMeans聚类方法的混合推荐系统,可以学习用户的兴趣和自动建议消费者最好的产品,应用于电子商务推荐系统;黄创光等[9]提出一种不确定近邻的协同过滤推荐算法,该算法基于用户以及产品的相似性计算,自适应地选择预测目标的近邻对象作为推荐群,同时计算推荐群中推荐把握概率较高的信任子群,最后通过不确定近邻的动态度量方法,来对预测结果进行平衡的推荐;贾大文等[10]分析了目前主流社会媒体网站基于用户自建组的信息共享机制所存在的问题以及传统推荐技术在效率上的问题,提出了一种新的基于用户偏好自动分类的社会媒体数据共享和推荐方法;刘树栋[11]提出一种基于移动用户位置的网络服务推荐方法,该方法有效地提高了网络服务推荐的准确性和可靠性,同时缓解了推荐过程中可能存在的数据稀疏性以及冷启动问题;孙光福等[12]通过衡量用户(产品)之间的关系寻找相似的邻居用户(产品),可以更准确地识别用户的个人兴趣,从而有效提高协同过滤推荐精度,为此,提出基于时序行为的协同过滤推荐算法;陈克寒等[13]提出一种基于两阶段聚类的推荐算法GCCR,将图摘要方法和基于内容相似度的算法结合,实现基于用户兴趣的主题推荐;李美子等[14]针对社交网络中无法有效管理陌生推荐安全性难题,提出了一种基于信任的评估推荐控制模型(TRCM);Ma等[15-16]研究了如何利用用户间的信任关系来进一步提高传统推荐算法的性能,并给出了一种能够将信任关系信息进行融合的概率矩阵分解框架. 王玙等[17]首先提出了社交圈检测算法,进而定义用户间的社交圈相似性,基于社交圈相似程度为用户推荐新朋友;张志军等[18]针对移动通信网络领域中个性化服务推荐问题,结合社会化网络分析方法,提出一种融合多种上下文信息的社交网络推荐算法. 该算法在利用用户的地理位置和时间信息的基础上,深入挖掘潜在的用户社会关系,辅助用户寻找与其偏好相似的用户,然后结合移动用户的社会关系进行相应的推荐,有效解决推荐的准确性问题. Silva等[19]利用拓扑图与遗传算法相结合,观察用户行为的相似度,从而实现推荐好友. 蒋盛益等[20]提出了一种协同过滤推荐算法,该算法的主要思路是先对大型社交网络进行快速的社区检测,在社区划分的基础上使用协同过滤推荐算法,以此能快速地得到推荐结果. 王勇等[21]针对传统推荐算法忽略了用户到商品的距离因素以及评价标准不一致对推荐系统带来的影响等问题,提出了一种基于距离衰减和评分趋势改进的协同推荐算法. 汪岭等[22]针对传统推荐算法没有考虑项目分类、用户兴趣和评分动态性、近邻项目选取方法的不合理等问题,提出了一种基于大数据集的混合动态协同过滤算法.
上述推荐方法是精准而有效的,但却容易被在线社区滥用,频繁推荐而造成用户恶感. 实际上,在线社区的好友推荐应是受限的,一般而言,用户并不希望系统频繁地将自己推荐给别人,或将别人推荐给自己,甚至因被频繁推荐与被推荐,关闭推荐功能,影响了在线社区的良序发展.
若将在线社区的好友视为系统管理资源,则受限推荐可视为资源优化问题,即可转换为资源指派. 但这种指派是建立在多对多基础上的,即一名用户可推荐给多名用户,也可接纳系统推荐的多名用户. 然而,以上推荐算法会向用户推荐大量的好友,而没有根据用户的需求量来推荐好友,故不能做到精准的好友推荐. 在线社交网络好友推荐其实也是一种多对多的指派问题,可以通过用户相似度评分矩阵进行多对多的指派,从而得到精准的好友推荐.
多对多指派是一个开问题. 在前期研究中,Zhu Haibin等[23]对其进行了研究,并在Kuhn-Munkres算法基础上引入了回溯,形成KM B算法(Kuhn-Munkres Algorithm with Backtracking),该算法在不改变KM算法时间复杂度量级的基础上(仍为立方级线性时间复杂度),解决了最优化多对多指派问题. 在此基础上,本文引入基于角色的协同模型E-CARGO对推荐机制进行建模,并以KM B对作为受限推荐下的核心指派算法,对相关问题进行了研究与处理.
2 基于E-CARGO的学者网建模 2.1 基于角色的协同及其E-CARGO模型基于角色的协同(Role-Based Collaboration,简称RBC)是由朱海滨教授提出的协同计算工程方法,其引入了角色作为工程建模与分工合作基础,E-CARGO是其形式化模型[3-6]. E-CARGO模型可以表示为9元组∑::=〈C, O, A, M, R, E, G, S 0, H〉抽象并描述了协作系统的组成部分. 其中A(Agent)表示协作个体单元集合;R(Role)表示角色集合(即任务与需求抽象);G(Group)表示群组集合,可用于表示团队;E用于抽象协作环境;而C和O作为类与对象,使E-CARGO建模得以引入面向对象方法.
RBC的指导思想及E-CARGO模型与在线社区的好友推荐情况是不谋而合的. 在线社区中,每名用户可视为一个代理(Agent),而在参与社区活动时,他们均扮演着不同的角色(Role),形成一定的群组(Group). 因此首先推荐问题即可转换为群组角色指派问题(Group Role Assignment)[3-6]. 据此本文使用E-CARGO模型对受限推荐下的多对多指派问题进行建模.
2.2 基于E-CARGO的学者网受限推荐建模学者网是一个大型教学与科研协作平台,能对学者构建自己的学术圈提供帮助. 该平台强调学者用户间的互动交流,为用户提供创建团队、个性化课程、发布动态信息、分享资源等功能. 分学科、方向与人群进行学术讨论与日常交流,是学者的特性. 在学者网中,用户一般希望结识一些兴趣相投的朋友,因此好友推荐对于学者网是非常重要的.
根据E-CARGO模型,可对学者网建模如下:
定义1 role(角色),r::=〈id, A r ,A o , A c 〉. 其中id是角色的标识号,不同的角色id不一致;A r 表示可以指派该角色的代理集,即用户集;A o 表示角色曾经拥有的代理集,即曾经扮演过这种角色身份的用户;A c 表示该角色当前拥有的代理集.
在学者网中,角色r可表示主动意向结识新朋友的用户.
定义2 agent(代理),a::=〈id, R o , R c , N g 〉. 其中id是代理的标识号;R o 表示曾经扮演过的角色集,如曾经是讲师,学生等;R c 表示当前扮演的角色集;N g 表示当前用户所在的群组.
在学者网中,代理a可表示被推荐结识新朋友的用户.
定义3 group(群组),g::=〈id, e, j, o〉. 其中id是群组的标识号;e表示群组所在的环境;j是一组代理及其扮演的角色对〈a,r〉,o表示群组的目标,即拥有某种特征.
在学者网中,群组g表示在共同环境下的用户群体,如网站中创建的团队或课程.
定义4 最少角色范围向量 L [j](0≤j<n),表示用户本历史周期最少想结识的好友数量,是角色范围向量的下界.
在学者网中,可根据学者前若干个历史周期中主动认识了多少个好友的历史数据,得到 L 向量,然后根据 L 向量预判用户本历史周期可能想认识多少个好友,从而对其进行好友推荐. L 向量是一种受限预判,严格限制推荐数量. 例如,若 L =[3, 2, 3]并使用其作为上限约束,则表示在本历史周期,系统能向且最少能向第一、二、三个用户分别推荐3、2、3个用户,从而做到采纳数受限.
定义5 最多角色范围向量 U [j]( L [j]≤j<n),表示预判学者本历史周期最多想结识的好友数量,是角色范围向量的上界.
相对于 L 向量, U 向量表示在本历史周期,系统能且最多能向用户推荐好友的上限值. 为更好体现受限推荐,减少用户厌烦,本文采用的最少推荐原则,即采用最少角色范围向量 L 进行好友推荐.
定义6 最少代理范围向量 La[i](0≤i<m),表示预判学者在本历史周期最少能被推荐给多少个用户认识,是代理范围向量的下界.
在学者网中,可根据学者前若干个历史周期中被多少个用户主动结识的历史数据,得到 La向量,然后根据 La向量预判学者本历史周期可能想被多少个用户认识. 例如 La=[2, 3, 2]并使用其作为上限约束,则表示在本历史周期,系统能向且最少能把第一、二、三个用户推荐给2、3、2个用户,从而做到推荐数受限.
定义7 最多代理范围向量 Ua[i]( La[i]≤i<m),表示预判学者在本历史周期最多能被推荐给多少个用户结识.
同样的,为更好体现受限推荐,减少用户厌烦,本文采用的最少推荐原则,即采用最少代理范围向量 La进行好友推荐.
实际上,不管是 L 向量还是 U 向量,抑或 La向量还是 Ua向量,作为上下界约束,已能明确好友的受限推荐与采纳范围.
定义8 用户相似度矩阵 Q [i,j](0≤i<m, 0≤j<n),表示学者之间的相似度评分值, Q [i,j]∈[0, 1].
在学者网中, Q 表示被推荐用户和推荐用户的相似度. Q 矩阵的行表示被推荐用户,列表示推荐用户. Q 的值越大表示被推荐用户和推荐用户的相似性越大,推荐的可能性也就越大. 本文中相似度矩阵随机产生,在此基础上进行多对多的仿真指派.
定义9 角色分配矩阵 T [i,j](0≤i<m,0≤j<n),表示该学者是否推荐给用户, T [i,j]∈{0,1}, T [i,j]=1表示推荐该学者给用户, T [i,j]=0表示不推荐该学者给用户.
在学者网中,推荐用户数量可能会比被推荐用户数量多,也就是
学者网的好友推荐是一种多对多的指派问题,例如一个学生可以结识多个教师,而一个教师可以结识多个学生,而指派问题是一种基本组合最优化问题. 多对多指派问题数学形式化如下:
| $\max \{ \sigma = \sum\limits_{i = 0}^{m - 1} {\sum\limits_{j = 0}^{n - 1} {{ Q}[i,j] \times { T}[i,j]} } \}. $ |
subject to
| $ {T}\left[ {i,j} \right] \in \{ 0,1\} \;\;\left( {{\rm{0}} \leqslant i < m,0 \leqslant j < n} \right).$ | (1) |
| $\sum\limits_{i = 0}^{m - 1} { {T}[i,j] = {L}[j]} \;\;\left( {{\rm{0}} \leqslant j < n} \right).$ | (2) |
| $\sum\limits_{j = 0}^{n - 1} { {T}[i,j] \leqslant { {L}^a}[i]} \;\;\left( {0 \leqslant i < m} \right).$ | (3) |
约束条件(1)表示角色分配矩阵 T 的值只能取0或1;约束条件(2)表示角色分配矩阵 T 每一列1的个数总和分别等于向量 L 的每个值;约束条件(3)表示角色分配矩阵 T 的每一行1的个数总和分别小于等于向量 La的每个值. 目标函数就是分配结果最优总值. 从上述可以看出多对多指派问题其实就是在约束条件下找到目标函数最大值,也即整数规划问题.
在推荐算法中,用户相似度 Q 矩阵的计算方法很多,例如根据共同好友比例,互动比例以及兴趣相似度来计算用户相似度 Q 矩阵. 但用户相似度 Q 矩阵的计算并非本文研究重点. 本文重点在于假定给出了用户相似度矩阵后( Q 矩阵),对其进行多对多的指派. 因此重点阐述多对多推荐机制,本文用户相似度 Q 矩阵仅通过实验随机产生,在此谨做说明.
对用于多对多指派的KM B受限推荐算法描述如下:
1) KM B算法的准备阶段.
(1) 随机产生一个m×n的用户相似度矩阵 Q ;
(2) 随机产生一个1×n的预判向量 L ;
(3) 随机产生一个1×m的预判向量 La;
(4) 根据预判向量 L 和预判向量 La分别对相似度矩阵 Q 的列和行进行扩展,扩展成一个k×k的矩阵 M ;
(5) 判断预判向量 L 的总和是否小于预判向量 La,如果是则相似度矩阵 Q 进行行和列置换,相应的 L 和 La也进行置换.
(6) 对于矩阵 M 列下标大于n的列填充0元素.
2) KM B算法的处理阶段.
(1) 简化矩阵 M :矩阵 M 的每行元素减去该行最小的元素,然后每列元素减去该列最小的元素.
(2) 初始化标星:在矩阵 M 中找到一个零元素(Z),如果在该行或者该列没有标记星的零元素,对Z零元素标记星,并调整属于同一个agent的不同行不同列的零元素为不可达.
(3) 覆盖含有标记星的零元素所在的列,如果所有列都覆盖了,跳转到步骤7,否则,继续步骤4.
(4) 没有覆盖的零元素标记撇:找到一个没有覆盖的零元素,对其标记撇,并调整属于同一个agent的不同行不同列的零元素为不可达(标记星的零元素除外).
① 如果含有标记撇的零元素所在的行没有带标记星的零元素,跳转到步骤5,否则,覆盖这一行并且取消覆盖带标记星的零元素所在的列.
② 继续执行以上步骤,直到没有没覆盖的零元素剩余.
③ 找到并保存没覆盖的最小元素值,并执行步骤6.
(5) 构建一系列互相变换的带标记撇的零元素和带标记星的零元素方法如下:
① Z 0代表没有覆盖的带标记撇的零元素.
② Z 1表示Z 0所在的列中带标记星的零元素.
③ Z 2表示Z 1所在的行中带标记撇的零元素.
④ 继续执行以上步骤,直到带标记撇的零元素所在列没有带标记星的零元素.
⑤ 在矩阵 M 中取消带标记星的零元素的星标记,对带标记撇的零元素标记星,擦除所有撇标记和取消覆盖的线.
⑥ 回撤:在矩阵 M 中根据擦除的星标记和撇标记的零元素来调整不可达元素为可达.
⑦ 返回步骤3.
(6) 覆盖行的所有元素加上步骤4找到的最小元素值,没覆盖的列的所有元素减去这个值. 返回步骤4,直到没有任何星标记、撇标记或者覆盖的线.
(7) 指派结果可以通过在矩阵 M 中带星标记的零元素的位置体现出来. 如果 M [i,j]是一个带星标记的零元素,行i关联的元素被分配给列j关联的元素.
通过上述KM B算法处理阶段后,会得到一个分配结果矩阵 T 以及最优用户相似度总评估值.
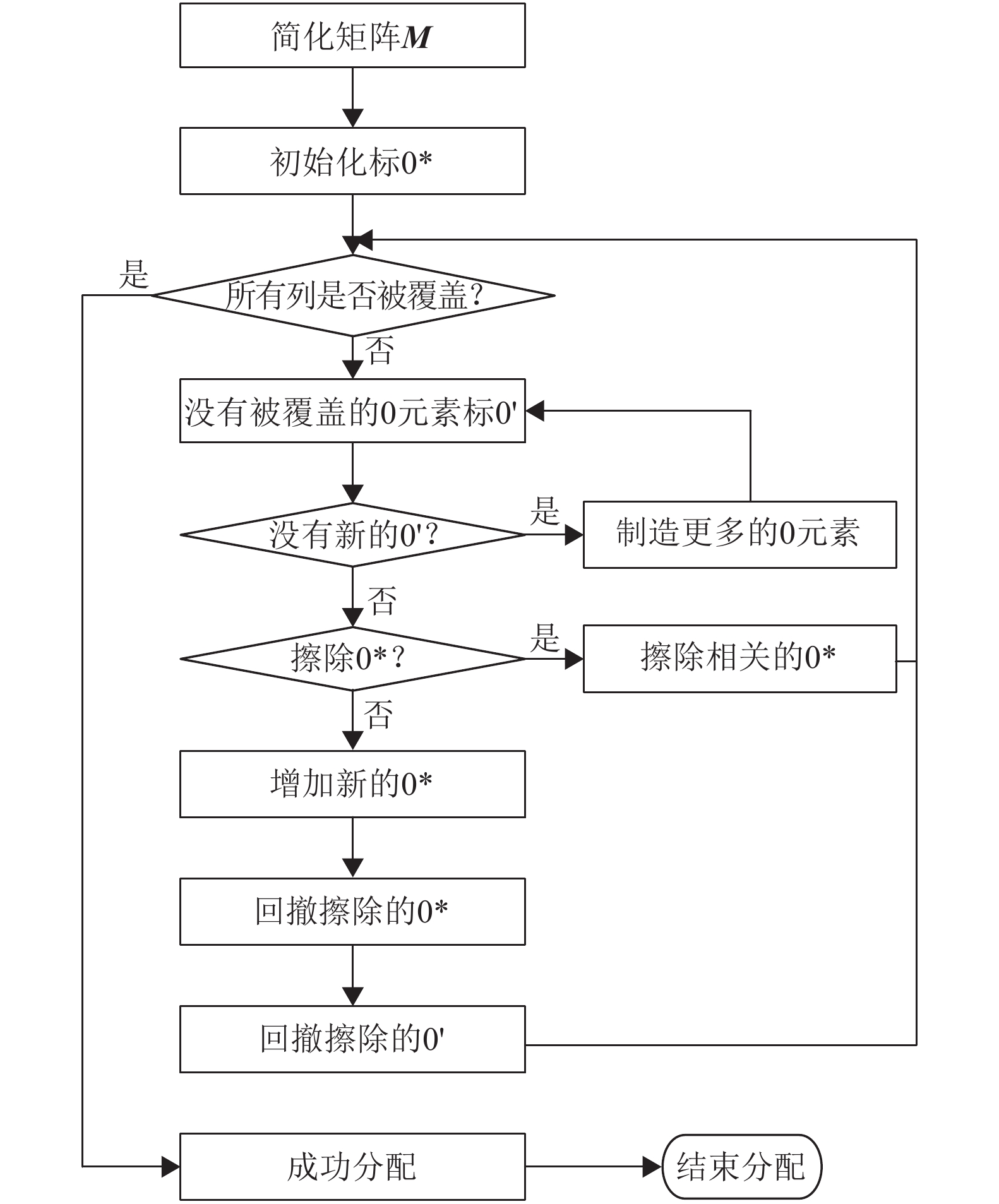
KM B算法的时间复杂度为O(m3)[23],KM B算法的处理阶段流程图如图1所示:
|
图 1 KM B算法的处理阶段流程图 Figure 1 The KM B algorithm flowchart of processing stage |
假定在学者网中有m=10个推荐用户,也就是E-CARGO模型中的10个代理a,n=5个被推荐用户,也就是E-CARGO模型中的5个角色r. 预判向量 L =[4, 2, 4, 1, 4],预判向量 La=[2, 1, 1, 3, 3, 2, 1, 2, 1, 1],假设给定的用户相似度矩阵 Q 为
| ${Q} = \left[ {\begin{array}{*{20}{c}}{{\rm{0}}{\rm{.16}}} & {{\rm{0}}{\rm{.70}}} & {{\rm{0}}{\rm{.83}}} & {{\rm{0}}{\rm{.59}}} & {{\rm{0}}{\rm{.22}}}\\[4pt]{{\rm{0}}{\rm{.40}}} & {{\rm{0}}{\rm{.76}}} & {{\rm{0}}{\rm{.86}}} & {{\rm{0}}{\rm{.32}}} & {{\rm{0}}{\rm{.07}}}\\[4pt]{{\rm{0}}{\rm{.43}}} & {{\rm{0}}{\rm{.54}}} & {{\rm{0}}{\rm{.40}}} & {{\rm{0}}{\rm{.60}}} & {{\rm{0}}{\rm{.28}}}\\[4pt]{{\rm{0}}{\rm{.71}}} & {{\rm{0}}{\rm{.85}}} & {{\rm{0}}{\rm{.13}}} & {{\rm{0}}{\rm{.34}}} & {{\rm{0}}{\rm{.72}}}\\[4pt]{{\rm{0}}{\rm{.69}}} & {{\rm{0}}{\rm{.18}}} & {{\rm{0}}{\rm{.30}}} & {{\rm{0}}{\rm{.80}}} & {{\rm{0}}{\rm{.36}}}\\[4pt]{{\rm{0}}{\rm{.18}}} & {{\rm{0}}{\rm{.79}}} & {{\rm{0}}{\rm{.26}}} & {{\rm{0}}{\rm{.37}}} & {{\rm{0}}{\rm{.44}}}\\[4pt]{{\rm{0}}{\rm{.25}}} & {{\rm{0}}{\rm{.58}}} & {{\rm{0}}{\rm{.58}}} & {{\rm{0}}{\rm{.72}}} & {{\rm{0}}{\rm{.92}}}\\[4pt]{{\rm{0}}{\rm{.61}}} & {{\rm{0}}{\rm{.02}}} & {{\rm{0}}{\rm{.30}}} & {{\rm{0}}{\rm{.68}}} & {{\rm{0}}{\rm{.55}}}\\[4pt]{{\rm{0}}{\rm{.67}}} & {{\rm{0}}{\rm{.35}}} & {{\rm{0}}{\rm{.55}}} & {{\rm{0}}{\rm{.35}}} & {{\rm{0}}{\rm{.10}}}\\[4pt]{{\rm{1}}{\rm{.00}}} & {{\rm{0}}{\rm{.08}}} & {{\rm{0}}{\rm{.08}}} & {{\rm{0}}{\rm{.75}}} & {{\rm{0}}{\rm{.84}}}\end{array}} \right].$ | (4) |
运行KM B算法后得到的最优多对多推荐角色分配矩阵 T 为
| ${T} = \left[ {\begin{array}{*{20}{c}}{\rm{0}} & {\rm{0}} & 1 & {\rm{0}} & {\rm{0}}\\[4pt]{\rm{0}} & {\rm{0}} & 1 & {\rm{0}} & {\rm{0}}\\[4pt]{\rm{0}} & {\rm{0}} & {\rm{1}} & {\rm{0}} & {\rm{0}}\\[4pt]{\rm{1}} & {\rm{1}} & {\rm{0}} & {\rm{0}} & {\rm{1}}\\[4pt]1 & {\rm{0}} & {\rm{0}} & {\rm{1}} & {\rm{0}}\\[4pt]{\rm{0}} & 1 & {\rm{0}} & {\rm{0}} & 1\\[4pt]{\rm{0}} & {\rm{0}} & {\rm{0}} & {\rm{0}} & {\rm{1}}\\[4pt]{\rm{1}} & {\rm{0}} & {\rm{0}} & {\rm{0}} & {\rm{1}}\\[4pt]{\rm{0}} & {\rm{0}} & {\rm{1}} & 0 & {\rm{0}}\\[4pt]{\rm{1}} & {\rm{0}} & 0 & {\rm{0}} & {\rm{0}}\end{array}} \right].$ | (5) |
根据角色分配矩阵 T 向用户推荐好友,减少了向用户推荐大量好友,做到了精准的好友推荐. 而且在约束条件下,用户相似度矩阵总评估值是最优的,上述例子中把角色分配矩阵 T 中值为1的对应于 Q 矩阵的值相加,得到最优的相似度总评估值为10.72,也就是目标函数
| $\max \sum\limits_{i = 0}^{m - 1} {\sum\limits_{j = 0}^{n - 1} {{Q}\left[ {i,j} \right] \times {T}\left[ {i,j} \right]} } = 10.{\rm{72}}.$ |
针对学者网的多对多好友推荐指派问题,以及为了评估KM B的性能,本文测试了不同规模下群组角色分配的平均时间. 由于学者网中,有可能存在推荐用户数比被推荐用户数多,或者推荐用户数比被推荐用户数少,以及推荐用户数和被推荐用户数相等的情况. 因此,本文的实验方案分3种情况[24]:
(1) m>n,即被推荐用户数比推荐用户数多,m表示老师,n表示学生,常用于老师和学生之间的推荐. 本文取
(2) m<n,即被推荐用户数比推荐用户数少,m表示老师,n表示学生,常用于老师和学生之间的推荐. 本文取
(3) m=n,即被推荐用户数和推荐用户数相等,常用于学生之间的推荐或者老师之间的推荐.
实验方案二中,KM B算法会对用户相似度 Q 矩阵进行行列置换, L 和 La也要进行对换处理;实验方案三中,KM B算法会把 L 和 La每个值分别加1以及用户相似度 Q 矩阵对角线的值置为1,因为用户自己可以向自己推荐.
本文实验方案如下:被推荐用户数m=20到m=200,步长20,共10组实验,随机 La=1-3, L =1-3和 La=1-5, L =1-3两类,本文中的用户相似度矩阵 Q 的值随机取0到1的小数,每组随机100次实验.
实验运行环境平台如表1所示.
| 表 1 实验运行环境 Table 1 The experimental running environment |
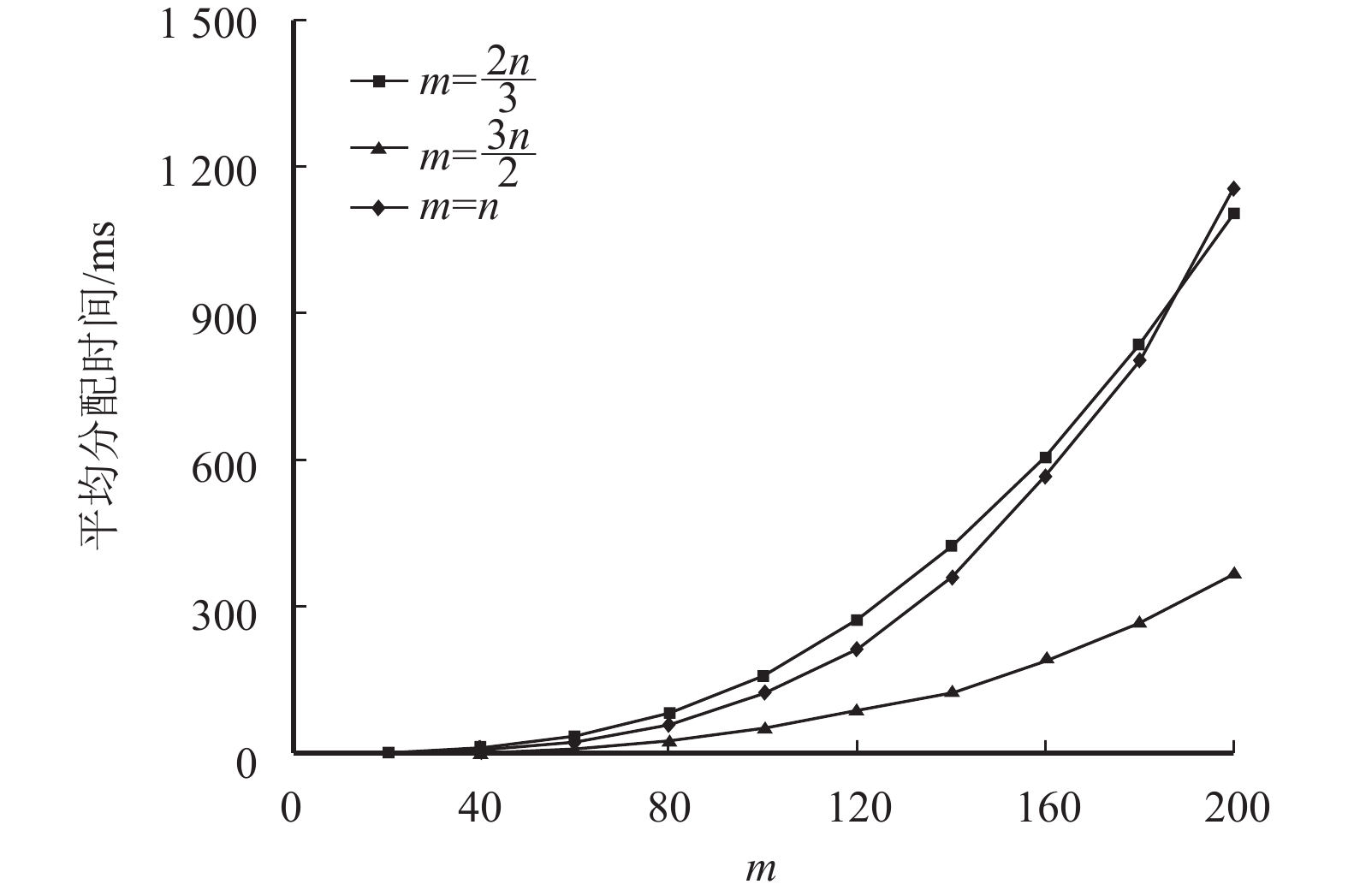
实验一: La=1-3, L =1-3. 实验结果如图2所示.
|
图 2 不同规模下平均分配时间(实验一) Figure 2 The average assignment time in different scales |
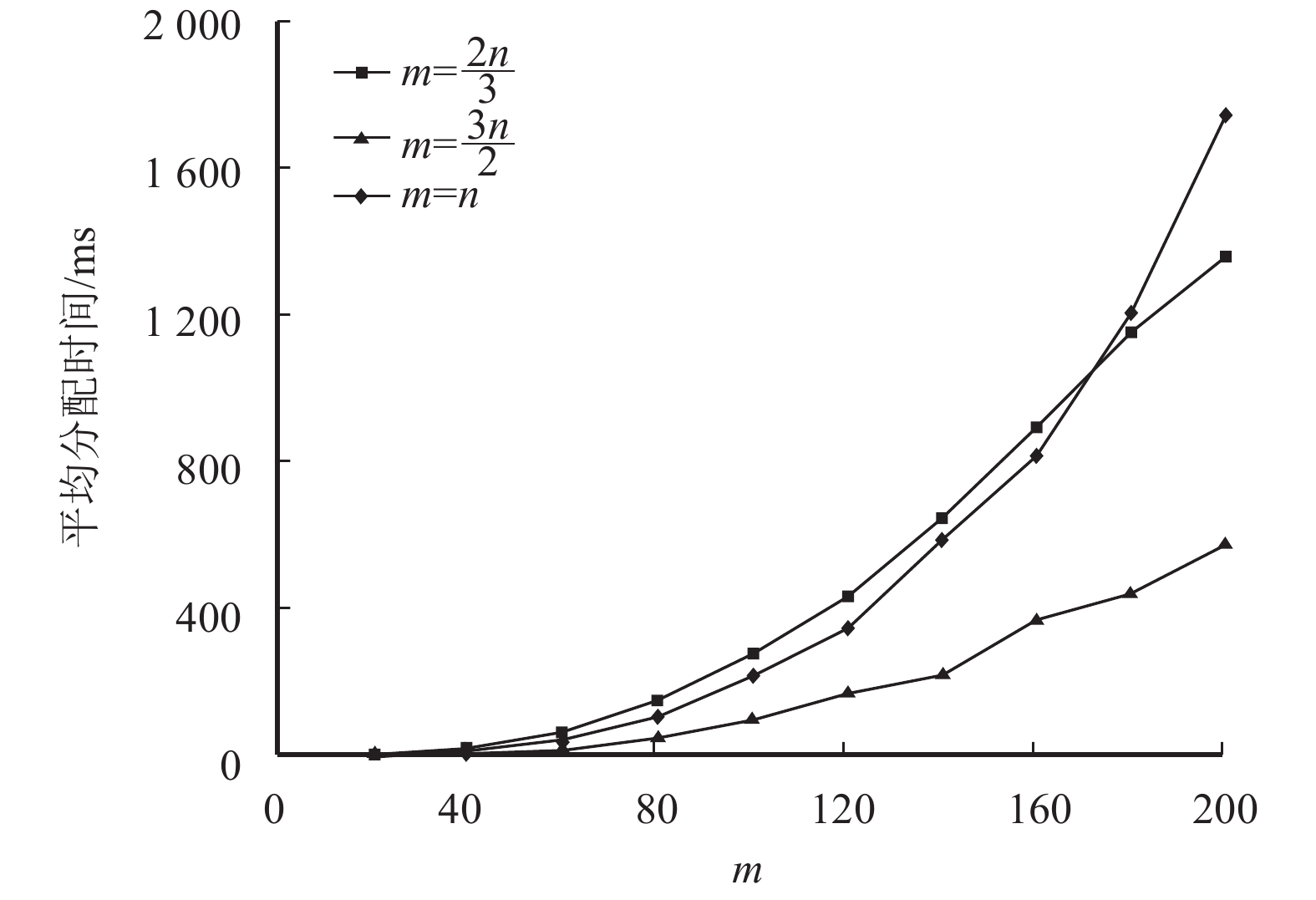
实验二: La=1-5, L =1-3. 实验结果如图3所示.
|
图 3 不同规模下平均分配时间(实验二) Figure 3 The average assignment time in different scales |
从图2和图3可以看出,随着被推荐用户数m的增大,所需要的平均分配时间就会增大,但是所需的平均分配时间也不是很大,当m=200时,所需要的平均分配时间也不超过1.8 s. 3种方案中,当m>n时所需的平均分配时间最小,而随着m的不断增大,m=n所需的平均分配时间大于m<n所需的平均分配时间.
综合上述实验结果,看出KM B算法应用到学者网的好友推荐是高效可行的. 由于其是基于最优化多对多指派的,因此准确度也得到了保证.
5 结束语仿真实验表明,本文提出的推荐机制能在一定程度内完善在线社区推荐机制,对在线社会健康发展形成助力. 相关研究与实验是以大型教学与科研协作平台学者网为研究背景的,由于引入了基于角色的协同模型E-CARGO对推荐机制进行建模,将好友推荐转化为多对多指派问题,并使用了带回溯的Kuhn-Munkres算法(KM B)对好友推荐数与接纳数受限情况下最优推荐指派进行了研究与解决,因此该推荐机制友好、高效、精准,能较好地提升用户体验. 由于本文的用户相似度是随机生成的,未对其如何计算作出研究,因此下一步工作将针对相似度计算做研究,进一步完善在线社区的用户推荐机制.
| [1] |
郭磊, 马军, 陈竹敏. 一种信任关系强度敏感的社会化推荐算法[J].
计算机研究与发展, 2013, 50(9): 1805-1813.
GUO L, MA J, CHEN Z M. Incorporating item relations for social recommendation[J]. Journal of Computer Research and Development, 2013, 50(9): 1805-1813. DOI: 10.7544/issn1000-1239.2013.20130449. |
| [2] |
杨阿祧, 汤庸, 王江斌, 等. 基于博弈的社会网络个性化好友推荐算法研究[J].
计算机科学, 2015, 42(9): 191-219.
YANG A T, TANG Y, WANG J B, et al. Personalized friends recommendation system based on game theory in social network[J]. Computer Science, 2015, 42(9): 191-219. DOI: 10.11896/j.issn.1002-137X.2015.09.036. |
| [3] | ZHU H, ZHOU M C. Role-based collaboration and its Kernel mechanisms[J]. IEEE Transactions on Systems, Man and Cybernetics, 2006, 36(4): 578-589. DOI: 10.1109/TSMCC.2006.875726. |
| [4] | ZHU H, ZHOU M C. Efficient role transfer based on Kuhn–Munkres algorithm[J]. IEEE Transactions on Systems, Man and Cybernetics, 2012, 42(2): 491-496. DOI: 10.1109/TSMCA.2011.2159587. |
| [5] | ZHU H, ZHOU M. M–M role-transfer problems and their solutions[J]. IEEE Transactions on Systems, Man and Cybernetics, 2009, 39(2): 448-459. DOI: 10.1109/TSMCA.2008.2009924. |
| [6] | ZHU H, ZHOU M C, ALKINS R. Group role assignment via a Kuhn-Munkres algorithm-based solution[J]. IEEE Transactions on Systems, Man and Cybernetics, 2012, 42(3): 739-750. DOI: 10.1109/TSMCA.2011.2170414. |
| [7] | RESINICK P, VARIAN H R. Recommender systems[J]. Communications of the ACM, 1997, 40(3): 56-58. DOI: 10.1145/245108.245121. |
| [8] |
高灵渲, 张巍, 霍颖翔, 等. 改进的聚类模式过滤推荐算法[J].
江西师范大学学报(自然科学版), 2012, 36(1): 106-110.
GAO L X, ZHANG W, HUO Y X, et al. Improved clustering filtering recommendation algorithm[J]. Journal of Jiangxi Normal University(Natural Science), 2012, 36(1): 106-110. |
| [9] |
黄创光, 印鉴, 汪静, 等. 不确定近邻的协同过滤推荐算法[J].
计算机学报, 2010, 33(8): 1369-1377.
HUANG C G, YIN J, WANG J, et al. Uncertain neighbor’s collaborative filtering recommendation algorithm[J]. Chinese Journal of Computers, 2010, 33(8): 1369-1377. |
| [10] |
贾大文, 曾承, 彭智勇, 等. 一种基于用户偏好自动分类的社会媒体共享和推荐方法[J].
计算机学报, 2012, 35(11): 2381-2391.
JIA D W, ZENG C, PENG Z Y, et al. A user preference based automatic potential group generation method for social media sharing and recommendation[J]. Chinese Journal of Computers, 2012, 35(11): 2381-2391. |
| [11] |
刘树栋, 孟祥武. 一种基于移动用户位置的网络服务推荐方法[J].
软件学报, 2014, 25(11): 2556-2574.
LIU S D, MENG X W. Approach to network services recommendation based on mobile user’s location[J]. Journal of Software, 2014, 25(11): 2556-2574. |
| [12] |
孙光福, 吴乐, 刘淇, 等. 基于时序行为的协同过滤推荐算法[J].
软件学报, 2013, 24(11): 2721-2733.
SUN G F, WU L, LIU Q, et al. Recommendations based on collaborative filtering by exploiting sequential behaviors[J]. Journal of Software, 2013, 24(11): 2721-2733. |
| [13] |
陈克寒, 韩盼盼, 吴健. 基于用户聚类的异构社交网络推荐算法[J].
计算机学报, 2013, 36(2): 349-359.
CHEN K H, HAN P P, WU J. User clustering based social network recommendation[J]. Chinese Journal of Computers, 2013, 36(2): 349-359. |
| [14] |
李美子, 黄震华, 向阳, 等. 社交网络中基于信任评估的推荐控制模型[J].
同济大学学报(自然科学版), 2014, 42(7): 1117-1122.
LI M Z, HUANG Z H, XIANG Y, et al. Trust evaluation-based recommendation control model in social network site[J]. Journal of Tongji University (Natural Science), 2014, 42(7): 1117-1122. |
| [15] | MA H, KING I, LYU M. Learning to recommend with social trust ensemble[C]//SIGIR '09 Proceedings of the 32nd international ACM SIGIR conference on Research and development in information retrieval. Boston, MA, USA: ACM, 2009: 203-210. |
| [16] | MA H, YANG H, LYU M, et al. Sorec: Social recommendation using probabilistic matrix factorization[C]//CIKM '08 Proceedings of the 17th ACM Conference on Information and Knowledge Management. Napa Valley, California, USA: ACM, 2008: 931-940. |
| [17] |
王玙, 高琳. 基于社交圈的在线社交网络朋友推荐算法[J].
计算机学报, 2014, 37(4): 801-808.
WANG Y, GAO L. Social circle-based algorithm for friend recommendation in online social networks[J]. Chinese Journal of Computers, 2014, 37(4): 801-808. |
| [18] |
张志军, 刘弘. 上下文感知的移动社交网络推荐算法研究[J].
模式识别与人工智能, 2015, 28(5): 404-410.
ZHANG Z J, LIU H. Research on context-awareness mobile SNS recommendation algorithm[J]. Pattern Recognition and Artificial Intelligence, 2015, 28(5): 404-410. |
| [19] | SILVA N B, TSANG I R, CAVALCANTI G D C, et al. A graph-based friend recommendation system using genetic algorithm[C]//IEEE Congress on Evolutionary Computation. [S.l.]: IEEE, 2011. |
| [20] |
蒋盛益, 杨博泓, 吴美玲. 基于快速社区检测的协同过滤推荐算法[J].
广西大学学报(自然科学版), 2013, 38(6): 1408-1412.
JIANG S Y, YANG B H, WU M L. Collaborative filter recommendation algorithm based on fast community detection[J]. Journal of Guangxi University(Natural Science Edition), 2013, 38(6): 1408-1412. |
| [21] |
王勇, 易庭. 基于距离衰减和评分趋势改进的协同推荐算法[J].
广东工业大学学报, 2015, 32(2): 38-42.
WANG Y, YI T. A distance decay and score trends improved collaborative recommendation algorithm[J]. Journal of Guangdong University of Technology, 2015, 32(2): 38-42. |
| [22] |
汪岭, 傅秀芬, 王晓牡. 基于大数据集的混合动态协同过滤算法研究[J].
广东工业大学学报, 2014, 31(3): 44-48.
WANG L, FU X F, WANG X M. Hybrid dynamic collaborative filtering algorithm based on big data sets[J]. Journal of Guangdong University of Technology, 2014, 31(3): 44-48. |
| [23] | ZHU H, LIU D N, ZHANG S Q, et al. Solving the many to many assignment problem by improving the Kuhn–Munkres algorithm with backtracking[J]. Theoretical Computer Science, 2016, 618(3): 30. |
| [24] | 刘艳. 基于E-CARGO的社会网络好友推荐机制研究与仿真[D]. 广州: 广东工业大学计算机学院, 2016. |
 2017, Vol. 34
2017, Vol. 34
