大数据环境下,知识发现更为容易,使得人或系统单元间的协同工作更为频繁与复杂[1-2]. 大数据支持下的“工业4.0”,更要求生产管理从高层上实现工业系统的横向协同以解决横向的企业间系统管理,与纵向协同以处理企业内部系统管理;从低层生产上,需确保工艺流程的灵活协作,保障多批次、小产量状态下产业的获利能力,提高资源利用率与提供高质量、个性化、人性化的产品. 然而存在于各协作单元之间的复杂数据耦合、时空冲突约束往往增加了团队生产与协同管理的难度与复杂度. 如表达任务分发先决条件关联的先序约束,即为最重要而又难于处理的时空约束之一[3].
协同工作[4]的本质在于分工与协作,如果分工明确具体,协作将轻松易行. 而分工的核心在于指派,如能在任务指派模型与算法中纳入对约束关系的表达与处理,则能理顺生产关系,协调生产管理,促进团队协作. 任务的高层抽象即为角色,在其位而谋其政,基于角色的协同管理相对于普通任务协作具有更高、更深远的内涵,目前已成为国内外研究任务分工与指派的重要方法之一[3, 5-7].
因此,为处理先序约束下的任务分工问题,本文于指派模型中引入角色,使用角色对任务分工进行抽象与建模,对先序约束下的多对多指派作表达与计算,并通过实验与仿真论证了相关方法的优化性能与有效性. 论文共分为6部分. 第1部分为相关工作分析;第2部分对先序约束下的生产管理进行了场景预设;第3、4部分使用了“基于角色协同”方法(Role-Based Collaboration, 简称RBC)及其E-CARGO模型对问题进行建模[3, 5-7]、计算与分析;第5部分为实验仿真;第6部分则对全文进行了总结并阐述了下一步工作.
1 相关工作针对指派算法的研究,最经典的即为匈牙利算法,该算法是一种在多项式时间内求解任务分配问题的组合优化算法. 1957年在Kuhn的工作基础上,美国数学家Munkres[8]对匈牙利算法进行了加速改进,将其时空复杂度由O(m4)降为O(m3),其中m表示矩阵行数,后人将其算法誉为Kuhn-Munkres算法(KM算法). 传统的KM算法,可高效解决一对一的指派最优化问题. 在后人研究中,朱海滨等[9]在KM算法中引入了回溯,提出了KM B算法(Kuhn-Munkres Algorithm with Backtracking),在不影响时间复杂度量级的情况下,使用KM算法处理了多对多指派问题;Balinski[10]通过签名去描述了一种在有限步骤内和有限时间内可找到最优分配方案的方法;王若鹏和徐红敏[11]针对生活中资源合理分配问题利用数理统计中X2拟合优度检验法建立了席地公平分配模型;张其亮和陈永生[12]针对最小化最大完工时间为目标的无等待柔性流水车间调度问题提出了一种混合粒子群-NEH算法,该算法解决了机械分配问题并进行了全局最优化;Lee等[13]在遗传算法的基础上通过引入一个贪婪的改造方案提出了新的算法来完成WTA问题的指派;Toroslu和Arslanoglu[14]通过引入二部图划分的结构和该结构的限制,使用匹配约束定义了标准指派问题的多样性并且基于分层和集合限制为指派问题提出了遗传算法解决方案;赵继军等[15]基于跨层联合设计思路建立一个混合整数非线性规划问题并得到问题的分簇最优结果和资源分配方案;Burkard等[16]对二维和三维指派问题进行了分析与处理;Hajri-Gabou[17]在服装产业上基于多层次的广义指派问题提出了一种模糊遗传多目标算法;Kim和Moon[18]在个性化市场的背景下为使目标准确性和顾客满意度最大化提出了多活动指派问题;孔维健等[19]基于镁砂熔炼工业制造在全厂供电容量约束下提出了基于工况优先级的电能分配策;Stützle[20]提出和分析了迭代本地搜索算法在二次指派问题(QAP)上的应用.
任务的高层抽象即为角色,为此加拿大学者朱海滨提出了群组角色指派方法(Group Role Assignment),以角色取代任务成为指派核心[3, 5-7]. 该指派方法区别于传统任务指派而引入角色建模与面向对象方法,形成了“基于角色的协同”的工程方法学及其E-CARGO模型. E-CARGO模型以9元组∑::=〈C, O, A, M, R, E, G, S 0, H〉抽象并描述了协作系统的组成部分. RBC方法与E-CARGO模型引入角色的概念,对任务需求与团队协作进行了高度抽象,赋予更丰富的工程内涵,为协同计算提供了可行、可靠的模型与方法. 而群组角色指派(GRA)则明确了以角色为核心的指派过程与计算方法. 因此成为了本文借鉴与使用的主要理论工具. 在此基础上,本文相关研究仍需进一步考虑将先序约束纳入到E-CARGO模型与GRA方法中,并提出可行有效的指派算法,以对该约束下的分工协作进行处理.
2 场景预设为具体清晰地呈现先序约束下的群组角色指派,本文对相关协同场景进行了预设:某公司X的执行总裁安妮签署了一个上百万的项目. 她要求人力资源部长鲍勃从公司所有员工中选择合适员工组成该项目小组. 表1是该项目的职位需求表,表示在该项目中集成设计员职位需要2名员工、接口设计员职位需要3名员工、界面设计员职位需要4名员工.
| 表 1 职位需求表 Table 1 Jobs wanted |
表2是候选员工职位能力表,体现了每位员工在每个工作岗位上的胜任度评分(0分为最低,1分为最高),该评分可由人力资源部门给出. 例:李浩执行集成设计职位的评分为0.8.
| 表 2 候选人员履职评估表 Table 2 Qualification of candidates |
一般而言,为确保项目高效运作,每一个员工应只担任一个职位. 但IT行业是一个特殊的行业. 例如为保证测试的完整性,集成测试员往往应从担任了该项目单元测试的人员中选择. 由此,一个担任集成测试工作的技术人员,也要担任单元测试的工作,在项目执行期间,该技术人员往往会多次交叉从事两个岗位的工作. 因此,先序约束下的指派问题实际为一类多对多指派问题.
据此,依项目需求人力资源部长鲍伯给出了各职位之间的关系图如图1所示.
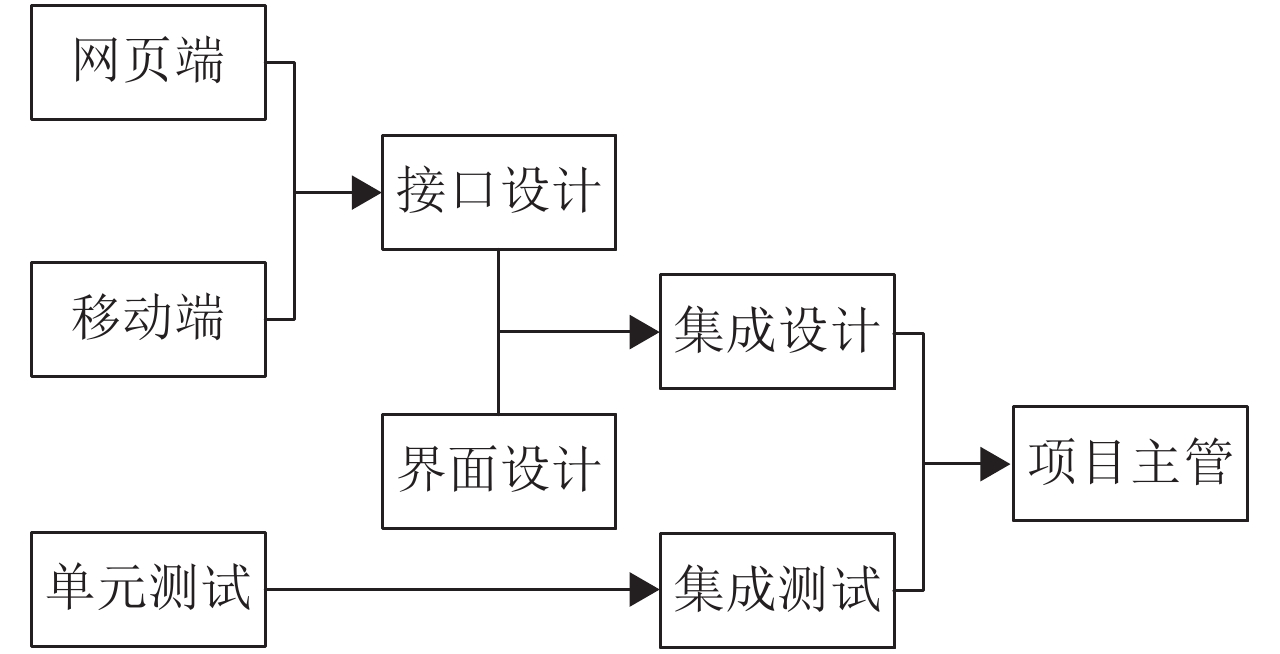
|
图 1 职位先序关系 Figure 1 Preorder constraints of job promotion |
从图1可知,岗位角色之间存在着先序约束关系如下:(1) 集成设计人员需至少参加过本项目的接口设计或界面设计工作之一项;(2) 接口设计人员需至少参加过本项目的移动端程序设计或网页端程序设计工作之一项;(3) 集成测试人员需参加过本项目单元测试.
据选拔条件,可将岗位角色的先序关系进一步细分为如图2和图3所示的两类情况.

|
图 2 与and约束 Figure 2 Constraint of AND |
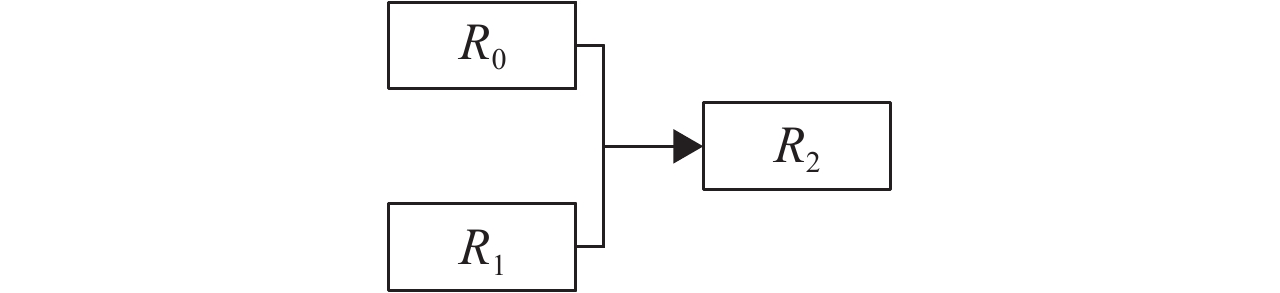
|
图 3 或or约束 Figure 3 Constraint of OR |
图2表明担任角色R 1的人员只能从担任角色R 0的人员中选拔,其中角色R 0是角色R 1的先序;角色R 1是角色R 0的后继,可称之为“先序与约束”. 图3则表明担任角色R 2的人员可以从担任角色R 0或者R 1的人员中选拔,其中角色R 0和R 1具有相同的后继R 2,可称之为“先序或约束”.
针对该问题,可采用E-CARGO模型与GRA方法进行表达与建模.
3 问题建模设以群组G表示协作全团队(Group)、角色集R表示岗位角色集(Role),代理集A表示候选人员集(Agent),则对角色、角色需求数、代理能力表(直观上如表2所示),指派方案等均可用向量和矩阵形式化表示. 其中,用非负整数m(=|A|,指集合A的基数)代表集合A的大小;n(|R|,指集合R的基数)代表集合R的大小. 用
定义1 角色需求向量 L :对每一角色的需求数可用向量 L 形式化表示.
根据表1项目职位需求表. 可得群组角色需求向量为 L =[2, 3, 4, 3, 3, 2, 4, 1].
定义2 资格矩阵
Q
:是一个m×n矩阵. 其中
Q
[i, j]∈{0, 1},代表Agent
i
(0
例如在表2中,黄英在执行接口设计岗位的执行力评分为0.45. Q [i, j]=0代表执行力评分最低分, Q [i, j]=1代表执行力评分最高分.
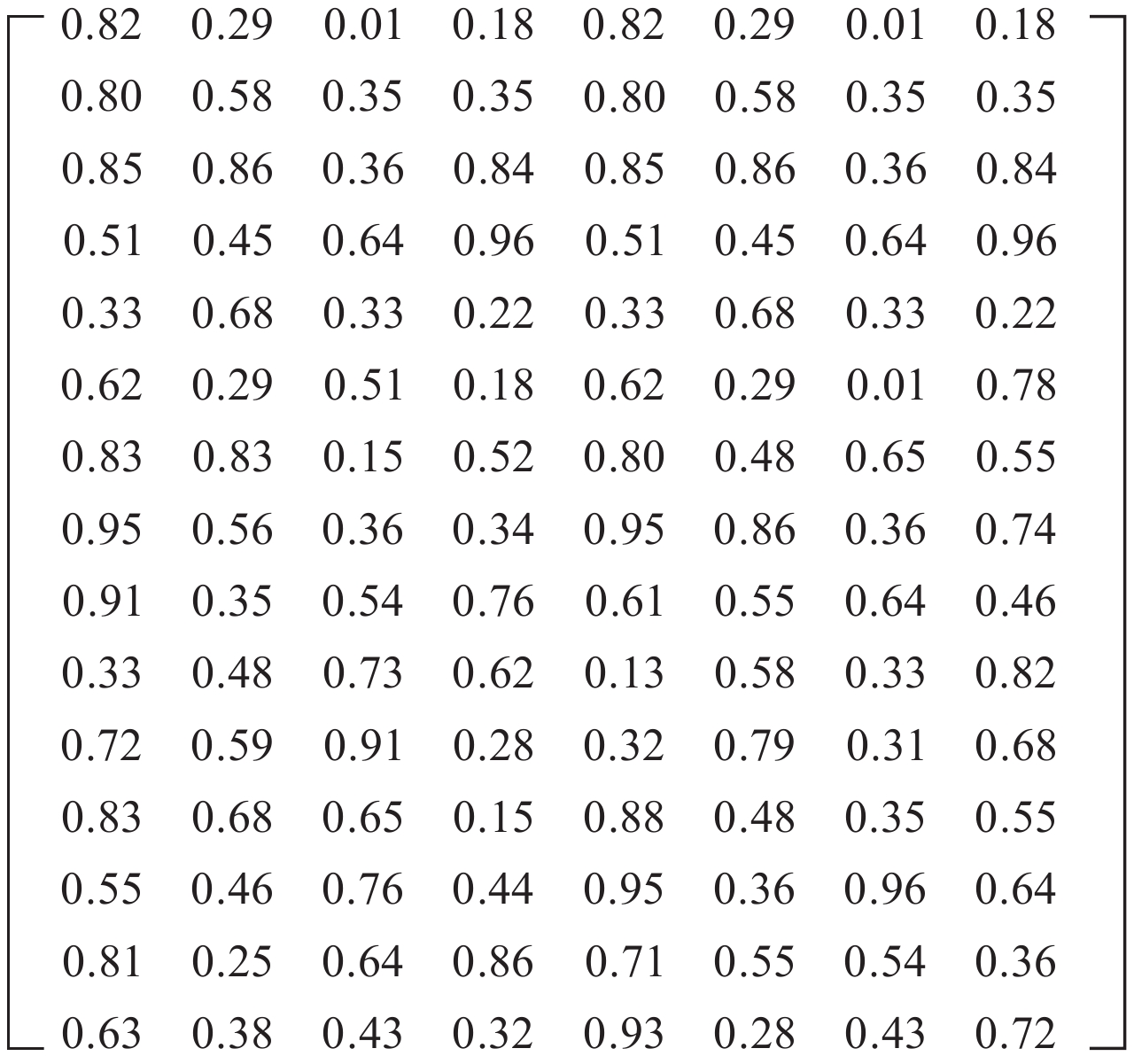
|
图 4 资格矩阵 Q Figure 4 Qualification matrix Q |
定义3 分配矩阵
T
,是一个m×n的矩阵. 其中
T
[i, j]∈{0, 1}(0
定义4 群组执行力σ :指派成功后,所有Agent的执行力评分总和. σ=
群组执行力σ的求解过程是将资格矩阵 Q 与分配矩阵 T 进行矩阵点乘.
定义5 角色j的可执行判定. 如果角色j被足够的Agent担任,即
定义6 分配矩阵
T
的可执行判定. 如果每一个角色j是可行的,即
以下定义先序约束关系,其实际可以通过角色之间的提升关系做定义7.
定义7 提升关系. 如果角色r i 要在角色r j 之前被指派,那么角色r j 是角色r i 的高级角色. 先序关系可以用符号 Λ来表示. Λ是二元组〈r j , r i 〉,其中r i 是r j 的低级角色且r j 是r i 的高级角色.
如图2所示,角色R 0一定要在角色R 1之前被指派. 角色R 0是角色R 1的低级角色,角色R 1是角色R 0的高级角色;R 0是R 1的先序,R 1是R 0的后继. 考虑到某些角色Role j1 和Role j2 可能存在共同的后继,因此可进一步将角色提升关系丰富,利用三值语义,以矩阵形式做表达,如定义8所示.
定义8 提升关系矩阵. 矩阵
Λ是一个n×n的提升关系矩阵. 其中,
Λ[j
1, j
2]∈{-1, 0, 1}, 0
| 表 3 提升关系矩阵 Table 3 Promotion matrix |
其中 Λ[集成设计, 接口设计]=-1说明:集成设计是接口设计的后继,接口设计是集成程序员的先序; Λ[界面设计, 接口程序员]=1说明:界面设计与接口设计有共同的后继; Λ[移动端, 集成设计]=0说明两个角色之间不存在任何关系.
据定义1至定义8,可对先序约束下群组角色的指派问题定义如定义9所示.
定义9 先序约束下的群组角色指派约束求解. 为一个可执行的分配矩阵 T ,使得
| $\max \{ \sigma = \sum\limits_{i = 0}^{m - 1} {\sum\limits_{j = 0}^{n - 1} {{Q}\left[ {i,j} \right] \times {T}[i,j]} } \}. $ |
限制于:
| ${T}\left[ {i,j} \right] \in \{ 0,1\} \;\;\;\left( {0 \leqslant i < m,0 \leqslant j < n} \right).$ | (1) |
| $\sum\limits_{j = 0}^{n - 1} {{T}\left[ {i,j} \right] \leqslant 1\;\;\left( {0 \leqslant i < m} \right)}.$ | (2) |
| $\forall {j_1}\neg \exists {j_{2.}}{j_1}{\varLambda} {j_2} \to \sum\limits_{i = 0}^{m - 1} {{T}\left[ {i,{j_1}} \right] = {L}[{j_1}]} .$ | (3) |
| $\begin{array}{l}\forall {j_1},{j_2},{j_3}.{j_1} {\varLambda} {j_3}{\rm{\& }}{j_2} {\varLambda} {j_3} \to \\\sum\limits_{i = 0}^{m - 1} {{T}\left[ {i,{j_1}} \right]} + \sum\limits_{i = 0}^{m - 1} {{T}\left[ {i,{j_2}} \right] = {L}\left[ {{j_1}} \right] + {L}\left[ {{j_2}} \right] - {L}\left[ {{j_3}} \right]} .\end{array}$ | (4) |
| $\begin{array}{l}\forall {j_1}\exists {j_2}\neg \exists {j_3}.{j_1} {\varLambda} {j_2}{\rm{\&}}{{{j}}_{\rm{3}}} {\varLambda} {{{j}}_{\rm{2}}} \to \sum\limits_{{\rm{i = 0}}}^{{{m - 1}}} {{T}} \left[ {{{i}},{{{j}}_{\rm{1}}}} \right]{\rm{ = }}\\{{L}}\left[ {{{{j}}_{\rm{1}}}} \right]{{ - L}}\left[ {{{{j}}_{\rm{2}}}} \right].\end{array}$ | (5) |
其中,式(1)指分配矩阵 T 是布尔型的. 其中 T [i, j]=1代表Agent i 执行角色Role j , T [i, j]=0代表Agent i 不执行角色Role j .
式(2)指 T 矩阵的每一行元素叠加总和小于等于1,代表一个Agent只能执行一个Role.
式(3)指角色j 1与角色j 2之间不存在约束关系. 整个公式代表不存在约束关系的两角色,执行角色j 1的代理个数与 L [j 1](其中, L [j 1]为j 1角色需求量)相等.
式(4)指角色j 1, j 2之间存在的约束关系为或(or)约束关系. 其中j 1, j 2拥有共同后继j 3. 整个公式代表执行角色j l与j 2代理个数之和等于 L [j 1]与 L [j 2]之和减去 L [j 3].
式(5)指角色j 1与角色j 2之间存在约束关系与(and)关系. 其中j 1是j 2的先序,j 2是j 1的后继. 整个公式代表执行先序角色j 1的代理总数等于 L [j 1]与 L [j 2]之差.
式(1)和(2)保证了GRA问题指派的可行性;式(3),(4)和(5)将先序约束下群组角色之间的先序约束关系逐一逻辑表示. 传统的群组角色指派需要满足式(1)和(2),先序约束下的群组角色指派不但要满足式(1)和(2),还必须满足角色之间的先序约束关系. 到目前为止,论文通过E-CARGO模型对问题进行了建模,并将角色之间的先序约束关系通过逻辑表达转换为约束求解问题. 在下一节,将把逻辑表达式转换为线性规划(Linear Programming)表达并作求解.
4 算法分析 4.1 穷举法目前无合适的收敛算法可解决先序约束下群组角色的指派问题. 为寻找问题的最优解,可尝试使用穷举法解决问题. 穷举法:将符合群组角色之间提升关系的指派方案一一枚举出来,然后找到群组执行力σ最高的一组作为最佳指派方案. 论文穷举法方案:先根据角色需求向量 L ,在满足群组角色指派问题(GRA)的限制:式(1)和(2)前提下,随机生成一个指派方案,再判断该指派方案是否符合群组角色的先序约束关系,最后在符合先序约束关系的指派方案里,选择群组执行力σ最高的一组.
根据问题规模,在满足所有先序约束关系前提下,如使用穷举法来完成指派,该问题是一个Σ2P级问题,即时间复杂度为
先序约束下群组角色指派问题允许一个代理可在不同时间点内执行多于一个不同但相关的角色(类似于操作系统进程并发的概念). 但目前其硬优化解法仍为开问题,尚无有效算法可解[14]. 因此,本文利用其同一时间点内一个代理只能执行一个角色的特点,将问题转化为一对一指派求较优解进行处理,继而做二次指派,处理多对多问题,如图5所示.

|
图 5 问题指派流程 Figure 5 Flow of problem assignment |
举例阐述算法思想如下:
根据图1,如果代理A想承担集成测试的角色,它必须也要承担单元测试员的角色. 其中,集成测试的角色需求量为2,单元测试的角色需求量为4. 因集成测试须从单元测试中提升选拨,可减少单元测试员的角色需求,修正为4-2=2. 但对于集成设计和接口设计,界面设计这3个角色的情况较为复杂. 设接口设计的角色需求量为x 1,界面设计的角色需求量为x 2,可得x 1+x 2=3+4-2=5,其中接口设计和界面设计角色需求量总和为5. 根据以上方法,可将图1群组对角色的需求量修改为如表4所示.
| 表 4 职位需求表 Table 4 Jobs wanted |
将章节3角色需求矩阵设为 L 1=[2, 3, 4, 3, 3, 2, 4, 1]修改后的角色需求矩阵设为 L 2=[2, x 1, x 2, x 3, x 4, 2, 2, 1],其中x 1+x 2=5;x 3+x 4=6-x 1. 将角色需求矩阵进行减少修正后,先序约束下群组角色指派的第一次指派符合同一时间内一个代理只能执行一个角色的要求. 根据定义8,章节3职位之间的约束关系可用 Λ矩阵表示如图6所示.

|
图 6 职位约束关系 Λ矩阵 Figure 6 Job constraint matrix Λ |
根据上述对角色需求的修正和定义8对群组角色之间约束关系的矩阵形式化表示,其一对一指派可转化为线性指派规划如定义10所示.
定义10 先序约束下的群组角色指派的线性求解,即寻找一个可行的分配矩阵 T ,其中
目标函数:
限制于:式(1)、(2)及
| $\begin{array}{l}\sum\limits_{i = 0}^{m - 1} {{{T}}\left[ {i,j} \right]} + \sum\limits_{k = 0}^{n - 1} {\left( {\varLambda} \right.} \left[ {k,j} \right] \times \sum\limits_{i = 0}^{m - 1} {\left. {{{T}}[i,k]} \right)} = {{L}}\left[ j \right] + \\[3pt]\sum\limits_{i = 0}^{n - 1} {{\varLambda}} \left[ {i,j} \right] \times {{L}}\left[ i \right] \small\left({\text{其中}} {\varLambda} \right.\left[ {k,j} \right] = \left. 1 \right).\end{array}$ | (6) |
注意:式(6)的含义是[角色j的代理总和]+[与角色j拥有共同后继的角色代理总和]=[j的角色需求量]+[角色i与角色j的提升关系 Λ]×[i的角色需求量].
定义10将先序约束下的群组角色指派问题转化为了线性规划问题,可借助工业优化工具IBM ILOG CPLEX完成指派. 先序约束下的群组角色指派之所以可被简化为一对一的指派,是因为对 L 中含有先序约束关系的角色需求数进行了减少修正. 因此在完成了一次的指派后,需进行二次指派,以弥补一次指派中减少的角色需求数. 第二次指派也需在群组角色之间的约束关系下完成.
例如,设图3中R 0、R 1和R 2的角色需求向量 L 例=[2, 3, 2],据章节4.2.1,一次指派中 L 1=[x 1, x 2, 2],其中x 1+x 2=3. 假设完成一次指派之后 L 1=[1, 2, 2],则二次指派需弥补一次减少修正的角色需求向量为 L 2= L 例- L 1=([2, 3, 2]-[1, 2, 2])=[1, 1, 0]. 二次指派中,根据R 0、R 1与R 2之间的约束关系,需从已执行了R 2的两个代理中分别指派足量代理执行R 1, R 2,且指派方案的执行力要求最高.
注意,因为本方法使用了二次指派,每次指派属于局部优化,因而本方法求得的不是全局最优解. 有必要通过实验,验证其优化程度.
4.2.2 问题求解本节将通过论文第2节工程项目职位的指派问题,对论文算法进详细分析,并作求解举例.
首先据图1,工程项目的职位需求矩阵可表示为 L =[2, 3, 4, 3, 3, 2, 4, 1];据图2,候选人履职评分表即职位资格矩阵可用 Q 矩阵表示如图7所示.
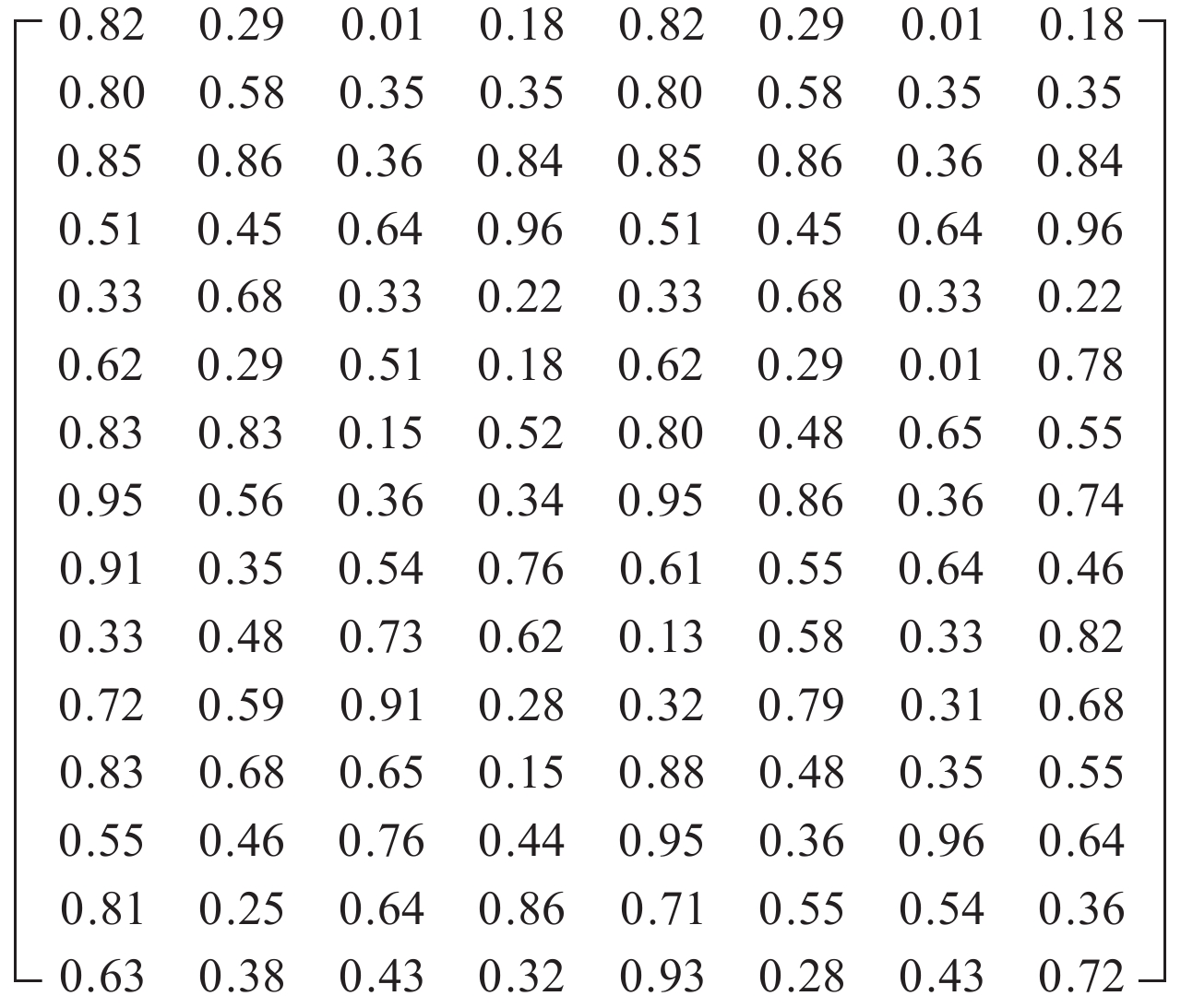
|
图 7 职位资格矩阵 Figure 7 Qualification matrix |
根据对该问题的线性指派规划,可将职位需求矩阵设为 L 1=[2, 3, 4, 3, 3, 2, 4, 1],减少修正后设为 L 2=[2, x 1, x 2, x 3, x 4, 2, 2, 1],其中x 1+x 2=5;x 3+x 4=6-x 1.
根据定义10,第一次指派结果如图8所示,一次指派成功 L 2=[1, 3, 2, 1, 2, 2, 2, 1].
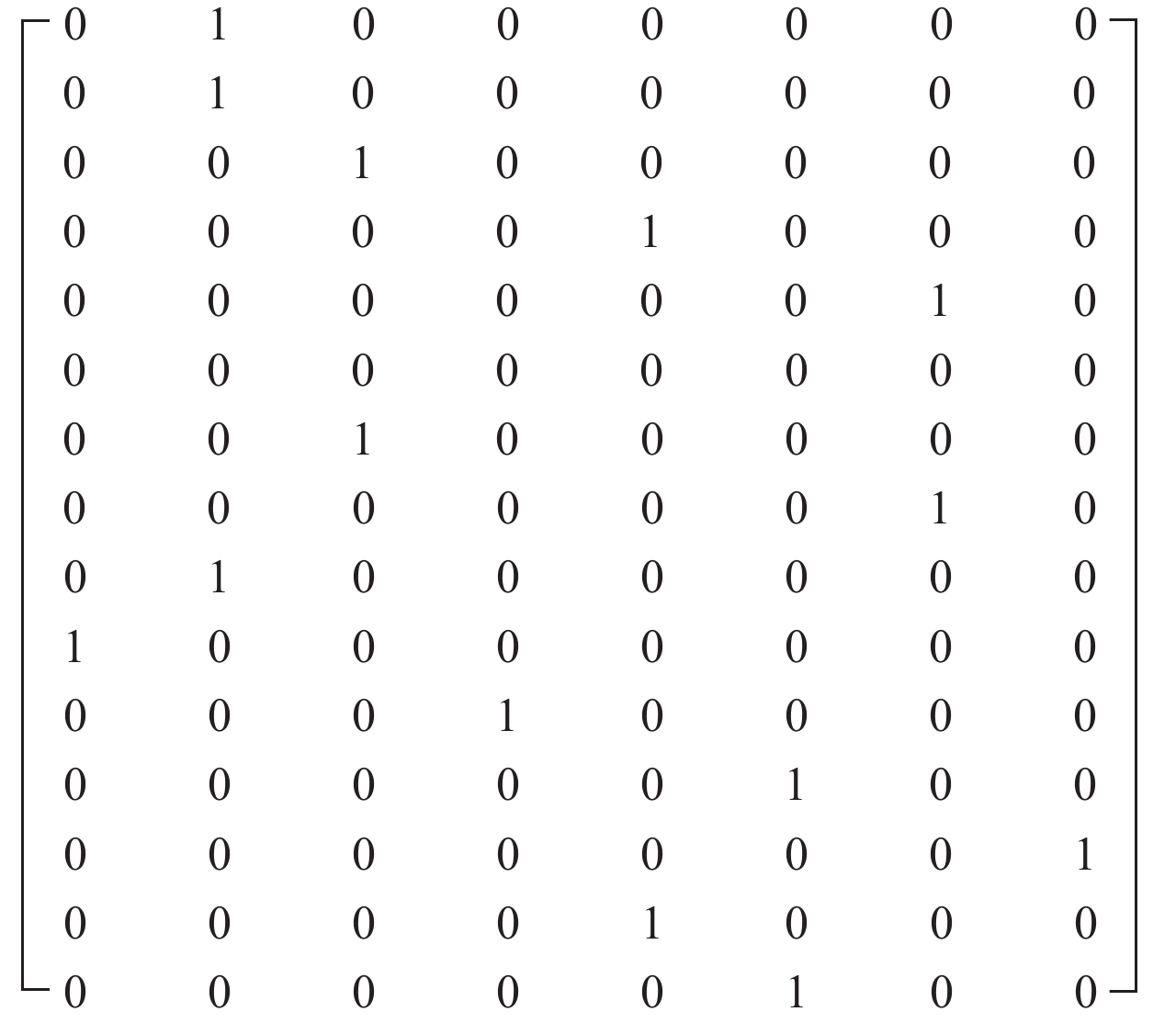
|
图 8 第一次指派结果 Figure 8 Results of first assignment |
根据4.2.1中对二次指派的解释, 则需弥补的角色需求向量为
| $\begin{array}{l}{{{L}}_3} \!=\! {{{L}}_2} \!- \!{{{L}}_1}\! =\! \left[ {2,3,4,3,3,2,4} \right] \!-\! \left[ {1,3,2,1,2,2,2,1} \right]\!=\\[8pt]\;\;\;\; \left[ {1,0,2,2,1,0,2,0} \right].\end{array}$ |
根据 L 3和资格矩阵 Q ,角色提升关系矩阵 Λ,进行第二次指派. 第二次指派结果如图9所示. 而最终指派结果为第一次指派结果与第二次指派结果之和,如图10所示. 根据图10,可得该工程项目整个分配方案的执行力为σ =15.54.

|
图 9 第二次指派结果 Figure 9 Results of second assignment |

|
图 10 最终指派结果 Figure 10 Results of final assignment |
实验将论文算法与穷举法,在m(行)=10,n(列)=5的问题规模下,进行了一百组随机实验对比(随机生成角色需求变量 L 、资格矩阵 Q 、提升关系矩阵 Λ). 相同问题规模和实验环境下,穷举法执行一次平均需消耗4 h,论文算法可在几秒内得到结果. 其中图11为穷举法与论文算法在执行力上的对比.
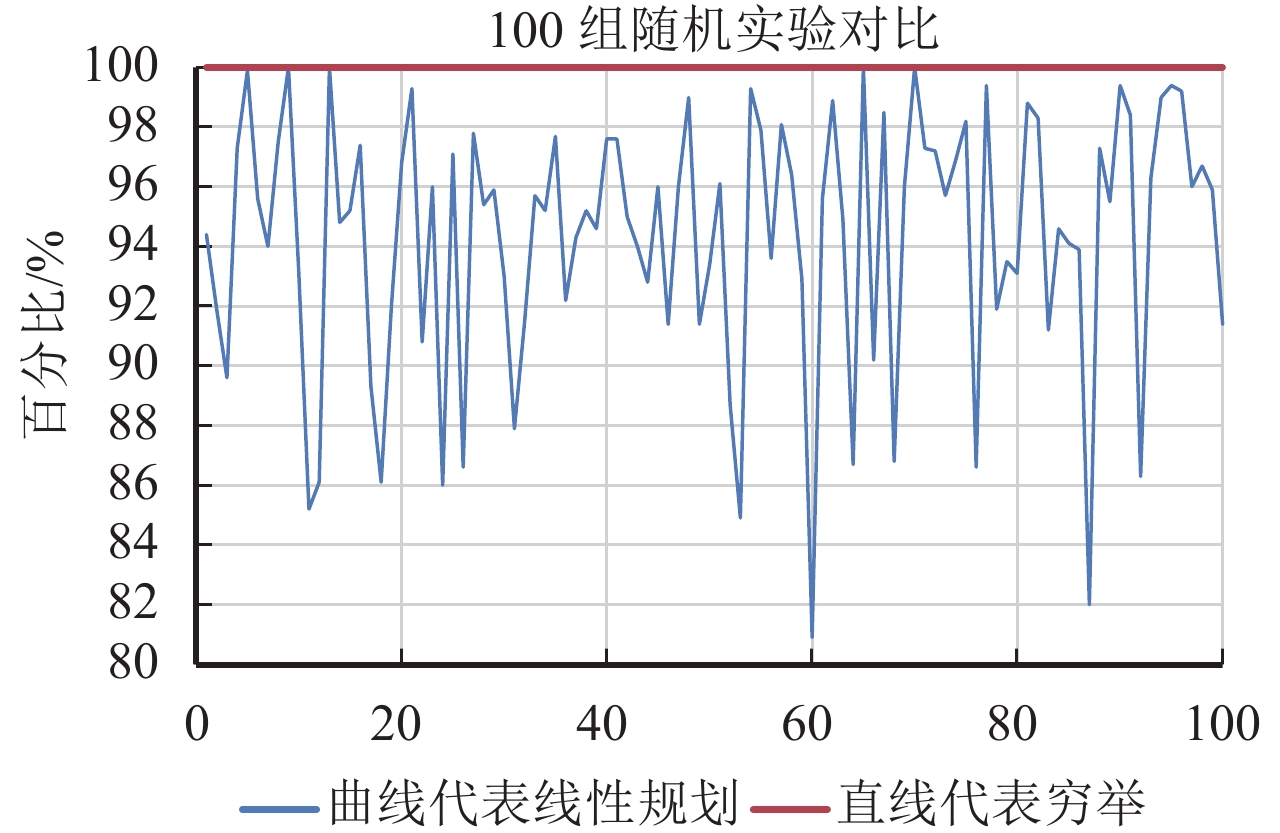
|
图 11 穷举法与论文算法执行力对比 Figure 11 Comparison between exhaustion method and proposed method |
从图11可得在100组随机实验中,本文方法最低效果达到穷举法的80%,最高效率达到穷举法的100%. 其中,有55次达到穷举法执行力的95%~100%,86次达到穷举法执行力的90%~100%,平均执行力达到穷举法的94%.
与穷举法对比的目的在于验证算法的有效性与精度,而非比较其效率. 事实上,在100组随机试验中,穷举法平均一次的执行时间约为4 h,但论文算法耗时最多为2 s. 虽然精度没有穷举法高,但却达到90%~100%的指派精度,更易被接受并得到应用.
5.2 算法性能分析在5.1节中,在固定问题规模:行m=10,列n=5的情况下,进行的100组随机实验说明了论文算法的可行性. 为证明论文算法可处理更大的问题规模,章节5.2以列n为基准,随机生成行m,资格矩阵 Q ,提升关系矩阵 Λ,再进行多组实验. 由于行m的随机受限于角色需求矩阵 L 的随机. 针对角色需求矩阵 L 的随机大小,本文对线性指派规划算法分别做了两组实验,其区别在于第一组实验角色需求矩阵 L 规模小,而第二组实验角色需求矩阵 L 规模大,以探究在有效时间内(论文规定为1 min),论文算法最高可处理的问题规模.
5.2.1 实验一:小规模角色需求矩阵 L实验方案:以列n为基准(10
| 表 5 实验一数据预设 Table 5 Parameters of experiment 1 |
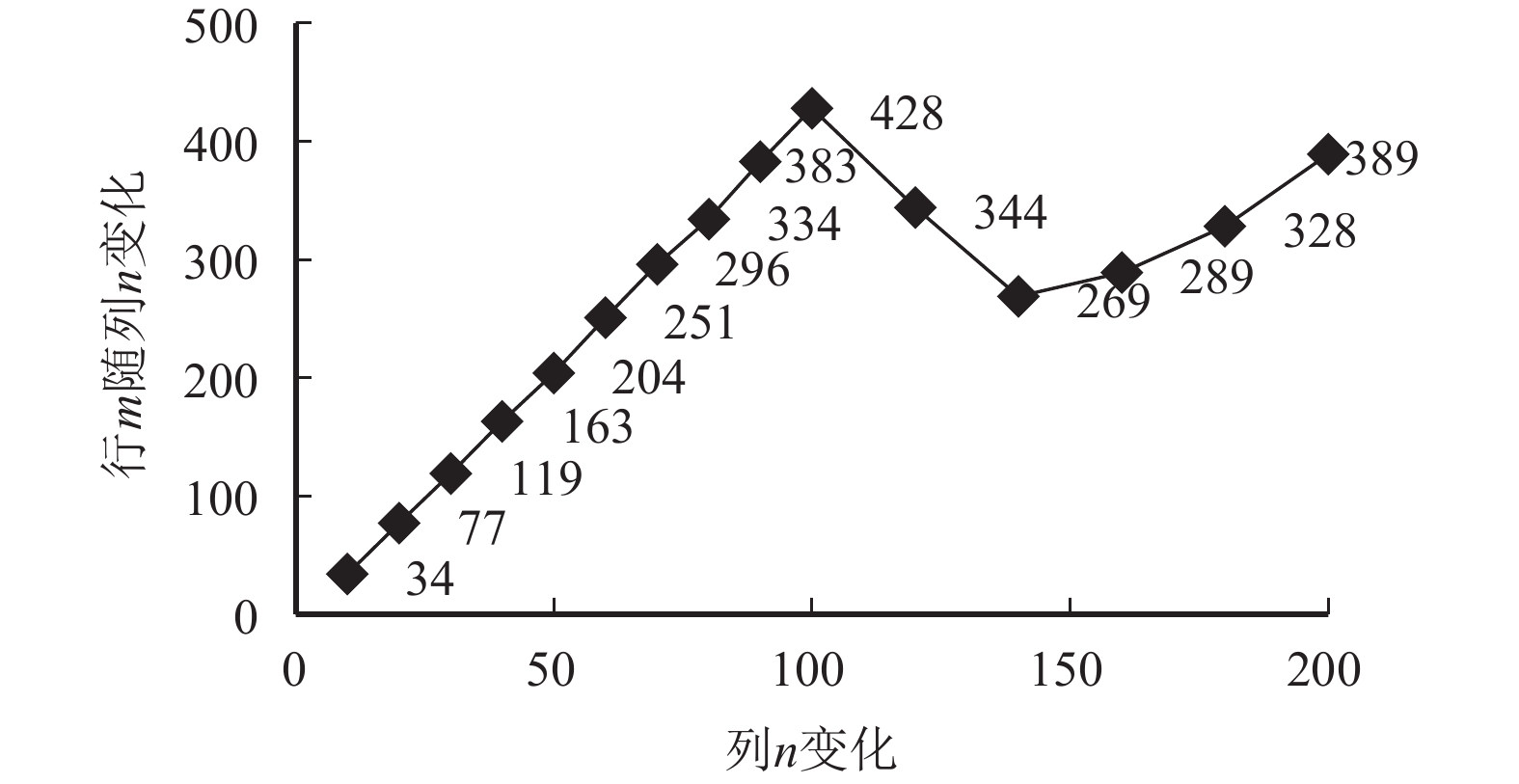
|
图 12 实验一行与列的随机 Figure 12 Relationships between rows and columns in experiment 1 |
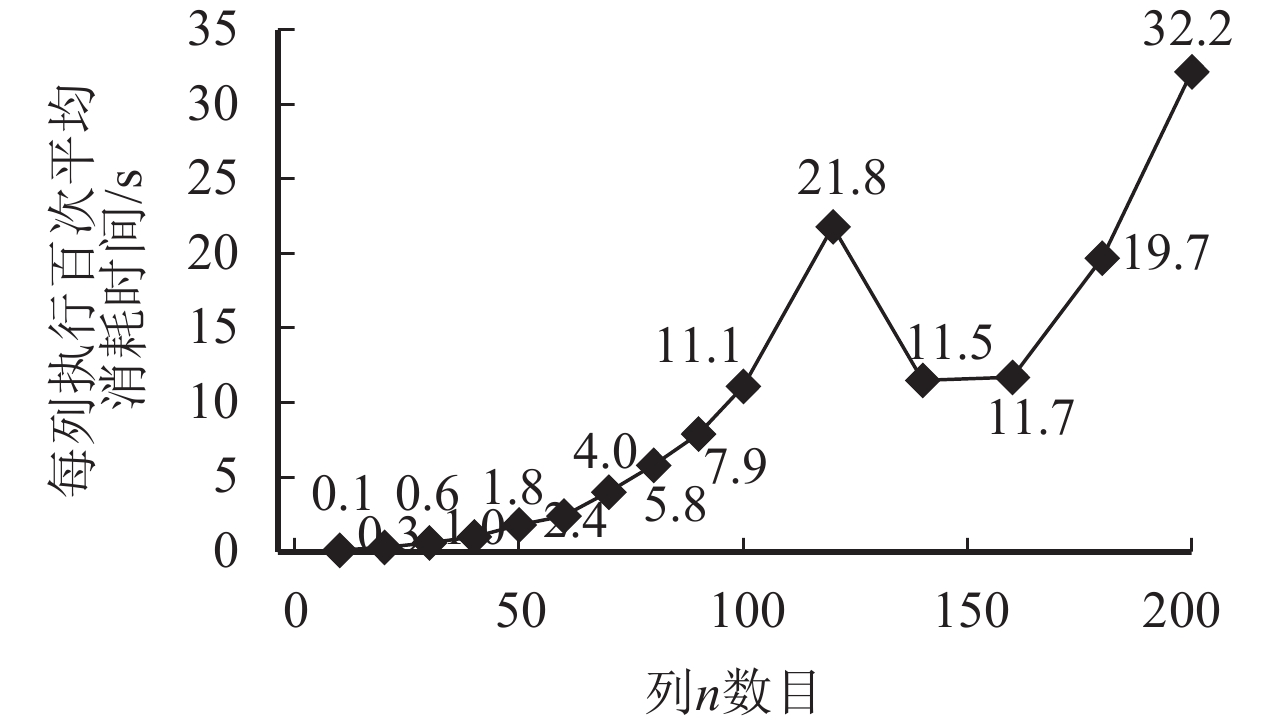
|
图 13 实验一论文算法消耗时间 Figure 13 Time consumption of proposed method in experiment 1 |
由于角色需求矩阵 L 随机范围不同,不同列对应生成的行成不规矩变化. 其中,当n=100时,由于角色需求矩阵 L 的随机范围为[1, 8],随机的行m=428;而当n=200时,由于角色需求矩阵 L 的随机范围[1, 3],随机的行m=389. 根据图12随机生成的行与列,使用论文算法处理相应问题规模,所消耗的时间如图13所示.
图13是图12中对应行、列使用论文算法执行100次平均每次消耗时间. 注意:n=120时比n=140的角色需求量随机范围大,致使其随机的m更大,算法消耗时间也更大,从而形成了图13曲线的下滑. 而随着n不断增大,算法消耗时间逐渐增加,曲线上升.
为探讨论文算法在有效时间内可处理更大的问题规模. 实验二增大了任意角色需求数的随机范围进行实验.
5.2.2 实验二:大规模角色需求矩阵 L实验方案:以列n为基准(20
| 表 6 实验二数据预设 Table 6 Parameters of experiment 2 |
|
图 14 实验二行与列的随机 Figure 14 Relationships between rows and columns in experiment 2 |
|
图 15 实验二论文算法耗费时间 Figure 15 Time consumption of proposed method in experiment 2 |
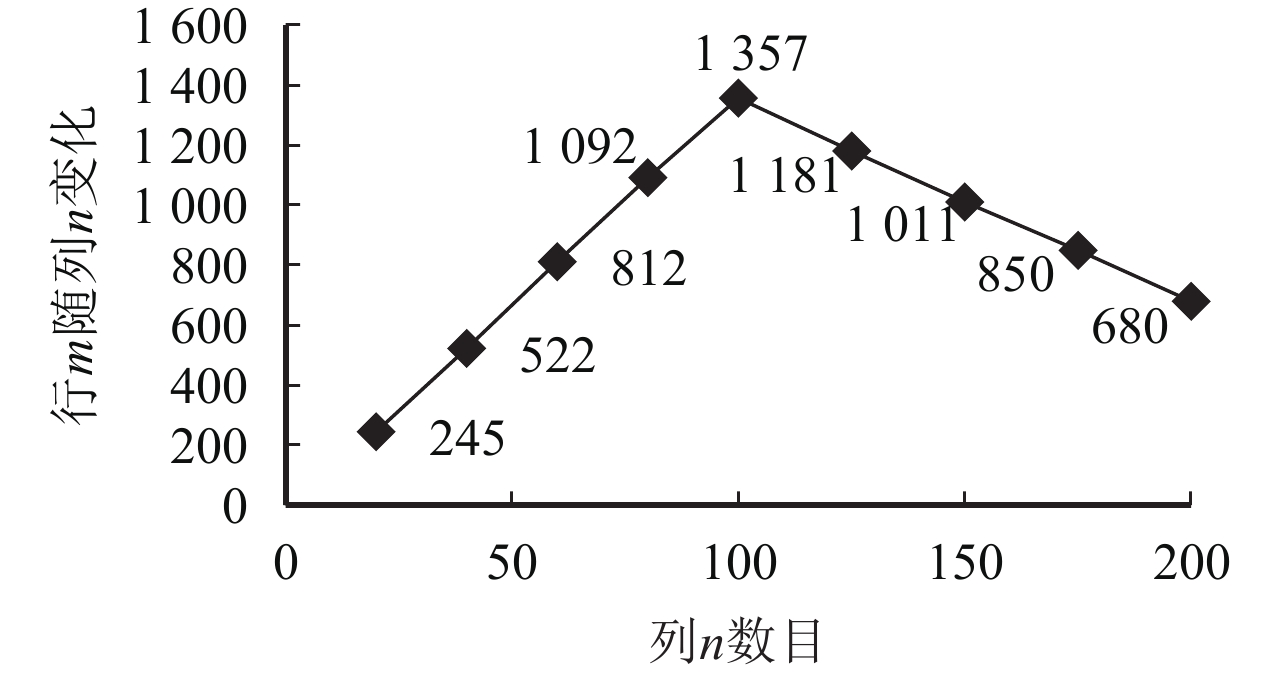
注意:由于角色需求矩阵 L 随机范围的不同,不同列对应生成的行成不规矩变化. 其中,当n=100时,由于角色需求矩阵 L 的随机范围为[5, 24],随机的行m=1 357;而当n=200时,由于角色需求矩阵 L 的随机范围[2, 5],随机的行m=680. 根据图15随机生成的行与列,使用本文线性规划指派算法处理相应问题规模,所消耗的时间如图15所示.
图15是图14中对应行、列使用论文算法执行多次平均每次消耗时间. 注意:n=150时比n=175的角色需求量随机范围大,致使其随机的m更大,算法消耗时间也更大,从而形成了图15曲线的下滑.
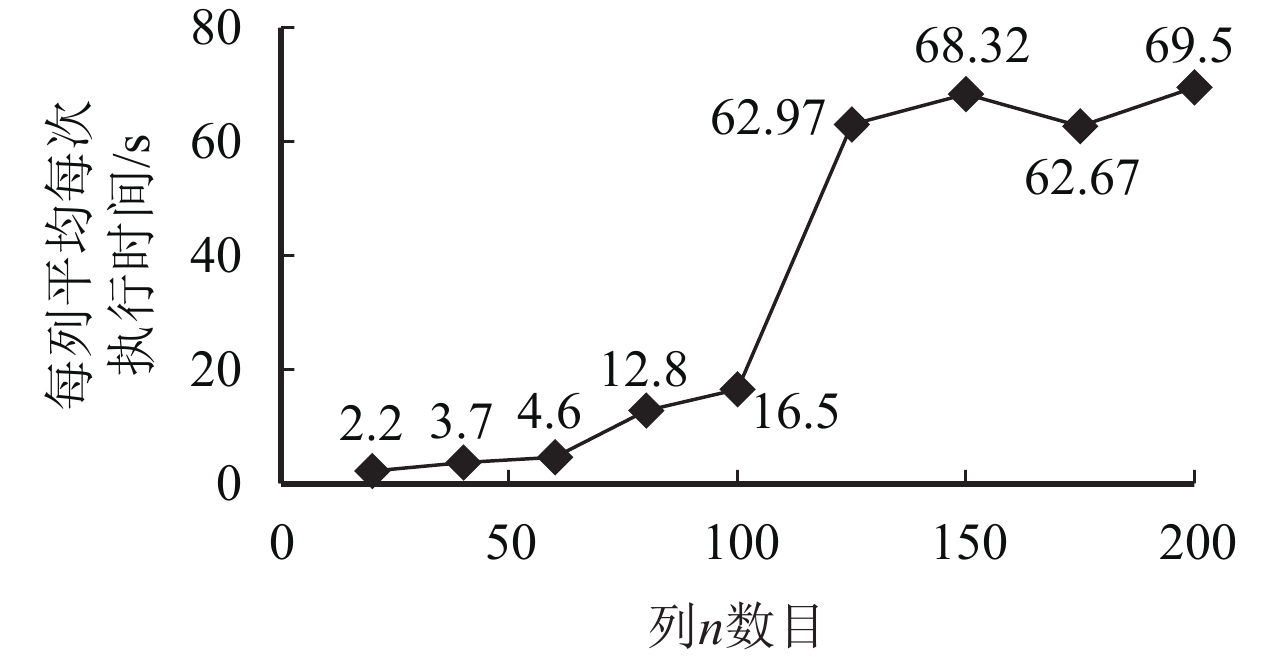
实验二是在实验一的基础上,增大角色需求矩阵的随机范围,对论文算法可处理问题规模大小进行更深一步的探讨. 通过实验一和二可发现:在有效时间内,论文算法可处理的最大问题规模已经达到:行m=200,列n=680和行m=100,列n=1 357. 规模性实验论证了本文方法是有效可行的.
6 结束语论文提出的多对多线性指派规划算法能满足在有限时间内对问题处理规模与团队性能保持的要求,对团队协作与伸长管理提供了有效支持. 论文在指派模型中引入角色,使用角色对任务分工进行抽象与建模,通过对先序约束下的指派作表达与计算,解决了先序约束下的群组角色指派问题.
在大数据环境下,知识发现变得容易,使得协同变得频繁与复杂. 而如果团队分工明确,协作必然轻松易行. 而解决时空约束之一:先序约束,更有利于任务的分工和指派. 论文下一步工作将对先序约束下的群组角色指派问题使用线性规划的方法重新定义问题等式,以求出该问题的最优解.
| [1] |
王元卓, 靳小龙, 程学旗. 网络大数据: 现状与展望[J].
计算机学报, 2013, 36(6): 1-15.
WANG Y Z, JIN X L, CHENG X Q. Network big data: present and future[J]. Chinese Journal of Computers, 2013, 36(6): 1-15. |
| [2] |
王勇, 许钟涛, 王瑛. 大数据环境下竞争情报系统的研究与实验[J].
广东工业大学学报, 2014, 31(3): 27-31.
WANG R, XU Z T, WANG Y. Research and implementation on competitive intelligence system based on big data[J]. Journal of Guangdong University of Technology, 2014, 31(3): 27-31. |
| [3] | ZHU H, ZHOU M C. Role-based collaboration and its kernel mechanisms[J]. IEEE Transactions on Systems, Man and Cybernetics, Part C, 2006, 36(4): 578-589. DOI: 10.1109/TSMCC.2006.875726. |
| [4] |
宋静静, 李振坤, 胡其伟, 等. MAOCW及其在Web选课中的应用[J].
广东工业大学学报, 2005, 22(2): 83-88.
SONG J J, LI Z K, HU Q W, et al. MAOCW and its application in course selecting on Web[J]. Journal of Guangdong University of Technology, 2005, 22(2): 83-88. |
| [5] | ZHU H, ZHOU M C. Efficient role transfer based on Kuhn-Munkres algorithm[J]. IEEE Trans. on Systems, Man and Cybernetics, Part A: Systems and Humans, 2012, 42(2): 491-496. DOI: 10.1109/TSMCA.2011.2159587. |
| [6] | ZHU H, ZHOU M. M-M role-transfer problems and their solutions[J]. IEEE Trans. on SMC(A), 2009, 39(2): 448-459. |
| [7] | ZHU H, ZHOU M C, ALKINS R. Group role assignment via a Kuhn-Munkres algorithm-based solution[J]. IEEE Transactions on Systems, Man and Cybernetics, Part A: Systems and Humans, 2012, 42(3): 739-750. DOI: 10.1109/TSMCA.2011.2170414. |
| [8] | MUNKRES J. Algorithms for the assignment and transportation problems[J]. Journal of the Society for Industrial and Applied Mathematics, 1957, 5(1): 32-38. DOI: 10.1137/0105003. |
| [9] | ZHU H B, LIU D N, ZHANG S Q, et al. Solving the many to many assignment problem by improving the Kuhn-Munkres algorithm with backtracking[J]. Theoretical Computer Science, 2016, 618: 30-41. DOI: 10.1016/j.tcs.2016.01.002. |
| [10] | BALINSKI M L. Signature methods for the assignment problem[J]. Operations Research, 1985, 33(3): 527-536. DOI: 10.1287/opre.33.3.527. |
| [11] |
王若鹏, 徐红敏. 基于X2拟合优度检验的席位公平分配模型[J].
系统工程理论与实践, 2014, 34(7): 1732-1738.
WANG R P, XU H M. A fair apportioning seats model based on chi square goodness of fit test[J]. Systems Engineering-Theory & Practice, 2014, 34(7): 1732-1738. DOI: 10.12011/1000-6788(2014)7-1732. |
| [12] |
张其亮, 陈永生, 等. 基于混合粒子群-NEH算法求解无等待柔性流水车间调度问题[J].
系统工程理论与实践, 2014, 34(3): 802-809.
ZHANG Q L, CHEN Y S. Hybrid PSO-NEH algorithm for solving no-wait flexible flow shop scheduling problem[J]. Systems Engineering-Theory & Practice, 2014, 34(3): 802-809. DOI: 10.12011/1000-6788(2014)3-802. |
| [13] | LEE Z J, SU S F, LEE C Y. Efficiently solving general weapon-target assignment problem by genetic algorithms with greedy eugenics[J]. Systems, Man, and Cybernetics, Part B: Cybernetics, IEEE Transactions on, 2003, 33(1): 113-121. DOI: 10.1109/TSMCB.2003.808174. |
| [14] | TOROSLU I H, ARSLANOGLU Y. Genetic algorithm for the personnel assignment problem with multiple objectives[J]. Information Sciences, 2007, 177(3): 787-803. DOI: 10.1016/j.ins.2006.07.032. |
| [15] |
赵继军, 谷志群, 薛亮, 等. WSN中层次型拓扑控制与网络资源配置联合设计方法[J].
自动化学报, 2015, 41(3): 646-660.
ZHAO J J, GU Z Q, XIE L, et al. A joint design method of Hierarchical topology control and network resource allocation for Wireless Sensor Network[J]. Acta Automatica Sinica, 2015, 41(3): 646-660. |
| [16] | BURKARD R E, DELL’AMICO M, MARTELLO S. Assignment problems [M]. Revised Reprint. Siam: [s. n. ], 2009. |
| [17] | HAJRI-GABOUJ S. A fuzzy genetic multi-objective optimization algorithm for a multilevel generalized assignment problem[J]. Systems, Man, and Cybernetics, Part C: Applications and Reviews, IEEE Transactions on, 2003, 33(2): 214-224. DOI: 10.1109/TSMCC.2003.814033. |
| [18] | KIM Y H, MOON B R. Multicampaign assignment problem[J]. Knowledge and Data Engineering, IEEE Transactions on, 2006, 18(3): 405-414. DOI: 10.1109/TKDE.2006.49. |
| [19] |
孔维健, 柴天佑, 丁进良, 等. 镁砂熔炼过程全厂电能分配实时多目标优化方法研究[J].
自动化学报, 2014, 40(1): 51-61.
KONG W J, CHAI T Y, DING J L, et al. A real-time multiobjective electric energy allocation optimization approach for the smelting process of magnesia[J]. Acta Automatica Sinica, 2014, 40(1): 51-61. |
| [20] | STÜTZLE T. Iterated local search for the quadratic assignment problem[J]. European Journal of Operational Research, 2006, 174(3): 1519-1539. DOI: 10.1016/j.ejor.2005.01.066. |
 2017, Vol. 34
2017, Vol. 34