数据挖掘技术如今已被广泛应用到实际生产，然而分类算法大多复杂度很高，模型训练与分类的时间效率低，如支持向量机的训练计算复杂度在 $O\left( {{N^3} + L \cdot {N^2} + d \cdot L \cdot N} \right)$ 和 $O\left( {d{\rm{ \cdot }}{L^2}} \right)$ 之间（其中N是支持向量的个数，L是训练集样本的个数，d是每个样本的维数），该问题很大程度上限制了分类算法在时间要求较高与大数据情况下的应用，如入侵检测问题^[1-8]，实时公车调度问题^[9-10]. 本文针对该问题提出一种基于降维的分类方法，能够快速建模与分类，同时有较好的分类准确率.

1 相关工作

分类算法被广泛应用于实际生产中^[11-12]，但数据量的急速增长，提高了对分类算法的效率的要求，分类算法若没有很好的运行效率则无法适应生产发展的需要. 入侵检测算法的实时性要求较高，在这个领域中已有许多方法针对分类方法的时间效率提出改进.

各种分类算法如决策树^[1-2]，贝叶斯^[3-4]，KNN^[5]，SVM^[6-8]已被改进并应用于入侵检测中. 在强调入侵检测准确率的同时，为了在入侵发生的第一时间能做出识别，降低损失，许多学者在时间效率上做出研究，文献[5]提出一种适应大样本集的网络入侵检测算法Cluster-KNN算法，该算法先进行离线预处理建立大样本集的聚簇索引，在线实时分类时利用该聚簇索引搜索得到近邻，再采用KNN算法得出分类结果，解决了KNN算法需要在分类过程中遍历数据集的问题，提高了算法分类过程的速度，让其能够应用于大数据集中. 但该算法在处理增量问题时，必须重新进行聚簇索引的建立，而K-means得到聚簇是一个非常耗时的过程. 文献[6]提出一种基于并行凸包分解计算和支持向量机的入侵检测分类算法(PCH-SVM)，该算法借助凸包的分解和并行计算快速提取训练样本空间几何凸包的顶点，构建约简SVM训练样本集. 该算法能在不造成精度损失的前提下，降低SVM训练的时空复杂度. 文献[7]提出了基于正区域快速属性约简算法，形成SVM最优约简属性集. 但是这类算法仅是从SVM训练样本的角度进行优化，未能根本解决SVM算法复杂度高的问题，故时间效率提高有限. 本文提出的基于正交投影的降维分类方法，其分类准确率略低于SVM方法，但其分类速度与训练速度远快于SVM方法，能够高效地处理实时分类问题.

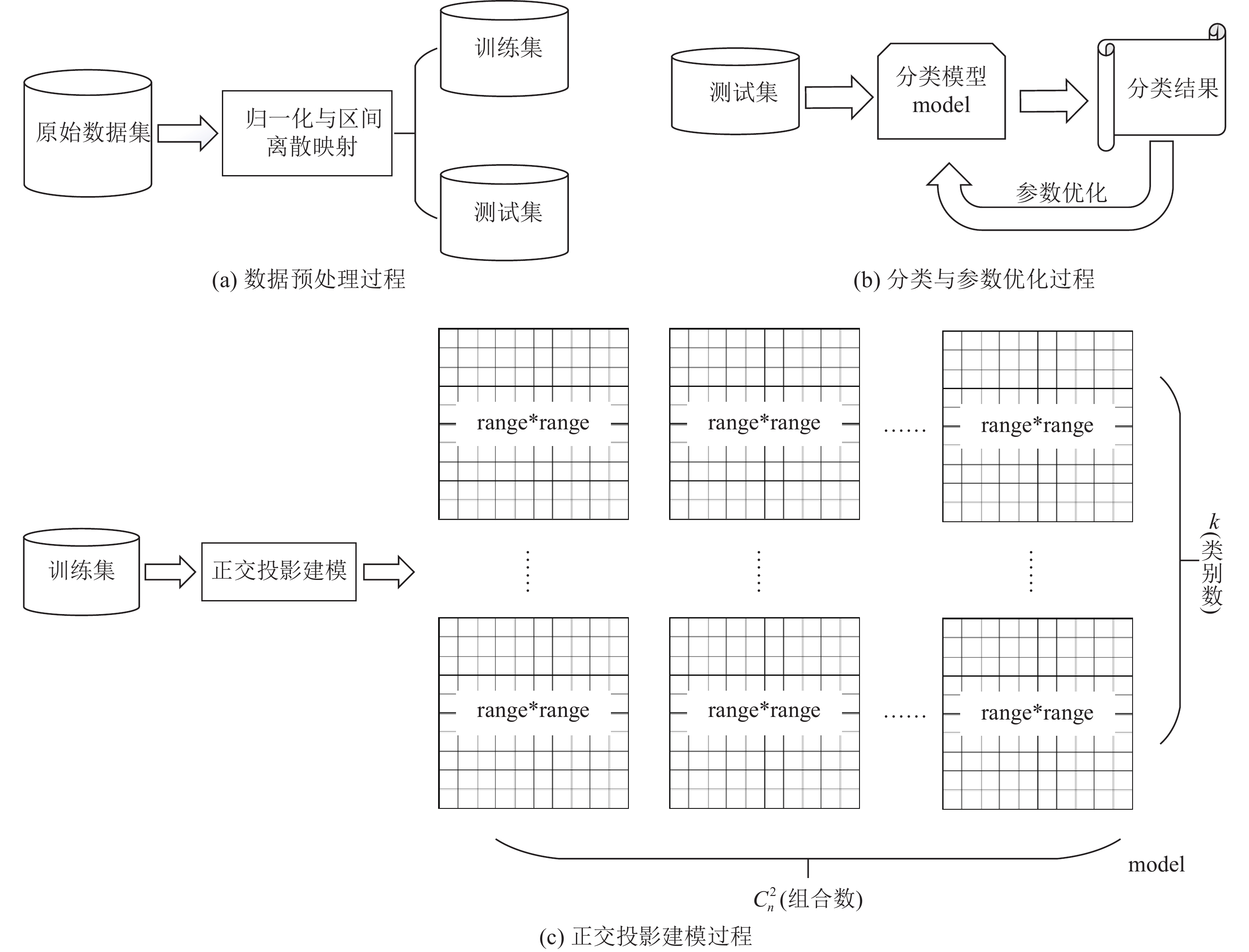
2 基于正交投影的降维分类方法 2.1 总体结构

本文从数据预处理，模型训练与分类3个步骤介绍基于正交投影的降维分类方法，预处理过程如图1(a)所示，对于原始数据集需要对其进行归一化与区间离散映射，这一过程是为了让数据变得规整均匀适合于投影至相同规格的矩阵中，且适合以数组形式来将投影模型保存在计算机中. 本文将处理后的数据按一定比例随机划分为训练集与测试集，对训练数据针对不同分类类别进行不同投影面的落点计数与模糊处理，如图1(c)所示，得到的是 $k \cdot C_n^2$ 个投影面密度模型，其中k为分类类别数，n表示数据维度数量，不同维度属性组合的二维投影面数量为 $C_n^2$ . 得到该模型后，用测试集对模型进行测试，如图1(b)，得到分类的准确率与耗时，分析分类结果，我们可以对模型的参数进行调整，如模糊过程中的模糊半径σ，映射区间范围大小range.

2.2 归一化与区间离散映射

基于正交投影的降维分类方法需要对数据进行归一化与区间离散映射处理. 模型训练的时候需要将数据投影至各个二维平面保存在矩阵数组中，这一过程需要根据矩阵数组的下标进行映射，数组的下标是离散而非连续的，为了让数据能够投影至同样规格的矩阵中，在模型训练前，不论连续的实数数据还是标量类型的数据都需要进行归一化与区间的离散化处理.

对于连续属性，基于正交投影的降维分类方法需要将实数处理为正整数，通过数据规范化的方法将数据规范化至区间[0, 1]，再进行映射取整.

假设A是数值属性，具有n个观测值 ${v_1},{v_2}, \cdots ,{v_n}$ ，且min _A 和max _A 分别为属性A的最小值和最大值，则有

$v_i' = \frac{{{v_i} - {\rm{mi}}{{\rm{n}}_A}}}{{{\rm{ma}}{{\rm{x}}_A} - {\rm{mi}}{{\rm{n}}_A}}} \cdot {\rm{range}}.$

(1)

把A的值v _i 离散化并映射为[0, range]中的 $v_i'$ ，其中的 ${\rm{range}} \in {Z^ + }$ 为离散化后范围的最大值，能够反映离散化的精度，当range取值越大时，数据的精度越高，但需要的存储空间也越大.

为了让降维分类方法能够处理标量型的数据，同样需要对标量数据进行离散值的映射，假设B是标量属性，具有n个观测值 ${b_1},{b_2}, \cdots ,{b_n}$ ，则有

$b_i' = \frac{{\left( {i - 1} \right)}}{n} \cdot {\rm{range}}.$

(2)

把B的值b _i 映射为[0, range]中的 $b_i'$ . 需要注意的是标量数据的排列顺序应与其物理意义的相对大小对应，如当B表示属性为评价时，B的排列顺序应为{差，中，良，优}，而非{中，差，优，良}.

2.3 建立投影面密度模型

经过预处理，得到[0, range]范围内规范的正整数数据，下面分二维数据建模与多维数据建模分别进行讨论.

2.3.1 二维数据建模

首先考虑二维一类的情况，假设现有已预处理的二维数据集 $P = \left\{ {{p_0},{p_1}, \cdots ,{p_m}} \right\}$ ， ${p_i} = \left( {{x_i},{y_i}} \right)$ ， ${x_i} \in \left[ {0,{\rm{range}}} \right],{y_i} \in \left[ {0,{\rm{range}}} \right]$ . P表示整个数据集，p _i 表示第i行数据，x _i 表示p _i 的第1维属性值，y _i 表示p _i 的第二维属性值，m表示数据量. 建立一个二维浮点型数组model，其初始值均为0，model的两个下标范围均为[0, range]，即其下标范围与P中数据的取值范围大小一致，故可以在model中找到与(x _i , y _i )对应的下标.

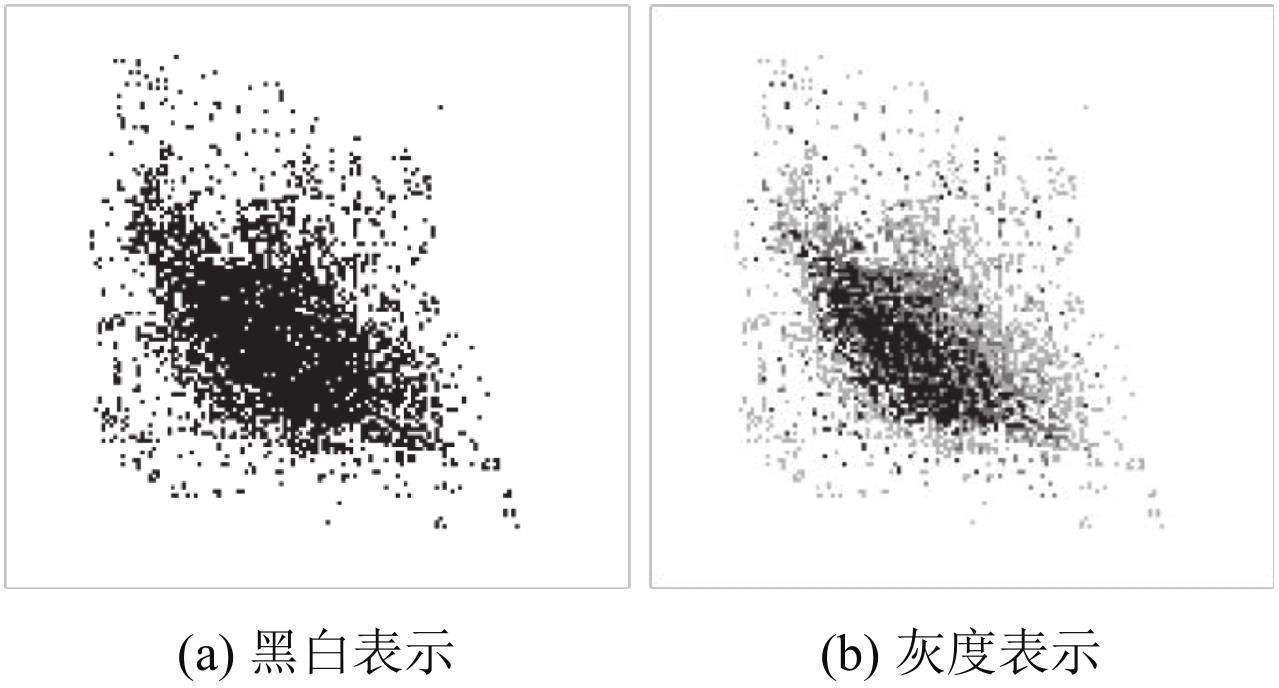
遍历数据集P，对于每一个p _i =(x _i , y _i )，找到model对应的下标，并让model对应下标的值自增. 为了方便说明，本文将model矩阵表示为一个二维图像，如图2(a)是一个二维一类数据集生成的model示例. 但图(a)仅能反映model中的某一位置有无数据，不能反映model中数据值的大小，即重叠的数据量，因此，本文通过灰度值来表示model中的数值的相对大小，如图2(b)所示.

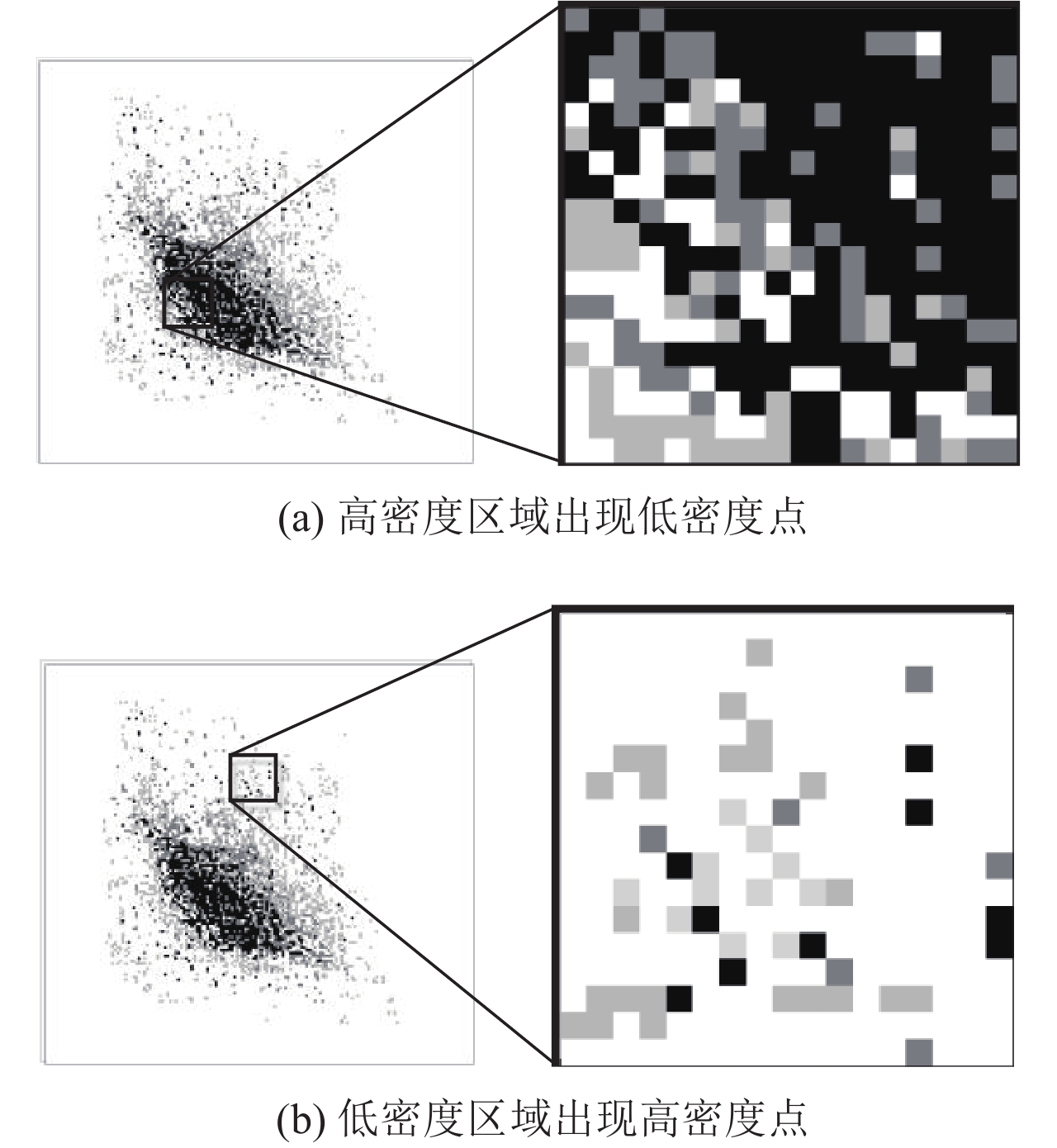
保存该模型，对于新的测试点，只需要查看model对应位置值的大小即可获得其分类信息. 但该模型易受噪声干扰，由于训练样本是有限的，在原本高密度的区域可能会出现低密度的点，如图3(a)，而在原本低密度的区域也可能会出现高密度的点，如图3(b)所示. 为了避免这种情况，需要对其进行高斯模糊处理. 进行高斯模糊时需要选择合适的模糊半径，如图4所示，这样能够在保证保留数据分布规律的同时，降低噪声. 若选择过小的模糊半径，去噪效果可能差，如图4(a)所示；若选择过度的模糊半径，则可能使数据的分布规律丢失，如图4(c)所示；图4(b)给出了合适的模糊半径.

上面讨论的情况类别数目唯一，即只能判断数据属于该类别的可能性，需要人工设置判定的阈值.

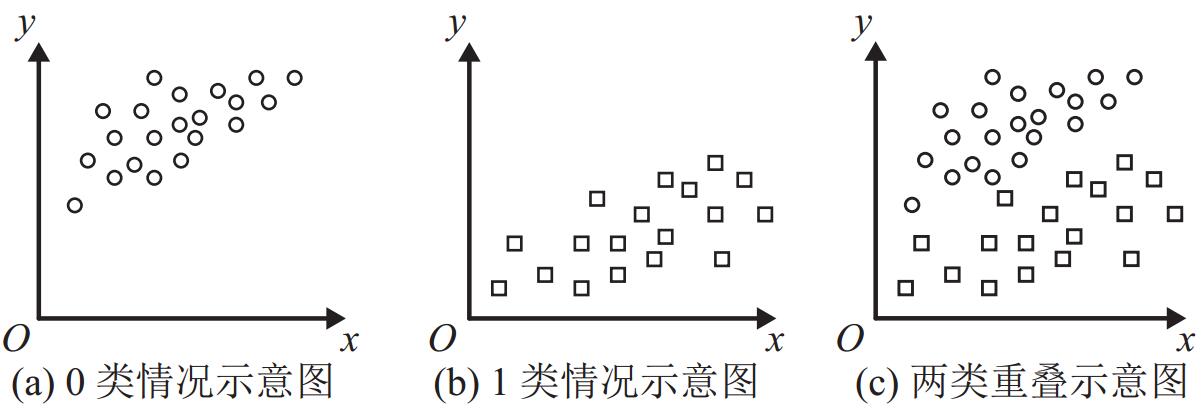
下面讨论二维多类数据的情况. 先考虑类别为2的情况，假设现有已预处理的二维二类数据集 $P = \left\{ {{p_0},{p_1}, \cdots ,{p_m}} \right\}\;,\;\;$ ${p_i} = \left( {{x_i},{y_i},{c_l}} \right)\;,\;\;$ ${x_i} \in \left[ {0,{\rm{range}}} \right]\;,$ ${y_i} \in \left[ {0,{\rm{range}}} \right],$ ${c_l} \in \left\{ {0,1} \right\}$ . P表示整个数据集，p _i 表示第i行数据，x _i 表示p _i 的第一维属性值，y _i 表示p _i 的第二维属性值，c _l 表示p _i 所属类别，m表示数据量. 即每行的数据p _i 都增加类别属性c _l ，此时可看作将数据集划分为两部分进行处理，即 $\alpha = \{ {p_i}|i \in \left[ {0,m} \right],{c_l} = 0\} $ 与 $\beta = \{ {p_i}|i \in \left[ {0,m} \right],{c_l} = 1\} $ 两部分，此时问题分解为求两个二维一类数据集的训练模型问题，采用前面介绍的方法，分别得到对应于不同类别的模型，如图5所示，图中以圆形表示第0类数据点，方形表示第1类数据点，则得到图1(a)和(b)两类的模型.

以相同方法进行扩展，推广到一般类别不唯一的情况，如假设此时的类别属性c _l 取值为0至k-1的自然数集，即此时类别数量为k个，那么针对这k个类别进行建模，即可得到k个表示不同类别的二维矩阵模型.

2.3.2 多维数据建模

下面将方法推广至多维的情况，先讨论类别数唯一的情况，假设现有已预处理的多维一类数据集 $P = \left\{ {{p_0},{p_1}, \cdots ,{p_m}} \right\}$ ， ${p_i} = \left( {{f_{i0}},{f_{i1}}, \cdots ,{f_{in}}} \right)$ ， ${f_{ij}} \in \left[ {0,{\rm{range}}} \right]$ . P表示整个数据集，m表示数据量，p _i 表示第i行数据，f _ij 表示p _i 的第j维属性值，维度数量为n. 此时无法像二维的情况一样将数据信息保存在一个二维矩阵中，本算法的做法是对多维属性进行投影，由于高维空间数据难以用图形示意，本文先以n=3的情况为例说明，如图6(a)所示，三维空间中的点 ${p_i} = \left( {{f_{i0}},{f_{i1}},{f_{i2}}} \right)$ ，可以找到3个相互正交的坐标平面xOy，xOz，yOz，将点p _i 向3个坐标构成的平面进行投影，可得 $a\left( {{f_{i0}},{f_{i1}}} \right)$ ， $b\left( {{f_{i0}},{f_{i2}}} \right)$ ， $c\left( {{f_{i1}},{f_{i2}}} \right)$ 3个投影点，如对于某三维数据点 ${p_i} = \left( {30,12,6} \right)$ ，对其向3个正交坐标轴组成的二维平面进行投影，分别得到3个坐标点(30, 12)，(30, 6)，(12, 6). 这样就将三维空间的问题通过投影的方式转化为3个二维空间组合的问题. 对于每一个投影的平面，采用与上述二维一类情况相同的做法，可以得到如图6(b)这样的模型. 当n>３时，方法是一样的，根据上面的投影方式可以计算三维情况下投影面的数量为 $C_3^2 = 3$ ，那么一般情况下一个数据点需要投影的二维平面数量则为 $C_n^2$ ，维度数量的增加只是增加了投影的数量且相应地增加了模型占用的内存，投影后按二维一类情况处理即可.

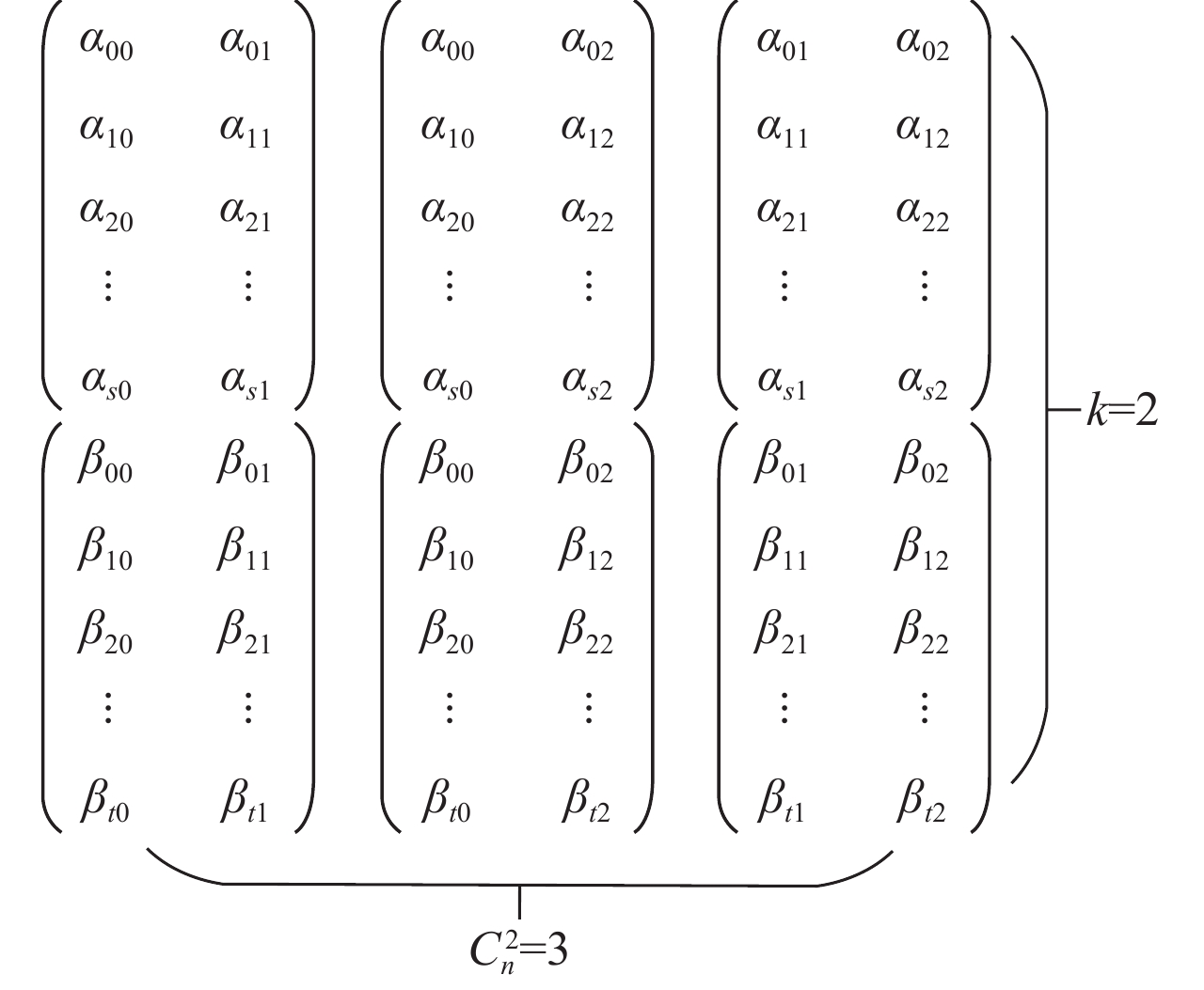
下面讨论多维数据类别不唯一、二维数据类别不唯一的情况，本文将问题转换为根据不同的类别建立多个二维一类模型，同理针对多维且类别不唯一的问题，本文将不同类别的数据分别建模，得到与类别对应的多维一类模型. 图7以三维二类为例展示了各类别对应的各投影面中投影的数据点，图中α表示类别为0的数据集，数据量为s，α _ij 表示数据集α的第i行数据的第j维属性，β表示类别为1的数据集，β _ij 表示数据集β的第i行数据的第j维属性，数据量为t. 投影后可得模型如图8所示. 根据α数据集(第0类)与β数据集(第1类)分别进行建模，可得到 $2 \cdot C_3^2 = 6$ 个投影面，那么对于类别数量为k，维度数量为n的数据集，此时需要存储的投影数量为 $k{\rm{ \cdot }}C_n^2$ . 由于本文应用一个浮点型数组存储该模型，在通常的编程环境中，浮点型数占用4字节的内存空间，则该模型所占用的内存空间为 $4{\rm{ \cdot rang}}{{\rm{e}}^2} \cdot k \cdot C_n^2$ 字节. 举例说明，当要处理的数据集为13维度二类的情况，若采用range=100处理数据集，则该模型需要占用的内存空间约为6 MB.

2.4 快速高斯模糊算法

建模过程中，需要对投影统计后的数据进行快速高斯模糊，高斯模糊算法本质上是一种数据平滑(Data Smoothing)算法，被广泛应用于信号处理领域.

一维高斯函数为

$G\left( x \right) = \frac{1}{{\sqrt {2{\rm{\uppi }}} \sigma }}{{\rm{e}}^{ - \frac{{{{\left( {x - \mu } \right)}^2}}}{{2{\sigma ^2}}}}}.$

(3)

二维高斯函数为

$G\left( {x,y} \right) = \frac{1}{{2{\rm{\uppi}}{\sigma ^2}}}{{\rm{e}}^{ - \frac{{{x^2} + {y^2}}}{{2{\sigma ^2}}}}}.$

(4)

其中x和y代表了相对于原始中心的偏移值，即距离中心点x轴向上的距离与y轴向上的距离. σ表示高斯模糊的标准差.

根据二维高斯函数，可以计算出一个N×N权重矩阵，其中N取值与σ相关. 通过将原始数据矩阵与该权重矩阵进行卷积运算，即可得到模糊后的矩阵数据. 但高斯模糊方法存在着两个问题，随着N的增加，模糊运算的时间消耗将逐级增加，其运算量如表1所示，另一个问题是，范围大于N的像素点，其权重为0，即对当前点无贡献，而实际情况是即使在3σ的像素点也对中心点有贡献.

快速高斯模糊在一定程度上解决了以上两个问题，具体步骤分为两步，首先对图像做一次前向滤波. 再对图像做一次后向滤波，前向滤波公式为

$w\left( n \right)\! =\! {a_0}x\left( n \right) + {a_1}x\left( {n\! -\! 1} \right) - {b_1}w\left( {n\! -\! 1} \right) - {b_2}w\left( {n \!-\! 2} \right).$

(5)

后向滤波公式为

$y\left( n \right) = {a_2}x\left( n \right) + {a_3}x\left( {n + 1} \right) - {b_1}y\left( {n + 1} \right) - {b_2}y\left( {n + 2} \right).$

(6)

其中，x为输入的数据序列，y为输出的结果序列，w为中间结果序列，a ₀，a ₁，a ₂，a ₃，b ₁，b ₂均为滤波系数.

从式(5)和式(6)可以看出，每个输出点的计算与N没有关系，而6个滤波系数是σ的函数，只需计算一次，对于不同的N，每个输出点的计算量是相同的，其计算量如表1所示，相对于原始的高斯模糊方法，其计算量大幅下降，能满足性能要求，且质量不会下降，甚至CPU也能达到实时处理要求.

2.5 分类

基于降维的分类方法，建立好模型以后，可以得到 $k \cdot C_n^2$ 个投影面，即针对每一类别均有 $C_n^2$ 个投影面，如图7所示，对于新输入的测试点，分别根据不同的类别取出该测试点在各投影面的密度值进行求和（或求平方和），此时可以得到k个和值，根据和值的大小，可以判断该测试点属于k个类别中的哪一类.

这一过程运算量极低，只需进行 $k \cdot C_n^2$ 次取数据操作与 $k \cdot \left( {C_n^2 - 1} \right)$ 次加法操作即可，这决定了本算法具有很高的时间效率.

3 实验及结果分析

本文通过4组实验数据对比传统分类方法支持向量机(SVM)、逻辑回归(LR)来验证基于正交投影的降维分类方法的可行性，比较不同类别数量，不同属性数量与不同数据量的情况下它们的分类准确率，建模效率与分类效率. 4组实验数据均来源于网络公开数据集. 数据具体情况如表2所示，实验环境如表3所示.

实验1的数据来源于真钞和假钞的图像，其图像通过工业相机拍摄，大小为400×400像素. 它的4个属性均是从图像中抽取的特征，其中属性1表示图像小波变换的方差(variance)，属性2表示图像小波变换的偏态(skewness)，属性3表示图像小波变换的峭度(kurtosis)，属性4表示图像的熵(entropy). 4个属性均为连续的实数，数据集共有两个类别标识，数据的基本情况如表4所示. 数据集的数据量并不大，本文取其中的50%作为训练集，另外的50%作为测试集.

取range=300对数据进行规范化与离散化处理，其中range需要人为调节，理论上其数值越大，表示精度越高，最后分类的准确率越高，但同时消耗的内存也越大，因此需要做出平衡，在维度数量与类别数量较低的情况下，可以选择较大的range，而当类别数量与维度都很大的时候，为了降低内存消耗，可以选择较小的range.

对数据进行建模，快速高斯模糊中取σ为6.02，可以得到 $2 \cdot C_4^2 = 12$ 个投影面，如图9所示，图中，本文假设4个维度属性分别对应于坐标w，x，y，z.

应用该模型进行分类，本文方法得到了约98.97%的分类准确率，且训练耗时与分类耗时都很低，只耗费了78 ms与小于1ms的时间，这里实验得出的时间均为多组实验的平均值. 作为对比，本文同时运用了两种应用广泛的分类方法：支持向量机与逻辑回归进行了测试，实验结果对比如表5中实验1所示，可以发现对于该数据集3种方法得到的分类准确率相差不多，且都比较高，其中SVM>本文>LR，但在耗时方面本文方法要远低于SVM与LR两种方法.

实验2、3、4采取与实验1相同的方法，在相同的运行环境中进行，这里不对其进行详细描述，给出4组试验的最终结果，如表5所示，文献[14-16]中有数据集的具体描述信息.

实验2的数据量较大，能够更清晰反映算法之间运算耗时的差距，实验1、2针对的是二分类问题，而实验3、4数据的维度与类别数量相对较大，反映了对于多分类问题算法的运行情况. 4组实验得到了相似的结果，其中多数情况下SVM方法在准确率上是最优的，本文方法得到的准确率稍低，但差距并不大，而在耗时方面本文方法要远远优于SVM与LR方法.

4 结论

本文介绍了一种基于降维的分类方法，能够把高维空间的问题转化为多个二维空间问题以降低分类算法复杂度，并给出了分类模型训练方法，通过3组实验的结果表明了基于正交投影的降维分类方法与传统的分类方法相比存在着明显的速度优势，且其预测准确率也只是稍低于以准确率著称的SVM分类方法. 降维分类方法算法简单，易于编程，具有实际应用价值. 当然该方法也存在着一些不足，如模型的存储占用内存比一般分类方法要大，对倾斜数据敏感等问题都需要在未来的工作中研究.