移动机器人的自主定位是机器人智能化的一种重要体现,已成为移动机器人领域中的热门研究方向。即时定位与地图构建[1-3](simultaneous localization and mapping,SLAM)解决的问题是指移动机器人在一个完全未知的环境中,仅使用自带的传感器,在移动过程中根据从传感器中获得的数据进行即时定位,并增量式地构建环境地图。目前SLAM算法已成为机器人研究的热点,被认为是实现完全自主智能的移动机器人的关键。
粒子滤波(Particle Filter,PF)[4-5]算法是贝叶斯滤波的一种实现,适用于非线性、非高斯时变系统,基于粒子滤波的SLAM算法是SLAM定位问题的主流解决方法之一。
机器人的SLAM定位结果常用于机器人的实时避障和路径规划,这要求SLAM定位具有较高的精度和实时性。基于粒子滤波的SLAM算法计算时间复杂度大,而SLAM定位结果又需要实时性,计算时间过长则增加定位延迟,这将导致较大的定位误差。目前大部分对基于粒子滤波SLAM算法的改进研究都集中于改进算法的定位精度或通过控制粒子数量来降低计算时间,如文献[6]利用人工鱼群算法优化粒子分布来提高SLAM算法的定位精度,这种方法在增加定位精度的同时增加了算法复杂度和计算时间;文献[7]通过KLD(Kullback-Leibler Distance)算法控制粒子数量,在数据不够收敛的时候仍需要大量的粒子,不能根本解决算法计算时间长的问题。
针对此问题,本文提出一种使用GPU并行计算[8]的方法对基于粒子滤波的SLAM算法进行改进优化,并对改进效果进行分析。
1 基于粒子滤波的SLAM算法SLAM利用传感器获得运动和环境测距信息进行实时定位,并同时根据定位结果进行实时的地图构建。SLAM可描述为式(1)[9]:
| $p \left( {\left. {{x_{\rm{k}}}} \right|{z_k},{u_k},{x_{k - 1}}} \right) = p \left( {{z_k}\left| {{{\tilde x}_k}} \right.} \right) \cdot p\left( {{{\tilde x}_k}\left| {{u_k},{x_{k - 1}}} \right.} \right),$ | (1) |
其中,k表示时刻;
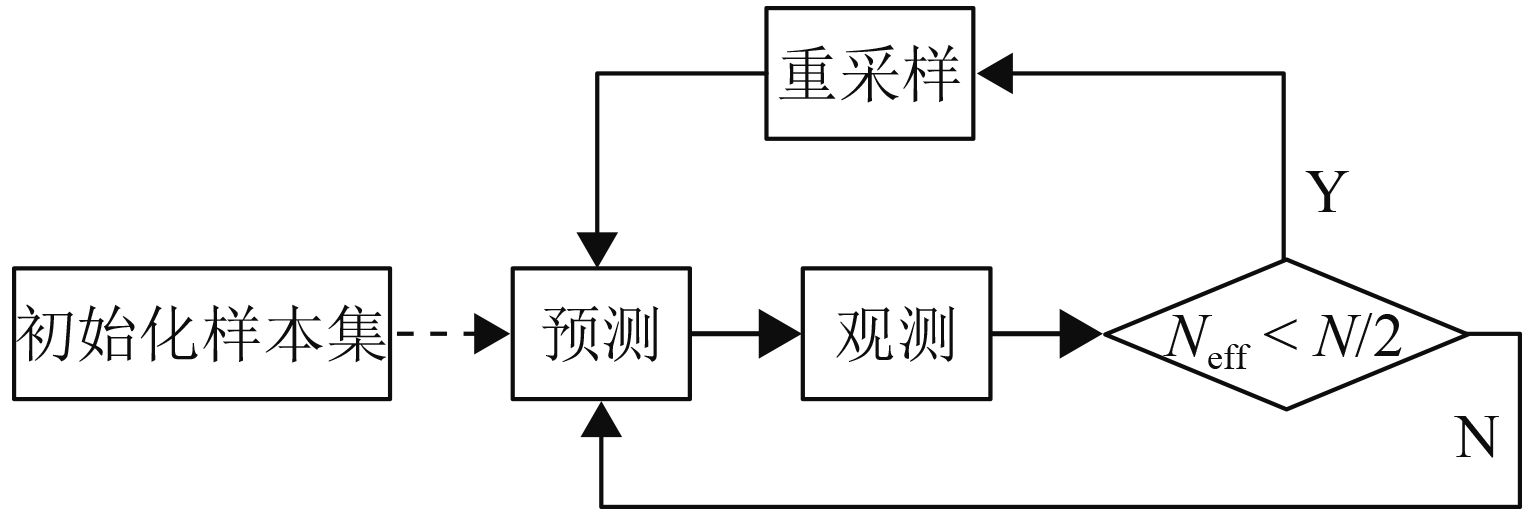
粒子滤波使用粒子的分布表示概率分布,是一种非线性滤波器,主要有预测、更新、重采样等过程[10-12],是基于粒子滤波SLAM算法的核心。算法利用粒子集表示移动机器人的定位结果的概率分布,粒子集中的每个粒子表示机器人的可能位姿,图1为算法实现基本流程。
|
图 1 SLAM算法基本流程 Figure 1 SLAM algorithm flow chart |
(1) 初始化.
初始化样本集,从先验分布P(x0)采样得到N个粒子
(2) 预测.
根据运动模型,由上一时刻粒子集和机器人移动数据,计算获得机器人定位粒子集的先验分布。由于从机器人内部传感器获得的移动数据存在误差,需要根据实际移动平台设置运动模型的噪声参数。
(3) 观测.
粒子集中每个粒子的观测似然率是观测阶段将获得的先验分布与传感器获得的测距数据结合,再利用观测模型计算出来的。然后根据每个粒子的观测似然率对每个粒子进行加权,得到后验分布。观测模型
(4) 是否需要重采样.
若有效粒子数Neff小于粒子数的一半N/2,则进行重采样,否则进入下一步。
(5) 重采样.
根据粒子的权值对粒子集进行采样,产生新的粒子集。通过除去权值较低的粒子,保留权值高的粒子[13],让粒子分布逐渐收敛接近最优值。
2 并行优化基于粒子滤波的SLAM算法使用粒子集表示定位的概率分布,粒子数量决定算法的抗干扰能力、鲁棒性和定位准确度等。在越复杂、宽广的环境下进行SLAM定位,对粒子数量的要求越高。粒子数量直接影响算法计算量及速度。目前对基于粒子滤波的SLAM算法的改进大多数都会增加算法复杂度,即在提高定位精度同时会降低算法执行速度。而移动机器人的定位结果具有时效性,所以SLAM的计算速度又将影响定位准确度。
本文提出一种结合粒子滤波和SLAM算法的,GPU并行计算优化的方式进行加速,从而减少计算带来的定位延迟。
2.1 并行优化分析基于粒子滤波的SLAM算法主要有预测、观测和重采样3个阶段。其中预测阶段使用运动模型对移动数据加入随机噪声,将上一时刻粒子集加入移动数据生成此时刻的粒子集先验分布。此过程中计算较为简单,每个粒子只执行一次对移动数据加操作。
重采样的实现过程主要是根据粒子的权值,决定粒子的去留。其中最容易的实现方法是把权值低的粒子去除,把权值高的粒子复制[14]。而其他一些较复杂方法需要在所有粒子中进行衡量,各个粒子计算的关联程度大,不适于并行计算。
算法的观测过程,主要利用观测模型计算每个粒子的观测似然率,而在粒子观测似然率的计算中,是以从测距传感器获得的测量数据和粒子作为输入,与已知地图进行比较计算得到观测似然率,再根据观测似然率对每个粒子进行加权。在计算过程中每个粒子分开计算,具有较高的计算独立性。
在实际环境使用中计算粒子的观测似然率是一个复杂的计算过程,基于激光雷达和栅格地图的观测模型将可能面临4种噪声数据:测量固有误差phit、预料外障碍物造成的误差pshort、测量失效误差pmax、随机误差prand。观测模型的主要任务是在存在多种噪声数据的情况下,使用先验分布和观测值估计出后验分布。其中观测模型可用式(2)表示:
| $\begin{array}{l}\!\! p\left( {z_k^i \left| {{{\tilde x}_k},m} \right.} \right) \!=\! {z_{\rm {hit}}} \! \cdot \! {p_{\rm {hit}}}\left( {z_k^i\left| {{{\tilde x}_k},m} \right.} \right) \!+\! {z_{\rm {short}}} \! \cdot \! {p_{\rm {short}}}\left( {z_k^i\left| {{{\tilde x}_k},m} \right.} \right) \!+\! \\\!\! {z_{{\rm{max}}}} \! \cdot \! {p_{\max }}\left( {z_k^i\left| {{{\tilde x}_k},m} \right.} \right) \!+\! {z_{\rm {rand}}} \! \cdot \! {p_{\rm {rand}}}\left( {z_k^i\left| {{{\tilde x}_k},m} \right.} \right),\end{array}$ | (2) |
式(2)中,
测量固有噪声在有效范围内呈正态分布,可用式(3)表示:
| ${p_{{\rm{hit}}}}\left( {z_k^i\left| {{{\tilde x}_k},m} \right.} \right) \!=\! \left\{ {\begin{array}{*{20}{c}}\!\! {\frac{1}{{\sqrt {2{\rm{\pi }}\sigma _{{\rm{hit}}}^2} }}{\rm e^{ - \frac{{{{\left( {z_k^i - z_k^{i*}} \right)}^2}}}{{2\sigma _{{\rm{hit}}}^2}}}},0 < z_k^i < {z_{\max }};}\\\!\! {0,\begin{array}{*{20}{c}}{z_k^i \leqslant 0} & {\rm {or}} & {{z_{\max \leqslant }}z_k^i.}\end{array}}\end{array}} \right.$ | (3) |
式(3)中,σhit是硬件固有噪声参数,
| ${p_{{\rm{short}}}}\left( {z_k^i\left| {{{\tilde x}_k},m} \right.} \right) = \left\{ {\begin{array}{*{20}{c}}{{\lambda _{{\rm{short}}}} \cdot {{\rm{e}}^{ - {\lambda _{{\rm{short}}}}z_k^i}},0 < z_k^i < z_k^{i*};}\\{0,z_k^i \leqslant 0orz_k^i \geqslant z_k^{i*}.}\end{array}} \right.$ | (4) |
式(4)中,λshort为观测模型的固有参数,需要根据实际环境设定。
| ${p_{\max }}\left( {z_k^i\left| {{{\tilde x}_k},m} \right.} \right) = \left\{ {\begin{array}{*{20}{c}}{1,z_k^i \geqslant {z_{\max }};}\\{0,z_k^i < {z_{\max }}.}\end{array}} \right.$ | (5) |
如式(5),zmax为扫描的有效范围,在观测距离不超过有效范围时,将不存在测量失效误差。
| ${p_{{\rm{rand}}}}\left( {z_k^i\left| {{{\tilde x}_k},m} \right.} \right) = \left\{ {\begin{array}{*{20}{c}}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{\frac{1}{{{z_{\max }}}},0 < z_k^i < {z_{\max }};}\\{0,z_k^i \leqslant 0orz_k^i \geqslant {z_{\max }}.}\end{array}} \right.$ | (6) |
式(6)表示在有效测量范围内存在的随机误差。
计算粒子观测似然率过程中,将从测距传感器获得的一系列测量点,并根据粒子表示位姿,分别转换为已知全局地图上的点,再分别对这些点周围n×n区域进行一次遍历,根据选择方法不同对此n×n区域进行相应计算,其中n为观测模型的有效计算范围。如使用式(2)的计算方法,将在全局地图中遍历测量障碍物点周围n×n区域,并寻找地图上一个与此测量障碍物点最近的已知障碍物点作为式(3)中的
在此假设每次可从传感器获得M个扫描点,间隔S个点取一个扫描点作为计算观测似然率的过程中的测量障碍物点,则每次计算观测似然率时需要进行M/S次坐标转换,并对n×n×M/S的栅格点进行遍历和计算。在实际应用中可能使用成千上万个粒子,如果按传统的流水线方式执行,则将在更新过程的计算耗费大量时间。
2.2 并行优化设计计算粒子观测似然率是算法中计算量最多的一个过程,而且粒子间的计算较为独立,适合进行GPU并行加速优化。
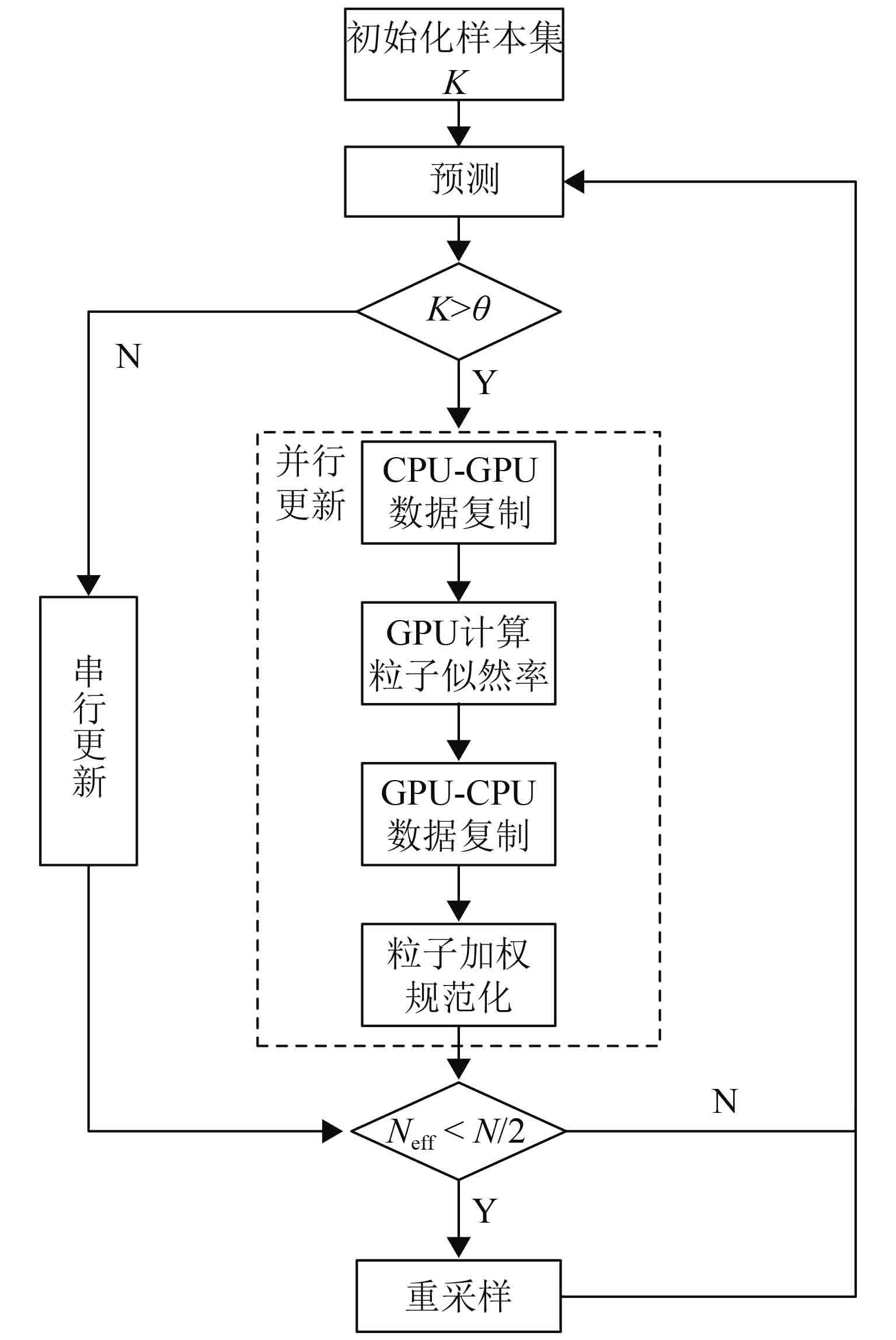
由上述分析,本文设计将计算粒子观测似然率部分移入GPU中进行大规模并行计算,加速前判断当前粒子数是否大于阈值(θ=868,加速比为1时粒子数),若大于则进行GPU并行加速,否则执行串行更新过程。并行优化后的算法执行框架如图2所示。
|
图 2 SLAM算法优化框架 Figure 2 SLAM algorithm optimization framework |
将算法中更新阶段的计算粒子观测似然率部分改用GPU并行执行。由于CPU与GPU不使用同一寻址空间,所以使用GPU的代价是增加了两个CPU内存和GPU内存间的数据复制过程。其中CPU-GPU数据复制包括已知地图、粒子集数据和观测数据。GPU-CPU的数据复制,只需要将每个粒子对应的观测似然率从GPU复制到CPU即可。最后再根据粒子的观测似然率对粒子进行加权和权值规范化,即完成观测阶段。
2.3 并行优化实现根据上节分析,使用CUDA进行GPU并行计算的开发,实现算法的并行优化,并对基于粒子滤波的SLAM的GPU并行优化验证。
使用原算法的预测和重采样,将更新阶段利用CUDA进行重新编程,使用GPU并行计算粒子的观测似然率。在实现对算法的GPU并行优化后,与原算的执行时间进行对比,分析优化结果。
3 实验结果与分析分别使用100、1 000、5 000、15 000、40 000、50 000、100 000个粒子进行实验,对比其加速部分的平均执行时间和总体的平均执行时间。实验数据如图3–图5所示。
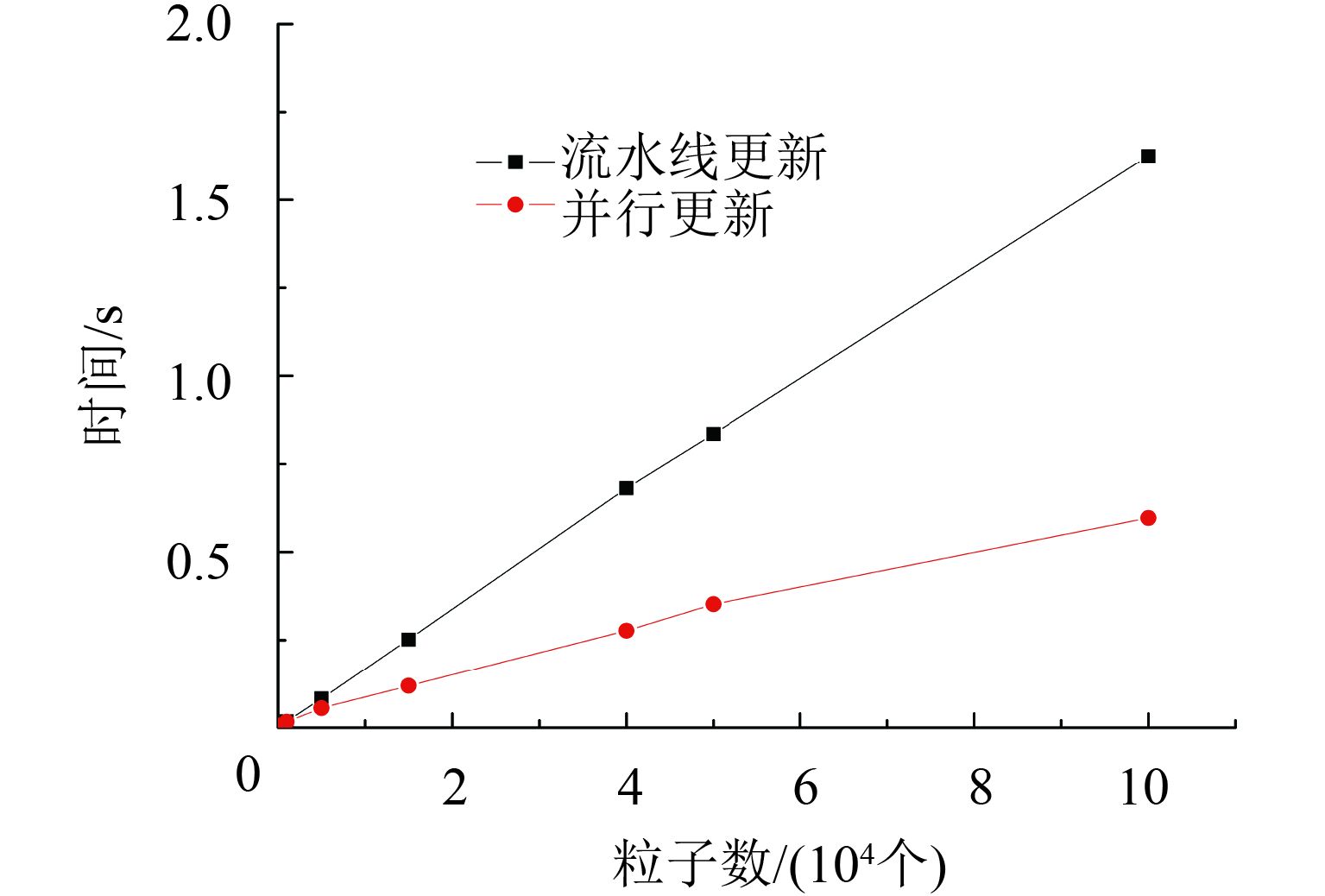
图3中对比了并行优化前后加速部分平均执行时间,即算法的更新部分平均执行时间。并行更新执行时间包括以下操作:将CPU内存中的粒子集数据、扫描数据和一些相关计算参数复制到GPU内存;粒子观测似然率由GPU计算;再将GPU计算出的观测似然率数据复制到CPU内存空间[15-16];根据粒子集观测似然率对粒子进行加权等。
|
图 3 加速部分平均执行时间比较 Figure 3 Comparison of the execution time of the parallel optimization of the acceleration part |
|
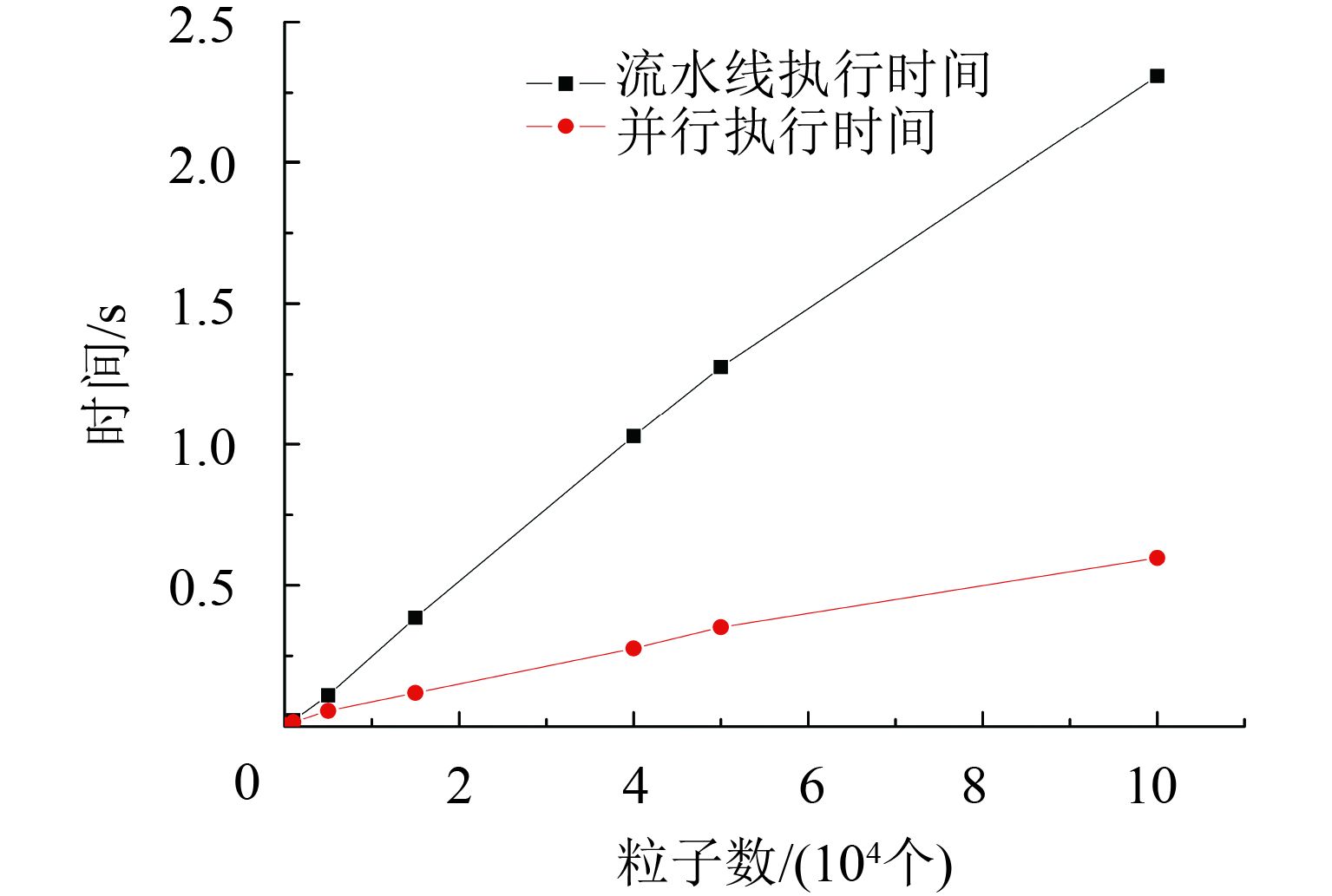
图 4 算法总执行时间比较 Figure 4 Comparison of execution time of parallel optimization algorithms |
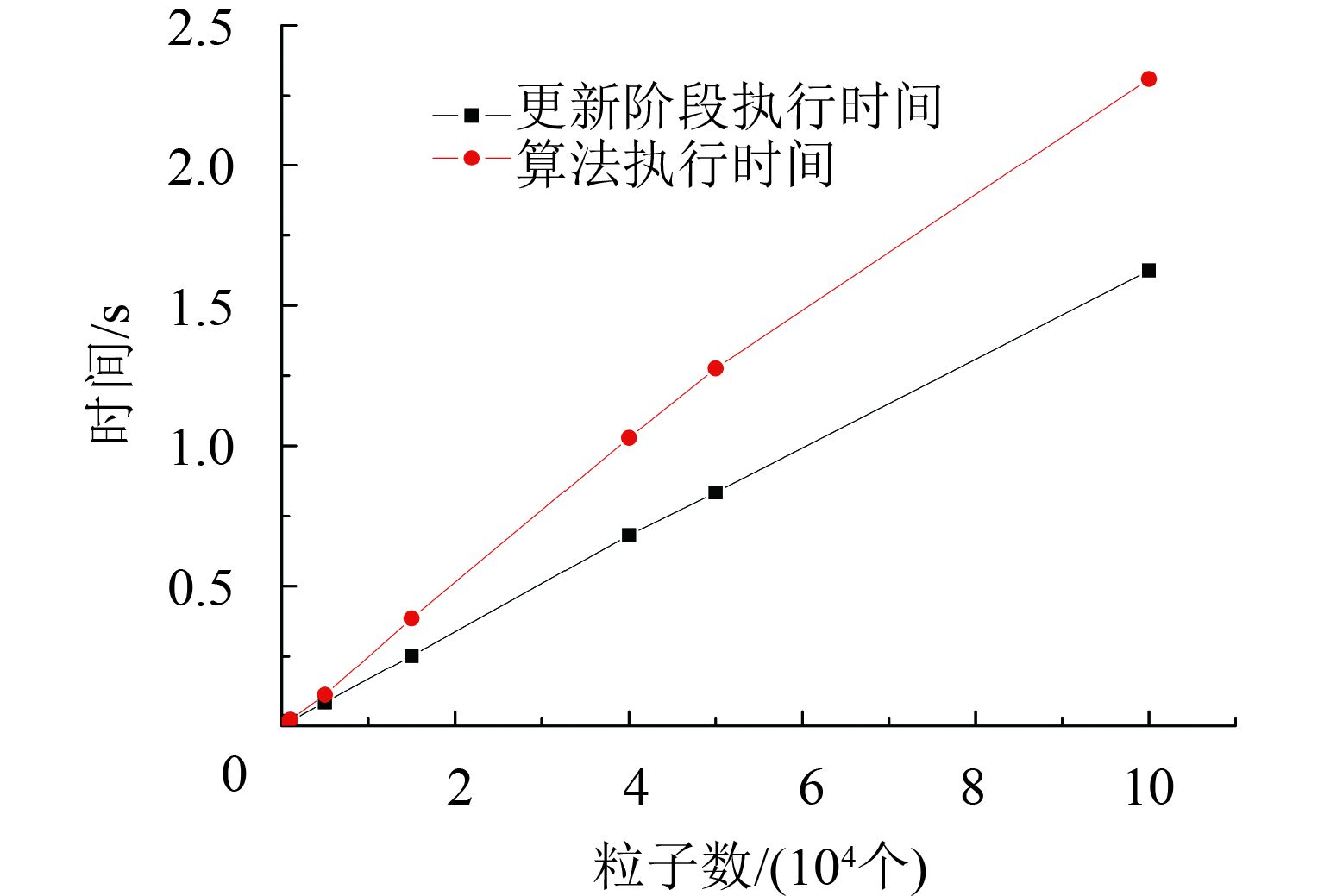
|
图 5 优化前算法执行时间比较 Figure 5 Comparison of algorithm execution time before optimization |

|
图 6 并行优化前后运动轨迹 Figure 6 The path of before and after parallel optimization |
由图3可见,在粒子数低于1 000时,使用GPU并行执行时间比使用CPU流水线执行更新操作相近或要更长,这是由于CPU主频高于GPU约3倍,处理相同任务的速度远远快于单个GPU。其次使用GPU进行并行计算,需要将粒子集数据、扫描数据和一些相关计算参数复制到GPU内存中,这需要耗费一定的时间。所以在使用粒子数量较少的时候,不能发挥GPU加速的优势,在粒子集中粒子数量达到15 000时,使用GPU并行计算的算法加速效果明显,算法更新阶段的执行速度达到原来的3.5倍。而在粒子集中粒子数量到达40 000后,GPU对算法的并行加速稳定在4.5倍左右,效果明显,大大降低算法中更新阶段的计算时间。
图4与图3的结果相近。图4比较了使用GPU并行优化前后算法的平均执行时间. 在粒子数较多时,GPU并行优化的加速效果明显。
图6为GPU并行加速前后机器人绕室内一圈的运动轨迹图(如图中蓝色所示)。图6(a)中由于机器人运动速度过快,而CPU处理速度较慢,从而导致观测数据之间关联较小,与真实运动轨迹偏差较大。图6(b)运用GPU并行加速,提高算法更新阶段的执行效率,解决了轨迹偏差较大的问题。实验证明,GPU并行加速不仅提高了算法执行效率,而且明显减小了由计算时间过长导致的定位误差。
4 结论基于粒子滤波的SLAM算法由于其实用性和创新性,已成为移动机器人领域中的热门研究。但算法计算量大,与机器人CPU计算资源紧张是一对明显的矛盾。SLAM定位结果具有时效性,算法计算时间过长将增加定位误差。本文针对此问题提出一种基于粒子滤波的SLAM算法的GPU并行优化方法,通过实验验证,算法的GPU并行优化效果明显,可减少由算法计算时间带来的定位误差,为移动机器人的SLAM算法提供一种全新的优化思路。
| [1] | DURRANT-WHYTEH. Simultaneous localization and mapping (SLAM): Part I The essential algorithms[J]. Robotics and Automation Magazine, 2006, 13(2): 99-110. DOI: 10.1109/MRA.2006.1638022. |
| [2] | SMITHR. Estimating uncertain spatial relationships in robotics[J]. Autonomous Robot Vehicles, 1990, 4: 167-193. |
| [3] | SHOWDONGH. Convergence and consistency analysis for extended Kalman filter based SLAM[J]. IEEE Transactions on Robotics, 2007, 23(5): 1036-1049. DOI: 10.1109/TRO.2007.903811. |
| [4] |
宋宇, 李庆玲. 平方根容积Rao-Blackwillised粒子滤波SLAM算法[J].
自动化学报, 2014, 40(2): 367-367.
SONG Y, LI Q L. SLAM with square-root cubature rao-blackwillisedparticle filter[J]. ACTA AUTOMATICA SINICA, 2014, 40(2): 367-367. |
| [5] | 王丁. 基于改进粒子滤波的检测前跟踪算法[D]. 成都: 电子科技大学电子工程学院, 2012. http://cn.bing.com/academic/profile?id=86196eb27975b9b4297de85e97ab085f&encoded=0&v=paper_preview&mkt=zh-cn |
| [6] |
朱磊. 未知环境下的移动机器人SLAM方法[J].
华中科技大学学报: 自然科学版, 2011, 39(7): 9-13.
ZHU L. SLAM method for mobile robot in unknown environment[J]. Huazhong University of Technology (Natural Science Edition), 2011, 39(7): 9-13. |
| [7] | DIETERFOX. Adapting the sample size in particle filters through KLD-sampling[J]. TheInternational Journal of Robotics Research, 2003, 22: 985-1003. DOI: 10.1177/0278364903022012001. |
| [8] |
卢风顺, 宋君强, 银福康. CPU/GPU协同并行计算研究综述[J].
计算机科学, 2011, 28(3): 5-9.
LU F S, SONG J Q, YIN F K. Survey of CPU/GPU synergetic parallel computing[J]. Computer Science, 2011, 28(3): 5-9. |
| [9] |
徐李超. 一种仿人机器人步态优化的新方法研究[J].
广东工业大学学报, 2012, 29(1): 50-54.
XU L C. Gait Optimizing of humanoid robots using a new method[J]. Journal of Guangdong University of Technology, 2012, 29(1): 50-54. |
| [10] |
王法胜, 鲁明羽, 赵清杰. 粒子滤波算法[J].
计算机学报, 2014, 37(8): 1679-1694.
WANG F S, LUM Y, ZHAO Q J. Particle filtering algorithm[J]. Chinese Journal of Computer, 2014, 37(8): 1679-1694. |
| [11] |
于金霞, 汤永利. 一种改进的自适应优化粒子滤波算法研究[J].
小型微型计算机系统, 2013, 34(6): 1446-1450.
YU J X, TANG Y L. Research on an improved particle filter algorithm based on adaptive optimization mechanism[J]. Journal of Chinese Computer Systems, 2013, 34(6): 1446-1450. |
| [12] |
左军毅, 张怡哲. 自适应不完全重采样粒子滤波器[J].
自动化学报, 2012, 38(4): 647-652.
ZUO J D, ZHANG Y Z. Particle filter based on adaptive part resampling[J]. Acta Automatica Sinica, 2012, 38(4): 647-652. DOI: 10.3724/SP.J.1004.2012.00647. |
| [13] |
冯驰. 粒子滤波器重采样算法的分析与比较[J].
系统仿真学报, 2009, 21(4): 1101-1110.
FENG C. Analysis and comparison of resampling algorithms in particle filter[J]. Journal of Systems Simulation, 2009, 21(4): 1101-1110. |
| [14] | 刘洞波. 移动机器人粒子滤波定位与地图创建方法研究[D]. 长沙: 湖南大学电气与信息工程学院, 2013. |
| [15] |
郭睿冉, 宋建新. 图像压缩感知的基于GPU的并行重构算法研究[J].
电视技术, 2014, 38(11): 15-19.
GUO R R, SONG J X. Research and implementation of parallel signal reconstruction about image compressed sensing based on GPU[J]. Digital Video, 2014, 38(11): 15-19. |
| [16] |
刘燕龙, 原玲. 基于Calculix的船舶疲劳强度并行计算方法研究与应用[J].
广东工业大学学报, 2015, 32(4): 77-82.
LIU Y L, YUAN L. Parallel mechanism research and application of calculix in ship fatigue analysis environment[J]. Journal of Guangdong University of Technology, 2015, 32(4): 77-82. |
 2017, Vol. 34
2017, Vol. 34

