无线传感器网络(Wireless Sensor Networks,WSNs)[1]由部署在监测区域内的大量具有感知对象、采集数据并处理数据和传输数据能力的传感器节点构成。传感器节点之间通过多跳方式进行无线通信,形成一个多跳自组织网络[2-3]。然而,网络中的每个传感器节点只有确定了自身的位置才能根据采集到的数据准确反映采集点的变化情况,同时提供给专业人员进行数据分析,以便采取相应的措施。因此,研究无线传感器网络中的节点定位机制有着重要的意义。
无线传感器网络定位机制分为与测距相关(Range-based)的定位算法和与测距无关(Range-free)的定位算法两大类[4]。Range-based定位需要额外的节点硬件条件支持,以实现对两节点之间距离或方位角的测量,而Range-free定位则不同,它是利用节点间信息的交换对节点间的距离进行估计,实现对未知节点的位置估计。Range-based定位技术有TOA、TDOA、RSSI和AOA,这类算法定位精度相对较高,但对节点的开销高,成本大。Range-free定位技术有Amorphous、质心算法[5]、APIT[6]、DV-Hop[7]等,这类定位算法的开销相对较低,对节点的配置要求不高,这有益于降低全网成本。因此,Range-free定位更适合大规模无线传感器网络的实际应用。
在数据挖掘中常对大量数据用聚类分析处理,分析数据的分布,每个类的特征,从而在特定的类的集合上进行更精确地集中分析,找到有用的信息。数据挖掘中的聚类算法有许多,其中经典的DBSCAN聚类算法[8-10]是一种基于密度的聚类算法,它能在带有噪声的环境下快速地发现任意形状的簇类,聚类能力较强,能够将数据样本划分多个簇类,使每个簇类中的元素相似性较大,簇类间元素相似性较小。由于该特点,它常常运用于web搜索、模式识别、数据分析、商务智能应用等领域[11-14]。
1 DV-Hop算法及三边测量法简介 1.1 DV-Hop算法定位过程Step1 实现网络上的所有节点获得各信标节点位置信息和最小跳数信息。首先,每一个信标节点向周围的邻居节点广播自身定位信息分组,分组中包含时间戳,发送者,跳数(跳数字段的初始化为0)以及自身位置信息。其次,所有节点通过以下方法获得与各信标节点的最小跳数值:若接收到同一个信标节点的多个跳数分组,则保留较小跳数的分组,较大分组则舍弃;同时让跳数字段值加一,再转发给周围的邻居节点。每个节点进行多次上述操作,最终网络中所有节点都能够获得与各信标节点的最小跳数和其位置信息。
Step2 获得未知节点与信标节点间的估计距离。每个信标节点使用第一个阶段中所获得的其余信标节点的位置信息和相距跳数,利用(1)式估算信标节点的平均跳距,然后通过平均跳距与跳数之积获得两者的估计距离。
| ${\rm{HopSiz}}{{\rm{e}}_i} = \frac{{\sum\limits_{i \ne j} {\sqrt {{{({x_j} - {x_i})}^2} + {{({y_j} - {y_i})}^2}} } }}{{\sum\limits_{i \ne j} {{h_{ij}}} }}.$ | (1) |
Step3 该阶段的目的是获得未知节点自身位置。当未知节点获得3个或3个以上的信标节点估计距离信息后,利用三边测量法或极大似然估计法计算未知节点定位坐标。
1.2 三边测量法在定位方法中,三边测量法是一种有效的定位方法。假设未知节点U和3个信标节点B1、B2、B3之间的距离分别为d1、d2、d3,信标节点的3个位置坐标分别为(x1,y1)、(x2,y2)、(x3,y3),如图1所示。
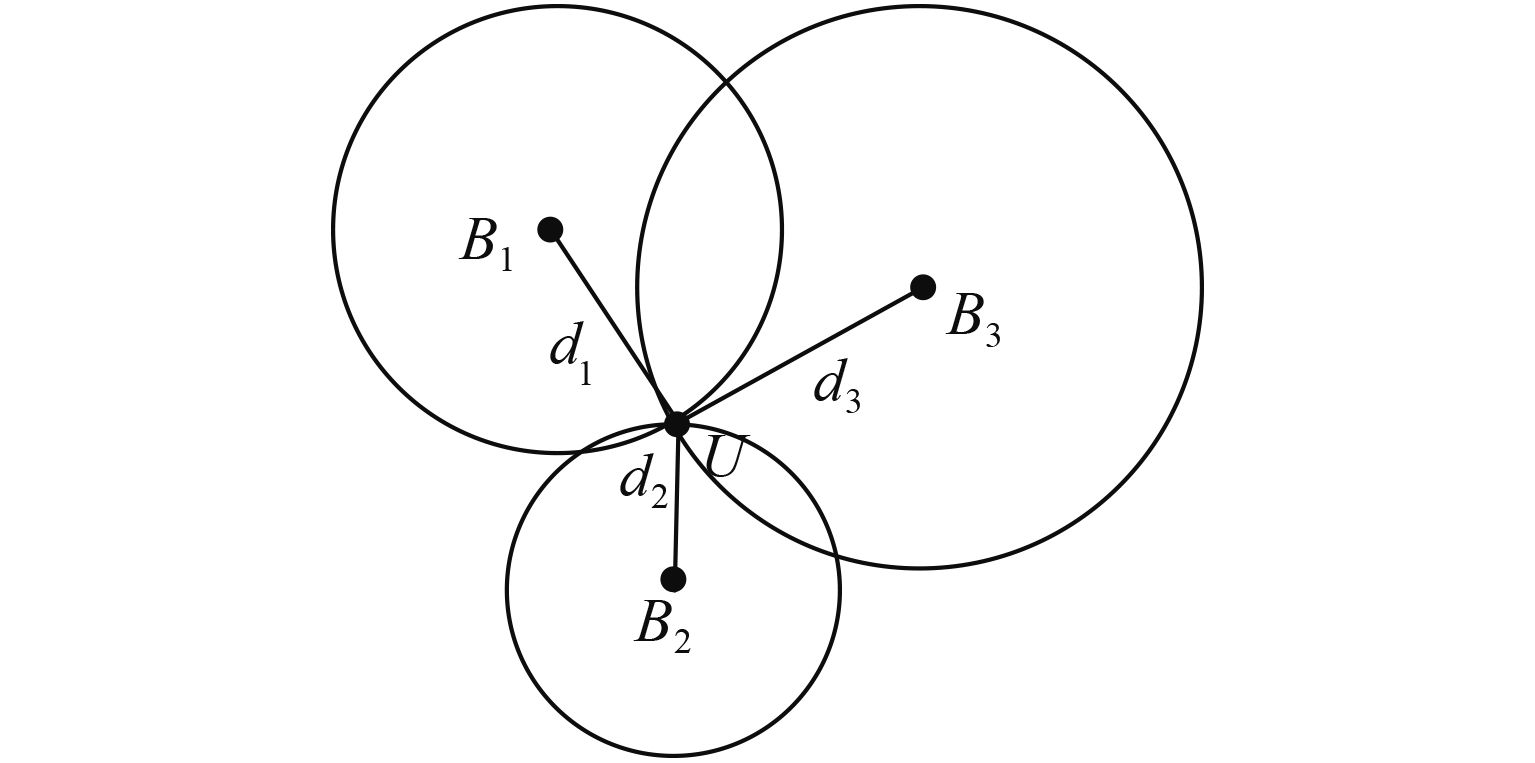
|
图 1 三边测量法示意图 Figure 1 The sketch map of trilateration |
| $\left\{ \begin{array}{l}\!\! {({x_1} - x)^2} + {({y_1} - y)^2} = {d_1}^2,\\\!\! {({x_2} - x)^2} + {({y_2} - y)^2} = {d_2}^2,\\\!\! {({x_3} - x)^2} + {({y_3} - y)^2} = {d_3}^2.\end{array} \right.$ | (2) |
解二元二次方程组得U的坐标为
| $\left[ \begin{array}{l} x\\ y \end{array} \right] = {\left[ \begin{array}{l} 2\left( {{x_1} - {x_3}} \right)2\left( {{y_1} - {y_3}} \right)\\ 2\left( {{x_2} - {x_3}} \right)2\left( {{y_2} - {y_3}} \right) \end{array} \right]^{ - 1}}\left[ \begin{array}{l} x_1^2 - x_3^2 + y_1^2 - y_3^2 - d_1^2 + d_3^2\\ x_2^2 - x_3^2 + y_2^2 - y_3^2 - d_2^2 + d_3^2 \end{array} \right].$ | (3) |
3个参与定位的信标节点所构成的三角形与待定位的未知节点之间的位置关系可分为两类,第1类是未知节点在三角形内部或边上(如图2所示),第2类是未知节点在三角形外部(如图3所示)。两者的区别可以通过一个等式判断:
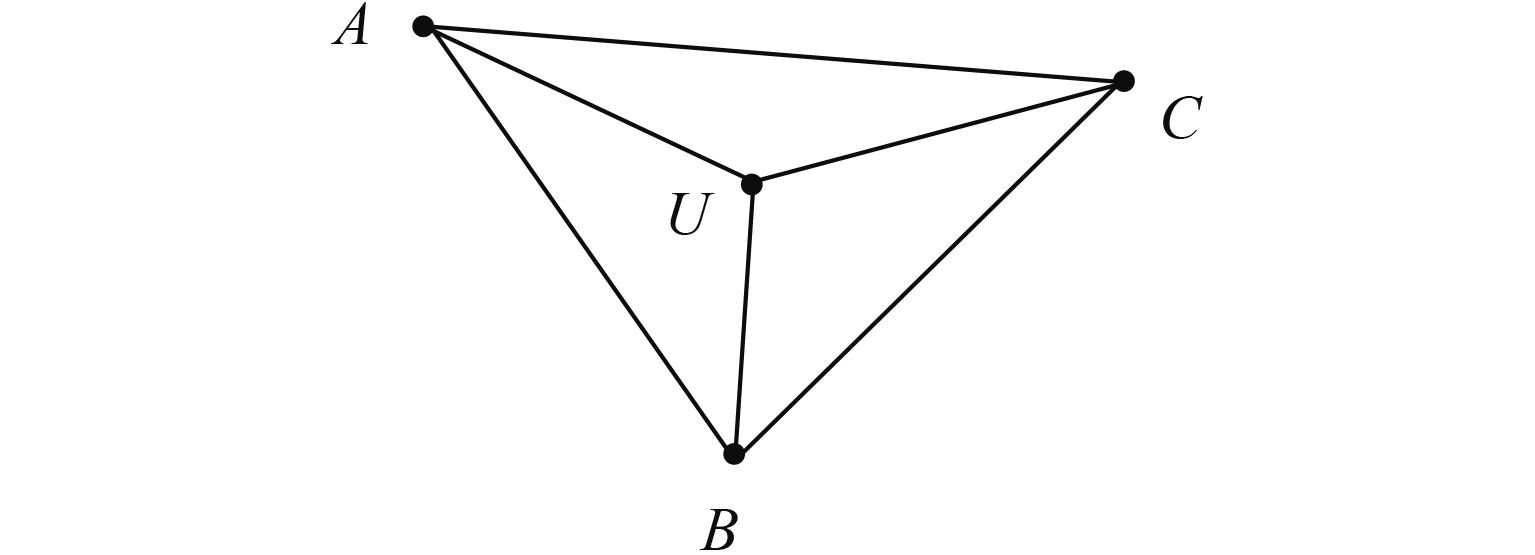
|
图 2 未知节点在三角形内部示意图 Figure 2 Unknown nodes in the related triangle |
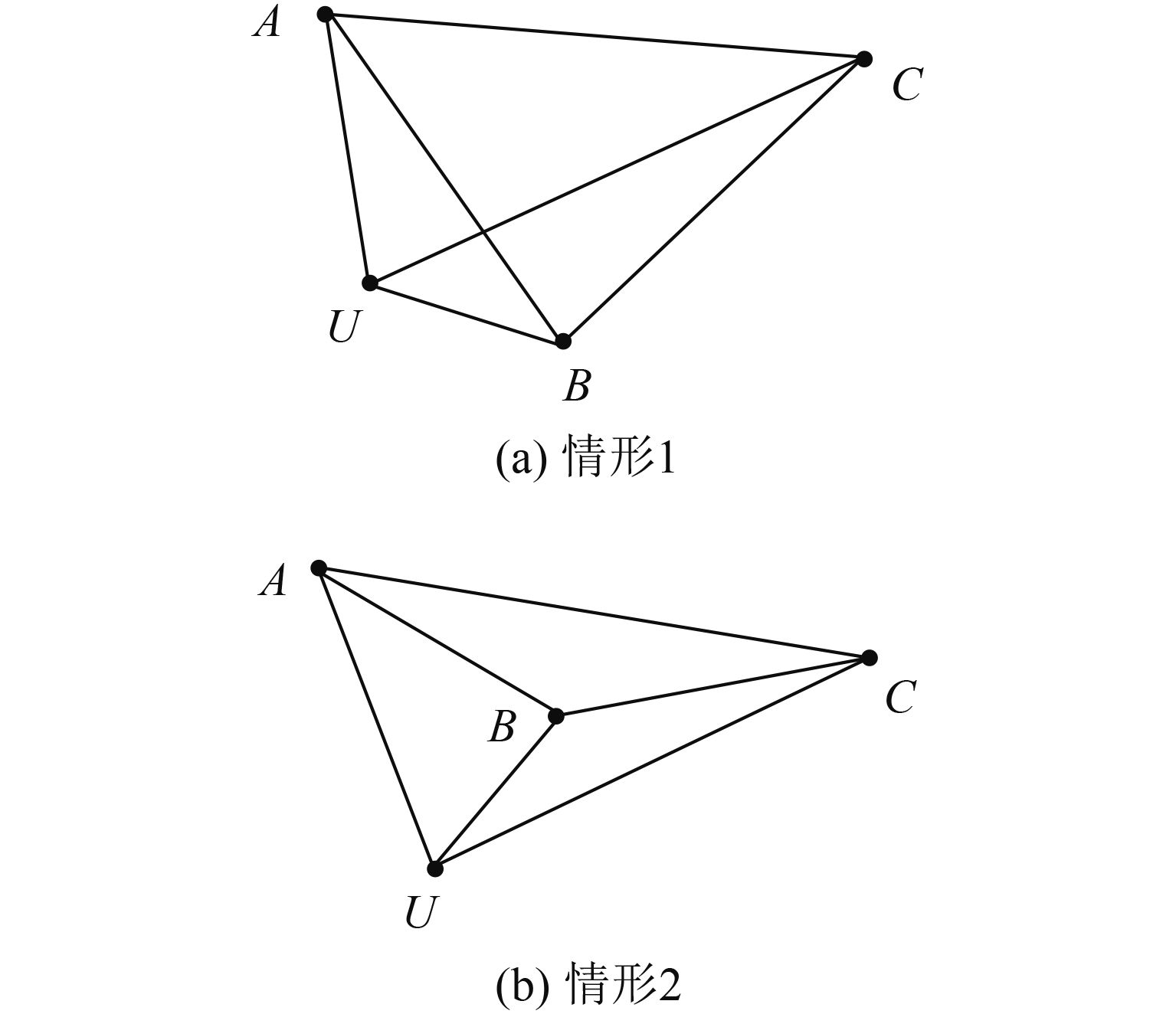
|
图 3 未知节点在三角形外部示意图 Figure 3 Unknown nodes out of the related triangle |
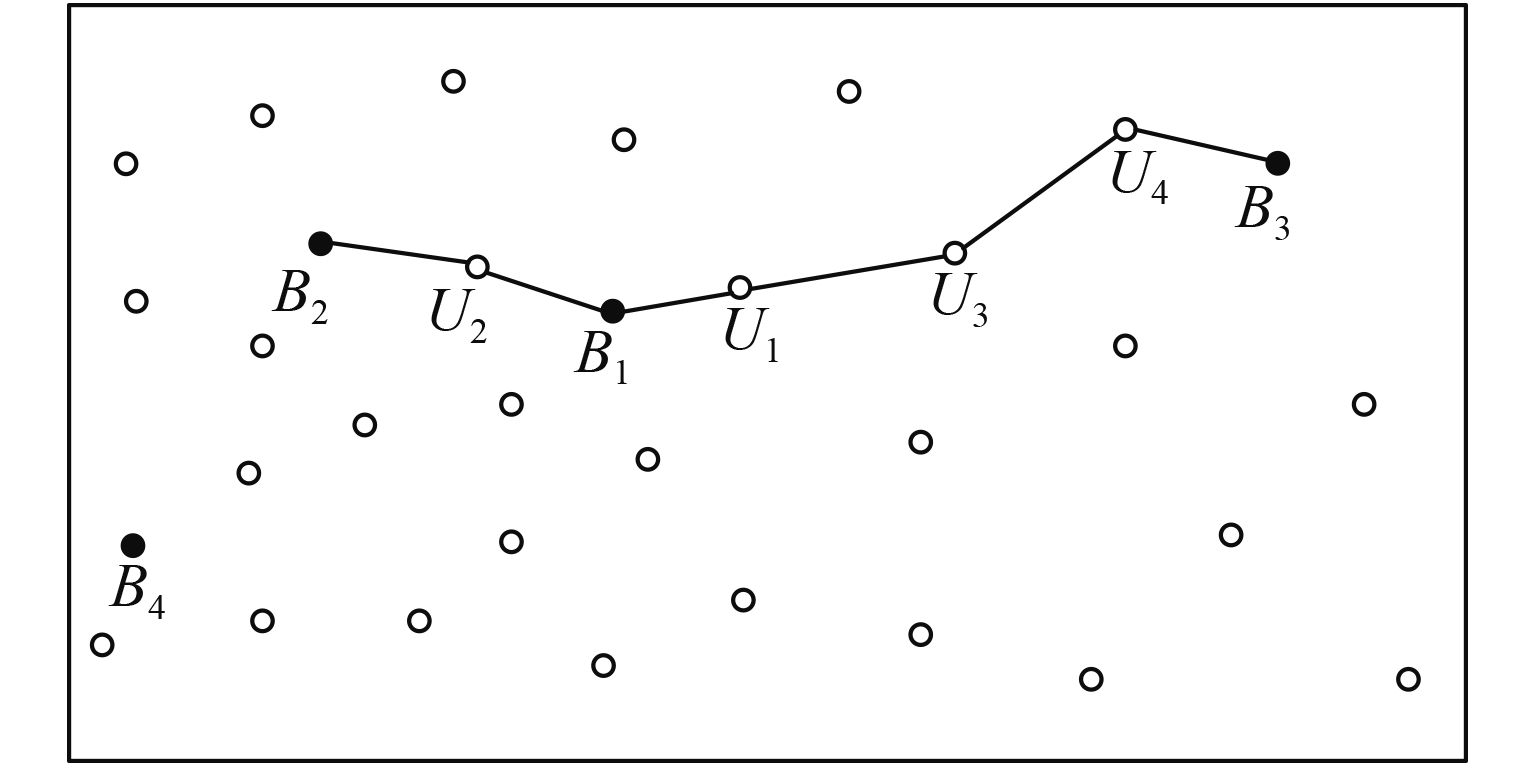
|
图 4 节点分布示意图 Figure 4 A sketch of nodes distribution |
当∠AUB+∠AUC+∠BUC=360°时,属于第一类,否则,属于第二类。
在第1类中,通过下面主要步骤对未知节点进行初步定位估计:
(1) 首先确定测量边和计算边。例如已知测量边AU和BU,待求解的计算边CU。
(2) 利用三角形中的已知三边距离,由两条测量边通过多次运用余弦定理,求解剩余的计算边。例如在△ABU上通过测量边AU和BU,运用余弦定理可以得到∠AUB和∠ABU,同理,在△ABC上再次使用余弦定理得到∠ABC,从而得到边CU对应的角∠UBC,有∠UBC=∠ABC–∠ABU。在△UBC上逆用余弦定理,求出计算边CU。
(3) 经步骤2之后,通过已知一条计算边和两条测量边,运用三边测量法对待定位的未知节点进行一次初步定位估计。
(4) 循环交换测量边和计算边,转到步骤1继续对待定位节点进行定位估计。如此循环操作,可以得到待定位节点的3次初步位置估计。
在第2类中,与第1类有所区别,需考虑两种情况,主要定位步骤如下:
(1) 首先从∠AUB,∠AUC和∠BUC中选取最大的角,以最大角对应的边作为划分边,判断其余两个顶点与划分边的位置关系,如果其余两个顶点在划分边的不同侧,则将这种情况归为第一种情况(如图3a所示),否则,归为第2种情况(如图3b所示)。若判断结果属于第一种情况,则转到第2步执行;若判断结果属于第2种情况,则转到第5步执行。
(2) 先确定测量边和计算边,然后根据3个信标节点构成的已知三边距离的三角形和两条测量边,多次利用余弦定理,求出计算边的值。例如,若计算边夹在两条测量边之间,如图3a所示,边CU夹在AU和BU之间,多次运用余弦定理可以计算得到∠ABU和∠ABC,则边CU对应的角∠CBU,有∠CBU=∠ABU+∠ABC。然后选择在离U最近的三角形△BCU上逆用余弦定理求出边CU。若计算边未夹在两条测量边之间,计算边AU未夹在CU和BU之间,用上述同样的方法,可以求出边AU对应的离U最近的角∠UBA,有∠UBA=∠UBC–∠ABC,再次逆用余弦定理,求解AU。
(3) 根据一条已经求出的计算边和两条已知的测量边,运用三边测量法对待定的未知节点进行一次初步定位估计。
(4) 若还有测量边和计算边的组合未参与了定位估计,则转到步骤2继续定位估计,否则转到步骤8。
(5) 此步骤的目的与步骤2相同,同样先确定测量边和计算边,然后通过现有的已知条件,求出计算边。但在计算角度过程中与步骤2有所区别,例如,如图3b所示,当计算边BU在两条测量边AU、CU之间时,则边BU所对应的离U最近的角∠UAB,有∠UAB=∠UAC–∠BAC。当计算边CU不在两条测量边AU、BU之间时,则边CU所对应的离U最近的角∠UBC,有∠UBC=360°–∠UBA–∠ABC。
(6) 此时满足三边测量法三边已知的条件,运用三边测量法对待定的未知节点进行一次初步定位估计。
(7) 转到步骤5继续定位估计,直到所有的测量边和计算边的组合都参与了定位估计。
(8) 结束一组信标节点的定位估计,获得待定位未知节点的三次初步位置估计。
上述的目的是通过选取其中两条边的距离,计算第3条边的距离,再应用三边测量法,以此反复计算,得到3次估计。利用3个信标节点两两之间的距离已知,实现用计算值代替测量值,以减小测量误差。因此,只需要已知两条边的距离和3个信标节点的位置关系就能对未知节点进行定位估计。
2.2 运用加权方式对平均跳距的改进图4为节点分布示意图,其中实心圆点代表信标节点,空心圆心代表未知节点。在图4的左侧为密集区域,右侧为稀疏区域,左侧网络与右侧网络相比,左侧网络跳距较短,在相同实际距离情况下跳数偏多。因此,若仅采用离未知节点U1最近的信标节点B1的平均跳距计算未知节点U1与各信标节点间的距离,那么未知节点U1与信标节点B3间的估计距离值将偏小,而未知节点U1与信标节点B2的估计距离值将偏大。为了有效地减少这种误差,本文对信标节点的平均跳距提出一种加权方式,信标节点加权系数λ为:
|
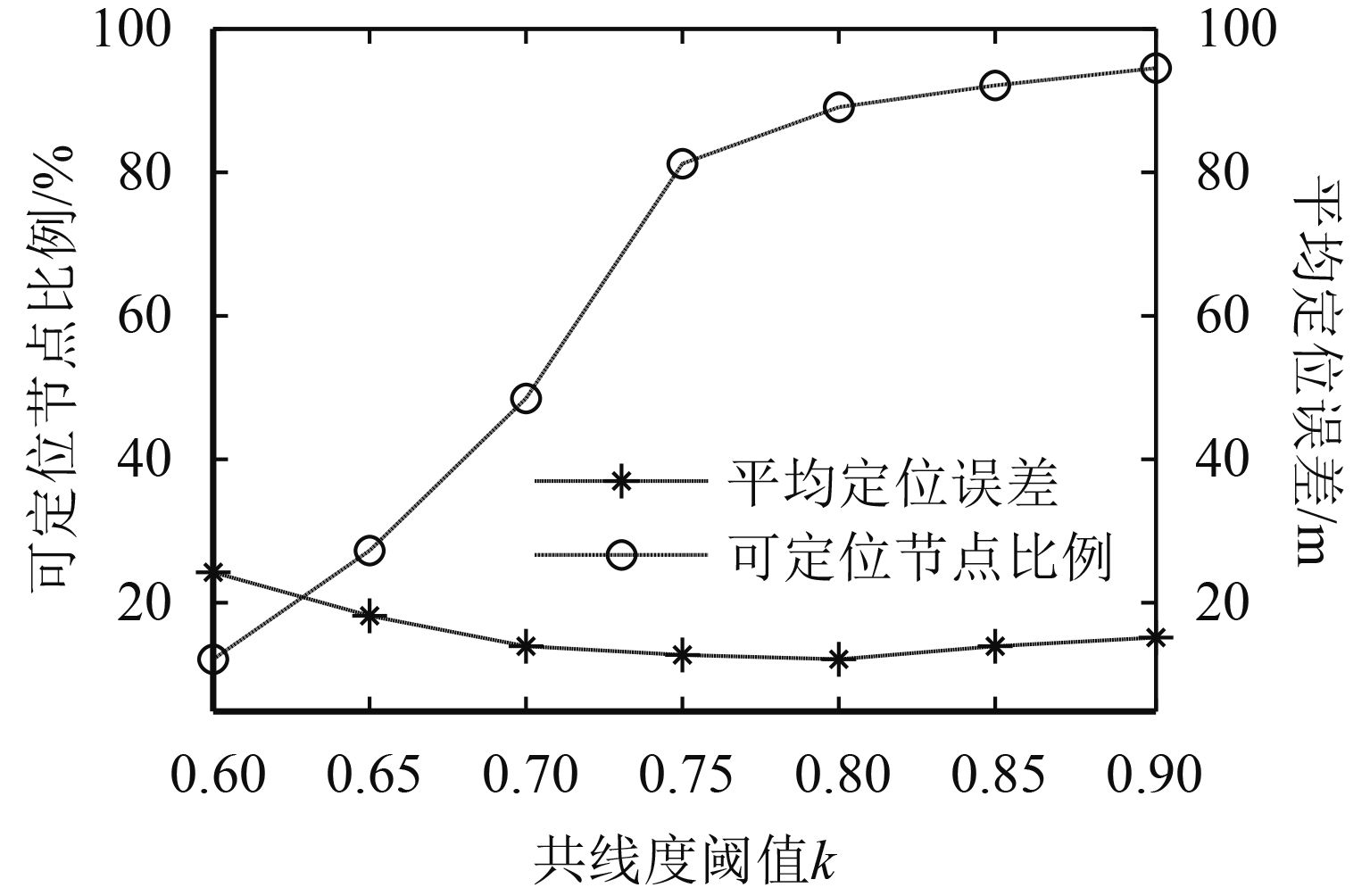
图 5 共线度阈值k与平均定位误差和可定位节点之间的关系 Figure 5 The relationship between thek and average localization error and the proportion of the localizable nodes |
| ${\lambda _i} = \frac{{{\omega _i}}}{{\sum\limits_{j = 1}^m {{\omega _j}} }}.$ | (4) |
| ${\omega _i} = \exp \left( { - \frac{{{h_{iU}} - {h_{\min }}}}{{\sum\limits_{j = 1}^m {{h_{jU}}} }}} \right).$ | (5) |
其中,hiU
是信标节点i与未知节点U之间的跳数,hmin是未知节点离其最近的信标节点之间的跳数,
所以,未知节点的平均跳距为
| ${\rm{HopSiz}}{{\rm{e}}_U} = \sum\limits_{i = 1}^m {{\lambda _i} \cdot {\rm{Hop}}} {\rm{Siz}}{{\rm{e}}_i}.$ | (6) |
在获得未知节点的平均跳距之后,未知节点与信标节点之间的估计距离为
| ${d_{ij}} = {\rm{Hopsiz}}{{\rm{e}}_i} \times {h_{ij}}.$ | (7) |
信标节点的筛选对定位误差有较大的影响,特别是,3个信标节点在一条直线上或近似在一条直线上会对定位产生较大的误差,对此,引入共线度概念[15],筛选满足一定共线度要求的信标节点组,提高三边测量法的定位精度。
共线度用于描述信标节点组在一条直线上的程度,将共线度定义为3个信标节点组成的三角形中最小内角的余弦值。所以,共线度的范围[0.5, 1],对应的角度范围[0, 60°];当共线度接近1时,也即3点接近一条直线,此时定位效果最差;当共线度接近0.5时,也即3点接近一个正三角形,此时定位误差最小。
将待定位节点筛选多组满足共线度要求的所有信标节点组,在每组中循环不重复地通过公式(7)估计两条边的距离,然后根据两条边的估计距离进行初步定位,以获得大量的待定位节点的初步定位结果,对大量初步定位结果视为一个点对象数据集合
DBSCAN是一种具有噪声应用的基于密度的聚类算法,它能找出核心对象,能够发现任意形状的簇,这有助于筛选上述改进DV-Hop算法中提出的多组信标节点多次定位估计产生的初步定位结果,将定位误差较大的噪声点去除,通过只选取最大簇类中的核心对象作为最终未知节点的位置估计的有效对象数据集,再对该集合求取平均值作为未知节点最终的定位估计。结合上述改进DV-Hop算法原理,如下将描述DBSCAN聚类算法的相关定义和DBSCAN对上述改进中产生的大量初步定位结果作为点对象数据集进行优化。
3.1 相关定义定义 1(Eps领域)在点对象中任意一点对象o的领域是以o为中心,Eps为半径的圆空间内包含的所有点对象的集合,也称之为点对象的Eps领域。
定义 2(密度)点对象中某个对象o的密度表示为以o为圆心,Eps为半径所在圆区域内所有点对象的总数。
定义 3(核心点对象)核心点对象是指点对象的密度大于或等于某个阈值MinPts的任意点对象。
定义 4(边界点对象)边界点对象的密度小于某个给定的阈值MinPts,并且属于点对象集合中某个核心点对象的Eps领域内。
定义 5(直接密度可达)假设核心点对象c,c的Eps领域中的任意一点对象x,则点对象x从核心点对象c直接密度可达。
定义 6(密度可达)设p为点对象集合中的任意点对象,q为点集合中的某一核心点对象,若存在核心点对象链q1,q2,q3,...,qn ,使p从q1直接密度可达,qn 从q直接密度可达,则点对象p从点对象q密度可达。
定义 7(密度相连)如果点对象集合中存在某一点对象o,使得点对象x和点对象y都从o密度可达,则点对象x和点对象y是密度相连的。
定义 8(聚类)关于Eps和MinPts的聚类是指该类中所有点对象均可以相互密度连接并通过密度连接包含更多的点对象直到不能添加为止所形成的集合。
定义 9(噪声点对象)不属于任何聚类的点对象称为噪声点对象。
3.2 DBSCAN算法优化步骤描述Step1 为了减少计算量,将DBSCAN聚类算法中的参数MinPts设置为4[16],然后计算每个对象到它的第4个最邻近的对象之间的距离,绘制k-dist图;然后根据所求的距离按从小到大排序绘制k-dist图的横坐标,纵坐标对应的是某一距离值的数据对象的个数,最后在k-dist图中找到凹陷处所对应的距离值作为DBSCAN算法中参数Eps的值[16]。
Step2 从数据点对象集合o中随机选择一个未访问的点S,检测S的领域内中包含的点对象数是否少于MinPts,如果不少于MinPts,则点S为核心点,将S的类号标记为ClassID,然后查找关于Eps和MinPts从S密度可达的所有点,并将它们的类号也标记为ClassID。如果S的领域内少于MinPts,则暂时将点S标记为噪声点。
Step3 对所有关于Eps和MinPts从S密度可达的点进行搜索,循环收集下一个该聚类中的核心点,不断扩展该聚类中的核心点的数量直到没有新的核心点添加为止,最终形成一个类号为ClassID的聚类。如果数据对象集合o中还有未访问的数据对象,则转至步骤2直到所有点对象均被访问。
Step4 在多个聚类中找出拥有数据点对象最多的聚类ClassID,并将其中的边界点去除,留下该聚类中的核心点,并对其求平均值作为未知节点的最终估计位置。
4 仿真实验仿真工具使用Matlab。设定所有节点随机部署在300 m×300 m正方形的二维监测区域内,每个节点都有一致的通信半径。
首先对共线度阈值的研究。在该监测区域内随机部署170个未知节点和30个信标节点(信标节点占比15%),所有的节点的通信半径设置为50 m,循环对共线度阈值k递增取值,研究k对平均定位误差和可定位节点比例的影响。图5反映了它们之间的关系。随着k值的增大,可定位节点数量也在增加,这说明有更多的信标节点组参与定位,而平均定位误差先减小后增大。当共线度阈值k低于0.6时,虽然此时产生的定位误差较小,但几乎没有信标节点组能够满足此共线度要求;当k超过0.8时,由于有些信标节点组接近或近似一条直线,产生的定位误差较大,从而对总体的平均定位误差有所增加,从图上看出,当k在0.8左右时,平均定位误差最小。因此,将0.8作为改进算法中共线度阈值参数k的取值。
|
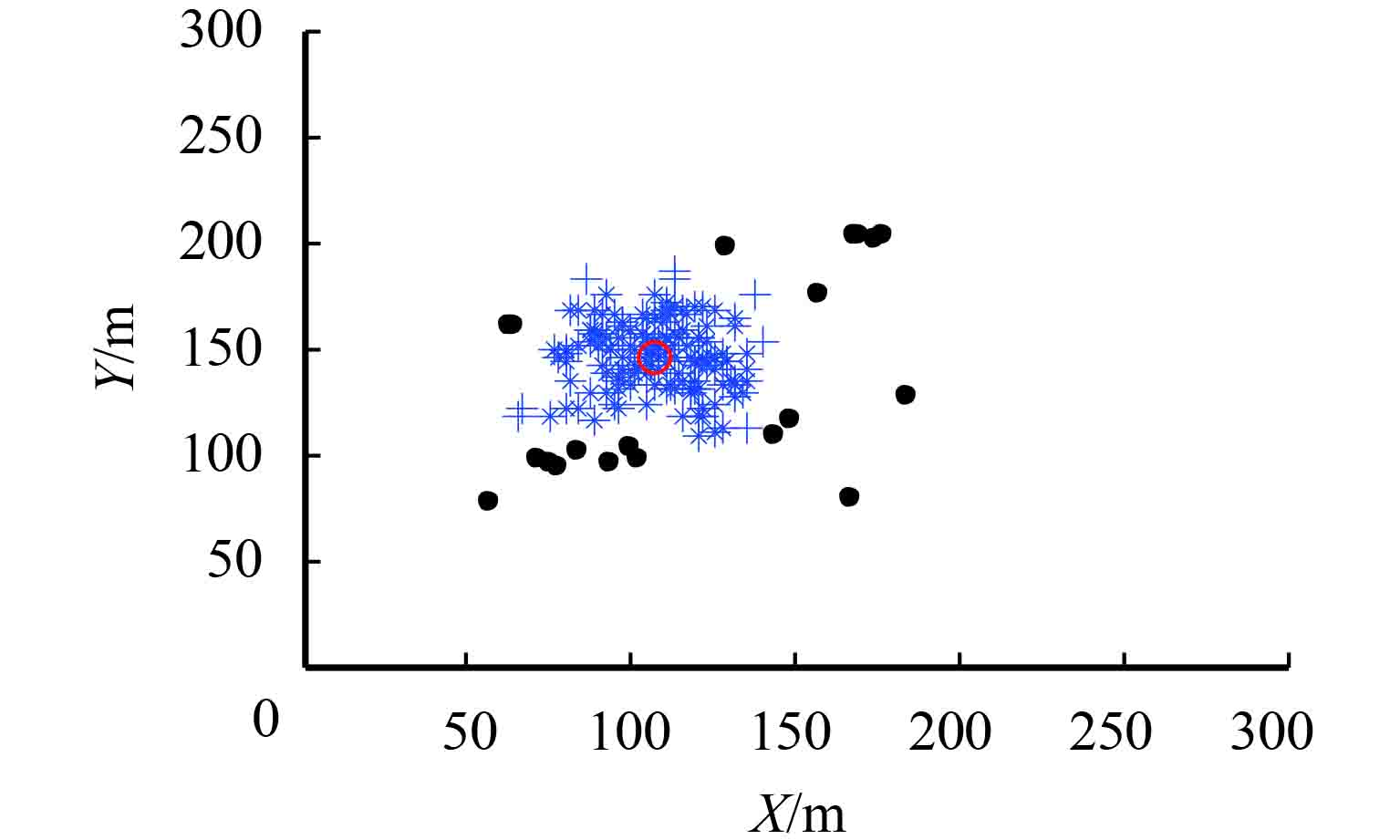
图 6 聚类优化实例图 Figure 6 An clustering case diagram of an unknown node’s location optimization |
图6显示了某个未知节点定位结果通过DBSCAN聚类优化的一个实例图。“*”代表簇类中的核心点,“+”代表簇类的边界点,“○”代表的是未知节点通过优化后的定位中心点. 从图6可以看出,DBSCAN聚类算法能够很好地获得定位中心点。
|
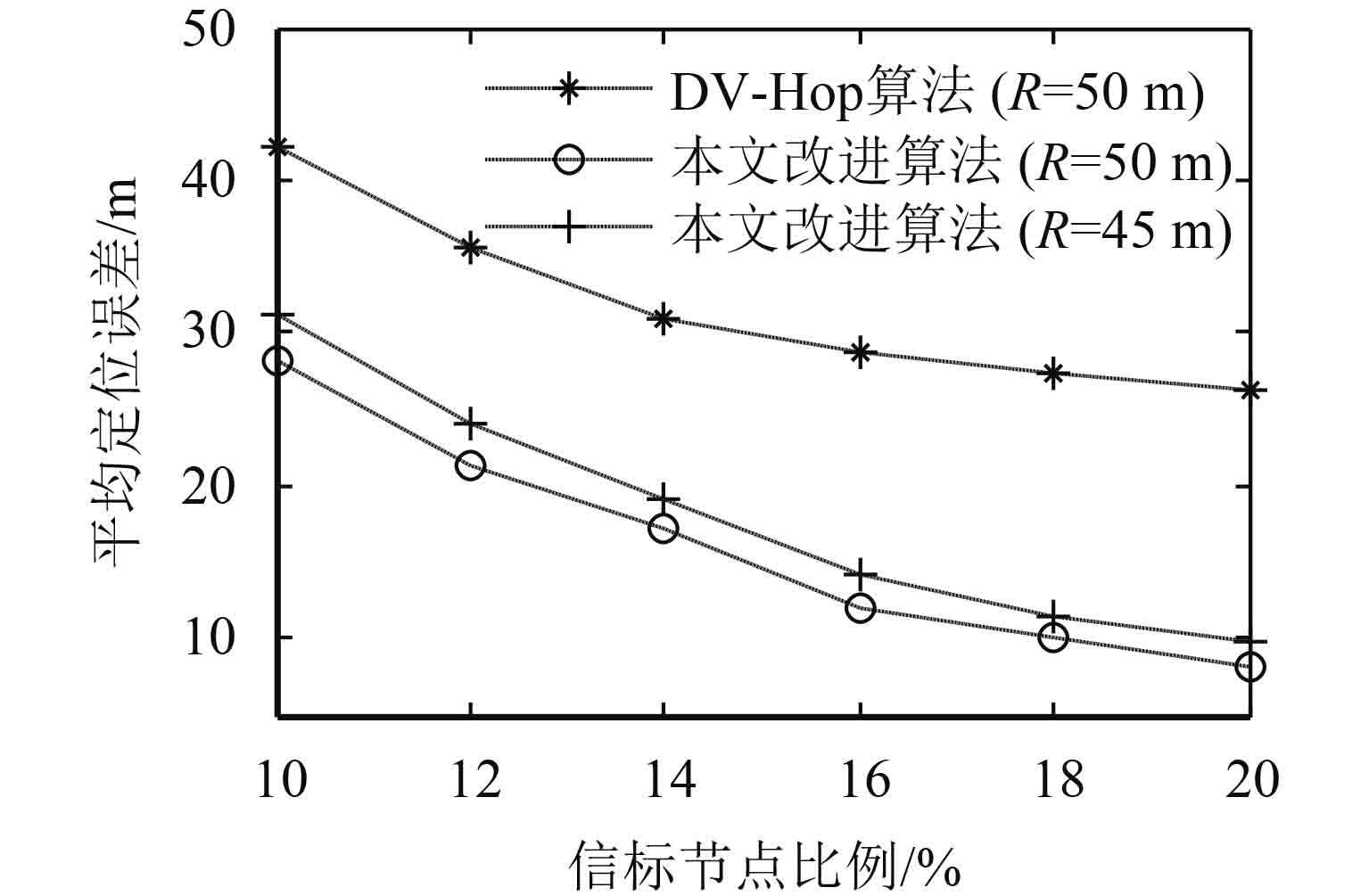
图 7 信标节点比例对平均定位误差的影响 Figure 7 The influence of the proportion of the anchor nodes to average localization error |
图7给出了通信半径R在45 m或50 m时,两种算法的平均定位误差与信标节点数的变化规律。从图中看出,在通信半径为50 m时,当信标节点占比为20%时,改进算法的平均定位误差比原始算法最大减小了18.22%,同时看到,对于相同算法,随着信标节点比例的增加,通信半径大的对应的平均定位误差较小。
|
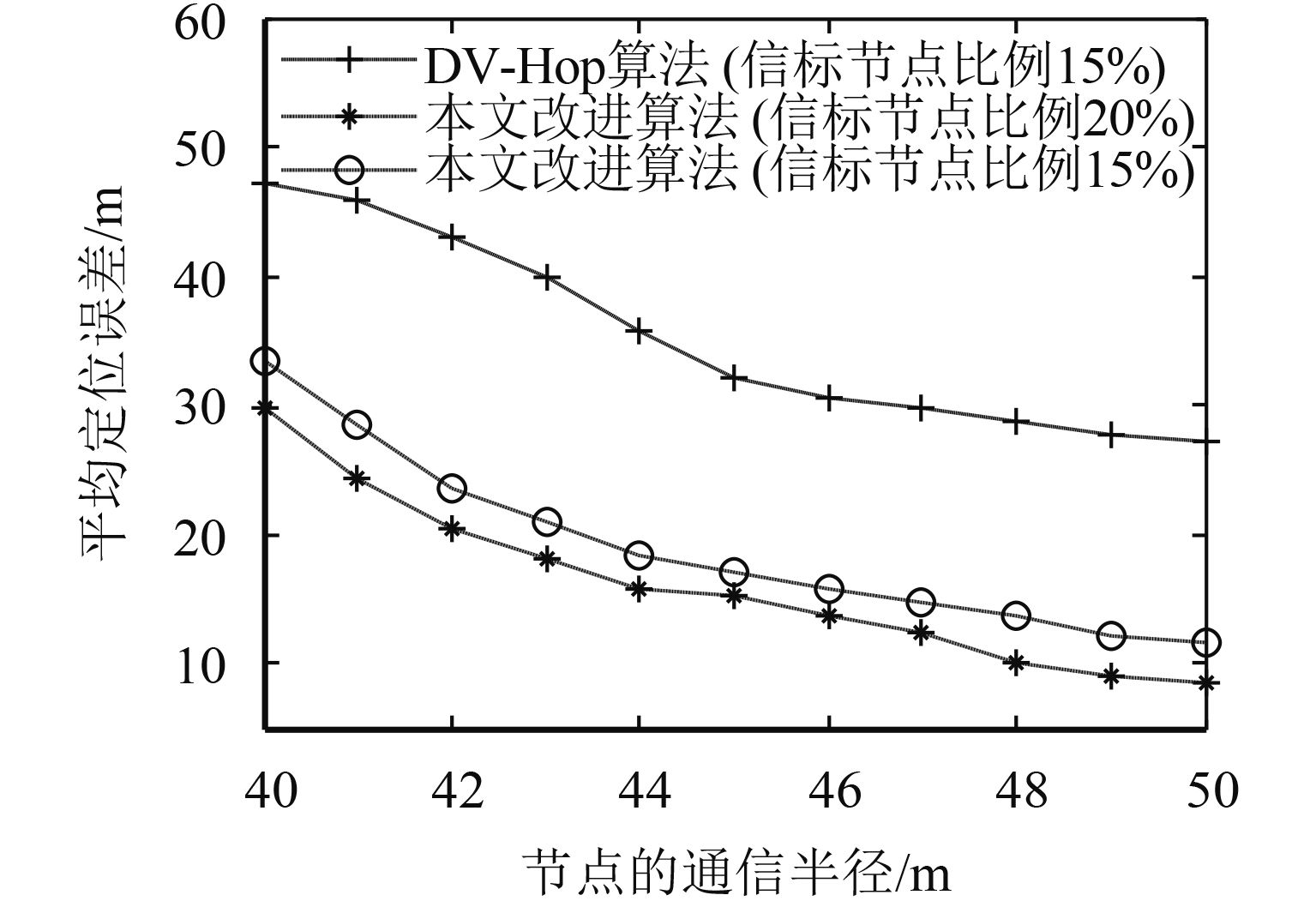
图 8 节点通信半径对平均定位误差的影响 Figure 8 The influence of the communication radius to average localization error |
图8给出了信标节点比例在15%或20%时,平均定位误差与节点通信半径之间的关系. 随着通信半径的增大,两种算法的平均定位误差都在减小,并随之趋于平缓。在通信半径R为50 m和信标节点占比为15%时,改进算法的平均定位误差大约减小了18.46%;由此可以看出改进算法的性能较原算法优越,有效地降低误差,提高定位的准确性。对于改进的算法而言,在相同的通信半径情形下,信标节点比例越大,平均定位误差越小,说明有更多的信标节点组参与了定位估计,加强了定位点的聚类程度,忽略了初步定位误差较大的影响。
5 结束语本文从数据挖掘领域中的DBSCAN聚类算法得到启发,分析了3个信标节点构成的定位三角形与待定位的节点之间的关系,充分利用已知的信标节点之间的距离,使用两个估计边对未知节点进行定位,进行多组多次定位估计,然后用聚类方法对大量的定位结果进行有效筛选,从而得到更精确的未知节点的坐标位置。从实验结果表明,本文改进算法的定位准确性比DV-Hop算法高,改进算法亦不受个别定位误差较大的影响,健壮性强。但在通信量和计算量方面,改进算法的开销较大,对节点的能量消耗大,缩短了整个网络寿命。对此,下一步将研究如何最大程度上减小节点间的通信量、平衡节点之间的能耗,降低算法开销,提高算法运行效率。
| [1] |
钱志鸿, 王义君. 面向物联网的无线传感器网络综述[J].
电子与信息学报, 2013, 35(1): 215-227.
H QIANZ, J WANGY. Internet of things-oriented wireless sensor networks review[J]. Journal of Electronics and Information Technology, 2013, 35(1): 215-227. |
| [2] |
李鹤. 无线传感器网络中基于能量比的簇首选择机制[J].
广东工业大学学报, 2014, 31(3): 83-87.
C LIH. Cluster-head Selection Mechanism Based on Energy Ratio in Wireless Sensor Networks[J]. Journal of Guangdong University of Technology, 2014, 31(3): 83-87. |
| [3] | CENEDESEA. Low-density wireless sensor networks for localization and tracking in critical environments[J]. IEEE Transactions on Vehicular Technology, 2010, 59(6): 2951-2962. DOI: 10.1109/TVT.2010.2049277. |
| [4] | MERT B, LIU M, SHEN W M, et al. Localization in cooperative wireless sensors networks: A review [C]//Proceedings of the 2009 13th International Conference on Computer Supported Cooperative Work in Design. Santiago: IEEE 2009: 438-443. http://cn.bing.com/academic/profile?id=1abdb40b2a20f5ef79f6e9ccc98bd610&encoded=0&v=paper_preview&mkt=zh-cn |
| [5] | BULUSUN. GPS-Less low cost outdoor localization for very small devices[J]. IEEE Personal Communication Magazine, 2000, 7(5): 28-34. DOI: 10.1109/98.878533. |
| [6] | HE T, HUANG C, BLUM B M, et al. Range-free localization schemes for large scale sensor networks [C] //Proc of the 9th Annual Int’1 Conf. on Mobile Computing and Networking. San Diego: ACM Press, 2003, 81-95. |
| [7] | NICULESCUD. DV-based positioning in ad hoc networks[J]. Telecommunication Systems, 2003, 22(1): 267-280. |
| [8] | ESTER M, KRIEGEL H P, SANDER J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise [C]//Proceedings of the 2th International Conference on Knowledge Discovery and Data Mining (KDD-96). Oregon: [s.n.], 1996. |
| [9] |
于亚飞, 周爱武. 一种改进的DBSCAN密度算法[J].
计算机技术与发展, 2011, 21(2): 30-33.
F YUY, W ZHOUA. An improved algorithm of DBSCAN[J]. Computer Technology and Development, 2011, 21(2): 30-33. |
| [10] |
朱炫璋. 基于DBSCAN的无线传感器网络定位方法[J].
计算机工程与应用, 2013, 49(11): 80-83.
Z ZHUX. Location method based on DBSCAN in wireless sensor networks[J]. Computer Engineering and Applications, 2013, 49(11): 80-83. |
| [11] | 郭世可. 基于颜色相似系数的图像分割方法研究[D]. 厦门: 厦门大学软件学院, 2008. |
| [12] |
蒋盛益, 王连喜. 聚类分析研究的挑战性问题[J].
广东工业大学学报, 2014, 31(3): 32-38.
Y JIANGS, X WANGL. Some challenges in clustering analysis[J]. Journal of Guangdong University of Technology, 2014, 31(3): 32-38. |
| [13] |
张丽杰. 具有稳定饱和度的DBSCAN算法[J].
计算机应用研究, 2014, 31(7): 1972-1975.
J ZHANGL. Stable saturation density of DBSCAN algorithm[J]. Application Research of Computers, 2014, 31(7): 1972-1975. |
| [14] | 蔡岳. 一种应用于搜索引擎的文本聚类算法 [D]. 北京: 北京林业大学信息学院, 2010. |
| [15] |
吴凌飞, 孟庆虎, 梁华为. 一种基于共线度的无线传感器网络定位算法[J].
传感技术学报, 2009, 22(5): 722-727.
F WUL, H MENGQ, W LIANGH. A collinearity-based localization algorithm for wireless sensor networks[J]. Chinese Journal of Sensors and Actuators, 2009, 22(5): 722-727. |
| [16] | 孙凌燕. 基于密度的聚类算法研究[D]. 太原: 中北大学理学院, 2009. |
 2017, Vol. 34
2017, Vol. 34

