广东工业大学学报  2017, Vol. 34Issue (2): 69-73.  DOI: 10.12052/gdutxb.160064.
0

引用本文 

孙安全, 陈林海, 潘永雄. 轻载下不存在电流倒灌现象的正激同步
整流电路研究 [J]. 广东工业大学学报, 2017, 34(2): 69-73. DOI: 10.12052/gdutxb.160064.
Sun An-quan, Chen Lin-hai, Pan Yong-xiong. A Study of Non-existent Current Intrusion in Forward Synchronous Rectifier Circuit under the Condition of Light Load[J]. JOURNAL OF GUANGDONG UNIVERSITY OF TECHNOLOGY, 2017, 34(2): 69-73. DOI: 10.12052/gdutxb.160064.

基金项目:

广东省高等学校学科建设专项资金资助项目(2014KTSCX058)；中山市科技强企项目(2013B3FC0002)

作者简介:

孙安全(1987–)，男，硕士研究生，主要研究方向为开关电源技术.。

文章历史

收稿日期：2016-04-26
Contents              Abstract              Full text              Figures/Tables              PDF
轻载下不存在电流倒灌现象的正激同步
整流电路研究
孙安全, 陈林海, 潘永雄     
广东工业大学 物理与光电工程学院， 广东 广州 510006
收稿日期：2016-04-26
基金项目：广东省高等学校学科建设专项资金资助项目(2014KTSCX058)；中山市科技强企项目(2013B3FC0002)
作者简介：孙安全(1987–)，男，硕士研究生，主要研究方向为开关电源技术.。
摘要: 为解决轻载下正激变换器电压自驱动同步整流电路Buck滤波电感电流倒灌造成电路效率下降问题，本文在分析了常用正激变换器拓扑去磁复位时间与Buck滤波电感电流回零时间关系基础上，找出了电流倒灌原因，提出了在承担续流功能的同步整流MOS管驱动电路中增加有源快速放电电路，使主变压器激磁磁通复位后强迫同步整流MOS管迅速截止，避免轻载下电感电流倒灌现象. 试验样机测试结果表明：本文提出的同步整流驱动方式可行、有效.
关键词: 工业电源    正激变换器    同步整流    DCM模式    电感电流倒灌    
A Study of Non-existent Current Intrusion in Forward Synchronous Rectifier Circuit under the Condition of Light Load
Sun An-quan, Chen Lin-hai, Pan Yong-xiong     
School of Physics and Optoelectronic Engineering, Guangdong University of Technology, Guangzhou 510006, China
To overcome the reduction of efficiency of circuit caused by the Buck filter inductor current flow backward in the circuit of voltage self-driven synchronous rectifier under light load, the relation between the demagnetization reset time of common forward converter topology and the current of Buck filter inductor back to zero time is analyzed. Based on this relation, the reason of the Buck filter inductor current flowing backward so that the forward converter with voltage self-driven synchronous rectifier circuit works at light load have been found. An active fast discharge circuit is proposed to be added in synchronous rectifier MOS transistor driven circuit whose function is freewheeling. And this circuit forces synchronous rectifier MOS to close rapidly after the magnetic field flux of main transformer reset. Thus it can prevent the inductor current flow backward. The prototype test results show that this design has been verified effective and feasible by the experiment result.
Key words: industrial power    forward converter    synchronous rectification    DCM mode    inductor current intrusion    

随着电子器件集成度及工作频率的不断提高，为降低器件功耗，将被迫采用低压、大电流供电方式，因此低压大电流输出DC/DC变换器已成为当前DC-DC变换器重要的发展方向之一[1]。尽管这类工业电源输出功率不大，但可靠性要求高。为降低成本，提高效率，一般采用由低导通内阻功率MOS管构成的同步整流方式代替肖特基二极管整流电路，主拓扑电路多采用正激(Forward)同步整流拓扑结构[2-5]。

正激同步整流变换器最大缺点是负载变化范围不宜太大，当负载小于某一特定值后次级输出滤波电感进入DCM状态，出现电流倒灌现象，使轻载状态下的效率迅速下降，并恶化了EMI指标[6]。为解决此缺陷，目前较成熟的技术方案主要有：通过控制单周期占空比方式避免电流倒灌[3]；借助反向限流电路控制电流倒灌[7]；通过外部信号驱动同步整流MOS管，控制策略是检测到输出滤波电感电流过零后立即关闭同步整流MOS管[8-9]；采用自驱动方式，通过检测采样电阻端电压方式控制同步整流MOS管的关、开动作[10]。然而文献[3]的单周期调节占空比旨在针对输入电压变化而动作；文献[7]控制逻辑复杂，成本较高；文献[8-9]同步整流MOS管所需两路信号的死区时间不易调节；文献[10]虽采用自驱方式，但需要的模拟元器件偏多，可靠性不高，且控制过程有延迟。本文在自驱模式下，利用变压器激磁电流回零时间小于滤波电感L去磁时间的特征，借助有源快速泄放电路，在变压器激磁电流回零后，强迫同步整流MOS管快速关断，避免滤波电感在DCM模式下出现电流倒灌现象。所用元器件少，可靠性高。

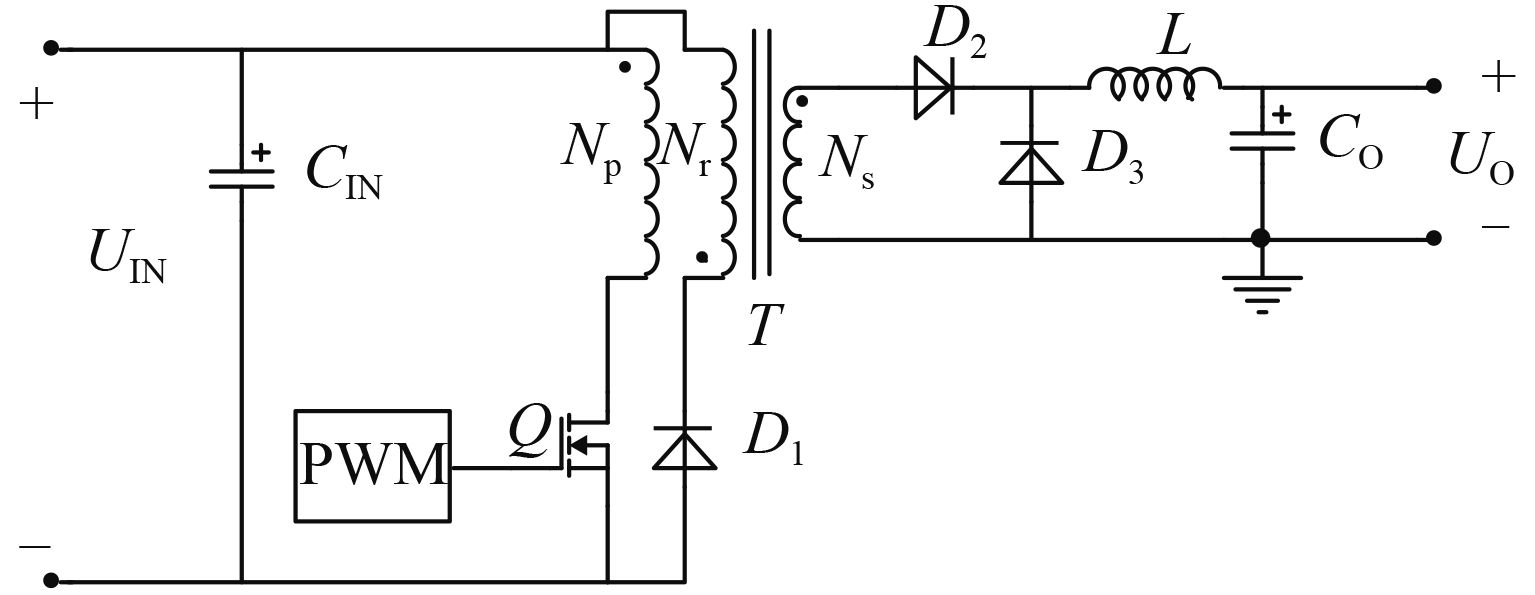
1 常用正激变换器拓扑特征分析 1.1 三绕组去磁复位正激变换器特征 1.1.1 激磁电流回零时间Toff与次级Buck滤波电感磁复位时间Toff_S关系

在图1所示的三绕组去磁复位正激变换器中，为避免开关管Q截止时，MOS管Q漏源极电压UDS 过高，主绕组NP 与磁复位绕组Nr 匝数往往相同[11]。

图 1 三绕组去磁复位正激变换器原理电路 Figure 1 Schematic circuit of three-winding demagnetization reset forward converter

假设激磁电感用LM 表示，则激磁电感电流峰值

${I_{{\rm{LMPK}}}} = \frac{{{U_{{\rm{IN}}}} - {U_{SW}}}}{{{L_M}}} \times {T_{{\rm{on}}}} = \frac{{{U_{{\rm{IN}}}} + {U_{{D_1}}}}}{{{L_M}}} \times {T_{{\rm{off}}}}$

当输入电压UIN较大，如100 V以上时，可忽略开关管Q导通电压USW 、磁复位二极管D1导通压降 $ {U_{{D_1}}} $ ，对初级侧来说，导通时间Ton与激磁电流iM 回零时间Toff近似相等。

由于次级Buck滤波输出电路由初级回路映射电压UINR 驱动，因此次级回路滤波电感L储能时间与初级开关管Q导通时间Ton相同。

在重载下，输出滤波电感L电流处于CCM模式，考虑到占空比d<0.5，次级回路Buck滤波电感L磁复位时间Toff_S一定大于变压器激磁电流iM 回零时间Toff。

在轻载下，输出滤波电感L电流处于DCM模式，Buck滤波电感L电流增量

$\begin{aligned}\Delta {I_L} = \frac{{{U_{INR}} - {U_{\rm{O}}} - {U_{{D_2}}}}}{L} \times {T_{{\rm{on}}}} = \\\frac{\displaystyle{\frac{{{U_{{\rm{IN}}}} - {U_{SW}}}}{n} - {U_{\rm{O}}} - {U_{{D_2}}}}}{L} \times {T_{{\rm{on}}}} = \end{aligned}$

其中n为匝比，UO为输出电压。如果忽略次级整流二极管D2导通电压 $ {U_{{D_2}}} $ 、续流二极管D3导通电压 $ {U_{{D_3}}} $ 、开关管Q导通电压USW 。依据伏秒积平衡原理，Buck滤波电感L去磁复位时间

${T_{{\rm{off}}\_S}} = \frac{{\frac{{{U_{{\rm{IN}}}}}}{n} - {U_{\rm{O}}}}}{{{U_{\rm{O}}}}} \times {T_{{\rm{on}}}}.$

考虑到 $\displaystyle \frac{{{U_{{\rm{IN}}}}}}{n} = \frac{{{U_{\rm{O}}}}}{d}$ ，其中d为CCM模式下的占空比，则Buck滤波电感L去磁复位时间

${T_{{\rm{off}}\_S}} = \frac{{1 - d}}{d}{T_{{\rm{on}}}} = \frac{{1 - d}}{d}{T_{{\rm{off}}}}.$

可见在输入电压UIN、输出电压UO保持不变条件下，在DCM模式下，电感L电流上升、下降斜率均保持不变，与CCM模式相比，电感储能时间Ton及去磁复位时间Toff_S等比例缩小。

由于占空比d<0.5，因此次级回路输出滤波电感L磁复位时间Toff_S也大于变压器激磁电流回零时间Toff。占空比d典型值与滤波电感L磁复位时间Toff_S及变压器激磁电流回零时间Toff关系如表1所示。

表 1 不同占空比下Toff_S与Toff之间关系 Table 1 Relation betweenToff_S andToff at different duty cycles
1.1.2 DCM模式下滤波电感储能时间Ton与去磁复位时间Toff_S

可以证明：在忽略初级侧开关管导通压降USW 、次级整流二极管导通压降UD2及UD3条件下，当负载电流由满载IO减小到轻载下的I'O时，处于DCM模式下的滤波电感L储能时间

${T_{{\rm{on}}}} = {T_{{\rm{off}}}} = \frac{d}{{{f_{SW}}}} \times \sqrt {\frac{2}{\gamma } \times \frac{{{{I'}_O}}}{{{I_O}}}} .$

滤波电感L去磁复位时间

${T_{{\rm{off}}\_S}} = \frac{{1 - d}}{{{f_{SW}}}} \times \sqrt {\frac{2}{\gamma } \times \frac{{{{I'}_O}}}{{{I_O}}}} .$

其中fSW 为开关频率，d为满载下的占空比，γ为满载下的电流纹波比，取值范围在0.6~1.0之间。在占空比d为0.45，电流纹波比γ为0.6的情况下，Toff_S、Ton随负载电流变化如表2所示。

表 2 Toff_S与Ton随负载电流变化趋势 Table 2 Trend ofToff_S andTon change with the load current

在电流纹波比γ为0.6，负载电流变化率I′O/IO为0.5的情况下，Toff_S、Ton随占空比d变化如表3所示。

表 3 Toff_S与Ton随占空比d变化趋势 Table 3 Trend ofToff_S andTon change with duty cycled
1.2 二极管去磁双管正激变换器特征

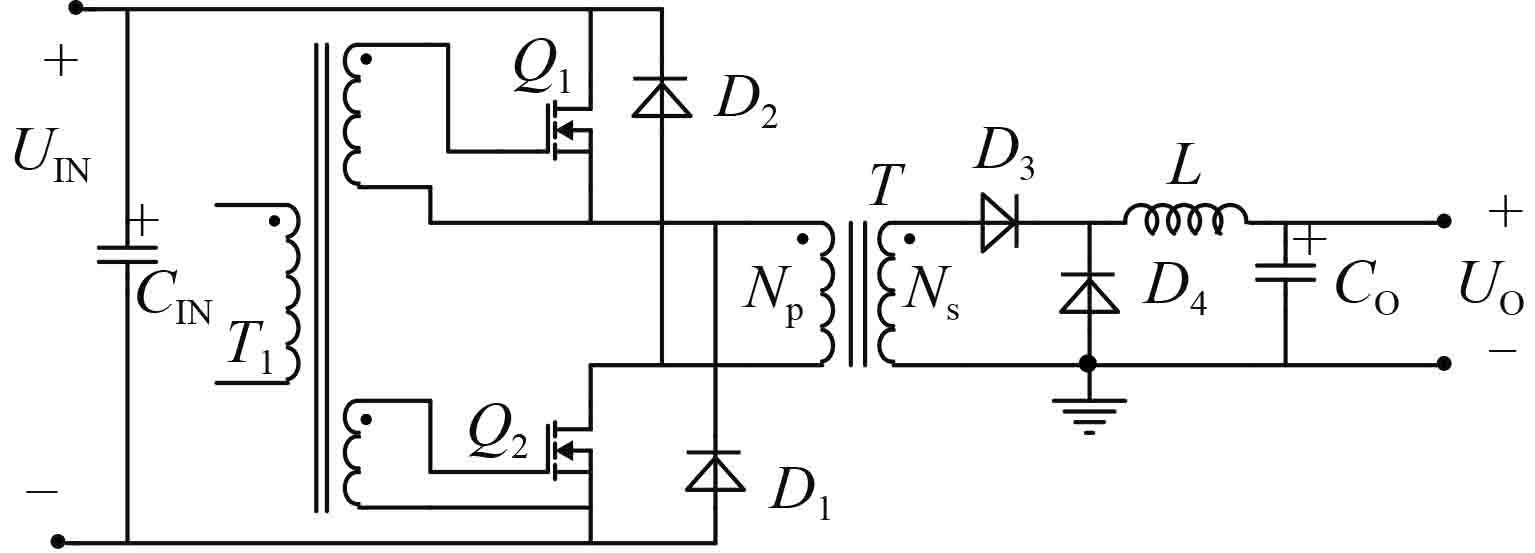
对于图2所示的二极管去磁双管正激变换器来说，如果输入电压UIN较大，在忽略开关管Q1、Q2导通电压USW1及USW2条件下，在Ton期间，初级绕组端电压UNP 近似为UIN；在忽略磁复位二极管D1、D2导通压降 $ {U_{{D_1}}} $ 及 $ {U_{{D_2}}} $ 条件下，在Toff期间，初级绕组端电压UNP 也近似为UIN，因此Ton=Toff同样成立，由此可见主开关管导通、截止期间初级绕组NP 端电压与三绕组去磁正激变换器相同，因此激磁电流回零时间Toff与次级Buck滤波电感L去磁复位时间Toff_S关系与三绕组去磁复位正激变换器相同。

图 2 二极管去磁双管正激变换器原理电路 Figure 2 Schematic circuit of diode demagnetization double forward converter
2 轻载下出现电流倒灌现象原因

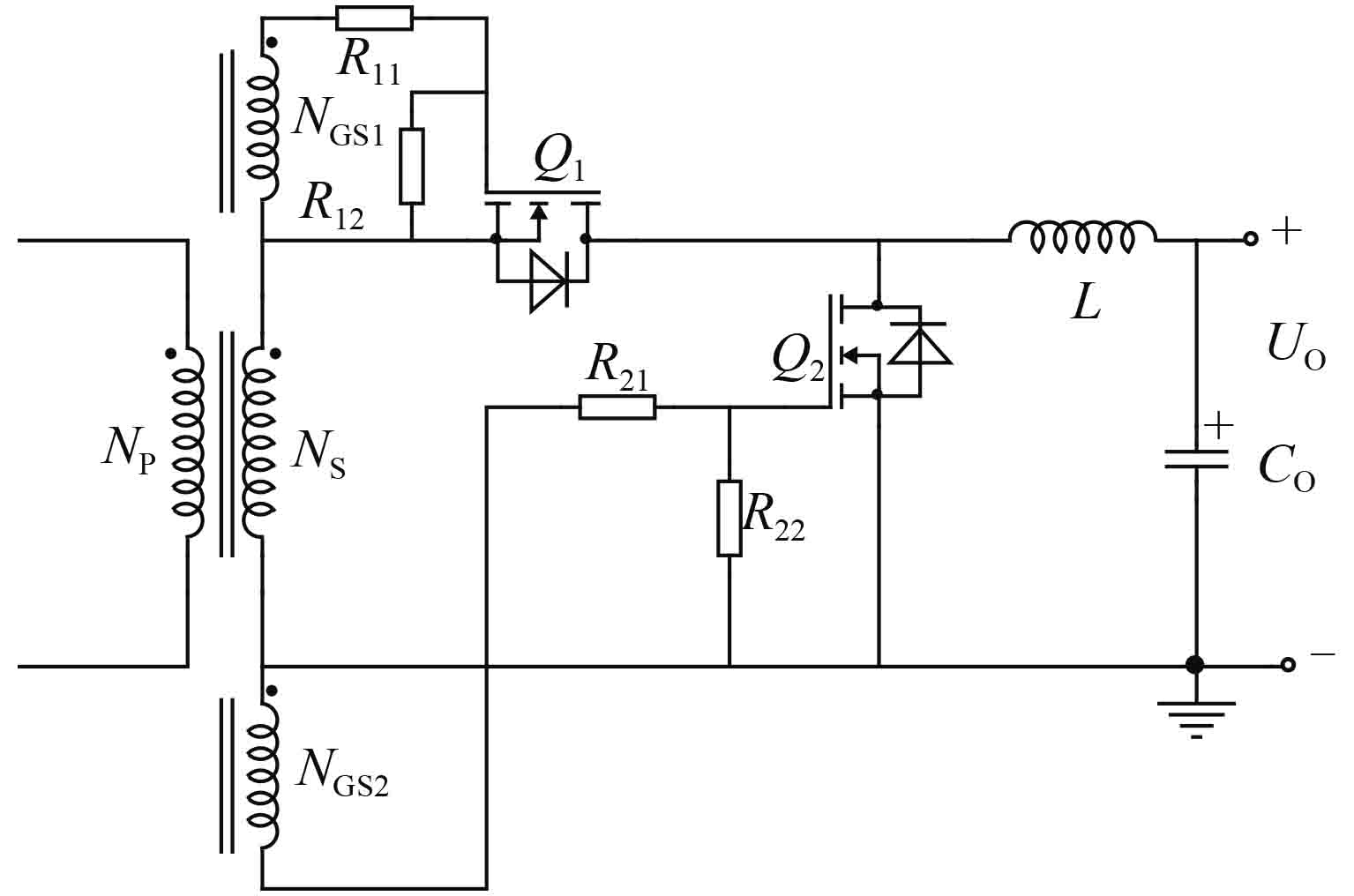
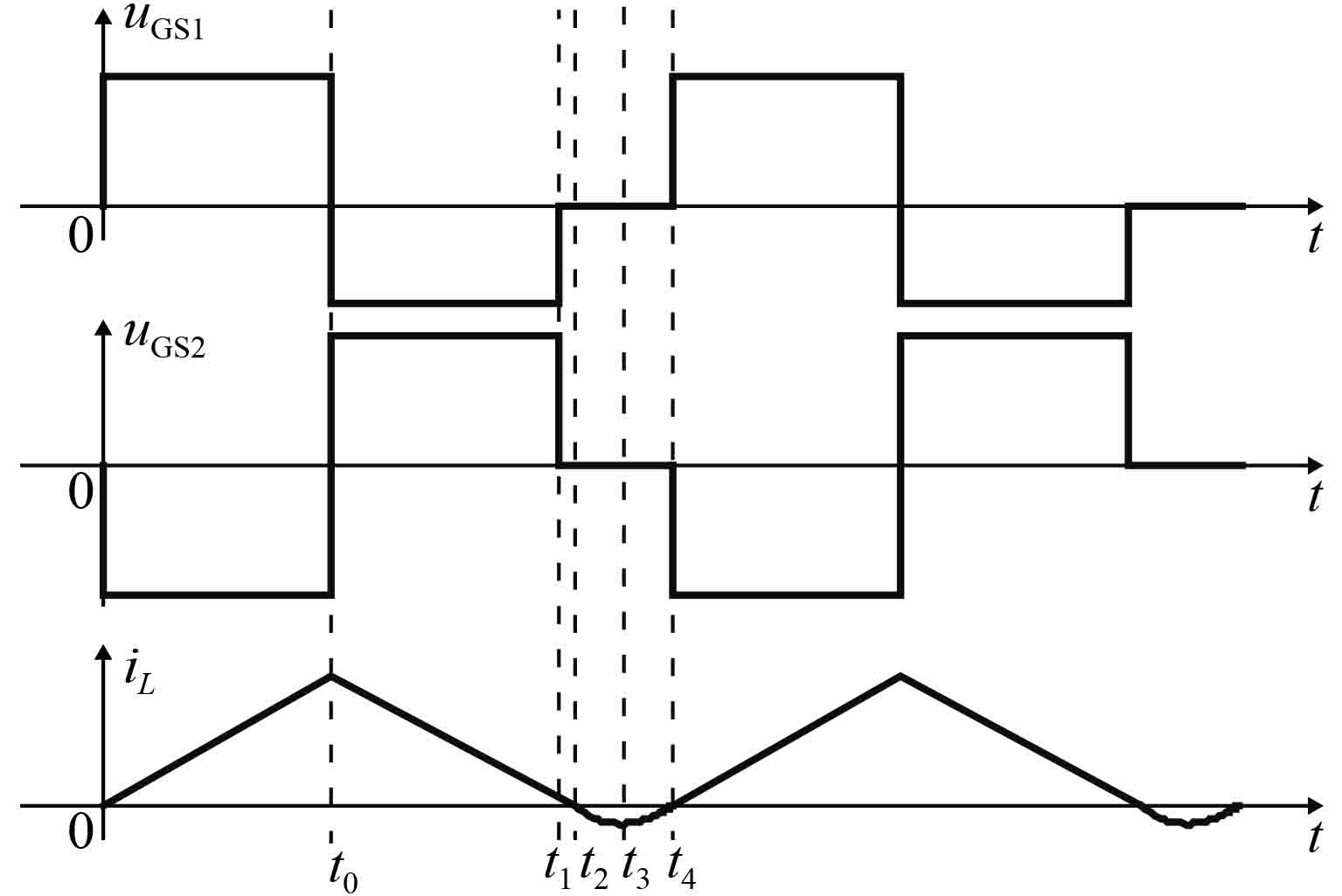
对于图3所示次级同步整流电路，在轻载下输出滤波电感L将工作在DCM模式[12]。如果占空比d较大，使Toff_S与Toff之比变小，在输出滤波电感L电流iL 回零后，承担续流功能的Q2未能在Toff_S-Toff时间内完全关闭，由于MOS管存在双向导通特性，将导致输出滤波电感L反向充电，引起电流倒灌现象[13-15]，如图4所示。

图 3 次级常见同步整流电路 Figure 3 Common secondary synchronous rectifier circuit
图 4 驱动时序及输出滤波电感L电流 Figure 4 Driving timing and the current of output filter inductor L

在t0时刻，初级回路开关管关闭，整流管Q1截止，续流管Q2导通，滤波电感L电流iL 线性下降；到t1时刻，主变压器激磁电流iM 回零，NGS2绕组驱动电压uGS2消失，承担续流功能的Q2管栅极电荷开始下降，到t2时刻滤波电感L电流iL 下降到零，但由于Q2管截止过程较慢，未能在t2-t1(即Toff_S-Toff)时间内完全关闭，滤波电感L就出现反向充电，充电路径为：输出电容Co正极→输出滤波电感L→Q2管D极→Q2管S极→输出滤波电容Co负极，出现了电流倒灌现象[16-17]。随着Q2管栅极电荷的不断下降，Q2管逐渐关闭，当Q2管uDS2接近输出电压UO时，反向电流iL 不再增加，如图4中的t3时刻。在t3时刻后，电感L借助Q2管DS极寄生电容COSS 释放反向存储的能量，并在Q2管DS之间形成很高的尖峰干扰电压。

3 正激同步整流电路设计与实验结果

考虑到变压器激磁电流iM 回零后，承担续流功能的Q2管驱动信号消失，截止速度慢，导致DCM模式下滤波电感电流回零时未能彻底关断，引起滤波电感L反向充电，为此可在Q2管驱动电路中增加以PNP BJT三极管Q21为核心的有源快速关断电路，如图5所示。当Q2驱动信号uGS2消失后，Q21导通，给MOS管Q2输入电容CINSS 提供快速放电通路，确保Q2管在滤波电感L电流iL 回零前可靠关闭，避免电流倒灌。

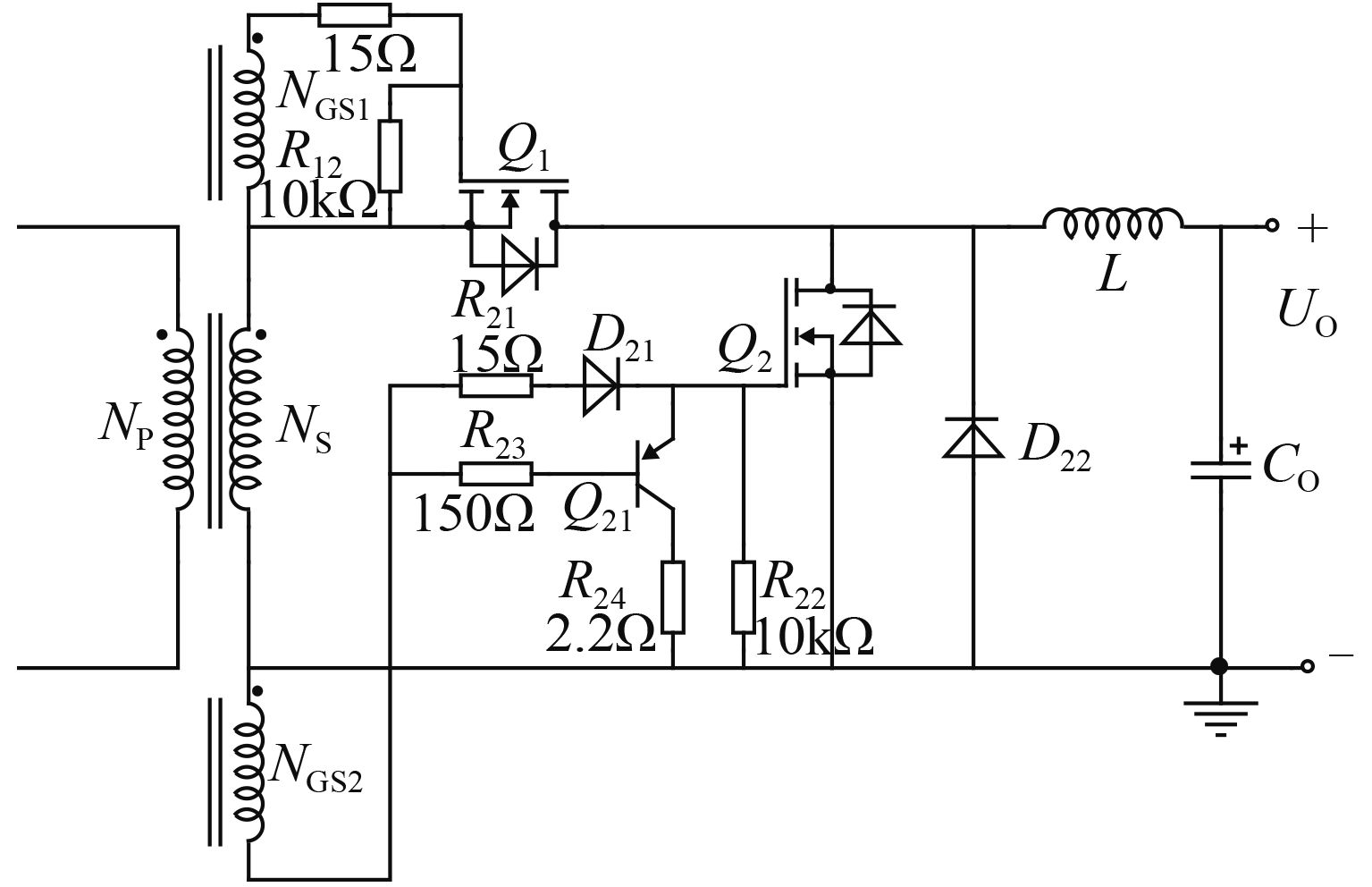
图 5 轻载下没有电流倒灌的正极电压自驱动同步整流电路 Figure 5 Positive voltage self-driven synchronous rectifier circuit without current intrusion under light load

表3计算数据表明：占空比d越大，在DCM模式下，滤波电感L电流iL 回零时间Toff_S与主变压器激磁电流iM 回零时间Toff差值就越小，使Q2管来不及关闭，当滤波电感L电流iL 回零时Q2管未能可靠关断时，将导致电流倒灌。为此，可适当降低占空比d，尤其是当开关频率较高，如133 kHz或以上时，将最小输入电压下对应的最大占空比dmax限制在0.42以下，缩短变压器激磁复位时间Toff，增加滤波电感电流回零时间Toff_S，使Q2有足够时间进入截止状态。但减小占空比d会引起Q2管提前关闭，使续流损耗上升，导致效率下降，为此可在Q2管DS极并联导通电压较小的肖特基二极管D22，以便在Q2管截止后，滤波电感L电流能借助低压降肖特基二极管D22续流。

为验证图5所示电路的可行性，制作了输出电压为12.0 V，输出电流为15 A二极管去磁复位双管正激同步整流变换器。

输入电压为340~420 V，开关频率为133 kHz，最大占空比d取0.42；匝比

$n = \frac{{{U_{{\rm{IN}}\min }}}}{{{U_O} + {U_{DS\_{Q_2}}}}} \times {d_{\max }} = \frac{{340}}{{12 + 0.2}} \times 0.42 = 11.7.$

用AP法估算磁芯参数，最终确定采用EE33磁芯，磁芯有效截面极Ae 为120.25 mm2，由此可推算出NP 取38匝，NS 取4匝，NGS1、NGS2均为1匝，同步整流MOS管为STP75NF75，肖特基二极管为MBRF30100；Buck滤波电感L电流纹波比γ取0.6。

测试数据如表4所示，DCM模式下滤波电感电流波形如图6所示。

表 4 测试数据 Table 4 Test data
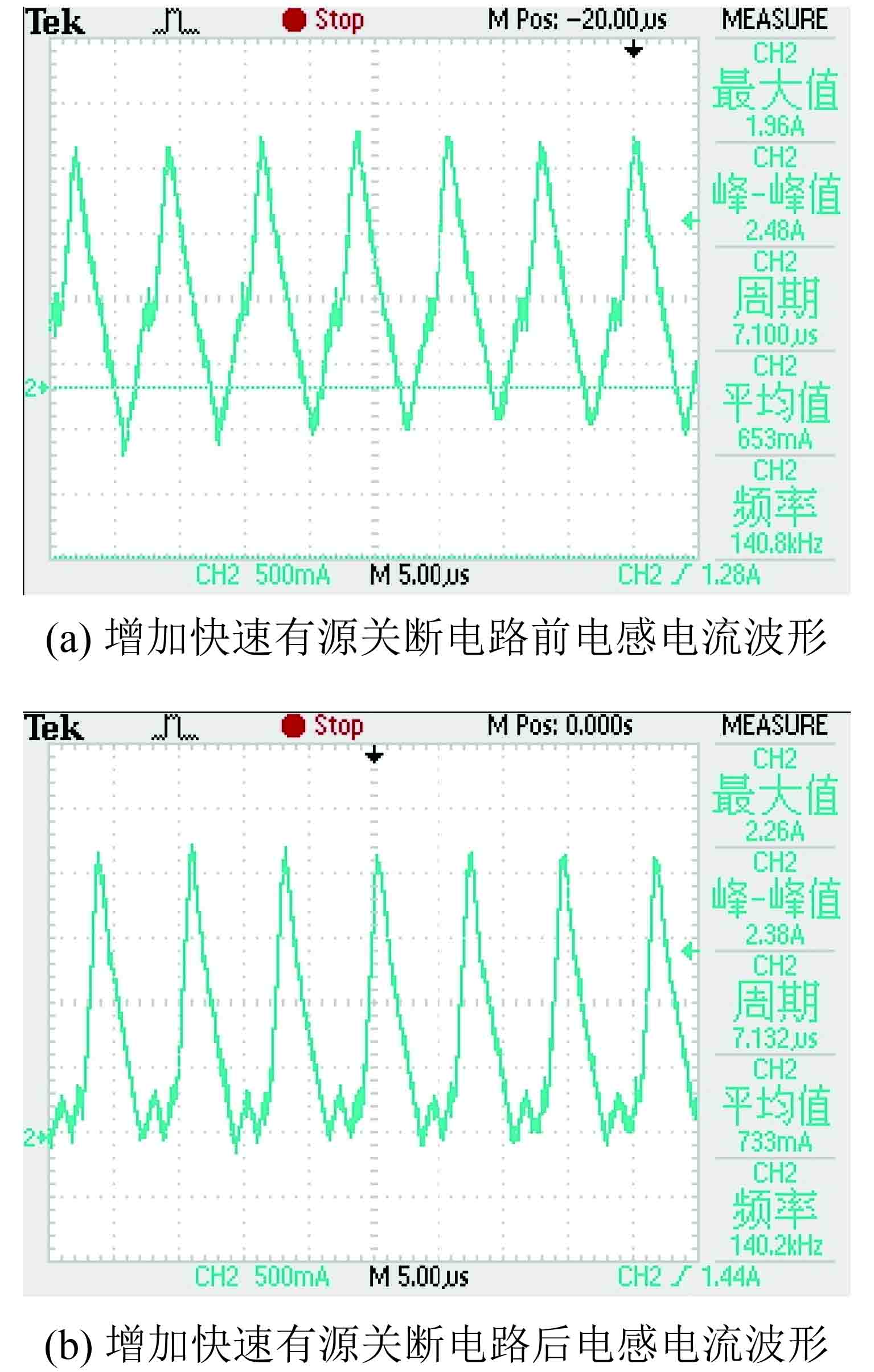
图 6 DCM模式下滤波电感电流波形 Figure 6 Filter inductor current waveform in DCM mode under light load

由表4测试看出：75%以上负载下AC-DC变换器整机效率大于87%(前级APFC变换器效率约为94%)。未在Q2管驱动电路中增加快速有源关断电路时，则负载电流小于15%，即2.25 A后，输出滤波电感L电流倒灌现象已非常明显，如图6(a)所示；增加快速有源关断电路后，负载电流小于5%，即0.75 A时，才开始出现电流倒灌现象，如图6(b)所示。

4 结论

本文提供的正激电压自驱动同步整流电路结构简单、元件数目少、可靠性高，没有采用同步整流驱动IC芯片，成本低。Buck滤波电感电流纹波比γ取值没有限制，即次级回路Buck滤波电感体积与肖特基二极管整流时相同。实验证实：重载效率高，当负载电流在5%以上时，变压器激磁电流iM 回零后，Q2管能迅速关闭，输出滤波电感L没有电流倒灌现象，具有较高的应用价值。

当开关频率较高时，适当降低最小输入电压对应的最大占空比d，使续流MOS管Q2提前关断，保证输出滤波电感L电流iL 回零时Q2可靠关断，能够避免轻载下电流倒灌现象。

参考文献
[1] 张登. 同步整流技术的研究[J]. 舰船电子对抗, 2014, 37(3): 109-111.
ZHANG D. Research into synchronous rectification technology[J]. Shipboard Electronic Countermeasure, 2014, 37(3): 109-111.
[2] 曹伟杰, 任小永, 阮新波. 同步整流技术在正激变换器中的应用研究[J]. 电力电子, 2010, 08(3): 39-44.
CAO W J, REN X Y, RUAN X B. Research on the application of synchronous rectification technology in forward converter[J]. Power Electronics, 2010, 08(3): 39-44.
[3] 钟才惠, 王德贤, 王之纯. 同步整流技术在低压大电流电源模块中的应用[J]. 电源技术, 2013, 37(5): 857-859.
ZHONG C H, WANG D X, WANG Z C. Application of synchronous rectification technology in low-voltage and high-current power supply Module[J]. Chinese Journal of Power Source, 2013, 37(5): 857-859.
[4] ABRAMOVITZA. Analysis and design of forward converter with energy regenerative snubber[J]. IEEE Transactions on Power Electronics, 2010, 25(3): 667-676. DOI: 10.1109/TPEL.2009.2033275.
[5] B PARKK, E KIMC, W MOONG. Three-switch active-clamp forward converter with Lowswitch voltage stress and wide ZVS range for high-input-voltage applications[J]. IEEE Transactions on Power Electronics, 2010, 25(4): 889-898. DOI: 10.1109/TPEL.2009.2036620.
[6] ZHOU X W. Improved light-load efficiency for synchronous rectifiervoltage regulator module[J]. IEEE Transactions on Power Electronics, 2000, 15(5): 826-834. DOI: 10.1109/63.867671.
[7] 黄苏平, 冯全源. 一种同步BUCK变换器反向限流电路的设计[J]. 微电子学与计算机, 2014, 31(2): 35-38.
HUANG S P, FENG Q Y. Design of a limiting reverse current circuit for synchronous BUCK converter[J]. Microelectronics & Computer, 2014, 31(2): 35-38.
[8] 邓超玄. 同步整流BUCK型DC-DC过零检测电路设计[D]. 成都: 西南交通大学信息科学与技术学院, 2014.
[9] 周朝阳, 冯全源. 一种低功耗同步BUCK芯片的过零检测电路设计[J]. 电源技术与应用, 2015, 41(11): 118-120+131.
ZHOU C Y, Y FENGQ. Design of a zero-crossing detection circuit for low-power synchronous BUCK converter[J]. Application of Electronic Technique, 2015, 41(11): 118-120+131.
[10] 谢运祥. 正激式变换器轻载条件下的同步整流分析[J]. 华南理工大学学报(自然科学版), 2003, 31(1): 60-64.
XIE Y X. Synchronous rectifier analysis of forward converter under the condition of light load[J]. Journal of South China University of Technology (Natural Science), 2003, 31(1): 60-64.
[11] 丁志亮. 双管正激同步整流变换器的研究 [D]. 武汉: 华中科技大学电气与电子工程学院, 2006.
[12] 陈坚. 电力电子学-电力电子变换和控制技术[M]. 北京: 高等教育出版社, 2004.
[13] 胡宗波. 同步整流器中 MOSFET 的双向导电特性和整流损耗研究[J]. 中国电机工程学报, 2002, 22(3): 88-93.
HU Z B. Research on bidirectional conduction characteristics and commutation losses of MOSFET in synchronous rectifier[J]. Proceedings of the Chinese Society for Electrical Engineering, 2002, 22(3): 88-93.
[14] 贺东. 基于同步整流技术的有源钳位正激变 换器的研究[D]. 成都: 电子科技大学通信与信息工程学院, 2014.
[15] 吴琼. 轻载下的正激同步整流变换器分析[J]. 电源技术应用, 2007, 10(3): 33-35.
WU Q. Analysis of the forward converter with synchronous rectification under light load[J]. Power Supply Technologies and Applications, 2007, 10(3): 33-35.
[16] 潘永雄. 开关电源技术与设计[M]. 西安: 西安电子科技大学出版社, 2016.
[17] 严尔梅, 韦远武. 一种适用于同步整流开关电源的过零检测电路[J]. 电子技术应用, 2013, 39(8): 47-49+53.
YAN E W, WEI Y W. Design of a zero-detect circuit for synchronous rectification mode switching power supply[J]. Application of Electronic Technique, 2013, 39(8): 47-49+53.