水火弯板作为船体外板弯曲成型的常见工艺,是利用钢板局部受热后急剧冷缩产生形变,从而使板材达到预期的形状[1]。
水火弯板工艺影响因素众多,火枪温度、焰道布置、板材厚度等因素都可能影响最后的弯板成型效果,实现自动化加工较为困难。国外对于水火弯板自动化设备研究已有多年,并取得了一定的研究成果,如日本IHI集团的IHI-α系统和首尔大学的ICALM系统[2]。国内此领域较早开展研究的有大连理工大学、上海交通大学、广东工业大学、广船国际等科研院所。然而国内外当前研究的重点大多集中在板形检测和匹配、火路规划和预报等方面,对于弯板机实时加工过程中的运动轨迹优化问题研究较少,尤其是对大曲率、大尺寸的板材进行加工时,火枪运动轨迹控制精度较差,单板加工无效路径过长,极大制约了水火弯板自动化加工设备的应用前景[3]。
本文以广东工业大学与广船国际合作研制的第三代全自动水火弯板机器人系统为研究对象,通过引进贪婪算法对多条待加工火路进行优化排序,缩短无效轨迹长度,提高加工效率;引进双NURBS曲线插补算法,通过对专家系统给出的火路离散特征点进行实时恒速插补,以实现加工轨迹的优化。
1 机械结构和系统组成 1.1 水火弯板机的机械结构
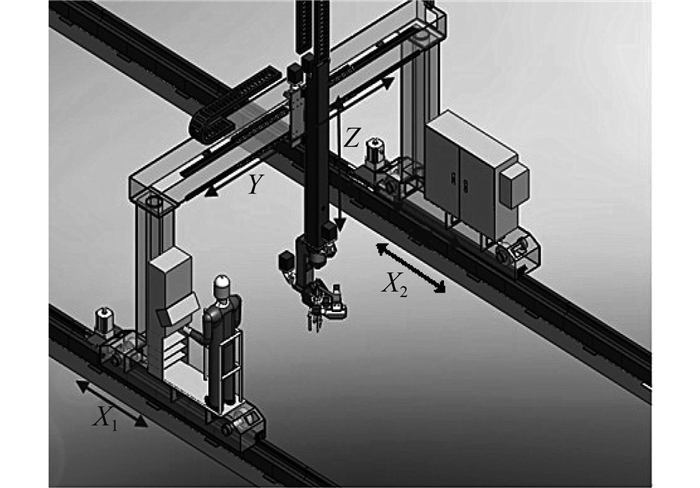
|
图 1 弯板机机械结构图 Figure 1 Mechanical structure of bending plate machining |
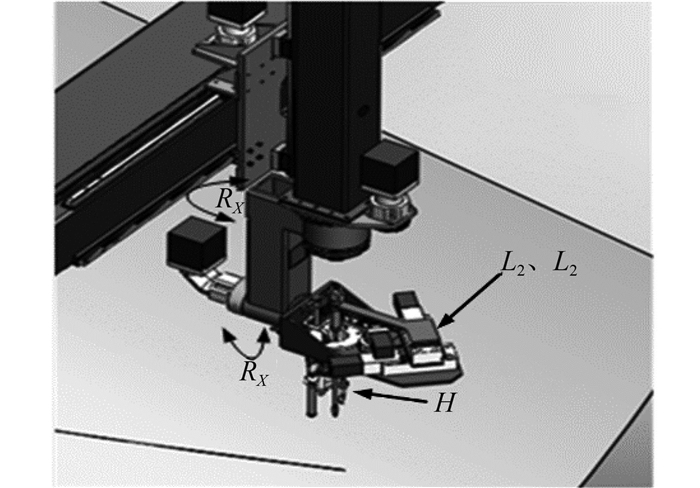
|
图 2 火枪头机械结构图 Figure 2 Mechanical structure of the head of heating machine |
由图 1和图 2可知,水火弯板机器人机械部分一共有9个能动轴组成,分别为X1、X2、Y、Z、RX、RZ、L1、L2、H。其中X1、X2两个同步轴统一认作X轴,X、Y、Z 3轴联动可以使火枪头到达加工位置的三维坐标点,RX、RZ两个旋转轴的旋动使火枪轴线矢量可以保证始终与轨迹上某点的切面法向矢量重合,即使火枪始终与待加工板面垂直,保证烧板效果。L1、L2联动能够使火枪自转,增大加热面积,H轴水枪转动跟随火枪轨迹,起冷却作用。X、Y、Z、RX、RZ 5轴联动决定了火枪的位置方向矢量,为本文研究的重点。
1.2 系统组成水火弯板机器人由火路规划与预报专家系统、板形数据提取测量系统、多轴联动运动控制系统组成[4]。在专家系统与运动控制系统之间增加轨迹优化服务,可以较大程度地提高控制精度和加工效率。结构如图 3所示。
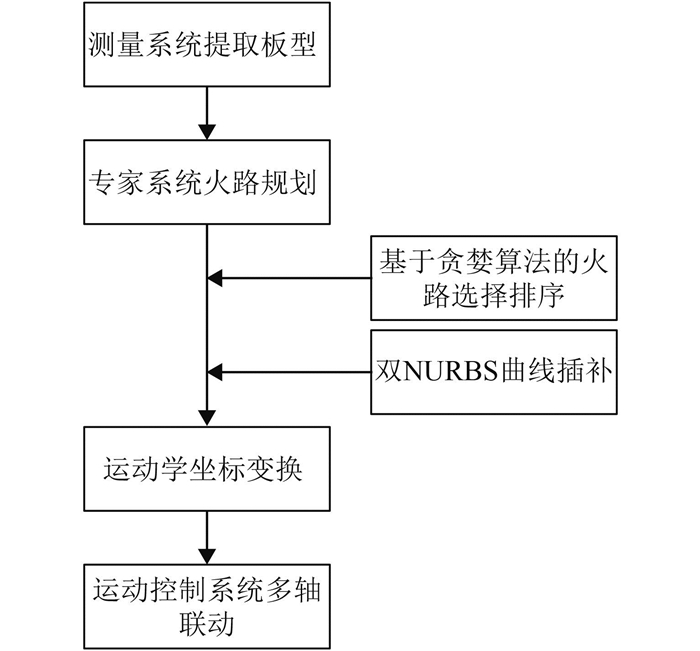
|
图 3 系统组成结构 Figure 3 The system composition structure |
专家系统是由自学习推理机、工人烧板经验数据组成专家库,将测量系统提取的板形与专家库做匹配,从而实现火路的规划预报[5]。然而专家系统给出的加工路径仅仅是火枪头的一些离散特征点的位置和方向矢量,平均每条火路上的特征点仅有7~12个,待加工板材曲率、尺寸越大,轨迹误差越明显,从而影响实际加工效果;一张板材上往往会规划多条路径,若加工次序随机必然会增加无效路径的长度,增加烧板时间[6]。
为了解决上述问题,引入CAM/CNC数控系统较为常见的双NURBS曲线插补方法和基于贪婪算法的火路次序选择方法[7],即先利用贪婪算法对专家系统给出的多条火路进行位置分析,调整火路行走次序,以使得总无效路径最短,然后利用双NURBS曲线插补对当前行走火路进行实时恒速插补,实现特征点的密化,最后调用坐标变换函数,将节点序列进行运动学坐标逆变换,使火枪头轨迹的位置矢量和火枪轴方向矢量转换为各轴进给量,驱动运动控制器移动。
2 基于贪婪算法的火路选择排序 2.1 运动轨迹的特点和约束条件图 4模拟火枪在一张有4条火路的待加工钢板上的行走轨迹。
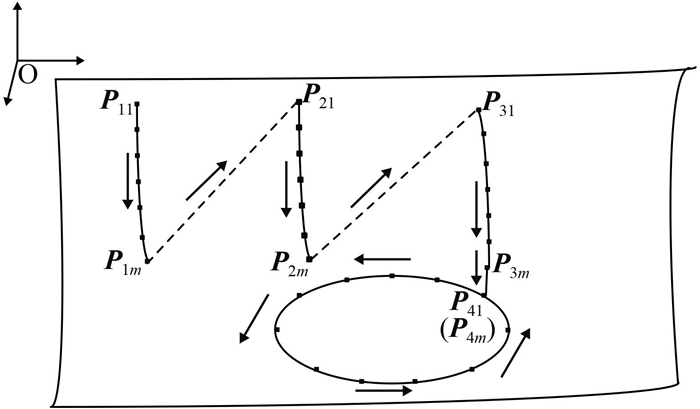
|
图 4 火枪头行走轨迹示例 Figure 4 Example of the path of the head of heating machine |
其中实线为专家系统规划火路,每条火路上布置m个特征点,P11和P1m分别代表第1条火路C1的起点和终点,虚线代表两条火路之间的无效路径,箭头方向代表火枪实际行走方向。运动轨迹的特点和约束条件为[8]:
(1) 每条火路上的每个特征点必须行走到位且不能重复,火枪头必须走完当前火路所有节点后才能寻找下一火路最近特征点。
(2) 要求虚线部分(即总无效路径)的长度之和最短。
(3) 单条火路行走方向无限定,即以无效路径最短为原则,允许其起点终点对调,如P1m→P11。
2.2 基于贪婪算法的火路排序规划在每条轨迹中都获取局部最优解的算法叫做贪婪算法,即在每一点选取离当前距离最短的特征点为下一跳点,以此类推,直到依次走过所有特征点[9]。目标函数:
| $ \boldsymbol{F} = \min \sum\limits_{j \ne k} {{d_{jk}}{\boldsymbol{X}_{jk}}} . $ | (1) |
其中,djk为两个特征点之间的距离,Xjk∈{0, 1},表示是否选取该路径。j,k=0, 1, 2,
| $ \left\{ \begin{array}{l} \sum\limits_{k = 1}^n {{\boldsymbol{X}_{jk}}} = 1,\;\;\;\;\;\;\;\;\;j = 1,2, \cdots ,n;\\ \sum\limits_{j = 1}^n {{\boldsymbol{X}_{jk}}} = 1,\;\;\;\;\;\;\;\;\;\;k = 1,2, \cdots ,n;\\ \sum\limits_{k,j \in s} {{\boldsymbol{X}_{jk}}} \leqslant \left| s \right| - 1,\;\;\;2 \leqslant \left| s \right| \leqslant n - 2,\;s \subset \left\{ {1,2, \cdots ,n} \right\}. \end{array} \right. $ |
考虑到水火弯板机火枪运动轨迹的特点和约束条件,所以对于非闭合曲线而言,只需比较各条火路起点和终点的位置到当前位置距离,以取较小值。
例如,如图 4所示,假设当前火枪头位于P1m,若d(P1m,P2m)=min (d(P1m,P21), d(P1m,P2m), d(P1m,P31), d(P1m,P3m)),则下一条轨迹为P1m→P2m→P21。火枪在到达P21后,按照前面方法继续判断,直到完成单板上总路径规划。
若存在闭合曲线火路,则需比较该条火路上所有特征点到当前位置的距离。若d(P1m,P4P)=min (d(P1m,P41), d(P1m,P42), d(P1m,P43), …d(P1m,P4p), …d(P1m,P4m), d(P1m,P21), d(P1m,P2m), d(P1m,P31), d(P1m,P3m)), 则下一条轨迹为P1m→P4p→P4(p+1) →…→P4m(P41)→…P4(p-1)→P4p,即P4p设为闭合火路轨迹C4的起点和终点。
综上,基于贪婪算法的火路排序流程如下:
(1)确定首条火路轨迹。判断非闭合曲线起点和终点以及闭合火路曲线所有特征点距坐标原点的距离,取最小值为首条火路起点。
(2)设置轨迹集合。设置P、Q两个集合,P中包含已经按次序规划完成的火路轨迹,Q中为尚未处理的火路集合。
(3)最近火路判断。按照贪婪算法逐步进行轨迹判断,并将判断后的元素依次放入P集合中,同时从Q中删除。
(4)判断集合Q是否为空,非空则返回(3)中继续判断,直到Q为空集合后完成排序。
3 火路轨迹的双NURBS曲线插补 3.1 NURBS曲线插补函数表示作为工业设计领域常见的几何形状数学表示方法,NURBS曲线可以由分段矢量函数p(u)表示[10],
| $ \begin{aligned} & \boldsymbol{p}\left( u \right) = \frac{{\sum\nolimits_{i = 0}^n {{\omega _i}{\boldsymbol{d}_i}{\boldsymbol{N}_{i,k}}\left( u \right)} }}{{\sum\nolimits_{i = 0}^n {{\omega _i}{\boldsymbol{N}_{i,k}}\left( u \right)} }},\;\;\\& i = \left( {0,1,2, \cdots ,n} \right). \end{aligned} $ | (2) |
其中,ωi为非负权因子,用于保证式(2)分母非零,di=(xi,yi,zi)为已知特征控制点.可按照式(3)求解B样条基函数Ni, k(u)所需节点矢量序列,
| $ \begin{aligned} & \boldsymbol{U} = \left( {{u_0},{u_1},{u_2}, \cdots ,{u_{n + k + 1}}} \right),\\& {u_{j + 1}} - {u_j} = \frac{{\sum\nolimits_{m = j + 1 - k}^{j - 1} {{l_m}} }}{{\sum\nolimits_{f = k + 1}^{n + 1} {\sum\nolimits_{h = f - k}^{f - 1} {{l_h}} } }}, \end{aligned} $ | (3) |
其中,li为两个相邻控制点之间的距离,有li=|di-di-1|, i=(0, 1, 2,
k次B样条基函数Ni, k(u)由德布尔-考克斯递推式迭代求得[11],
| $ \begin{aligned} {\boldsymbol{N}_{i,k}}\left( u \right) =& \frac{{\left( {u - {u_i}} \right){\boldsymbol{N}_{i,k - 1}}\left( u \right)}}{{{u_{i + k}} - {u_i}}} + \\ & \frac{{\left( {{u_{i + k + 1}} - u} \right){\boldsymbol{N}_{i + 1,k - 1}}\left( u \right)}}{{{u_{i + k + 1}} - {u_{i + 1}}}}. \end{aligned} $ | (4) |
NURBS曲线的s阶导矢:
| $ {\boldsymbol{p}^{\left( s \right)}}\left( u \right) = \sum\limits_{i = 0}^n {\boldsymbol{N}_{i,k}^{\left( s \right)}\left( u \right)\boldsymbol{R}_{i,k}^{\left( s \right)}\left( u \right)} , $ | (5) |
其中,
| $ \begin{aligned} \boldsymbol{R}{'_{i,k}}\left( u \right) =& \frac{{{\omega _i}\sum\nolimits_{i = 0}^n {\boldsymbol{N}{'_{i,k}}\left( u \right)} }}{{\sum\nolimits_{i = 0}^n {{\omega _i}{\boldsymbol{N}_{i,k}}\left( u \right)} }} - \\& \frac{{{\omega _i}{N_{i,k}}\left( u \right)\sum\nolimits_{i = 0}^n {{\omega _i}\boldsymbol{N}{'_{i,k}}\left( u \right)} }}{{{{\left[ {\sum\nolimits_{i = 0}^n {{\omega _i}{\boldsymbol{N}_{i,k}}\left( u \right)} } \right]}^2}}}. \end{aligned} $ | (6) |
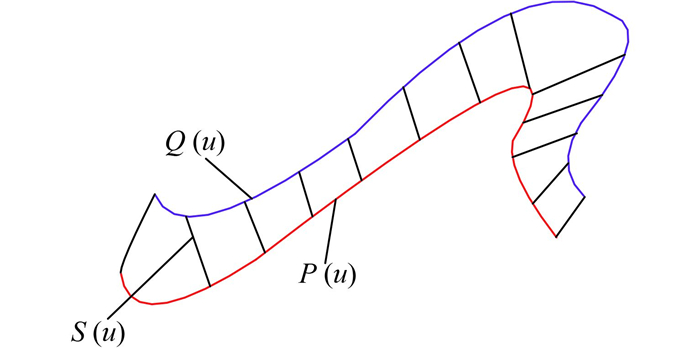
常见的单NURBS曲线插补一般只应用于2轴或3轴机床,水火弯板机器人火枪轴由X、Y、Z、RX、RZ 5轴驱动,所以要构造两条NURBS曲线,实现5轴实时插补,如图 5所示[12]。
|
图 5 双NURBS曲线示例 Figure 5 Example of double NURBS curve |
如图 5所示,P(u)为火枪头位置的NURBS曲线,Q(u)是火枪轴线上距火枪头距离为H的点的NURBS曲线,H为定常数。两条NURBS曲线有相同节点矢量,S(u)为轴线方向矢量.
| $ \boldsymbol{P}\left( u \right) = \left[ {{x_t}\left( u \right),{y_t}\left( u \right),{z_t}\left( u \right)} \right], $ | (7) |
| $ \boldsymbol{Q}\left( u \right) = \left[ {{x_h}\left( u \right),{y_h}\left( u \right),{z_h}\left( u \right)} \right], $ | (8) |
| $ \boldsymbol{S}\left( u \right) = \frac{{\boldsymbol{Q}\left( u \right) - \boldsymbol{P}\left( u \right)}}{{\left| {\boldsymbol{Q}\left( u \right) - \boldsymbol{P}\left( u \right)} \right|}}. $ | (9) |
为了保证烧板过程中火枪头速度稳定、减少抖动,采取恒速插补方法,给定速度VH=v(t)、插补周期T。
| $ v\left( t \right) = \frac{{{\rm{d}}s}}{{{\rm{d}}t}} = \frac{{{\rm{d}}s}}{{{\rm{d}}u}}\frac{{{\rm{d}}u}}{{{\rm{d}}t}}, $ | (10) |
则
| $ \frac{{{\rm{d}}u}}{{{\rm{d}}t}} = \frac{{v\left( t \right)}}{{\sqrt {{{\left( {x{'_t}} \right)}^2} + {{\left( {y{'_t}} \right)}^2} + {{\left( {z{'_t}} \right)}^2}} }}, $ | (11) |
其中,x't、y't、z't由式(4)、(5)、(6)联立求得。
对式(11)作二阶泰勒展开,以求得每一插补周期内的所有节点矢量,有[13]
| $ u\left( {\left( {k + 1} \right)t} \right) = u\left( {kT} \right) + T\frac{{{\rm{d}}u}}{{{\rm{d}}t}}{|_{t = kt}} + \xi , $ | (12) |
其中,ξ为高阶无穷小。
将求得所有插补周期内的节点矢量代入式(2)、(4),求得插补点坐标后,再联立并代入式(7)、(8)、(9),最终求得火枪头插补点的位置及火枪轴方向矢量序列为
| $ \begin{aligned} & {\boldsymbol{P}_T} = \left[ {{\boldsymbol{P}_{0T}}{\boldsymbol{P}_{1T}}{\boldsymbol{P}_{2T}}{\boldsymbol{P}_{3T}} \cdots } \right],\\ & {\boldsymbol{S}_T} = \left[ {{\boldsymbol{S}_{0T}}{\boldsymbol{S}_{1T}}{\boldsymbol{S}_{2T}}{\boldsymbol{S}_{3T}} \cdots } \right]. \end{aligned} $ |
最后调用坐标变换函数,将节点序列进行运动学坐标逆变换,使PT和ST组成的火枪头工件坐标转换为机床坐标(x, y, z, θrx, θrz),驱动运动控制器各轴移动。
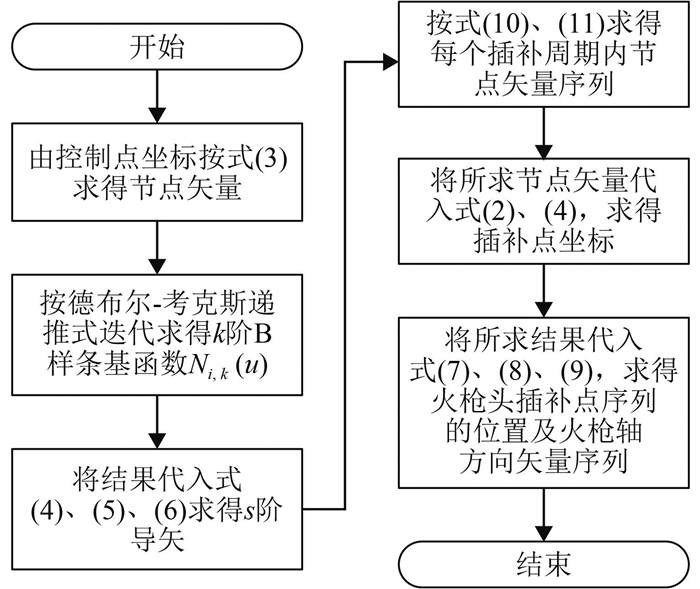
综上,双NURBS曲线插补的流程图如图 6所示。
|
图 6 NURBS曲线插补流程图 Figure 6 Flow chart of NURBS curve interpolation |
在WIN8.1系统下的Visual Studio 2013中,使用C++编写基于贪婪算法的轨迹排序优化和双NURBS曲线插补优化的服务软件,在广船国际股份有限公司龙穴造船厂烧板现场进行现场试验。
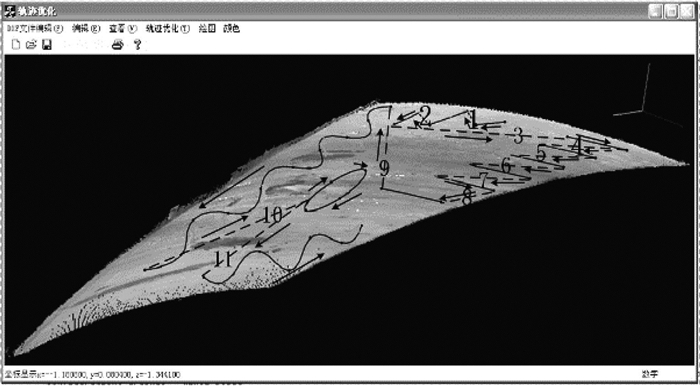
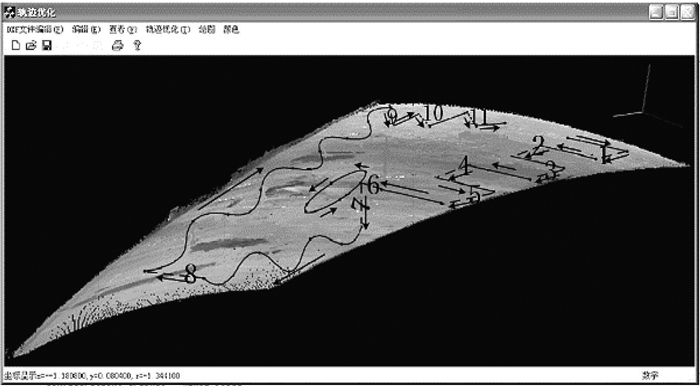
4.1 单板无效轨迹长度分析选取广船国际5.00 m×12.00 m大尺寸船体外板作为实验对象,通过3D扫描仪提取钢板三维图像。图 7为未经排序优化的火枪轨迹,图 8为通过贪婪算法规划排序的火枪轨迹,数字1~11为无效路径的序号,分别测得对应各段无效轨迹长度,如表 1所示。
|
图 7 未经优化的火路轨迹 Figure 7 Fire paths without optimizing |
|
图 8 经贪婪算法优化的火路轨迹 Figure 8 Fire paths optimization by greedy algorithm |
| 表 1 贪婪算法优化前后无效路径长度比较 Table 1 Comparison of invalid path length before and after optimization of greedy algorithm |
由表 1可知,通过使用贪婪算法对火路轨迹进行优化排序,大大减少了无效轨迹长度,有利于水火弯板机节省实际加工时间,提高运行效率。
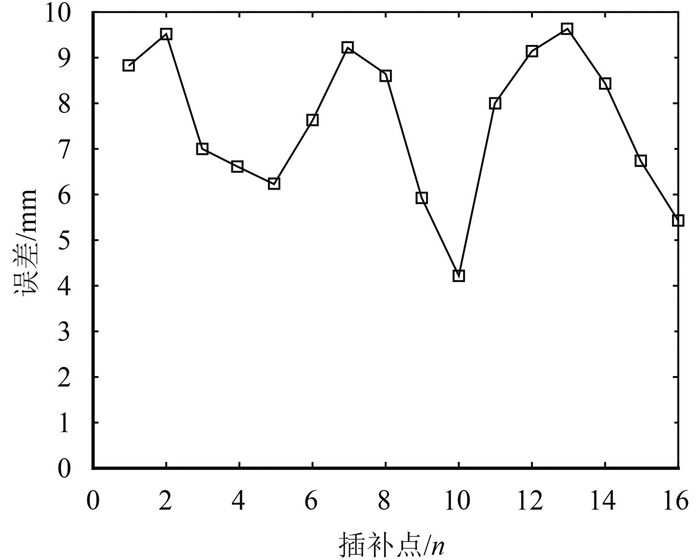
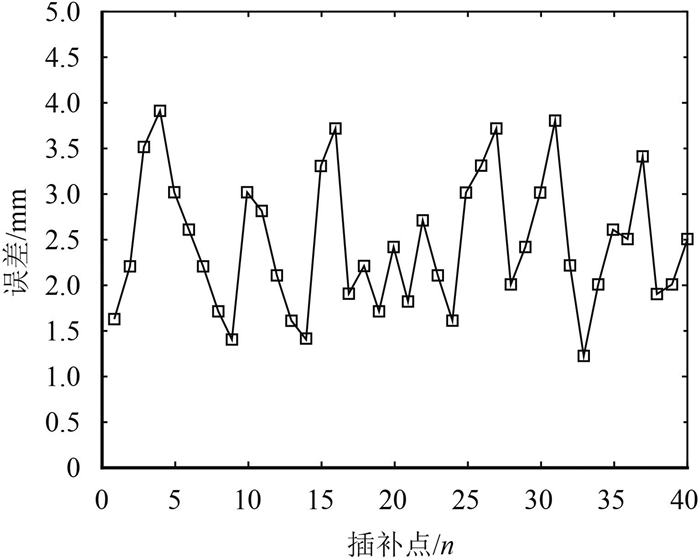
4.2 双NURBS插补点误差分析将一条经过双NURBS曲线插补的弯板机实际行走火路轨迹通过扫描仪进行提取,并在插补点作非线性误差分析,同时选取线性插补作对照实验。其中,进给速度VH取0.5 m/min,周期T=5 ms。图 9和图 10分别为采用线性插补和双NURBS曲线插补插补点的误差曲线。
|
图 9 线性插补误差 Figure 9 The error of linear interpolation |
|
图 10 双NURBS曲线插补误差 Figure 10 The error of double NURBS curve interpolation |
由图 9、10可知,在水火弯板机器人轨迹优化方面,较传统线性插补,双NURBS曲线插补可以较明显地减小非线性误差,提高火枪沿火路行走的精确性。
5 结语将基于贪婪算法的火路选择排序方法与双NURBS曲线插补运用到水火弯板机器人运动轨迹优化中,通过“先规划,后插补”的优化流程,减小单板无效轨迹长度和火路行走偏差,较大程度地提升了设备生产效率和烧板质量,有助于促进水火弯板自动化加工水平的提高。
| [1] |
唐伟, 杨澍, 许江淳, 等. 数控水火弯板机及其工艺的发展现状[J].
材料开发与应用, 2010, 25 (3): 75-78.
TANG W, YANG S, XU J C, et al. Progress in numerical control device of line heating and technology[J]. Development and Application of Materials, 2010, 25 (3): 75-78. |
| [2] |
郭培军. 中国船舶产业现状分析及发展思索[J].
中国远洋航务, 2008 (1): 68-69.
GUO P J. Analysis of the current situation of China Shipbuilding Industry and its development thinking[J]. Chinese ocean shipping, 2008 (1): 68-69. |
| [3] | JING H J, YAO Y X, CHEN S D. Machining accuracy enhancement by modifying NC program[J]. Key Engineering Materials, 2006, 315 : 71-75. |
| [4] | 汪骥.水火弯板自动化加工工艺的关键技术研究[D].大连:大连理工大学船舶工程学院, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10141-2007207270.htm |
| [5] |
邓燕萍, 郭培军, 刘玉君, 等. 船体外板水火成型工艺参数预报系统设计与实现[J].
船舶工程, 2008, 30 (1): 61-65.
DENG Y P, GUO P J, LIU Y J, et al. Design and implementation of technological parameter prediction system for hull plate formed by line heating[J]. Ship Engineering, 2008, 30 (1): 61-65. |
| [6] | 李敢.高频感应弯板成型计算机辅助系统的开发[D].上海:上海交通大学船舶海洋与建筑工程学院, 2007. http://d.wanfangdata.com.cn/Thesis/D029466 |
| [7] |
熊小安, 曾碧, 余永权. CAD/CAM系统中NURBS曲线修改的研究[J].
广东工业大学学报, 2002, 19 (2): 14-17.
XIONG X A, ZENG B, YU Y Q. Research on the Modification of NURBS Curve in CAD/CAM System[J]. Journal of Guangdong University of Technology, 2002, 19 (2): 14-17. |
| [8] |
童行行, 王凌, 何京芮. 旅行商问题基于参考点的相邻插入法及其改进[J].
计算机工程与应用, 2002, 20 (2): 63-65.
TONG X X, WANG L, HE J R. Reference point-based near insertion approach and its improvement for traveling salesman problem[J]. Computer Engineering and Application, 2002, 20 (2): 63-65. |
| [9] |
孔令夷. 面向有约束TSP的一种混合启发式算法[J].
西安邮电大学学报, 2013, 18 (1): 86-89.
KONG L Y. A hybrid heuristic algorithm for constrained TSP[J]. Journal of Xi'an University of Posts and Telecommunications, 2013, 18 (1): 86-89. |
| [10] |
赖金涛, 傅建中, 沈洪壵. 基于NURBS曲面敏感点的曲面检测测点优化[J].
浙江大学学报:工学版, 2015, 49 (7): 1201-1207.
LAI J T, FU J Z, SHEN H Y. Measuring points optimization in machining error inspection based on reconstruction of NURBS control points driven by sensitive points[J]. Journal of Zhejiang University:Engineering Science, 2015, 49 (7): 1201-1207. |
| [11] | Wu J C, ZHOU H C, TANG X Q. A NURB interpolation algorithm with continuous federate[J]. The International Journal of Advanced Manufacturing Technology, 2012, 59 (5/8): 865-873. |
| [12] | 马朝阳.自由型曲线曲面直接插补技术研究[D].山东:山东大学机械工程学院, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10422-2008189538.htm |
| [13] | 吴继春.曲面数控加工编程轨迹的NURBS拟合及插补算法研究[D].武汉:华中科技大学机械科学与工程学院, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10487-1013011026.htm |
 2017, Vol. 34
2017, Vol. 34