2. 中国电子科技集团公司第七研究所, 广东 广州 510310 ;
3. 中南民族大学 智能无线通信湖北省重点实验室, 湖北 武汉 430074
2. China Electronics Technology Group Corporation No. 7 Research Institute, Guangzhou 510310, China ;
3. Hubei Key Laboratory of Intelligent Wireless Communications, South-Central University for Nationalities, Wuhan 430074, China
认知无线电网络中,次用户(SU, secondary user)须以不影响主用户(PU, primary user)的正常通信为前提[1],选择空闲频段进行通信[2].如果SU合作感知定位到PU空间位置[3-4]时,则SU可有更多次的频谱接入机会,且有效地提高频谱的利用率.目前在认知无线网络中测距算法与非测距算法是常见的定位算法[5],但由于小型移动主用户的随意移动特性;发射功率只有10~50 mW,信号覆盖范围小;开关模式的时空特性变化大,因此在对小型移动主用户定位的问题上依然存在很大的难点.
文献[6]研究了通过简单的能量感知方法对移动目标进行定位.当一个检测区域内的传感器收集到能量时,选取几个收集能量最强的传感器信号,通过平均权重的方法来对移动目标进行定位.但是该移动目标移动速度慢于小型移动主用户,发送的能量值远高于小型移动主用户,并不能将其看待成小型移动主用户.文献[7]提出了一种检测小型移动主用户的方法.为使检测小型移动主用户的虚警概率与漏检概率满足要求而采用基于数学的理论分析,得出了检测小型移动主用户的最小感知密度.可文章中并未涉及小型移动主用户定位问题.文献[8]提出基于能量感知的追踪方案,基于带有阴影衰落的序列蒙特卡洛(Sequential Monte Carlo),称为SOLID的定位方法.但算法追踪性能深深地依赖于粒子的数量,计算复杂度过大.
本文提出一种基于加权质心算法[9-10]与粒子滤波算法[11-12]结合且带有追踪调整机制的(with Adjustment mechanism based Weighted Centroid Localization and Particle Filter)小型移动主用户定位算法用来追踪小型移动主用户.考虑到实际环境与噪声的影响,加入调整机制,确保算法整体的跟踪效果.仿真结果显示,AWCPF算法的定位误差可控制在10 m之内.
1 系统模型假设N个SU与一个小型移动主用户在一个Q×Q的仿真范围内.小型移动主用户可随机出现在任意位置并进行着非线性无规则的运动;N个SU有规则地安放在该区域内,同时在该网络模型下所有的SU都知道自身的位置点,合作追踪小型移动主用户. AWCPF算法先依据次用户接收到的主用户信号强度(Received Signal Strength, RSS)值来选取参与定位的SU个数.为确保RSSI值结果更加精准,无线信号传输模型采用对数正态阴影路径损耗模型.
1.1 对数正态阴影路径损耗模型当SU接收到小型移动主用户的信号能量时[13-14],SU获取到的能量值可表示为
| ${\rm{RSSI(}}d) = {\rm{RSSI(}}{d_0}{\rm{) - }}10n{\rm{lg}}\left( {\frac{d}{{{d_0}}}} \right) + {X_\sigma }.$ | (1) |
由式(1)可得出
| $d = {d_0} \times {10^{\frac{{{\rm{RSSI}}({d_0}) - {\rm{RSSI}}(d) + {X_\sigma }}}{{10n}}}}.$ | (2) |
其中,d为小型移动主用户与SU之间的距离;d0为参考距离,一般取1 m;n为信号动态衰减因子,该值随着周围环境变化而变化,根据经验取值范围为2~6;RSSI (d0)代表SU在d0米处测量到的小型移动主用户的能量值;RSSI (d)代表距离小型移动主用户d米远处的SU接收到的能量值;考虑到受环境影响,引入服从高斯分布的随机变量Xσ.
1.2 选取SU根据无线传播特性,SU测量到小型移动主用户信号强度后,采用二元假设模型判断SU是否在小型移动主用户的覆盖范围内,表示为
| $\left\{ {\begin{array}{*{20}{c}} {{H_0}:{\rm{RSS}}{{\rm{I}}_i} \geqslant T,}\\ {{H_1}:{\rm{RSS}}{{\rm{I}}_i} \leqslant T.} \end{array}} \right.$ | (3) |
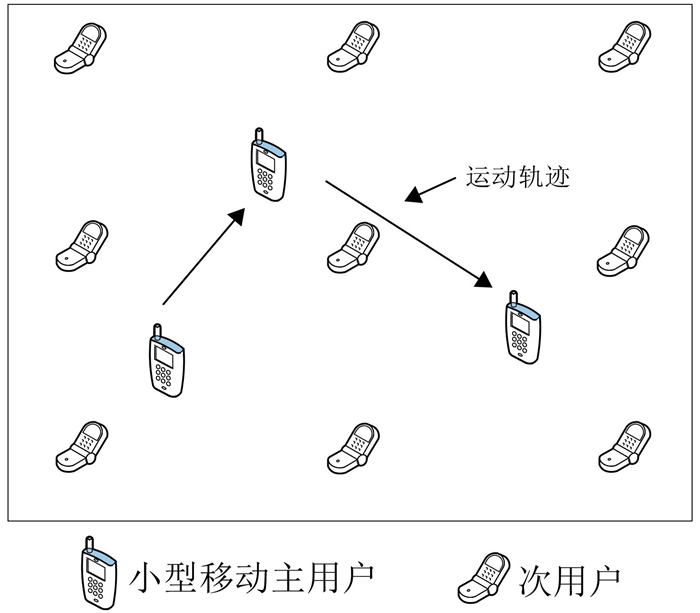
其中H0事件中的RSSIi代表第i个SU接收到的主用户信号强度,T为信号强度阈值.根据上式来判断选取参与定位的SU.若RSSIi大于阈值T,则表示在小型移动主用户的信号覆盖范围内存在该SU,则将选取该SU参与主用户的定位,反之则舍弃.图 1描述了PU与SU的网络模型.
|
图 1 网络模型图 Figure 1 Network model |
本文提出AWCPF定位算法首先采用加权质心定位(Weighted Centroid Localization)可缩小定位范围,为粒子滤波算法(Particle Filter)提供观测量,随之粒子滤波算法进行追踪定位.与此同时为防止定位误差过大,调制机制适时启动确保定位效果.基于以上思路,具体算法如下.
2.1 加权质心算法由于小型移动主用户与SU之间的距离越近则相应的SU获取的能量值越大,所以将基于接收信号强度的加权质心定位算法的结果作为粒子滤波算法中的观测量.根据上述的信道传输模型可知,在加权质心定位算法中能量值越大的SU对定位结果影响越大.加权质心定位算法得到的定位值由下式得出
| $\left\{ {\begin{array}{*{20}{c}} {x = \dfrac{{{\rm{RSS}}{{\rm{I}}_1} \times {x_1} + {\rm{RSS}}{{\rm{I}}_2} \times {x_2} + \cdot \cdot \cdot + {\rm{RSS}}{{\rm{I}}_n} \times {x_n}}}{{{\rm{RSS}}{{\rm{I}}_1} + {\rm{RSS}}{{\rm{I}}_2} + \cdot \cdot \cdot + {\rm{RSS}}{{\rm{I}}_n}}},}\\ {y = \dfrac{{{\rm{RSS}}{{\rm{I}}_1} \times {y_1} + {\rm{RSS}}{{\rm{I}}_2} \times {y_2} + \cdot \cdot \cdot + {\rm{RSS}}{{\rm{I}}_n} \times {y_n}}}{{{\rm{RSS}}{{\rm{I}}_1} + {\rm{RSS}}{{\rm{I}}_2} + \cdot \cdot \cdot + {\rm{RSS}}{{\rm{I}}_n}}}.} \end{array}} \right.$ | (4) |
其中(xi, yi)表示的是第i个SU的坐标位置.第i个SU的权重为wi=RSSIi/(RSSI1+RSSI2+.....+RSSIn),其中i=1, 2, 3...n.
为了确保质心定位的精准度,设定能量阈值T,只选取能量值大于T的SU.为方便起见根据设定好的阈值T与式(2),直接选取与主用户距离小于等于参数d的SU,再由式(4)得到小型移动主用户初步的位置信息.同时如果SU接收信号强度值出现误差时也会影响定位精度,本文将在仿真部分讨论RSSI值误差对AWCPF算法的影响.
2.2 粒子滤波算法在粒子滤波算法中,一个动态系统可以由状态方程与测量方程表述[15],如下所示
| $ \left\{ {\begin{array}{*{20}{c}} {{\boldsymbol{X}_{k + 1}} = {f_k}\left( {{x_k}\boldsymbol{,}{\boldsymbol{w}_k}} \right),}\\ {{\boldsymbol{Z}_{k + {\rm{1}}}} = {g_k}\left( {{x_k}\boldsymbol{,}{\boldsymbol{v}_k}} \right).} \end{array}} \right. $ | (5) |
其中f和g分别是状态函数与测量函数,X表示状态向量,Z表示测量向量,w与v分别表示过程噪声向量和测量噪声向量.
2.2.1 运动模型本文将一个弧线运动模型作为小型移动主用户的移动模型,且假设小型移动主用户的运动状态方程已知.主用户运动状态方程由下式表示
| $\begin{array}{c} \boldsymbol{X}\left( {:,k} \right) = \boldsymbol{X}\left( {:,k - 1} \right) + {\rm{dis}} \times \left[ {\left( { - \cos \left( {k\theta } \right)} \right);\sin \left( {k\theta } \right)} \right] + \\ {\rm{wgn}}\left( {2,1,10\lg \left( Q \right)} \right). \end{array}$ | (6) |
其中dis代表每次移动的距离;θ代表旋转的角度;Q代表过程噪声方差.
2.2.2 粒子滤波先根据系统的初始化分布P(x)随机抽取M个样本粒子(xt(i), wt(i)),i=1, 2...M.每个xt(i)代表粒子,wt(i)为权重,其中w=1/M.接着根据小型移动主用户的运动状态方程,由式(6)预测出M个粒子的位置来估计小型移动主用户的位置信息
| $\begin{aligned} P(:,k) = & P(:,k{\rm{ - 1}}) + {\rm{dis \times }}[({\rm{ - cos}}(k \theta ));{\rm{sin}}(k \theta )] + \\ & {\rm{wgn}}(2,1,10{\rm{lg}}(Q)). \end{aligned}$ | (7) |
其中P(:, k)代表粒子在时刻k的位置信息.进而得出每个粒子的权重
| $\begin{aligned} \boldsymbol{w}_t^{(i)} = \frac{1}{{{\rm{sqrt(}}R{\rm{)sqrt(2}}pi)}}\exp ( - \frac{{{{(dist)}^2}}}{{2R}}). \end{aligned}$ | (8) |
其中R代表测量噪声方差;dist代表粒子估计值与测量值的差值.最后进行重采样,对粒子更新并标准化相应权重.最终小型移动主用户的位置可表示为
| ${\hat x_t} = \sum\limits_{i = 1}^{{N_{{\rm{particle}}}}} {\boldsymbol{w}_t^{(i)}x_t^{(i)}} .$ | (9) |
由于噪声等其他因素的干扰,粒子滤波算法并不能确保准确地追踪小型移动主用户的位置.因此我们提出一个调整机制,确保AWCPF算法的整体追踪效果.小型移动主用户运动的每一时刻误差可表示为
| ${\rm{err}} = {\rm{norm(}}\boldsymbol{X}(:,k) - {\rm{PC}}(:,k)).$ | (10) |
其中X(:, k)代表小型移动主用户的真实位置;PC (:, k)代表估计的小型移动主用户位置;err代表定位误差;norm代表Matlab中的函数.接着采用二元假设模型来判断是否启用调整机制,表示为
| $\left\{ {\begin{array}{*{20}{c}} {{\rm{err}} \geqslant \alpha ,}\\ {{\rm{err}} < \alpha .} \end{array}} \right.$ | (11) |
当某时刻的定位误差大于所设定的门限阈值α时,将启用调整机制,在下一时刻定位前更新主用户的位置信息,替换粒子算法中的主用户位置观测量,确保追踪效果.AWCPF算法具体流程如下.
(1) 采用加权质心定位算法初步定位,获得小型移动主用户位置信息(x, y).
从时刻t=1开始循环执行:
(2) 粒子滤波算法进行追踪定位,得到每时刻的定位误差;
(3) 如果某时刻定位误差大于阈值α,则启用调整机制,更新主用户的位置信息,继续执行(2);
(4) 反之不启用,持续执行步骤(2);
结束循环。
3 仿真结果假设认知无线网络中SU有规则地分布在100 m×100 m的仿真范围内.小型移动主用户初始位置随机放置,其发射功率为250 mW[4].路径损耗n=4,过程噪声的方差为10,测量噪声的方差为5.仿真中将小型移动主用户以弧线运动模型移动20次,每次移动距离设定8 m,旋转角度为π/10.
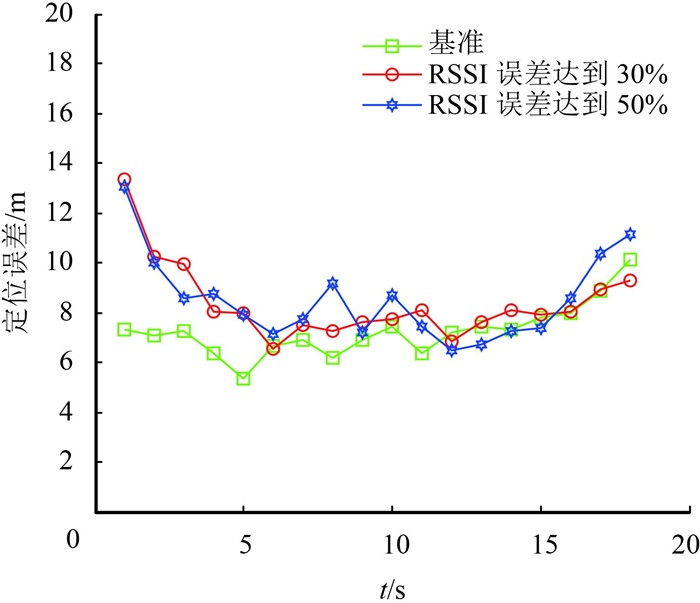
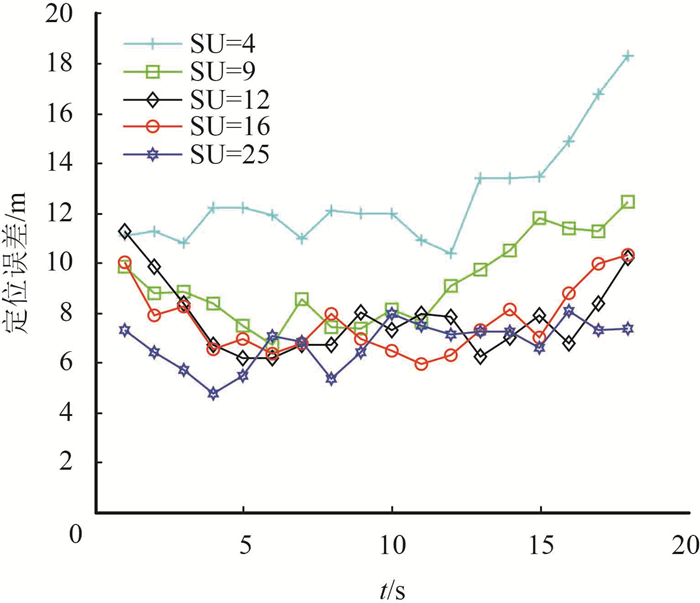
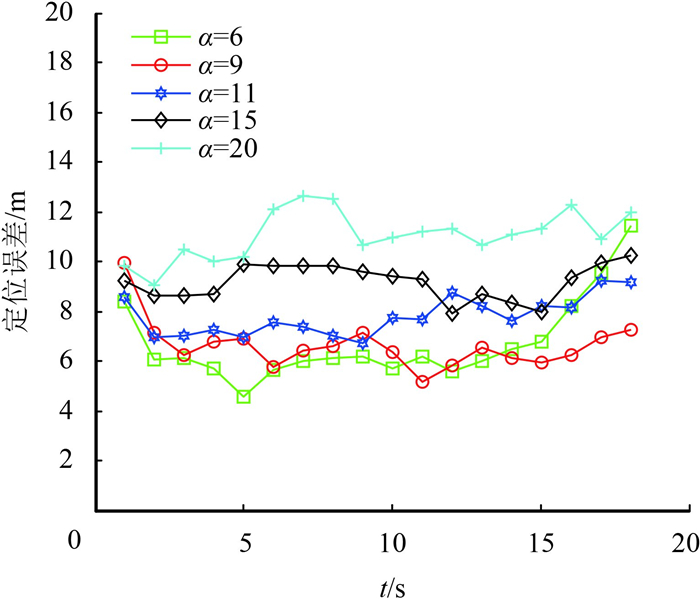
图 2为SU接收小型移动主用户信号强度值出现误差对定位算法的影响.选取RSSI值无误差情况为基准,当检测到的RSSI值与基准时相比误差分别达到30%与50%时,算法的定位精度有所降低.这是由于RSSI值出现误差导致可参与定位的SU数量减少,影响加权质心初步定位结果进而导致AWCPF算法定位精度降低.后续在AWCPF算法的调整机制启用后,定位效果逐步相近并趋于稳定;图 3为SU数量不同时的定位误差.从图中可看出当参与定位的SU个数过少时定位效果差.这是因为协作定位的SU数量少,致使算法的初步定位精度低,在调整机制启用时无法更新小型移动主用户的当前位置信息;图 4为调整机制中的门限α(称为误差阈值)对定位算法的影响.由图可知当选取的阈值α越小时,定位误差越小.这是由于阈值α越小,启用调整机制的次数则会越多,确保对小型移动主用户位置的实时把控,进而提升定位精度.
|
图 2 接收信号强度误差对定位的影响 Figure 2 Effects of RSSI error |
|
图 3 SU数量对定位的影响 Figure 3 Effects of sensor |
|
图 4 误差阈值α对定位的影响 Figure 4 Effects of threshold α |
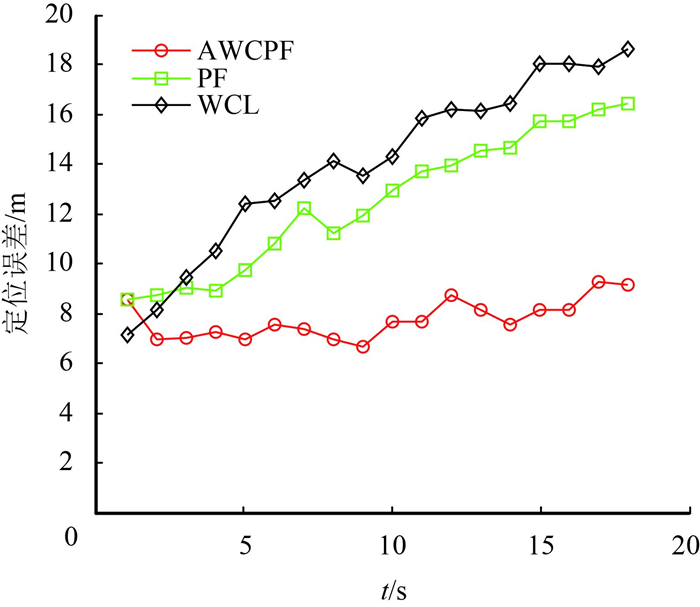
图 5为AWCPF算法与其他定位算法的性能对比.由于PF算法没有调整机制,故而在后期由于噪声等因素的影响会逐渐偏离小型移动主用户,无法精准地跟踪小型移动主用户的行踪.同时,提出的AWCPF算法可以连续定位,定位效果更是优于WCL算法.
|
图 5 定位算法对比 Figure 5 Performance comparison of tracking algorithms |
本文提出AWCPF算法去追踪小型移动主用户.算法先采用权重质心定位算法获得小型移动主用户的初始位置信息,后由粒子滤波算法进行对小型移动主用户跟踪,得到定位误差.并在每时刻的定位过程中加入调整机制,确保算法整体的跟踪效果.仿真结果表明,对于小型移动主用户的追踪定位,提出的AWCPF算法比其他定位算法有更好的定位效果.
| [1] | MIN A W, ZHANG X Y, SHIN K G. Detection of small-scale primary users in cognitive radio networks[J]. IEEE Journal on Selected Areas in Communications, 2011, 29 (2): 349-361. DOI: 10.1109/JSAC.2011.110208. |
| [2] | YUCEK T, ARSLAN H. A survey of spectrum sensing algorithms for cognitive radio applications[J]. IEEE Communications Surveys and Tutorials, 2009, 11 (1): 116-130. DOI: 10.1109/SURV.2009.090109. |
| [3] | MA Z, BEN L K, CHEN W, et al. A semi range-based iterative localization algorithm for cognitive radio networks[J]. IEEE Transactions on Vehicular Technology, 2009, 59 (2): 2214-2218. |
| [4] | SHARMA P, CHANDRA K. Prediction of state transitions in rayleigh fading channels[J]. IEEE Transactions on Vehicular Technology, 2007, 56 (2): 416-425. DOI: 10.1109/TVT.2007.891421. |
| [5] | VIANI F, LIZZI L, ROCCA P, et al. Object tracking through rssi measurements in wireless sensor networks[J]. Electronics Letters, 2008, 44 (10): 653-654. DOI: 10.1049/el:20080509. |
| [6] | LIANG X, GREENSTEIN L J, MANDAYAM N B. Sensor-assisted localization in cellular systems[J]. IEEE Transactions on Wireless Communications, 2007, 6 (12): 4244-4248. DOI: 10.1109/TWC.2007.060316. |
| [7] | WU Q, DING G, WANG J, et al. Spatial-temporal opportunity detection for spectrum-heterogeneous cognitive radio networks:two-dimensional sensing[J]. IEEE Transactions on Wireless Communications, 2013, 12 (2): 516-526. DOI: 10.1109/TWC.2012.122212.111638. |
| [8] | MIN A W, SHIN K G. Robust tracking of small-scale mobile primary user in cognitive radio networks[J]. IEEE Transactions on Parallel and Distributed Systems, 2013, 24 (4): 778-788. DOI: 10.1109/TPDS.2012.191. |
| [9] | WANG J, CHEN J, CABRIC D. Stansfield localization algorithm:theoretical analysis and distributed implementation[J]. Wireless Communications Letters IEEE, 2013, 2 (3): 327-330. DOI: 10.1109/WCL.2013.032013.130052. |
| [10] | WANG J, URRIZA P, HAN Y, et al. Weighted centroid localization algorithm:theoretical analysis and distributed implementation[J]. IEEE Transactions on Wireless Communications, 2011, 10 (10): 3403-3413. DOI: 10.1109/TWC.2011.081611.102209. |
| [11] | SCHIKORA M, GNING A, MIHAYLOVA L, et al. Box-particle probability hypothesis density filtering[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50 (3): 1660-1672. DOI: 10.1109/TAES.2014.120238. |
| [12] | YOO J, KIM W, KIM H J. Distributed estimation using online semi-supervised particle filter for mobile sensor networks[J]. Control Theory and Applications Iet, 2015, 9 (3): 418-427. DOI: 10.1049/iet-cta.2014.0495. |
| [13] |
彭越, 吴多龙, GuillaumeAndrieux, 等. 基于最小能量法的无线传感器网络节点能量有效性研究[J].
广东工业大学学报, 2014, 31 (1): 86-89.
PENG Y, WU D L, GUILLAUME A, et al. Research on energy-efficiency in wireless sensor networks based on minimum energy coding[J]. Journal of Guangdong University of Technology, 2014, 31 (1): 86-89. |
| [14] |
李鹤, 刘广聪, 胡蝶. 无线传感器网络中基于能量比的簇首选择机制[J].
广东工业大学学报, 2014, 31 (3): 83-87.
LI H, LIU G C, HU D. Cluster-head selection mechanism based on energy ratio in wireless sensor networks[J]. Journal of Guangdong University of Technology, 2014, 31 (3): 83-87. |
| [15] | CANDY J V. Bootstrap particle filtering[J]. IEEE Signal Processing Magazine, 2007, 24 (4): 73-85. DOI: 10.1109/MSP.2007.4286566. |
 2017, Vol. 34
2017, Vol. 34