近年来，随着我国节能减排政策的大力推广，清洁新能源的开发和利用受到广泛关注和重视，这就推动了我国风力发电事业的发展。然而，风电具有较强的不确定性和间歇性，而且大型风力涡轮机不能储存电能，这就使得风电输出功率表现出很强的波动性以及随机性。当大规模的风电场接入电网时，风电场出力的不确定性就会对整个电力系统的安全运行以及规划产生很重要的影响。因此，计及风电场并网的电力系统机组组合优化问题便成为提高系统运行稳定性亟待解决的研究课题^[1]。

文献[2]建立了基于模糊理论计及风电场并网的动态经济调度模型，较好地解决了风电有功出力的随机性，但优化后的结果较依赖于人为设置的满意度，并且不能使风电资源的利用最大化；文献[3]利用机会约束来描述风电出力的不确定性，建立了计及风电并网的机会约束规划机组组合模型，采用粒子群算法进行求解，但是没有考虑多目标问题；文献[4]在利用对风速进行预测的基础上，建立了计及风电场并网的电力系统动态经济调度模型，但忽略了系统中机组的启停问题。

风速具有一定的随机性和间歇性，因此单一的确定性模型无法真实反映风电出力的实际情况。机会约束规划是指在一定程度上考虑不确定因素，将传统优化中完全满足的约束条件转化为满足约束条件的概率高于某一置信水平。考虑到机会约束规划和风力化问题，以使含风电场的机组组合更具实用性。

在此基础，本文针对含风机组的发电系统，提出基于机会约束规划下的机组组合优化数学模型，采用混沌文化粒子群(CCPSO)算法对标准粒子群(PSO)算法进行改进，利用混沌算法提高种群的搜索遍历性与多样性；利用文化算法的双层进化机制，改善粒子群算法初始化随机性及易陷入局部最优的缺陷。利用混沌离散粒子(CDPSO)算法对机组进行启停安排，通过CCPSO算法安排机组出力；制定了节能减排下的多目标优化，分析了机会约束条件在不同置信度要求下协调方案利润和风险的优势。

1 含风电场并网的多目标机组组合优化模型

由于风电出力的不确定性，使得电力系统经济调度的目标函数和约束条件中包含随机变量。本文引入机会约束规划理论，用随机数来表示风电场出力的不确定性，以数学期望值最小为目标函数，以概率形式描述相关约束条件。本文含风电场机组组合问题建立的目标函数是在满足系统约束和发电机自身约束的前提下，确定各时段机组的启停状态及有功出力情况，以式(1)中燃料耗量及考虑环境效益中污染气体SO₂、CO₂排放量最小为目标函数。

$ \left\{ \begin{aligned} \!\!\! & \min {f_1} \!\! =\!\! E\left[ {\sum\limits_{t = 1}^T \sum\limits_{i = 1}^{{N_g}} {\left( {{u_i}^tf\left( {\boldsymbol{P}_i^t} \right) \!\! +\!\!\! \sum\limits_{t = 1}^T \sum\limits_{i = 1}^{{N_g}} {\boldsymbol{S}_i}^t*{u_i}^t(1 \!\! - \!\! {u_i}^{(t - 1)})} \right)} } \right],\\ \!\!\! & \min {f_2} \!\! =\!\! E\left[ {\sum\limits_{t = 1}^T {\sum\limits_{i = 1}^{{N_g}} {\left( {{u_i}^t({\alpha _{{\rm{c}}i}} + {\beta _{ci}}\boldsymbol{P}_i^t + {\gamma _{ci}}{{(\boldsymbol{P}_i^t)}^2}} \right)} } } \right],\\ \!\!\! & \min {f_3} \!\! =\!\! E\left[ {\sum\limits_{t = 1}^T {\sum\limits_{i = 1}^{{N_g}} {\left( {{u_i}^t({\alpha _{si}} + {\beta _{si}}\boldsymbol{P}_i^t + {\gamma _{si}}{{(\boldsymbol{P}_i^t)}^2}} \right)} } } \right]. \end{aligned} \right. $

(1)

含风场机组组合问题的机会约束规划模型所需考虑的约束条件见式(2)。

$ \left\{ \begin{aligned} & \sum\limits_{i = 1}^{{N_g}} {{u_i}^t\boldsymbol{P}{{_i^g}^t} + \sum\limits_{k = 1}^{{N_w}} {\boldsymbol{P}{{_k^w}^t}} - {\boldsymbol{P}_D}^t} {\rm{ = }}0,\\ & {P_r}\left\{ {\sum\limits_{i = 1}^{{N_g}} {{u_i}^t{\boldsymbol{P}_{{\rm{MAX}}}}_i^t + \sum\limits_{k = 1}^{{N_w}} {\boldsymbol{P}_k^{wt} \ge {\boldsymbol{P}_D}^t} (1 + {\boldsymbol{R}_u}^t)} } \right\}\geqslant \beta ,\\ & {P_r}\left\{ {\sum\limits_{i = 1}^{{N_g}}{{u_i}^t{\boldsymbol{P}_{{\rm{MAX}}}}_i^t + \sum\limits_{k = 1}^{{N_w}} {\boldsymbol{P}_k^{wt} \leqslant {\boldsymbol{P}_D}^t} (1 - {\boldsymbol{R}_d}^t)} } \right\} \geqslant \beta ,\\ & {\boldsymbol{P}_{{\rm{MAX}}}}_i \leqslant \boldsymbol{P}_i^t \leqslant {\boldsymbol{P}_{{\rm{MIN}}}}_i,\\ & \boldsymbol{P}_i^{t - 1} - \boldsymbol{P}_i^t \leqslant \boldsymbol{P}_i^{{\rm{down}}},\\ & \boldsymbol{P}_i^t - \boldsymbol{P}_i^{t - 1} \leqslant \boldsymbol{P}_i^{{\rm{up}}},\\ & (\boldsymbol{U}_{\rm{i}}^{t - 1} - \boldsymbol{U}_{\rm{i}}^t)({\rm{Ton}}_i^{t - 1} - {\rm{MU}}{{\rm{T}}_i}) \geqslant 0,\\ & (\boldsymbol{U}_{\rm{i}}^t - \boldsymbol{U}_{\rm{i}}^{t - 1})( - {\rm{Toff}}_i^{t - 1} - {\rm{MD}}{{\rm{T}}_i}) \geqslant 0. \end{aligned} \right. $

(2)

式(1)、(2)中，N_w为并网的风机组数；$\boldsymbol{P}_k^{wt}$为风电机组k在时段t的有功出力，是一随机变量；$\boldsymbol{P}_D^t$为t时段的系统负荷需求量。${\boldsymbol{R}_u}^t \geqslant {\boldsymbol{P}_R}^t + us\% {\boldsymbol{P}_W}^t$，${\boldsymbol{R}_d}^t \geqslant ds\% {\boldsymbol{P}_W}^t$，${\boldsymbol{P}_W}_t = {k^w}\displaystyle\sum\limits_{k = 1}^{{N_w}} {\boldsymbol{P}_k^{wt}} $。式中，${\boldsymbol{R}_u}^t$、${\boldsymbol{R}_d}^t$分别为系统在t时刻系统的上备用容量和下备用容量；β为置信度水平，${\boldsymbol{P}_W}^t$表示t时刻风电场的额定容量；k^w为风机同时率系数(k^w≤1)，本文取近似值为1；${\boldsymbol{P}_R}^t$表示在t时刻系统的负荷旋转备用；u_s%、d_s%分别表示因风功率预测误差而所需旋转备用率；f₁为火电机组运行总成本；T表示一个调度周期内的时段数；N_g表示系统中发电机组的数量；${u_i}^t$为发电机组i在时段t的运行状态，若${u_i}^t = 1$，表示机组为开机运行状态，若${u_i}^t = 0$，则表示发电机组为停机状态；${\boldsymbol{P}_i^{gt}}$表示发电机组i在t时段的有功出力。${f\left( {\boldsymbol{P}_i^{gt}} \right)}$表示发电机组i在t时段的发电成本，${\boldsymbol{S}_i}^t$表示发电机组i在时段t的启动成本。f₂、f₃分别表示系统CO₂与SO₂排放量；α_ci、β_ci、γ_ci为机组i的污染气体CO₂的排放函数系数；α_si、β_si、γ_si为机组i的污染气体SO₂的排放函数系数。

2 混沌文化粒子群优化算法 2.1 文化算法

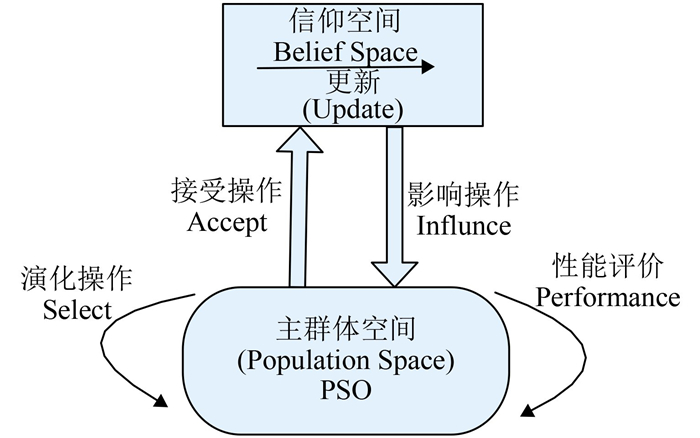
Reynolds于1994年最早提出了文化算法(Culture Algorithm，CA)，近年来引起了国外的关注^[5]。文化算法是多进化过程的算法，其具有宏观和微观两个方面。宏观方面是指文化算法信仰空间内部的更新进化；微观方面是指内部种群之间的进化，两者首先采用接收函数从种群空间中来获得经验知识，然后通过影响操作利用较好的经验知识来指导搜索过程，从而提高算法的搜索效率。其模型建立如图 1所示^[6]。

根据个体在进化过程中的信息和经验的不同情况可以将信仰空间分为以下5类：历史知识、形式知识、地势知识、领域知识以及形势知识。文献[7]提出了最常用的规范化知识与形势知识，即信仰空间为 < S, N > 结构，其中$\boldsymbol{S} = \left\{ {s_1^t,s_2^t,\boldsymbol{L},s_m^t} \right\}$表示形势知识，为最优个体集合，$s_i^t$为个体i在迭代次数为t时的最优个体，m为最优个体规模的大小；$\boldsymbol{N} = \left\langle {{\boldsymbol{X}_1},{\boldsymbol{X}_2},\boldsymbol{L},{\boldsymbol{X}_n}} \right\rangle $表示规范知识，是指当前信仰空间种群的可行解空间为；${\boldsymbol{X}_i} = [{\boldsymbol{I}_i},{\boldsymbol{L}_i},{\boldsymbol{U}_i}]$，${\boldsymbol{I}_i} = \{ {x_i}|{l_i} \leqslant {x_i} \leqslant {u_i}\} $，n为个体的变量，l_i、u_i分别为x_i的下限和上限，L_i、U_i分别是l_i、u_i对应的适应度值。

(1) 形势知识的更新规则

形势知识用来储存种群最优个体，本文选取最优个体s^t来更新信仰空间中的形势知识，即：

${s^{t + 1}} = \left\{ \begin{gathered} x_{{\text{best}}}^t,\;\;\;\;\;\;f(x_{{\text{best}}}^t) < f({s^t}); \hfill \\ {s^t},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他. \hfill \\ \end{gathered} \right.$

(3)

式(3)中，$x_{{\rm{best}}}^t$表示在第t次迭代时产生的最优个体。

(2) 规范知识的更新规则

假定个体i和个体k分别影响参数j的下边界和上边界，则其上下边界以及对应的适应度值可表示为：

$\left\{ \begin{array}{l} l_j^{t + 1} = \left\{ \begin{array}{l} x_{i,j}^t,\;\;x_{i,j}^t \le l_j^t\;\;{\rm{or}}\;\;{\rm{f}}\left( {x_j^t} \right) < L_j^t;\\ l_j^t,\;\;\;\;\;\;\;\;\;\;{\rm{其他}}{\rm{.}} \end{array} \right.\\ \boldsymbol{L}_j^{t + 1} = \left\{ \begin{array}{l} f\left( {x_j^t} \right),\;\;x_{i,j}^t \le l_j^t\;\;{\rm{or}}\;\;f\left( {x_i^t} \right) < \boldsymbol{L}_j^t;\\ L_j^t,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{其他}}{\rm{.}} \end{array} \right.\\ u_j^{t + 1} = \left\{ \begin{array}{l} x_{k,j}^t,\;\;\;x_{k,j}^t \ge u_j^t\;\;{\rm{or}}\;\;f\left( {x_k^t} \right) < U_j^t;\\ u_j^t,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{其他}}. \end{array} \right.\\ \boldsymbol{U}_j^{t + 1} = \left\{ \begin{array}{l} f\left( {x_K^t} \right),\;\;\;x_{k,j}^t \ge u_j^t\;\;{\rm{or}}\;\;f\left( {x_k^t} \right) < U_j^t;\\ U_j^t,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{其他}}. \end{array} \right. \end{array} \right.$

(4)

式(4)中，$l_j^t$、$\boldsymbol{L}_j^t$分别是指迭代次数为t时个体j的下边界及与之对应的适应度函数值；$u_j^t$、$\boldsymbol{U}_j^t$分别代表迭代次数为t时个体j的上边界及与之对应的适应度函数值。

(3) 接受函数(Accept)

本文利用Accept函数将主群体中的精英个体映射到信仰空间，而当前信仰空间中的个体也会受到Accept函数选择的影响。

(4) 影响函数(Influence)

影响函数表示信仰空间中的信息反过来引导主群体空间进行进一步演化的影响方式。本文使用规范知识调整个体变量步长，通过形势知识调整群体前进方向。定义如下

$ x_j^{t + 1} = \left\{ \begin{aligned} * x_{i,j}^t + \left| {(u_j^t - l_j^t)*{\rm{rand}}} \right|,\quad x_{i,j}^t < {s^t};\\ * x_{i,j}^t - \left| {(u_j^t - l_j^t)*{\rm{rand}}} \right|,\quad x_{i,j}^t > {s^t};\\ * x_{i,j}^t + \left| {(u_j^t - l_j^t)*{\rm{rand}}} \right|,\quad x_{i,j}^t = {s^t}. \end{aligned} \right. $

(5)

2.2 混沌粒子群算法

混沌(Chaos)指在确定性非线性系统中，不需附加随机因素可实现类似随机的行为。混沌运动是一种对初始条件具有敏感依赖性、永不重复性的非周期运动，是有序与无序的统一、确定性与随机性的统一^[8-10]。设粒子群种群规模为m，在变量区间随机生成初始值位置${\boldsymbol{X}_1} = {[{x_{11}},{x_{12}}, \ldots \ldots {\rm{,}}{x_{1N}}]^{\rm{T}}}$和速度${\boldsymbol{V}_1} = {[{v_{11}},{v_{12}}, \ldots \ldots {\rm{,}}{v_{1N}}]^{\rm{T}}}$，根据变量的区间，首先进行归一化处理，再将其映射到区间(0，1)之间。如将粒子位置${\boldsymbol{X}_1} = {[{x_{11}},{x_{12}}, \ldots \ldots {\rm{,}}{x_{1N}}]^{\rm{T}}}$映射到(0，1)区间$x'_{ij} = ({x_{ij}} - {x_{\min }})/({x_{\max }} - {x_{\min }})$。然后利用Logistic函数对归一化操作变量进行混沌操作$x{'^{(t + 1)}} = 4x{'^t}(1 - x{'^t})$，从而产生混沌变量，接着将其进行反归一化处理${x_{ij}} = {x_{\min }} + ({x_{\max }} - {x_{\min }})x_{ij}^t$，将产生的混沌变量映射到变量取值的区间。

混沌算法既不改变粒子群优化算法在初始化时的随机本质，又能利用混沌提高种群的搜索遍历性与多样性。

3 含风电场的多目标机组组合优化求解

利用CDPSO算法确定机组启停计划，通过CCPSO算法实现经济负荷分配，计算多目标函数中煤耗量及污染气体排放量，具体实现步骤如下.

(1) 输入各机组参数及各时段负荷数据，设置离散粒子种群的迭代次数I_TERMAX，种群个数N_P，学习因子c₁、c₂，最大速度V_max，随机初始化粒子位置与速度.

(2) 机组满足最小连续开停机时间约束以及备用容量约束时，利用CDPSO算法按照优先顺序法安排机组启停状态.

(3) 根据风速服从的Weibull分布进行风速概率抽样，求出相应的风电功率P_w.

(4) 采用Monte-Carlo随机模拟的方法校验含随机变量的约束条件，若否则转至步骤(2)，若是则利用CCPSO算法进行负荷经济分配.

(5) 初始化文化算法中主群体空间。对初始化粒子的速度和位置进行混沌操作，产生N个混沌变量，分别计算粒子多目标的适应度函数值；再对文化算法中信仰空间的规范知识以及形势知识 < S, N > 进行初始化.

(6) 利用Update更新函数对主群体空间中的父代种群进行更新操作；而信仰空间利用Influence影响函数对主群体空间的父代种群来生成子代种群.

(7) 父子种群中个体的数量为2N_P，利用竞争淘汰规则选取最为接近目标函数种群为新一代的种群N_P，采用权重系数法来计算多目标适应度函数值，再更新粒子个体极值p_best以及最优极值g_best.

(8) 在最优极值g_best的附近进行一定次数的混沌搜索操作，并计算多目标适应度函数的值，选取最接近全局最优值的个体来替换最优极值g_best的个体。再按照某种一定的概率来更新信仰空间中的规范知识以及形势知识 < S, N > .

(9) 判断收敛条件是否满足，若满足收敛条件则输出对应的发电费用以及各机组的开停机状态和最优有功功率P，然后计算各粒子适应度值，更新个体极值p_best与最优极值g_best，若不满足收敛条件，则转至步骤(6).

(10) 判断迭代次数是否满足最大迭代次数I_TERMAX，若是则迭代结束，若否则转至步骤(2)。

4 仿真结果及分析

本文采用Matlab进行仿真，CDPSO算法控制参数设置如下：初始化种群规模N_P=10，粒子维数为n=10，机组最大迭代次数I_termax=20，惯性权重变化范围为[0.4，0.9]，学习因子c₁=c₂=2。CCPSO算法控制参数设置如下：初始化种群规模N_P=200，粒子维数为n=10，机组最大迭代次数I_termax=2000，惯性权重变化范围[0.4，0.9]，学习因子c₁=c₂=2。

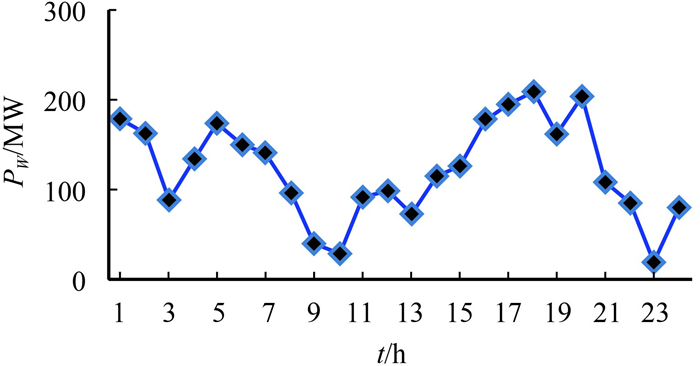
本文假设所研究的系统中含有1个风电场和10台火电机组，该风电场有并联运行的120台风力机组，每台风机的额定功率P_R为2 MW，额定总功率为240 MW，风电场在各时段预测的平均输出功率见图 2^[11]。设切入风速V_CI、切出风速V_CO、额定风速V_N分别为3 m/s、25 m/s、12 m/s。因风功率预测误差而所需旋转备用率u_s%、d_s%分别为额定风功率的20%。风机出力抽样样本为1 000，火电机组的机组特性参数与负荷数据及污染气体排放系数见文献[12-13]。

以一天24 h为优化调度周期，在不同置信度水平下，以总煤耗量、CO₂气体排放总量以及SO₂气体排放总量作为优化的目标函数，比较不同权重系数下对含风电场机组组合优化问题的影响。求解多目标优化问题的最优折中解时权重系数可以设为：ω₁=0.4、ω₂=0.3和ω₃=0.3，具体分析过程参见文献[11]，CO₂和SO₂的排放总量均较理想，而且符合工程实际节能较重于减排的情况。

由表 1可以看出，在不同的置信度水平下，整个调度周期内系统运行总成本随着置信度水平的提高而增多。因为随着置信度水平的提高，系统旋转备用容量不断增大，一方面其提高了整个系统运行的可靠性，另一方面增加了系统机组的启动成本。在输送相同功率的情况下，小容量机组的运行成本必然会有所增加，这就导致整个调度周期内系统运行总成本增大。此外，随着置信度水平提高，系统CO₂排放总量不断减小，这是因为在同等条件下，大容量机组较小容量机组相比CO₂排放量要多。在较高置信度水平条件下，小容量机组承担了部分负荷，从而降低了CO₂排放总量。而SO₂排放总量随着置信度水平的提高而不断增大，这是因为系统SO₂气体排放总量是由各个出力机组的SO₂气体排放系数所决定的，所以小容量机组的SO₂气体排放量比输送相同功率的大容量机组的SO₂气体排放量要多。而在较高置信度水平下小容量机组承担部分负荷，从而使得系统SO₂排放总量增大。

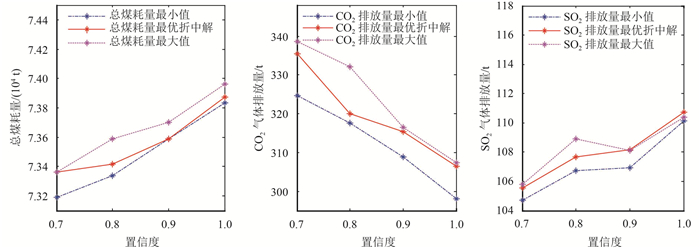
由表 2和图 3可知，对于节能减排条件下的计及风电场并网的多目标机组组合优化，随着约束条件中置信度水平减小，优化后系统CO₂气体排放总量有所增加，而机组总的运行成本和系统SO₂气体排放总量相对减少。这就意味着置信度水平的高低与系统运行的经济性和稳定性有关。因此，在合理的置信度水平条件下，通过改变系统运行总成本与污染气体排放总量之间的权重系数，可以使得系统运行经济性最优和环保性最优进行折中。在较高置信度水平的条件下，提高了系统运行的稳定性，有效降低污染气体排放总量，提高了环保效益，但牺牲了系统运行的经济性，增加了机组运行总成本。反之，则降低了系统安全可靠性和环保效益，但是提高了系统的经济性。因此，选取适当置信度水平是既能保证经济最优同时也能使环境污染最小的多目标优化问题的关键。

5 结论

本文研究了计及风电场并网的电力系统机组组合优化问题，建立了基于机会约束规划的含风电场机组组合优化模型，目标函数中考虑了机组总运行成本以及污染气体的排放量。提出采用混沌文化粒子群算法对标准粒子群算法进行改进，利用混沌算法提高种群的搜索遍历性与多样性以及文化算法存在双层进化机制可以更精准反映进化过程，改善粒子群算法初始化随机性以及易陷入局部最优的缺陷。利用混沌离散粒子群优化算法对机组进行启停安排，通过混沌文化粒子群优化算法实现经济负荷分配；10机系统的算例证明，合适的置信度水平既能保证系统的经济性也能使环保效益最优，调度人员可以根据实际情况协调风险、利润以及环境因素指标，以实现最优化决策。