2. 深圳市市政设计研究院有限公司, 广东 深圳 518029 ;
3. 广东工业大学 土木与交通工程学院, 广东 广州 510006
2. Shenzhen Municipal Design and Research Institute Co. Ltd., Shenzhen 518029, China ;
3. School of Civil and Transportation Engineering, Guangdong University of Technology, Guangzhou 510006, China
由于我国经济发达地区如珠三角地区存在着大面积的软土区域,该土层具有含水量高、渗透性差、强度低、孔隙大、密度低并具一定的结构性的特点,而且其分布往往不均匀,因而若对软土特性认识不足,选择处理方法不当,技术控制不严,就会在施工过程中出现地基失稳而滑动,并产生较大的不均匀沉降,以及持续长时间的较大工后沉降,不能满足工程设计的要求,因此合理有效地处理这种软土地基已成为我国珠三角地区进一步快速发展需要解决的一个关键问题.
在真空预压基础上发展起来的真空–堆载联合预压技术不仅能满足上述需求,而且适合大面积软土地基处理和一些对地基承载力要求高的建筑物场地的需要.与传统预压方法相比,它能大大缩短施工工期;同时由于真空预压使土体向内侧收缩,而堆载预压使土体向外侧扩张,从而增强了堆载的稳定性,具有显著的经济效应.因此对其使用也越来越广泛,相应的深入研究迫在眉睫[1-4].刘汉龙、李豪和彭劼[5]利用室内实验从微观角度解释真空预压以及真空–堆载联合预压的加固机理;吴跃东和赵维炳[6]采用真空–堆载联合预压处理京珠高速公路地基,发现抽真空能引起软土的曼德尔现象;高晖[7]采用Duncan-Chang模型,利用Abaqus对堆载预压软基进行了沉降计算;江辉煌[8]对二维单井轴对称固结问题进行了研究,认为大变形的固结速率小于小变形的.本文依托珠海横琴岛多联供燃气能源站项目的真空–堆载联合预压处理地基的工程监测资料,借用Abaqus有限元软件对其加固机理进行较深入的研究,获得了一些新的认识.
1 工程概述本文所采用的工程实例为珠海横琴岛多联供燃气能源站的软基处理项目,其地基处理共分为A、B、C、D、E、F、G和H等7个大区,采用了真空–堆载联合预压的方法进行地基处理.水平排水系统采用500 mm厚的砂垫层,竖向排水系统采用间距为1 m的C型塑料排水板,塑料排水板呈正方形布置,排水板打设深度为25 m.要求在抽真空时保持真空度为–85 kPa.
场地地貌属于珠江三角洲海陆交互冲积平原,区内河网发育,鱼塘密布.根据钻孔揭露,软基处理技术场地第四系覆盖层主要有人工填土、海积淤泥、淤泥质土、粉质黏土、砂土层以及残积砂质黏性土.这种土质由于沉积历史较短,具有含水率高、渗透性差、强度低、孔隙大的特点.其各层土主要土工参数如表 1所示.
| 表 1 土体的物理力学参数 Table 1 Physical and mechanical parameters of soils |
采用塑料排水板进行地基处理严格来讲应采用三维固结有限元来进行计算,但由于塑料排水板及因其造成的涂抹区的存在会导致三维固结模型划分的单元大为增加,计算非常复杂.同时三维计算所需的土工参数很难通过常规实验得到,计算精度难以控制.故而本文使用二维平面应变有限元建模分析.
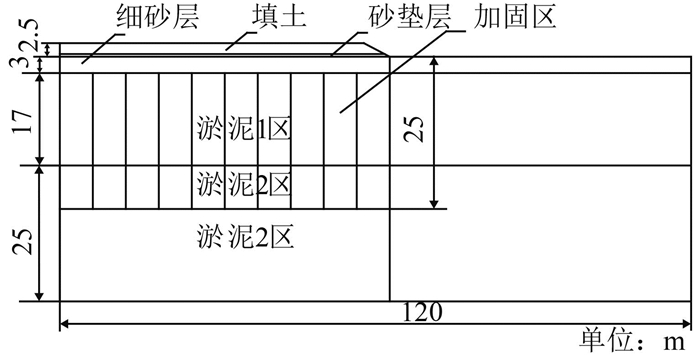
2.1 几何建模该实例中加固区域宽度为120 m,利用结构的对称性,取加固区一半作分析,中心为对称轴.因此根据土质条件及真空预压的影响范围,取地基的计算宽度为120 m,其中60 m是加固区,60 m是加固区以外的影响区.加固区塑料排水板的打设深度为25 m.按土质条件及真空预压的影响深度,向下计算深度取45 m.其断面图如图 1所示.土体单元采用耦合的孔隙流体/应力耦合单元CPE4P[9-10],Abaqus中的土体渗流与耦合分析过程包括了孔隙介质的有效应力原理、土体渗流变形耦合的本构方程以及达西定律,从而能够充分地模拟土体渗透变形性状[11-12].
|
图 1 计算范围 Figure 1 Calculating scope |
3 m的细砂层采用摩尔-库伦破坏准则.淤泥1区和淤泥2区采用修正剑桥模型[13],其计算参数共有5个,分别是土体泊松比ν、膨胀指标κ、压缩指标λ、破坏比M以及初始孔隙比e0,如表 1所示.膨胀指标和压缩指标可分别用等向固结试验或三轴压缩试验确定,破坏比M即为土体破坏时p'-q直线的斜率.为了简化,对模型做了以下基本假设:
(1) 同一土层为均匀连续并且为各向同性的.
(2) 土体为完全饱和,孔隙水渗流符合达西定律.
2.2 砂井地基参数的选取依据等效固结度的原则,目前对砂井的处理方法主要有两类:一是将砂井加固的地基简化为渗透系数较大的均质地基(天然地基)来进行处理[14-15];二是将砂井地基转化为平面砂墙,将砂墙间距以及渗透系数进行调整来简化计算[16].
在一般的工程设计中,通常是把砂井群地基简化为单井地基来进行处理,利用轴对称固结情况分析其固结过程,但在有限元模拟计算中通常将三维空间问题转化为二维平面应变问题,其转化前提是保证三维空间问题的平均固结度等于二维平面应变问题的平均固结度.其方法就是将原来沿着路基、堤坝等建筑物的纵向有一定间隔分布的砂井等效成沿着纵向连续分布的砂墙,即把原来的砂井地基等效为打设了一排排砂墙的地基,而这种砂墙地基就可以当作平面应变问题来分析.
赵维炳[10]从巴隆固结理论出发,在考虑涂抹效应的同时也考虑了地基的侧向渗透变形和竖向渗流变形的影响,得到了砂墙地基的双向渗流平均固结度表达式,并在平均固结度相等的原则下,通过调整砂墙间距和渗透系数将三维问题转化为二维问题来简化计算,推导出的计算公式如下:
| ${k_{xp}} = {D_x}{k_{ra}}.$ | (1) |
| ${k_{zp}} = {D_z}{k_{za}}.$ | (2) |
式中,
Dx为水平向渗透系数的调整系数:
| ${D_x} = \frac{{4{{\left( {{n_p} - {s_p}} \right)}^2}\left( {1 + \nu } \right){L^2}}}{{9n_p^2{\mu _a} - 12\beta \left( {{n_p} - {s_p}} \right)\left( {{s_p} - 1} \right)\left( {1 + \nu } \right){L^2}}}.$ | (3) |
Dz为竖直向渗透系数的调整系数:
| ${D_z} = \frac{{2\left( {1 + \nu } \right)}}{3}.$ | (4) |
式中,
其中
在本文有限元计算中假设砂井间距2B=4.8 m,s=1.2,sp=1.2,β=7.0。通过式(1)~(4)计算得到的砂井地基调整参数如表 2所示。
| 表 2 排水砂井参数调整 Table 2 Adjusting parameters of drainage sand wells |
模型的边界条件如下:地基底部为不排水边界,且X、Y方向为固定约束;地基左右两边均为不透水边界,X方向为固定约束,Y方向为自由;地基表面不施加位移约束,为完全自由面。加固区外地基与大气相连通,为孔压为0的自由排水边界。
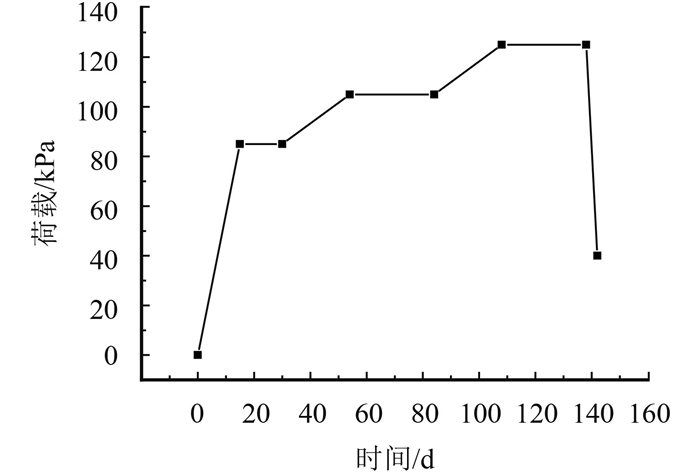
2.4 荷载区域的确定真空–堆载联合预压的加载分为真空荷载和堆载的施加.真空荷载加载是通过让加固区表面以及所转化的砂墙各点的孔压按线性从0变化为–85 kPa,然后保持不变来实现。而堆载则是按实际加载曲线分级施加上去。其真空荷载与堆载的加载过程如图 2所示。Abaqus提供了step分析模块用于模拟整个过程。本文设计了9个分析步骤模拟整个过程,分别为1个geo和8个soil(Trasient),前者是用于重力与地应力平衡的荷载步,后者用于软土沉降固结分析的过程。(1) 为初始地应力平衡;(2) 为将砂垫层置于地基表面,时间为3 d;(3) 为施加真空荷载至–85 kPa,时间为15 d;(4) 为恒载固结,时间为15 d;(5) 为施加第一级堆载,时间为20 d;(6) 为恒载固结,时间为34 d;(7) 为施加第二级堆载,时间为20 d;(8) 为恒载固结,时间为34 d;(9) 5 d卸真空。
|
图 2 荷载-时间曲线 Figure 2 Load-time curve |
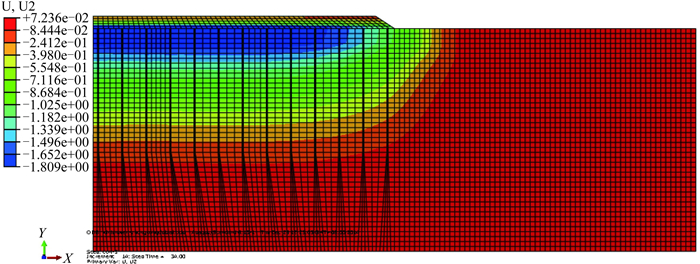
图 3所示为卸真空前真空–堆载联合预压的地基沉降计算云图,可以看出加固区土体表面中心点处的沉降最大,加固区地基表面的平均沉降约为1.8 m,整个沉降等值线呈锅状,且地基土体的沉降随着深度的增加而减小;而未加固区地基表面的影响范围大致为15 m,其地基表面的平均沉降为70 cm。加固区边缘处的沉降比中心点处的小,主要是由于加固区边缘受真空度和堆载的影响较小,导致加固区地基土体边缘沉降量小。
|
图 3 卸真空前真空–堆载联合预压地基沉降计算云图 Figure 3 Soil settlement contours under vacuum-surcharge preloading before unloading |
图 4所示为实测的场地中心区域沉降过程线与有限元计算得到的场地中心区域沉降过程线。从图 4可以看出,二者曲线的发展趋势基本趋于一致;有限元计算得到的沉降过程线与实测得到的沉降过程线略有偏差,地基表面该位置141 d沉降量的有限元计算值与实测值分别为1.80 m和1.9 m。现有计算模型、计算参数与实际情况的偏差以及没考虑蠕变、只在小变形情况下计算沉降可能是偏差产生的主要原因。

|
图 4 计算与实测场地地基表面沉降过程线 Figure 4 Comparing settlement calculation results with settlement measuring results as time proceeding |
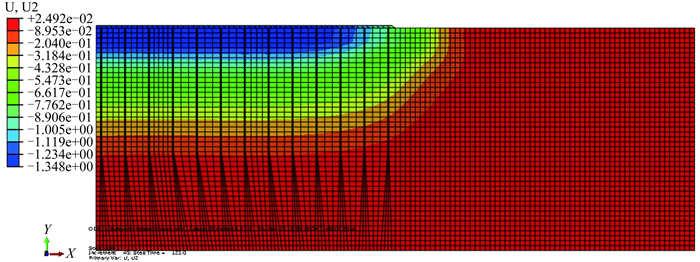
图 5为上述模型在单独采用真空预压进行数值模拟情况下所得到的沉降计算云图,可以看出,真空预压的沉降等值迹线与图 3的基本相似,最大沉降同样位于地基土体中心区域,且其沉降值从中间向两边缘逐步递减,沉降值从上向下逐步递减,符合实际情况。
|
图 5 卸真空前85 kPa真空预压地基沉降计算云图 Figure 5 Soil settlement contours under 85 kPa vacuum preloading before unloading |
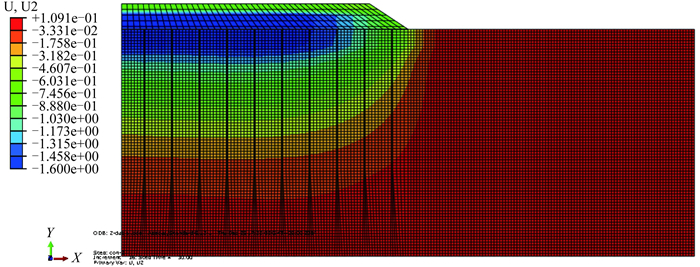
图 6为将真空荷载等效为85 kPa的堆载之后,与原有堆载40 kPa相加,得到125 kPa堆载预压下的沉降计算云图。从图 6可以看出在125 kPa的堆载作用下,地基土体同样呈现中心区域沉降大两边沉降小、沉降值从上向下逐步递减的特点,且其对地表未加固区边缘的影响区域明显不如真空预压大。
|
图 6 卸载前125 kPa堆载预压沉降计算云图 Figure 6 Soil settlement contours under 125 kPa surcharge preloading before unloading |
将图 3与图 6进行对比分析可以看出以下几方面不同。一是在同样的地表荷载下,真空–堆载联合预压导致的地基沉降较堆载预压产生的地基沉降值大,说明相对于堆载预压,真空–堆载联合预压的加固效果更好。二是真空–堆载联合预压与125 kPa堆载预压对地基的作用效果是完全不同的,真空–堆载联合预压不仅作用效果更明显,而且地基沉降更均匀。也说明将真空预压等效为等重上覆土重来计算其固结度是存在问题的,因为堆载预压导致地基k0固结,而真空预压导致地基三维等向固结。
对比图 3、图 5与图 6可知,单纯从地基沉降角度,真空预压导致地基的固结效果最好,但真空预压产生的荷载有限,常常需在真空预压的基础上叠加堆载以满足实际荷载大的工程地基固结的需求;真空预压导致地基向内侧移,而堆载导致地基向外侧移,两者在地基侧移上有一定程度相互抵消,有利于地基的侧移变形稳定。
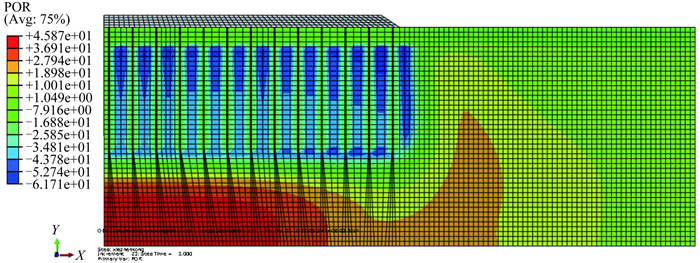
3.3 孔隙水压力分析图 7所示为真空–堆载联合预压处理地基的孔隙水压力分布云图。从图 7的孔隙水压力分布云图可以看出,由于3 m厚细砂层与平面砂墙、砂垫层的渗透系数差别不大,造成卸去真空荷载后这些区域的孔隙水压力消散很快且大小基本一致。在塑料排水板加固区范围内,卸去真空荷载后,由于平面砂墙的存在,在相邻两砂墙之间土体孔隙水压力呈条纹状分布,离砂墙最远处土体的负孔压绝对值最大,向着砂墙方向土体的负孔压绝对值逐渐减小;从竖向距离来讲,离排水板顶部排水砂层的距离越远,土体中的孔隙水压力越大。由于存在堆载的压力,在塑料排水板底部以下土体中的孔隙水压力为正值。
|
图 7 真空–堆载联合预压孔隙水压力分布云图 Figure 7 Soil pore water pressure contours under 125 kPa vacuum-surcharge preloading after unloading |
此外,由于该工程实例采用了排水板作为竖向排水通道,其井阻相对砂井较小[7],故本文模拟中未考虑其井阻的存在,这与实际情况有所不符,故而造成孔隙水压力的分布存在一定的误差。
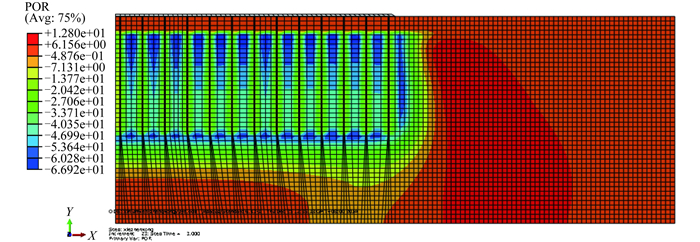
图 8为85 kPa真空预压后计算得到的孔隙水压力分布云图,卸去真空荷载后,图 8与图 7的孔隙水压力分布云图基本相似,只是由于缺少40 kPa堆载的影响,图 8中加固区内负孔隙水压力的绝对值更大一些,而排水板底部以下土体中的孔隙水压力的正值更小一些。
|
图 8 85 kPa真空预压孔隙水压力分布云图 Figure 8 Soil pore water pressure contours under 85 kPa vacuum preloading after unloading |
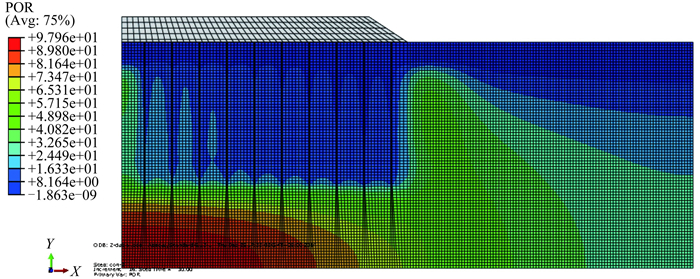
图 9为将85 kPa的真空荷载等效为等量重85 kPa的堆载后与原有的40 kPa堆载相加之后得到的125 kPa堆载预压的孔隙水压力分布云图。从图 9可看出,在地基土体的3 m厚细砂层,由于渗透系数较大,故而孔隙水压力消散得快,接近于0。在排水板加固区的范围,从水平距离来讲,距离中心区越近,堆载效果越好,正的超孔隙水压力越大,因此孔隙水压力也越大,而在之后固结过程中孔隙水压力也未能及时消散,这就导致距离中心区越近,孔隙水压力越大,而在堆载边缘位置土体中孔隙水压力相对较小;从竖向距离来讲,离排水板顶部排水砂层的距离越远,土体中的孔隙水压力越大。而在排水板底部以下的土体中,由于堆载及差的排水条件,土体中积聚了最大的孔隙水压力。
|
图 9 125 kPa堆载预压孔隙水压力分布云图 Figure 9 Soil pore water pressure contours under 125 kPa surcharge preloading |
图 7与图 8二者的孔隙水压力等值迹线基本相似,但相比之下真空预压相同位置的负孔隙水压力的绝对值更大。之所以这样,从加固机理来分析,真空荷载是直接作用在土体的水气流体上,直接产生负的孔隙水压力,导致孔隙水压力的减少,根据有效应力原理,总应力不变,有效应力的增加量就是孔隙水压力的减少量,这即为真空预压加固的基本原理;而真空–堆载联合预压不仅存在真空预压作用,也存在堆载作用,其中真空荷载会产生负的超孔隙水压力,结合图 9的分析可知堆载作用在土骨架上会产生正的超孔隙水压力,二者共同作用使水力梯度比单独作用的大,从而使孔隙水能够更快地流出,这最后导致了真空–堆载联合预压负的孔隙水压力的绝对值小于真空预压的。因此,正是加固机理的区别导致真空预压的负孔隙水压力的绝对值更大。也说明了堆载预压产生的孔隙水压力对孔隙水是“挤出”,而真空预压对孔隙水则是“吸出”,故而在二者共同作用时,它们的孔隙水压力不是直接相互抵消的,而是形成更大的水力梯度加快孔隙水的渗透排出。
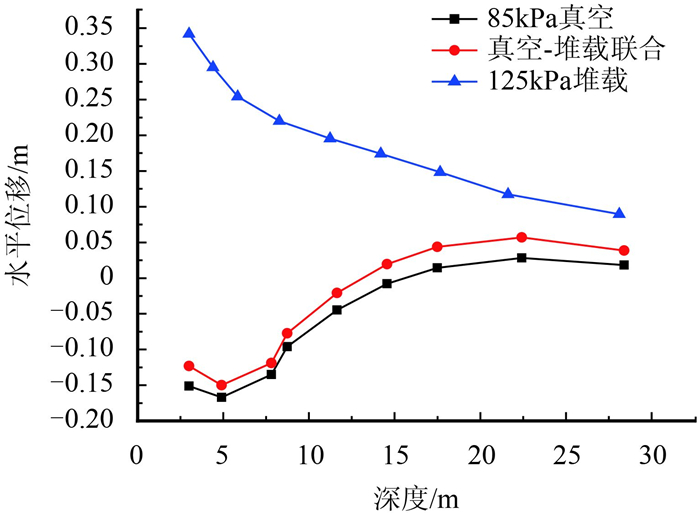
3.4 水平向地基变形分析图 10为85 kPa真空预压、真空–堆载联合预压以及125 kPa堆载预压在不同深度处的水平位移图,其中正的水平位移为向外扩张,负的水平位移为向内收缩。从图 10中可以看出,在加固区边缘,堆载预压的水平位移为向外扩张,真空预压以及真空–堆载联合预压在此处的水平位移为向内收缩的,且真空预压大于真空–堆载联合预压的向内收缩的幅度。
|
图 10 3种预压方式加固区边缘不同深度处的水平位移 Figure 10 The curves of soil horizontal displacement with depth for three preloading types around the preloading area edge |
图 11所示为85 kPa真空预压地基的水平向位移的分布云图,在图 11上部红色区域存在向外扩张的侧向变形,是由于其位于3 m厚的细砂层,在仿真模拟时,将砂垫层的作用施加于其上,故而在该处存在不大的指向未加固区的水平位移。从图 11及图 10中可以看出,其水平位移主要发生在加固区边缘,在边缘以下3~16 m的淤泥深度范围内存在向内压缩的水平位移,在边缘16 m以下淤泥深度范围存在着较小的向外伸展的水平位移。在加固区内部,如图 11所示,在横向向着加固区的内部方向,依次存在着边缘的向内收缩区、靠近边缘的土体伸展区以及靠近中部的大面积向内收缩区,靠近边缘的土体伸展区主要是由于两侧区域土体的收缩给出了其水平变形空间而引起的。总的来说,真空预压的水平位移主要是指向加固区内部,为向内压缩的。
|
图 11 85 kPa真空预压水平位移计算云图 Figure 11 Horizontal displacement contours of 85 kPa vacuum preloading |
图 12所示为等效为125 kPa的堆载预压,从图 12以及图 10可以看出,其整个水平位移图均为正值,即为向外扩张态势,最大的水平位移发生在堆载边缘处,加固区内部越靠近堆载边缘土体的水平位移越大;沿深度方向,随深度增加加固区土体的水平位移逐步衰弱,与实际监测情况相符。这说明了堆载预压导致的水平位移指向未加固区,为向外扩张的。

|
图 12 125 kPa堆载预压水平位移计算云图 Figure 12 Horizontal displacement contours of 125 kPa surcharge preloading |
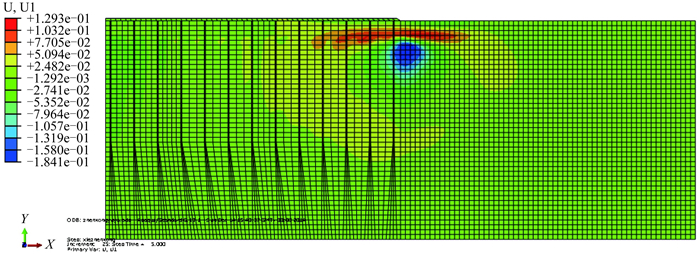
图 13所示为真空–堆载联合预压地基的水平向位移的分布云图。图 13的水平位移等值迹线反映的是计算断面的整体位移情况。与图 11相似,图 13的红色区域也是由于其位于3 m厚的细砂层,有堆载施加在其上,故而在该处存在指向未加固区的水平位移。从图 10和图 13可以看出,在加固区边缘附近处的地基土体的水平位移最大,在边缘以下3~13 m的淤泥深度范围内存在向内压缩的水平位移,在边缘13 m以下淤泥深度范围存在着较小的向外伸展的水平位移。在加固区内部,如图 13所示,在横向向着加固区的内部方向,依次存在着边缘的向内收缩区、靠近边缘的土体伸展区以及靠近中部的大面积向内收缩区,只不过由于堆载的影响使土体伸展区域变大,特别是减小了靠近中部的向内收缩区的大小,也最终减小了土体向内收缩值的大小。
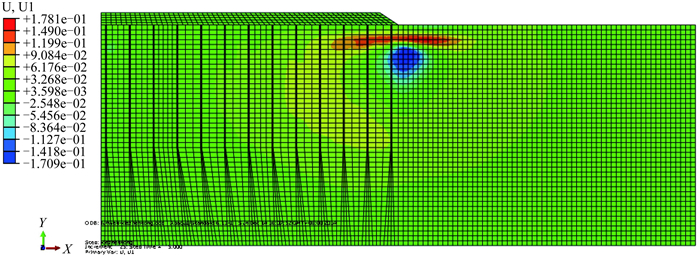
|
图 13 真空-堆载联合预压水平位移计算云图 Figure 13 Horizontal displacement contours of vacuum combined with surcharge preloading |
结合图 10、图 11及图 13可知,在真空–堆载联合作用下,相应真空荷载所占的比例较大,总的来讲加固区水平位移以向内收缩为主,说明此时真空预压占主导地位,由于堆载的影响减小了土体向内收缩的程度,说明真空–堆载联合预压能充分结合真空预压与堆载预压的优点,确保土体的安全稳定以及填土的快速堆载。
4 结论(1) 在本文的真空–堆载联合预压处理软土地基实例中,在固结度等效的前提下,将塑料排水板地基等效成砂墙地基,采用修正剑桥模型进行有限元计算,之后通过监测沉降数据与计算所得沉降数据进行对比分析可以发现二者的结果是较为吻合的。这说明利用Abaqus有限元进行淤泥类土体的沉降计算是切实可行的。
(2) 通过模拟对比分析真空预压、堆载预压以及真空–堆载联合预压的孔隙水压力计算云图,发现真空预压的孔隙水是被“吸出”,堆载预压的孔隙水是被“挤出”,而真空–堆载预压是在二者的共同作用下,产生更大的水力梯度,使孔隙水更快渗流出,从而证实了是由于加固机理的不同导致了这3种地基处理方法加固效果的区别。
(3) 对真空预压地基,在加固区内部,如图 11所示,在横向向着加固区的内部方向,依次存在着边缘的向内收缩区、靠近边缘的向外伸展区以及靠近中部的大面积向内收缩区,夹在中间的土体伸展区主要是由于两侧区域土体的收缩给出了其水平变形空间而引起的;同理,在真空预压地基的四周以下土体,也依次存在着向内收缩范围及向外伸展范围。这是一个新的认识,所以以往认为真空预压加固区内部土体均处于向内收缩状态的观点是值得讨论的。
(4) 通过模拟对比真空预压、堆载预压以及真空–堆载联合预压,证实相比前面二者,真空–堆载联合预压对地基处理的加固效果更好;并且由于真空预压主要使土体水平位移发生向内压缩,堆载预压使土体水平位移发生向外扩张,因此在二者联合作用下能充分结合真空预压与堆载预压的优点,既能够保证加固效果,又能确保土体侧移的安全稳定以及填土的快速堆载。
| [1] |
陈环, 鲍秀清. 负压条件下土的固结有效应力[J].
岩土工程学报, 1984 (5): 39-47.
CHEN H, BAO X Q. Consolidation effective stress of soil under vacuum condition[J]. Chinese Journal of Geotechnical Engineering, 1984 (5): 39-47. |
| [2] |
沈珠江, 陆瞬英. 软土地基真空排水预压的固结变形分析[J].
岩土工程学报, 1986, 8 (3): 7-15.
SHEN Z J, LU S Y. Analysis of consolidation and deformation of soft subsoil under vacuum[J]. Chinese Journal of Geotechnical Engineering, 1986, 8 (3): 7-15. |
| [3] |
陈兰云, 朱建才. 真空预压影响区安全措施有限元分析[J].
岩石力学与工程学报, 2005, 24 (2): 5712-5715.
CHEN L Y, ZHU J C. Finite element analysis of safety measures for affected soft ground area by vacuum preloading[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24 (2): 5712-5715. |
| [4] | KHAN A Q, MESRI G. Vacuum distribution with depth in vertical drains and soil during preloading[J]. Geomechanics and Engineering, 2014, 6 (4): 377-389. DOI: 10.12989/gae.2014.6.4.377. |
| [5] |
刘汉龙, 李豪, 彭劼. 真空-堆载联合预压加固软基室内试验研究[J].
岩土工程学报, 2004, 26 (1): 145-149.
LIU H L, LI H, PENG J. Laboratory test on vacuum preloading combined with surcharge[J]. Chinese Journal of Geotechnical Engineering, 2004, 26 (1): 145-149. |
| [6] |
吴跃东, 赵维炳. 真空-堆载预压加固高速公路软基的研究[J].
河海大学学报, 1999, 27 (6): 77-81.
WU Y D, ZHAO W B. Study on strengthening of soft foundations of express highway by vacuum-surcharge preloading[J]. Journal of Hehai University, 1999, 27 (6): 77-81. |
| [7] | 高辉.Abaqus在软基固结过程分析中的应用研究[D].武汉:武汉理工大学土木工程与建筑学院, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10497-2006061175.htm |
| [8] | 江辉煌.砂井处理超软基地基的固结计算[D].北京:中国铁道科学研究院, 2009. |
| [9] | 王金昌, 陈页开. ABAQUS在土木工程中的应用[M]. 2006. |
| [10] | 费康, 张建伟. ABAQUS在岩土工程中的应用[M]. 北京: 中国水利水电出版社, 2010. |
| [11] | 梁磊, 真空-堆载联合预压加固软土地基的应用研究及数值模拟[D].广州:广东工业大学土木与交通工程学院, 2009. |
| [12] | 钱家欢, 殷宗泽. 土工原理与计算[M]. 二版. 北京: 中国水利水电出版社, 1996. |
| [13] |
杨雪强, 张建龙, 刘勇健. 修正Cam模型与Lade-Duncan屈服准则的合理耦合[J].
广东工业大学学报, 2008, 25 (3): 90-94.
YANG X Q, ZHANG J L, LIU Y J. Combination of modified Cam-Clay model and Lade-Duncan yield criterion[J]. Journal of Guangdong University of Technology, 2008, 25 (3): 90-94. |
| [14] | 赵维炳, 施建勇. 软土固结与流变[M]. 南京: 河海大学出版社, 1996. |
| [15] |
李豪, 高玉峰, 刘汉龙, 等. 真空-堆载联合预压加固软基简化计算方法[J].
岩土工程学报, 2003, 25 (1): 58-62.
LI H, GAO Y F, LIU H L, et al. Simplified method for subsoil improved by vacuum combined with surcharge preloading[J]. Chinese Journal of Geotechnical Engineering, 2003, 25 (1): 58-62. |
| [16] |
赵维炳, 陈永辉, 龚友平. 平面应变有限元分析中砂井的处理方法[J].
水利学报, 1998 (6): 53-57.
ZHAO W B, CHEN Y H, GONG Y P. Methodology for modeling sand-drain ground in plain strain analysis[J]. Journal of Hydraulic Engineering, 1998 (6): 53-57. |
 2017, Vol. 34
2017, Vol. 34

