2. 广东工业大学 可拓学与创新方法研究所, 广东 广州 510006 ;
3. 广东工业大学 广东省创新方法与决策管理系统重点实验室, 广东 广州 510006
2. Research Institute of Extenics and Innovation Methods, Guangdong University of Technology, Guangdong University of Technology, Guangzhou 510006, China ;
3. Key Laboratory of Innovation Method and Decision Management System of Guangdong Province, Guangdong University of Technology, Guangzhou 510006, China
产品的创新是提高企业竞争力的保障。随着竞争和科技不断的发展,越来越多的学者开始关注创新方法的研究,我国学者蔡文教授经过深入研究,挖掘创新的本质,创立了一门横断性学科--可拓学。可拓学从创立至今已经发展了30多个年头,其发展逐步进入到应用阶段的研究[1-2]。目前可拓学的基本理论已经用于概念设计[3-6]、数据挖掘[7-8]、检测[9-10]、识别[11-12]、可拓策略[13-16]等方面,其在解决矛盾问题方面提供了有效的方法手段。
本文主要根据需求分析及目前条件限制所产生的矛盾问题,采用可拓学菱形思维方式,按照可拓创新过程,对矛盾问题的目标和条件进行拓展分析、可拓变换及相关分析,逐步形成新的创新方案。
1 可拓创新概念设计基于可拓学的产品构思实际上就是产品的概念设计,从本质上就是解决矛盾问题的过程。从用户的需求及已有的产品出发构思新的产品及解决方案,其具体的解决过程如下:
(1)从用户对产品功能的需求出发,根据需求分析,目前的产品无法满足这一功能需求,从而构成该问题的目标G及条件L,则其矛盾问题为
| $P = G * L ,$ |
并对目标G和条件L进行形式化表达。
(2)拓展分析。根据发散分析、相关分析、蕴含分析及可扩分析等方法,对目标及条件的特征及量值进行拓展,并对基元进行重新组合,从而找到解决矛盾的方法。
(3)可拓变换。根据分解、置换、增删、扩缩等变换,由原基元变换成新基元,从而形成解决问题的创新方法。
(4)优度评价。用以判断解决矛盾方案好坏的方法。通过建立关联函数来定量地分析各特征与目标值之间的关系,计算优度,对各方案进行评价。
上述过程中,拓展分析、可拓变换及优度评价的具体过程见文献[1]。
2 实例分析打印机是目前普遍使用的家庭及办公用品,打印机型号各异。然而在一般的办公室及家庭,由于受空间限制,其规格型号一般都适合于A4及其以下纸张,故适合A4打印纸的打印机更加普遍。在实际使用中,经常遇到需要将两页内容打印在A3纸上的情况,目前的解决方法:一是找适合A3打印纸的打印机输出,但是普通的办公室少有这样的设备;二是将内容打印在两张A4打印纸上,然后再复印在A3打印纸上,这不仅浪费了时间还浪费了两张打印纸。在现有的A4打印机上有效无误地实现在A3纸上的打印,则既节约了用户的成本,又减少资源的浪费。目前并没有相关的研究及产品能够很好地解决这个矛盾。
本文将利用可拓创新方法,研究这个矛盾问题,并提出解决方案,其具体过程如下:
步骤1 根据用户需求,将问题的目标和条件进行形式化描述。
本问题需求目标为在A4纸打印机上将内容打印到A3规格打印纸上,其具体的形式化描述如下
| $ G = \left[ {\begin{array}{*{20}{c}} {打\;\;印,}&{支配对象,}&{文字图像} \\ {}&{工\;\;具,}&{打印机{\text{B}}} \\ {}&{地\;\;点,}&{{\text{A3打印纸}}} \end{array}} \right]. $ |
而目前的条件是现有的打印机仅适合A4打印纸,而A3打印纸的尺寸远远超过打印机所允许的纸张规格,其形式化描述如下
| $ \begin{gathered} {L_1} = \left[ {\begin{array}{*{20}{c}} {{\text{打印机B,}}}&{打印幅面,}&{{\text{A4打印机}}} \\ {}&{进纸盒尺寸,}&{{a_1} \times {b_1}} \end{array}} \right] \wedge \hfill \\ {L_2} = \left[ {\begin{array}{*{20}{c}} {{\text{A}}3打印纸,}&{长度,}&{{a_2}} \\ {}&{宽度,}&{{b_2}} \end{array}} \right]. \hfill \\ \end{gathered} $ |
根据一般规格的打印机B可知,进纸盒尺寸可调节,211 mm≤a1≤356 mm,147 mm≤b1≤216 mm,即a1∈(211,356),b1∈(147,216)。A3打印纸规格a2=420 mm,b2=297 mm。根据分析,打印纸的尺寸与进纸盒尺寸相关,按照打印机B使用A4纸张居多,故设打印纸在宽度为210 mm和长度297 mm为最优点。下面以打印纸宽度进行分析,说明该问题的矛盾性。
根据基本要求的区间和质变的区间相同,对宽度尺寸,有限区间x=〈a,b〉=〈147,216〉,其最优点M=210 mm,则其宽度方向的关联函数为
| $ k(x) = \left\{ \begin{aligned} & {\frac{{x - a}}{{M - a}}},\;\;\;\;\;x \leqslant M;\\ & {\frac{{b - x}}{{b - M}}},\;\;\;\;\;x \geqslant M. \end{aligned} \right. $ |
即为
| $k(x) = \left\{ \begin{aligned} & \frac{{x - 147}}{{210 - 147}}{\rm{ = }}\frac{{x - 147}}{{63}},\;\;\;\;\;x \leqslant 210;\\ & \frac{{216 - x}}{{216 - 210}}{\rm{ = }}\frac{{216 - x}}{6},\;\;\;\;\;x \geqslant 210. \end{aligned} \right.$ | (1) |
当x=297 mm时,代入式(1),k(x)=–13.5 < 0。同理在长度方向上,进行同样的推导,其关联函数仍然是负的,很明显,这是一个矛盾问题。
步骤2 根据该问题的需要,目标需求不能变换,只能对矛盾问题的条件进行分析。
根据上述问题分析,进行相关分析可知
| $ \begin{aligned} & \left( \! {{\rm{A}}3 {\small{\text{打印纸,长度}}},{a_2}} \! \right) \! \sim \! \left\{ \begin{array}{l} \!\!\!\! \left({ {\small{\text{打印机B}}},{\small{\text{打印幅面}}},{\rm{A}}4} \right)\\ \!\!\!\! \left({ {\small{\text{打印机B}}},{\small{\text{进纸盒尺寸}}},{a_1} \! \times \! {b_1}} \right), \end{array} \right.\\ & \left( \! {{\rm{A}}3 {\small{\text{打印纸,长度}}},{b_2}} \! \right) \! \sim \! \left\{ \begin{array}{l} \!\!\!\! \left({ {\small{\text{打印机B}}},{\small{\text{打印幅面}}},{\rm{A}}4} \right)\\ \!\!\!\! \left({ {\small{\text{打印机B}}},{\small{\text{进纸盒尺寸}}},{a_1} \! \times \! {b_1}} \right), \end{array} \right. \end{aligned} $ |
故对A3打印纸的变换可以找到解决问题的途径。
在拓展过程中,根据物元的“一物多征,一征多物,一值多物”,进行发散性思维,从而为问题的求解提供路径。
下面对条件L2进行拓展分析。按照“一物多征”可知
| $ {L_2}\dashv{L_{21}} = \left\{ \begin{array}{l} {L_{211}}{\rm{ = }}({\rm{A}}3 {\small{\text{打印纸,长度}}}, {a_{21}})\\ {L_{212}}{\rm{ = }}({\rm{A}}3 {\small{\text{打印纸,宽度}}}, {b_{21}})\\ {L_{213}}{\rm{ = }}({\rm{A}}3 {\small{\text{打印纸,放置方式,平铺}}})\\ {L_{214}}{\rm{ = }}({\rm{A}}3 {\small{\text{打印纸,放置方向,横向}}}) \end{array} \right.\;\;\;\;\;\;\;\;\;\;, $ |
根据“一征多值”可知
| $ \begin{array}{l} {L_{213}} \dashv {L_{2131}}{\rm{ = (A}}3打印纸,放置方式,折叠),\\ {L_{214}} \dashv {L_{2141}}{\rm{ = (A3打印纸,放置方向,纵向)}}{\rm{.}} \end{array} $ |
A3打印纸折叠放置,则L2131可拓展
| $ {L_{2131}} \dashv \left\{ \begin{array}{l} {L_{21311}} = \left[ {\begin{array}{*{20}{c}} \rm{A3打印纸,}&{放置方式,}&{折叠}\\ {}&{折叠方向,}&{长轴}\\ {}&{折叠线位置,}&{\left\langle {0,148.5} \right\rangle } \end{array}} \right]\\ {L_{21312}} = \left[ {\begin{array}{*{20}{c}} {{\rm{A3打印纸,}}}&{放置方式,}&{折叠}\\ {}&{折叠方向,}&{短轴}\\ {}&{折叠线位置,}&{\left\langle {0,210} \right\rangle } \end{array}} \right] \end{array} \right., $ |
根据相关分析,折叠放置后,A3打印纸的长度和宽度尺寸会发生变化,即
| ${L_{2131}} \sim \left\{ \begin{array}{l} {L_{211}}\\ {L_{212}} \end{array} \right.,$ |
而放置方向与打印机B的打印幅面相关,即
| $ {L_{214}} \sim ({\small{\text{打印机}}}{\rm{B}},{\small{\text{进纸盒尺寸}}},{a_1} \times {b_1}). $ |
根据上述分析,A3打印纸的尺寸随着折叠线位置不同而变化。当沿长轴折叠到对称轴时,则A3打印纸的尺寸a21=420 mm,b21=148.5 mm;而当沿短轴折叠到对称轴时,则A3打印纸的尺寸为a21=297 mm,b21=210 mm,将上述尺寸代入等式(1)中可知,其宽度方向关联函数值k(x) > 0;但是在长度方向上,第一组数据的关联函数值仍然为负。据此,把A3打印纸沿着短轴对折后,A3打印纸的尺寸与A4打印纸尺寸相同,满足两个方向的关联函数值为正。这样折叠后的A3打印纸可以顺利地放入进纸盒中,打印完一面后,将折叠后的打印纸翻转180°,打印另一面,即可将两页的内容打印到一张A3打印纸上。但是经实践证明,折叠后的A3打印纸在A4打印机上打印时,经常会出现卡纸的现象,说明并未根本解决问题,出现了新的矛盾。
折叠后的A3打印纸在轴线一侧,由于纸张的连接关系,打印进纸时相当于一张纸;但是在另一侧相当于是两张纸,导致打印纸两侧进纸速度不同而发生卡纸现象。目前问题的目标和条件
| $ G = \left[ {\begin{array}{*{20}{c}} {\small{\text{打 印}}},&{\small{\text{支配对象}}},&{\small{\text{文 字 图 像}}}\\ {}&{\small{\text{工 具}}},&{\small{\text{打印机 }}}B\\ {}&{\small{\text{地 点}}},&{\rm{A}3 {\small{\text{打印纸}}}}\\ {}&{\small{\text{程 度}}},&{\small{\text{顺 畅}}} \end{array}} \right], $ |
条件为L1和L3
| $ {L_3} = \left[ \begin{array}{l} \!\!\!\! \rm{A}3 {\small{\text{打印纸}}},\;\;{\small{\text{尺 寸}}},\;\;297\; {\rm mm} \times 210\;{\rm mm}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\small{\text{放置方式}}},\;\;{\small{\text{折叠}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\small{\text{放置方向}}},\;\;{\small{\text{纵向}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\small{\text{放置方向}}},\;\;{\small{\text{短轴}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\small{\text{折叠线位置}}},\;\;210\;{\rm mm} \end{array} \right]. $ |
根据物元的可拓展性
| $ \begin{aligned} & {L_{11}} = \left[ {\begin{array}{*{20}{c}} {\small{\text{打印机}}}{\rm B},&{\small{\text{打 印幅面}}},&{\rm{A}4}\\ {}&{\small{\text{进纸盒尺寸}}},&{{a_1} \times {b_1}}\\ {}&{\small{\text{进纸页数}}}&1 \end{array}} \right], \\ & {L_{31}} = \left[ \begin{array}{l} \! \rm{A}3{\small{\text{打印纸}}},\;\;{\small{\text{尺寸}}},\;\;297\;mm \times 210\;mm\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\small{\text{放置方式}}},\;\;{\small{\text{折叠}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\small{\text{放置方向}}},\;\;{\small{\text{纵向}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\small{\text{折叠方向}}},\;\;{\small{\text{短轴}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\small{\text{折叠线位置}}},\;\;210\;{\rm mm}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{页数},\;\;1 \vee 2 \end{array} \right]. \end{aligned} $ |
从上述分析看,打印机B的进纸页数和折叠后的A3打印纸页数不同,存在矛盾,从而造成打印机卡纸的问题。
对折后的A3打印纸放置在进纸盒中,它们之间的接触关系可以用关系元表示为
| $ R = \left[ {\begin{array}{*{20}{c}} {\small{\text{接触关系}}},&{\small{\text{前项}}},&{{L_{31}}}\\ {}&{\small{\text{后项}}},&{\small{\text{进纸盒}}}\\ {}&{\small{\text{程度}}},&{\small{\text{直接接触}}} \end{array}} \right] $ |
根据“一征多值”,上述的关系元可拓展为
| $ {R_1} = \left[ {\begin{array}{*{20}{c}} {\small{\text{接触关系}}},&{\small{\text{前项}}},&{L_{31}}\\ {}&{\small{\text{后项}}},&{\small{\text{进纸盒}}}\\ {}&{\small{\text{程度}}},&{\small{\text{间接接触}}}\\ {}&{\small{\text{方式}}},&{\small{\text{中介物}}} \end{array}} \right] $ |
按照上述关系元,可将对折后的A3打印纸间接地放在进纸盒上,即将对折后的A3打印纸放在中介物中,然后再一起放置在进纸盒中,这样解决对折后A3打印纸两侧张数不同的矛盾,从而克服卡纸的问题。
步骤3 可拓变换,即为
| $ M = \left[ \begin{array}{l} \!\!\!{L_{31}} \oplus {\small{\text{中介物}}},\;\;{\small{\text{尺寸}}},\;\;a\;{\rm{mm}} \times b\;{\rm{mm}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\small{\text{放置方向}}},\;\;{\small{\text{纵向}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\small{\text{页数}}},\;\;\;\;\;\;\;\;\;1 \end{array} \right], $ |
M的尺寸取决于中介物的尺寸,即打印夹的尺寸,而且要满足式(1),关联函数值为正。
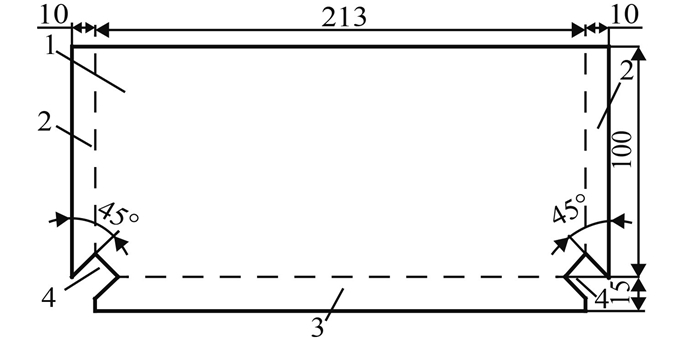
打印夹的尺寸设计如图 1和图 2所示。图 1为打印夹的展开图,虚线为折叠线,1为支撑底板,2为横向折叠板,3为纵向折叠板;图 2为打印夹折叠后的示意图。折叠后的打印夹总体尺寸为213 mm×100 mm,比对折后A3打印纸的宽度(210 mm)略大,则非常轻松即可将对折后的A3打印纸放入打印夹中;横向折叠板各折叠10 mm,因为页面有一定的页边距,不会影响打印内容;打印纸放入打印夹时,将打印面朝纵向折叠板3。将打印夹宽度方向213 mm代入式(1),其关联函数值k(x)=0.5 > 0,满足尺寸要求。

|
图 1 未折叠的打印夹示意图(单位:mm) Figure 1 Schematic diagram of unfolded print clip |
|
图 2 折叠后的打印夹示意图(单位:mm) Figure 2 Schematic diagram of folded print clip |
本文根据需求与条件的矛盾关系,即偶尔需要使用A4打印机在A3打印纸上打印内容,采用可拓创新方法,建立了矛盾问题的基元;根据基元的可拓展性,菱形思维引导创新过程;最后设计出折叠纸打印夹,并已经成功申请实用新型专利,专利号为201420030129.2。可拓创新方法有效解决矛盾问题,创新过程有章可循,为创新设计提供一种新的方法。
| [1] | 杨春燕, 蔡文. 可拓工程[M]. 北京: 科学出版社, 2007. |
| [2] | 赵燕伟, 苏楠. 可拓设计[M]. 北京: 科学出版社, 2010. |
| [3] |
张雷, 彭宏伟, 刘志峰, 等. 绿色产品概念设计中的知识重用[J].
机械工程学报, 2013, 49 (7): 72-79.
ZHANG L, PENG H W, LIU Z F, et al. Knowledge reuse in green product concept design process[J]. Journal of Mechanical Engineering, 2013, 49 (7): 72-79. DOI: 10.3901/JME.2013.07.072. |
| [4] |
齐宁宁, 杨春燕. 基于可拓学第三创造法的产品概念设计[J].
数学的实践与认识, 2015, 45 (5): 226-238.
QI N N, YANG C Y. Product conceptual design based on third creative method of Extenics[J]. Mathematics in Practice and Theory, 2015, 45 (5): 226-238. |
| [5] | TANG W Y, LI S Y, ZHANG X W, et al. Selection and evaluation of mechanical motion scheme based on extension theory[C]//CAI W, YANG C Y, FLORENTIN S, et al. Extenics and Innovation Methods. New York:CRC Press, 2013:297-304. |
| [6] |
唐文艳, 张晓伟, 李苏洋, 等. 基于可拓学的刨床刨刀往复运动机构设计[J].
机械科学与技术, 2014, 33 (6): 811-814.
TANG W Y, ZHANG X W, LI S Y, et al. Design of reciprocating motion mechanism for plane blade of planer based on Extenics[J]. Mechanical Science and Technology for Aerospace Engineering, 2014, 33 (6): 811-814. |
| [7] |
丁俐娟, 邹广天, 郭强, 等. 可拓建筑策划数据挖掘理论探讨[J].
广东工业大学学报, 2015, 32 (1): 1-5.
DING L J, ZOU G T, GUO Q, et al. Research on the theory of extension architecture programming data mining[J]. Journal of Guangdong University of Technology, 2015, 32 (1): 1-5. |
| [8] |
叶广仔, 李卫华. 可拓数据挖掘在教师科研考核评价中的应用[J].
数学的实践与认识, 2015, 45 (12): 53-59.
YE G Z, LI W H. The application of extension data mining teachers scientitic research evaluation[J]. Mathematics in Practice and Theory, 2015, 45 (12): 53-59. |
| [9] |
刘林, 黄英, 贺振华. 基于可拓检测的医学图像分割[J].
广东工业大学学报, 2013, 30 (3): 18-22.
LIU L, HUANG Y, HE Z H. Segmentation of medical images based on extension detecting technology[J]. Journal of Guangdong University of Technology, 2013, 30 (3): 18-22. |
| [10] |
谢蓝, 曾韬, 余永权, 等. 可拓检测的可拓变换机理[J].
计算机工程与应用, 2011, 47 (5): 149-151.
XIE L, ZENG T, YU Y Q, et al. Extension transformation mechanism of extension detecting[J]. Computer Engineering and Applications, 2011, 47 (5): 149-151. |
| [11] |
许可, 王金广. 基于可拓思维模式的产品形象识别系统设计研究[J].
西部皮革, 2016, 1 : 48-50.
XU K, WANG J G. Research on products identity system based on extension thinking modes[J]. West Leather, 2016, 1 : 48-50. |
| [12] |
张文会, 马俊, 罗文文, 等. 基于可拓学的事故路段风险等级识别模型[J].
重庆交通大学学报(自然科学版), 2016, 35 (1): 107-110.
ZHANG W H, MA J, LUO W W, et al. Identification model for risk level of traffic accident section based on extension science[J]. Journal of ChongQing Jiaotong University (Natural Science), 2016, 35 (1): 107-110. |
| [13] |
陈萍, 田双亮. 确定市场营销策略的可拓方法[J].
西北民族学院学报(自然科学版), 1999, 20 (3): 26-29.
CHEN P, TIAN S L. The extension method about determination of marketing tactics[J]. Journal of Northwest Minorities University (Natural Science), 1999, 20 (3): 26-29. |
| [14] |
方耀楣, 李俭, 崔霁. 基于可拓方法的城市拆迁的策略生成[J].
哈尔滨工业大学学报, 2006, 38 (7): 1179-1183.
FANG Y M, LI J, CUI J. Strategy formation for urban house pulling down and migration using extension methods[J]. Journal of Harbin Institute of Technology, 2006, 38 (7): 1179-1183. |
| [15] |
黄海鸥. 可拓策略生成系统及其应用[J].
吉林农业科技学院学报, 2010, 19 (2): 89-91.
HUANG H O. Extension strategy generating system and its utilization[J]. Journal of Jilin Agricultural Science and Technology College, 2010, 19 (2): 89-91. |
| [16] |
李承晓, 李卫华. 租房可拓策略生成系统[J].
智能系统学报, 2011, 6 (3): 272-278.
LI C X, LI W H. Research on a tenement extension strategy generation system[J]. CAAI Transactions on Intelligent Systems, 2011, 6 (3): 272-278. |
 2017, Vol. 34
2017, Vol. 34
