智能网联汽车与5G通信技术结合，为无人自动驾驶服务提供关键技术支撑，以支持车载终端设备深度神经网络学习与推理计算任务^[1]。由于车载终端距离云数据中心较远，其高延迟难以保障车辆智能驾驶相关推理任务的服务质量(Quality of Service, QoS)^[2]。为克服移动云计算高延迟的缺点，移动边缘计算(Mobile Edge Computing, MEC)^[3]通过将云计算的算力部署在移动终端附近，例如路边单元(Road Side Unit, RSU)等，大大降低了移动云计算的传输通信延迟^[4]。然而，实际应用中为覆盖所有区域而放置大量边缘服务器往往因成本控制而不可行。因此，在低密度部署下，RSU在高峰时段随着车辆数量的增加，将不可避免地出现计算负载过载，损害车辆推理任务的QoS。为解决该问题，车辆雾计算(Vehicle Fog Computing, VFC)^[5]通过充分利用高配车辆车载计算机的空闲算力资源^[6]，可有效减轻RSU的负载^[7]。

现有移动边缘计算研究大多考虑在服务缓存与任务卸载方面优化系统吞吐量、处理延迟以及设备能耗等问题，而较少考虑服务公平性。在系统吞吐量优化中，文献[8]研究了在延迟约束下的车辆优先级异构任务RSU卸载问题，设计了基于深度强化学习的卸载算法以最大化累积任务优先完成率，然而其未考虑RSU算力、存储等资源约束。文献[9]研究了在服务模型加载延迟存在下的服务缓存与请求卸载问题，并设计了近似算法与贪心算法最大化系统吞吐量。文献[10]在边云协同场景中联合研究了多子任务并行下的卸载问题，在延迟约束下最大化服务推理吞吐量。然而，文献[9-10]假设边缘端拥有较充分的算力资源。在处理延迟优化中，文献[11]在算力约束下，提出了一个在线任务卸载算法以最小化所有任务的总延迟。文献[12]在算力、带宽资源约束下研究了车联网中车到车的随机任务卸载延迟问题，使用李雅普诺夫优化与分布式在线算法优化系统延迟能耗权衡。文献[13]研究了服务缓存和请求路由的联合优化问题，提出了一个深度强化学习算法以最小化任务的平均时延。在设备能耗优化中，文献[14]研究了一个多源多中继的无线传感器边缘网络的能耗问题，提出了一种基于二分匹配的最优加权平均总能耗算法以最小化任务执行能耗。文献[15]考虑了WiFi网络和蜂窝网络并存的异构网络场景，提出了一个联合服务部署与任务缓存的管理问题，设计了一个基于交替优化技术的迭代算法来最小化终端设备的能耗。文献[16]研究了车辆边缘计算中依赖性任务感知的服务部署与请求卸载问题，设计了一种基于动态规划的半分布式算法以降低车辆的能耗。然而，上述研究均假设网络控制节点可以全局感知节点的算力，且接收任务节点将自己的可用算力完全用于协助服务请求节点，鉴于用户自私性，这一假设在现实场景中过于理想化。

此外，移动边缘计算在实际执行中仍面临缺失公平服务机制、缺少有效的激励机制等亟待解决的难题。首先，车辆自身资源和能耗受限，为其他车辆提供边缘计算服务将占用对应资源并消耗其自身电量，因此亟需提供相应的激励机制，作为车辆协助RSU计算服务的补偿。其次，如果优化系统总吞吐量，会导致小计算量推理任务比大计算量推理任务优先被车辆卸载处理，从而造成请求服务车辆之间的不公平服务。文献[17]针对自私性问题，研究了基于合同的匹配激励机制，优化车载任务的完成时间，然而其假设服务模型已经部署，且忽视了动态任务卸载带来的不公平服务问题。文献[18]采用遗传算法解决了面向任务级别的服务公平性调度问题，然而其忽略了节点自私性且假设边缘节点资源充足。

为解决上述存在的问题，本研究主要贡献为：

(1) 针对提供服务车辆的自私性，提出一种新的合同激励机制，鼓励高配车辆出让其计算资源以降低高峰时期的RSU服务器负载，并给出了完整的合同模型设计，用卡罗需−库恩−塔克(Karush-Kuhn-Tucker, KKT)条件求解合同最优值和面向VFC网络的合同生成算法。

(2) 针对服务请求车辆的自私性，从公平性的新颖角度出发，基于最大最小公平性原则，在提供服务车辆存储资源、算力资源以及计算任务完成时间约束下，以最大化最小的任务完成率为优化目标，提出了面向VFC网络的任务卸载与服务缓存联合优化问题，并证明了该问题的NP难解性。

(3) 提出了基于合同的随机舍入算法解决任务卸载与服务缓存的联合优化问题，并给出了近似比证明。同时，针对随机舍入策略复杂度较高的不足，还提出了一个快速高效的基于合同的贪心算法。实验结果表明，提出的两个算法可有效提升最小服务完成率。

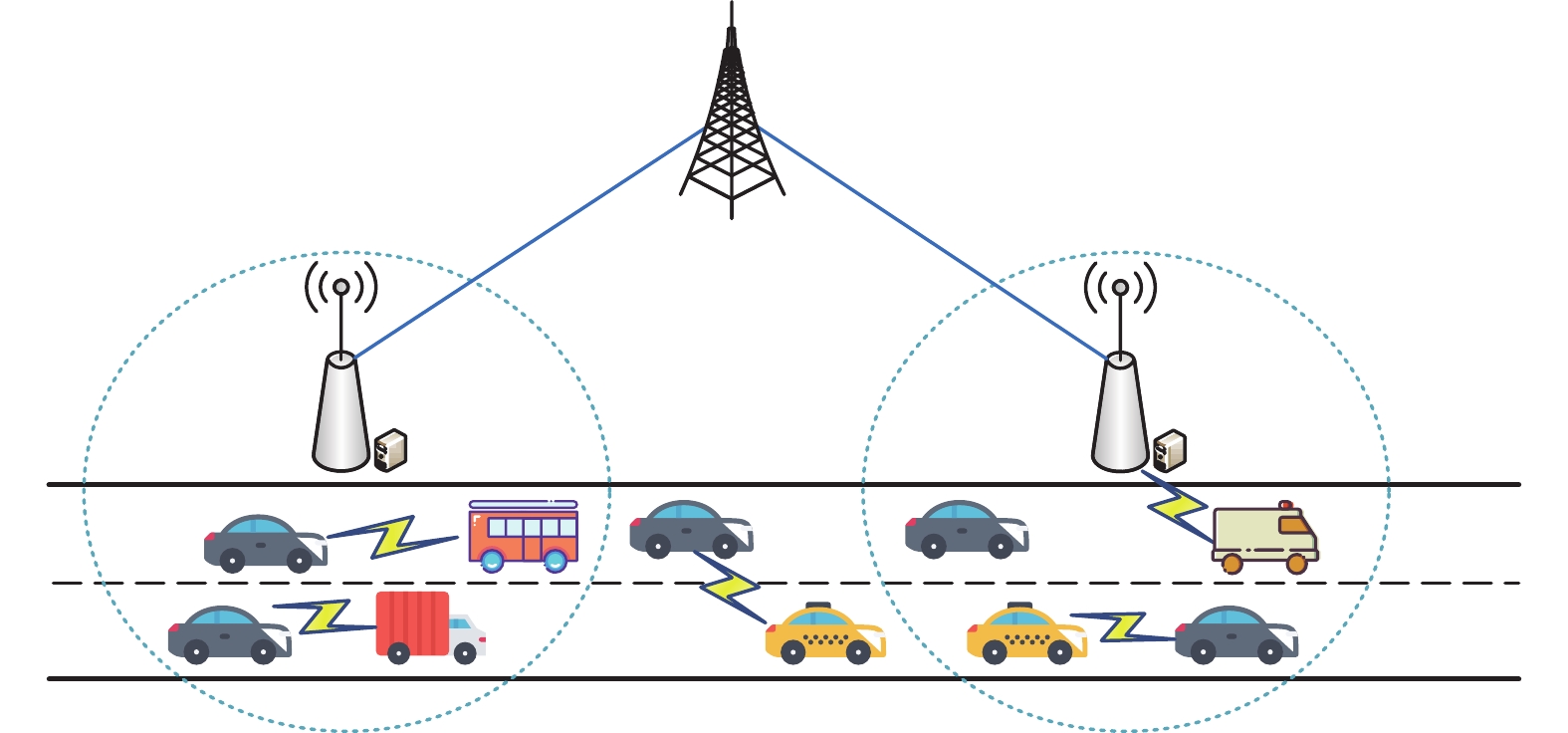
1 系统模型

如图1所示的车联网，由一个宏基站与若干RSU以及多辆车组成，宏基站通过有线光纤与各个RSU相连，RSU通过无线通信与覆盖范围内的车辆相连。设$ {\cal{I}}=\{1,2, \cdots, I\} $表示发送计算任务的请求车辆集合，设${\cal{M}} = \{ 1,2,\cdots,M\} $表示接收计算任务的服务车辆集合，这些车均匀分布在两条单向行驶的车道上。在RSU信号覆盖范围内的车辆，每辆车可以与RSU进行(Vehicle-to-Infrastructure, V2I) 通信，也可以在RSU的帮助下与其他车辆进行车对车(Vehicle-to-Vehicle, V2V) 通信，即使车辆驶出RSU信号范围，已经建立的V2V通信连接仍然可以继续工作。对于不同功能和种类的深度神经网络(Deep Neural Network, DNN) 模型，设${\cal{V}} = \{ 1,2,\cdots,V\} $表示不同种类的服务模型集合。将时间划分为离散的区间，用时隙模型表示一段时间。RSU可通过车辆的任务卸载来缓解自身的过载，如果对应车辆缓存了相应的服务模型，那么该车辆就能够处理请求该服务的任务。

1.1 任务模型

令0-1二元变量$x_m^v$表示服务模型的缓存策略，若$x_m^v = 1$，则表示服务车辆$m$缓存有DNN服务模型$v$，否则$x_m^v = 0$，故有

$ x_m^v=\left\{{\begin{array}{*{20}{l}}1,&\text{表示车辆}m\text{缓存模型}v\\0,&\text{其他}\end{array}} \right.,m\in{\cal{M}},v\in{\cal{V}} $

(1)

假设每个车辆发送的一个计算任务对应一个服务模型。令0-1二元变量$y_i^v$表示请求车辆$i$发出的对于服务模型$v$的请求，若$y_i^v = 1$，则表示请求车辆$i$请求服务$v$，否则$y_i^v = 0$，故有

$ y_i^v=\left\{{\begin{array}{*{20}{l}}1,&\text{表示车辆}i\text{请求模型}v\\0,&\text{其他}\end{array}} \right.,i\in{\cal{I}},v\in{\cal{V}} $

(2)

令0-1二元变量$z_m^i$表示车辆的计算任务卸载策略，若$z_m^i = 1$，则表示将请求车辆$i$的计算任务卸载到车辆$m$，否则$z_m^i = 0$，故有

$ {z}_{m}^{i}=\left\{ {\begin{array}{*{20}{l}} 1,&\text{表示车辆}i{\text{卸载任务到}}m\\ 0,&\text{其他}\end{array}} \right.,i\in {\cal{I}},m\in {\cal{M}}$

(3)

请求车辆发出的计算任务既可以被服务车辆处理，也可以在RSU上处理，故有约束

$ \sum\limits_{m \in {\cal{M}} \cup {\text{RSU}}} {z_m^i} = 1,i \in {\cal{I}} $

(4)

请求车辆发出的计算任务如果能被服务车辆处理，其前提是该服务车辆一定缓存有对应的服务模型，故有约束

$ y_i^vz_m^i \leqslant x_m^v,i \in {\cal{I}},m \in {\cal{M}},v \in {\cal{V}} $

(5)

缓存服务模型需要消耗车辆的存储资源，然而车辆提供的存储资源有限，服务部署时所存储的模型总和不能超过已提供存储资源的上限，故有约束

$ \sum\limits_{v \in {\cal{V}}} {x_m^v{c_v}} \leqslant R_m^{\max },m \in {\cal{M}} $

(6)

式中：${c_v}$为服务模型$v$的大小，$R_m^{\max }$为服务车辆$m$的最大存储容量。

1.2 传输模型

在任务卸载场景中，请求车辆发出任务后，在RSU的帮助下可以通过V2V通信和正交频分多址(Orthogonal Frequency Division Multiple Access, OFDMA) 技术与服务车辆建立无线连接。设请求车辆$i$与服务车辆$m$进行通信时的传输速率为${r_{i,m}}$，其可由香农公式得到，故有

$ {r_{i,m}} = {b_{i,m}}{\log _2}\bigg(1 + \frac{{{p_i}{H_{i,m}}}}{{\sigma _m^2}}\bigg) ,i \in {\cal{I}},m \in {\cal{M}} $

(7)

式中：${b_{i,m}}$为请求车辆$i$和服务车辆$m$之间的传输带宽，${p_i}$为请求车辆$i$的发送功率，$\sigma _m^2$为服务车辆$m$的环境噪音功率，${H_{i,m}}$为请求车辆$i$和服务车辆$m$之间的无线信道功率增益，其与车辆之间的欧几里得距离${L_{i,m}}$和瑞利衰落信道系数${h_{i,m}}$有关^[19]。

无线信道功率增益的公式为

$ {H_{i,m}} = {({L_{i,m}}) ^{ - n}}{\left| {{h_{i,m}}} \right|^2},i \in {\cal{I}},m \in {\cal{M}} $

(8)

式中：常数$n$通常取3~4^[20]。

设请求服务模型$v$的任务数据包的大小为${s_v}$，则请求车辆$i$到服务车辆$m$之间花费的传输延迟为

$ t_{i,m}^{{\text{tra}}} = \frac{{\displaystyle\sum\nolimits_{v \in {\cal{V}}} {y_i^v{s_v}} }}{{{r_{i,m}}}},i \in {\cal{I}},m \in {\cal{M}} $

(9)

1.3 计算模型

计算任务的计算延迟与被分配到的计算资源大小有关，计算任务在执行前需要服务车辆启动对应的虚拟机。设服务车辆$m$分配给请求车辆$i$的计算资源大小为${f_{i,m}}$，请求服务模型$v$的计算量大小为${d_v}$，虚拟机启动时间为${t^{{\text{VW}}}}$，则服务车辆处理来自请求车辆的计算任务所需要花费的处理延迟为

$ t_{i,m}^{{\text{exe}}} = \frac{{\displaystyle\sum\nolimits_{v \in {\cal{V}}} {y_i^v{d_v}} }}{{{f_{i,m}}}} + {t^{{\text{VM}}}},i \in {\cal{I}},m \in {\cal{M}} $

(10)

计算任务需要消耗车辆的计算资源，然而车辆提供的计算资源是有限的，任务卸载时需要的计算资源总和不能超过已提供计算资源的上限，故有约束

$ \sum\limits_{i \in {\cal{I}}} {z_m^i{f_{i,m}}} \leqslant C_m^{\max },m \in {\cal{M}} $

(11)

1.4 求解目标

由于计算任务处理完毕后返回的数据包很小，故这部分延迟通常可以忽略^[21]。因此，计算任务从请求车辆$i$发出到服务车辆$m$处理完毕所花费的总延迟分为传输延迟$t_{i,m}^{{\text{tra}}}$和处理延迟$t_{i,m}^{{\text{exe}}}$两部分，故有

$ {t_{i,m}} = t_{i,m}^{{\text{tra}}} + t_{i,m}^{{\text{exe}}},i \in {\cal{I}},m \in {\cal{M}} $

(12)

每个计算任务都有可能完成时间和最大容忍时间，若计算任务的可能完成时间不超过最大容忍时间时可卸载到服务车辆进行处理，否则应卸载到RSU处理，因此计算任务的可能完成时间可作为任务卸载的依据之一。为了降低高峰时期RSU的负载，设请求车辆$i$的任务请求卸载到RSU处理的时间等于任务的最大容忍时间${t_{i,0}}$。设二进制变量${l_i}$表示请求车辆发出的计算任务是否被成功处理，若${l_i} = 1$则表示未超过最大容忍时间，计算任务被成功处理，否则${l_i} = 0$。设${A_v}$表示请求服务$v$的请求车辆集合，则有

$ {A_v} = \{ i|y_i^v = 1,i \in {\cal{I}}\} ,v \in {\cal{V}} $

(13)

由于有限资源的限制，服务车辆不一定能同时满足所有请求车辆的任务请求。设${a_v}$表示请求服务$v$的成功处理的任务数量，则有

$ {a_v} = \sum\limits_{i \in {\cal{I}}} {y_i^v{l_i}} ,v \in {\cal{V}} $

(14)

令服务$v$的任务完成率为请求服务$v$的计算任务成功处理数量与请求服务$v$的计算任务总数量的比值，故有

$ {g_v} = \frac{{{a_v}}}{{{A_v}}},v \in {\cal{V}} $

(15)

对于每个请求车辆来说，自私性会导致其希望自己的任务能被优先处理，不同计算任务请求的服务模型需要的资源大小也不同，需要较多计算资源和存储资源的DNN模型称为大服务模型，例如VGG13，相反称之为小服务模型，例如AlexNet。因此在宏观的最大化系统吞吐量的优化方案中，请求车辆的自私性和服务的异构性会使得请求小服务模型的车辆比请求大服务模型的车辆有更高的任务完成率。为了降低自私性等带来的影响，提高优化方案的公平性，故求解目标为最大化最小任务的完成率。问题的形式化定义为

$ \begin{split} &({\cal{P}}) {\text{ }}\max {\text{ }}\min {g_v}\\ &\mathrm{s.t.}{\text{ }}(4) ,(5) ,(6) ,(11) , \\ &x_m^v,z_m^i \in \{ 0,1\} ,i \in {\cal{I}},m \in {\cal{M}},v \in {\cal{V}} \end{split} $

式中：约束式(4)确保任务能被顺利卸载到一个处理对象，约束式(5)确保处理计算任务的服务车辆缓存了相应服务，约束式(6)为服务车辆的存储资源约束，约束式(11)为服务车辆的计算资源约束。

2 激励机制

在VFC网络场景中，理想状况下RSU可以将计算任务卸载到临近的车辆来扩充其有限的计算和存储资源，然而，在实际情况中这种假设过于乐观。由于车辆是私人拥有的，处理这些卸载请求需要花费额外的开销，故具有天然自私性的服务车辆往往不愿意充当计算节点，除非有对应的补偿。除此之外，自私性使得车辆不愿意公开一些私有信息，例如其对资源出让的偏好以及出让资源大小等。这使得RSU和车辆之间是信息不对称的，RSU无法准确知道当前接入的每个车辆出让资源的大小。为了解决上述问题，需要设计一个高效的激励机制。大多数方法如拍卖理论^[22]和斯塔克尔伯格博弈^[23]是基于迭代机制的且需要多次交换信息，这在提供延迟敏感服务的VFC网络中会导致额外的高信令开销。为了降低开销并解决上述问题，故选择合同论作为高效的激励机制。

2.1 合同描述

对于服务车辆集合${\cal{M}}$，考虑到车辆资源的异构性，按照RSU所需要的资源大小将其划分为$K$种类型的集合${\cal{K}} = \{ 1,2,\cdots,K\} $且$k \in {\cal{K}}$。除此之外，设服务车辆中能够提供的最小和最大计算资源满足$C_m^{\min },C_m^{\max } \in [{C^{\min }},{C^{\max }}]$，其中有${C^{\min }} = \min C_m^{\min }$，${C^{\max }} = \max C_{m'}^{\max }$，$m,m' \in {\cal{M}}$。基于上述，再将区间$[{C^{\min }},{C^{\max }}]$划分为具有相同长度的$K$个子区间，设权重值${\theta _k}$大小等同于第$k$个子区间的下限大小，可得

$ {\theta _k} = {C^{\min }} + \frac{{k - 1}}{K}({C^{\max }} - {C^{\min }}) ,k \in {\cal{K}} $

(16)

由于${\theta _k}$单调，故有

$ {\theta _1} < \cdots < {\theta _k} < \cdots < {\theta _K},k \in {\cal{K}} $

(17)

对于服务车辆$m$，若其最大可提供的资源大小为类型$k$，则

$ {\theta _k} \leqslant C_m^{\max } < {\theta _{k + 1}} $

(18)

如图2所示为激励机制，根据RSU所需要的资源类型和大小的不同，设计了$K$种类型的合同，其集合${\cal{C}}{\text{ = \{ }}\{ {\varphi _k},{\varPhi _k}\} {\text{|}}{ }\forall k \in {\cal{K}}{\text{\} }}$，其中${\varphi _k}$表示在资源类型$k$范围内的值且满足${\theta _k} \leqslant {\varphi _k}$，${\varPhi _k}$表示出让拥有的类型为$k$的资源所获得的资源回报或者奖励。每个车辆在收到合同后可以选择接受或者拒绝，即每辆车有选择是否出让自身资源的权力。为激励车辆，假设车辆出让的计算资源越多，车辆获得的回报越多。当${\varphi _k} = 0$时表示车辆拒绝当前合同，对应的奖励为${\varPhi _k} = 0$。由于车辆实际算力资源信息具有隐私性，用户不愿意将其公开，而RSU提供的合同集合${\cal{C}}$可以让服务车辆根据其当前愿意出让的算力资源偏好自主选择合同内容$\{ {\varphi _k},{\varPhi _k}\} $，从而隐藏了实际算力信息，保护了车辆算力数据隐私。在信息不对称的情况下，RSU不能准确知道每个服务车辆所属类型的准确信息，设接收车辆属于资源类型$k$的概率为${\lambda _k}$，则有$\displaystyle\sum\nolimits_{k = 1}^K {{\lambda _k}} = 1$，其可以通过统计历史信息得到。

2.2 车辆效用模型

对于服务车辆$m$，针对RSU提供的合同${\cal{C}}$，如果其接受并出让自己的资源给别的车辆发出的任务请求，则该车根据合同内容会得到对应的报酬。出让资源大小为${\varphi _k}$的车辆的效用函数为

$ U_k^m = {\theta _k}{\varPhi _k} - {\varphi _k},k \in {\cal{K}} $

(19)

为鼓励车辆多多出让它们的资源，可令出让资源更高的车辆拥有更高的回报。因此，将具有单调递增属性的${\theta _k}$作为出让资源类型$k$的合同权重。

2.3 RSU效用模型

对于RSU，其负责调度来自请求车辆的任务并将其计算任务卸载到出让资源的车辆，以减轻RSU自身负担。由于车辆出让计算资源相当于增大了VFC网络可用计算资源大小，故RSU的效用可以通过减少任务处理延迟进行提升。这里使用线性函数^[24]以表征RSU在VFC网络接入一个出让资源大小为${\varphi _k}$的服务车辆的效用，得到

$ \begin{split} U_k^{{\text{RSU}}} =& {\lambda _k}(u \cdot \Delta t - {\varPhi _k}) =\\ &{\lambda _k} [u\bigg({t_{i,0}} - \frac{{{d_n}}}{{\dfrac{{{d_n}}}{{{t_{i,0}}}} + {\varphi _k}}}\bigg) - {\varPhi _k}],k \in {\cal{K}} \end{split} $

(20)

式中：$\Delta t$表示资源扩充后降低的延迟，$u$表示延迟下降所带来的单位效用提升。

对于$M$个车辆的所有$K$个类型的情况，RSU的总效用函数为

$ {U^{{\text{RSU}}}} = \sum\limits_{m = 1}^M {\sum\limits_{k = 1}^K {U_k^{{\text{RSU}}}} } $

(21)

2.4 求解目标

考虑到车辆的自私性和为降低RSU自身负担，进行RSU的设计和优化。基于此，求解目标是已知各个资源类型权重${\theta _k}$，在出让资源类型下限约束、出让资源大小单调性、个体理性和激励相容性的约束条件下，最大化RSU系统总效用^[25]。记该问题为${\cal{Q}}$，则

$ ({\cal{Q}})\;\; \max {U^{{\text{RSU}}}} $

$ {\mathrm{s.t.}}\;\; {\theta _k} \leqslant {\varphi _k},k \in {\cal{K}} $

(22)

$ 0 \leqslant {\varphi _1} < \cdots < {\varphi _k} < \cdots < {\varphi _K},k \in {\cal{K}} $

(23)

$ {\theta _k}{\varPhi _k} - {\varphi _k} \geqslant 0,k \in {\cal{K}} $

(24)

$ {\theta _k}{\varPhi _k} - {\varphi _k} \geqslant {\theta _{k'}}{\varPhi _{k'}} - {\varphi _{k'}},k,k' \in {\cal{K}},k \ne k' $

(25)

式(22)为出让资源大小的下限约束，式(23)为出让资源大小单调性约束，式(24)为个体理性(Individual Rationality, IR)约束，式(25)为激励相容性(Incentive Compatibility, IC)约束。下限约束和单调性约束确保资源较多的车辆会出让更多的计算资源。IR约束确保服务车辆始终会选择对自己有益的合同项目。IC约束确保服务车辆始终会选择对自己效用最大的合同项目。

2.5 合同优化

根据文献[17]，可得到引理1和引理2。

引理1　对于集合${\cal{K}}$中的任意的$k$和$k'$，如果${\theta _k} > {\theta _{k'}}$，那么${\varPhi _k} > {\varPhi _{k'}}$，当且仅当${\theta _k} = {\theta _{k'}}$时满足${\varPhi _k} = {\varPhi _{k'}}$。

引理2　若合同$\{ {\varphi _k},{\varPhi _k}\} $具有可行性，则当且仅当满足条件${\theta _{k + 1}}({\varPhi _{k + 1}} - {\varPhi _k}) \geqslant {\varphi _{k + 1}} - {\varphi _k} \geqslant {\theta _k}({\varPhi _{k + 1}} - {\varPhi _k}) $。

基于引理1和引理2，可得出引理3。

引理3　优化后的合同问题满足以下条件

$ {\theta _1}{\varPhi _1} - {\varphi _1} = 0 $

(26)

$ {\varphi _k} = {\varphi _{k - 1}} + {\theta _k}({\varPhi _k} - {\varPhi _{k - 1}}) ,2 \leqslant k \leqslant K $

(27)

证明　假设$k' \in \{ 1,\cdots, k\} $，根据权重大小为${\theta _k}$的车辆的IC条件，有

$ U_k^m = {\theta _k}{\varPhi _k} - {\varphi _k} \geqslant {\theta _k}{\varPhi _{k'}} - {\varphi _{k'}} $

(28)

由于${\theta _k} > {\theta _{k'}}$，有

$ {\theta _k}{\varPhi _{k'}} - {\varphi _{k'}} \geqslant {\theta _{k'}}{\varPhi _{k'}} - {\varphi _{k'}} = U_{k'}^m $

(29)

根据不等式的传递性，将上述不等式结合，有

$ U_k^m > U_{k'}^m $

(30)

以此类推，对于${\theta _1} < \cdots < {\theta _k} < \cdots < {\theta _K}$，有

$ U_1^m < \cdots < U_k^m < \cdots < U_K^m $

(31)

至此，可以将$K$个权重大小为${\theta _k}$的IR条件全部都推导到权重大小为${\theta _1}$的车辆的IR条件，故有

$ U_1^m = {\theta _1}{\varPhi _1} - {\varphi _1} \geqslant 0 $

(32)

由于RSU可以通过降低${\varPhi _1}$或提高${\varphi _1}$直到不等式变成等式来获得最大效益，并同时满足合同可行性，故此时有

$ U_1^m = {\theta _1}{\varPhi _1} - {\varphi _1} = 0 $

(33)

此外根据引理2，有

$ {\theta _k}{\varPhi _k} - {\varphi _k} \geqslant {\theta _k}{\varPhi _{k - 1}} - {\varphi _{k - 1}} $

(34)

与上面相似，RSU可以通过降低或提高直到不等式变成等式来获得最大效用，并同时满足合同可行性，故有

$ {\theta _k}{\varPhi _k} - {\varphi _k} = {\theta _k}{\varPhi _{k - 1}} - {\varphi _{k - 1}} $

(35)

引理3证毕。

2.6 合同求解

通过上一小节中的合同优化，除去初始化约束式(22) 与式(23)，问题${\cal{Q}}$被转换为问题${\cal{Q}}1$，则有

$ \begin{split} &({\cal{Q}}1) \;\; \max {U^{{\text{RSU}}}}\\ &\mathrm{s.t.}\;\;(22) ,(23) ,(26) ,(27) \end{split} $

式中：式(26) 为IR约束，式(27) 为IC约束。

转换后的问题${\cal{Q}}1$为标准凸规划问题，对于标准凸规划问题，KKT(Karush-Kuhn-Tucker) 条件求解求得的极值点一定是该问题的全局最优解，这是充分必要条件。因此，使用KKT条件求解${\cal{Q}}1$。问题${\cal{Q}}1$的拉格朗日相关函数为

$ \begin{split} &L({\varphi _k},{\varPhi _k},{\alpha _k},{\beta _k},{\gamma _k}) = {U^{{\text{RSU}}}} + {\alpha _1}({\theta _1}{\varPhi _1} - {\varphi _1}) +\\ &\quad\sum\limits_{k = 2}^K {{\alpha _k}} ({\theta _k}({\varPhi _k} - {\varPhi _{k - 1}}) + {\varphi _{k - 1}} - {\varphi _k}) +{\beta _1}{\varphi _1} +\\ &\quad \sum\limits_{k = 2}^K {{\beta _k}({\varphi _k} - {\varphi _{k - 1}}) } +\sum\limits_{k = 1}^K {{\gamma _k}({\varphi _k} - {\theta _k}) } \end{split} $

(36)

式中：${\alpha _1}$是对应约束条件(26) 的拉格朗日乘子，$\{ {\alpha _k}|2 \leqslant k \leqslant K\} $和$\{ {\beta _k}|k \in {\cal{K}}\} $是对应约束条件(27) 和(23) 的拉格朗日乘子向量，$\{ {\gamma _k}|k \in {\cal{K}}\} $是对应约束条件(22) 的拉格朗日乘子向量。

至此，可以列出所有的KKT条件，故有下列：

(1) 初始约束条件(22) 和(23)。

(2) 对偶约束条件$ \alpha_{k} \geq 0, \beta_{k} \geq 0, \gamma_{k} \geq 0, k \in K $。

(3) 互补松弛条件${\beta _1}{\varphi _1} = 0,{\beta _k}({\varphi _k} - {\varphi _{k - 1}}) = 0,2 \leqslant k \leqslant K$。

(4) 拉格朗日一阶偏导数条件

$ \frac{{\partial L}}{{\partial ({\varphi _k}) }} = \frac{{\partial ({U^{RSU}}) }}{{\partial ({\varphi _k}) }} - {\alpha _k} + {\alpha _{k + 1}} + {\beta _k} - {\beta _{k + 1}} + {\gamma _k} = 0,k \ne K $

$ \frac{{\partial L}}{{\partial ({\varphi _K}) }} = \frac{{\partial ({U^{RSU}}) }}{{\partial ({\varphi _K}) }} - {\alpha _K} + {\beta _K} + {\gamma _K} = 0 $

$ \frac{{\partial L}}{{\partial ({\varPhi _k}) }} = \frac{{\partial ({U^{RSU}}) }}{{\partial ({\varPhi _k}) }} + {\alpha _k}{\theta _k} - {\alpha _{k + 1}}{\theta _{k + 1}} = 0,k \ne K $

$ \frac{{\partial L}}{{\partial ({\varPhi _K}) }} = \frac{{\partial ({U^{RSU}}) }}{{\partial ({\varPhi _K}) }} + {\alpha _K}{\theta _K} = 0 $

通过列出KKT条件，将权重大小${\theta _k}$代入对应的方程组，使用待定系数法可迭代求解出所有的值，舍去不满足约束条件的值后，便可得到完整的合同内容。这里设计了一个算法用于求解问题${\cal{Q}}1$，如算法1所示。

算法1第1行根据式(16) 和(18) 将服务车辆按计算资源大小进行分类，第2行根据上面提出的KKT条件求解问题${\cal{Q}}1$并得到最优合同内容${{\cal{C}}^*}$，第3行到第5行遍历服务车辆集合${\cal{M}}$，签订合同并接收服务车辆出让的计算资源$\varphi _k^*$，第6行返回最优合同${{\cal{C}}^*}$。

算法1　基于KKT的RSU合同生成算法(KKT-based RSU Contract Generation Algorithm, KCGA)

输入：请求车辆$ {{\cal{M}}}$，权重$ {{\theta _k},k \in {\cal{K}}}$，概率$ {{\lambda _k},k \in {\cal{K}}}$。

输出：合同$ {{{\cal{C}}^*}{\text{ = \{ (}}{\varphi _k},{\varPhi _k}{\text{) |}}{ }\forall k \in {\cal{K}}{\text{\} }}}$。

1. 基于式 (16) 和(18) 对车辆类型分类

2. 求解问题$ {{\cal{Q}}1}$，得到最优合同值 $ {{{\cal{C}}^*}}$

3. for $ {m \in {\cal{M}}}$ do

4. 　车辆$ {m}$与RSU签署合同项目$ {(\varphi _k^*,\varPhi _k^*) }$,，并出让空闲资源

5. end for

6. return $ {{{\cal{C}}^*}}$

3 算法与分析 3.1 基于合同的舍入算法

由于问题${\cal{P}}$是一个混合非线性整数规划问题，且具有NP难解性。为此，先将问题${\cal{P}}$转化为一个整数线性规划问题，利用线性规划和随机舍入技术给出一个多项式时间复杂度的随机舍入求解策略，并给出近似比证明。

3.1.1 问题转化

引入一个连续变量$f_{im}^{\min }$，其表示请求车辆$i$的任务卸载至服务车辆$m$被成功处理所需的最小计算资源大小，故有

$ f_{i,m}^{\min } = \frac{{\displaystyle\sum\nolimits_{v \in {\cal{V}}} {y_i^v{d_v}} }}{{{t_{i,0}} - t_{i,m}^{tra}}},i \in {\cal{I}},m \in {\cal{M}} $

(37)

引入连续变量后，$z_m^i$不再表示将请求车辆$i$的计算任务卸载到服务车辆$m$，而是表示将请求车辆$i$的计算任务卸载到服务车辆$m$且该计算任务可以成功被处理，则有

$ \sum\limits_{m \in {\cal{M}}} {z_m^i} \leqslant 1,i \in {\cal{I}} $

(38)

$ \sum_{i \in {\cal{I}}} z_{m}^{i} f_{i, m}^{\min } \leq \varphi_{k}, m \in {\cal{M}}, k \in K $

(39)

约束式(38)确保计算任务至多被卸载至一个服务车辆，式(39)表示计算资源约束。

此时变量${l_i}$的计算方式变为

$ l_{i}=\sum_{m \in \cal{M}} z_{m}^{i}, i \in \cal{I} $

(40)

为解决求解目标的非连续性，引入连续变量$\lambda $，其满足

$ \lambda \leqslant {g_v},v \in {\cal{V}} $

(41)

综上所述，在引入两个连续变量后，可得到混合整数线性规划(ILP) 问题${\cal{P}}1$，问题的形式化定义为

$ \begin{split} &({\cal{P}}1)\;\; \max \lambda \\ &\mathrm{s.t.}\;\;(5) ,(6) ,(38) ,(39) ,(41) , \\ &x_m^v,z_m^i \in \{ 0,1\} ,i \in {\cal{I}},m \in {\cal{M}},v \in {\cal{V}} \end{split} $

通过松弛问题${\cal{P}}1$中的整型变量，可以得到线性规划问题${\cal{P}}2$，则有

$ \begin{split} &({\cal{P}}2) \;\;\max \lambda \\ &\mathrm{s.t.}\;\;(5) ,(6) ,(38) ,(39) ,(41) , \\ &x_m^v,z_m^i \in [0,1],i \in {\cal{I}},m \in {\cal{M}},v \in {\cal{V}} \end{split} $

3.1.2 算法

对于线性规划问题${\cal{P}}2$，用线性规划求解器得到最优解为分数解，而不是整数线性规划问题${\cal{P}}1$的解。因此，需要进行舍入操作以适配原问题。基于此，设计一个基于合同的随机舍入算法，如算法2所示。

第1行执行算法1，进行一个RSU合同的生成与求解过程，并完成RSU与服务车辆之间的合同匹配。第2行利用求解器求解线性规划问题得到$\bar x_m^v$和$\bar z_m^i$，第3行到第8行表示首先以$\bar x_m^v$的概率将$x_m^v$舍入为1，其中$x_m^v = 1$表示服务模型已经部署完毕后，此时再以$\dfrac{{\bar z_m^iy_i^v}}{{\bar x_m^v}}$的概率将$z_m^i$舍入为1，最后第9行返回服务部署策略$x_m^v$和任务卸载策略$z_m^i$。

算法2　基于合同的舍入算法(Contract-based Rounding Algorithm, CRA)

输入：请求车辆$ {{\cal{I}}}$，服务车辆$ {{\cal{M}}}$，服务模型$ {{\cal{V}}}$，请求车辆请求$ {y_i^v,v \in {\cal{V}},i \in {\cal{I}}}$，车辆存储资源$ {R_m^{\max },m \in {\cal{M}}}$，权重$ {{\theta _k},k \in {\cal{K}}}$，概率$ {{\lambda _k},k \in {\cal{K}}}$。

输出：服务缓存策略$ {x_m^v,v \in {\cal{V}},m \in {\cal{M}}}$，任务卸载策略$ {z_m^i,i \in {\cal{I}},m \in {\cal{M}}}$，合同$ {{{\cal{C}}^*}{\text{ = \{ (}}{\varphi _k},{\varPhi _k}{\text{) |}}{ }\forall k \in {\cal{K}}{\text{\} }}}$。

1. $ {[\{ {\varphi _1},{\varPhi _1}\} ,\{ {\varphi _2},{\varPhi _2}\} , \cdots ,\{ {\varphi _K},{\varPhi _K}\} ]}$ = KCGA$ {({\theta _1},{\theta _2}, \cdots ,{\theta _k}},$ $ {{\lambda _1},{\lambda _2}, \cdots ,{\lambda _k})} $

2. 求解问题$ {{\cal{P}}2}$，得到$ {\bar x_m^v}$和$ {\bar z_m^i}$

3. for $ {m \in {\cal{M}}}$ do

4. 　for $ {i \in {\cal{I}}}$

5. 　　以概率$ {\bar x_m^v}$令$ {x_m^v \leftarrow 1}$

6. 　　以概率$ {\dfrac{{\bar z_m^iy_i^v}}{{\bar x_m^v}}}$令$ {z_m^i \leftarrow 1}$

7. 　end for

8. end for

9. return $ {x_m^v}$ and $ {z_m^i}$

定理1　算法2的时间复杂度为${\cal{O}}{(IM + MV) ^3}$，其中$I$表示请求车辆的数量，$M$表示服务车辆的数量，$V$表示服务模型的数量。

证明　第1行执行算法1的时间复杂度为${\cal{O}}(M) $，第2行求解线性规划问题的时间复杂度为${\cal{O}}(IM + MV) ^3$^[26]，之后3到8行为了生成$x_m^v$和$z_m^i$而嵌套执行两个循环，此时的时间复杂度为${\cal{O}}(IM) $。故最终算法2的时间复杂度为${\cal{O}}{(IM + MV) ^3}$。

引理4　随机舍入策略能以$1 - {1}/{M}$的概率获得$\dfrac{{I\sqrt I }}{{V(\sqrt I - \sqrt {2\ln M} ) }}$的近似比，其中$V$表示服务模型数量，$I$表示请求车辆数量，$M$表示服务车辆数量。

证明　设$T$表示系统的吞吐量，$\mu $表示$T$的期望，则有

$ T = \sum\limits_{i \in {\cal{I}}} {\sum\limits_{m \in {\cal{M}}} {z_m^i} } $

(42)

$ \mu = {\text{E}}[T] = \sum\limits_{i \in {\cal{I}}} {\sum\limits_{m \in {\cal{M}}} {\Pr {\text{(}}z_m^i = 1) } } = \sum\limits_{i \in {\cal{I}}} {\sum\limits_{m \in {\cal{M}}} {\bar z_m^i} } $

(43)

由于$z_m^i$独立且属于$[0,1]$，此时由切诺夫界^[27]可知，对于$\forall \varepsilon > 0$满足有

$ \Pr (T \leqslant (1 - \varepsilon ) \cdot \mu ) \leqslant {{\text{e}}^{\tfrac{{ - {\varepsilon ^2}\mu }}{2}}} $

(44)

设${g_{\min }}$表示算法2求得的最小任务完成率，则有

$ {g_{\min }} \leqslant \frac{{\displaystyle\sum\nolimits_{i \in {\cal{I}}} {\displaystyle\sum\nolimits_{m \in {\cal{M}}} {y_i^vz_m^i} } }}{{{A_v}}} $

(45)

$ \sum\limits_{v \in {\cal{V}}} {\sum\limits_{i \in {\cal{I}}} {\sum\limits_{m \in {\cal{M}}} {y_i^vz_m^i} } } \geqslant \sum\limits_{v \in {\cal{V}}} {{A_v}{g_{\min }}} = I{g_{\min }} $

(46)

设${g_{\max }}$表示${g_v}$的最大值，并假设每个服务的计算任务至少能完成1个，则有

$ \frac{{I{g_{\min }}}}{V} \geqslant 1 \geqslant {g_{\max }} $

(47)

将上述式(42)~(47) 结合得

$ I{g_{\min }} \leqslant T \leqslant I{g_{\max }} \leqslant \frac{{{I^2}{g_{\min }}}}{V} $

(48)

设$g*$表示线性规划最优解对应的最小任务完成率，同时也是整数线性规划最优的最小任务完成率的上界。设${g^ + }$表示整数线性规划最优解对应的最小任务完成率，则有${g^ + } \leqslant g*$。与上式同理，结合$\mu $，有

$ Ig* \leqslant \sum\limits_{i \in {\cal{I}}} {\sum\limits_{m \in {\cal{M}}} {\bar z_m^i} } \leqslant \frac{{{I^2}g*}}{V} $

(49)

$ Ig* \leqslant \mu \leqslant \frac{{{I^2}g*}}{V} $

(50)

结合上述所有不等式，有

$ \Pr \bigg(\frac{{{I^2}{g_{\min }}}}{V} \leqslant (1 - \varepsilon ) Ig*\bigg) \leqslant {{\text{e}}^{\tfrac{{ - {\varepsilon ^2}\mu }}{2}}} $

(51)

由于${g^ + } \leqslant g*$，可以化简得

$ \Pr \bigg(\frac{{I{g_{\min }}}}{V} \leqslant (1 - \varepsilon ) {g^ + }\bigg) \leqslant {{\text{e}}^{\tfrac{{ - {\varepsilon ^2}\mu }}{2}}} $

(52)

令上述不等式右边的值为${1}/{M}$，即不等式左边成立的概率为${1}/{M}$，有

$ \varepsilon = \sqrt {\frac{{2\ln M}}{\mu }} $

(53)

实际中$\mu $近似地与请求车辆$I$的数量呈正比，故有

$ \varepsilon = \sqrt {\frac{{2\ln M}}{I}} $

(54)

根据近似比的定义，此时有

$ \frac{{{g^ + }}}{{{g_{\min }}}} \geqslant \frac{I}{{V(1 - \varepsilon ) }} = \frac{{I\sqrt I }}{{V(\sqrt I - \sqrt {2\ln M} ) }} $

(55)

3.2 基于合同的贪心算法

算法2在求解线性规划过程中需要消耗太多的时间，故针对算法2中随机舍入策略复杂度较高的不足设计了一个基于贪心策略的高效算法。基本思想是优先缓存任务完成率最小的服务，并优先卸载服务对应的计算任务，直到最小的任务完成率无法提升为止。算法的形式化过程如算法3所示。

与之前的算法类似，第1行执行算法1，进行一个RSU合同的生成与求解过程，并完成RSU与服务车辆之间的合同匹配。第2行计算从每个请求车辆到所有服务车辆的传输延迟，并按升序排列生成有序序列${M_i}$。第3行到第16行表示首先随机选择一个任务完成率最小的服务，检查该请求服务的终端用户集合${A_v}$。若集合中终端用户的请求任务未被卸载，则依次遍历有序序列${M_i}$中的服务车辆。若服务车辆缓存了对应的服务模型，且其剩余计算资源能成功处理终端用户的请求任务，则将该终端用户的请求任务卸载至此服务车辆，并重复执行这一过程。第17行到第29行表示在有限的存储资源条件下，对于随机选择的任务完成率最小的服务，检查该请求服务的终端用户集合${A_v}$。若集合中终端用户的请求任务未被卸载，则依次遍历有序序列${M_i}$中的服务车辆。若服务车辆没有缓存对应的服务模型，但剩余的存储资源和计算资源能容纳该服务模型，则将该服务模型缓存至此服务车辆，并将该终端用户的请求任务卸载至此服务车辆，之后重复执行这一过程。最后第30行返回服务部署策略$x_m^v$和任务卸载策略$z_m^i$。

算法3　基于合同的贪心算法(Contract-based Greedy Algorithm, CGA)

输入：请求车辆$ {{\cal{I}}}$，服务车辆$ {{\cal{M}}}$，服务模型$ {{\cal{V}}}$，请求车辆请求$ {y_i^v,v \in {\cal{V}},i \in {\cal{I}}}$，车辆存储资源$ {R_m^{\max },m \in {\cal{M}}}$，权重$ {{\theta _k},k \in {\cal{K}}}$，概率$ {{\lambda _k},k \in {\cal{K}}}$。

输出：服务缓存策略$ {x_m^v,v \in {\cal{V}},m \in {\cal{M}}}$，任务卸载策略$ {z_m^i,i \in {\cal{I}},m \in {\cal{M}}}$，合同$ {{{\cal{C}}^*}{\text{ = \{ (}}{\varphi _k},{\varPhi _k}{\text{) |}}{ }\forall k \in {\cal{K}}{\text{\} }}}$。

1. $ {[\{ {\varphi _1},{\varPhi _1}\} ,\{ {\varphi _2},{\varPhi _2}\} , \cdots ,\{ {\varphi _K},{\varPhi _K}\} ]}$ = KCGA$ {({\theta _1},{\theta _2}, \cdots ,{\theta _k}},$ $ {{\lambda _1},{\lambda _2}, \cdots ,{\lambda _k}) }$

2. 计算$ {t_{i,m}^{{\mathrm{tra}}}}$，生成有序序列$ {{{\cal{M}}_i}}$

3. 令$ {{\mathrm{flag}} \leftarrow 1}$和$ {{g_v} \leftarrow 0}$

4. while $ {{\mathrm{flag}} = 1}$ do

5. 　遍历值$ {{g_v}}$，随机挑选服务模型$ {v}$

6. 　令$ {{\mathrm{flag}} \leftarrow 0}$

7. 　for $ {i \in {A_v}}$ do

8. 　　for $ {m \in {M_i}}$ do

9. 　　　while 满足式(5) 和(39) do

10. 　　　　令$ {z_m^i \leftarrow 1}$

11. 　　　　令$ {{A_v} \leftarrow {A_v}\backslash \{ i\}} $

12. 　　　　更新$ {C_m^{\max }}$

13. 　　　　令$ {{\mathrm{flag}} \leftarrow 1}$，更新$ {{g_v}}$

14. 　　　end while

15. 　　end for

16. 　end for

17.　 if $ {{\mathrm{flag}} = 0}$ do

18. 　　for $ {i \in {A_v}}$ do

19. 　　　for $ {m \in {M_i}}$ do

20. 　　　　while 满足式(5) 、(6) 和(39) do

21. 　　　　　令$ {x_m^v \leftarrow 1,z_m^i \leftarrow 1}$

22. 　　　　　令$ {{A_v} \leftarrow {A_v}\backslash \{ i\} }$

23. 　　　　　更新$ {C_m^{\max }}$和$ {R_m^{\max }}$

24. 　　　　　令$ {{\mathrm{flag}} \leftarrow 1}$，更新$ {{g_v}}$

25. 　　　　end while

26. 　　　end for

27. 　　end for

28. 　end if

29. end while

30. return $ {x_m^v}$ and $ {z_m^i}$

定理2　算法3的时间复杂度为${\cal{O}}((M + V) {I^2}) $，其中$I$表示请求车辆的数量，$M$表示服务车辆的数量，$V$表示服务模型的数量。

证明　第1行执行算法1的时间复杂度为${\cal{O}}(M) $，之后为了挑选任务完成率最小的服务和请求任务未被卸载的终端用户，需要遍历服务集合和请求车辆，故此时的时间复杂度为${\cal{O}}(IV) $。在寻找最佳的服务车辆去缓存服务和卸载请求时，需要遍历请求车辆和服务车辆，故此时的时间复杂度为${\cal{O}}(IM) $。最外层的循环次数不会超过请求车辆数量$I$，故算法3总的时间复杂度为${\cal{O}}((M + V) {I^2}) $。

4 实验

实验在搭载Intel(R) i7-10700F处理器的工作站上进行，设置随机部署的请求车辆和服务车辆之间的欧几里得距离为[0,100] m，且请求车辆的数量远大于服务车辆。请求车辆的传输带宽设为5 MHz，发送功率为25 dBm。请求车辆和服务车辆之间的环境噪音功率为−174 dBm。服务车辆出让的计算能力范围为[100,150] GFLOPs，内存大小为[800,1200] MB。当前越来越多的DNN模型可以用于提供低延时的推断服务，因此，选择18种不同的DNN模型(ResNet50、VGG13等) 作为请求车辆请求的服务，请求车辆对服务的请求任务是随机产生的。这些人工智能推断服务输入的RGB图片尺寸为224 pixels $ \times $ 224 pixels $ \times $ 3 channel，大小约为147 kB。推断服务所需的存储空间和计算量对应DNN模型的模型大小和计算量，可事先测量得到。实验结果为100次重复随机实验的平均值。

4.1 基准算法

CSPR：SPR算法^[9]联合考虑服务缓存和请求调度，最大化整个系统的吞吐量，在VFC场景中，该算法最大化请求车辆的服务数量。由于未考虑车辆自私性等因素，故对SPR算法进行改进得到CSPR算法。CSPR算法首先执行算法1计算最优合同并与服务车辆签订资源出让条约，然后求解线性规划问题得到最优的分数解为$\bar x_m^v$和$\bar z_m^i$。以$\bar x_m^v$的概率将服务缓存到服务车辆，以${{\bar z_m^i}}/{{\bar x_m^v}}$的概率将请求车辆的任务卸载到服务车辆，再依次按升序排列移除相应的服务和任务直到计算和存储资源满足。

CSPRG：基于贪心思想对CSPR算法进行改进得到CSPRG算法，其目标是最大化系统的吞吐量。CSPRG算法在执行完CSPR算法后，不断迭代将未被卸载的任务卸载到计算资源消耗最少的服务车辆中，直到所有剩余资源无法满足任意的任务。

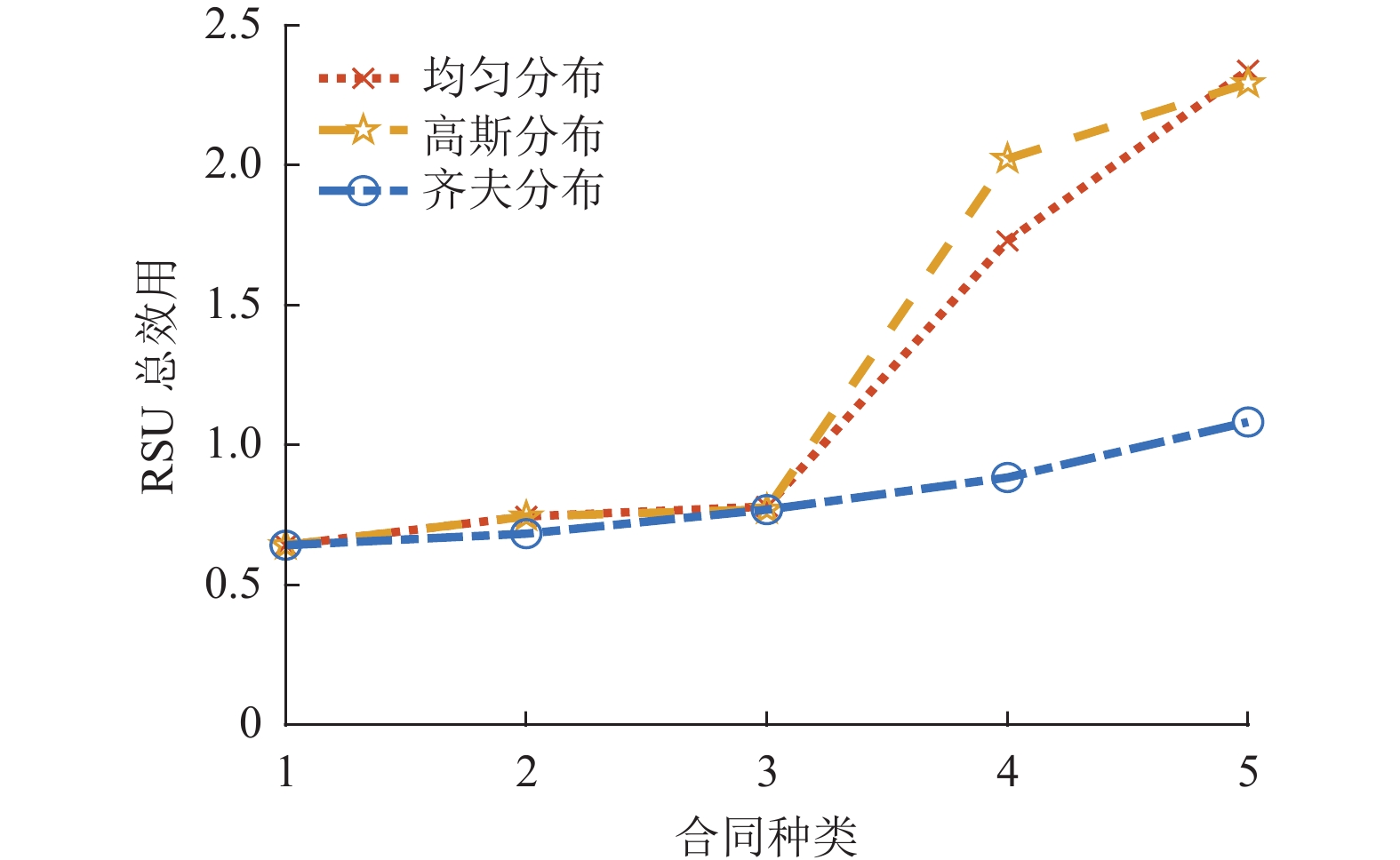
4.2 实验结果

图3展示了在不同合同种类下，出让资源的服务车辆类型属于不同分布概率时的RSU总效用对比。根据不同数量的合同种类将区间[100,150] GFLOPs划分为对应数量的子区间，为不失一般性，对出让资源的服务车辆类型属于哪种子区间的概率分布考虑均匀分布^[28]、高斯分布^[29]和齐夫分布^[30]3种情况。均匀分布意味着每个出让资源的服务车辆属于每种类型的概率相同，高斯分布意味着每个出让资源的服务车辆属于中间类型的概率更大，齐夫分布意味着每个出让资源的服务车辆属于低出让计算能力类型的概率更大。从图3中可以看出，不论满足哪种概率分布类型，RSU的效用都会随着合同种类的上升而上升，不同于齐夫分布的缓慢上升，均匀分布和高斯分布在合同种类大于3后迅速上升。实验结果说明RSU总效用会随着概率分布类型的不同而变化。

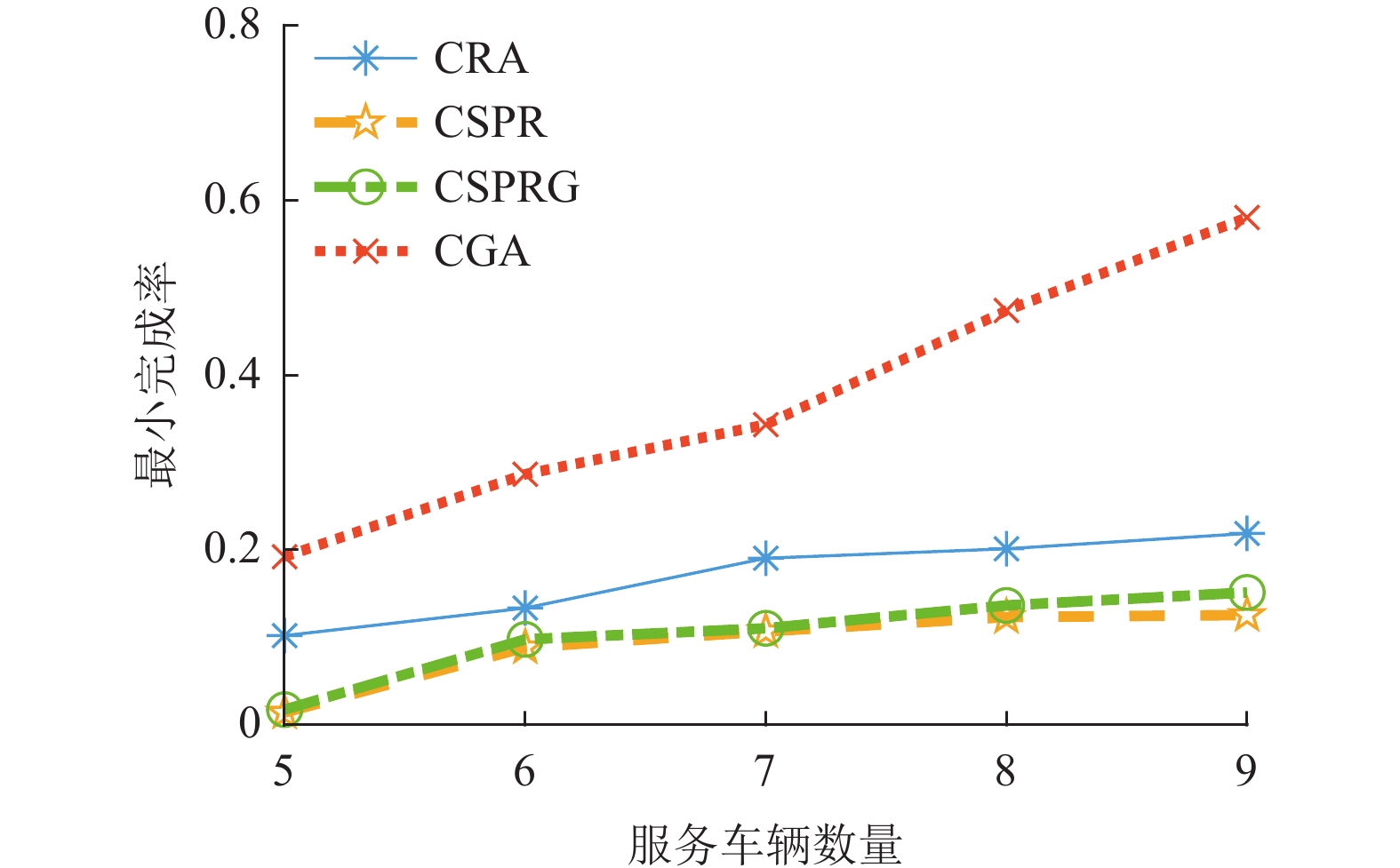
图4展示了当发送计算任务的请求车辆数量为40、最大容忍延迟为0.5 s时，不同服务车辆数量下算法关于最小任务完成率的性能对比。从图4中可以看出，提出的CRA算法和CGA算法性能优于经过改进的基准算法CSPR和CSPRG。去掉基准算法最小完成率几乎等于零的情况，CRA算法相比于CSPR算法和CSPRG算法平均分别有66.63%和50.27%的性能提升，而CGA算法相比于CSPR算法和CSPRG算法更有平均272.58%和233.41%的性能提升。当愿意出让资源的服务车辆数量偏少时，CSPR算法和CSPRG算法获得的最小服务完成率几乎为0，这是因为在系统资源非常有限时，最大化系统吞吐量的目标会导致大服务的请求几乎无法得到服务。随着出让资源的服务车辆数目的增多，最小服务完成率逐渐增大，这是因为网络的计算资源越来越充足，可为更多的请求车辆提供服务。即使系统资源非常有限，提出的CRA和CGA算法也能保证各个服务都有一定的完成率。

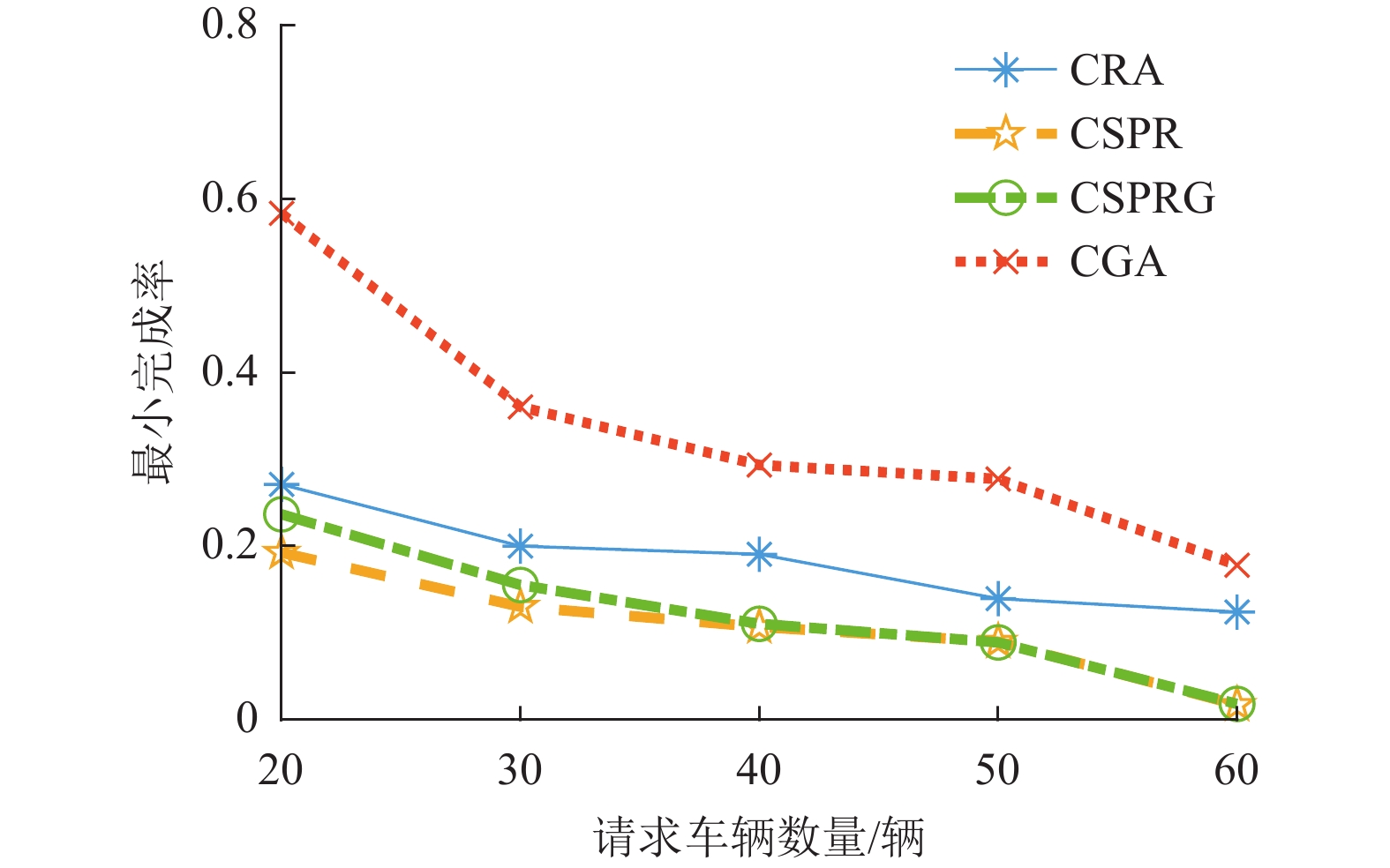
图5展示了当出让资源的服务车辆数量为7、最大容忍延迟为0.5 s时，不同请求车辆数量下算法关于最小任务完成率的性能对比。从图5中可以看出，提出的CRA算法和CGA算法性能优于经过改进的基准算法CSPR和CSPRG。去掉基准算法最小完成率几乎等于0的情况，CRA算法相比于CSPR算法和CSPRG算法平均分别有56.92%和43.12%的性能提升，而CGA算法相比于CSPR算法和CSPRG算法更有平均190.57 %和163.83 %的性能提升。当发送计算任务的请求车辆数量偏多时，CSPR算法和CSPRG算法获得的最小服务完成率几乎为0，这是由于在系统资源有限时，请求小服务的请求车辆逐渐增多，故最大化系统吞吐量的目标导致大服务的请求几乎无法得到服务。因此，在系统资源有限时即使请求小服务的任务增多，提出的CRA和CGA算法也能保证各个服务都有一定的完成率。

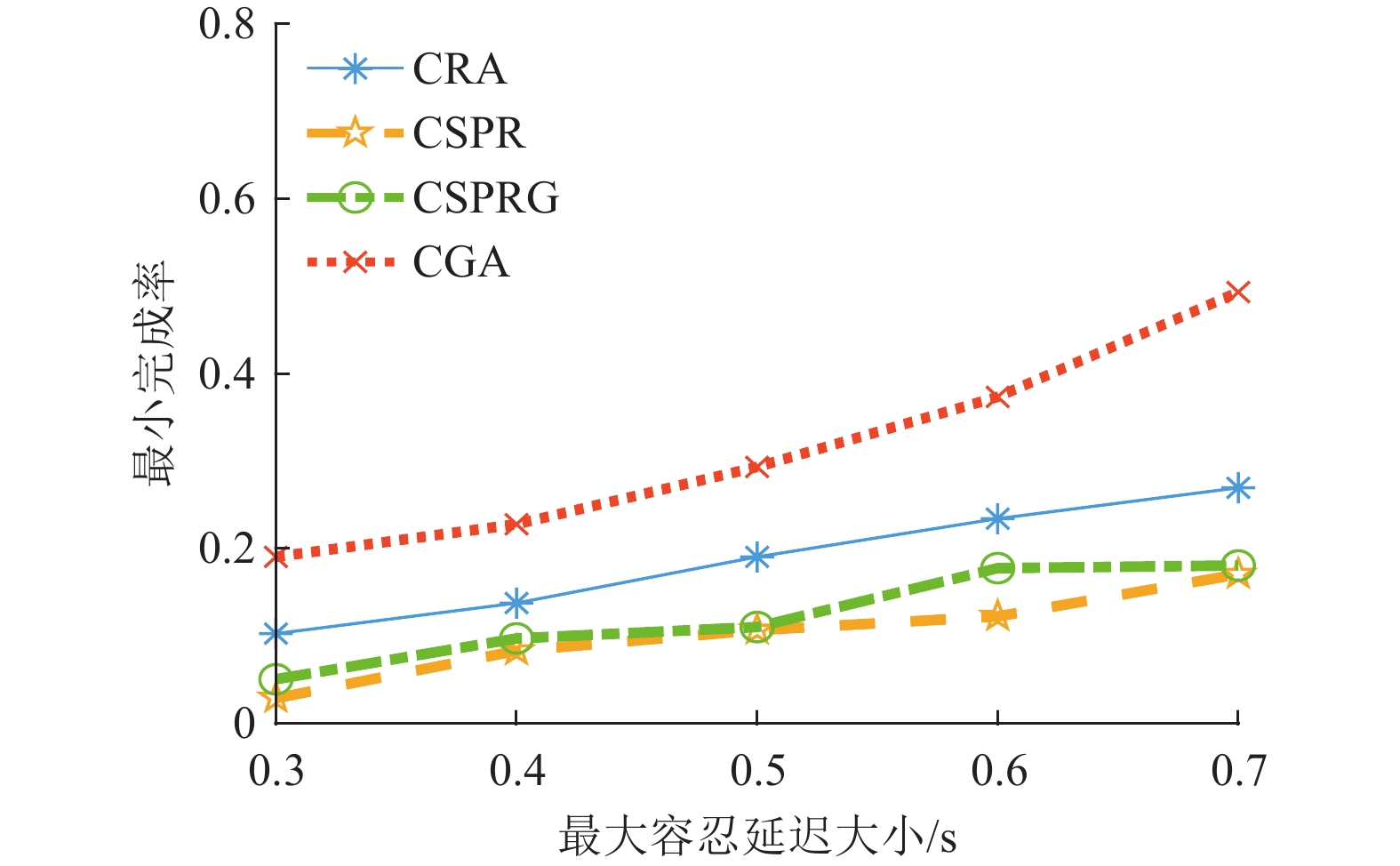
图6和图7分别展示了当发送计算任务的请求车辆数量为40，出让资源的服务车辆数量为7时，不同最大容忍延迟下算法关于最小任务完成率和系统平均吞吐量的性能对比。从图6中可以看出，提出的CRA算法和CGA算法性能优于经过改进的基准算法CSPR和CSPRG。去掉基准算法最小完成率几乎等于零的情况，CRA算法相比于CSPR算法和CSPRG算法平均分别有73.16%和48.72%的性能提升，而CGA算法相比于CSPR算法和CSPRG算法更有平均185.27%和145.53%的性能提升。当最大容忍延迟较小时，CSPR算法和CSPRG算法获得的最小服务完成率几乎为0，这是由于在系统资源有限时，请求任务为了满足更低的处理时延需要更多的计算资源，故最大化系统吞吐量的目标导致大服务的请求几乎无法得到服务。因此在系统资源有限时即使最大容忍延迟较小，提出的CRA和CGA算法也能保证各个服务都有一定的完成率。从图7中可以看出，提出的CGA算法相比于CSPR算法和CSPRG算法系统平均系统吞吐量降低了24.81%和33.69%，CRA算法只降低了3.39%和14.96%。对比图6和图7，和现有的基准算法对比，可以发现CGA算法能在损失一部分吞吐量下极大提升最小服务完成率，CRA算法能在几乎不损失吞吐量下也能保证所有服务都有一定的最小服务完成率，并且当系统资源越来越充足时，吞吐量的损失会越来越低。

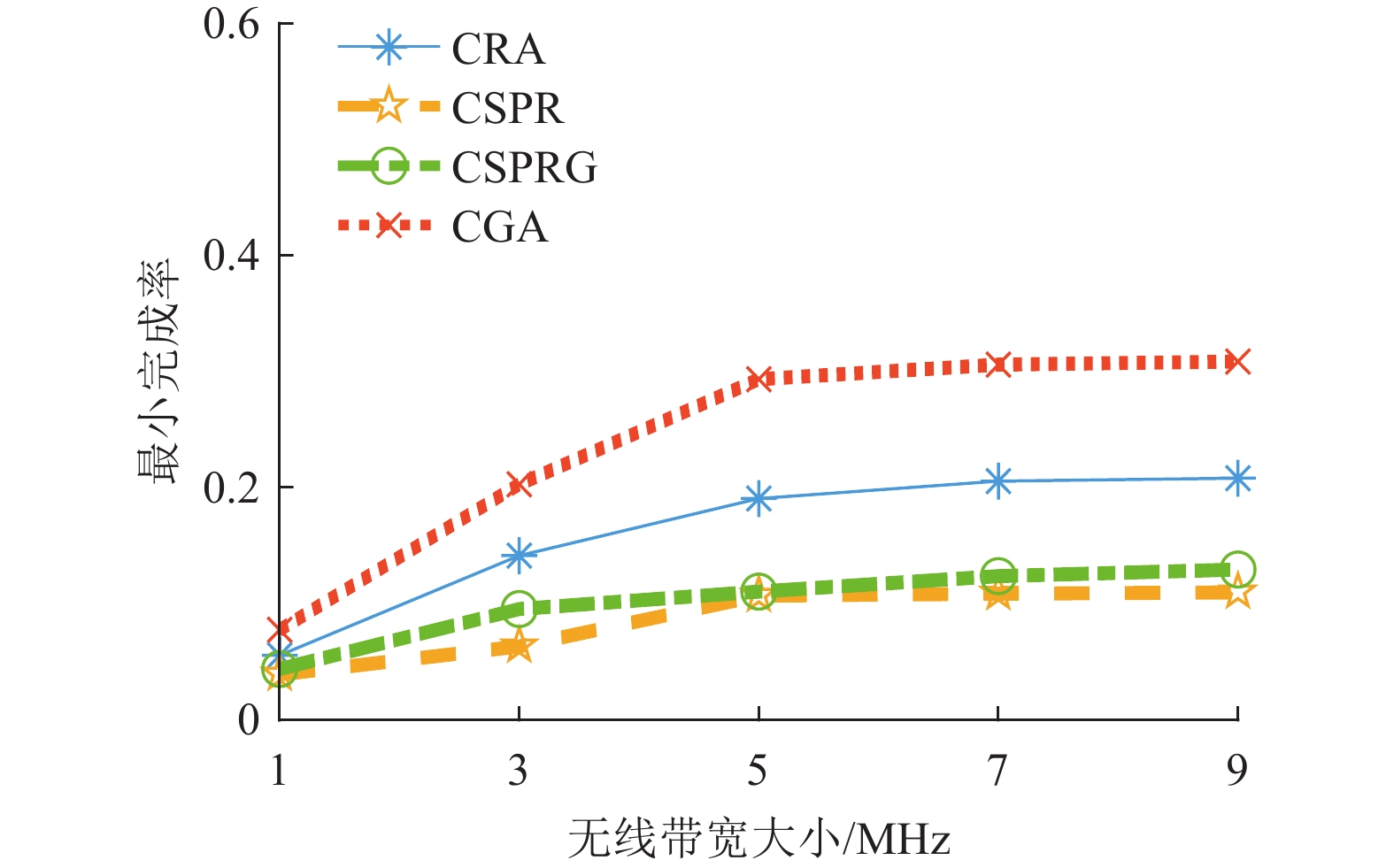
图8 展示了当发送计算任务的请求车辆数量为40，出让资源的服务车辆数量为7，最大容忍延迟为0.5 s时，不同无线带宽大小下算法关于最小任务完成率的性能对比。从图8中可以看出，提出的CRA算法和CGA算法性能优于经过改进的基准算法CSPR和CSPRG。当无线带宽资源较少时，此时的任务传输延迟大小成为影响卸载决策的因素之一，故所有算法的最小任务完成率都较低，随着系统资源越来越充足，传输延迟大小对于卸载决策的影响逐渐降低，故所有算法的最小任务完成率逐渐趋近平稳。

5 总结

在车辆雾计算网络中，考虑服务车辆的自私性现象，设计了合同论模型，同时给出了KKT条件求解过程和合同生成算法。在应对服务请求车辆公平性保障的过程中，在满足存储资源、计算资源和延迟约束等条件下，联合考虑了服务缓存与任务卸载下的最大化最小任务完成率。为解决上述问题，首先提出了一个基于合同的随机舍入算法，并证明了算法的近似比，与此同时，为解决随机舍入策略计算复杂度较高的缺陷，还提出了一个基于合同的贪心算法。大量的实验结果表明，与现有的算法相比，提出的算法在激励机制方面和保障异构服务公平性方面有了较大的提升。未来将引入深度强化学习算法，实现算法的自适应部署。